Nysiad: Practical Protocol Transformation to Tolerate Byzantine Failures¹

Chi Ho, Robbert van Renesse
Cornell University - Mark Bickford
ATC-NY - Danny Dolev
Hebrew University of Jerusalem

Abstract

The paper presents and evaluates Nysiad,² a system that implements a new technique for transforming a scalable distributed system or network protocol tolerant only of crash failures into one that tolerates arbitrary failures, including such failures as freeloading and malicious attacks. The technique assigns to each host a certain number of guard hosts, optionally chosen from the available collection of hosts, and assumes that no more than a configurable number of guards of a host are faulty. Nysiad then enforces that a host either follows the system's protocol and handles all its inputs fairly, or ceases to produce output messages altogether--a behavior that the system tolerates. We have applied Nysiad to a link-based routing protocol and an overlay multicast protocol, and present measurements of running the resulting protocols on a simulated network.

1 Introduction

Scalable distributed systems have to tolerate nondeterministic failures from causes such as Heisenbugs and Mandelbugs [14], aging related or bit errors (e.g., [23]), selfish behavior (e.g., freeloading), and intrusion. While all these failures are prevalent and it would seem that large distributed systems have sufficient redundancy and diversity to handle such failures, developing software that delivers scalable Byzantine fault tolerance has proved difficult, and few such systems have been built and deployed. Distributed systems and protocols like DNS, BGP, OSPF, IS-IS, as well as most P2P communication systems tolerate only crash failures. Secure versions of such systems aim to prevent compromise of participants. While important, this issue is orthogonal to tolerating Byzantine failures as a host is not faulty until it is compromised.

We know how to build practical scalable Byzantine-tolerant data stores (e.g., [1,2,27]). Various work has also focused on Byzantine-tolerant peer-to-peer protocols (e.g., [3,9,20,17,19]). However, the only known and general approach to developing a Byzantine version of a protocol or distributed system is to replace each host by a Replicated State Machine (RSM) [18,25]. As replicas of a host can be assigned to existing hosts in the system, this does not necessarily require a large investment of hardware.

This paper presents Nysiad, a technique that uses a variant of RSM to make distributed systems tolerant of Byzantine failures in asynchronous environments, and evaluates the practicality of the approach. Nysiad leverages that most distributed systems already deal with crash failures and, rather than masking arbitrary failures, translates arbitrary failures into crash failures. Doing so avoids having to solve consensus [12] during normal operation. Nysiad invokes consensus only when a host needs to communicate with new peers or when one of its replicas is being replaced.

Instead of treating replicas as symmetric, Nysiad's replication scheme is essentially primary-backup with the host that is being replicated acting as primary. Different from RSM's original specification [18], Nysiad allows the entire RSM to halt in case the host does not comply with the protocol. A voting protocol ensures that the output of the RSM is valid. A credit-based flow control protocol ensures that the RSM processes all its inputs (including external input) fairly. As a result of combining both properties, the worst that the Byzantine host can accomplish is to stop processing input, a behavior that the original system will treat as a crash failure and recover accordingly.

We believe that the cost of Nysiad, while significant, is within the range of practicality for mission-critical applications. End-to-end message latencies grow by a factor of 3 compared to message latencies in the original system. The overhead caused by public key cryptography operations are manageable. Most alarmingly, the total number of messages sent in the translated system per end-to-end message sent in the original system can grow significantly depending on factors such as the communication behavior of the original system. However, the message overhead does not grow significantly as a function of the total number of hosts, and grows only linearly as a function of the number of failures to be tolerated. Most of the additional traffic is in the form of control messages that do not carry payload.

The paper

• evaluates for the first time the overheads involved when applying RSM to scalable distributed systems;
• shows that RSM does not require solving consensus if the original system is already tolerant of crash failures;
• presents a novel technique that forces hosts to process input fairly in a Byzantine environment, or leave;
• demonstrates how automatic reconfiguration can be supported in a Byzantine-tolerant distributed system.

Section 2 presents background and related work on countering Byzantine behavior. Section 3 describes an execution model and introduces terminology. The Nysiad design is presented in Section 4. Section 5 provides notes on the implementation. Section 6 evaluates the performance of systems generated by Nysiad using various case studies. Limitations are discussed in Section 7. Section 8 concludes.

2 Background

The RSM approach can be applied to systems like DNS [7]. While overheads are practical, the approach does not handle reconfiguration in the DNS hierarchy.

The idea of automatically translating crash-tolerant systems into Byzantine systems can be traced back to the mid-eighties. Gabriel Bracha presents a translation mechanism that transforms a protocol tolerant of up to $t$ crash failures into one that tolerates $t$ Byzantine failures [6]. Brian Coan also presents a translation [11] that is similar to Bracha's. These approaches have two important restrictions. One is that input protocols are required to have a specific style of execution, and in particular they have to be round-based with each participant awaiting the receipt of $n-t$ messages before starting a new round. Second, the approaches have quadratic message overheads and as a result do not scale well. Note that these approaches were primarily intended for a certain class of consensus protocols, while we are pursuing arbitrary protocols and distributed systems.

Toueg, Neiger and Bazzi worked on an extension of Bracha's and Coan's approaches for translation of synchronous systems [4,5,24]. Mpoeleng et al. [22] present a scalable translation that is also intended for synchronous systems, and transforms Byzantine faults to so-called signal-on-failure faults. They replace each host with a pair, and assume only one of the hosts in each pair may fail. In the Internet, making synchrony assumptions is dangerous. Byzantine hosts can easily trigger violations of such assumptions to attack the system.

Closely related to Nysiad is the recent PeerReview system [15], providing accountability [28] in distributed systems. PeerReview detects those Byzantine failures that are observable by a correct host. Like Nysiad, PeerReview assumes that each host implements a protocol using a deterministic state machine. PeerReview maintains incoming and outgoing message logs and, periodically, runs incoming logs through the state machines and checks output against outgoing logs. PeerReview can only detect a subclass of Byzantine failures, and only after the fact. Like reputation management and intrusion detection systems, accountability deters intentionally faulty behavior, but does not prevent or tolerate it.

Nysiad is based on our prior work described in [16], in which we developed a theoretical basis for a similar translation technique, but one that does not scale, does not handle reconfiguration, and does not prevent a Byzantine host from considering its input selectively.

3 Model

A system is a collection of hosts that exchange messages as specified by a protocol. Below we will use the terms original and translated to refer to the systems before and after translation, respectively. The original system tolerates only crash failures, while the translated system tolerates Byzantine failures as well. For simplicity we will assume that each host runs a deterministic state machine that transitions in response to receiving messages or expiring timers. (Nysiad may handle nondeterministic state machines by considering nondeterministic events as inputs.) As a result of input processing, a state machine may produce messages, intended to be sent to other hosts. The system is assumed to be asynchronous, with no bounds on event processing, message latencies, or clock drift.

The hosts are configured in an undirected communication graph $(V, E)$, where $V$ is the set of hosts and $E$ the set of communication links. A host only communicates directly with its adjacent hosts, also called neighbors. The graph may change over time, for example as hosts join and leave the system. We will initially assume that the graph is static and known to all hosts. We later weaken this assumption and address topology changes.

Figure 1: A communication graph (left) and a possible guard graph (right) for $t = 1$. In this particular case, each host has exactly $3t+1$ guards, and each set of neighbors exactly $2t+1$ monitors.

The Nysiad transformation requires that the communication graph has a guard graph. A $t$-guard graph of $(V, E)$ is a directed graph $(V', E')$ with the following requirements:

1. Each host in $V$ has a (directed) edge to at least $3t+1$ hosts in $V'$ (including itself) called the guards of the host.
2. For each two neighboring hosts in $V,$ the two hosts have edges to at least $2t+1$ common guards in $V'$ (including themselves). We call such guards the monitors of the two hosts.

We assume that for each host in $V$ at most $t$ of its guards are Byzantine. We also assume that messages between correct guards of the same host are eventually delivered (using an underlying retransmission protocol that recovers from message loss). Note that a monitor of two hosts is a guard of both hosts, and that neighbors in $V$ are each other's guards. Moreover, each host is one of its own guards.

Within the constraints of these requirements, Nysiad works with any guard graph. For efficiency it is important to create as few guards per host as possible, as all guards of a host need to be kept synchronized. However, the requirements on guards and monitors may produce guard graphs with some of the hosts needing more than $3t+1$ guards.

If $V = V'$, no additional hosts are added to the system and hosts guard one another. Figure 1 presents an example communication graph and a possible guard graph for $t = 1$ where no additional hosts were added. Some deployments may favor adding additional hosts for the sole purpose of guarding hosts in the original system.

In the current implementation of Nysiad, the guard graph is created and maintained by a logically centralized, Byzantine-tolerant service called the Olympus, described in Section 4.4. The Olympus certifies the guards of a host, and is involved only when the communication graph changes as a result of host churn or new communication patterns in the original system. The Olympus does not need to be aware of the protocol that the original system employs.

Figure 2: Host $h_i$ initiates an OARcast execution for $t = 1$. The time diagram shows all guards of $h_i$, where only $h_{g3}$ is faulty.

4 Design

Nysiad translates the original system by replicating the deterministic state machine of a host onto its guards. Nysiad is composed of four subprotocols. The replication protocol ensures that guards of a host remain synchronized. The attestation protocol guarantees that messages delivered to guards are messages produced by a valid execution of the protocol. The credit protocol forces a host to either process all its input fairly, or to ignore all input. Finally, the epoch protocol allows the guard graph to be bootstrapped and reconfigured in response to host churn. The following subsections describe each of these protocols. The final subsection describes how Nysiad deals with external I/O.

4.1 Replication

The state machine of a host is replicated onto the guards of the host, together constituting a Replicated State Machine (RSM). It is important to keep in mind that we replicate a host only for ensuring integrity, not for availability or performance reasons. After all, the original system can already maintain availability in the face of unavailable hosts.

Say $\alpha_j^i$ is the replica of the state machine of host $h_i$ on guard $h_j$. A host $h_i$ broadcasts input events for its local state machine replica $\alpha_i^i$ to its guards. A guard $h_j$ delivers an input event to $\alpha^i_j$ when $h_j$ receives such a broadcast message from $h_i$. In order to guarantee that the guards of $h_i$ stay synchronized in the face of Byzantine behavior, the hosts use a reliable ordered broadcast protocol called OARcast (named for Ordered Authenticated Reliable Broadcast) [16] for communication.

Using OARcast a host can send a message that is intended for all its guards. When a guard host $h_j$ delivers a message $m$ from $h_i$ it means that $h_j$ received $m$, believes it came from $h_i$, and delivers $m$ to $\alpha^i_j$, the replica of $h_i$'s state machine on guard $h_j$. OARcast guarantees the following properties:

• Relay. If $h_j$ and $h_k$ are correct, and $h_j$ delivers $m$ from $h_i$, then $h_k$ delivers $m$ from $h_i$ (even if $h_i$ is Byzantine);
• Ordering. If two hosts $h_j$ and $h_k$ are correct and $h_j$ and $h_k$ both deliver $m_1$ from $h_i$ and $m_2$ from $h_i$, then they do so in the same order (even if $h_i$ is Byzantine);
• Authenticity. If two hosts $h_i$ and $h_j$ are correct and $h_i$ does not send $m$, then $h_j$ does not deliver $m$ from $h_i$;
• Persistence. If two hosts $h_i$ and $h_j$ are correct, and $h_i$ sends a message $m$, then $h_j$ delivers $m$ from $h_i$;
• FIFO. If two hosts $h_i$ and $h_j$ are correct, and $h_i$ sends a message $m_1$ before $m_2$, then $h_j$ delivers $m_1$ from $h_i$ before delivering $m_2$ from $h_i$.

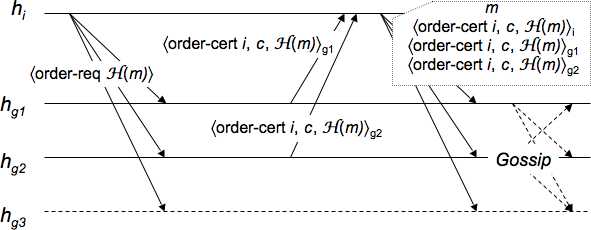
Relay guarantees that all correct guards deliver a message if one correct guard does. Ordering guarantees that all correct guards deliver messages from the same host in the same order. These two properties together guarantee that the correct replicas of a host stay synchronized, even if the host is Byzantine. Authenticity guarantees that Byzantine hosts cannot forge messages of correct hosts. Persistence rules out a trivial implementation that does not deliver any messages. FIFO stipulates that correct guards deliver messages from a correct host in the order sent.

These properties are not as strong as those for asynchronous consensus [12] and indeed consensus is not necessary for our use, as only the host whose state is replicated can issue updates (i.e., there is only one proposer). If that host crashes or stops producing updates for some other reason, no new host has to be elected to take over its role, and the entire RSM is allowed to halt as a result. Indeed, unlike consensus, the OARcast properties can be realized in an asynchronous environment with failures, as we shall show next.

Figure 3: Normal case attestation when $t = 1$. Here the state machine of $h_i$ sends a message $m$ to the state machine of $h_j$. The guards of $h_j$ are $h_i$, $h_k$, $h_d$, and $h_j$ itself, and each run a replica of $h_j$'s state machine. Hosts $h_i$, $h_j$, and $h_k$ monitor $h_i$ and $h_j$. $h_j$ collects attestations for $m$ and OARcasts the event to its guards. In this case only $h_d$ needs the attestations.

The implementation of OARcast used in this paper is as follows. Say a sending host $h_i \in V$ wants to OARcast an input message $m$ to its $n_i$ guards in $V'$, where ($n_i > 3t$). Each guard $h_j$ maintains a sequence number $c$ on behalf of $h_i$. Using private (MAC-authenticated) FIFO point-to-point connections, $h_i$ sends $\langle \texttt{order-req} ~ {\cal H}(m) \rangle$ to each guard, where $\cal H$ is a cryptographic one-way hash function. On receipt, $h_j$ sends an order certificate $\langle \texttt{order-cert} ~ i, c, {\cal H}(m) \rangle_j$ back to $h_i$, where the subscript $j$ means that $h_j$ digitally signed the message such that any host can check its origin.

As at most $t$ of $h_i$'s guards are Byzantine, $h_i$ is guaranteed to receive order-cert messages from at least $n_i - t$ different guards with the correct sequence number and message hash. We call such a collection of order-cert messages an order proof for $(c, m)$. Byzantine orderers cannot generate conflicting order proofs (same sequence number, different messages) even if $h_i$ itself is Byzantine, as two order proofs have at least $t+1$ order-cert messages in common, one of which is guaranteed to be generated by a correct guard [21].

$h_i$ delivers $m$ locally to $\alpha^i_i$ and forwards $m$ along with an order proof to each of its guards. On receipt, a guard $h_j$ checks that the order proof corresponds to $m$ and is for the next message from $h_i$. If so, $h_j$ delivers $m$ to $\alpha^i_j$.

To guarantee the Relay property, $h_j$ gossips order proofs with the other guards. A similar implementation of OARcast is proved correct in [16]. That paper also presents an implementation that does not use public key cryptography, but has higher message overhead.

Figure 2 shows an example of an OARcast execution. Optimizations are discussed in Section 5. Not counting the overhead of gossip and without exploiting hardware multicast, a single OARcast to $3t$ guards uses at most $9t$ messages. Gossip can be largely piggybacked on existing traffic.

4.2 Attestation

While the replication protocol above guarantees that guards of a host synchronize on its state, it does not guarantee that the host OARcasts valid input events, because the sending host $h_i$ may forge arbitrary input events. We consider two kinds of input events: message events and timer events. Checking validity for each is slightly different.

First let us examine message sending. Say in the original system host $h_i \in V$ sends a message $m$ to a host $h_j \in V$. Because $h_j$ is a neighbor of $h_i$ it is also a guard of $h_i$, and thus in the translated system $\alpha^i_j$ will produce $m$ as an input event for $\alpha^j_j$. Accordingly $h_j$ OARcasts $m$ to its guards, but the guards, not sure whether to trust $h_j$, need a way to verify the validity of $m$ before delivering $m$ to local replicas. To protect against Byzantine behavior of $h_j$, we require that $h_j$ includes a proof of validity with every OARcast in the form of a collection of $t+1$ attestations from guards of $h_i$.

Because the guards of $h_i$ implement an RSM, each (correct) guard $h_k \in V'$ has a replica $\alpha^i_k$ of the state of $h_i$ that produces $m$. Each guard $h_k$ of $h_i$ (including $h_i$ and $h_j$) sends $\langle \texttt{attest} ~ i, j, s_{ij}, {\cal H}(m) \rangle_k$ to $h_j$. $s_{ij}$ is a sequence number for messages from $i$ to $j$, and prevents replay attacks. $h_j$ has to collect $t$ of these attestations in addition to its own and include them in its OARcast to convince $h_j$'s guards of the validity of $m$. Again, correct guards have to gossip attestations in order to guarantee that every correct guard receives them in case one does.

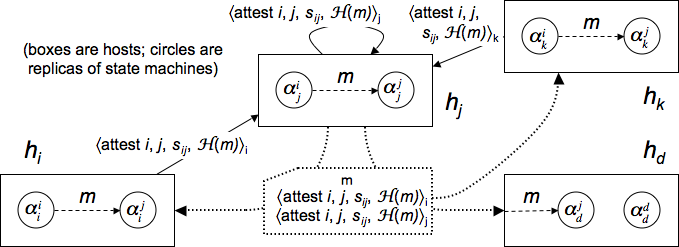
There are two important optimizations to this. First, as $h_j$ only needs $t+1$ attestations, only the monitors of $h_i$ and $h_j$ need to send attestations to guarantee that $h_j$ gets enough attestations. This not only reduces traffic, but the monitors are neighbors of $h_j$ and thus no additional communication links need be created. Second, $h_j$ does not need the attestations until the last phase of the OARcast protocol, thus $h_j$ can request order certificates before it has received the attestations. This way ordering and attestation can happen in parallel rather than sequentially. Both these optimizations are exploited in the implementation (Section 5). Figure 3 shows an example of the flow of traffic when using attestations.

Figure 4: Credit mechanism with $t = 1$. $h_i$ and $h_k$ are neighbors of $h_j$, each sending a message to $h_j$. $h_j$ tries to order the message from $h_k$ while ignoring the message from $h_i$. The credit mechanism renders the OARcast illegal.

In case of a timer event at a host $h$, $h$ needs to collect $t$ additional attestations of its own guards in addition to its own attestation. This prevents $h$ from producing timer events at a rate higher than that of the fastest correct host. While theoretically this may appear useless in an asynchronous environment, in practice doing so is important. Consider, for example, a system in which a host pings its neighbors in order to verify that they are alive. Without timer attestation, a Byzantine host may force a failure detection by not waiting long enough for the response to those pings. While in an asynchronous system one cannot detect failures accurately using a pinging protocol, timer attestation ensures in this case that a host has to wait a reasonable amount of time. Also, because hosts only wait for $t$ attestations from more than $2t$ guards, Byzantine guards cannot delay or block timer events emitted by correct hosts.

4.3 Credits

While attestation prevents a host from forging invalid input events, a host may still selectively ignore input events and fail to produce certain output events. For example, in the pinging example above, a host could respond to pings, avoiding failure detection, but neglect to process other events. In a multicast tree application a host could accept input but neglect to forward output to its children (freeloading). Such a host could even deny wrongdoing by claiming that it has not yet received the input events or that the output events have already been sent but simply not yet delivered by the network--after all, we assume that the system is asynchronous.

We present a credit-based approach that forces hosts either to process input from all sources fairly and produce the corresponding output events, or to cease processing altogether. The essence of the idea is to require that a host obtain credits from its guards in order to OARcast new input events, and a guard only complies if it has received the OARcast from the host for previous input events. As such, credits are the flip-side of attestations: while attestations prevent a host from producing bad output, credits force a host to either process all input or process none of it. If a host elects to process no input, it cannot produce output and will eventually be considered as a crashed host by the original system.

We will exploit that a single OARcast from a host can order a sequence of pending input events for its state machine, rather than one input message at a time. The OARcast's order certificate binds a single sequence number to the ordered list of input events. We say that the OARcast orders the events in the list.

A credit is a signed object of the form $\langle \texttt{credit} ~ j, c, \vec{v}_{i,j} \rangle_i$, where $h_i$ has to be a guard of $h_j$. $h_i$ sends such a credit to $h_j$ to approve delivery of the $c^\textit{th}$ OARcast message from $h_j$, provided a certain ordering condition specified by $\vec{v}_{i,j}$ holds. Including $c$ prevents replay attacks. The ordering constraint $\vec{v}_{i,j}$ is a vector that contains an entry for each state machine that $h_i$ and $h_j$ both guard. Such an entry contains how many events (possibly 0) the corresponding state machine replica on $h_i$ has produced for $\alpha_i^j$.

For each neighbor $h_k$ of $h_j$, $h_j$ has to collect at least $t+1$ credits for OARcast $c$ from monitors of $h_j$ and $h_k$. However, $h_j$ can only use a credit for an OARcast if the OARcast orders all messages specified in the credit's ordering constraint that were not ordered already by OARcasts numbered less than $c$. These two constraints taken together guarantee that an OARcast contains a credit from a correct monitor for each of its neighbors, and prevents $h_j$ from ignoring input messages that correct monitors observe while ordering other input messages.

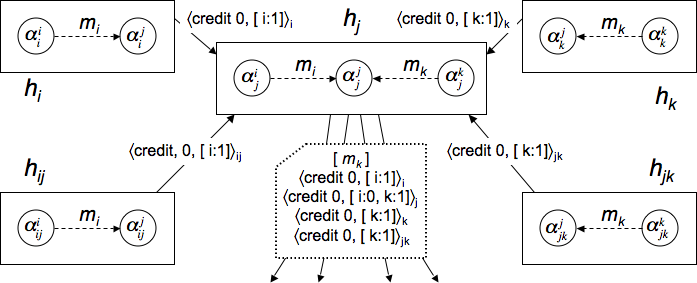
For example, consider Figure 4, showing five hosts. $h_i$ and $h_k$ are neighbors of $h_j$. $h_{ij}$ is a monitor for hosts $h_i$ and $h_j$, while $h_{jk}$ is a monitor for $h_j$ and $h_k$. Assume $t = 1$. Consider a situation in which $h_j$ has not yet sent any OARcasts, but $\alpha^i_i$ has produced a message $m_i$ for $h_j$ on hosts $h_i$ and $h_{ij}$, while $\alpha^k_k$ has produced a message $m_k$ for $h_j$ on hosts $h_k$ and $h_{jk}$. Each guard of $h_j$ sends credit for the first OARcast that reflects the messages produced locally for $h_j$.

Now assume that $h_j$ is Byzantine and trying to ignore messages from $h_i$ but process messages from $h_k$. $h_j$ has to include a credit from either $h_i$ or $h_{ij}$. Because $h_j$ is Byzantine and $t = 1$, both $h_i$ and $h_{ij}$ have to be correct and will not collude with $h_j$. If $h_j$ tries to order only $m_k$ as shown in the figure, receiving hosts will note that at least one credit requires that a message from $h_i$ has to be ordered and will therefore ignore the OARcast (and report the message to authorities as proof of wrongdoing).

As with other credit-based flow control mechanisms, a window $w$ may be used to allow for pipelining of messages. Initially, each guard of $h_j$ sends credits for the first $w$ OARcasts from $h_j$, specifying an empty ordering constraint. Then, on receipt of the $c^\textit{th}$ OARcast, a guard sends a credit for OARcast $c + w$, using an ordering constraint that reflects the current set of produced messages for $h_j$. If $w = 1$, the next OARcast cannot be issued until it has been received by at least $t+1$ monitors of each neighbor and the new credits have been communicated to $h_j$. If $w > 1$ pipelining becomes possible, but at the expense of additional freedom for $h_j$. In practice we found that $w=2$ enables good performance while monitors still have significant control over the order of messages produced by the hosts they guard.

4.4 Epochs

So far we have assumed that the communication graph $(V, E)$ and its $t$-guard graph $(V', E')$ are static and well-known to all hosts. This is necessary, because when a host receives an OARcast it has to check that the order certificates, the attestations, and the credits were generated by qualified hosts. In particular, order certificates and credits have to be generated by a guard of the sending host of an OARcast message, and each attestation of a message has to be generated by monitors of the source and destination of the message. Also, the receiving host of an OARcast has to know how many guards the sending host has in order to check that a message contains a sufficient number of ordering certificates and credits.

While Nysiad, in theory, could inspect the code of the state machines, it has no good way of determining which hosts will be communicating with which other hosts, and so in reality even the communication graph $(V, E)$ is initially unknown, let alone its guard graph. Making matters worse, such a communication graph often evolves over time.

Figure 5: Example of an execution of the reconfiguration protocol. $h_{i1}$, $h_{i2}$, and $h_{i3}$ are guards of $h_i$. When the Olympus suspects that $h_{i3}$ has failed, it requests the current epoch of $h_i$ to be concluded and installs a new set of guards, replacing $h_{i3}$ with $h_{i3'}$.

In order to handle this problem, we introduce a logically centralized (but Byzantine-replicated [10]) trusted certification service that we call the Olympus. The Olympus is not involved in normal communication, but only in charge of tracking the communication graph and updating the guard graph accordingly. The Olympus produces signed epoch certificates for hosts, which contain sufficient information for a receiver of an OARcast message to check its validity. In particular, an epoch certificate for a host $h_i$ describes

• the host identifier $(i)$;
• the set of the identifiers of all $h_i$'s guards;
• the epoch number (described below);
• a hash of the final state of the host in the previous epoch.

The Olympus does not need to know the protocol that the original system uses. Initially, the Olympus assigns $3t$ guards to each host arbitrarily, in addition to the host itself. Each guard starts in epoch 0 and runs the state machine starting from a well-defined initial state. Order certificates and credits have to contain the epoch number in order to prevent replay attacks of old certificates in later epochs. Next we describe a general protocol for changing guards and how this protocol is used to handle reconfigurations.

Changing-of-the-guards

While the Olympus assigns guards to hosts, the changing-of-the-guards protocol starts with the guards themselves. In response to triggers that we will describe below, each guard of $h_i$ sends a state certificate containing the current epoch number and a secure hash of its current state to $h_i$. After the guard receives an acknowledgment from $h_i$ it is free to clean up its replica, unless the guard is $h_i$ itself. However, in order to avoid replay attacks the guard needs to remember that this epoch of $h_i$'s execution has terminated.

When $h_i$ has received $n_i - t$ such certificates (typically including its own) that correspond to its own state, $h_i$ sends the collection of state certificates to the Olympus. $n_i - t$ certificates together guarantee that there are at most $t$ correct guards and $t$ Byzantine guards that are still active, not enough to order additional OARcast messages. Effectively, the collection certifies that the state machine of $h_i$ has halted in the given state.

In response, the Olympus assigns new guards to $h_i$ and creates a new epoch certificate using an incremented epoch number and the state hash, and sends the certificate to $h_i$. On receipt, $h_i$ sends its signed state and the new epoch certificate to its new collection of guards. Recipients check validity of the state using the hash in the epoch certificate and resume normal operation.

Reconfiguration

One scenario in which the changing-of-the-guards protocol is triggered is when guards of $h_i$ produce a message $m$ for another host $h_j$ for the first time. Each correct guard sends a state certificate to $h_i$ when it produces the message. The state has to be such that the message $m$ is about to be produced, so that when the state machine is later restarted, possibly on a different guard, $m$ is produced and processed the normal way. The state certificate also indicates that a message for $h_j$ is being produced, so that the Olympus may know the reason for the invocation.

$h_i$ collects $n_i - t$ state certificates, and sends the collection to the Olympus. The Olympus, now convinced that $h_i$ has produced a message for $h_j$, requests $h_j$ to change its guards as well. $h_j$ does this by OARcasting a special end-epoch message, triggering the changing-of-the-guards protocol at each guard in the same state. (Should $h_j$ not respond then it is up to the Olympus to decide when to declare $h_j$ faulty, block $h_j$'s guards, and restart $h_i$.)

Assuming the Olympus has received the state certificates for both $h_i$ and $h_j$, the Olympus can assign new guards to each in order to satisfy the constraints of the guard graph. The Olympus then sends new epoch certificates to both $h_i$ and $h_j$, after which each sends its certificate to its new guards. These guards start in a state where they first produce $m$, which can now be processed normally.

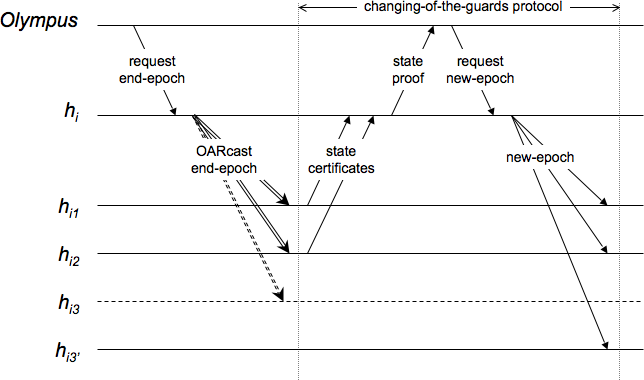
The Olympus also undertakes reconfiguration when it determines that a guard of a host has failed. In order to detect crash failures, the Olympus may periodically ping all guards to determine responsiveness. (A more scalable solution is described in [17]. Note that while a false positive may introduce overhead, it is not a correctness issue.) Also, guards send proof of observable Byzantine behavior to the Olympus. In response to detection of a failure of a guard of a host other than the host itself, the Olympus requests the host to OARcast an end-epoch message to invoke the changing-of-the-guards protocol. Figure 5 shows an example.

Should a host $h_i \in V$ be detected as faulty then the Olympus sends a message to all $h_i$'s guards, requesting them to block further OARcasts from $h_i$. Once the Olympus has received acknowledgments from $n_i - t$ guards, the Olympus knows that $h_i$ can no longer produce input for other hosts successfully.

4.5 External I/O

So far we have assumed that Nysiad translates a system in its entirety. However, often such a system serves external clients that cannot easily be treated in the same way. We cannot expect to be able to replicate those clients onto multiple hosts, and it becomes impossible to verify that the clients send valid data using a general technique. To wit, a Byzantine-tolerant storage service does not verify the validity of the data that it stores, nor does a Byzantine-tolerant multicast service check the data from the broadcaster. The usual assumption, from the system's point of view, is to trust clients.

In Nysiad, we treat external clients as trusted hosts. Such hosts may crash or leave, but there is no need to replicate their state machines, nor to attest the data they generate. However, when a trusted host $h_i$ sends a message to an untrusted host $h_j$, we do want to make sure that $h_j$ treats the input fairly with respect to other inputs that it receives. Vice versa, when $h_j$ sends a message to $h_i$, $h_i$ has to collect attestations in order to verify the validity of the message. We also want to prevent $h_j$ from withholding messages for $h_i$.

The methodology we developed so far can be adapted to achieve these requirements. We assign the pair $(h_i, h_j)$ $2t+1$ half-monitors. Each half-monitor runs a full replica of $h_j$'s state machine, but for $h_i$ only keeps track of the messages that $h_i$ sends. Unlike normal monitors, $h_i$ itself does not run a half-monitor, but $h_j$ does.

When $h_i$ wants to send a message to $h_j$, it sends a copy of the message to each half-monitor using authenticated FIFO channels. (The half-monitors gossip the receipt of this message with one another to ensure that either all or none of the correct half-monitors receive the message in a situation in which $h_i$ crashes during sending.) Like normal monitors, half-monitors generate attestations for messages from $h_i$ so that $h_j$ can convince others of the validity of that input. More importantly, half-monitors generate credits for $h_j$ forcing $h_j$ to treat $h_i$'s messages fairly with respect to its other inputs.

In a similar manner, half-monitors generate attestations for messages from $h_j$ to $h_i$ so that $h_i$ can verify the validity of those messages. Should $h_j$ itself fail to send messages to $h_i$ then the half-monitors can provide the necessary copy.

5 Implementation Details

In order to evaluate overheads we implemented Nysiad in Java. In this section we provide details on how we construct guard graphs and how we combine the various subprotocols into a single coherent protocol.

Given a communication graph and a parameter $t$ many different guard graphs are often possible. For efficiency and fault tolerance it is prudent to minimize the number of guards per host (see Section 3). We are not aware of an optimal algorithm for determining such a graph. We devised the following algorithm to create a $t$-guard graph of the communication graph. It runs in two phases. In the first phase the algorithm considers each pair of neighbors $(h_i, h_j)$. Initially $h_i$ and $h_j$ are assigned as monitors. The algorithm then determines the hosts that are 1 hop away from the current set of monitors, and adds, randomly, such hosts to the set of monitors until there are no such hosts left or until the number of monitors has reached $2t+1$. This step is repeated until the set of monitors has reached the required size. Note that the monitors are guards to both $h_i$ and $h_j$. In the next phase, the algorithm considers all hosts individually. If a host has fewer than $3t+1$ guards then the closest hosts in terms of hop distance are added, randomly as before, until the desired number of guards is reached.

Figure 6: Message overhead factor (a) and public key signing and checking overheads (b) as a function of the number of hosts for running SSR on a Random graph using $k = 3$ and various $t$.

(a)	(b)

While best understood separately, the OARcast, attestation, and credit protocols combine into a single replication protocol. Doing so reduces message and CPU overheads significantly, while also simplifying implementation. Consider the $c^\textit{th}$ OARcast from some host $h_i$, and assume $h_i$ has the necessary credits and has produced the messages required by those credits. At this point $h_i$ creates an order-req, containing a list of hashes of the messages that it has produced but not yet ordered in previous OARcasts, and sends the request to each of its $n_i$ guards.

On receipt, each guard signs a single certificate that contains the credit for OARcast $c + w$, an order certificate for OARcast $c$, and any attestations that it can create for messages in OARcast $c$. This way the signing and checking costs of all certificate types can be amortized. The guard sends the resulting certificate back to $h_i$. $h_i$ awaits $n_i - t$ certificates, which collectively are guaranteed to contain the necessary order certificates and attestations for completing the current OARcast, and the necessary credits for OARcast $c + w$.

In the third and final round, $h_i$ sends these aggregate certificates to its guards. On receipt, a guard has to check the signatures on all certificates except its own. The end-to-end latency consists of three network latencies, plus the latency of signing (done in parallel by each of the guards) and checking $n_i - 1$ certificates (executed in parallel as well). The more messages can be ordered by a single OARcast, the more these costs can be amortized.

An execution of OARcast requires $3 \cdot (n_i - 1)$ FIFO messages. Since $n_i > 3t$, the minimum number of FIFO messages per OARcast is $9t$. In order to further reduce traffic, Nysiad also tries to combine messages for different OARcasts--if two FIFO messages are sent at approximately the same time between two different hosts, they are combined in a manner similar to back-to-back messages in the TCP protocol.

6 Case Studies

While one cannot test if a system tolerates Byzantine failures, it is possible to measure the overheads involved. In this section we report on two case studies: a point-to-point link-level routing protocol and a peer-to-peer multicast protocol. We applied Nysiad to each and ran the result over a simulated network to measure network overheads and overheads caused by cryptographic operations.

For the point-to-point routing protocol we selected Scalable Source Routing (SSR) [13]. SSR is inspired by the Chord overlay routing protocol [26], but can be deployed on top of the link layer. (SSR is similar to Virtual Ring Routing [8], which applies the same idea to Pastry.)

The basic idea of SSR is simple. Each host initially knows its own (location-independent) identifier and those of the neighbors it is directly connected to. The SSR protocol organizes the hosts into a Chord-like ring by having each host discover a source route to its successor and predecessor. This is done as follows. Initially a host $h_i$ sends a message to its best guess at its successor. Should this tentative successor host know of a better successor for $h_i$, or discover one later, then the successor host sends a source route for the better successor back to $h_i$. On receipt $h_i$ sends a message to its new best guess at its successor, and so on. This protocol converges into the desired ring and terminates. Once the ring is established routing can be done in a Chord-like manner, whereby a message travels around the ring, but taking shortcuts whenever possible. In our simulations we measure the ring-discovery protocol, not the routing itself.

Figure 7: Message overhead (a) and public key signing and checking overheads (b) as a function of the number of hosts for the SSR protocol on a Random graph using $t = 2$ and various $k$, the minimum number of neighbors per host.

(a)	(b)

The multicast protocol is even simpler. Here we assume that the hosts are organized in a balanced binary tree, and that each host forwards messages from its parent to its children (if any). We call this protocol MCAST. We measured the overhead of sending a message from the root host to all hosts.

We considered two network graph configurations. In the first, Tree, the network graph is a balanced binary tree. In the second, Random, we placed hosts uniformly at random on a square metric space, and connected each host to its $k$ closest peers.

We report on three configurations:

• SSR/Random The SSR protocol on top of a Random graph;
• SSR/Tree The SSR protocol on a Tree graph;
• MCAST/Tree The MCAST protocol on a Tree graph.

For the evaluation we developed a simple discrete time event network simulator to evaluate message overheads. The fidelity of the simulation was kept low in order to scale the simulation experiments to interesting sizes. While the simulator models network latency, we assume bandwidth is infinite. The public key signature operations were replaced by simple hash functions. We focus our evaluation on the failure-free ``normal case'' executions. We vary the number of hosts and $t$, and in the case of the Random graph we also vary $k$, the (minimum) number of neighbors of each host. In all experiments, the credits window $w$ was chosen to be $2$.

By and large, the increase in latency is close to a factor of 3 for all experiments, independent of what parameters are chosen. (No graphs shown.) This amount of increase was expected as the OARcast protocol consists of three rounds of communication (see Section 5). This can be decreased to two rounds by having the guards broadcast certificates directly to each other, but this results in a message overhead that is quadratic in $t$ rather than linear.

When measuring message overhead, we report on the ratio between the number of FIFO messages sent in the translated protocol and the number of FIFO messages sent in the original protocol. We call this the message overhead factor, and report the minimum, average, and maximum over 10 executions. We ignore messages sent on behalf of the gossip protocol that implement the Relay property of OARcast. These messages do not require additional cryptographic operations and contribute only a small and constant load on the network.

For measuring CPU overhead, we report only the number of public key signing and checking operations per message per guard. Such operations tend to dominate protocol processing overheads. We found the variance for these measurements to be low, the minimum and maximum usually being within 1 operation from the average number of operations, and so we report only the averages.

Figure 8: Message overhead factor (a) and public key signing and checking overheads (b) as a function of the number of hosts for various protocols and graphs using $t = 1$ and $k = 3$.

(a)	(b)

In the first set of experiments, we used the SSR/Random configuration using a Random graph with $k = 3$. In Figure 6(a) we show the message overhead factor for $t = 1, 2, 3$. As we described in Section 5, an OARcast to $n$ guards uses at most $3n$ messages, and we see that this explains the trends well. There is an increase in overhead as we increase the number of hosts due to an increase in the average number of guards per host and reduced opportunity for aggregation as traffic becomes less concentrated due to the larger graph. Small graphs necessitate more sharing of guards, which reduces overhead.

Figure 6(b) reports, per guard the average number of public key sign and check operations per message in the original system. Due to aggregation, the number of sign operations message in the original system per guard is always less than 1 and does not significantly depend on $t$, as can be understood from Section 5. However, guards have to check each other's signatures and The number of check operations per message per guard may exceed $3t$ because a host may have more than $3t+1$ guards, and, as stated above larger graphs tend to have more guards. Nonetheless, these graphs should also reach an asymptote.

Next, for the same SSR/Random configuration, we fix $t = 2$ and range $k$ from 3 to 6. We show the message and public key signature overhead measurements in Figure 7. Even though $t$ is fixed, an increase in the number of neighbors per host requires additional monitors, and thus the average number of guards per host tends to increase beyond the required $3t+1$, causing additional message and CPU overhead. It is thus important for overhead of translation and indeed for fault tolerance to configure the original protocol to use as sparse a graph as possible. This tends to increase the diameter of the communication graph, and thus a suitable trade-off has to be designed.

In the final experiments, we compare the three different configurations for $t = 1$. For the Random graph we chose $k = 3$. In the case of a Tree graph, the average number of neighbors per host is approximately 2, internal hosts having 3 neighbors, leaf hosts having 1 neighbor, and the root host having 2 neighbors. We report results in Figure 8.

MCAST suffers most message overhead. This is because there is no opportunity for message aggregation in the experiment--each host receives only one message (from its parent). However, when multiple messages are streamed, the opportunity for message aggregation is excellent--any backlog that builds up can be combined and ordered using a single OARcast operation--and thus throughput is not limited by this overhead. Even if messages cannot be aggregated, order certificates, attestations, and credits still can, and thus signature generation and checking overheads are still good.

SSR performs significantly better on the Tree graph than on the Random graph. Because communication opportunities are more limited in the Tree graph with fewer neighbors to choose from, many messages can be aggregated and ordered simultaneously. For such situations the message overhead can indeed completely disappear.

Finally, note that if hardware multicast were available the overhead of Nysiad could be significantly reduced (from $9t$ point-to-point messages for an OARcast in the best case to $3t$ point-to-point messages and 2 multicasts).

7 Discussion

Nysiad can generate a Byzantine-tolerant version of a system that was designed to tolerate only crash failures. This comes with significant overheads. When developing a Byzantine-tolerant file system, such overheads are easily masked by the overhead of accessing the disk and large data transfers. When applied to message routing protocols where there is no disk overhead and payload sizes are relatively small, overheads cannot be masked as easily.

In practice, Nysiad may be used to generate a first cut at a Byzantine-tolerant protocol or distributed system, and then apply application-specific optimizations that maintain correctness. For example, if it is possible to distinguish the retransmission of a data packet from the original transmission, then it may be possible for the original transmission to be routed unguarded. Doing so could potentially mask most overhead of Nysiad.

But even if such optimizations are not possible, some applications may choose robustness over raw speed. Byzantine fault tolerance can be a part of increasing security, but it does not solve all security problems. Nysiad is not intended to defend against intrusion, but to tolerate intrusions. Defense against intrusion involves authentication and authorization techniques, as well as intrusion detection, and these are essential to guarantee that there is sufficient diversity among guards and no more than a small fraction are compromised. In the face of a limited number of successful intrusions Nysiad maintains integrity and availability of a system, but it does not provide confidentiality of data. Worse still, the replication of state complicates confidentiality. Hosts cannot trust their guards for confidentiality, and confidential data has to be encrypted in an end-to-end fashion.

Another possibility is to run some of the mechanisms that Nysiad uses inside secured hosts that are more difficult to compromise than hosts ``in the field.'' Such secured hosts may have reduced general functionality and use their resources to guard a relatively large number of state machines.

Nysiad makes strong assumptions about how many hosts can fail using the threshold value $t$. But what happens if more than $t$ guards of a host become Byzantine? Now the host can in fact behave in a Byzantine fashion and break the system. As a system becomes larger it becomes more likely that a host has more than $t$ Byzantine guards, and thus $t$ should the chosen large enough to handle the maximum system size. If $N$ is the maximum system size, then $t$ should be chosen $O(\log N)$ in order to keep the probability that any host in the system has more than $t$ Byzantine guards sufficiently low. As [17] demonstrates, a value for $t$ of 2 or 3 is probably sufficient for most applications. It is also important that, as much as possible, proofs of observed Byzantine behavior are sent to the Olympus immediately so that faulty hosts can be removed quickly [28].

Nysiad exploits diversity and is defenseless against deterministic bugs that either cause a host to make an incorrect state transition or allow an attacker to compromise more than $t$ host. The use of configuration wizards, high-level languages, and bug-finding tools may help avoid such problems. Similarly, Nysiad is helpless in the face of link-level Denial-of-Service attacks. These should be controlled by network-level anti-DoS techniques.

Nysiad in its current form uses the Olympus, a logically centralized service, to handle configuration changes. Because the Olympus is not invoked during normal operation, the load on the Olympus is likely sufficiently low for many practical applications. This architecture does not deal well with high churn, nor does the translated protocol handle network partitions well: hosts that cannot communicate with the Olympus are excluded from participating.

Finally, we have evaluated the use of Nysiad for systems where each host has a relatively small number of neighbors with which it communicates actively. Figure 7 shows that overhead grows as a function of the number of neighbors. In systems where hosts have many active neighbors the overhead of the Nysiad protocols could be substantial. We are considering a variant of Nysiad where not all neighbors of a host are guards in order to contain overhead.

8 Conclusion

Nysiad is a general technique for developing scalable Byzantine-tolerant systems and protocols in an asynchronous environment that does not require consensus to be solved. Starting with a system tolerant of crash failures only, Nysiad assigns a set of guards to each host that verify the output of the host and constrain the order in which the host handles its inputs. A logically centralized service assigns guards to hosts in response to churn in the communication graph. Simulation results show that Nysiad may be practical for a large class of distributed systems.

Bibliography

1

ADYA, A., BOLOSKY, W., CASTRO, M., CERMAK, G., CHAIKEN, R., DOUCEUR, J., HOWELL, J., LORCH, J., THEIMER, M., AND WATTENHOFER, R.
FARSITE: Federated, Available, and Reliable Storage for an Incompletely Trusted Environment.
In Proc. of the 5th Symp. on Operating Systems Design and Implementation (Boston, MA, Dec. 2002), USENIX.

2

AMIR, Y., DANILOV, C., KIRSCH, J., LANE, J., DOLEV, D., NITA-ROTARU, C., OLSEN, J., AND ZAGE, D.
Scaling Byzantine fault-tolerant replication to wide area networks.
In Proc. of the Int. Conf. on Dependable Systems and Networks (DSN O6) (Washington, DC, June 2006).

3

AWERBUCH, B., AND SCHEIDELER, C.
Group Spreading: A protocol for provably secure distributed name service.
In Proc. of the 31st International Colloquium on Automata, Languages and Programming (ICALP 2004) (Turku, Finland, July 2004), vol. 3142 of Lecture Notes in Computer Science, Springer.

4

BAZZI, R.
Automatically increasing fault tolerance in distributed systems.
PhD thesis, Georgia Institute of Technology, Atlanta, GA, 1995.

5

BAZZI, R., AND NEIGER, G.
Simplifying fault-tolerance: providing the abstraction of crash failures.
J. ACM 48, 3 (2001), 499-554.

6

BRACHA, G.
Asynchronous Byzantine agreement protocols.
Inf. Comput. 75, 2 (1987), 130-143.

7

CACHIN, C., AND SAMAR, A.
Secure distributed DNS.
In Proc. of the Int. Conf. on Dependable Systems and Networks DSN O4 (Florence, Italy, June 2004).

8

CAESAR, M., CASTRO, M., NIGHTINGALE, E., O'SHEA, G., AND ROWSTRON, A.
Virtual Ring Routing: Network routing inspired by DHTs.
In Proc. of SIGCOMM'06 (Pisa, Italy, Sept. 2006).

9

CASTRO, M., DRUSCHEL, P., GANESH, A., ROWSTRON, A., AND WALLACH, D.
Secure routing for structured peer-to-peer overlay networks.
In Proc. of the 5th Usenix Symposium on Operation System Design and Implementation (OSDI) (Boston, MA, Dec. 2002).

10

CASTRO, M., AND LISKOV, B.
Practical Byzantine Fault Tolerance.
In Proc. of the 3rd Symposium on Operating Systems Design and Implementation (OSDI) (New Orleans, LA, Feb. 1999).

11

COAN, B.
A compiler that increases the fault tolerance of asynchronous protocols.
IEEE Transactions on Computers 37, 12 (1988), 1541-1553.

12

FISCHER, M., LYNCH, N., AND PATTERSON, M.
Impossibility of distributed consensus with one faulty process.
J. ACM 32, 2 (Apr. 1985), 374-382.

13

FUHRMANN, T.
The use of Scalable Source Routing for networked sensors.
In Proc. of the 2nd IEEE Workshop on Embedded Networked Sensors (Sydney, Australia, May 2005), pp. 163-165.

14

GROTTKE, M., AND TRIVEDI, K.
Fighting bugs: Remove, retry, replicate, and rejuvenate.
IEEE Computer 40, 2 (Feb. 2007).

15

HAEBERLEN, A., KOUZNETSOV, P., AND DRUSCHEL, P.
PeerReview: Practical accountability for distributed systems.
In Proc. of the 21st ACM Symp. on Operating Systems Principles (Stevenson, WA, Oct. 2007).

16

HO, C., DOLEV, D., AND VAN RENESSE, R.
Making distributed systems robust.
In Proc. of the 11th Int. Conf. on Principles Of Distributed Systems (OPODIS'07) (Guadeloupe, French West Indies, Dec. 2007).

17

JOHANSEN, H., ALLAVENA, A., AND VAN RENESSE, R.
Fireflies: Scalable support for intrusion-tolerant network overlays.
In Proc. of Eurosys 2006 (Leuven, Belgium, Apr. 2006).

18

LAMPORT, L.
Using time instead of timeout for fault-tolerant distributed systems.
Trans. on Programming Languages and Systems 6, 2 (Apr. 1984), 254-280.

19

LI, H., CLEMENT, A., WONG, E., NAPPER, J., ROY, I., ALVISI, L., AND DAHLIN, M.
BAR gossip.
In Proc. of the 2006 USENIX Symposium on Operating Systems Design and Implementation (OSDI'06) (Nov. 2006).

20

M., H., AND VAN RENESSE, R.
Defense against intrusion in a live streaming multicast system.
In Proc. of the Sixth IEEE International Conference on Peer-to-Peer Computing (P2P '06) (Washington, DC, Sept. 2006), IEEE Computer Society.

21

MALKHI, D., AND REITER, M.
Byzantine Quorum Systems.
Distributed Computing 11 (June 1998), 203-213.

22

MPOELENG, D., EZHILCHELVAN, P., AND SPEIRS, N.
From crash tolerance to authenticated Byzantine tolerance: A structured approach, the cost and benefits.
In Proc. of the Int. Conf. on Dependable Systems and Networks (DSN O3) (Los Alamitos, CA, 2003), IEEE Computer Society.

23

MUKHERJEE, S., EMER, J., AND REINHARDT, S.
The soft error problem: An architectural perspective.
In Proc. of the Symposium on High-Performance Computer Architecture (Feb. 2005).

24

NEIGER, G., AND TOUEG, S.
Automatically increasing the fault-tolerance of distributed systems.
In Proc. of the 7th ACM Symp. on Principles of Distributed Computing (Toronto, Ontario, Aug. 1988), ACM SIGOPS-SIGACT.

25

SCHNEIDER, F.
Implementing fault-tolerant services using the state machine approach: A tutorial.
ACM Computing Surveys 22, 4 (Dec. 1990), 299-319.

26

STOICA, I., MORRIS, R., KARGER, D., AND KAASHOEK, M.
Chord: A scalable peer-to-peer lookup service for Internet applications.
In Proc. of the '95 Symp. on Communications Architectures & Protocols (Cambridge, MA, Aug. 1995), ACM SIGCOMM.

27

WEATHERSPOON, H., EATON, P., CHUN, B.-G., AND KUBIATOWICZ, J.
Antiquity: exploiting a secure log for wide-area distributed storage.
In Proc. of the 2007 EuroSys Conf. (Lisbon, Portugal, 2007).

28

YEMEREFENDI, A., AND CHASE, J.
The role of accountability in dependable distributed systems.
In Proc. of the First Workshop on Hot Topics in System Dependability (HotDep'05) (Yokohama, Japan, June 2005), IEEE.

About this document ...

Nysiad: Practical Protocol Transformation to Tolerate Byzantine Failures¹

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -init_file .latex2html_init -split 0 -show_section_numbers -local_icons -no_navigation nysiad_html

The translation was initiated by Robbert VanRenesse on 2008-02-19

Footnotes

... Failures¹

The authors were supported by AFRL award FA8750-06-2-0060 (CASTOR), NSF award 0424422 (TRUST), AFOSR award FA9550-06-1-0244 (AF-TRUST), DHS award 2006-CS-001-000001 (I3P), as well as by ISF, ISOC, CCR. and Intel Corporation. The views and conclusions herein are those of the authors.

...Nysiad,²

The Nysiads nursed Dionysos and rendered him immortal.