Information Slicing: Anonymity Using
Unreliable Overlays

Sachin Katti	Jeff Cohen	Dina Katabi
skatti@mit.edu	jscohen@mit.edu	dk@mit.edu

Abstract:

This paper proposes a new approach to anonymous communication called information slicing. Typically, anonymizers use onion routing, where a message is encrypted in layers with the public keys of the nodes along the path. Instead, our approach scrambles the message, divides it into pieces, and sends the pieces along disjoint paths. We show that information slicing addresses message confidentiality as well as source and destination anonymity. Surprisingly, it does not need any public key cryptography. Further, our approach naturally addresses the problem of node failures. These characteristics make it a good fit for use over dynamic peer-to-peer overlays. We evaluate the anonymity of information slicing via analysis and simulations. Our prototype implementation on PlanetLab shows that it achieves higher throughput than onion routing and effectively copes with node churn.

1 Introduction

Suppose Alice wants to send a confidential and anonymous message to Bob. Bob, however, does not have a public key that Alice could use to encrypt her message. Further, Alice does not feel comfortable exposing her unencrypted message to her ISP or an anonymizer. Alice's dilemma might seem simple, but underlying it is the general issue of online privacy. How do we send anonymous and confidential messages, when most of us do not have public keys and the sender does not trust a third party?

Our objective is to leverage popular existing peer-to-peer overlays to send confidential and anonymous messages without public keys. We focus on practical low-delay anonymity for everyday applications, rather than perfect anonymity at all costs. Popular peer-to-peer overlays have thousands of nodes and much traffic [5], creating an ideal environment for hiding anonymous communications. The dynamic nature of their participants makes them hard to track, and their diverse constituency allows dividing trust among nodes that are unlikely to collude. Some prior work has envisioned using these overlays for anonymity [15,24,21,23,16,27]. Current proposals, however, fall into two camps: either they do not address the high node churn in these environments and need all overlay nodes to have public keys [15,24,21,16], or they address churn but need very expensive solutions such as group key management [31] or broadcast [27].

This paper presents information slicing, a single technique that provides source and destination anonymity and churn resilience, without using any public key cryptography. It can also provide message confidentiality as long as the attacker cannot snoop on all traffic going to the destination. These characteristics make it suitable for use over popular peer-to-peer overlays. For example, say Alice knows that Bob, like many of us, uses a popular file sharing overlay to download content, and the overlay software supports information slicing. Then Alice can send Bob a confidential anonymous message without any public keys and in a manner robust to node churn and failures.

To provide confidentiality, our technique employs a properly chosen coding scheme to randomize the message. It then divides the randomized message into pieces, and sends the pieces along node disjoint paths that meet only at the destination. As a result, an attacker that gets all but one of the pieces of the randomized message cannot decode and recover the original message. Only the destination receives all pieces and can decode the message.

Information slicing also provides anonymity without requiring the overlay nodes to have public keys. Typically, anonymizers use onion routing, which assumes the sender has the public keys of all the nodes in the overlay. Onion routing hides the correspondence between a source and destination by sending the route setup message through a chain of nodes, wrapped in layers of public key encryption, such that each node along the path knows only its previous and next hops. Instead, to create an anonymous path, we send to each intermediate node its routing information (i.e., its next hop) in a confidential message sliced over multiple disjoint paths. The technical challenge is to perform this process efficiently. To send a relay node the identity of its next hop along different paths, we need to tell each node along these paths about its own next hop anonymously. Performed naively, this needs an exponential number of disjoint paths, and thus an exponential number of nodes. To avoid exponential blow-up, we build efficient forwarding graphs that reuse the overlay nodes without leaking information.

Finally, information slicing naturally provides protection against node churn and failures. The standard approach to address node failures is to employ multiple paths and add redundancy to the data. The challenge however is to minimize the redundancy overhead for the same amount of resilience. Typically, communication channels use coding to address such a challenge. We show that the same codes that we use to send confidential messages can simultaneously provide resilience to churn and failures. We also boost robustness by using network coding, which is proven to minimize redundancy while maximizing resilience to failures [18].

We show analytically and demonstrate experimentally that information slicing provides high anonymity and is resilient to node churn. We implement our protocol and evaluate its real-world performance in PlanetLab. Our experimental results show that information slicing provides higher throughput than onion routing. Further, it provides strong resilience to node churn, while using minimal redundancy.

2 Related Work

First generation anonymizers used a single intermediate node to relay traffic between senders and receivers (e.g., Anonymizer [1] and Safeweb [6]). Users had to trust the anonymizing node, which knows the identities of the source and destination.

Most modern anonymizers are based on Chaum's mixes [9] and its near realtime variant, onion routing [17]. The sender constructs a route by picking intermediate hops from a list of mixing nodes. The mixers may delay and re-order the packets depending on the traffic's timing constraints. The sender encrypts the IP address of each node along the path with the public key of its previous hop. This creates layers of encryption, like layers of an onion. Each node decrypts the packets, discovers its next hop and forwards the packet to the next hop and so on until the entire path is set up. Once the path is established, nodes exchange computationally efficient symmetric secret keys to transmit the actual data itself.

A few anonymizers rely on static and dedicated overlays [12,4,3,2]. For example, Tor [12] is a widely used anonymous system based on onion routing. Tor's infrastructure contains a small set of distributed nodes. Admission to the Tor network is tightly controlled. Tor has a centralized trusted directory server that provides the users with IP addresses and public keys of all the nodes in the system.

Some proposals [31,15,24,16] aim to build anonymity out of global peer-to-peer overlays. Most of these systems employ onion routing and use public key cryptography. Only one of them addresses churn explicitly [31]. For example, Tarzan [15] uses onion routing, assumes each overlay node has a public key, and distributes these keys to interested senders using a gossip protocol. Tarzan sets up tunnels along each path, which are rebuilt upon node failures or departures. MorphMix's design is fairly similar to Tarzan and differs only in the details of the tunnel setup procedure [24]. Herbivore [16] builds on DC-nets [9] to provide anonymity in large overlays. It divides nodes into cliques and requires shared secrets across cliques via either a PKI or offline key exchanges. Freenet [10] is a decentralized censorship-resistant peer-to-peer data storage facility, intended for anonymous publishing, not communication.

Similar to ours, some prior work does not use public key cryptography. In Crowds [23], each intermediate node flips a coin to decide whether to forward a packet to the destination or to a random node in the overlay. In contrast to our work, Crowds does not provide destination anonymity, and uses a centralized admission server to admit nodes into the overlay. AP3 [21] is based on the same random routing idea, and similarly does not provide destination anonymity. $P^5$ [27] achieves anonymity by broadcasting encrypted packets at a constant rate to all participants. When a node has no packets to send, it broadcasts noise, which is then propagated through the network in the same manner as data packets. In comparison, our system does not broadcast messages and thus has a lower overhead. Finally, Malkhi et al. propose a system based on Secure Multi-Party Communication, which does not require cryptography [20]. They do, however, require secure channels between all participants. Such a requirement is hard to achieve in a large global overlay where most of the participants do not know each other a priori, and one cannot distinguish between good and bad participants.

To the best of our knowledge, there is only one prior proposal for addressing churn in anonymizing overlays. Cashmere [31] tackles churn by using a multicast group at each hop instead of a single node. Any node in the multicast group can forward the message. Cashmere assumes a trusted public key infrastructure (PKI) that assigns the same key to all nodes in each multicast group. Hence, Cashmere needs group key management and key redistribution, whenever group membership changes, which happens often in dynamic peer-to-peer overlays.

Finally, our information slicing idea is related to the theoretical work on secure communication [13,29]. This work bounds the adversarial strength under which perfectly secure communication is possible. Our work on the other hand considers the problem of anonymous, confidential, and resilient communication. We provide stronger resilience to churn, a system implementation and evaluation of the performance of our protocol.

Some of the coding techniques used in our work are related to secret sharing [26]. A secret-sharing scheme is a method for distributing a secret among a group of participants, each of which is allotted a share of the secret. The secret can only be reconstructed when the shares are combined together, individual shares are of no use on their own. Our work, however, is significantly different from prior work on secret sharing; we focus on building a practical anonymizing overlay. Furthermore, our ideas about node reuse, the graph construction algorithm, and churn resilience are all different from secret sharing.

3 Model & Assumptions

(a) Goals: This paper aims to hide the source and destination identities, as well as the message content, from both external adversaries and the relay nodes. Further, the destination also does not know the identity of the actual source. Said differently, we are interested in the same type of anonymity exhibited in onion routing, where a relay node cannot identify the source or the destination, or decipher the content of the message; all it knows are its previous and next hops.

We also want a system that is practical and simple to deploy in a dynamic and unmanaged peer-to-peer overlay. The design should deal effectively with node churn. It must not need a trusted third party or a public key infrastructure, and preferably should not use any public key cryptography. The system also should not impose a heavy load on individual overlay nodes or require them to provide much bandwidth.

(b) Threat model: We assume an adversary who can observe a fraction of network traffic, operate relay nodes of his own, and compromise some fraction of the relays. Further, the compromised relays may also collude among themselves. Like prior proposals for low-latency anonymous routing, we do not address a global attacker who can snoop on all links in the network [12,21,15,31]. Such a global attacker is unlikely in practice. We also assume that the attacker cannot snoop on all paths leading to the destination. If this latter assumption is unsatisfied, i.e., the attacker can snoop on all of the destination's traffic, the attacker can decode the content of the message but cannot identify the source of the message.

(c) Assumptions: We assume the source has an uncompromised IP address to access the Internet, $S$. Additionally, we assume the source has access to one or more IP addresses from which she can send. These IPs, which we call pseudo-sources $S'$, should not be on the same local network as $S$. We assume that the source has a shared key with each of the pseudo-sources and communicates with them over a secure channel.

We believe these assumptions are reasonable. Many people have Internet access at home and at work or school, and thus can use one of these addresses as the source and the rest as pseudo-sources. Even when the user has only one IP address, she is likely to have a spouse, a friend, or a parent whose IP address she can use. When none of that is available, the user can go to an Internet cafe and use her home address as the source and the cafe's IP as a pseudo-source.

Note that the pseudo-sources cannot identify the destination or decipher the content of the message. They can only tell that the source is sending an anonymous message. In our system, we assume that the source wants to keep the pseudo-sources anonymous because they are personally linked to her, i.e., we protect the anonymity of the pseudo-sources in the same way as we protect the anonymity of the source. We conservatively assume that if the anonymity of any one of them is compromised then the source anonymity is also compromised. Thus, in the rest of this paper, the anonymity of the source comprises the anonymity of all pseudo-sources.

4 Information Slicing

The design of information slicing involves answering three questions:

• How do we send a confidential message without keys?
• How do we construct an anonymous overlay path? In particular, how do we hide the identities of the source and destination from the overlay nodes along the path and also hide the identity of the source from the destination?
• How do we make the protocol resilient to node churn?

We address each of these questions in the following sections, starting with message confidentiality.

Figure: Alice wants to send a confidential message to Bob but does not know his key. Alice first multiplies the message $\vec m$ with a random matrix, $A$, then splits the resulting information, $\vec I^* = A \vec m$, into multiple pieces, $I^*_1, ..., I^*_d$. She sends each piece on a disjoint overlay path to Bob. Only Bob receives enough information bits to decode the original message as $\vec m = A^{-1} I^*$.

1 Confidentiality Without Keys

Information slicing enables a source to send a confidential message to a destination without knowing the destination's key. Consider the scenario in Fig. 1. Alice wants to send the message ``Let's meet at 5pm'' to Bob. Alice divides the message into $d$ pieces, e.g., $m_1=$``Let's meet'' and $m_2=$``at 5pm'' when $d=2$, so that the original message can be recovered only when a node has access to all $d$ pieces. We call this process slicing the message.

Sending a message slice in the clear is undesirable, as the slice may expose partial information to intermediate nodes along the path. For example, a node that sees $m_1=$``Let's meet'' knows that Alice and Bob are arranging for a meeting. Thus, Alice multiplies the message vector $\vec m= (m_1,..., m_d)$ with a random but invertible $d \times d$ matrix $A$ and generates $d$ slices which constitute a random version of the message:

$$\vec{I}^{*} = \left( \begin{array}{c} A_{1} \\ \vdots \\ A_{d} \end{array} \right) \vec m = A\vec m$$

Then, Alice picks $d$ disjoint overlay paths to Bob. She sends on path $i$ both the slice $I^*_i$ and $A_i$, where $A_i$ is row $i$ of matrix $A$. An intermediate node sees only some random values $I^*_i$ and $A_i$, and thus cannot decipher the content of the message. Once Bob receives all slices, he decodes the original message as:

$$\vec m = A^{-1} \vec I^*.$$

Figure: Alice wants to send an anonymous message to Bob without any public keys. Each node along the path needs to learn the IP addresses of its next hops in a confidential message, which is done by splitting each IP address and sending the pieces on disjoint paths. Alice has access to two machines $Alice$ and $Alice'$. A message like $\{Z_l, Bob_l\}$ refers to the low-order words of the IDs of nodes $Z$ and $Bob$, and $rand$ refers to random bits.

2 Anonymous Routing Without Keys

Next, assume that Alice wants to send her message anonymously. How can Alice set up an anonymous path without keys? Each node along an anonymous path should know its previous hop and its next hop but nothing more. In onion routing, a node along the path learns its next hop from its previous hop - its parent. Though the parent delivers this information to its child, it cannot access it itself because the information is encrypted with the child's public key. In the absence of keys, the path cannot be included in the message, as that allows any intermediate node to learn the whole path from itself to the destination. We need an alternative method to tell a node about its next hop without revealing this information to other nodes, particularly parent nodes.

Our approach to anonymity without keys relies on a simple idea: anonymity can be built out of confidentiality. For anonymous communication, the source needs to send to every relay node along the path its routing information (i.e., its next hop) in a confidential message, accessible only to the intended relay. Information slicing enables a source to send such confidential messages without keys.

Using information slicing for anonymity, however, is challenging. To send a particular node the identity of its next hop along different anonymous paths, one needs to anonymously tell each node along these paths about its own next hop. This requires an exponential number of disjoint paths, and thus an exponential number of nodes. To avoid exponential blow-up, it is essential that the source constructs efficient forwarding graphs that reuse the overlay nodes without giving them too much information. The construction of such graphs in the general case is discussed in §4.2.1, but we first explain a simple example to give the reader an intuition about how the protocol works.

1 Example

Alice wants to send an anonymous message to Bob. Alice retrieves the DNS names of a few overlay nodes that she or her friends have used in the past to download music via a P2P file-sharing network. She can use DNS to retrieve the IP addresses of these overlay nodes. Alice does not know the public keys of the overlay nodes, or whether they have keys. She does, however, know that the software of the peer-to-peer overlay supports information slicing.

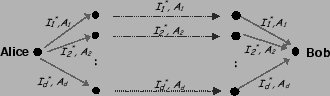
Alice has Internet at home and work, and hence has access to two IP addresses: $Alice$ and $Alice'$. Alice arranges the overlay nodes into stages. Let's say she uses the graph in Fig. 2, which contains 3 stages (path length $L=3$), each containing 2 nodes (split factor $d=2$) (we will show how to pick appropriate values for $L$ and $d$ in §6). The $0^{th}$ stage is the source stage itself. Each node in this graph is connected to every node in its successive stage. Note that the destination node, i.e. Bob's node, is randomly assigned to one of the stages in the graph.

Alice needs to send to each relay node the IP addresses of its next hops, without revealing this information to other nodes. To do so, she splits each IP into two pieces and sends this information over two paths. Alice could have split each IP address to its most significant and least significant words. This, however, is undesirable as the most significant word may indicate the owner of the IP prefix. Instead Alice first transforms the IP addresses of the relay nodes by multiplying each address by an invertible matrix $A$ of size $d \times d$ (i.e., $2 \times 2$). (For simplicity, assume that $A$ is known to all nodes; in §4.3, we explain how the sender anonymously sends $A$ to the relays on the graph.) Let $Z_{l}$ and $Z_{h}$ be the low and high words of the IP address of node $Z$; Alice splits the IP address as follows:

$$\left( \begin{array}{c} Z_{L} \\ Z_{H} \end{array} \ri... ...t( \begin{array}{c} Z_{l} \\ Z_{h} \end{array} \right).$$ (1)

She sends $Z_L$ and $Z_H$ to node $Z$'s parents, $V$ and $W$, along two different paths.

Fig. 2 shows how messages are forwarded so that each node knows no more than its direct parents and children. Consider an intermediate node in the graph, say $V$. It receives the message `` $\{Z_H,Bob_H\}\{X_H,Y_H\}\{rand_H\}$'' from its first parent. It receives ``$\{Z_L,Bob_L\}$'' from its second parent. After receiving both messages, $V$ can discover its children's IP addresses as follows:

$$\left( \begin{array}{cc} Z_{l} & Bob_{l} \\ Z_{h} & Bob_... ...ay}{cc} Z_L & Bob_{L}\\ Z_H & Bob_{H} \end{array} \right)$$ (2)

But $V$ cannot, however, identify the children of its children (i.e., the children of nodes $Z$ and $Bob$) because it misses half the bits in these addresses, nor does it know the rest of the graph. Node $V$ also does not know that Bob is the destination and Alice is the sender. From its perspective, Alice may have received the message from someone upstream, and Bob may be just another forwarder.

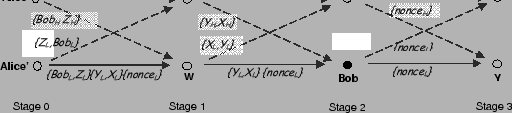
You might be wondering how the graph in Fig. 2 will be used to anonymously send data to Bob. Indeed, as it is, Bob does not even know he is the intended destination; but this is easy to fix. In addition to sending each node its next-hop IPs, Alice sends him: (1) a symmetric secret key, (2) and a flag indicating whether he is the destination. Similar to the next-hop IPs, the key and the flag of each node are split along disjoint paths, and thus inaccessible to other nodes. To send a confidential data message, Alice encrypts the data with the key she sent to Bob during the route setup phase, chops the data into $d$ pieces, and forwards the pieces along the forwarding graph to Bob. Once Bob receives the $d$ slices of the data, he can decode the encrypted data and invert the encryption using the key previously sent to him. No other node can decipher the data even if it gets all $d$ slices.

Table 1: Variables used in the paper.

Var	Definition
$d$	Split factor, i.e., the number of slices a message is split to.
$L$	Path length, i.e., the number of relay stages along a path.
$N$	Number of nodes in the peer-to-peer network excluding the source stage.
$f$	Fraction of subverted nodes in the anonymizing network.

3 Protocol Specification

This section rigorously describes our protocol. Our anonymous routing protocol delivers packets along a forwarding graph as explained in §4.2.1. The protocol has two phases. First, the source anonymously and confidentially informs each of the relay nodes on the graph of its forwarding information, i.e., it establishes the graph. Second, the source uses the forwarding graph to send data. If the source does not need to send much data, it is possible to collapse the two phases together and concatenate the data slices with the slices that build the graph. Before delving into the details of the protocol, we refer the reader to Table 1, which describes the variables used in the rest of the paper.

Figure: Packet Format. Each packet contains $L$ information slices.

1 Per Node Information

Let $x$ be one of the nodes in the forwarding graph. $I_x$ is the routing information the source needs to anonymously deliver to node $x$. $I_x$ consists of the following fields:

• Nexthop IPs. The IP addresses of the $d$ children of node $x$.
• Nexthop flow-ids. These are $d$ 64-bit ids whose values are picked randomly by the source and are to be put in the clear in the packets going to the corresponding $d$ next-hops. The source ensures that different nodes sending to the same next-hop put the same flow-id in the clear. This allows the next-hop to determine which packets belong to the same flow. The flow-id changes from one relay to another to prevent the attacker from detecting the path by matching flow-ids.
• Receiver Flag. This flag indicates whether the node is the intended destination.
• Secret Key. The source sends each node along the path a symmetric secret key that can be used to encrypt any further messages intended to this node.
• Slice-Map. This field describes which of the slices the relay receives go to which child (see §4.3.4).
• Data-Map. This field describes how the data packets flow down the graph (see §4.3.7).

Figure: An example showing how to split information slices along disjoint paths. Node R is the destination, S and S' are the sources. The text on the arrows refers to the information slices traversing that edge. The text next to each node describes the information slices collected by that node.

2 Creating Information Slices

The source chops the node information $I_{x}$ into $d$ blocks of $\frac{\vert I_{x}\vert}{d}$ bits each and constructs a $d$ length vector, $\vec{I_x}$. Further, it transforms $\vec{I_x}$ into coded information slices using a full rank $d \times d$ random matrix $A$ as follows:

$$\vec{I}^{*}_{x} = \left( \begin{array}{c} A_{1} \\ \vdots \\ A_{d} \end{array} \right) \vec{I_x} = A\vec{I_x}$$ (3)

The source concatenates each element in $\vec{I}^{*}_{x}$ with the row of the matrix $A$ that created it (i.e., it concatenates $I_{xi}^{*}$ with $A_i$). The result is what we call an information slice. The source delivers the $d$ slices to node $x$ along disjoint paths.

3 Packet Format

Fig. 3 shows the format of a packet used in our system. In addition to the IP header, a packet has a flow-id, which allows the node to identify packets from the same flow and decode them together. The packet also contains $L$ slices. The first slice is always for the node that receives the packet. The other slices are for nodes downstream on the forwarding graph.

4 Constructing the Forwarding Graph

The source constructs a forwarding graph that routes the information slices to the respective nodes along vertex disjoint paths, as explained in Algorithm 1.

We demonstrate the algorithm by constructing such a graph in Fig. 4, where $L=3$ and $d=2$. The source starts with the $2$ nodes in the last stage, $X$ and $Y$. It assigns both the slices, $I_{X1}^{*}$, $I_{X2}^{*}$ to $X$. The source then has to decide from whom node $X$ will receive its slices. The source goes through the preceding stages, one by one, and distributes $(I_{X1}^{*},I_{X2}^{*})$ among the $2$ nodes at each stage. The distribution can be random as long as each node receives only one of the slices. The path taken by slice $I_{X1}^{*}$ to reach $X$ can be constructed by tracing it through the graph. For e.g., the slice $I_{X1}^{*}$ traverses $(S',W,Z,X)$, which is disjoint from the path taken by $I_{X2}^{*}$, i.e., $(S,V,R,X)$. The source repeats the process for the slices of $Y$, and for the slices of every node in all the other stages.

5 Decoding the Information Slices

A node decodes its information from the $d$ slices it receives from its parents, as shown in Fig. 5. The first slice in every packet that node $x$ receives is for itself. It consists of one of the $d$-slices of $x$'s information, $I^*_{xi}$, and the row of the transform matrix that helped create it, $A_i$. Node $x$ constructs the vector $\vec{I}_{x}^{*}$ from the $d$ slices it receives, and assembles a $d \times d$ matrix $A = {[A_{1}; \ldots; A_{d}]}$ from the $d$ rows of the transform matrix sent in the slices. Then, node $x$ computes its information vector, $\vec{I_x}$, as $\vec{I_x} = A^{-1}\vec{I}_{x}^{*}$.

Figure: An example of how a node decodes its information from its incoming slices. It uses the $d$ incoming slices and reconstructs the original information by inverting the matrix $A$ and gets the IP addresses of its next-hops as well as the flows ids, its secret key, its slice-map, and its data-map.

6 How to Forward Information Slices

After the relay decodes its own information, it has to decide what to send to each one of its children. As is apparent from Figs. 2 and 4, a relay does not send the same information slices to all of its $d$ children. The relay needs a map that tells it which of the information slices it received from its parents goes to which child, and in what order. This information is provided by the source in the slice-map.

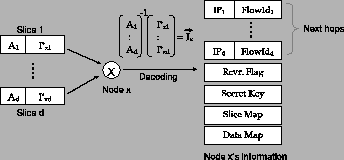Fig. 6 shows an example slice-map. The slice-map is a $d \times L$ matrix that tells the relay how to construct the packets it sends to its children. For example, in Fig. 6, node $x$ has received 2 packets from its parents. The number of slices in each packet is fixed to the path length $L=4$. Note that $x$ should first extract its own slice from each of the packets, which is the first slice in the packet, as explained in §4.3.5. The other three slices in each packet are to be forwarded downstream, as prescribed by $x$'s slice-map. For example, the figure shows that the third slice in the packet received from $V$ should be the first slice in the packet sent to node $C$. Entries labeled ``rand'' refer to padding slices with random bits that are inserted by the relay node to replace its own slices and maintain a constant packet size.

Additionally, all packets headed to a child node should contain the child node's slice as the first slice. The source constructs the slice maps of the parent nodes such that the packets meant for the child node always have the child node's slice as the first slice in the packet. Also the child node needs to be able to identify which $d$ packets go together. The source arranges for all of the parent relays to use the same flow-id for packets going to the same child. The parent learns these flow-ids as part of its information, as shown in Fig. 5.

7 Data Transmission

Once the forwarding graph is established, the source can send anonymous data messages to the destination until it explicitly terminates the connection or the routing information times out. Also the destination can use a similar procedure to transmit to the source along the reverse path.

The source encrypts each data message with the key it sent to the destination node. Then it chops the data message into $d$ pieces, converts them into $d$ slices and multicasts the slices to the nodes in the first stage of the forwarding graph. Each relay node in the first stage receives all $d$ data slices, but they cannot multicast whatever they receive to the nodes in the next stage, since each child then will receive $d^2$ data slices leading to bandwidth overhead. On the other hand, if each node forwards a random slice to each of its children, then each child will get $d$ data slices; but these slices may overlap and thus be useless. To solve the problem, the source sends each relay a data-map as part of its information. The data-map tells the node how to forward the data slices between each parent-child pair. The data map is very similar to the slice map shown in Fig. 6, except that instead of slice numbers the entries correspond to data packets. The source picks the entries in the data-map to ensure that each child gets all useful data slices, and no more. Each node in the graph including the destination therefore gets $d$ slices, but since the data slices are encrypted using the destination's keys, only the destination can recover the original data.

Figure: An example showing the slice-map of node $X$, which has $V$ and $W$ as parents and $C$ and $D$ as children.

4 Resilience to Churn and Failures

Overlays with open membership suffer from churn because nodes join and leave frequently. Node churn causes data loss. The standard way to deal with loss is to add redundancy. The challenge, however, is to maximize the probability of recovery for the same amount of redundancy. Communication systems typically use coding to achieve this goal. Our design naturally extends the codes used to provide confidentiality to also provide resilience against churn and failures.

(a) Basic idea: Take a vector of $d$ elements $\vec m = (m_1, \ldots ,m_d)$ and multiply it by a random matrix $A'$ of rank $d$ and size $d'\times d$ where $d' > d$. The result will be a a vector of $d'$ elements, $\vec m' = (m'_1, \ldots , m'_{d'})$; it is a redundant version of your original vector. What is interesting about this process is that it is possible to retrieve the original message from any $d$ elements of $\vec m'$ and their corresponding rows in the matrix [18].

(b) Adding redundancy to graph establishment phase: Instead of slicing the per-node information into $d$ independent pieces that are all necessary for decoding, we use $d' > d$ dependent slices. Replace Eq. 3 with:

$$\vec{I^*_{x}} = A'\vec{I_{x}}$$ (4)

where $A'$ is a $d'\times d$ matrix with the property that any $d$ rows of $A^{'}$ are linearly independent. The source picks $d'$ disjoint paths to send the message. A node can recover its information from any $d$ out of $d'$ slices that it successfully receives.

(c) Adding redundancy to the data transfer phase: As mentioned earlier, the source encrypts the data with the symmetric key it sent to the destination during path establishment. The source then chops the encrypted message into $d$ pieces, creating a message vector $\vec m$. Before it sends the message, however, it multiplies it by a random matrix $A'$ of size $d'\times d$ and rank $d$, where $d' > d$. This creates $d'$ data slices that the source sends along $d'$ disjoint paths. The destination can recover the original information as long as it receives any $d$ slices out of the $d'$ data slices the source created.

1 Boosting Resilience to Churn Via Network Coding

The resilience scheme above is far from optimal. Consider an example where $d=2$ and $d'=3$, and assume that at some stage $i$ along the path, one of the three relays fails. Its children in stage $i+1$ will receive two data slices instead of three. This is sufficient for recovering the original data. The problem, however, is that the redundancy is lost. Unless the redundancy is restored, downstream relays cannot recover from any additional failures.

We use network coding to solve the problem. Network coding allows intermediate nodes to code the data too. In our scheme, during the data transmission phase, a relay can easily restore the redundancy after its parent fails. To do so, the relay creates a linear combination of the slices it received, i.e., $m'_{new} = \sum p_i m'_i$, where $p_i$ are random numbers. The relay also creates $A'_{new} = \sum p_i A'_i$, where $p_i$ are the same numbers above. The new slice is the concatenation of $A'_{new}$ and $m'_{new}$ and can effectively replace the lost slice. Any relay that receives $d$ or more slices can replace all lost redundancy. Thus, with a small amount of redundancy, we can survive many node failures because at each stage the nodes can re-generate the lost redundancy.

5 Security Analysis

Instead of standard key-based encryption, our scheme uses information slicing. To understand the level of confidentiality, i.e., the security obtained with such an approach, we estimate the amount of information a malicious node can glean from the messages it receives. We borrow the following definition from [8,28].

A pi-secure information slicing algorithm implies that to decrypt a message, an attacker needs to obtain all $d$ information slices; partial information is equivalent to no information at all. The proof of the following lemma is in a technical report [19]:

Lemma 5.1   Information slicing is pi-secure.

We note that there are many types of security, e.g., cryptographic security, pi-security, and information theoretic security. The strongest among these is information theoretic security. Information slicing can be made information theoretically secure, albeit with increased overhead. Instead of chopping the data into $d$ parts and then coding them, we can combine each of the $d$ parts with $d-1$ random parts. This will increase the space required $d$-fold, but provides extremely strong information-theoretic security.

6 Evaluation of Anonymity

The basic threat to anonymity in peer-to-peer overlays are attackers who compromise the overlay network. They can hack nodes, operate their own nodes, or eavesdrop on links to do traffic analysis. They can further collude to compromise anonymity. In this section we evaluate the anonymity of information slicing against such adversaries via simulations.

1 Anonymity Metric

The anonymity of a system is typically measured by its entropy [25,11], and is usually expressed in comparison with the maximum anonymity possible in such a system, i.e.:

$$Anonymity= \frac{H(x)}{H_{max}} = \frac{\sum_{x}-P(x)log(P(x))}{log(N)},$$ (5)

where $N$ is the total number of nodes in the network, $P(x)$ is the probability of a node being the source/destination, and $H_{max}=log(N)$ is the maximum entropy that occurs when the attacker has no information. Anonymity is a number between $0$ and $1$. For example, the source is perfectly anonymous when it is equally likely to be any node in the network, in which case $P(x)=\frac{1}{N}$ and the $Anonymity =\frac{H(x)}{H_{max}} = 1$.

Note that $Anonymity = 0.5$ is quite high. It does not mean that the attacker knows the source or the destination with probability $0.5$. Rather it means the attackers are still missing half the information necessary to discover the anonymous source or destination.

2 Simulation Environment

We would like to measure how the anonymity of the source and destination depends on the strength of the attackers. We simulate a scenario in which the attacker subverts a fraction $f$ of the overlay nodes and the subverted nodes collude together. We assume that all attackers collude and consider them together as one powerful attacker. Note that this scenario subsumes attacks in which the attacker eavesdrops (i.e. does traffic analysis) on a fraction of the links because compromising a node is always a stronger attack than snooping on its input and output links. Further, this also subsumes ``intersection'' attacks in which attackers across multiple stages collude to compromise anonymity.

We assume that the source picks the relays randomly from the set of all nodes in the network, and that every node appears only once in the anonymity graph. These assumptions degrade anonymity, making our results conservative.

In each simulation, we randomly pick $f\times N$ nodes to be controlled by the attacker, where $N$ is the number of overlay nodes. Then we pick $L \times d$ nodes randomly and arrange them into $L$ stages of $d$ nodes each. We randomly pick the destination out of the nodes on the graph. We identify the malicious nodes in the graph and analyze the part of the graph known to the attacker. Once we know the part of the graph known to the attacker, the anonymity for that particular scenario is computed. The details of how to compute source and destination anonymity for a particular simulation scenario are kept in a technical report [19]. Depending on the random assignment, the part of the graph known to the attacker will vary and so will the anonymity. Hence the simulation procedure is repeated $1000$ times and the average anonymity is plotted.

3 Simulation Results

Figure: Source and destination anonymity as functions of the fraction of malicious nodes in the network ( $N=10000, L=8, d=3$). The anonymity obtained via information slicing is close to what Chaum mixes provide.

1 How does information slicing compare to Chaum mixes?

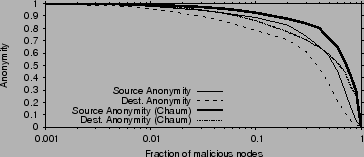In this section we evaluate the anonymity provided by information slicing and compare it to Chaum mixes. Consider attackers who compromise a fraction $f$ of all nodes or links and collude together to discover the identities of the source and destination. Fig. 7 plots the anonymity of the source and destination as functions of the fraction of compromised nodes, for the case of $N=10000, L=8, d=3$. When less than $20\%$ of the nodes in the network are malicious, anonymity is very high and comparable to Chaum mixes, despite no keys. As the fraction of malicious nodes increases, the anonymity falls. But even when the attackers control half of the nodes, they are still missing half the information necessary to detect the source or destination. Destination anonymity drops faster with increased $f$ because discovering the destination is possible if the attacker controls any stage upstream of the destination, while discovering the source requires the attacker to control stage 1, as we show in [19].

Figure: Source and destination anonymity as functions of the splitting factor ($N=10000, L=8$). For small $f$, increasing $d$ decreases anonymity because it exposes more nodes to the attacker. For large $f$, the probability that attackers control an entire stage dominates, hence increasing $d$ increases anonymity. Anonymity of $0.5$ is still quite high since the attackers are missing half the information necessary to compromise the anonymity of the source and destination.

2 Impact of Protocol Parameters

We evaluate how anonymity is affected by the parameters under the source's control: how many slices each piece of information is split into and the number of stages in the routing graph.

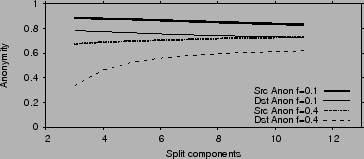Fig. 8 plots source and destination anonymity as functions of the splitting factor $d$. When $f$ is low, information leakage is due primarily to the malicious nodes knowing their neighbors on the graph. In this case, increasing $d$ increases the exposure of non-malicious nodes to attackers which results in a slight loss of anonymity. When $f$ is high, information leakage is mainly due to attackers being able to compromise entire stages. Hence, increasing $d$ increases anonymity. However, even an anonymity as low as 0.5 is fairly strong; it means that the attacker is still missing half the bits necessary to identify the source/destination.

Figure: The anonymity of the source and destination increases with the path length ( $N=10000, d=3, f=0.1$).

Fig. 9 plots the source and destination anonymity as functions of the path length $L$. Both source and destination anonymities increase with $L$. The attacker knows the source and destination have to be on the graph; thus, for moderate values of $f$, putting more nodes on the graph allows the communicators to hide among a larger crowd.

Figure: The anonymity of the destination decreases with the redundancy added ($d$ = 3, $L$ = 8, $f$ = 0.1), source anonymity is not that adversely affected by redundancy since it is mainly a function of how many attackers are present in the graph.

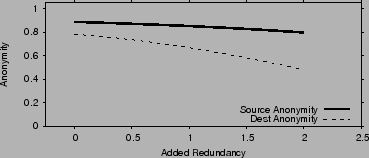We also evaluate how anonymity and churn resilience trade off against each other. The theoretical analysis is in [19]. Fig. 10 plots the source and destination anonymity as functions of the redundancy added to combat churn. Redundancy is calculated as $(d'-d)/d$, and in the figure $d=3$. As the added redundancy increases, it becomes more likely that the attacker compromises an entire stage of nodes. Hence destination anonymity decreases. Source anonymity is not much affected because it depends on whether specifically the first stage is compromised.

7 Evaluation of Performance

We evaluate the performance of information slicing via a prototype implementation run on the local and wide-area networks. Our wide-area experiments use 256 PlanetLab nodes, including nodes in North America, South America, Europe, and Asia. In each experiment, we pick a random subset of the above nodes depending on the size of the graph being set. We repeat each experiment $25$ times by changing the randomly chosen subset of PlanetLab nodes and we take the average of the measured quantity. Our local-area experiments are performed on a 1 Gbps switched network with the nodes being 2.8 GHz Pentium boxes with 1 GB of RAM.

1 Implementation and Benchmarks

We have built a prototype of information slicing in Python. It includes two programs: an overlay daemon and a source utility. Each overlay node runs a multi-threaded daemon that listens on a special port. The daemon maintains a hash table keyed on the flow-id. For each anonymous flow, the table contains all the relevant forwarding information including the flow's next-hop IPs. When the daemon receives a packet, it forks a thread to process the packet and appropriately update the flow table. Additionally, the daemon periodically garbage collects the flow table to remove stale entries. The source utility program takes as input a list of willing overlay nodes, and a few configuration parameters such as the path length $L$, the number of parallel paths $d'$, and the number of independent slices $d$.

The overhead of information slicing is low. We have performed benchmarks on a Celeron $800$MHz machine with $256$MB RAM connected to the local $1$Gbps network. Coding and decoding require on average $d$ finite-field multiplications per byte. Hence, the maximum achievable throughput is limited by how fast the multiplications can be accomplished. For $d=5$, coding takes on average $60\mu s$ per 1500B packet, which limits the maximum output rate to $200$Mbps. The memory footprint is determined by $d$, since we need the $d$ packets to generate outgoing coded packets. Thus the memory consumed for packet storage is $d \times 1500B$ which is negligible.

2 Per-Flow Throughput

Fig. 11 and 12 show the throughput obtained when a transfer is run for 150 seconds using onion routing and our protocol for the local area network and PlanetLab respectively. The onion routing protocol uses computationally efficient symmetric session keys for the data transfer; public key cryptography is used only for the route setup. Both protocols use 1500 byte packets. On the local-area network (Fig. 11), our protocol can send at about 40-60 Mb/s. The parallelism in our protocol allows it to achieve higher throughput than onion routing. On PlanetLab (Fig. 12), the nodes are highly loaded, reducing the achievable throughput. Yet, the transfer achieves about 1 Mb/s, which is a good throughput for the wide-area network.

Figure: Comparison of the throughput of information slicing and onion routing on the local-area network. Information slicing achieves higher throughput due to the inherent parallelism involved in multiple paths.

Figure: Comparison of the throughput of information slicing and onion routing on PlanetLab. Information slicing achieves higher throughput than onion routing.

The overhead of information slicing in path setup is higher compared to onion routing. Specifically, since each message is split into $d$ components, and each node outputs $d$ packets in every round, the total number of packets between any two stages is $d^2$. For onion routing $d=1$, whereas $d$ can be varied in information slicing. But on the other hand, information slicing delivers higher throughput, since it used $d$ parallel paths to deliver the data.

3 Scaling with the Number of Users

Figure: Network Throughput as a function of the number of flows using an overlay of $100$ PlanetLab nodes. As load increases, the network throughput from information slicing scales almost linearly. At sufficiently high load, the network throughput levels off.

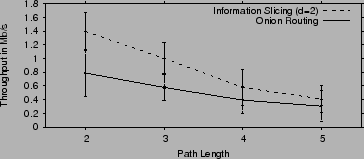
We examine how the throughput scales as the number of sources using the anonymizing overlay increases. Fig. 13 shows the total throughput as a function of the average load on the overlay nodes. The total throughput is the sum of the throughputs of the anonymous flows in the experiment. Load is quantified as the number of concurrent anonymous flows using the overlay. The experiment is performed on a set of $100$ PlanetLab nodes that have long uptimes, so that churn does not affect the result (for churn results see 8). We set $d=3$ and $L=5$, hence each flow uses $15$ nodes from the set of $100$ nodes.

The figure shows that, as load increases, the total throughput scales linearly. At significantly high load, the throughput levels off and the overlay reaches saturation. The saturation threshold is a function of the used set of PlanetLab nodes and the loads imposed on these nodes by other users/experiments. Information slicing therefore scales well with the amount of load placed on the overlay up to moderate loads.

4 Route Setup Latency

Setup latency is measured end-to-end, from when the sender initiates the route establishment until the receiver sends back an ack (the ack is for measurement collection and not part of the protocol.) Our protocol allows the receiver to be randomly placed anywhere in the graph to obscure its identity. For purposes of our experiments, however, we place the receiver in the last stage of the graph, so that the measured setup times are the times to set up the entire graph, not just those stages up to the receiver's stage.

Figure: Average graph setup times on the local-area network as functions of path length $L$ and splitting factor $d$. Increasing $d$ means higher setup times, since each node has to wait for more packets before it can decode and forward its packet.

Fig. 14 plots the average graph setup times on the local-area network. As one would expect, the setup time increases with increased path length $L$ and splitting factor $d$. A large $d$ affects the setup time because a relay has to wait to hear from all of its $d$ parents and thus, the delay at each stage will be dominated by the slowest relay in that stage. In general however, the setup time is less than a couple of seconds. Furthermore, for $d=2$, the setup time is a few hundred milliseconds.

We repeat the same experiments on PlanetLab to measure how much the conditions in the wide area network affect our setup times. Fig. 15 shows the average graph setup times in that environment. The setup times have increased beyond their values in the local-area network because of the larger RTT, but more importantly because PlanetLab nodes have a high CPU utilization leading up to the conference deadline. Despite this increase, the setup time is still within a few seconds.

Figure: Average graph setup times on the wide-area network (PlanetLab) as functions of path length $L$ and splitting factor $d$. Setup times are high since nodes have been picked all around the world and PlanetLab nodes were heavily loaded before the conference deadline.

8 Evaluation of Churn Resilience

Churn is an inescapable reality of dynamic peer-to-peer overlay networks. In §4.4 we presented a novel technique that recreates lost redundancy to combat churn. Here we evaluate its performance via analysis and an actual implementation. First we show analytically how coding helps us achieve high resilience with a small amount of added redundancy. Then we evaluate information slicing's churn resilience on PlanetLab and show that it can successfully cope with failures and make long anonymous transfers practical.

1 Analysis

We first show the efficiency of our coding approach compared to onion routing via analysis; but comparing it to standard onion routing would be unfair, as onion routing does not have any redundancy added and it would show very bad performance. Hence we compare it to a modified version of onion routing which has the same amount of redundancy as information slicing.

Imagine making onion routing resilient to failures by having the sender establish multiple onion-routing paths to the destination. The most efficient approach we can think of would allow the sender to add redundancy by using erasure codes (e.g., Reed-Solomon codes) over multiple onion routing paths. Assuming the number of paths is $d'$, and the sender splits the message into $d$ parts, she can then recover from any $d'-d$ path failures. We call this approach onion routing with erasure codes. Recall that in information slicing as well, the sender adds redundancy by increasing the number of paths $d' > d$, i.e., $d$ slices of information are expanded to $d'$ slices. But the key difference in information slicing is that relays inside the overlay network can regenerate lost redundancy.

To evaluate analytically, consider a message of $S$ bytes. Suppose a sender has sent $S(1+R)$ bytes, where $R$ is the amount of redundancy in your transfer. $R$ is also the overhead in the system; it limits the useful throughput. Now, let us compare the probability of successfully transferring the data under our scheme and onion routing with erasure codes when the same amount of redundancy is added. In particular, assume the path length is $L$, and that failures are independent and the probability of a node failing is $p$, the redundancy in both schemes is $R= \frac {d'-d}{d}$, hence $d' = (R+1)d$.

Onion routing with erasure codes succeeds when there are at least $d$ operational paths. A path is operational if none of the nodes on that path fail. Thus, the probability of a path success is $P(path succeeds) = (1-p)^L$. The probability of the scheme succeeding is the probability of having at least $d$ non-failing paths, i.e.,

$$\begin{array}{cc} P(success) & = \sum^{i=d'}_{i=d} \binom{d'}{i} {(1-p)}^{Li}{(1-{(1-p)}^{L})}^{(d'-i)} \end{array}$$ (6)

The information slicing approach, on the other hand, can tolerate $d'-d$ failures in each stage. The scheme succeeds if all stages succeed. A stage succeeds if at least $d$ nodes in the stage do not fail, i.e.,

$$\begin{array}{l} P(stage succeeds) = \sum^{i=d'}_{i=d} \binom{d'}{i} (1-p)^{i} p^{d'-i} \end{array}$$

The slicing scheme succeeds if all stages succeed, i.e.:

$$P(success /slicing)= \left( P(stage succeeds) \right)^L.$$ (7)

Fig. 16 illustrates the two success probabilities as a function of the amount of redundancy for $d=2$, and $L=5$. The probability of a node failure during the transfer is set to $p=0.1$ in the top graph and $p=0.3$ in the bottom graph. The figure shows that, for the same amount of overhead, the slicing approach has a substantially higher probability of successfully completing its transfer.

Figure: The probability of completing a transfer in information slicing and onion routing with redundancy as a function of the added redundancy. Figure shows that for the same level of redundancy, information slicing achieves much higher resilience to node failures ($L=5, d=2$).

Figure: Resilience to node failures in PlanetLab for L = 5. Information slicing achieves very high resilience since it regenerates redundancy inside the network when a node fails.

2 Resilience to Churn on PlanetLab

We complement the analytical evaluation with real experiments on a failure-prone overlay network, i.e., the PlanetLab network. We run our experiments with all nodes in our PlanetLab slice including the ones which are very failure prone. ``Failure-prone'' are nodes which are often inaccessible due to myriad reasons, either due to heavy CPU overload or network disconnectivity. These nodes have short ``perceived'' lifetimes of less than $20$ minutes, and are extremely likely to fail during an experiment. The rationale for picking such nodes is that the sender usually has a list of overlay nodes, some of which are up and some are down. The sender cannot ping the nodes to identify the operational ones because this might jeopardize its anonymity.

We focus on the following question: ``Given PlanetLab churn rate and failures, what is the probability of successfully completing a session that takes $30$ minutes?'' Given the throughput figures presented earlier, a $30$-minute flow can transfer over $90$ MB, which is typical of P2P file transfers. We compare information slicing with the modified version of onion routing which has redundancy added as described in the previous section.

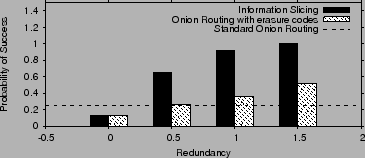
Fig. 17 compares the probability of successfully finishing the transfer under our approach, standard onion routing (one path), and onion routing with redundancy added using erasure codes. As we saw in the previous section, for the same number of paths, onion routing with erasure codes has the same level of redundancy as our scheme. Redundancy is added by increasing the number of paths $d' > d$, in this case the added redundancy $R$ is given by $(d'-d)/d$. The results are for $L=5$ and $d=2$. We vary the level of added redundancy by varying $d'$, and measure the probability of successfully completing a session lasting $30$ minutes.

The figure shows that with standard onion routing completing such a transfer is extremely unlikely. The probability of success increases with onion routing with erasure codes but stays relatively low. In contrast, with information slicing, adding a little amount of redundancy results in a very high success probability, making such relatively long anonymous transfers practical.

9 Robustness to Attacks

The biggest threat to peer-to-peer anonymizing overlays are from attackers who control nodes or can eavesdrop on links. Under conservative assumptions, i.e., even after assuming that an attacker who can eavesdrop on links leading to a node is as powerful as one who controls the node itself; we have shown that information slicing achieves anonymity comparable to Chaum mixes in §6. This section describes a few other attacks and how we address them. These attacks are fairly generic and apply to almost all anonymizers.

1 Limiting Malicious Nodes on the Graph

How does a sender choose relays for the anonymous graph it is setting up? One may be tempted to choose nodes completely at random from all available nodes; but an attacker could control large address spaces and increase the likelihood that the sender chooses colluding malicious nodes. To counter this attack, we leverage the structure of the IP address space. While an adversary can potentially control as many nodes as IP addresses to which he has access, these addresses are rarely scattered uniformly through the IP address space or through multiple autonomous systems (AS). IP addresses are divided into prefixes that are allocated to various networks worldwide. The prefixes appear in the inter-domain routing tables with their corresponding routes. These routing tables are publicly available from multiple vantage points [7]. It is realistic to assume that the attacker cannot compromise a large fraction of the inter-domain routing tables. Indeed if she can, then the attack has already jeopardized the Internet connectivity. By analyzing the publicly available routing tables, the sender can choose its relay nodes to be under different ASes potentially in different countries (e.g., Iran, US, China etc). This makes the above attack significantly more difficult because the attacker now needs to control many IP addresses belonging to many different ASes potentially spread around the world. Though this is possible, it is much more difficult. In the general case, picking overlay nodes that are independent and are guaranteed not to collude is a very difficult problem. Even if one knew the physical connectivity of the network, it is still not possible to guarantee non-collusion. Picking nodes based on their AS membership ensures that with high probability nodes are unlikely to collude.

2 Denial of Service Attack

It is always possible for a subverted relay to drop messages. It is also possible for a malicious source to try to consume the resources of the overlay nodes, denying other sources access to these resources. Overall, we believe that our approach neither increases nor decreases the vulnerability of an anonymizing overlay to denial of service; in comparison to onion routing, our approach allows the sender to store a small state (the per-node information) on the overlay nodes, but onion routing allows the sender to force the overlay nodes to do CPU-expensive public key cryptography.

In general, the best way to deal with denial of service attacks on anonymizing systems is to increase the size of the network. By allowing unmanaged peer-to-peer overlays with no trusted authority, our scheme has the potential to increase the size of these networks, thus increasing the resilience of the service.

3 Powerful Firewall

Consider a sender who lives under a repressive government that censors international online communications. The sender wants to anonymously communicate with an outside destination. To do so, it has to traverse the government's firewall. There are two cases. First the sender knows a pseudo-source outside the country. In this case, the sender splits the communication and securely tunnels a slice or more to outside pseudo-sources. The firewall, though it sees all slices, cannot reconstruct the message because some slices are encrypted. (Recall that a pseudo-source cannot read the message content or tell who the destination is.)

In the second case, the sender does not have access to a pseudo-source outside the firewall. In this case, the sender chooses some of the relays in some stage $i$ to be outside the country and the rest inside -i.e., the firewall does not cut the graph at a single stage. For the firewall to be able to decipher the message, it needs to pick the right $d^2$ packets out of all packets in a particular interval (say 0.5s). These packets do not come from the same set of senders (because of the cross-stage cut) and the bits in these packets are hard to correlate. Furthermore, there are potentially billions of packets traversing the firewall during that interval. Picking the right $d^2$ packets therefore is a very difficult problem.

4 Traffic Analysis Attacks

There is always a tradeoff between robustness to attacks and increased overhead. Most solutions either send excessive amount of traffic or increase complexity making the system less usable. The right operation point usually depends on the application scenario. Our system focuses on providing practical low-delay anonymity for everyday applications rather than providing perfect anonymity at all costs. As mentioned in §3 we cannot protect against a global eavesdropper who can observe all traffic. Further if an attacker can snoop on all links leading to the destination, message confidentiality is compromised. But the attacker still cannot discover the identity of the sender.

Traffic analysis attacks become significantly harder to mount in a global overlay with thousands of nodes and a large amount of normal filesharing traffic. In predecessor attacks [30], the attacker forces frequent rebuilding of paths and tries to identify the sender and destination by identifying specific responders outside the overlay to which connections are made. For this attack, the attacker needs to observe all traffic across the global overlay which is unrealistic in practice. Murdoch et.al. [22] present an attack in which the attacker pings nodes in the overlay and identifies how the load offered by the adversary affects the delay of other anonymous communication streams at the source node. The attacker has to ping potentially thousands of nodes in the global overlay before he can observe any significant statistical change in the senders anonymous communication. Further the large amount of P2P filesharing traffic already present makes such attacks based on statistical analysis hard to mount in a global overlay network. We describe below some other specific traffic analysis attacks and how our system protects against them.

(a) Inserting a pattern in the data: Colluding attackers who are not in consecutive stages might try to track a connection by inserting a particular pattern in the packet and observing the path of the inserted pattern downstream. To prevent such attacks the sender makes the nodes along the path intelligently scramble each slice such that no pattern can percolate through the network. We will demonstrate the algorithm through a single slice $K$, which belongs to an intermediate node $N$ in stage $i$. As we have seen before this slice passes through $i-1$ nodes before it reaches node $N$. Before transmitting the slice, the sender passes the slice through $i-1$ random transformations $T_1*T_2*\ldots*T_{i-1}$ successively. Now the sender has to ensure that when node $N$ receives the slice, all of these random transformations have been removed, else the slice will be useless to node $N$. Therefore the sender confidentially sends each of the inverses of the $i-1$ random transformations applied above to the $i-1$ nodes which handle this slice. Each intermediate node applies one inverse transform to the slice $K$, hence by the time the slice reaches node $N$, the slice is through $i-1$ inverse transformations and is back to its original unmodified state. Node $N$ can then decode and recover his own information.

The source repeats this process for all slices. This ensures that a slice is guaranteed to not look the same at any two links in the graph. Hence though the attacker might insert a particular pattern, the pattern will change in the immediate next stage without the attacker knowing how it changed. As a result, colluding non-consecutive attackers never see the same bit pattern, thereby nullifying the attack.

(b) End-to-End Time analysis attacks: The attacker may study the timing pattern in the traffic at various nodes in the overlay network in an attempt to identify where an anonymous flow enters and exits the overlay. Feamster et al [14] have shown that such an attack is possible in the Tor network. In particular, they report that Tor [12] has many nodes in the same AS. Hence, it is probable that the entry and exit nodes of an anonymous flow end up in the same AS. If this AS is adversarial, it can conduct timing analysis attacks to determine the sender and receiver. This attack becomes much harder in a large peer-to-peer overlay. In a large peer-to-peer network spread across the world, it is unlikely that a significant fraction of the nodes belong to the same AS. Furthermore, the node selection strategy outlined in §9.1 ensures that nodes are picked from different ASes, hence it is significantly hard for any single AS to mount a timing analysis attack.

(c) Resilience to packet size analysis: Looking at Fig. 4, the reader may think that the packet size decreases as it travels along the forwarding graph, and thus the attacker can analyze the position of a relay on the graph by observing the packet size. This is not the case, however. As explained in §4.3.4, each relay replaces its own information slices with random padding and shuffles the slices according to the sender's instructions sent in the slice-map. The map ensures that the packet size stays constant.

10 Conclusion

Anonymity spans a large design space; different anonymizers optimize for different objectives with corresponding tradeoffs. Information slicing presents a unique point in this design space. It provides confidentiality, anonymity and churn resilience without public key cryptography but with the tradeoff that the anonymity and confidentiality guarantees are slightly weaker than if we had public keys. We have analyzed the security and anonymity of the protocol and shown that it presents good guarantees against a variety of important attacks. We have also implemented the protocol, run it over PlanetLab, and shown that it is feasible and robust to node churn and failures. We believe information slicing simplifies the implementation and deployment of global peer-to-peer anonymizing networks, which is an important step towards scalable and practical online privacy.

11 Acknowledgments

We thank Jeremy Stribling, Vinod Vaikuntanathan, Hariharan Rahul, Maxwell Krohn and Frank Dabek for their comments on the paper. Cohen and Katabi are supported by the NSF Career Award CNS-0448287, whereas Katti is supported by NSF award CNS-0627021. The opinions and findings in this paper are those of the authors and do not necessarily reflect the views of NSF.

Bibliography

1

Anonymizer- Anonymous Web Surfing.
https://www.anonymizer.com.

2

Freedom Network.
https://www.freedom.net/.

3

JAP Anonymity and Privacy.
https://anon.inf.tu-dresden.de/index_en.html/.

4

MixMinion- Anonymous Remailer.
https://www.mixminion.net.

5

Peer-to-Peer in 2005.
https://www.cachelogic.com/home/pages/research/p2p2005.php.

6

Safeweb- Anonymous Web Surfing.
https://www.safeweb.com.

7

University of Oregon Route Views Project.
https://www.routeviews.org/.

8

J. Byers, M. C. Cheng, J. Considine, G. Itkis, and A. Yeung.
Securing Bulk Content Almost for Free.
Journal of Computer Communications, Special Issue on Network Security, pages 280-290, February 2006.

9

D. L. Chaum.
Untraceable electronic mail, return addresses and digital pseudonyms.
Commun. of the ACM, pages 84-90, February 1981.

10

I. Clarke.
FreeNet.
https://freenet.sourceforge.net/.

11

C. Díaz, S. Seys, J. Claessens, and B. Preneel.
Towards measuring anonymity.
In Proc. of PET 2002.

12

R. Dingledine, N. Mathewson, and P. Syverson.
TOR: The second-generation onion router.
In Proc. of USENIX Security 2004, San Diego, CA, USA.

13

D. Dolev, C. Dwork, O. Waarts, and M. Yung.
Perfectly secure message transmission.
Journal of the ACM, 40(1), 1993.

14

N. Feamster and R. Dingledine.
Location diversity in anonymity networks.
In In Proc. of ACM WPES 2004.

15

M. J. Freedman and R. Morris.
Tarzan: A peer-to-peer anonymizing network layer.
In Proc. of ACM CCS 2002, Washington, DC, USA.

16

S. Goel, M. Robson, M. Polte, and E. Sirer.
Herbivore: A scalable and efficient protocol for anonymous communication.
In Proc. of the European SIGOPS Workshop 2004, Leuven, Belgium.

17

D. M. Goldschlag, M. G. Reed, and P. F. Syverson.
Hiding Routing Information.
In Proc. of Workshop on Information Hiding, Cambridge, UK, 1996.

18

T. Ho, M. Médard, J. Shi, M. Effros, and D. Karger.
On randomized network coding.
In Proc. of Allerton Conference on Communication, Control, and Computing, Monticello, IL, 2003.

19

S. Katti, J. Cohen, and D. Katabi.
Information slicing: Anonymity using unreliable overlays.
Technical Report MIT-CSAIL-TR-2007-013, CSAIL, MIT, February 2007.

20

D. Malkhi and E. Pavlov.
Anonymity without cryptography.
In Financial Cryptography 2001, Grand Cayman, British West Indies.

21

A. Mislove, G. Oberoi, A. Post, C. Reis, P. Druschel, and D. Wallach.
Ap3: A cooperative, decentralized service providing anonymous communication.
In Proc. of the ACM SIGOPS European Workshop, 2004, Leuven, Belgium.

22

S. Murdoch and G. Danezis.
Low-cost traffic analysis for TOR.
In Proc. of IEEE Symposium on Security and Privacy 2005, Oakland, CA, USA.

23

M. Reiter and A. Rubin.
Crowds: Anonymity for web transactions.
ACM Transactions on Information and System Security, 1(1), June 1998.

24

M. Rennhard and B. Plattner.
Introducing MorphMix: Peer-to-Peer based Anonymous Internet Usage with Collusion Detection.
In Proc. of WPES 2002, Washington, DC, USA.

25

A. Serjantov and G. Danezis.
Towards an information theoretic metric for anonymity.
In Proc. of PET 2002, San Francisco, CA, USA.

26

A. Shamir.
How to share a secret.
Communications of the ACM, pages 612-613, November 1979.

27

R. Sherwood, B. Bhattacharjee, and A. Srinivasan.
P5: A protocol for scalable anonymous communication.
In Proc. of the IEEE Symposium on Security and Privacy, 2002, Oakland, CA, USA.

28

D. Stinson.
Something about all or nothing transforms.
Designs, Codes and Cryptography, pages 133-138, March 2001.

29

L. Subramanian.
Decentralized Security Mechanisms for Routing Protocols.
PhD thesis, University of California, Berkeley, Nov. 2005.

30

M. Wright, M. Adler, B. Levine, and C. Shields.
An analysis of the degradation of anonymous protocols.
In Proc. of NDSS 2002, San Diego, CA, USA.

31

L. Zhuang, F. Zhou, B. Y. Zhao, and A. Rowstron.
Cashmere: Resilient anonymous routing.
In Proc. of NSDI 2005, Cambridge, MA, USA.

About this document ...

Information Slicing: Anonymity Using
Unreliable Overlays

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons paper.tex

The translation was initiated by Sachin Katti on 2007-02-22

Footnotes

... \let

... follows:

Elements of $\vec{I_x}$ and $A$ belong to a finite field $F_{p^{q}}$ where $p$ is a prime number and $q$ is a positive integer. All operations are therefore defined in this field and differ from conventional arithmetic.

...InformationTheory,InformationTheory1,

The entropy of a random variable $x$ is $H(x)= - \sum_{x} P(x) log (P(x))$, where $P(x)$ is the probability function.