
4th USENIX Symposium on Networked Systems Design & Implementation
Pp. 43–56 of the Proceedings
Information Slicing: Anonymity Using
Unreliable
Overlays
| Sachin Katti |
Jeff Cohen |
Dina Katabi |
| skatti@mit.edu |
jscohen@mit.edu |
dk@mit.edu |
Abstract:
This paper proposes a new approach to anonymous communication called
information slicing. Typically, anonymizers use onion routing, where a
message is encrypted in layers with the public keys of the nodes along
the path. Instead, our approach scrambles the message, divides it into
pieces, and sends the pieces along disjoint paths. We show that
information slicing addresses message confidentiality as well as
source and destination anonymity. Surprisingly, it does not need any
public key cryptography. Further, our approach naturally addresses the
problem of node failures. These characteristics make it a good fit for
use over dynamic peer-to-peer overlays. We evaluate the anonymity of
information slicing via analysis and simulations. Our prototype
implementation on PlanetLab shows that it achieves higher throughput
than onion routing and effectively copes with node churn.
1 Introduction
Suppose Alice wants to send a confidential and anonymous message to
Bob. Bob, however, does not have a public key that Alice could use to
encrypt her message. Further, Alice does not feel comfortable
exposing her unencrypted message to her ISP or an anonymizer. Alice's
dilemma might seem simple, but underlying it is the general issue of
online privacy. How do we send anonymous and confidential messages,
when most of us do not have public keys and the sender does not trust
a third party?
Our objective is to leverage popular existing peer-to-peer overlays to
send confidential and anonymous messages without public keys. We
focus on practical low-delay anonymity for everyday applications,
rather than perfect anonymity at all costs. Popular peer-to-peer
overlays have thousands of nodes and much traffic [5],
creating an ideal environment for hiding anonymous communications. The
dynamic nature of their participants makes them hard to track, and
their diverse constituency allows dividing trust among nodes that are
unlikely to collude. Some prior work has envisioned using these
overlays for
anonymity [15,24,21,23,16,27]. Current
proposals, however, fall into two camps: either they do not address
the high node churn in these environments and need all overlay nodes
to have public keys [15,24,21,16], or they
address churn but need very expensive solutions such as group key
management [31] or broadcast [27].
This paper presents information slicing, a single technique that
provides source and destination anonymity and churn resilience,
without using any public key cryptography. It can also provide
message confidentiality as long as the attacker cannot snoop on all
traffic going to the destination. These characteristics make it
suitable for use over popular peer-to-peer overlays. For example, say
Alice knows that Bob, like many of us, uses a popular file sharing
overlay to download content, and the overlay software supports
information slicing. Then Alice can send Bob a confidential anonymous
message without any public keys and in a manner robust to node churn
and failures.
To provide confidentiality, our technique employs a properly chosen
coding scheme to randomize the message. It then divides the
randomized message into pieces, and sends the pieces along node
disjoint paths that meet only at the destination. As a result, an
attacker that gets all but one of the pieces of the randomized message
cannot decode and recover the original message. Only the destination
receives all pieces and can decode the message.
Information slicing also provides anonymity without requiring the
overlay nodes to have public keys. Typically, anonymizers use onion
routing, which assumes the sender has the public keys of all the nodes
in the overlay. Onion routing hides the correspondence between a
source and destination by sending the route setup message through a
chain of nodes, wrapped in layers of public key encryption, such that
each node along the path knows only its previous and next hops.
Instead, to create an anonymous path, we send to each intermediate
node its routing information (i.e., its next hop) in a confidential
message sliced over multiple disjoint paths. The technical challenge
is to perform this process efficiently. To send a relay node the
identity of its next hop along different paths, we need to tell each
node along these paths about its own next hop anonymously. Performed
naively, this needs an exponential number of disjoint paths, and thus
an exponential number of nodes. To avoid exponential blow-up, we
build efficient forwarding graphs that reuse the overlay nodes without
leaking information.
Finally, information slicing naturally provides protection against
node churn and failures. The standard approach to address node
failures is to employ multiple paths and add redundancy to the
data. The challenge however is to minimize the redundancy overhead for
the same amount of resilience. Typically, communication channels use
coding to address such a challenge. We show that the same codes that
we use to send confidential messages can simultaneously provide
resilience to churn and failures. We also boost robustness by using
network coding, which is proven to minimize redundancy while
maximizing resilience to failures [18].
We show analytically and demonstrate experimentally that information
slicing provides high anonymity and is resilient to node churn. We
implement our protocol and evaluate its real-world performance in
PlanetLab. Our experimental results show that information slicing
provides higher throughput than onion routing. Further, it provides
strong resilience to node churn, while using minimal redundancy.
2 Related Work
First generation anonymizers used a single intermediate node to relay
traffic between senders and receivers (e.g.,
Anonymizer [1] and Safeweb [6]). Users had
to trust the anonymizing node, which knows the identities of the
source and destination.
Most modern anonymizers are based on Chaum's mixes [9] and
its near realtime variant, onion routing [17]. The sender
constructs a route by picking intermediate hops from a list of mixing
nodes. The mixers may delay and re-order the packets depending on the
traffic's timing constraints. The sender encrypts the IP address of
each node along the path with the public key of its previous hop.
This creates layers of encryption, like layers of an onion. Each node
decrypts the packets, discovers its next hop and forwards the packet
to the next hop and so on until the entire path is set up. Once the
path is established, nodes exchange computationally efficient
symmetric secret keys to transmit the actual data itself.
A few anonymizers rely on static and dedicated
overlays [12,4,3,2]. For example,
Tor [12] is a widely used anonymous system based on onion
routing. Tor's infrastructure contains a small set of distributed
nodes. Admission to the Tor network is tightly controlled. Tor has a
centralized trusted directory server that provides the users with IP
addresses and public keys of all the nodes in the system.
Some proposals [31,15,24,16] aim to build
anonymity out of global peer-to-peer overlays. Most of these systems
employ onion routing and use public key cryptography. Only one of
them addresses churn explicitly [31]. For example,
Tarzan [15] uses onion routing, assumes each overlay node has
a public key, and distributes these keys to interested senders using a
gossip protocol. Tarzan sets up tunnels along each path, which are
rebuilt upon node failures or departures. MorphMix's design is fairly
similar to Tarzan and differs only in the details of the tunnel setup
procedure [24]. Herbivore [16] builds on
DC-nets [9] to provide anonymity in large overlays. It
divides nodes into cliques and requires shared secrets across cliques
via either a PKI or offline key exchanges. Freenet [10] is
a decentralized censorship-resistant peer-to-peer data storage
facility, intended for anonymous publishing, not communication.
Similar to ours, some prior work does not use public key cryptography.
In Crowds [23], each intermediate node flips a coin to
decide whether to forward a packet to the destination or to a
random node in the overlay. In contrast to our work, Crowds does not
provide destination anonymity, and uses a centralized
admission server to admit nodes into the overlay. AP3 [21]
is based on the same random routing idea, and similarly does not
provide destination anonymity. 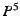 [27] achieves
anonymity by broadcasting encrypted packets at a constant rate to all
participants. When a node has no packets to send, it broadcasts noise,
which is then propagated through the network in the same manner as
data packets. In comparison, our system does not broadcast messages
and thus has a lower overhead. Finally, Malkhi et al. propose a
system based on Secure Multi-Party Communication, which does not
require cryptography [20]. They do, however, require secure
channels between all participants. Such a requirement is hard to
achieve in a large global overlay where most of the participants do
not know each other a priori, and one cannot distinguish between good
and bad participants. [27] achieves
anonymity by broadcasting encrypted packets at a constant rate to all
participants. When a node has no packets to send, it broadcasts noise,
which is then propagated through the network in the same manner as
data packets. In comparison, our system does not broadcast messages
and thus has a lower overhead. Finally, Malkhi et al. propose a
system based on Secure Multi-Party Communication, which does not
require cryptography [20]. They do, however, require secure
channels between all participants. Such a requirement is hard to
achieve in a large global overlay where most of the participants do
not know each other a priori, and one cannot distinguish between good
and bad participants.
To the best of our knowledge, there is only one prior proposal for
addressing churn in anonymizing overlays. Cashmere [31]
tackles churn by using a multicast group at each hop instead of a
single node. Any node in the multicast group can forward the message.
Cashmere assumes a trusted public key infrastructure (PKI) that
assigns the same key to all nodes in each multicast group. Hence,
Cashmere needs group key management and key redistribution,
whenever group membership changes, which happens often in dynamic
peer-to-peer overlays.
Finally, our information slicing idea is related to the theoretical
work on secure communication [13,29]. This work bounds
the adversarial strength under which perfectly secure communication is
possible. Our work on the other hand considers the problem of
anonymous, confidential, and resilient communication. We provide
stronger resilience to churn, a system implementation and evaluation
of the performance of our protocol.
Some of the coding techniques used in our work are related to secret
sharing [26]. A secret-sharing scheme is a method for
distributing a secret among a group of participants, each of which is
allotted a share of the secret. The secret can only be
reconstructed when the shares are combined together, individual shares
are of no use on their own. Our work, however, is significantly
different from prior work on secret sharing; we focus on building a
practical anonymizing overlay. Furthermore, our ideas about node
reuse, the graph construction algorithm, and churn resilience are all
different from secret sharing.
3 Model & Assumptions
(a) Goals: This paper aims to hide the source and destination
identities, as well as the message content, from both external
adversaries and the relay nodes. Further, the destination also does
not know the identity of the actual source. Said differently, we are
interested in the same type of anonymity exhibited in onion routing,
where a relay node cannot identify the source or the destination, or
decipher the content of the message; all it knows are its previous
and next hops.
We also want a system that is practical and simple to deploy in a
dynamic and unmanaged peer-to-peer overlay. The design should deal
effectively with node churn. It must not need a trusted third party
or a public key infrastructure, and preferably should not use any
public key cryptography. The system also should not impose a heavy
load on individual overlay nodes or require them to provide much
bandwidth.
(b) Threat model: We assume an adversary
who can observe a fraction of network traffic, operate relay nodes of
his own, and compromise some fraction of the relays. Further, the
compromised relays may also collude among themselves. Like prior
proposals for low-latency anonymous routing, we do not address a
global attacker who can snoop on all links in the
network [12,21,15,31]. Such a global attacker is
unlikely in practice. We also assume that the attacker cannot snoop on
all paths leading to the destination. If this latter assumption is
unsatisfied, i.e., the attacker can snoop on all of the destination's
traffic, the attacker can decode the content of the message but cannot
identify the source of the message.
(c) Assumptions: We assume the source has
an uncompromised IP address to access the Internet, 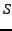 . Additionally,
we assume the source has access to one or more IP addresses from which
she can send. These IPs, which we call pseudo-sources . Additionally,
we assume the source has access to one or more IP addresses from which
she can send. These IPs, which we call pseudo-sources 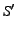 , should
not be on the same local network as , should
not be on the same local network as 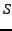 . We assume that the source
has a shared key with each of the pseudo-sources and communicates with
them over a secure channel. . We assume that the source
has a shared key with each of the pseudo-sources and communicates with
them over a secure channel.
We believe these assumptions are reasonable. Many people have
Internet access at home and at work or school, and thus can use one of
these addresses as the source and the rest as pseudo-sources. Even
when the user has only one IP address, she is likely to have a spouse,
a friend, or a parent whose IP address she can use. When none of that is
available, the user can go to an Internet cafe and use her home
address as the source and the cafe's IP as a pseudo-source.
Note that the pseudo-sources cannot identify the destination or
decipher the content of the message. They can only tell that the
source is sending an anonymous message. In our system, we assume that
the source wants to keep the pseudo-sources anonymous because they are
personally linked to her, i.e., we protect the anonymity of the
pseudo-sources in the same way as we protect the anonymity of the
source. We conservatively assume that if the anonymity of any one of
them is compromised then the source anonymity is also compromised.
Thus, in the rest of this paper, the anonymity of the source comprises
the anonymity of all pseudo-sources.
The design of information slicing involves answering three questions:
- How do we send a confidential message without keys?
- How do we construct an anonymous overlay path?
In particular, how do we hide the identities of the source and destination
from the overlay nodes along the path and also hide the identity of the source
from the destination?
- How do we make the protocol resilient to node churn?
We address each of these questions in the following sections, starting with
message confidentiality.
Figure:
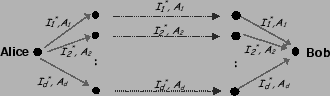 |
1 Confidentiality Without Keys
Information slicing enables a source to send a confidential message to
a destination without knowing the destination's key. Consider the
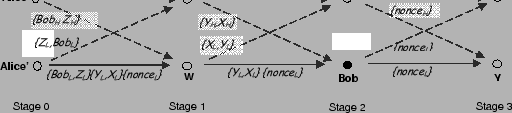
scenario in Fig. 1. Alice wants to send the message
``Let's meet at 5pm'' to Bob. Alice divides the message into
 pieces, e.g., pieces, e.g.,  ``Let's meet'' and ``Let's meet'' and  ``at
5pm'' when ``at
5pm'' when 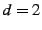 , so that the original message can be recovered only
when a node has access to all , so that the original message can be recovered only
when a node has access to all  pieces. We call this process slicing the message. pieces. We call this process slicing the message.
Sending a message slice in the clear is undesirable, as the slice may
expose partial information to intermediate nodes along the path. For
example, a node that sees  ``Let's meet'' knows that Alice
and Bob are arranging for a meeting. Thus, Alice multiplies the
message vector ``Let's meet'' knows that Alice
and Bob are arranging for a meeting. Thus, Alice multiplies the
message vector
 with a random but
invertible with a random but
invertible 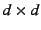 matrix matrix 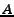 and generates and generates  slices which
constitute a random version of the message: slices which
constitute a random version of the message:
Then, Alice picks  disjoint overlay paths to Bob. She sends on
path disjoint overlay paths to Bob. She sends on
path 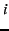 both the slice both the slice  and and 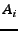 , where , where 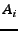 is row is row 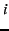 of
matrix of
matrix 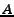 . An intermediate node sees only some random values . An intermediate node sees only some random values  and and
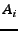 , and thus cannot decipher the content of the message.
Once Bob receives all slices, he decodes the original message as: , and thus cannot decipher the content of the message.
Once Bob receives all slices, he decodes the original message as:
Figure:
 |
2 Anonymous Routing Without Keys
Next, assume that Alice wants to send her message anonymously. How
can Alice set up an anonymous path without keys? Each node along an
anonymous path should know its previous hop and its next hop but
nothing more. In onion routing, a node along the path learns its next
hop from its previous hop - its parent. Though the parent delivers
this information to its child, it cannot access it itself because the
information is encrypted with the child's public key. In the absence
of keys, the path cannot be included in the message, as that allows
any intermediate node to learn the whole path from itself to the
destination. We need an alternative method to tell a node about its
next hop without revealing this information to other nodes,
particularly parent nodes.
Our approach to anonymity without keys relies on a simple idea:
anonymity can be built out of confidentiality. For anonymous
communication, the source needs to send to every relay node along the
path its routing information (i.e., its next hop) in a confidential
message, accessible only to the intended relay. Information slicing
enables a source to send such confidential messages without keys.
Using information slicing for anonymity, however, is challenging. To
send a particular node the identity of its next hop along different
anonymous paths, one needs to anonymously tell each node along these
paths about its own next hop. This requires an exponential number of
disjoint paths, and thus an exponential number of nodes.
To avoid exponential blow-up, it is essential that the source
constructs efficient forwarding graphs that reuse the overlay nodes
without giving them too much information.
The construction of such graphs in the general case is discussed
in §4.2.1, but we first explain a simple example to
give the reader an intuition about how the protocol works.
1 Example
Alice wants to send an anonymous message to Bob. Alice retrieves the
DNS names of a few overlay nodes that she or her friends have used in
the past to download music via a P2P file-sharing network. She can
use DNS to retrieve the IP addresses of these overlay nodes. Alice
does not know the public keys of the overlay nodes, or whether they
have keys. She does, however, know that the software of the
peer-to-peer overlay supports information slicing.
Alice has Internet at home and work, and hence has access to two IP
addresses:  and and 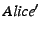 . Alice arranges the overlay nodes
into stages. Let's say she uses the graph in
Fig. 2, which contains 3 stages (path length . Alice arranges the overlay nodes
into stages. Let's say she uses the graph in
Fig. 2, which contains 3 stages (path length
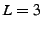 ), each containing 2 nodes (split factor ), each containing 2 nodes (split factor 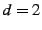 ) (we will show how
to pick appropriate values for ) (we will show how
to pick appropriate values for 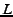 and and  in §6). The in §6). The
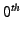 stage is the source stage itself. Each node in this graph is
connected to every node in its successive stage. Note that the
destination node, i.e. Bob's node, is randomly assigned to one of the
stages in the graph. stage is the source stage itself. Each node in this graph is
connected to every node in its successive stage. Note that the
destination node, i.e. Bob's node, is randomly assigned to one of the
stages in the graph.
Alice needs to send to each relay node the IP addresses of its next
hops, without revealing this information to other nodes. To do so, she
splits each IP into two pieces and sends this information over two
paths. Alice could have split each IP address to its most significant
and least significant words. This, however, is undesirable as the most
significant word may indicate the owner of the IP prefix. Instead
Alice first transforms the IP addresses of the relay nodes by
multiplying each address by an invertible matrix 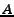 of size of size 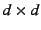 (i.e., (i.e.,  ). (For simplicity, assume that ). (For simplicity, assume that 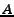 is
known to all nodes; in §4.3, we explain how the sender
anonymously sends is
known to all nodes; in §4.3, we explain how the sender
anonymously sends 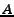 to the relays on the graph.) Let to the relays on the graph.) Let  and and
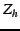 be the low and high words of the IP address of node be the low and high words of the IP address of node 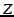 ; Alice
splits the IP address as follows: ; Alice
splits the IP address as follows:
 |
(1) |
She sends  and and  to node to node 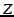 's parents, 's parents,  and and 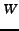 , along
two different paths. , along
two different paths.
Fig. 2 shows how messages are forwarded so that
each node knows no more than its direct parents and children.
Consider an intermediate node in the graph, say  . It receives the
message `` . It receives the
message ``
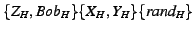 '' from its first
parent. It receives `` '' from its first
parent. It receives ``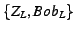 '' from its second
parent. After receiving both messages, '' from its second
parent. After receiving both messages,  can discover its
children's IP addresses as follows: can discover its
children's IP addresses as follows:
 |
(2) |
But  cannot, however, identify the children of its children (i.e.,
the children of nodes cannot, however, identify the children of its children (i.e.,
the children of nodes 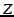 and and  ) because it misses half the bits
in these addresses, nor does it know the rest of the graph. Node ) because it misses half the bits
in these addresses, nor does it know the rest of the graph. Node  also does not know that Bob is the destination and Alice is the
sender. From its perspective, Alice may have received the message
from someone upstream, and Bob may be just another forwarder.
also does not know that Bob is the destination and Alice is the
sender. From its perspective, Alice may have received the message
from someone upstream, and Bob may be just another forwarder.
You might be wondering how the graph in Fig. 2
will be used to anonymously send data to Bob. Indeed, as it is, Bob
does not even know he is the intended destination; but this is easy to
fix. In addition to sending each node its next-hop IPs, Alice sends
him: (1) a symmetric secret key, (2) and a flag indicating whether he
is the destination. Similar to the next-hop IPs, the key and the flag
of each node are split along disjoint paths, and thus inaccessible to
other nodes. To send a confidential data message, Alice encrypts the
data with the key she sent to Bob during the route setup phase, chops
the data into  pieces, and forwards the pieces along the forwarding
graph to Bob. Once Bob receives the pieces, and forwards the pieces along the forwarding
graph to Bob. Once Bob receives the  slices of the data, he can
decode the encrypted data and invert the encryption using the key
previously sent to him. No other node can decipher the data even if it
gets all slices of the data, he can
decode the encrypted data and invert the encryption using the key
previously sent to him. No other node can decipher the data even if it
gets all  slices. slices.
Table 1:
Variables used in the paper.
|
|
3 Protocol Specification
This section rigorously describes our protocol. Our anonymous routing
protocol delivers packets along a forwarding graph as explained
in §4.2.1. The protocol has two phases. First, the source
anonymously and confidentially informs each of the relay nodes on the
graph of its forwarding information, i.e., it establishes the graph.
Second, the source uses the forwarding graph to send data. If the
source does not need to send much data, it is possible to collapse the
two phases together and concatenate the data slices with the slices
that build the graph. Before delving into the details of the protocol,
we refer the reader to Table 1, which describes the
variables used in the rest of the paper.
Figure:
 |
Let  be one of the nodes in the forwarding graph. be one of the nodes in the forwarding graph. 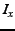 is the
routing information the source needs to anonymously deliver to
node is the
routing information the source needs to anonymously deliver to
node  . . 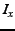 consists of the following fields: consists of the following fields:
Figure:
 |
The source chops the node information 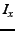 into into  blocks of blocks of
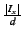 bits
each and constructs a bits
each and constructs a  length vector, length vector, 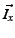 .
Further, it transforms .
Further, it transforms 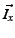 into coded information
slices using a full rank into coded information
slices using a full rank 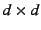 random matrix random matrix 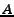 as follows: as follows:![[*]](footnote.png)
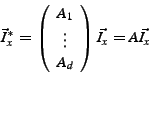 |
(3) |
The source concatenates each element in
 with the row of the
matrix with the row of the
matrix 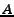 that created it (i.e., it concatenates that created it (i.e., it concatenates  with with 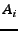 ).
The result is what we call an information slice.
The source delivers the ).
The result is what we call an information slice.
The source delivers the  slices to node slices to node  along disjoint paths. along disjoint paths.
Fig. 3 shows the format of a packet used in our system.
In addition to the IP header,
a packet has a flow-id, which allows the
node to identify packets from the same flow and decode them together.
The packet also contains 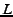 slices.
The first slice is always for the node that receives the packet.
The other slices are for nodes downstream on the forwarding graph. slices.
The first slice is always for the node that receives the packet.
The other slices are for nodes downstream on the forwarding graph.
4 Constructing the Forwarding Graph
The source constructs a forwarding graph that routes the information slices
to the respective nodes along vertex disjoint paths, as explained in Algorithm 1.
![\begin{algorithm}
% latex2html id marker 673
[ht!]
{\footnotesize
\caption{I...
...n $e$
\ENDFOR
\ENDFOR
\vskip -0.15in
\end{algorithmic}
}
\end{algorithm}](img69.png)
We demonstrate the algorithm by constructing such a graph in
Fig. 4, where 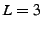 and and 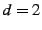 .
The source starts with the .
The source starts with the  nodes in
the last stage, nodes in
the last stage,  and and  . It assigns both the slices, . It assigns both the slices,
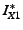 , , 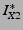 to to  .
The source then has to decide from whom node .
The source then has to decide from whom node  will receive its slices.
The source goes through the preceding stages, one by one,
and distributes will receive its slices.
The source goes through the preceding stages, one by one,
and distributes
 among the among the  nodes at each stage.
The distribution can be random as long as each node receives only one of the slices.
The path taken by slice nodes at each stage.
The distribution can be random as long as each node receives only one of the slices.
The path taken by slice 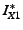 to
reach to
reach  can be constructed by tracing it through the graph.
For e.g., the slice can be constructed by tracing it through the graph.
For e.g., the slice 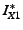 traverses traverses
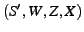 , which is disjoint from the path taken by , which is disjoint from the path taken by 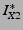 , i.e., , i.e.,  .
The source repeats the process for
the slices of .
The source repeats the process for
the slices of  , and for the slices of every node in all the other stages. , and for the slices of every node in all the other stages.
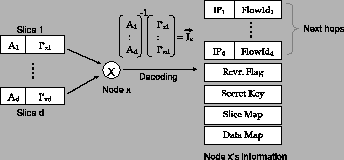
5 Decoding the Information Slices
A node decodes its information from the  slices it receives from its
parents, as shown in Fig. 5.
The first slice in every packet that node slices it receives from its
parents, as shown in Fig. 5.
The first slice in every packet that node  receives is for itself. It consists of
one of the receives is for itself. It consists of
one of the  -slices of -slices of  's information, 's information,  , and the row of the
transform matrix that helped create it, , and the row of the
transform matrix that helped create it, 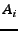 .
Node .
Node  constructs the vector constructs the vector
 from the from the
 slices it receives, and
assembles a slices it receives, and
assembles a 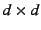 matrix matrix
![$A = {[A_{1}; \ldots; A_{d}]}$](img79.png) from the
from the  rows of the transform matrix sent in the slices.
Then, node rows of the transform matrix sent in the slices.
Then, node  computes its information vector, computes its information vector, 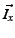 , as , as
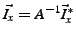 . .
Figure:
 |
After the relay decodes its own information, it has to decide what to
send to each one of its children. As is apparent from
Figs. 2 and 4, a relay does
not send the same information slices to all of its  children. The
relay needs a map that tells it which of the information slices it
received from its parents goes to which child, and in what order. This
information is provided by the source in the slice-map. children. The
relay needs a map that tells it which of the information slices it
received from its parents goes to which child, and in what order. This
information is provided by the source in the slice-map.
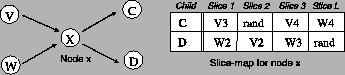
Fig. 6 shows an example slice-map. The slice-map is
a 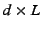 matrix that tells the relay how to construct the
packets it sends to its children. For example, in
Fig. 6, node matrix that tells the relay how to construct the
packets it sends to its children. For example, in
Fig. 6, node  has received 2 packets from its
parents. The number of slices in each packet is fixed to the path
length has received 2 packets from its
parents. The number of slices in each packet is fixed to the path
length  . Note that . Note that  should first extract its own slice from
each of the packets, which is the first slice in the packet, as
explained in §4.3.5. The other three slices in each packet
are to be forwarded downstream, as prescribed by should first extract its own slice from
each of the packets, which is the first slice in the packet, as
explained in §4.3.5. The other three slices in each packet
are to be forwarded downstream, as prescribed by  's slice-map. For
example, the figure shows that the third slice in the packet received
from 's slice-map. For
example, the figure shows that the third slice in the packet received
from  should be the first slice in the packet sent to node should be the first slice in the packet sent to node 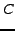 .
Entries labeled ``rand'' refer to padding slices with random bits that
are inserted by the relay node to replace its own slices and maintain
a constant packet size. .
Entries labeled ``rand'' refer to padding slices with random bits that
are inserted by the relay node to replace its own slices and maintain
a constant packet size.
Additionally, all packets headed to a child node should contain the
child node's slice as the first slice. The source constructs the slice
maps of the parent nodes such that the packets meant for the child
node always have the child node's slice as the first slice in the
packet. Also the child node needs to be able to identify which  packets go together. The source arranges for all of the parent relays
to use the same flow-id for packets going to the same child. The
parent learns these flow-ids as part of its information, as shown in
Fig. 5.
packets go together. The source arranges for all of the parent relays
to use the same flow-id for packets going to the same child. The
parent learns these flow-ids as part of its information, as shown in
Fig. 5.
7 Data Transmission
Once the forwarding graph is established, the source can send
anonymous data messages to the destination until it explicitly
terminates the connection or the routing information times out. Also
the destination can use a similar procedure to transmit to the source
along the reverse path.
The source encrypts each data message with the key it sent to the
destination node. Then it chops the data message into  pieces,
converts them into pieces,
converts them into  slices and multicasts the slices to the nodes
in the first stage of the forwarding graph. Each relay node in the
first stage receives all slices and multicasts the slices to the nodes
in the first stage of the forwarding graph. Each relay node in the
first stage receives all  data slices, but they cannot multicast
whatever they receive to the nodes in the next stage, since each child
then will receive data slices, but they cannot multicast
whatever they receive to the nodes in the next stage, since each child
then will receive 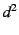 data slices leading to bandwidth overhead. On
the other hand, if each node forwards a random slice to each of its
children, then each child will get data slices leading to bandwidth overhead. On
the other hand, if each node forwards a random slice to each of its
children, then each child will get  data slices; but these slices
may overlap and thus be useless. To solve the problem, the source
sends each relay a data-map as part of its information. The data-map
tells the node how to forward the data slices between each
parent-child pair. The data map is very similar to the slice map shown
in Fig. 6, except that instead of slice numbers the
entries correspond to data packets. The source picks the entries in
the data-map to ensure that each child gets all useful data slices,
and no more. Each node in the graph including the destination therefore
gets data slices; but these slices
may overlap and thus be useless. To solve the problem, the source
sends each relay a data-map as part of its information. The data-map
tells the node how to forward the data slices between each
parent-child pair. The data map is very similar to the slice map shown
in Fig. 6, except that instead of slice numbers the
entries correspond to data packets. The source picks the entries in
the data-map to ensure that each child gets all useful data slices,
and no more. Each node in the graph including the destination therefore
gets  slices, but since the data slices are encrypted using the
destination's keys, only the destination can recover the original data. slices, but since the data slices are encrypted using the
destination's keys, only the destination can recover the original data.
Figure:
 |
4 Resilience to Churn and Failures
Overlays with open membership suffer from churn because nodes join
and leave frequently. Node churn causes data loss. The standard way
to deal with loss is to add redundancy. The challenge, however, is to
maximize the probability of recovery for the same amount of
redundancy. Communication systems typically use coding to
achieve this goal. Our design naturally extends the codes used to
provide confidentiality to also provide resilience against churn and
failures.
(a) Basic idea:
Take a vector of  elements elements
 and
multiply it by a random matrix and
multiply it by a random matrix  of rank of rank  and size and size 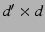 where
where  . The result will be a a vector of . The result will be a a vector of  elements, elements,
 ; it is a redundant version of your
original vector. What is interesting about this process is that it is
possible to retrieve the original message from any ; it is a redundant version of your
original vector. What is interesting about this process is that it is
possible to retrieve the original message from any  elements
of elements
of  and their corresponding rows in the
matrix [18]. and their corresponding rows in the
matrix [18].
(b) Adding redundancy to graph establishment phase:
Instead of slicing the per-node information into  independent
pieces that are all necessary for decoding, we use independent
pieces that are all necessary for decoding, we use  dependent
slices. Replace Eq. 3 with: dependent
slices. Replace Eq. 3 with:
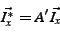 |
(4) |
where  is a is a 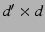 matrix with the property that any matrix with the property that any  rows of
rows of 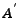 are linearly independent. The source picks are linearly independent. The source picks  disjoint paths to send the message. A node can recover its information
from any
disjoint paths to send the message. A node can recover its information
from any  out of out of  slices that it successfully receives. slices that it successfully receives.
(c) Adding redundancy to the data transfer phase:
As mentioned earlier, the source encrypts the data with the symmetric
key it sent to the destination during path establishment. The source
then chops the encrypted message into  pieces, creating a message
vector pieces, creating a message
vector 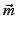 . Before it sends the message, however, it multiplies
it by a random matrix . Before it sends the message, however, it multiplies
it by a random matrix  of size of size 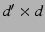 and rank and rank  , where , where
 . This creates . This creates  data slices that the source sends along data slices that the source sends along
 disjoint paths. The destination can recover the original
information as long as it receives any disjoint paths. The destination can recover the original
information as long as it receives any  slices out of the slices out of the  data
slices the source created. data
slices the source created.
The resilience scheme above is far from optimal.
Consider an example where 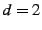 and and 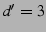 , and
assume that at some stage , and
assume that at some stage  along the path, one of the three relays
fails. Its children in stage along the path, one of the three relays
fails. Its children in stage 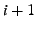 will receive two data slices
instead of three. This is sufficient for recovering the original
data. The problem, however, is that the redundancy is lost. Unless
the redundancy is restored, downstream relays cannot recover from any
additional failures. will receive two data slices
instead of three. This is sufficient for recovering the original
data. The problem, however, is that the redundancy is lost. Unless
the redundancy is restored, downstream relays cannot recover from any
additional failures.
We use network coding to solve the problem.
Network coding allows intermediate nodes to code the
data too.
In our scheme, during the data transmission phase,
a relay can easily restore the redundancy after its parent
fails. To do so, the relay creates a linear combination of the slices it
received, i.e.,
 , where , where 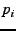 are random
numbers. The relay also creates are random
numbers. The relay also creates
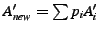 , where , where
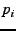 are the same numbers above. The new slice is the
concatenation of are the same numbers above. The new slice is the
concatenation of 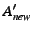 and and  and can effectively replace
the lost slice. Any relay that receives and can effectively replace
the lost slice. Any relay that receives  or more slices can
replace all lost redundancy.
Thus, with a small amount of redundancy, we can survive many node failures
because at each stage the nodes can re-generate the lost redundancy. or more slices can
replace all lost redundancy.
Thus, with a small amount of redundancy, we can survive many node failures
because at each stage the nodes can re-generate the lost redundancy.
5 Security Analysis
Instead of standard key-based encryption, our scheme uses information
slicing. To understand the level of confidentiality, i.e., the
security obtained with such an approach, we estimate the amount of
information a malicious node can glean from the messages it receives.
We borrow the following definition
from [8,28].
A pi-secure information slicing algorithm implies that to
decrypt a message, an attacker needs to obtain all  information
slices; partial information is equivalent to no information at all.
The proof of the following lemma is in a technical
report [19]: information
slices; partial information is equivalent to no information at all.
The proof of the following lemma is in a technical
report [19]:
Lemma 5.1
Information slicing is pi-secure.
We note that there are many types of security, e.g., cryptographic
security, pi-security, and information theoretic security. The
strongest among these is information theoretic security. Information
slicing can be made information theoretically secure, albeit with
increased overhead. Instead of chopping the data into  parts and
then coding them, we can combine each of the parts and
then coding them, we can combine each of the  parts with parts with 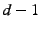 random parts. This will increase the space required
random parts. This will increase the space required  -fold, but
provides extremely strong information-theoretic security. -fold, but
provides extremely strong information-theoretic security.
6 Evaluation of Anonymity
The basic threat to anonymity in peer-to-peer overlays are attackers
who compromise the overlay network. They can hack nodes, operate their
own nodes, or eavesdrop on links to do traffic analysis. They can
further collude to compromise anonymity. In this section we evaluate
the anonymity of information slicing against such adversaries via
simulations.
The anonymity of a system is typically measured by its
entropy [25,11],![[*]](footnote.png) and is usually
expressed in comparison with the maximum anonymity possible in such a
system, i.e.: and is usually
expressed in comparison with the maximum anonymity possible in such a
system, i.e.:
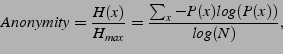 |
(5) |
where 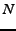 is the total number of nodes in the network, is the total number of nodes in the network,  is the
probability of a node being the source/destination, and is the
probability of a node being the source/destination, and
 is the maximum entropy that occurs when the attacker
has no information. Anonymity is a number between is the maximum entropy that occurs when the attacker
has no information. Anonymity is a number between  and and  . For
example, the source is perfectly anonymous when it is equally likely
to be any node in the network, in which case . For
example, the source is perfectly anonymous when it is equally likely
to be any node in the network, in which case
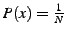 and
the and
the
 . .
Note that
 is quite high. It does not mean that the
attacker knows the source or the destination with probability is quite high. It does not mean that the
attacker knows the source or the destination with probability 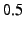 . Rather it
means the attackers are still missing half the information necessary
to discover the anonymous source or destination. . Rather it
means the attackers are still missing half the information necessary
to discover the anonymous source or destination.
2 Simulation Environment
We would like to measure how the anonymity of the source and
destination depends on the strength of the attackers. We simulate a
scenario in which the attacker subverts a fraction 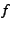 of the overlay
nodes and the subverted nodes collude together. We assume that all
attackers collude and consider them together as one powerful attacker.
Note that this scenario subsumes attacks in which the attacker
eavesdrops (i.e. does traffic analysis) on a fraction of the links
because compromising a node is always a stronger attack than snooping
on its input and output links. Further, this also subsumes
``intersection'' attacks in which attackers across multiple stages
collude to compromise anonymity. of the overlay
nodes and the subverted nodes collude together. We assume that all
attackers collude and consider them together as one powerful attacker.
Note that this scenario subsumes attacks in which the attacker
eavesdrops (i.e. does traffic analysis) on a fraction of the links
because compromising a node is always a stronger attack than snooping
on its input and output links. Further, this also subsumes
``intersection'' attacks in which attackers across multiple stages
collude to compromise anonymity.
We assume that the source picks the relays randomly from the set of
all nodes in the network, and that every node appears only once in the
anonymity graph. These assumptions degrade anonymity, making our
results conservative.
In each simulation, we randomly pick 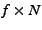 nodes to be
controlled by the attacker, where nodes to be
controlled by the attacker, where 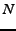 is the number of overlay nodes.
Then we pick is the number of overlay nodes.
Then we pick  nodes randomly and arrange them into nodes randomly and arrange them into 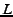 stages of
stages of  nodes each. We randomly pick the destination out of the
nodes on the graph. We identify the malicious nodes in the graph and
analyze the part of the graph known to the attacker. Once we know the
part of the graph known to the attacker, the anonymity for that
particular scenario is computed. The details of how to compute
source and destination anonymity for a particular simulation scenario
are kept in a technical report [19].
Depending on the random assignment, the part of the graph known to the
attacker will vary and so will the anonymity. Hence the simulation
procedure is repeated nodes each. We randomly pick the destination out of the
nodes on the graph. We identify the malicious nodes in the graph and
analyze the part of the graph known to the attacker. Once we know the
part of the graph known to the attacker, the anonymity for that
particular scenario is computed. The details of how to compute
source and destination anonymity for a particular simulation scenario
are kept in a technical report [19].
Depending on the random assignment, the part of the graph known to the
attacker will vary and so will the anonymity. Hence the simulation
procedure is repeated  times and the average anonymity is
plotted. times and the average anonymity is
plotted.
Figure:
 |
In this section we evaluate the anonymity provided by information
slicing and compare it to Chaum mixes. Consider attackers who
compromise a fraction 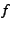 of all nodes or links and collude together
to discover the identities of the source and destination.
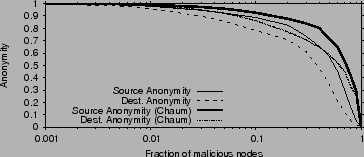
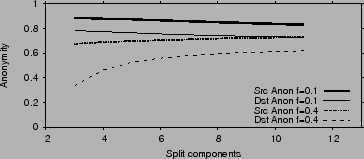
Fig. 7 plots the anonymity of the source and
destination as functions of the fraction of compromised nodes, for the
case of of all nodes or links and collude together
to discover the identities of the source and destination.
Fig. 7 plots the anonymity of the source and
destination as functions of the fraction of compromised nodes, for the
case of
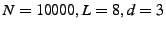 . When less than . When less than  of the nodes in the
network are malicious, anonymity is very high and comparable to Chaum
mixes, despite no keys. As the fraction of malicious nodes increases,
the anonymity falls. But even when the attackers control half of the
nodes, they are still missing half the information necessary to detect
the source or destination. Destination anonymity drops faster with
increased of the nodes in the
network are malicious, anonymity is very high and comparable to Chaum
mixes, despite no keys. As the fraction of malicious nodes increases,
the anonymity falls. But even when the attackers control half of the
nodes, they are still missing half the information necessary to detect
the source or destination. Destination anonymity drops faster with
increased  because discovering the destination is possible if the
attacker controls any stage upstream of the destination, while
discovering the source requires the attacker to control stage 1, as
we show in [19]. because discovering the destination is possible if the
attacker controls any stage upstream of the destination, while
discovering the source requires the attacker to control stage 1, as
we show in [19].
Figure:
 |
We evaluate how anonymity is affected by the parameters under the
source's control: how many slices each piece of information is split
into and the number of stages in the routing graph.
Fig. 8 plots source and destination anonymity as
functions of the splitting factor  . When . When  is low, information
leakage is due primarily to the malicious nodes knowing their
neighbors on the graph. In this case, increasing is low, information
leakage is due primarily to the malicious nodes knowing their
neighbors on the graph. In this case, increasing  increases the
exposure of non-malicious nodes to attackers which results in a slight
loss of anonymity. When increases the
exposure of non-malicious nodes to attackers which results in a slight
loss of anonymity. When 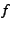 is high, information leakage is mainly
due to attackers being able to compromise entire stages. Hence,
increasing is high, information leakage is mainly
due to attackers being able to compromise entire stages. Hence,
increasing  increases anonymity. However, even an anonymity as low
as 0.5 is fairly strong; it means that the attacker is still missing
half the bits necessary to identify the source/destination. increases anonymity. However, even an anonymity as low
as 0.5 is fairly strong; it means that the attacker is still missing
half the bits necessary to identify the source/destination.
Figure:
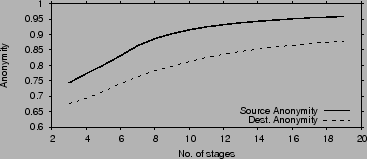 |
Fig. 9 plots the source and destination anonymity
as functions of the path length 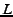 . Both source and destination
anonymities increase with . Both source and destination
anonymities increase with 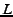 . The attacker knows the source and
destination have to be on the graph; thus, for moderate values of . The attacker knows the source and
destination have to be on the graph; thus, for moderate values of 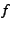 ,
putting more nodes on the graph allows the communicators to hide among
a larger crowd. ,
putting more nodes on the graph allows the communicators to hide among
a larger crowd.
Figure:
 |
We also evaluate how anonymity and churn resilience trade off against
each other. The theoretical analysis is
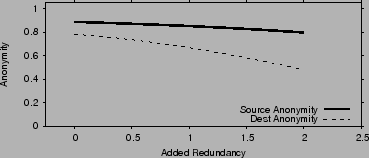
in [19]. Fig. 10 plots the source
and destination anonymity as functions of the redundancy added to
combat churn. Redundancy is calculated as 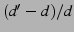 , and in the
figure , and in the
figure 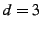 . As the added redundancy increases, it becomes more
likely that the attacker compromises an entire stage of nodes. Hence
destination anonymity decreases. Source anonymity is not much
affected because it depends on whether specifically the first stage is
compromised. . As the added redundancy increases, it becomes more
likely that the attacker compromises an entire stage of nodes. Hence
destination anonymity decreases. Source anonymity is not much
affected because it depends on whether specifically the first stage is
compromised.
We evaluate the performance of information slicing via a prototype
implementation run on the local and wide-area networks. Our wide-area
experiments use 256 PlanetLab nodes, including nodes in North America,
South America, Europe, and Asia. In each experiment, we pick a random
subset of the above nodes depending on the size of the graph being
set. We repeat each experiment  times by changing the randomly
chosen subset of PlanetLab nodes and we take the average of the
measured quantity. Our local-area experiments are performed on a 1
Gbps switched network with the nodes being 2.8 GHz Pentium boxes with
1 GB of RAM. times by changing the randomly
chosen subset of PlanetLab nodes and we take the average of the
measured quantity. Our local-area experiments are performed on a 1
Gbps switched network with the nodes being 2.8 GHz Pentium boxes with
1 GB of RAM.
1 Implementation and Benchmarks
We have built a prototype of information slicing in Python. It
includes two programs: an overlay daemon and a source utility. Each
overlay node runs a multi-threaded daemon that listens on a special
port. The daemon maintains a hash table keyed on the flow-id. For
each anonymous flow, the table contains all the relevant forwarding
information including the flow's next-hop IPs. When the daemon
receives a packet, it forks a thread to process the packet and
appropriately update the flow table. Additionally, the daemon
periodically garbage collects the flow table to remove stale
entries. The source utility program takes as input a list of willing
overlay nodes, and a few configuration parameters such as the path
length 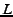 , the number of parallel paths , the number of parallel paths  , and the number of
independent slices , and the number of
independent slices  . .
The overhead of information slicing is low. We have performed
benchmarks on a Celeron  MHz machine with MHz machine with 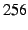 MB RAM connected to
the local MB RAM connected to
the local  Gbps network. Coding and decoding require on average Gbps network. Coding and decoding require on average  finite-field multiplications per byte. Hence, the maximum achievable
throughput is limited by how fast the multiplications can be
accomplished. For
finite-field multiplications per byte. Hence, the maximum achievable
throughput is limited by how fast the multiplications can be
accomplished. For 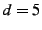 , coding takes on average , coding takes on average  per 1500B
packet, which limits the maximum output rate to per 1500B
packet, which limits the maximum output rate to 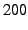 Mbps. The memory
footprint is determined by Mbps. The memory
footprint is determined by  , since we need the , since we need the  packets to
generate outgoing coded packets. Thus the memory consumed for packet
storage is packets to
generate outgoing coded packets. Thus the memory consumed for packet
storage is
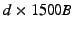 which is negligible. which is negligible.
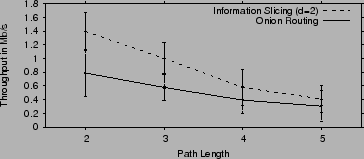
Fig. 11 and 12 show the throughput
obtained when a transfer is run for 150 seconds using onion routing
and our protocol for the local area network and PlanetLab
respectively. The onion routing protocol uses computationally
efficient symmetric session keys for the data transfer; public key
cryptography is used only for the route setup. Both protocols use
1500 byte packets. On the local-area network
(Fig. 11), our protocol can send at about 40-60
Mb/s. The parallelism in our protocol allows it to achieve higher
throughput than onion routing.
On PlanetLab (Fig. 12), the nodes are
highly loaded, reducing the achievable throughput. Yet, the transfer
achieves about 1 Mb/s, which is a good throughput for the wide-area network.
Figure:
 |
Figure:
 |
The overhead of information slicing in path setup is higher compared
to onion routing. Specifically, since each message is split into  components, and each node outputs
components, and each node outputs  packets in every round, the
total number of packets between any two stages is packets in every round, the
total number of packets between any two stages is 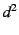 . For onion
routing . For onion
routing 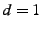 , whereas , whereas  can be varied in information slicing. But
on the other hand, information slicing delivers higher throughput,
since it used can be varied in information slicing. But
on the other hand, information slicing delivers higher throughput,
since it used  parallel paths to deliver the data. parallel paths to deliver the data.
Figure:
 |
We examine how the throughput scales as the number of sources using
the anonymizing overlay increases. Fig. 13 shows the
total throughput as a function of the average load on the
overlay nodes. The total throughput is the sum of the throughputs of
the anonymous flows in the experiment. Load is quantified as the
number of concurrent anonymous flows using the overlay. The experiment
is performed on a set of 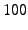 PlanetLab nodes that have long uptimes,
so that churn does not affect the result (for churn results
see 8). We set PlanetLab nodes that have long uptimes,
so that churn does not affect the result (for churn results
see 8). We set 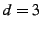 and and  , hence each
flow uses , hence each
flow uses 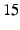 nodes from the set of nodes from the set of 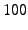 nodes. nodes.
The figure shows that, as load increases, the total throughput scales
linearly. At significantly high load, the throughput levels off and
the overlay reaches saturation. The saturation threshold is a
function of the used set of PlanetLab nodes and the loads imposed on
these nodes by other users/experiments. Information slicing therefore
scales well with the amount of load placed on the overlay up to
moderate loads.
Setup latency is measured end-to-end, from when the sender initiates
the route establishment until the receiver sends back an ack (the ack
is for measurement collection and not part of the protocol.)
Our protocol allows the receiver to be randomly placed anywhere in the
graph to obscure its identity. For purposes of our experiments,
however, we place the receiver in the last stage of
the graph, so that the measured setup times are the times to set up
the entire graph, not just those stages up to the receiver's stage.
Figure:
 |
Fig. 14 plots the average graph setup times on the
local-area network. As one would expect, the setup time increases with
increased path length 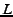 and splitting factor and splitting factor  . A large . A large  affects the setup time because a relay has to wait to hear from all of
its
affects the setup time because a relay has to wait to hear from all of
its  parents and thus, the delay at each stage will be dominated by
the slowest relay in that stage. In general however, the setup time
is less than a couple of seconds. Furthermore, for parents and thus, the delay at each stage will be dominated by
the slowest relay in that stage. In general however, the setup time
is less than a couple of seconds. Furthermore, for 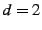 , the setup
time is a few hundred milliseconds. , the setup
time is a few hundred milliseconds.
We repeat the same experiments on PlanetLab to measure how much the
conditions in the wide area network affect our setup
times. Fig. 15 shows the average graph setup times in
that environment. The setup times have increased beyond their values
in the local-area network because of the larger RTT, but more
importantly because PlanetLab nodes have a high CPU utilization
leading up to the conference deadline. Despite this increase, the
setup time is still within a few seconds.
Figure:
 |
8 Evaluation of Churn Resilience
Churn is an inescapable reality of dynamic peer-to-peer overlay
networks. In §4.4 we presented a novel technique that
recreates lost redundancy to combat churn. Here we evaluate its
performance via analysis and an actual implementation. First we show
analytically how coding helps us achieve high resilience with a small
amount of added redundancy. Then we evaluate information slicing's
churn resilience on PlanetLab and show that it can successfully cope
with failures and make long anonymous transfers practical.
We first show the efficiency of our coding approach compared to onion
routing via analysis; but comparing it to standard onion routing would
be unfair, as onion routing does not have any redundancy added and it
would show very bad performance. Hence we compare it to a modified
version of onion routing which has the same amount of redundancy as
information slicing.
Imagine making onion routing resilient to failures by having the
sender establish multiple onion-routing paths to the destination. The
most efficient approach we can think of would allow the sender to add
redundancy by using erasure codes (e.g., Reed-Solomon codes) over
multiple onion routing paths. Assuming the number of paths is  ,
and the sender splits the message into ,
and the sender splits the message into  parts, she can then recover
from any parts, she can then recover
from any 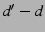 path failures. We call this approach onion
routing with erasure codes. Recall that in information slicing as
well, the sender adds redundancy by increasing the number of paths path failures. We call this approach onion
routing with erasure codes. Recall that in information slicing as
well, the sender adds redundancy by increasing the number of paths  , i.e., , i.e.,  slices of information are expanded to slices of information are expanded to  slices. But
the key difference in information slicing is that relays inside
the overlay network can regenerate lost redundancy. slices. But
the key difference in information slicing is that relays inside
the overlay network can regenerate lost redundancy.
To evaluate analytically, consider a message of 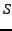 bytes. Suppose a sender has sent bytes. Suppose a sender has sent  bytes,
where bytes,
where 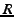 is the
amount of redundancy in your transfer. is the
amount of redundancy in your transfer. 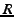 is also the
overhead in the system; it limits the useful throughput.
Now, let us compare the probability of successfully transferring the
data under our scheme and onion routing with erasure codes when the same amount
of redundancy is added.
In particular,
assume the path length is is also the
overhead in the system; it limits the useful throughput.
Now, let us compare the probability of successfully transferring the
data under our scheme and onion routing with erasure codes when the same amount
of redundancy is added.
In particular,
assume the path length is 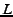 , and that failures are independent
and the probability of a node failing is , and that failures are independent
and the probability of a node failing is 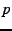 ,
the redundancy in both schemes is ,
the redundancy in both schemes is
 , hence , hence 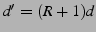 . .
Onion routing with erasure codes succeeds when there are at least  operational paths.
A path is operational if none of the nodes on that path fail. Thus, the probability of a path
success is operational paths.
A path is operational if none of the nodes on that path fail. Thus, the probability of a path
success is
 . The probability of the scheme succeeding is
the probability of having at least . The probability of the scheme succeeding is
the probability of having at least  non-failing paths, i.e., non-failing paths, i.e.,
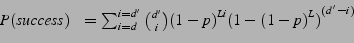 |
(6) |
The information slicing approach, on the other hand, can tolerate 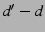 failures in each stage. The scheme succeeds if all stages succeed.
A stage succeeds if at least
failures in each stage. The scheme succeeds if all stages succeed.
A stage succeeds if at least  nodes in the stage do not fail, i.e., nodes in the stage do not fail, i.e.,
The slicing scheme succeeds if all stages succeed, i.e.:
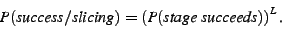 |
(7) |
Fig. 16 illustrates the two success probabilities as
a function of the amount of redundancy for 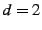 , and , and  . The
probability of a node failure during the transfer is set to . The
probability of a node failure during the transfer is set to 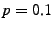 in
the top graph and in
the top graph and 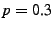 in the bottom graph. The figure shows that,
for the same amount of overhead, the slicing approach has a
substantially higher probability of successfully completing its
transfer. in the bottom graph. The figure shows that,
for the same amount of overhead, the slicing approach has a
substantially higher probability of successfully completing its
transfer.
Figure:
 |
Figure:
 |
We complement the analytical evaluation with real experiments on a failure-prone
overlay network, i.e., the PlanetLab network. We run our experiments
with all nodes in our PlanetLab slice including the ones which are very failure
prone. ``Failure-prone'' are nodes which are often inaccessible due to myriad reasons,
either due to heavy CPU overload or network disconnectivity. These nodes
have short ``perceived'' lifetimes of less than 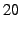 minutes, and are extremely likely to
fail during an experiment.
The rationale for picking such nodes is that the sender usually has a list of
overlay nodes, some of which are up and some are down. The sender
cannot ping the nodes to identify the operational ones because this might jeopardize its anonymity. minutes, and are extremely likely to
fail during an experiment.
The rationale for picking such nodes is that the sender usually has a list of
overlay nodes, some of which are up and some are down. The sender
cannot ping the nodes to identify the operational ones because this might jeopardize its anonymity.
We focus on the following question: ``Given PlanetLab churn rate and failures,
what is the probability of successfully completing a session that
takes  minutes?''
Given the throughput figures presented earlier, a minutes?''
Given the throughput figures presented earlier, a  -minute flow can
transfer over -minute flow can
transfer over 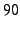 MB, which is typical of P2P file transfers.
We compare information slicing with the modified version of onion
routing which has redundancy added as described in the previous section. MB, which is typical of P2P file transfers.
We compare information slicing with the modified version of onion
routing which has redundancy added as described in the previous section.
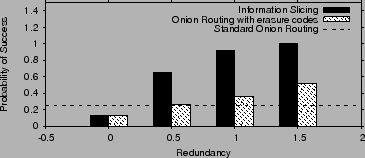
Fig. 17 compares the probability of successfully
finishing the transfer under our approach, standard onion routing (one
path), and onion routing with redundancy added using erasure codes.
As we saw in the previous section, for the same number of paths, onion
routing with erasure codes has the same level of redundancy as our
scheme. Redundancy is added by increasing the number of paths  , in this case the added redundancy , in this case the added redundancy 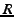 is given by is given by 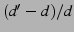 . The
results are for . The
results are for  and and 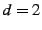 . We vary the level of added redundancy
by varying . We vary the level of added redundancy
by varying  , and measure the probability of successfully
completing a session lasting , and measure the probability of successfully
completing a session lasting  minutes. minutes.
The figure shows that with standard onion routing completing such a
transfer is extremely unlikely. The probability of success increases
with onion routing with erasure codes but stays relatively low. In
contrast, with information slicing, adding a little amount of
redundancy results in a very high success probability, making such
relatively long anonymous transfers practical.
9 Robustness to Attacks
The biggest threat to peer-to-peer anonymizing overlays are from attackers who
control nodes or can eavesdrop on links. Under conservative assumptions,
i.e., even after assuming that an attacker who can eavesdrop on links
leading to a node is as powerful as one who controls the node itself; we
have shown that information slicing achieves anonymity comparable to
Chaum mixes in §6. This section describes a few other
attacks and how we address them. These attacks are fairly
generic and apply to almost all anonymizers.
1 Limiting Malicious Nodes on the Graph
How does a sender choose relays for the anonymous graph it is setting
up? One may be tempted to choose nodes completely at random from all
available nodes; but an attacker could control large address spaces
and increase the likelihood that the sender chooses colluding
malicious nodes. To counter this attack, we leverage the structure of
the IP address space. While an adversary can potentially control as
many nodes as IP addresses to which he has access, these addresses are
rarely scattered uniformly through the IP address space or through
multiple autonomous systems (AS). IP addresses are divided into
prefixes that are allocated to various networks worldwide. The
prefixes appear in the inter-domain routing tables with their
corresponding routes. These routing tables are publicly
available from multiple vantage points [7]. It is
realistic to assume that the attacker cannot compromise a large
fraction of the inter-domain routing tables. Indeed if she can, then
the attack has already jeopardized the Internet connectivity. By
analyzing the publicly available routing tables, the sender can choose
its relay nodes to be under different ASes potentially in different
countries (e.g., Iran, US, China etc). This makes the above attack
significantly more difficult because the attacker now needs to control
many IP addresses belonging to many different ASes potentially spread
around the world. Though this is possible, it is much more
difficult. In the general case, picking overlay nodes that are
independent and are guaranteed not to collude is a very difficult
problem. Even if one knew the physical connectivity of the network, it
is still not possible to guarantee non-collusion. Picking nodes based
on their AS membership ensures that with high probability nodes are
unlikely to collude.
It is always possible for a
subverted relay to drop messages. It is also possible for a
malicious source to try to consume the resources of the overlay nodes,
denying other sources access to these resources. Overall, we believe that our
approach neither increases nor decreases the vulnerability of an
anonymizing overlay to denial of service; in comparison to onion
routing, our approach allows the sender to store a small state (the
per-node information) on the overlay nodes, but onion routing allows
the sender to force the overlay nodes to do CPU-expensive public key
cryptography.
In general, the best way to deal with denial of service
attacks on anonymizing systems is to increase the size of the
network. By allowing unmanaged peer-to-peer overlays with no trusted
authority, our scheme has the potential to increase the size of these
networks, thus increasing the resilience of the service.
Consider a sender who lives under a repressive government that censors
international online communications. The sender wants to
anonymously communicate with an outside destination. To do so, it has
to traverse the government's firewall.
There are two cases. First the sender knows a pseudo-source outside
the country. In this case, the sender splits the communication and
securely tunnels a slice or more to outside
pseudo-sources. The firewall, though it sees all slices, cannot
reconstruct the message because some slices are encrypted.
(Recall that a pseudo-source cannot read the message content or tell who the destination is.)
In the second case, the sender does not have access to a pseudo-source
outside the firewall. In this case,
the sender chooses some of the relays in some stage 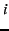 to be outside the country
and the rest inside -i.e., the firewall does not cut the
graph at a single stage. For the firewall to be able to decipher the
message, it needs to pick the right to be outside the country
and the rest inside -i.e., the firewall does not cut the
graph at a single stage. For the firewall to be able to decipher the
message, it needs to pick the right 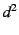 packets out of all packets
in a particular interval (say 0.5s).
These packets do not come from the same set of senders
(because of the cross-stage cut) and the bits in these packets are hard to correlate.
Furthermore, there are
potentially billions of packets traversing the firewall during that
interval. Picking the right packets out of all packets
in a particular interval (say 0.5s).
These packets do not come from the same set of senders
(because of the cross-stage cut) and the bits in these packets are hard to correlate.
Furthermore, there are
potentially billions of packets traversing the firewall during that
interval. Picking the right 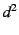 packets therefore is a very difficult problem. packets therefore is a very difficult problem.
There is always a tradeoff between robustness to attacks and increased overhead.
Most solutions either send excessive amount of traffic or increase complexity
making the system less usable. The right operation point usually depends on the
application scenario. Our system focuses on providing practical low-delay
anonymity for everyday applications rather than providing perfect anonymity at
all costs. As mentioned in §3 we cannot protect against a global
eavesdropper who can observe all traffic. Further if an attacker can snoop on
all links leading to the destination, message confidentiality is compromised.
But the attacker still cannot discover the identity of the sender.
Traffic analysis attacks become significantly harder to mount in a global
overlay with thousands of nodes and a large amount of normal filesharing
traffic. In predecessor attacks [30], the attacker forces frequent rebuilding
of paths and tries to identify the sender and destination by identifying
specific responders outside the overlay to which connections are made.
For this attack, the attacker needs to observe all traffic across the global
overlay which is unrealistic in practice. Murdoch et.al. [22] present an attack in which the
attacker pings nodes in the overlay and identifies how the load offered by the
adversary affects the delay of other anonymous communication streams at the
source node. The attacker has to ping potentially thousands of nodes in the
global overlay before he can observe any significant statistical
change in the senders anonymous communication. Further the large amount of P2P
filesharing traffic already present makes such attacks
based on statistical analysis hard to mount in a global overlay network. We describe below some other
specific traffic analysis attacks
and how our system protects against them.
(a) Inserting a pattern in the data:
Colluding attackers who are not in consecutive stages might try to track a
connection by inserting a particular pattern in the packet and
observing the path of the inserted pattern downstream.
To prevent such attacks the sender makes the nodes along
the path intelligently scramble each slice such that no pattern can
percolate through the network. We will demonstrate the algorithm through a
single slice  , which belongs to an intermediate
node , which belongs to an intermediate
node 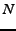 in stage in stage 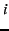 . As we have seen before this slice passes through . As we have seen before this slice passes through 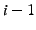 nodes before it reaches node
nodes before it reaches node 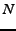 .
Before transmitting the slice, the sender passes the
slice through .
Before transmitting the slice, the sender passes the
slice through 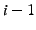 random transformations random transformations
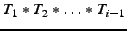 successively. Now the sender has to ensure that when node
successively. Now the sender has to ensure that when node 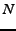 receives the
slice, all of these random transformations have been removed, else the slice
will be useless to node receives the
slice, all of these random transformations have been removed, else the slice
will be useless to node 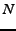 . Therefore the sender confidentially sends each of the inverses
of the . Therefore the sender confidentially sends each of the inverses
of the 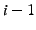 random transformations applied above to the random transformations applied above to the 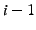 nodes which handle this slice.
Each intermediate node applies one inverse transform to the slice nodes which handle this slice.
Each intermediate node applies one inverse transform to the slice  , hence by
the time the slice reaches node , hence by
the time the slice reaches node 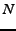 , the slice is through , the slice is through 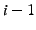 inverse
transformations and is back to its original
unmodified state. Node inverse
transformations and is back to its original
unmodified state. Node 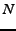 can then decode and recover his own information. can then decode and recover his own information.
The source repeats this process for all slices. This ensures that a slice is guaranteed to not look the same
at any two links in the graph. Hence though the attacker
might insert a particular pattern, the pattern will change in the immediate next
stage without the attacker knowing how it changed. As a result, colluding
non-consecutive attackers never see the same bit pattern, thereby nullifying the attack.
(b) End-to-End Time analysis attacks:
The attacker may study the timing pattern in the traffic at various nodes in the overlay network
in an attempt to identify where an anonymous flow enters and exits the overlay.
Feamster et al [14] have shown that such an attack is possible in
the Tor network.
In particular, they report that Tor [12]
has many nodes in the same AS. Hence,
it is probable that the entry and exit nodes of an anonymous flow end up in the same AS.
If this AS is adversarial, it can conduct timing analysis attacks to
determine the sender and receiver.
This attack becomes much harder in a large peer-to-peer overlay.
In a large peer-to-peer network spread across the world, it is unlikely that a
significant fraction of the nodes belong to the same AS.
Furthermore, the node
selection strategy outlined in §9.1 ensures that nodes are
picked from different ASes, hence it is significantly hard for any single AS to
mount a timing analysis attack.
(c) Resilience to packet size analysis:
Looking at Fig. 4, the reader may
think that the packet size decreases as it travels along the forwarding
graph, and thus the attacker can analyze the position of a relay on
the graph by observing the packet size. This is not the case, however. As explained in §4.3.4,
each relay replaces its own information slices with random padding and
shuffles the slices according to the sender's instructions sent in
the slice-map. The map ensures that the packet size stays constant.
Anonymity spans a large design space; different anonymizers optimize
for different objectives with corresponding tradeoffs. Information
slicing presents a unique point in this design space. It provides
confidentiality, anonymity and churn resilience without public key
cryptography but with the tradeoff that the anonymity and
confidentiality guarantees are slightly weaker than if we had public
keys. We have analyzed the security and anonymity of the protocol and
shown that it presents good guarantees against a variety of important
attacks. We have also implemented the protocol, run it over
PlanetLab, and shown that it is feasible and robust to node churn and
failures. We believe information slicing simplifies the
implementation and deployment of global peer-to-peer anonymizing
networks, which is an important step towards scalable and practical
online privacy.
We thank Jeremy Stribling, Vinod Vaikuntanathan, Hariharan Rahul,
Maxwell Krohn and Frank Dabek for their comments on the paper. Cohen
and Katabi are supported by the NSF Career Award CNS-0448287, whereas
Katti is supported by NSF award CNS-0627021. The opinions and
findings in this paper are those of the authors and do not necessarily
reflect the views of NSF.
- 1
-
Anonymizer- Anonymous Web Surfing.
https://www.anonymizer.com.
- 2
-
Freedom Network.
https://www.freedom.net/.
- 3
-
JAP Anonymity and Privacy.
https://anon.inf.tu-dresden.de/index_en.html/.
- 4
-
MixMinion- Anonymous Remailer.
https://www.mixminion.net.
- 5
-
Peer-to-Peer in 2005.
https://www.cachelogic.com/home/pages/research/p2p2005.php.
- 6
-
Safeweb- Anonymous Web Surfing.
https://www.safeweb.com.
- 7
-
University of Oregon Route Views Project.
https://www.routeviews.org/.
- 8
-
J. Byers, M. C. Cheng, J. Considine, G. Itkis, and A. Yeung.
Securing Bulk Content Almost for Free.
Journal of Computer Communications, Special Issue on Network
Security, pages 280-290, February 2006.
- 9
-
D. L. Chaum.
Untraceable electronic mail, return addresses and digital pseudonyms.
Commun. of the ACM, pages 84-90, February 1981.
- 10
-
I. Clarke.
FreeNet.
https://freenet.sourceforge.net/.
- 11
-
C. Díaz, S. Seys, J. Claessens, and B. Preneel.
Towards measuring anonymity.
In Proc. of PET 2002.
- 12
-
R. Dingledine, N. Mathewson, and P. Syverson.
TOR: The second-generation onion router.
In Proc. of USENIX Security 2004, San Diego, CA, USA.
- 13
-
D. Dolev, C. Dwork, O. Waarts, and M. Yung.
Perfectly secure message transmission.
Journal of the ACM, 40(1), 1993.
- 14
-
N. Feamster and R. Dingledine.
Location diversity in anonymity networks.
In In Proc. of ACM WPES 2004.
- 15
-
M. J. Freedman and R. Morris.
Tarzan: A peer-to-peer anonymizing network layer.
In Proc. of ACM CCS 2002, Washington, DC, USA.
- 16
-
S. Goel, M. Robson, M. Polte, and E. Sirer.
Herbivore: A scalable and efficient protocol for anonymous
communication.
In Proc. of the European SIGOPS Workshop 2004, Leuven, Belgium.
- 17
-
D. M. Goldschlag, M. G. Reed, and P. F. Syverson.
Hiding Routing Information.
In Proc. of Workshop on Information Hiding, Cambridge, UK,
1996.
- 18
-
T. Ho, M. Médard, J. Shi, M. Effros, and D. Karger.
On randomized network coding.
In Proc. of Allerton Conference on Communication, Control, and
Computing, Monticello, IL, 2003.
- 19
-
S. Katti, J. Cohen, and D. Katabi.
Information slicing: Anonymity using unreliable overlays.
Technical Report MIT-CSAIL-TR-2007-013, CSAIL, MIT, February 2007.
- 20
-
D. Malkhi and E. Pavlov.
Anonymity without cryptography.
In Financial Cryptography 2001, Grand Cayman, British West
Indies.
- 21
-
A. Mislove, G. Oberoi, A. Post, C. Reis, P. Druschel, and D. Wallach.
Ap3: A cooperative, decentralized service providing anonymous
communication.
In Proc. of the ACM SIGOPS European Workshop, 2004, Leuven,
Belgium.
- 22
-
S. Murdoch and G. Danezis.
Low-cost traffic analysis for TOR.
In Proc. of IEEE Symposium on Security and Privacy 2005,
Oakland, CA, USA.
- 23
-
M. Reiter and A. Rubin.
Crowds: Anonymity for web transactions.
ACM Transactions on Information and System Security, 1(1), June
1998.
- 24
-
M. Rennhard and B. Plattner.
Introducing MorphMix: Peer-to-Peer based Anonymous Internet Usage
with Collusion Detection.
In Proc. of WPES 2002, Washington, DC, USA.
- 25
-
A. Serjantov and G. Danezis.
Towards an information theoretic metric for anonymity.
In Proc. of PET 2002, San Francisco, CA, USA.
- 26
-
A. Shamir.
How to share a secret.
Communications of the ACM, pages 612-613, November 1979.
- 27
-
R. Sherwood, B. Bhattacharjee, and A. Srinivasan.
P5: A protocol for scalable anonymous communication.
In Proc. of the IEEE Symposium on Security and Privacy, 2002,
Oakland, CA, USA.
- 28
-
D. Stinson.
Something about all or nothing transforms.
Designs, Codes and Cryptography, pages 133-138, March 2001.
- 29
-
L. Subramanian.
Decentralized Security Mechanisms for Routing Protocols.
PhD thesis, University of California, Berkeley, Nov. 2005.
- 30
-
M. Wright, M. Adler, B. Levine, and C. Shields.
An analysis of the degradation of anonymous protocols.
In Proc. of NDSS 2002, San Diego, CA, USA.
- 31
-
L. Zhuang, F. Zhou, B. Y. Zhao, and A. Rowstron.
Cashmere: Resilient anonymous routing.
In Proc. of NSDI 2005, Cambridge, MA, USA.
Information Slicing: Anonymity Using
Unreliable
Overlays
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons paper.tex
The translation was initiated by Sachin Katti on 2007-02-22
Footnotes
- ...
\let
-
- ... follows:
![[*]](footnote.png)
- Elements of
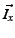 and
and 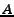 belong to a finite field belong to a finite field 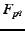 where where 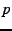 is a prime number and is a prime number and 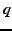 is a positive integer.
All operations are therefore defined in this field and differ from conventional arithmetic. is a positive integer.
All operations are therefore defined in this field and differ from conventional arithmetic.
- ...InformationTheory,InformationTheory1,
![[*]](footnote.png)
- The
entropy of a random variable
 is is
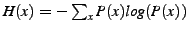 , where , where  is the probability function. is the probability function.
Sachin Katti
2007-02-22
|
