Performance Modeling and System Management
for Multi-component Online Services¹

Christopher Stewart and Kai Shen
Department of Computer Science, University of Rochester
{stewart, kshen}@cs.rochester.edu

Abstract:

Many dynamic-content online services are comprised of multiple interacting components and data partitions distributed across server clusters. Understanding the performance of these services is crucial for efficient system management. This paper presents a profile-driven performance model for cluster-based multi-component online services. Our offline constructed application profiles characterize component resource needs and inter-component communications. With a given component placement strategy, the application profile can be used to predict system throughput and average response time for the online service. Our model differentiates remote invocations from fast-path calls between co-located components and we measure the network delay caused by blocking inter-component communications. Validation with two J2EE-based online applications show that our model can predict application performance with small errors (less than 13% for throughput and less than 14% for the average response time). We also explore how this performance model can be used to assist system management functions for multi-component online services, with case examinations on optimized component placement, capacity planning, and cost-effectiveness analysis.

1 Introduction

Recent years have witnessed significant growth in online services, including Web search engines, digital libraries, and electronic commerce. These services are often deployed on clusters of commodity machines in order to achieve high availability, incremental scalability, and cost effectiveness [14,16,29,32]. Their software architecture usually comprises multiple components, some reflecting intentionally modular design, others developed independently and subsequently assembled into a larger application, e.g., to handle data from independent sources. A typical service might contain components responsible for data management, for business logic, and for presentation of results in HTML or XML.

Previous studies have recognized the value of using performance models to guide resource provisioning for on-demand services [1,12,27]. Common factors affecting the system performance include the application characteristics, workload properties, system management policies, and available resources in the hosting platform.

However, the prior results are inadequate for predicting the performance of multi-component online services, which introduce several additional challenges. First, various application components often have different resource needs and components may interact with each other in complex ways. Second, unlike monolithic applications, the performance of multi-component services is also dependent upon the component placement and replication strategy on the hosting cluster. Our contribution is a comprehensive performance model that accurately predicts the throughput and response time of cluster-based multi-component online services.

Our basic approach (illustrated in Figure 1) is to build application profiles characterizing per-component resource consumption and inter-component communication patterns as functions of input workload properties. Specifically, our profiling focuses on application characteristics that may significantly affect the service throughput and response time. These include CPU, memory usage, remote invocation overhead, inter-component network bandwidth and blocking communication frequency. We perform profiling through operating system instrumentation to achieve transparency to the application and component middleware. With a given application profile and a component placement strategy, our model predicts system throughput by identifying and quantifying bottleneck resources. We predict the average service response time by modeling the queuing effect at each cluster node and estimating the network delay caused by blocking inter-component communications.

**Figure 1:** Profile-driven performance modeling for an online service containing a front-end Web server, a back-end database, and several middle-tier components (A, B, and C).
$\begin{figure}\centerline{\psfig{figure=figures/overview.eps, width=5.3in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

Based on the performance model, we explore ways that it can assist various system management functions for online services. First, we examine component placement and replication strategies that can achieve high performance with given hardware resources. Additionally, our model can be used to estimate resource needs to support projected future workload or to analyze the cost-effectiveness of hypothetical hardware platforms. Although many previous studies have addressed various system management functions for online services [5,6,10,31], they either deal with single application components or they treat a complex application as a non-partitionable unit. Such an approach restricts the management flexibility for multi-component online services and thus limits their performance potentials.

The rest of this paper is organized as follows. Section 2 describes our profiling techniques to characterize application resource needs and component interactions. Section 3 presents the throughput and response time models for multi-component online services. Section 4 validates our model using two J2EE-based applications on a heterogeneous Linux cluster. Section 5 provides case examinations on model-based component placement, capacity planning, and cost-effectiveness analysis. Section 6 describes related work. Section 7 concludes the paper and discusses future work.

2 Application Profiling

Due to the complexity of multi-component online services, an accurate performance model requires the knowledge of application characteristics that may affect the system performance under any possible component placement strategies. Our application profile captures three such characteristics: per-component resource needs (Section 2.1), the overhead of remote invocations (Section 2.2), and the inter-component communication delay (Section 2.3).

We perform profiling through operating system instrumentation to achieve transparency to the application and component middleware. Our only requirement on the middleware system is the flexibility to place components in ways we want. In particular, our profiling does not modify the application or the component middleware. Further, we treat each component as a blackbox (i.e., we do not require any knowledge of the inner-working of application components). Although instrumentation at the application or the component middleware layer can more easily identify application characteristics, our OS-level approach has wider applicability. For instance, our approach remains effective for closed-source applications and middleware software.

2.1 Profiling Component Resource Consumption

A component profile specifies component resource needs as functions of input workload characteristics. For time-decaying resources such as CPU and disk I/O bandwidth, we use the average rates $\theta_$ cpu and $\theta_$ disk to capture the resource requirement specification. On the other hand, variation in available memory size often has a severe impact on application performance. In particular, a memory deficit during one time interval cannot be compensated by a memory surplus in the next time interval. A recent study by Doyle et al. models the service response time reduction resulting from increased memory cache size for Web servers serving static content [12]. However, such modeling is only feasible with intimate knowledge about application memory access pattern. To maintain the general applicability of our approach, we use the peak usage $\theta_$ mem for specifying the memory requirement in the component profile.

**Figure 2:** Linear fitting of CPU usage for two RUBiS components.
$\begin{figure}\centerline{\psfig{figure=figures/profile_bidweb.eps, width=2.5in}}\vspace*{-0.1in} \end{figure}$

Component	CPU usage (in percentage)
Web server	1.525 $\cdot$ $\lambda _$ workload + 0.777
Database	0.012 $\cdot$ $\lambda _$ workload + 3.875
`Bid`	0.302 $\cdot$ $\lambda _$ workload + 0.807
`BuyNow`	0.056 $\cdot$ $\lambda _$ workload + 0.441
`Category`	0.268 $\cdot$ $\lambda _$ workload + 1.150
`Comment`	0.079 $\cdot$ $\lambda _$ workload + 0.568
`Item`	0.346 $\cdot$ $\lambda _$ workload + 0.588
`Query`	0.172 $\cdot$ $\lambda _$ workload + 0.509
`Region`	0.096 $\cdot$ $\lambda _$ workload + 0.556
`User`	0.403 $\cdot$ $\lambda _$ workload + 0.726
`Transaction`	0.041 $\cdot$ $\lambda _$ workload + 0.528

The input workload specifications in component profiles can be parameterized with an average request arrival rate $\lambda _$ workload and other workload characteristics $\delta_$ workload including the request arrival burstiness and the composition of different request types (or request mix). Putting these altogether, the resource requirement profile for a distributed application component specifies the following mapping $\stackrel{f}{\longrightarrow}$ :

$\displaystyle (\lambda_$ workload $\displaystyle , \delta_$ workload $\displaystyle ) \stackrel{f}{\longrightarrow} (\theta_$ cpu $\displaystyle , \theta_$ disk $\displaystyle , \theta_$ mem $\displaystyle )$

Since resource needs usually grow by a fixed amount with each additional input request per second, it is likely for $\theta_$ cpu, $\theta_$ disk, and $\theta_$ mem to follow linear relationships with $\lambda _$ workload.

We use a modified Linux Trace Toolkit (LTT) [38] for our profiling. LTT instruments the Linux kernel with trace points, which record events and forward them to a user-level logging daemon through the relayfs file system. We augmented LTT by adding or modifying trace points at CPU context switch, network, and disk I/O events to report statistics that we are interested in. We believe our kernel instrumentation-based approach can also be applied for other operating systems. During our profile runs, each component runs on a dedicated server and we measure the component resource consumption at a number of input request rates and request mixes.

2.1.0.1 Profiling Results on Two Applications

We present profiling results on two applications based on Enterprise Java Beans (EJB): the RUBiS online auction benchmark [9,28] and the StockOnline stock trading application [34]. RUBiS implements the core functionality of an auction site: selling, browsing, and bidding. It follows the three-tier Web service model containing a front-end Web server, a back-end database, and nine movable business logic components (Bid, BuyNow, Category, Comment, Item, Query, Region, User, and Transaction). StockOnline contains a front-end Web server, a back-end database, and five EJB components (Account, Item, Holding, StockTX, and Broker).

Component	CPU usage (in percentage)
Web server	0.904 $\cdot$ $\lambda _$ workload + 0.779
Database	0.008 $\cdot$ $\lambda _$ workload + 4.832
`Account`	0.219 $\cdot$ $\lambda _$ workload + 0.789
`Item`	0.346 $\cdot$ $\lambda _$ workload + 0.781
`Holding`	0.268 $\cdot$ $\lambda _$ workload + 0.674
`StockTX`	0.222 $\cdot$ $\lambda _$ workload + 0.490
`Broker`	1.829 $\cdot$ $\lambda _$ workload + 0.533

Profiling measurements were conducted on a Linux cluster connected by a 1Gbps Ethernet switch. Each profiling server is equipped with a 2.66GHz Pentium 4 processor and 512MB memory. For the two applications, the EJB components are hosted on a JBoss 3.2.3 application server with an embedded Tomcat 5.0 servlet container. The database server runs MySQL 4.0. The dataset for each application is sized according to database dumps published on the benchmark Web sites [28,34].

After acquiring the component resource consumption at the measured input rates, we derive general functional mappings using linear fitting. Figure 2 shows such a derivation for the Bid component and the Web server in RUBiS. The results are for a request mix similar to the one in [9] (10% read-write requests and 90% read-only requests). The complete CPU profiling results for all 11 RUBiS components and 7 StockOnline components are listed in Table 1 and Table 2 respectively. We do not show the memory and disk I/O profiling results for brevity. The memory and disk I/O consumption for these two applications are relatively insignificant and they never become the bottleneck resource in any of our test settings.

2.2 Profiling Remote Invocation Overhead

Remote component invocations incur CPU overhead on tasks such as message passing, remote lookup, and data marshaling. When the interacting components are co-located on the same server, the component middleware often optimizes away these tasks and some even implement local component invocations using direct method calls. As a result, the invocation overhead between two components may vary depending on how they are placed on the hosting cluster. Therefore, it is important to identify the remote invocation costs such that we can correctly account for them when required by the component placement strategy.

It is challenging to measure the remote invocation overhead without assistance from the component middleware. Although kernel instrumentation tools such as LTT can provide accurate OS-level statistics, they do not directly supply middleware-level information. In particular, it is difficult to differentiate CPU usage of normal component execution from that of passing a message or serving a remote lookup query. We distinguish the remote invocation cost of component A invoking component B in a three step process. First, we isolate components A and B on separate machines. Second, we intercept communication rounds initiated by component A. We define a communication round as a sequence of messages between a pair of processes on two different machines in which the inter-message time does not exceed a threshold. Finally, we associate communication rounds with invocations. Thus, the remote invocation cost incurred between components A and B is the sum of resource usage during communication rounds between them. Since the components are isolated during the profiling, communication rounds are not likely to be affected by network noises.

2.2.0.1 Profiling Results

Figure 3 shows the application profile on remote invocation overhead for RUBiS.

**Figure 3:** Profile on remote invocation overhead for RUBiS. The label on each edge indicates the per-request mean of inter-component remote invocation CPU overhead (in percentage).
$\begin{figure}\centerline{\psfig{figure=figures/profile_rmi.eps,width=3.15in}}\vspace{-0.2in} \vspace{-0.1in}\end{figure}$

2.3 Profiling Inter-Component Communications

We profile component interaction patterns that may affect bandwidth usage and network service delay between distributed application components. We measure inter-component bandwidth consumption by intercepting all network messages between components during off-line profile runs. Note that the bandwidth usage also depends on the workload level, particularly the input user request rate. By measuring bandwidth usage at various input request rates and performing linear fitting, we can acquire per-request communication data volume for each inter-component link.

The processing of a user request may involve multiple blocking round-trip communications (corresponding to request-response rounds) along many inter-component links. We consider the request processing network delay as the sum of the network delays on all inter-component links between distributed components. The delay on each link includes the communication latency and the data transmission time. Inter-component network delay depends on the link round-trip latency and the number of blocking round-trip communications between components. We define a round trip as a synchronous write-read interaction between two components.

**Figure 4:** Identifying blocking round trip communications based on an intercepted network system call trace. #132 $\longrightarrow$ #135 is counted as only one round trip interaction because #132, #133, and #134 occur very close to each other (less than a single network round-trip latency in the profiling environment).
$\begin{figure}\centerline{\psfig{figure=figures/trace.eps, width=5.8in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

Figure 5: Inter-component communication profile for RUBiS. In the left figure, the label on each edge indicates the per-request mean of data communication volume in bytes. In the right figure, the label on each edge indicates the per-request mean of the blocking round-trip communication count.

3.15in!figures/profile_bw.eps

3.15in!figures/profile_rt.eps

Due to the lack of knowledge on the application behavior, it is challenging to identify and count blocking round trip communications at the OS level. Our basic approach is to intercept system calls involving network reads and writes during profile runs. System call interception provides the OS-level information nearest to the application. We then count the number of consecutive write-read pairs in the message trace between two components. We also compare the timestamps of consecutive write-read pairs. Multiple write-read pairs occurring within a single network round-trip latency in the profiling environment are counted as only one. Such a situation could occur when a consecutive write-read pair does not correspond to each other in a blocking interaction. Figure 4 illustrates our approach for identifying blocking round trip communications. To avoid confusion among messages belonging to multiple concurrent requests, we process one request at a time during profile runs.

2.3.0.1 Profiling Results

Our profiling results identify the per-request communication data volume and blocking round-trip interaction count for each inter-component link. Figure 5 shows inter-component communication profiles for RUBiS. The profiling result for each inter-component link indicates the per-request mean of profiled target.

2.4 Additional Profiling Issues

Non-Linear functional mappings. In our application studies, most of the workload parameter (e.g., request arrival rate) to resource consumption mappings follow linear functional relationships. We acknowledge that such mappings may exhibit non-linear relationships in some cases, particularly when concurrent request executions affect each other's resource consumption (e.g., extra CPU cost due to contention on a spin-lock). However, the framework of our performance model is equally applicable in these cases, as long as appropriate functional mappings can be extracted and included in the application profile. Non-linear fitting algorithms [4,30] can be used for such a purpose. Note that a non-linear functional mapping may require more workload samples to produce an accurate fitting.

Profiling cost. To improve measurement accuracy, we place each profiled component on a dedicated machine. This eliminates the interference from co-located components without the need of complex noise-reduction techniques [8]. However, the profiling of isolated components imposes a large demand on the profiling infrastructure (i.e., the cluster size equals the number of components). With a smaller profiling infrastructure, it would require multiple profile runs that each measures some components or inter-component links. At a minimum, two cluster nodes are needed for per-component resource consumption profiling (one for the profiled component and the other for the rest) and three machines are required to measure inter-component communications. At these settings for an -component service, it would take profile runs for per-component measurement and $\frac{N \cdot (N-1)}{2}$ runs for inter-component communication profiling.

3 Performance Modeling

We present our performance model for cluster-based multi-component online services. The input of our model includes the application profile, workload properties, available resources in the hosting platform, as well as the component placement and replication strategy. Below we describe our throughput prediction (Section 3.1) and response time prediction (Section 3.2) schemes. We discuss several remaining issues about our performance model in Section 3.3.

3.1 Throughput Prediction

Our ability to project system throughput under each component placement strategy can be illustrated by the following three-step process:

We first derive the mapping between the input request rate $\lambda _$ workload and runtime resource demands for each component. The CPU, disk I/O bandwidth, and memory needs $\theta_$ cpu $, \theta_$ disk $, \theta_$ mem can be obtained with the knowledge of the component resource consumption profile (Section 2.1) and input workload characteristics. The remote invocation overhead (Section 2.2) is then added when the component in question interacts with other components that are placed on remote servers. The component network resource demand $\theta_$ network can be derived from the inter-component communication profile (Section 2.3) and the placement strategy. More specifically, it is the sum of communication data volume on all non-local inter-component links adjacent to the component in question.
Given a component placement strategy, we can determine the maximum input request rate that can saturate the CPU, disk I/O bandwidth, network I/O bandwidth, or memory resources at each server. Let $\tau_$ CPU, $\tau_$ disk, $\tau_$ network, and $\tau_$ memory denote such saturation rates at server . When a component is replicated, its load is distributed to all server replicas. The exact load distribution is dependent on the policy employed by the component middleware. Many load distribution strategies have been proposed in previous studies [13,25,26,40]. However, most of these have not been incorporated into component middleware systems in practice. Particularly, we are only able to employ round-robin load distribution with the JBoss application server, which evenly distributes the load among replicas. Our validation results in Section 4 are therefore based on the round-robin load distribution model.
The system reaches its maximum throughput as soon as one of the servers cannot handle any more load. Therefore, the system throughput can be estimated as the lowest saturation rate for all resource types at all servers:
$\displaystyle \min_{\text{for all servers}} \{\tau_\text{CPU}(s), \tau_\text{disk}(s), \tau_\text{network}(s), \tau_\text{memory}(s)\}$

3.2 Response Time Prediction

The service response time for a cluster-based online service includes two elements: 1) the request execution time and the queueing time caused by resource competition; and 2) network delay due to blocking inter-component communications.

3.2.0.1 Request Execution and Queuing

The system-wide request execution and the queueing time is the sum of such delay at each cluster server. We use an M/G/1 queue to simplify our model of the average response time at each server. The M/G/1 queue assumes independent request arrivals where the inter-arrival times follow an exponential distribution. Previous studies [7,11] found that Web request arrivals may not be independent because Web workloads contain many automatically triggered requests (e.g., embedded Web objects) and requests within each user session may follow particular user behavioral patterns. We believe our simplification is justified because our model targets dynamic-content service requests that do not include automatically triggered embedded requests. Additionally, busy online services observe superimposed workloads from many independent user sessions and thus the request inter-dependencies with individual user sessions are not pronounced, particularly at high concurrencies.

The average response time at each server can be estimated as follows under the M/G/1 queuing model:

$\displaystyle E[r] = E[e] + \frac{\rho E[e] ( 1 + C_e^2)}{2(1-\rho)}$

where

is the average request execution time; $\rho$ is the workload intensity (i.e., the ratio of input request rate to the rate at which the server resource is completely exhausted); and

is the coefficient of variation (i.e., the ratio of standard deviation to the sample mean) of the request execution time.

The average request execution time at each component is the resource needs per request at very low request rate (when there is no resource competition or queuing in the system). The average request execution time at each server is the sum of such time for all hosted components. The workload intensity at each server $\rho$ can be derived from the component resource needs and the set of components that are placed at the server in question. The coefficient of variation of the request execution time can be determined with the knowledge of its distribution. For instance, if the request execution time follows an exponential distribution. Without the knowledge of such distribution, our application profile maintains an histogram of execution time samples for each component and we then use these histograms to determine for each server under a particular placement strategy.

3.2.0.2 Network Delay

Our network delay prediction is based on the inter-component communication profile described in Section 2.3. From the profile, we can acquire the per-request communication data volume (denoted by $\nu_l$ ) and round-trip blocking interaction count (denoted by $\kappa_l$ ) for each inter-component link

. Under a particular cluster environment, let $\gamma_l$ and $\omega_l$ be the round-trip latency and bandwidth, respectively, of link

. Then we can model the per-request total network delay as:

$\displaystyle \Gamma = \sum_{\text{for each non-local inter-component link } l} [\kappa_l \cdot \gamma_l + \frac{\nu_l}{\omega_l}]$

3.3 Additional Modeling Issues

Cache pollution due to component co-location. When components are co-located, interleaved or concurrent execution of multiple components may cause processor cache pollution on the server, and thus affect the system performance. Since modern operating systems employ affinity-based scheduling and large CPU quanta (compared with the cache warm-up time), we do not find cache pollution to be a significant performance factor. However, processor-level multi-threading technologies such as the Intel Hyper-Threading [19] allow concurrent threads executing on a single processor and sharing level-1 processor cache. Cache pollution is more pronounced on these architectures and it might be necessary to model such cost and its impact on the overall system performance.

Replication consistency management. If replicated application states can be updated by user requests, mechanisms such as logging, undo, and redo may be required to maintain consistency among replicated states. Previous studies have investigated replication consistency management for scalable online services [15,29,32,39]. Consistency management consumes additional system resources which our current model does not consider. Since many component middleware systems in practice do not support replication consistency management, we believe this limitation of our current model should not severely restrict its applicability.

Cross-architecture performance modeling. A service hosting cluster may comprise servers with multiple types of processor architectures or memory sizes. Our current approach requires application profiling on each of the architectures present in the cluster. Such profiling is time consuming and it would be desirable to separate the performance impact of application characteristics from that of server properties. This would allow independent application profiling and server calibration, and thus significantly save the profiling overhead for server clusters containing heterogeneous architectures. Several recent studies [22,33] have explored this issue in the context of scientific computing applications and their results may be leveraged for our purpose.

4 Model Validation

Table 3: Component placement strategies (on a 12-node cluster) used for measurements in Section 4.1.

Servers

Pentium4

Xeon

Account

Stock

Item

Holding

StockTX

Holding

Online

Holding

StockTX

Broker

StockTX

Broker

Bid

Item

User

Region

BuyNow

Region

BuyNow

Region

BuyNow

**Figure 6:** Validation results on system throughput.
$\begin{figure}\centerline{\psfig{figure=figures/overallaccu_thrput.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

**Figure 7:** Validation results on per-node CPU resource usage (at the input workload rate of 230 requests/second).
$\begin{figure}\centerline{\psfig{figure=figures/overallaccu_resusage.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

4.1 Model Accuracy at a Typical Setting

**Figure 8:** Validation results on service response time.
$\begin{figure}\centerline{\psfig{figure=figures/overallaccu_resptime.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

The measurement results in this section are based on a 12-machine service cluster (four are type-1 and the other eight are type-2). For each application, we employ an input request mix with 10% read-write requests and 90% read-only requests. The placement strategy for each application we use (shown in Table 3) is the one with highest modeled throughput out of 100 random chosen candidate strategies. We compare the measured performance with three variations of our performance model:

#1.: The base model: The performance model that does not consider the overhead of remote component invocation and network delays.
#2.: The RI model: The performance model that considers remote invocation overhead but not network delays.
#3.: The full model: The performance model that considers both.

Figure 6 shows validation results on the overall system throughput for StockOnline and RUBiS. We measure the rate of successfully completed requests at different input request rate. In our experiments, a request is counted as successful only if it returns within 10 seconds. Results show that our performance model can accurately predict system throughput. The error for RUBiS is negligible while the error for StockOnline is less than 13%. This error is mostly attributed to instable results (due to timeouts) when the system approaches the saturation point. There is no difference between the prediction of the RI model and that of the full model. This is expected since the network delay modeling does not affect the component resource needs and subsequently the system throughput. Comparing between the full model and the base model, we find that the modeling of remote invocation overhead has a large impact on the prediction accuracy. It improves the accuracy by 36% and 14% for StockOnline and RUBiS respectively.

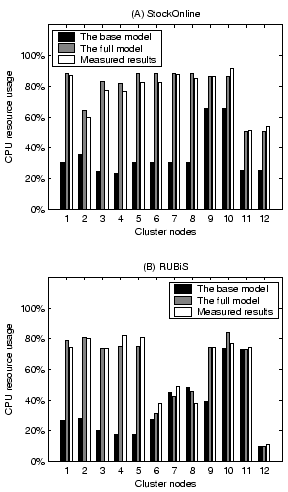
Since the system throughput in our model is derived from resource usage at each server, we further examine the accuracy of per-node resource usage prediction. Figure 7 shows validation results on the CPU resource usage at the input workload rate of 230 requests/second (around 90% workload intensity for both applications). We do not show the RI model since its resource usage prediction is the same as the full model. Comparing between the full model and the base model, we find that the remote invocation overhead can be very significant on some of the servers. The failure of accounting it results in poor performance prediction of the base model.

**Figure 9:** Validation results on system saturation throughput at various cluster sizes.
$\begin{figure}\centerline{\psfig{figure=figures/scalability_thrput.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

**Figure 10:** Validation results on service response time at various cluster sizes. The response time is measured at the input workload that is around 85% of the saturation throughput.
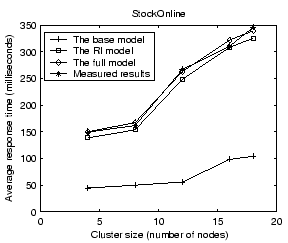$\begin{figure}\centerline{\psfig{figure=figures/scalability_resptime.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

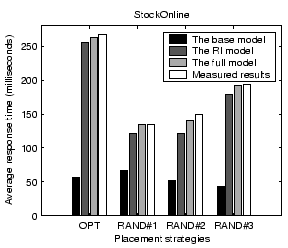
Figure 8 shows validation results on the average service response time for StockOnline and RUBiS. For each application, we show the average response time when the input workload is between 50% and 90% of the saturation throughput, defined as the highest successful request completion rate achieved at any input request rate. Results show that our performance model can predict the average response time with less than 14% error for the two applications. The base model prediction is very poor due to its low resource usage estimation. Comparing between the full model and the RI model, we find that the network delay modeling accounts for an improved accuracy of 9% and 18% for StockOnline and RUBiS respectively.

4.2 Impact of Factors

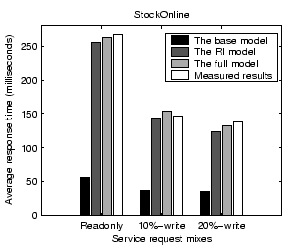
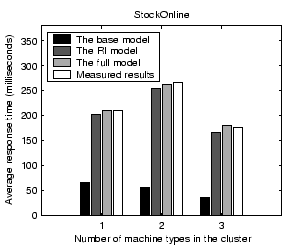
We examine the impact of various factors on the accuracy of our performance model. When we vary one factor, we keep other factors unchanged from settings in Section 4.1.

4.2.0.1 Impact of cluster sizes

We study the model accuracy at different cluster sizes. Figure 9 shows the throughput prediction for the StockOnline application at service clusters of 4, 8, 12, 16, and 18 machines. At each cluster size, we pick a high-throughput placement strategy out of 100 random chosen candidate placements. Figure 10 shows the validation results on the average response time. The response time is measured at the input workload that is around 85% of the saturation throughput. Results demonstrate that the accuracy of our model is not affected by the cluster size. The relative accuracies among different models are also consistent across all cluster sizes.

**Figure 11:** Validation results on system saturation throughput at various service request mixes.
$\begin{figure}\centerline{\psfig{figure=figures/mix_thrput.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

**Figure 12:** Validation results on service response time at various service request mixes. The response time is measured at the input workload that is around 85% of the saturation throughput.
$\begin{figure}\centerline{\psfig{figure=figures/mix_resptime.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

4.2.0.2 Impact of request mixes

Figure 11 shows the throughput prediction for StockOnline at input request mixes with no writes, 10% read-write request sequences, and 20% read-write request sequences. Figure 12 shows the validation results on the average response time. Results demonstrate that the accuracy of our model is not affected by different types of input requests.

**Figure 13:** Validation results on system saturation throughput at various cluster settings.
$\begin{figure}\centerline{\psfig{figure=figures/hetero_thrput.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

**Figure 14:** Validation results on service response time at various cluster settings. The response time is measured at the input workload that is around 85% of the saturation throughput.
$\begin{figure}\centerline{\psfig{figure=figures/hetero_resptime.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

4.2.0.3 Impact of heterogeneous machine architectures

Figure 13 shows the throughput prediction for StockOnline at service clusters with one, two, and three types of machines. All configurations have twelve machines in total. Figure 14 illustrates the validation results on the average response time. Results show that the accuracy of our model is not affected by heterogeneous machine architectures.

**Figure 15:** Validation results on system saturation throughput at various placement strategies.
$\begin{figure}\centerline{\psfig{figure=figures/place_thrput.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

**Figure 16:** Validation results on service response time at various placement strategies. The response time is measured at the input workload that is around 85% of the saturation throughput.
$\begin{figure}\centerline{\psfig{figure=figures/place_resptime.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

4.2.0.4 Impact of placement and replication strategies

Finally, we study the model accuracy at different component placement and replication strategies. Figure 15 shows the throughput prediction for StockOnline with the throughput-optimized placement and three random chosen placement strategies. Methods for finding high-performance placement strategies will be discussed in Section 5.1. Figure 16 shows the validation results on the average response time. Small prediction errors are observed at all validation cases.

Table 4: Component placement strategies (on a 12-node cluster) used for measurements in Section 5.1. The ``all replication'' strategy is not shown.

Servers

Pentium4

Xeon

Simulate

Holding

Item

Holding

Account

annealing

StockTX

Holding

Broker

OPT

Broker

Item

Account

Holding

Account

Random

StockTX

Broker

Item

StockTX

Item

sampling

Broker

Holding

Broker

StockTX

OPT

StockTX

Broker

Low

Item

Account

Holding

StockTX

Broker

replication

Broker

4.3 Summary of Validation Results

Our model can predict the performance of the two J2EE applications with high accuracy (less than 13% error for throughput and less than 14% error for the average response time).
The remote invocation overhead is very important for the accuracy of our performance model. Without considering it, the throughput prediction error can be up to 36% while the prediction for the average response time can be much worse depending on the workload intensity.
Network delay can affect the prediction accuracy for the average response time by up to 18%. It does not affect the throughput prediction. However, the impact of network delay may increase with networks of lower bandwidth or longer latency.
The validation results are not significantly affected by factors such as the cluster size, the mix of input request types, the heterogeneity of the hosting servers, and the placement strategy.

5 Model-based System Management

We explore how our performance model can be used to assist system management functions for multi-component online services. A key advantage of model-based management is its ability to quickly explore the performance tradeoff among a large number of system configuration alternatives without high-overhead measurements. Additionally, it can project system performance at hypothetical settings.

5.1 High-performance Component Placement

Our objective is to discover a component placement and replication strategy that achieves high performance on both throughput and service response time. More specifically, our target strategy should be able to support a large input request rate while still maintaining an average response time below a specified threshold. Our model proposed in this paper can predict the performance with any given component placement strategy. However, the search space of all possible placement strategies is too large for exhaustive check. Under such a context, we employ optimization by simulated annealing [21,24]. Simulated annealing is a random sampling-based optimization algorithm that gradually reduces the sampling scope following an ``annealing schedule''.

We evaluate the effectiveness of our approach on a 12-node cluster (the same as in Section 4.1) using the StockOnline application. We set the response time threshold of our optimization at 1 second. The number of samples examined by our simulated annealing algorithm is in the order of 10,000 and the algorithm takes about 12 seconds to complete on a 2.00GHz Xeon processor. For comparison, we also consider a random sampling optimization which selects the best placement out of 10,000 randomly chosen placement strategies. Note that both of these approaches rely on our performance model.

For additional comparison, we introduce two placement strategies based on ``common sense'', i.e., without the guidance of our performance model. In the first strategy, we replicate all components (except the database) on all nodes. This is the suggested placement strategy in the JBoss application server documentation. High replication may introduce some overhead, such as the component maintenance overhead at each replica that is not directly associated with serving user requests. In the other strategy, we attempt to minimize the amount of replication while still maintaining balanced load. We call this strategy low replication. Table 4 lists the three placement strategies except all replication.

**Figure 17:** System throughput under various placement strategies.
$\begin{figure}\centerline{\psfig{figure=figures/opt_thrput.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

**Figure 18:** Average service response time under various placement strategies.
$\begin{figure}\centerline{\psfig{figure=figures/opt_resptime.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

**Figure 19:** Capacity planning using various models.
$\begin{figure}\centerline{\psfig{figure=figures/capacity_thrput.eps, width=2.5in}}\vspace{-0.1in} \vspace{-0.1in}\end{figure}$

Figure 17 illustrates the measured system throughput under the above four placement strategies. We find that the simulated annealing optimization is slightly better than the random sampling approach. It outperforms all replication and low replication by 7% and 31% respectively. Figure 18 shows the measured average response time at different input workload rates. The response time for low replication rises dramatically when approaching 220 requests/second because it has a much lower saturation throughput than the other strategies. Compared with random sampling and all replication, the simulated annealing optimization achieves 22% and 26% lower response time, respectively, at the input workload rate of 250 requests/second.

5.2 Capacity Planning

The ability of predicting future resource needs at forecast workload levels allows an online service provider to acquire resources in an efficient fashion. Figure 19 presents our capacity planning results for StockOnline on simulated annealing-optimized placement and all replication placement. The base platform for capacity planning is a 12-node cluster (four type-1 nodes and eight type-2 nodes). Our performance model is used to project resource needs at workload levels that could not be supported in the base platform. We assume only type-2 nodes will be added in the future. Previous work [23] has suggested linear projection-based capacity planning where future resource requirement scales linearly with the forecast workload level. For the comparison purpose, we also show the result of linear projection. The base performance for linear projection is that of all replication on the 12-node cluster.

**Figure 20:** Cost-effectiveness of various machine types.
$\begin{figure}\centerline{\psfig{figure=figures/capacity_dollars.eps, width=2.5in}}\end{figure}$

Results in Figure 19 illustrate that our optimized strategy consistently saves resources compared with all replication. The saving is at least 11% for projected workload of 1000 requests/second or higher. Comparing between the modeled all replication and linearly projected all replication, we find that the linear projection significantly underestimates resource needs (by about 28%) at high workload levels. This is partially due to heterogeneity in the machines being employed. More specifically, four of the original nodes are type-1, which are slightly more powerful than the type-2 machines that are expected to be added. Additionally, linear projection fails to consider the increased likelihood of remote invocations at larger clusters. In comparison, our performance model addresses these issues and provides more accurate capacity planning.

5.3 Cost-effectiveness Analysis

We provide a model-based cost-effectiveness analysis. In our evaluation, we plan to choose one of the three types of machines (described in the beginning of Section 4) to expand the cluster for future workloads. We examine the StockOnline application in this evaluation. Figure 20 shows the estimated cost when each of the three types of machines is employed for expansion. We acquire the pricing for the three machine types from www.epinions.com and they are $1563, $1030, and $1700 respectively. Although type-2 nodes are less powerful than the other types, it is the most cost-effective choice for supporting the StockOnline application. The saving is at least 20% for projected workload of 1000 requests/second or higher. Such a cost-effectiveness analysis would not be possible without an accurate prediction of application performance at hypothetical settings.

6 Related Work

Previous studies have addressed application resource consumption profiling. Urgaonkar et al. use resource usage profiling to guide application placement in shared hosting platforms [36]. Amza et al. provide bottleneck resource analysis for several dynamic-content online service benchmarks [3]. Doyle et al. model the service response time reduction with increased memory cache size for static-content Web servers [12]. The Magpie tool chain actually extracts per-request execution control flow through online profiling [8]. The main contribution of our profiling work is that we identify a comprehensive set of application characteristics that can be employed to predict the performance of multi-component online services with high accuracy.

A very recent work by Urgaonkar et al. [35] models a multi-tier Internet service as a network of queues. Their view of service tiers is not as fine-grained as application components in our model. Additionally, service tiers are organized in a chain-like architecture while application components can interact with each other in more complex fashions. As a result, their model cannot be used to directly guide component-level system management such as distributed component placement. On the other hand, our approach uses a simple M/G/1 queue to model service delay at each server while their model more accurately captures the dependencies of the request arrival processes at different service tiers.

Recent studies have proposed the concept of component-oriented performance modeling [17,37]. They mainly focus on the design of performance characterization language for software components and the way to assemble component-level models into whole-application performance model. They do not describe how component performance characteristics can be acquired in practice. In particular, our study finds that the failure of accounting the remote invocation overhead can significantly affect the model accuracy.

Distributed component placement has been examined in a number of prior studies. Coign [18] examines the optimization problem of minimizing communication time for two-machine client-server applications. ABACUS [2] focuses on the placement of I/O-specific functions for cluster-based data-intensive applications. Ivan et al. examine the automatic deployment of component-based software over the Internet subjected to throughput requirements [20]. Most of these studies heuristically optimize the component placement toward a performance objective. In comparison, our model-based approach allows the flexibility to optimize for complex objectives (e.g., a combination of throughput and service response time) and it also provides an estimation on the maximum achievable performance.

7 Conclusion and Future Work

This paper presents a profile-driven performance model for cluster-based multi-component online services. We construct application profiles characterizing component resource needs and inter-component communication patterns using transparent operating system instrumentation. Given a component placement and replication strategy, our model can predict system throughput and the average service response time with high accuracy. We demonstrate how this performance model can be employed to assist optimized component placement, capacity planning, and cost-effectiveness analysis.

In addition to supporting static component placement, our model may also be used to guide dynamic runtime component migration for achieving better performance. Component migration requires up-to-date knowledge of runtime dynamic workload characteristics. It also desires a migration mechanism that does not significantly disrupt ongoing service processing. Additionally, runtime component migration must consider system stability, especially when migration decisions are made in a decentralized fashion. We plan to investigate these issues in the future.

7.0.0.1 Project Website

More information about this work, including publications and releases of related tools and documentations can be found on our project website: www.cs.rochester.edu/u/stewart/component.html.

7.0.0.2 Acknowledgments

We would like to thank Peter DeRosa, Sandhya Dwarkadas, Michael L. Scott, Jian Yin, Ming Zhong, the anonymous referees, and our shepherd Dina Katabi for helpful discussions and valuable comments. We are also indebted to Liudvikas Bukys and the rest of the URCS lab staff for maintaining the experimental platform used in this study.

Bibliography

1: G. A. Alvarez, E. Borowsky, S. Go, T. H. Romer, R. Becker-Szendy, R. Golding, A. Merchant, M. Spasojevic, A. Veitch, and J. Wilkes.
Minerva: An Automated Resource Provisioning Tool for Large-Scale Storage Systems.
ACM Trans. on Computer Systems, 19(4):483-418, November 2001.
2: K. Amiri, D. Petrou, G. Ganger, and G. Gibson.
Dynamic Function Placement for Data-Intensive Cluster Computing.
In Proc. of the USENIX Annual Technical Conf., San Diego, CA, June 2000.
3: C. Amza, A. Chanda, A. L. Cox, S. Elnikety, R. Gil, K. Rajamani, W. Zwaenepoel, E. Cecchet, and J. Marguerite.
Specification and Implementation of Dynamic Web Site Benchmarks.
In Proc. of the 5th IEEE Workshop on Workload Characterization, Austin, TX, November 2002.
4: E. Anderson.
Simple Table-based Modeling of Storage Devices.
Technical Report HPL-SSP-2001-04, HP Laboratories, July 2001.
5: K. Appleby, S. Fakhouri, L. Fong, G. Goldszmidt, M. Kalantar, S. Krishnakumar, D. Pazel, J. Pershing, and B. Rochwerger.
Oceano - SLA Based Management of A Computing Utility.
In Proc. of the 7th Int'l Symp. on Integrated Network Management, Seattle, WA, May 2001.
6: M. Aron, P. Druschel, and W. Zwaenepoel.
Cluster Reserve: A Mechanism for Resource Management in Cluster-based Network Servers.
In Proc. of the ACM SIGMETRICS, pages 90-101, Santa Clara, CA, June 2000.
7: P. Barford and M. Crovella.
Generating Representative Web Workloads for Network and Server Performance Evaluation.
In Proc. of the ACM SIGMETRICS, pages 151-160, Madison, WI, June 1998.
8: P. Barham, A. Donnelly, R. Isaacs, and R. Mortier.
Using Magpie for Request Extraction and Workload Modeling.
In Proc. of the 6th USENIX OSDI, pages 259-272, San Francisco, CA, December 2004.
9: E. Cecchet, J. Marguerite, and W. Zwaenepoel.
Performance and Scalability of EJB Applications.
In Proc. of the 17th ACM Conf. on Object-oriented Programming, Systems, Languages, and Applications, pages 246-261, Seattle, WA, November 2002.
10: J. S. Chase, D. C. Anderson, P. N. Thakar, A. M. Vahdat, and R. P. Doyl.
Managing Energy and Server Resources in Hosting Centers.
In Proc. of the 18th ACM SOSP, pages 103-116, Banff, Canada, October 2001.
11: S. Deng.
Empirical Model of WWW Document Arrivals at Access Link.
In Proc. of the IEEE Conf. on Communications, pages 1797-1802, Dallas, TX, June 1996.
12: R. P. Doyle, J. S. Chase, O. M. Asad, W. Jin, and A. M. Vahdat.
Model-based Resource Provisioning in a Web Service Utility.
In Proc. of the 4th USENIX Symp. on Internet Technologies and Systems, Seattle, WA, March 2003.
13: D. L. Eager, E. D. Lazowska, and J. Zahorjan.
Adaptive Load Sharing in Homogeneous Distributed Systems.
IEEE Trans. on Software Engineering, 12(5):662-675, May 1986.
14: A. Fox, S. D. Gribble, Y. Chawathe, E. A. Brewer, and P. Gauthier.
Cluster-Based Scalable Network Services.
In Proc. of the 16th ACM SOSP, pages 78-91, Saint Malo, France, October 1997.
15: S. D. Gribble, E. A. Brewer, J. M. Hellerstein, and D. Culler.
Scalable, Distributed Data Structures for Internet Service Construction.
In Proc. of the 4th USENIX OSDI, San Diego, CA, October 2000.
16: S. D. Gribble, M. Welsh, E. A. Brewer, and D. Culler.
The MultiSpace: An Evolutionary Platform for Infrastructural Services.
In Proc. of the USENIX Annual Technical Conf., Monterey, CA, June 1999.
17: S. A. Hissam, G. A. Moreno, J. A. Stafford, and K. C. Wallnau.
Packaging Predictable Assembly.
In Proc. of the First IFIP/ACM Conf. on Component Deployment, Berlin, Germany, June 2002.
18: G. C. Hunt and M. L. Scott.
The Coign Automatic Distributed Partitioning System.
In Proc. of the Third USENIX OSDI, New Orleans, LA, February 1999.
19: Hyper-Threading Technology.
https://www
[1].intel
[1].com
[1]/technology/hyperthread.
20: A.-A. Ivan, J. Harman, M. Allen, and V. Karamcheti.
Partitionable Services: A Framework for Seamlessly Adapting Distributed Applications to Heterogeneous Environments.
In Proc. of the 11th IEEE Symp. on High Performance Distributed Computing, pages 103-112, Edinburgh, Scotland, July 2002.
21: S. Kirkpatrick, C. D. Gelatt Jr., and M. P. Vecchi.
Optimization by Simulated Annealing.
Science, 220(4598):671-680, May 1983.
22: G. Marin and J. Mellor-Crummey.
Cross-Architecture Performance Predictions for Scientific Applications Using Parameterized Models.
In Proc. of the ACM SIGMETRICS, pages 2-13, New York, NY, June 2004.
23: D. A. Menascé and V. A. F. Almeida.
Capacity Planning for Web Performance: Metrics, Models, and Methods.
Prentice Hall, 1998.
24: N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller.
Equation of State Calculations by Fast Computing Machines.
J. Chem. Phys., 21(6):1087-1092, 1953.
25: M. Mitzenmacher.
On the Analysis of Randomized Load Balancing Schemes.
In Proc. of the 9th ACM SPAA, pages 292-301, Newport, RI, June 1997.
26: V. S. Pai, M. Aron, G. Banga, M. Svendsen, P. Druschel, W. Zwaenepoel, and E. Nahum.
Locality-Aware Request Distribution in Cluster-based Network Servers.
In Proc. of the 8th ASPLOS, pages 205-216, San Jose, CA, October 1998.
27: D. Petriu and M. Woodside.
Analysing Software Requirements Specifications for Performance.
In Proc. of the Third Int'l Workshop on Software and Performance, Rome, Italy, July 2002.
28: RUBiS: Rice University Bidding System.
https://rubis
[1].objectweb
[1].org.
29: Y. Saito, B. N. Bershad, and H. M. Levy.
Manageability, Availability, and Performance in Porcupine: a Highly Scalable, Cluster-based Mail Service.
ACM Trans. on Computer Systems, 18(3):298-332, August 2001.
30: G. A. Seber.
Nonlinear Regression Analysis.
Wiley, New York, 1989.
31: K. Shen, H. Tang, T. Yang, and L. Chu.
Integrated Resource Management for Cluster-based Internet Services.
In Proc. of the 5th USENIX OSDI, pages 225-238, Boston, MA, December 2002.
32: K. Shen, T. Yang, and L. Chu.
Clustering Support and Replication Management for Scalable Network Services.
IEEE Trans. on Parallel and Distributed Systems - Special Issue on Middleware, 14(11):1168-1179, November 2003.
33: A. Snavely, L. Carrington, and N. Wolter.
Modeling Application Performance by Convolving Machine Signatures with Application Profiles.
In Proc. of the 4th IEEE Workshop on Workload Characterization, Austin, TX, December 2001.
34: The StockOnline Benchmark.
https://forge
[1].objectweb
[1].org
[1]/projects/stock-online.
35: B. Urgaonkar, G. Pacifici, P. Shenoy, M. Spreitzer, and A. Tantawi.
An Analytical Model for Multi-tier Internet Services and Its Applications.
In Proc. of the ACM SIGMETRICS (to appear), Banff, Canada, June 2005.
36: B. Urgaonkar, P. Shenoy, and T. Roscoe.
Resource Overbooking and Application Profiling in Shared Hosting Platforms.
In Proc. of the 5th USENIX OSDI, pages 239-254, Boston, MA, December 2002.
37: X. Wu and M. Woodside.
Performance Modeling from Software Components.
In Proc. of the 4th Int'l Workshop on Software and Performance, pages 290-301, Redwood City, CA, January 2004.
38: K. Yaghmour and M. R. Dagenais.
Measuring and Characterizing System Behavior Using Kernel-Level Event Logging.
In Proc. of the USENIX Annual Technical Conf., San Diego, CA, June 2000.
39: H. Yu and A. Vahdat.
Design and Evaluation of a Continuous Consistency Model for Replicated Services.
In Proc. of the 4th USENIX OSDI, San Diego, CA, October 2000.
40: S. Zhou.
A Trace-Driven Simulation Study of Dynamic Load Balancing.
IEEE Trans. on Software Engineering, 14(9):1327-1341, September 1988.

About this document ...

Performance Modeling and System Management
for Multi-component Online Services¹

This document was generated using the LaTeX2HTML translator Version 2002 (1.62)

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons nsdi05.tex

The translation was initiated by Christopher Stewart on 2005-03-26

Footnotes

... Services ¹: This work was supported in part by the National Science Foundation grants CCR-0306473, ITR/IIS-0312925, and CCF-0448413.

Christopher Stewart 2005-03-26

Performance Modeling and System Management for Multi-component Online Services1

Abstract:

1 Introduction

2 Application Profiling

2.1 Profiling Component Resource Consumption

2.2 Profiling Remote Invocation Overhead

2.3 Profiling Inter-Component Communications

2.4 Additional Profiling Issues

3 Performance Modeling

3.1 Throughput Prediction

3.2 Response Time Prediction

3.3 Additional Modeling Issues

4 Model Validation

4.1 Model Accuracy at a Typical Setting

4.2 Impact of Factors

4.3 Summary of Validation Results

5 Model-based System Management

5.1 High-performance Component Placement

5.2 Capacity Planning

5.3 Cost-effectiveness Analysis

6 Related Work

7 Conclusion and Future Work

Footnotes

Performance Modeling and System Management
for Multi-component Online Services¹