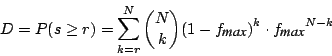|
NSDI '05 Paper
[NSDI '05 Technical Program]
Glacier: Highly durable, decentralized storage despite
massive correlated failures
Andreas Haeberlen Alan Mislove Peter Druschel
Department of Computer Science, Rice University
{ahae,amislove,druschel}@cs.rice.edu
Abstract:
Decentralized storage systems aggregate the available disk space of
participating computers to provide a large storage
facility. These systems rely on data redundancy to ensure durable
storage despite of node failures. However, existing systems
either assume independent node failures, or they rely on introspection to carefully place redundant data on nodes with low
expected failure correlation. Unfortunately, node failures are not
independent in practice and constructing an accurate failure model is
difficult in large-scale systems. At the same time, malicious worms
that propagate through the Internet pose a real threat of large-scale
correlated failures. Such rare but potentially catastrophic failures
must be considered when attempting to provide highly durable storage.
In this paper, we describe Glacier, a distributed storage system
that relies on massive redundancy to mask the effect of large-scale
correlated failures. Glacier is designed to aggressively minimize the
cost of this redundancy in space and time: Erasure coding and garbage
collection reduces the storage cost; aggregation of small objects and
a loosely coupled maintenance protocol for redundant fragments
minimizes the messaging cost. In one configuration, for instance, our system can
provide six-nines durable storage despite correlated failures of up to
60% of the storage nodes, at the cost of an eleven-fold storage
overhead and an average messaging overhead of only 4 messages per node
and minute during normal operation. Glacier is used as the storage
layer for an experimental serverless email system.
Distributed, cooperative storage systems like FarSite and OceanStore
aggregate the often underutilized disk space and network bandwidth of
existing desktop computers, thereby harnessing a potentially huge and
self-scaling storage
resource (1,27). Distributed
storage is also a fundamental component of many other recent
decentralized systems, for instance, cooperative backup, serverless
messaging or distributed hash
tables (15,17,20,28,31).
Since individual desktop computers are not sufficiently dependable,
redundant storage is typically used in these systems to enhance data
availability. For instance, if nodes are assumed to fail
independently with probability p, a system of k replicas fails
with probability pk << p; the parameter k can be adjusted to achieve the desired level
of availability. Unfortunately, the assumption of failure
independence is not realistic (3,4,25,41,43).
In practice, nodes may be located in the same building, share the same
network link, or be connected to the same power grid.
Most importantly, many of the nodes may run the same software.
Results of our own recent survey of 199 random Gnutella nodes,
which is consistent with other statistics (34), showed
that 39% of the nodes were using the Morpheus client;
more than 80% were running the Windows operating system. A
failure or security vulnerability associated with a widely shared
software component can affect a majority of nodes within a short
period of time. Worse, worms that propagate via email, for instance,
can even infect computers within a firewalled corporate intranet.
On the other hand, stored data represents an important asset and has
considerable monetary value in many environments. Loss or corruption
of business data, personal records, calendars or even user email could
have catastrophic effects. Therefore, it is essential that a storage
system for such data be sufficiently dependable. One aspect of
dependability is the durability of a data object, which we
define, for the purposes of this paper, as the probability that a
specific data object will survive an assumed worst-case system
failure.
Large-scale correlated failures can be observed in the Internet, where
thousands of nodes are regularly affected by virus or worm
attacks. Both the frequency and the severity of these attacks have
increased dramatically in recent years (39).
So far, these attacks have rarely caused data losses. However, since
the malicious code can often obtain administrator privileges on
infected machines, the attackers could easily have erased the locals
disks had they intended to do serious harm.
In this paper, we describe Glacier, a distributed storage system that is robust
to large-scale correlated failures. Glacier's goal is to provide highly
durable, decentralized storage suitable for important and otherwise
unrecoverable data, despite the potential for correlated, Byzantine
failures of a majority of the participating storage nodes. Our approach
is `extreme' in the sense that, in contrast to other approaches (23,27),
we assume the exact nature of the correlation to be unpredictable. Hence,
Glacier must use redundancy to prepare for a wide range of failure scenarios.
In essence, Glacier trades efficiency in storage utilization for durability,
thus turning abundance into reliability.
Since Glacier does not make any
assumptions about the nature and correlation of faults, it can
provide hard, analytical durability guarantees. The system can be
configured to prevent data loss even under extreme conditions, such as
correlated failures with data loss on 85% of the storage nodes or
more.
Glacier makes use of erasure codes to spread data
widely among the participating storage nodes, thus generating a degree
of redundancy that is sufficient to survive failures of this
magnitude. Aggregation of small objects and a loosely coupled
fragment maintenance protocol reduce the message overhead for maintaining this
massive redundancy, while the use of erasure codes and garbage
collection of obsolete data mitigate the storage cost.
Despite these measures, there is a substantial storage cost for
providing strong durability in such a hostile environment. For
instance, to ensure an object survives a correlated failure of 60% of
the nodes with a probability of .999999, the storage overhead is
about 11-fold. Fortunately, disk space on desktop PCs is a vastly
underutilized resource. A recent study showed that on average, as much
as 90% of the local disk space is unused (9). At
the same time, disk capacities continue to follow Moore's law (22).
Glacier leverages this abundant but unreliable storage space to
provide durable storage for critical data. To the best of our
knowledge, Glacier is the first system to provide hard durability
guarantees in such a hostile environment.
The rest of this paper is structured as follows: In the next section,
we give an overview of existing solutions for ensuring long-term data
durability. Section 3 describes the assumptions we
made in the design of our system, and the environment it is intended
for. In the following two sections, we demonstrate how Glacier can
lend a distributed hash table data durability in the face of
large-scale correlated failures. We discuss security aspects in
Section 6 and describe our experimental evaluation
results in Section 7. Finally, Section 8
presents our conclusions.
OceanStore (27) and
Phoenix (23,24) apply
introspection to defend against the threat of correlated
failures. OceanStore relies primarily on inferring correlation by
observing actual failures, whereas Phoenix proactively infers possible
correlations by looking at the configuration of the system, e.g. their
operating system and installed software. In both systems, the
information is then used to place replicas of an object on nodes that
are expected to fail with low correlation.
However, the failure model can only make accurate predictions if it
reflects all possible causes of correlated failures. One
possible conclusion is that one has to carefully build a very detailed
failure model. However, a fundamental limitation of the introspective
approach is that observation does not reveal low-incidence failures
and it is difficult for humans to predict all sources of correlated
failures. For instance, a security vulnerability that exists in two
different operating systems due to a historically shared codebase is
neither observable, nor are developers or administrators likely to be
aware of it prior to its first exploit.
Moreover, introspection itself can make the system vulnerable to a
variety of attacks. Selfish node operators may have an incentive to
provide incorrect information about their nodes. For example, a user
may want to make her node appear less reliable to reduce her share of
the storage load, while an attacker may want to do the opposite in an
attempt to attract replicas of an object he wants to censor. Finally,
making failure-related information available to peers may be of
considerable benefit to an attacker, who may use it to choose
promising targets.
Introspective systems can achieve robustness to correlated failures
at a relatively modest storage overhead, but they assume an accurate
failure model, which involves risks that are hard to quantify.
Glacier is designed to provide very high data durability for important data.
Thus, it chooses a point in the design space that relies on minimal
assumptions about the nature of failures, at the expense of larger storage
overhead compared to introspective systems.
TotalRecall (5) is an example of a system
that uses introspection to optimize availability under churn. Since this
system does not give any worst-case guarantees, our criticism of
introspection does not apply to it.
OceanStore (27), like Glacier, uses
separate mechanisms to maintain short-term availability and to ensure
long-term durability. Unlike Glacier, OceanStore cannot sustain
Byzantine failures of a large fraction of storage
nodes (44).
Many systems use redundancy to guard against data loss. PAST (20)
and Farsite (1) replicate objects across multiple nodes,
while Intermemory (14),
FreeHaven (18), Myriad (13),
PASIS (45) and other systems (2) use
erasure codes to reduce the storage overhead for the redundant data.
Weatherspoon et al. (42) show that erasure
codes can achieve mean time to failures many orders of magnitude higher than
replicated systems with similar storage and bandwidth requirements.
However, these systems assume only small-scale correlated failures or
failure independence. Systems with support for remote writes typically rely on
quorum techniques or Byzantine fault tolerance to serialize writes and
thus cannot sustain a catastrophic failure.
Cates (12) describes a data management scheme
for distributed hashtables that keeps a small number of
erasure-coded fragments for each object to decrease fetch
latency and to improve robustness against small-scale fail-stop
failures. The system is not designed to sustain large-scale correlated
failures or Byzantine faults.
Glacier spends a high amount of resources to provide strong worst-case
durability guarantees. However, not all systems require this level of
protection; in some cases, it may be more cost-effective to optimize
for expected failure patterns. Keeton et al. (26)
present a quantitative discussion of the tradeoff between cost
and dependability.
Glacier uses leases to control the lifetime of stored objects, which
need to be periodically renewed to keep an object alive. Leases are a
common technique in distributed storage systems; for example, they have
been used in Tapestry (46) and
CFS (17).
A particularly common example of correlated failures are Internet worm
attacks. The course, scope and impact of these attacks has been studied
in great detail (29,30,38,39,47).
3 Assumptions and intended environment
In this section, we describe assumptions that underlie the design of
Glacier and the environment it is intended for.
Glacier is a decentralized storage layer providing data durability in
the event of large-scale, correlated and Byzantine storage node
failures. It is intended to be used in combination with a
conventional, decentralized replicating storage layer that handles
normal read and write access to the data. This primary storage
layer might typically keep a small number of replicas of each data
object, sufficient to mask individual node failures without loss in
performance or short-term availability.
Glacier is primarily intended for an environment consisting of desktop
computers within an organizational intranet, though some fraction of
nodes are assumed to be notebooks connected via a wireless LAN or home
desktops connected via cable modems or DSL. Consistent with this
environment, we assume modest amounts of churn and relatively good
network connectivity. A substantial fraction of the nodes is assumed
to be online most of the time, while the remaining nodes (notebooks
and home desktops) may be disconnected for extended periods of time.
In the following, we outline key assumptions underlying Glacier's
design.
We define the lifetime of a node as the time from the instant
when it first joins the system until it either permanently departs or
it loses its locally stored data. The session time of a node is
the time during which it remains connected to the overlay network. We
assume that the expected lifetime of a node is high, at least on the
order of several weeks. Without a reasonably long lifetime a
cooperative, persistent storage system is infeasible since the
bandwidth overhead of moving data between nodes would be
prohibitive (6). Glacier is intended for an
environment similar to the one described by Bolosky et
al. (8), where an expected lifetime of 290 days was reported.
However, session times can be much shorter, on the order of hours or
days. Nodes may go offline and return with their disk contents intact,
as would be expected of notebooks, home desktops, or desktops that are
turned off at night or during weekends.
3.2 Failure model
We assume that Glacier is in one of three operating modes at any given
time: normal, failure or recovery. During normal operation, only a small fraction of nodes is assumed to be
faulty at any time, though a strong minority of the nodes may be
off-line. In this mode, Glacier performs the background tasks of
aggregation, coding and storage of newly written data, garbage
collection, and fragment maintenance.
During a large-scale failure, a majority of the storage nodes,
but not more than a fraction fmax,
have suffered Byzantine failures virtually simultaneously. In this
mode, we cannot assume that communication within the system is
possible, and Glacier's role is limited to protecting the data stored
on non-faulty nodes. It is sufficient to choose fmax
as a loose upper bound, which can be estimated from the overall
amount of diversity in the system. The failure state is assumed to
last less than Glacier's object lease period LO.
Glacier enters recovery mode when sysadmins have recovered or
taken off-line enough of the faulty nodes so that communication within
the system is once again possible. In this mode, Glacier reconstitutes
aggregates from surviving fragments
and restores missing fragments. Note that Glacier does not
explicitly differentiate between the three modes.
Glacier assumes that the participating storage nodes form an overlay
network. The overlay is expected to provide a distributed directory
service that maps numeric keys to the address of a live node that is
currently responsible for the key. Glacier assumes that the set of
possible keys forms a circular space, where each live participating
node is responsible for an approximately uniformly sized segment of
the key space. This segment consists of all keys closest to the node's
identifier. Participating nodes store objects with keys in their
segment. If a node fails, the objects in its local store may be lost.
To prevent Sybil attacks (19), node identifiers
are assigned pseudo-randomly and it is assumed that an attacker cannot
acquire arbitrarily many legitimate node identifiers. This can be
ensured though the use of certified node
identifiers (10).
Structured overlay networks with a distributed hash table (DHT) layer
like DHash/Chord (16,40) or
PAST/Pastry (20,37) provide
such a service, though other implementations are possible. Glacier
requires that it can always reliably identify, authenticate and
communicate with the node that is currently responsible for a given
key. If the overlay provides secure routing techniques, such as those
described by Castro et al. (10), then
Glacier can tolerate Byzantine failures during normal operation.
Glacier assumes that the participating nodes have loosely synchronized
clocks, for instance by running NTP (33). Glacier does not depend
on the correctness of its time source, nor the correctness of the
overlay directory services during large-scale failures.
4 Glacier
The architecture of Glacier is depicted in Figure 1.
Glacier operates alongside a primary store, which maintains a
small number of full replicas of each data object (e.g., 2-3 replicas). The
primary store ensures efficient read and write access and provides
short-term availability of data by masking individual node
failures. Glacier acts as an archival storage layer, ensuring
long-term durability of data despite large-scale failure. The
aggregation layer, described in Section 5,
aggregates small objects prior to their insertion into Glacier for
efficiency. Objects of sufficient size can be inserted directly into
Glacier.
Figure 1:
Structure of a multi-tier system with Glacier and an additional aggregation layer.
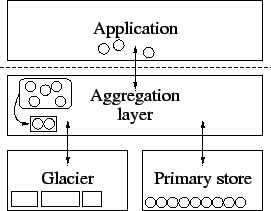 |
During normal operation, newly written or updated data objects are
aggregated asynchronously. Once a sufficiently large aggregate has
accumulated or a time limit is reached, Glacier erasure codes the
aggregate and places the fragments at pseudo-randomly selected storage
nodes throughout the system. Periodically, Glacier consolidates
remaining live objects into new aggregates, inserts the new fragments
and discards fragments corresponding to old aggregates.
Once an object is stored as part of an erasure coded aggregate,
Glacier ensures that the object can be recovered even if the system
suffers from a large-scale, correlated Byzantine failure. The
durability guarantee given by Glacier implies that, if the
failure affects a fraction f ≤ fmax of the
storage nodes, each object survives with probability P ≥ Pmin.
The parameters fmax and Pmin
determine the overhead and can be adjusted to the requirements of the
application.
Glacier ensures durability by spreading redundant data for each object
over a large number of storage nodes. These nodes periodically
communicate with each other to detect data loss, and to re-create
redundancy when necessary. After a large-scale failure event, Glacier
reconstitutes aggregates from surviving fragments and reinserts
objects into the primary store. The recovery proceeds gradually to
prevent network overload. Additionally, an on-demand primitive is
available to recover objects synchronously when requested by the
application.
Glacier is designed to protect data against Byzantine failures,
including a failures of the node that inserted an object. Therefore,
there are no primitives to either delete or overwrite existing data
remotely. However, leases are used to limit the time for which
an object is stored; when its lease expires, the object can be removed
and its storage is reclaimed. Application must renew the leases of all
objects they care about once per lease period. The lease period is
chosen to exceed the assumed maximal duration of a large-scale failure
event, typically several weeks or months. Also, since objects in
Glacier are effectively immutable, updated objects must be inserted
with a different version number.
Applications interact with Glacier by invoking one of the following
methods:
- put(i,v,o,l) stores an object o under identifier i and version number v,
with a lease period of l.
- get(i,v) -> o retrieves the object stored under identifier i and version number v.
If the object is not found, or if its lease has expired, nil is returned.
- refresh(i,v,l) extends the lease of an existing object. If the current lease period of the
object already exceeds l, the operation has no effect.
Glacier uses an erasure code (35) to reduce
storage overhead. We use a variant of
Reed-Solomon codes based on Cauchy matrices (7),
for which efficient codecs exist. However, any other erasure code could
be used as well. An object O of size |O| is recoded into
n fragments F1, F2, ..., Fn of size 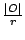 , any r of
which contain sufficient information to restore the entire object. If possible, each
fragment is stored on a different node, or fragment holder, to
reduce failure correlation among fragments. , any r of
which contain sufficient information to restore the entire object. If possible, each
fragment is stored on a different node, or fragment holder, to
reduce failure correlation among fragments.
If the object O is stored under a key k, then its fragments are stored
under a fragment key (k,i,v), where i is the index of the fragment
and v is a version number. For each version, Glacier maintains an independent
set of fragments. If an application creates new versions frequently, it can
choose to bypass Glacier for some versions and apply the corresponding
modifications to the primary storage system only.
For each object O, Glacier also maintains an authenticator
AO = (H(O), H(F1),H(F2),...,H(Fn),v,l)
where H(f) denotes a secure hash (e.g., SHA-1) of f. This is
necessary to detect and remove corrupted fragments during recovery,
since any modification to a fragment would cause the object to be
reconstructed incorrectly. The value l represents the lease associated
with the object; for permanent objects, the value 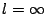 is used. is used.
The authenticator is part of a manifest MO, which
accompanies the object and each of its fragments. The manifest may
contain a cryptographic signature that authenticates the object and
each of its fragments; it can also be used to store metadata such as
credentials or billing information. For immutable objects that do not
require a specific, chosen key value, it is sufficient to choose MO=AO
and k=H(AO); this makes the object and each of its
fragments self-certifying.
In structured overlays like Pastry or Chord, keys are assigned to
nodes using consistent hashing. For instance, in Pastry, a key is
mapped to the live node with the numerically closest node identifier. In
the event of a node departure, keys are immediately reassigned to
neighboring nodes in the id space to ensure availability.
In Glacier, this is both unnecessary and undesirable because fragments
stored on nodes that are temporarily off-line do not need to be
available and therefore do not need to be reassigned. For this reason,
Glacier uses a modified assignment of keys to nodes, where keys are
assigned by consistent hashing over the set of nodes that are either
on-line or were last online within a period Tmax.
In order to determine which node should store a particular fragment (k,i,v),
Glacier uses a placement function P. This function
should have the following properties:
- Fragments of the same object should be placed on different,
pseudo-randomly chosen nodes to reduce
inter-fragment failure correlation.
- It must be possible to locate the fragments after a failure, even if all
information except the object's key is lost.
- Fragments of objects with similar keys should be grouped together so as to
allow the aggregation of maintenance traffic.
- The placement function should be stable, i.e. the node on which a
fragment is placed should change rarely.
A natural solution would be to use a `neighbor set', i.e. to map (k,i,v) to the i.th
closest node relative to k. Unfortunately,
this solution is not stable because the arrival of a new node in the
vicinity of k would change the placement of most fragments. Also,
choosing P(k,i,v) as the content hash of the corresponding fragment
is not a solution because it does not allow fragments to be located
after a crash. Instead, Glacier uses
This function maps the primary replica at position k and its n fragments to
n+1 equidistant points in the circular id space
(Figure 2). If multiple versions exist, the hash H(v)
prevents a load imbalance by placing their fragments on different nodes.
When a new object (k,v) must be inserted, Glacier uses the overlay
to send probe messages to each location P(k,i,v), i=1..N. If the owner of
P(k,i,v) is currently online, it responds to this message, and Glacier
sends the fragment directly to that node. Otherwise, the fragment is
discarded and restored later by the maintenance mechanism.
Figure 2:
Fragment placement in a configuration with five fragments and three replicas in the primary store.
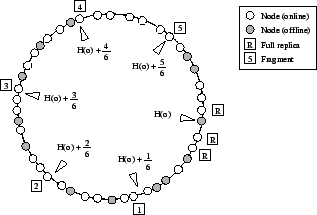 |
If the availability of the nodes is very low, there may be situations
where fewer than  fragment holders are online during insertion. In
this case, the inserting node sends additional probe messages, which
are answered by one of the owners' neighbors. These neighbors then
act as temporary fragment holders. When an owner rejoins the overlay,
its neighbors learn about it using the standard overlay mechanisms and
then deliver their fragments to the final destination. fragment holders are online during insertion. In
this case, the inserting node sends additional probe messages, which
are answered by one of the owners' neighbors. These neighbors then
act as temporary fragment holders. When an owner rejoins the overlay,
its neighbors learn about it using the standard overlay mechanisms and
then deliver their fragments to the final destination.
Ideally, all N fragments of each object would be available in the
network and stored on their respective fragment holders. However,
there are various reasons why real Glacier installations may deviate
from this ideal state: Nodes may miss fragment insertions due to
short-term churn, key space ownership may change due to node joins and
departures, and failures may cause some or all fragments stored on a
particular node to be lost. To compensate for these effects, and to
avoid a slow deterioration of redundancy, Glacier includes a
maintenance mechanism.
Fragment maintenance relies on the fact that the placement function
assigns fragments with similar keys to a similar set of nodes.
If we assume for a moment that the nodeId distribution is perfectly
uniform, each fragment holder has N-1 peers which are storing fragments
of the exact same set of objects as itself. Then, the following simple
protocol can be used:
- The node compiles a list of all the keys (k,v) in its local
fragment store, and sends this list to some of its peers.
- Each peer checks this list against its own fragment store and
replies with a list of manifests, one for each object missing from the list.
- For each object, the node requests k fragments from its peers,
validates each of the fragments against the manifest, and then computes the
fragment that is to be stored locally.
With realistic nodeId distributions, the local portion of key space may not perfectly
match that of the peer, so the node may have to divide up the list among
multiple nodes. In very small networks, the placement
function may even map more than one fragment to a single node,
which must be accounted for during maintenance.
Glacier uses Bloom filters as a compact representation for the lists.
To save space, these filters are parametrized such that they have a fairly
high collision rate of about 25%, which means that about one out of
four keys will not be detected as missing. However, the hash functions in
the Bloom filter are changed after every maintenance cycle. Since
maintenance is done periodically (typically once per hour), collisions
cannot persist, and every fragment is eventually recovered.
Glacier's maintenance process works whenever overlay communication is
possible. Thus, the same mechanism covers normal maintenance and
recovery after a large-scale failure. Compromised nodes either fail
permanently, in which case other nodes take over their key segments,
or they are eventually repaired and re-join the system with an empty
fragment store. In both cases, the maintenance mechanism eventually
restores full redundancy. Hence, there is no need for Glacier to
explicitly detect that a correlated failure has occurred.
However, care must be taken to prevent congestive collapse during
recovery. For this reason, Glacier limits the number of simultaneous
fragment reconstructions to a fixed number Rmax. Since the load spreads
probabilistically over the entire network, the number of requests at
any particular node is also on the order of Rmax. Since Glacier relies on TCP for
communication, this approach has the additional advantage of being
self-clocking, i.e. the load is automatically reduced when the network
is congested.
When the lease associated with an object expires, Glacier is no longer
responsible for maintaining its fragments and may reclaim
the corresponding storage. Since the lease is part of the authenticator,
which accompanies every fragment, this process can be carried out
independently by each storage node.
However, assuming closely synchronized clocks among the storage
nodes would be unrealistic. Therefore, fragments are not deleted
immediately; instead, they are kept for an additional
grace period TG, which is set to exceed the assumed maximal
difference among the clocks. During this time, the fragments are still
available for queries, but they are no longer advertised to other
nodes during maintenance. Thus, nodes that have already deleted their
fragments do not attempt to recover them.
Glacier has explicit protection against attacks on its time source,
such as NTP. This feature is discussed in
Section 6.
4.8 Configuration
Glacier's storage overhead is determined by the overhead for the erasure
code, which is 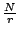 , while the message overhead is determined
by the number of fragments N that have to be maintained per object.
Both depend on the guaranteed durability Pmin
and the maximal correlated failure fraction fmax,
which are configurable. , while the message overhead is determined
by the number of fragments N that have to be maintained per object.
Both depend on the guaranteed durability Pmin
and the maximal correlated failure fraction fmax,
which are configurable.
Figure 3:
Number of fragments required for 99.9999% durability, and the
resulting storage overhead.
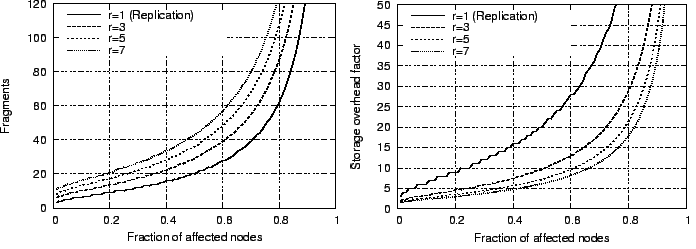 |
Since suitable values for N and r have to be chosen a
priori, i.e. before the failure has occurred, we do not know which
of the nodes are going to be affected. Hence, all we can assume is
that the unknown failure will affect any particular node with
probability fmax. Note that this differs from
the commonly assumed Byzantine failure model, where the attacker gets
to choose the nodes that will fail. In our failure model, the attacker
can only compromise nodes that share a common vulnerability, and these
are distributed randomly in the identifier space because of the
pseudo-random assignment of node identifiers.
Consider an object O whose N fragments are
stored on N different nodes. The effect of the unknown correlated failure
on O can be approximated by N Bernoulli trials; the object
can be reconstructed if at least r trials have a positive outcome, i.e. with probability
The parameters N and r should be chosen such that P meets the
desired level of durability. Figure 3 shows the
lower bound on N and the storage overhead for different assumed
values of fmax and for different choices of r.
Table 1 shows a few example configurations.
Table 1:
Example configurations for Glacier. For comparison, a
configuration with simple replication (r=1) is included.
Failure
fmax |
Durability
D |
Code
r |
Fragments
N |
Storage
S |
| 0.30 |
0.9999 |
3 |
13 |
4.33 |
| 0.50 |
0.99999 |
4 |
29 |
7.25 |
| 0.60 |
0.999999 |
5 |
48 |
9.60 |
| 0.70 |
0.999999 |
5 |
68 |
13.60 |
| 0.85 |
0.999999 |
5 |
149 |
29.80 |
| 0.63 |
0.999999 |
1 |
30 |
30.00 |
|
While D represents the durability for an individual object, the user is
probably more concerned about the durability of his entire collection of
objects. If we assume that the number of storages nodes is large and that
keys are assigned randomly (as is the case for content-hash keys), object
failures are independent, and the probability that a collection of n
objects survives the failure unscathed is PD(n) = Dn.
Figure 4 shows a graph of PD for different
values of D.
Figure 4:
Probability of survival for collections of multiple objects.
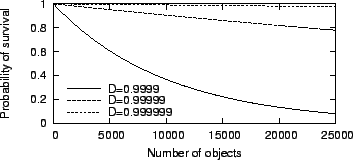 |
If the value for fmax is accidentally chosen
too low, Glacier still offers protection; the survival probability
degrades gracefully as the magnitude of the actual failure
increases. For example, if fmax=0.6 and
Pmin=0.999999 were chosen, P is still
0.9997 in a failure with f=0.7, and 0.975 for f=0.8.
This is different in an introspective system, where an incorrect failure
model can easily lead to a catastrophic data loss.
Another important parameter to consider is the lease time. If leases
are short, then storage utilization is higher, since obsolete
objects are removed more quickly; on the other hand, objects have to
be refreshed more often. Clearly, the lease time must exceed both the
maximal duration of a large-scale failure and the maximal absence of a
user's node from the system. In practice, we recommend leases on the
order of months. With shorter leases, users leaving for a long
vacation might accidentally lose some of their data if they keep their
machine offline during the entire time.
5 Object aggregation
Glacier achieves data durability using massive redundancy. As a
result, the number of internal objects Glacier must maintain is
substantially larger than the number of application objects stored in
Glacier. Each of these internal objects has a fixed cost; for example,
each fragment is stored together with a manifest, and its key must be
sent to other nodes during maintenance. To mitigate this cost, Glacier
aggregates small application objects in order to amortize the cost of
creating and maintaining fragments over a sufficient amount of
application data.
In Glacier, each user is assumed to access the system through one node
at a time. This node, which we call the user's proxy, holds the
user's key material and is the only node in the system trusted by the
user. All objects are inserted into Glacier from the object owner's
proxy node. A user can use different proxy nodes at different times.
When a user inserts objects into Glacier, they are buffered at the
user's proxy node. To ensure their visibility at
other nodes, the objects are immediately inserted into Glacier's
primary store, which is not aggregated. Once enough objects have been gathered or enough
time has passed, the buffered objects are inserted as a single object
into Glacier under an aggregate key. In the case of a proxy
failure while an object is buffered, the next refresh operation will
re-buffer the object for aggregation. Of course, buffered objects are
vulnerable to large-scale correlated failures. If this is not
acceptable, applications may invoke a
flush method for important objects, which ensures that an aggregate
with these objects is created and immediately stored in Glacier.
The proxy is also responsible for refreshing the owner's objects and
for consolidating aggregates that contain too many expired
objects. Performing aggregation and aggregate maintenance on a
per-user basis avoids difficult problems due to the lack of trust
among nodes. In return, Glacier foregoes the opportunity to bundle
objects from different users in the same aggregate and to eliminate
duplicate objects inserted by different users. In our experience, this
is a small price to pay for the simplicity and robustness Glacier
affords.
The proxy maintains a local aggregate directory, which maps
application object keys to the key of the aggregate that contains the
object. The directory is used when an object is refreshed and when an
object needs to be recovered in response to an application request.
After a failure of the proxy node, the directory needs to be
regenerated from the aggregates. To do so, an owner's aggregates are
linked in order of their insertion, forming a linked list, such that each aggregate contains
the key of the previously inserted aggregate. The head of the list is
stored in an application-specific object with a well-known key. To
avoid a circularity, this object is not subject to
aggregation in Glacier. The aggregate directory can be recovered
trivially by traversing the list.
Aggregates are reclaimed in Glacier once all of the contained objects
have expired. However, if aggregates expire in an order other than
their insertion order, the aggregate list might become
disconnected. To fix this problem, aggregates in the linked list may
contain references to multiple other aggregates; thus, the aggregates
actually form a directed acyclic graph (DAG, see
Figure 5).
Figure 5:
Reference graph. The object labeled `D' has expired.
 |
Glacier monitors the indegree of every aggregate in the DAG and tries to
keep it above a fixed number dmin. If the indegree of an
aggregate falls below this threshold, a pointer to it is added from the
next aggregate to be inserted. This requires little extra overhead as long
as insertions occur regularly; however, if a disconnection is imminent while
no objects are inserted for an extended period of time, an empty
aggregate may have to be created. This wastes a small amount of storage but,
in our experience, occurs very rarely.
Figure 6:
DAG of aggregates and the list head (left), and fragments of a single aggregate with the authenticator in detail (right).
 |
An aggregate consists of tuples (oi, ki, vi), where
oi is an object, ki is the object's key, and vi
is the version number. Additionally,
each aggregate contains one or more references to other aggregates. Note
that the leases of the component objects are not stored; they are kept only
in the aggregate directory, where they can be updated efficiently. The lease
of the entire aggregate is the maximum of the component leases; for efficiency, Glacier
tries to aggregate objects with similar leases.
After a correlated failure, we must assume that all information that
is not stored in Glacier is lost. In particular, this includes the
contents of the primary store and, for most nodes, the aggregate
directory.
The aggregate directory can be recovered by walking the DAG. First,
the key of the most recently inserted aggregate is retrieved using a
well-known key in Glacier. Then, the aggregates are retrieved in
sequence and objects contained in each aggregate are added to the
aggregate directory. The subleases of the component objects are set to
the lease of the aggregate. Since aggregate leases are always higher
than component leases, this is conservative. The primary store can
either be re-populated lazily on demand by applications, or eagerly
while walking the aggregate DAG.
Note that some of the references may be pointing to expired
aggregates, so some of the queries issued to Glacier will fail. It is
thus important to distinguish actual failures, in which at
least N-k+1 fragment holders have been contacted but no fragments are
found, from potential failures, in which some fragment holders
are offline. In the latter case, recovery of the corresponding
aggregate must be retried at a later time.
In order to maintain a low storage overhead, we use a mechanism
similar to the segment cleaning technique in
LFS (36). Glacier periodically checks the
aggregate directory for aggregates whose leases will expire soon, and
decides whether to renew their leases. If the aggregate in question
is small or contains many objects whose leases have already expired,
the lease is not renewed. Instead, the non-expired objects are
consolidated with new objects either from the local buffer or from
other aggregates, and a new aggregate is created. The old aggregate
is abandoned and its fragments are eventually garbage collected by the
storing nodes.
Consolidation is particularly effective if object lifetimes are
bimodal, i.e. if objects tend to be either short-lived or
long-lived. By the time of the first consolidation cycle, the
short-lived objects may have already expired, so the consolidated
aggregate contains mostly long-lived objects. Such an aggregate then
requires little maintenance, except for an occasional refresh
operation.
6 Security
In this section, we discuss potential attacks against either the
durability or the integrity of data stored in Glacier.
Attacks on integrity:
Since Glacier does not have remote delete or update operations,
a malicious attacker can only overwrite fragments that are stored on
nodes under his control.
However, each fragment holder stores a signed manifest, which includes
an authenticator. Using this authenticator, fragment holders can validate
any fragments they retrieve and replace them by other fragments if they
do not pass the test. Assuming, as is customary, that SHA-1 is second
pre-image resistant, generating a second fragment with the same hash value
is computationally infeasible.
Attacks on durability:
If an attacker can successfully destroy all replicas of an object in
the primary store, as well as more than n-r of its fragments, that
object is lost. However, since there is no way to delete fragments
remotely, the attacker can only accomplish this by either a targeted
attack on the storage nodes, or indirectly by interfering with
Glacier's fragment repair or lease renewal. The former requires
successful attacks on n-r specific nodes within a short time frame,
which is highly unlikely to succeed due to the pseudo-random selection
of storage nodes. The latter cannot go unnoticed because Glacier
relies on secure and authenticated overlay communication for fragment
repair and lease renewal. This leaves plenty of time for corrective
action by system administrators before too many fragments disappear
due to uncorrelated failures, churn or lease expiration.
Attacks on the time source:
Since the collection process is based on timestamps, an attacker might
try to destroy an object by compromising a time source such as an
NTP server and advancing the time beyond the object's expiration time.
For this reason, storage nodes internally maintain all timestamps as
relative values, translating them to absolute values only during shutdown
and when communicating with another node.
Space-filling attacks:
An attacker can try to consume all available storage by inserting a large
number of objects into Glacier. While this does not affect existing data,
no new data can be inserted because the nodes refuse to accept additional
fragments. Without a remote deletion primitive, the storage can only
be reclaimed gradually as the attacker's data expires. To prevent this
problem, incentive mechanisms (32) can be added.
Attacks on Glacier:
If a single implementation of Glacier is shared by all the nodes,
Glacier itself must be considered as a potential source of failure
correlation. However, data loss can result only due to a failure in
one of the two mechanisms that actually delete fragments, handoff and
expiration. Both are very simple (about 210 lines of code) and are
thus unlikely to contain bugs.
Haystack-needle attacks:
If an attacker can compromise his victim's personal node, he has, in the
worst case, access to the cryptographic keys and can thus sign valid
storage requests. Existing data cannot be deleted or overwritten; however,
the attacker can try to make recovery infeasible by inserting decoy
objects under existing keys, but with higher version numbers. The victim
is thus forced to identify the correct objects among a gigantic number of
decoys, which may be time-consuming or even infeasible.
However, notice that the attacker cannot compromise referential integrity.
Hence, if the data structures are linked (as, for example, the aggregate
log), the victim can recover them by guessing the correct key of a single
object. One way to facilitate this is to periodically insert reference objects
with well-known version numbers, such as the current time stamp. Thus,
knowledge of the approximate time of the attack is sufficient to recover
a consistent set of objects.
7 Experimental evaluation
To evaluate Glacier, we present the result of two sets of
experiments. The first set is based on the use of
Glacier as the storage layer for ePOST, a cooperative, serverless email
system (28) that provides email service to a small group of
users. ePOST has been in use for several months and it has
used Glacier as its data store for the past 140 days. The second set is
based on trace-driven simulations, which permit us to examine the system under a
wider range of conditions, including a much larger workload corresponding to
147 users, up to 1,000 nodes, a wider range of failure scenarios and
different types of churn.
The Glacier prototype is built on top of the
FreePastry (21) implementation of the
Pastry (37) structured overlay and makes use of
the PAST (20) distributed hash table service as its primary
store. Since the ePOST system relies on PAST for storage, Glacier now
provides durable storage for ePOST.
Over time, our experimental ePOST overlay grew from 20 to currently 35 nodes.
The majority of these nodes are desktop PCs running Linux; however, there
are also machines running OS X and Windows. Our user base consists of
8 passive users, which are still primarily using
server-based email but are forwarding their incoming mail to the
ePOST, and 9 active users, which rely on ePOST as
their main email system.
ePOST uses Glacier with aggregation to store email and the
corresponding metadata. For each object, Glacier maintains 48 fragments
using an erasure code with r=5, i.e. any five fragments are sufficient
to restore the object. In this configuration, each object can survive a
correlated failure of fmax=60% of all nodes with
probability Pmin=0.999999. We are aware of the
fact that with only 35 nodes, our experimental deployment is too small to
ensure that fragment losses are uncorrelated. Nevertheless, we chose this
configuration to get realistic numbers for the per-node overhead.
Each of the nodes in the overlay periodically writes statistics to
its log file, including the number of objects and aggregates it maintains,
the amount of storage consumed locally, and the number and type of
the messages sent. We combined these statistics to obtain a view of the
entire system.
While working with Glacier and ePOST, we were able to collect much practical
experience with the system. We had to handle several node failures, including
kernel panics, JVM crashes and a variety of software problems and configuration errors.
Also, there were some large-scale correlated failures; for instance, a configuration error
once caused an entire storage cluster of 16 nodes to become disconnected. Glacier was able to
handle all of these failures. Also, note that Glacier was still under active development
when it was deployed. During our experiments, we actually found two bugs, which we were
able to fix simply by restarting the nodes with the updated software.
We initially configured Glacier so that it would consider nodes to have failed if they
did not join the overlay for more than 5 days. However, it turned out that some of the
early ePOST adopters started their nodes only occasionally, so their regions of key space
were repeatedly taken over by their peers and their fragments reconstructed. Nevertheless,
we decided to include these results as well because they show how Glacier responds to an
environment that is heavily dynamic.
Figure 7:
Storage load in ePOST.
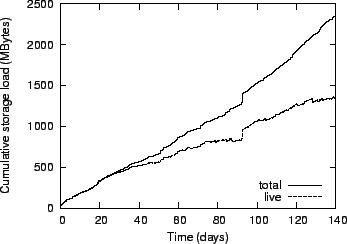 |
We first examined the workload generated by ePOST in our experimental
overlay. Figure 7 shows the cumulative size of
all objects inserted over time, as well as the size of the objects that
have not yet expired. Objects are inserted with an initial lease of one
month and are refreshed every day until they are no longer referenced.
Figure 8 shows a histogram of the object sizes. The
histogram is bimodal, with a high number of small objects ranging
between 1-10kB, and a lower number of large objects. Out of the 274,857 objects, less than
1% were larger than 600kB (the maximum was 9.1MB); these are not shown for readability. The small
objects typically contain emails and their headers, which are stored
separately by ePOST, while the large objects contain
attachments. Since most objects are small compared to the fixed-size
manifests used by Glacier (about 1kB), this indicates that
aggregation can considerably increase storage efficiency.
Figure 8:
Object sizes in ePOST.
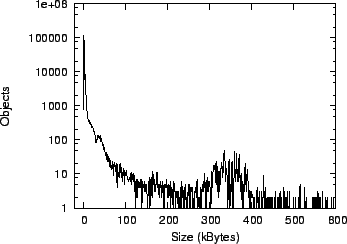 |
Next, we looked at the amount of storage required by Glacier to store
the above workload. Figure 9 shows the combined size
of all fragments in the system. The
storage grows slowly, as new email is entering the system; at the
same time, old email and junk mail is deleted by the users and
eventually removed by the garbage collector.
In this deployment, garbage is not physically deleted but rather moved
to a special trash storage, whose size is also shown. We used a lease time
of 30 days for all objects. For compatibility reasons, ePOST maintains
its on-disk data structures as gzipped XML. On average, this creates an
additional overhead of 32%, which is included in the figures shown.
Figure 9:
Storage consumed by Glacier fragments and trash.
 |
Figure 10:
Storage factor, including serialization overhead.
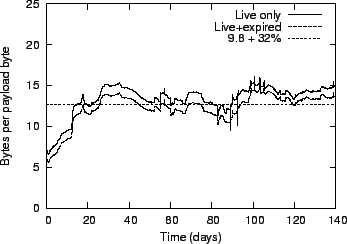 |
Figure 10 compares the size of the on-disk data
structures to the actual email payload. It shows the average number
of bytes Glacier stored for each byte of payload, excluding trash, but
including the 32% overhead from XML serialization, for live data
and for all data stored in Glacier. The average storage overhead over
time is very close to the expected factor of 9.6 plus the 32% due to
XML serialization.
Figure 11 shows the average traffic generated by an
ePOST node in bytes and in Pastry-level messages sent per minute (the messages
are sent over TCP, so small messages may share a single packet, and large
messages may require multiple packets). For comparison, we also report
traffic statistics for the other subsystems involved in ePOST, such
as PAST and Scribe (11).
Figure 11:
Average traffic per node and day (left) and average number of messages
per node and minute (right).
 |
The traffic pattern is heavily bimodal. During quiet periods (e.g. days 30-50),
Glacier generally sends fewer messages than PAST because it can mask short-term
churn, but since the messages are larger because of the difference in storage
factors (9.6 versus 3), the overall traffic is about the same. In periods
with a lot of node failures (e.g. days 80-120), Glacier must recover the
lost fragments by reconstructing them from other fragments, which creates
additional load for a short time. The increase in Pastry traffic on day 104
was caused by an unrelated change in Pastry's leaf set stabilization protocol.
The traffic generated by Glacier can be divided into five categories:
- Insertion: When new objects are inserted, Glacier identifies the fragment
holders and transfers the fragment payload to them.
- Refresh: When the leases for a set of objects are extended, Glacier sends
the updated part of the storage manifest to the current fragment holders.
- Maintenance: Peer nodes compare their key lists, and lost fragments
are regenerated from other fragments.
- Handoff: Nodes hand off some of their fragments to a new node who has
taken over part of their key space.
- Lookup: Aggregates are retrieved when an object is lost from the object
cache, or when small aggregates are consolidated into larger ones.
In Figure 12, the Glacier traffic is broken down by
category. In times with a low number of failures, the traffic is
dominated by insertions and refreshes. When the network is unstable,
the fraction of handoff and maintenance traffic increases. In all
cases, the maintenance traffic remains below 15 packets per
host and minute, which is very low.
Figure 12:
Messages sent by Glacier, by activity.
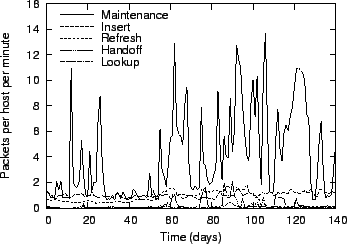 |
To determine the effectiveness of aggregation, we also collected statistics
on the number of objects and aggregates in the system. We distinguished between
live objects, whose lease is still valid, and expired objects,
which are still stored as part of an aggregate but are eligible for
garbage collection.
Figure 13:
Aggregation factor.
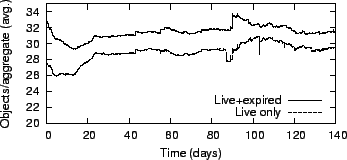 |
Figure 13 shows the average number of objects in
each aggregate. In our system, aggregation reduced the number of keys by
more than an order of magnitude. Moreover, our results show that the
number of expired objects remains low, which indicates that aggregate
consolidation is effective.
To study Glacier's behavior in the event of a large-scale correlated
failure, we randomly selected 13 of the 31 nodes in our experimental
ePOST overlay and copied their local fragment store to 13 fresh
nodes (note that, since our overlay has fewer than N=48 nodes, some nodes
store more than one fragment of the same object). The primary PAST store
and the metadata were not copied. We then started a new Pastry overlay
with only these 13 nodes. The resulting situation corresponds to a 58%
failure in the main overlay, which is close to our assumed fmax=60%.
We then completely re-installed ePOST on a fourteenth node and let it
join the ring. One of the authors entered his email address and an
approximate date when he had last used ePOST. From this information,
ePOST first determined the key of its metadata backup in Glacier by
hashing the email address; then it retrieved the backup and extracted
from it the root key of the aggregate DAG. The aggregation layer then
reconstructed the DAG and restored the objects in it to the primary store.
This process took approximately one hour to complete but could be sped up
significantly by adding some simple optimizations. Afterwards, ePOST
was again ready for use; all data that had been stored using Glacier
was fully recovered.
7.7 Simulations: Diurnal behavior
For this and the following experiments, we used a trace-driven
simulator that implements Glacier and the aggregation layer. Since we
wanted to model a system similar to
ePOST, we used a trace from our department's email server, which
contains 395,350 delivery records over a period of one week
(09/15-09/21). Some email is carbon-copied to multiple recipients; we
delivered each copy to a separate node, for a total of 1,107,504
copies or approximately 8 GBytes. In the simulation, Glacier
aggregates of up to 100 objects using a simple, greedy first-fit
policy.
In our first simulation, we explore the impact of diurnal short-term
churn. In their study of a large deployment of desktop machines,
Bolosky et al. (8) report that the number
of available machines, which was generally around approximately
45,000, dropped by about 2,500 (5.5%) at night time and by about
5,000 (11.1%) during weekends. In our simulations, we modeled a
ring of 250 nodes with the behavior from the study, where
M% of the nodes are unavailable between 5pm and 7am on weekdays and
2M% on weekends. The experiment was run for one week of simulation time,
starting from Wednesday, 09/15, and the entire trace was used. Glacier
was configured with the maximum offline time Tmax
set to one week.
Figure 14:
Impact of diurnal short-term churn on message overhead.
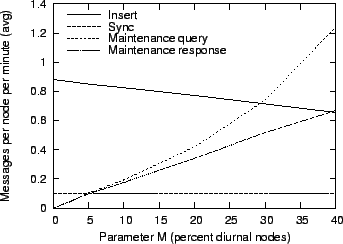 |
Figure 14 shows how this behavior affects the total message overhead,
which includes all messages sent over the entire week, for different values of M.
As churn increases, fewer fragments can be delivered directly to their respective
fragment holders, so insertion traffic decreases. However, the lost fragments must
be recovered when the fragment holders come back online, so the maintenance overhead
increases. As an additional complication, the probability that fragments are available
at the designated fragment holder decreases, so maintenance requires more attempts to
successfully fetch a fragment. This causes the disparity between maintenance requests
and replies, which are shown separately in the figure.
In our second simulation, we study how the load influences the message
overhead. We again used a overlay of 250 nodes and the trace from our mail server, but
this time, we used only a fraction f of the messages. Instead of diurnal churn,
we simulated uncorrelated short-term churn with a mean session time of 3 days and a
mean pause time of 16 hours, as well as long-term churn with a mean node lifetime
of 8 days. We varied the parameter f between 0 and 1.
Figure 15:
Impact of increasing load on message overhead.
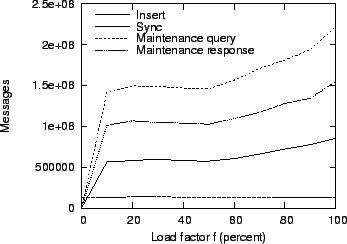 |
Figure 15 shows how the load influences the cumulative
message overhead over the entire week. Under light load, the message overhead remains
approximately constant. This is because aggregates are formed periodically by every
node, even if less than 100 objects are available in the local buffer. As the load
increases further, the increase in overhead is approximately linear, as expected.
Figure 16 shows the same overhead in bytes. Here,
the threshold effect does not appear. Also, note the high maintenance
overhead, as expected. This is due to the aggressive parameters we
used for churn; at a node lifetime of eight days, almost all the nodes
are replaced at least once during the simulation period, their local
fragment store being fully regenerated every time. For their desktop
environment, Bolosky et al. (8) report an
expected machine lifetime of 290 days and low short-term churn,
which would reduce the maintenance overhead considerably.
Figure 16:
Impact of increasing load on total traffic.
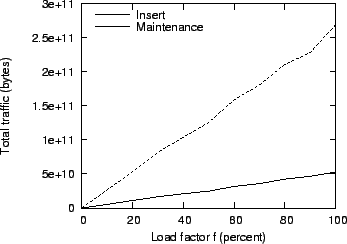 |
In our third simulation, we examine Glacier's scalability in terms of the number of
participating nodes. We used the same trace as before, but scaled it such that the
storage load per node remained constant; the full trace was used for our maximum
setting of N=1000 nodes. The churn parameters are the same as before.
Figure 17:
Message overhead for different overlay sizes and a constant per-node storage
load.
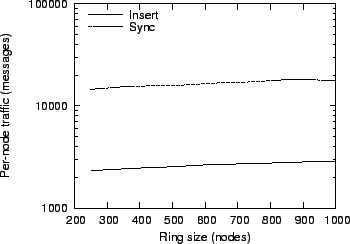 |
Figure 17 shows the message overhead per node for
different overlay sizes. As expected, the net overhead remains
approximately constant; however, since query messages are sent using
the Pastry overlay, the total number of messages grows slowly with N log N.
The storage overhead required to sustain large-scale correlated
failures is substantial. In our experiments, we used fairly
aggressive parameters (fmax=60%, Pmin=0.999999), which resulted in an
11-fold storage overhead. However, this cost is mitigated by the fact
that Glacier can harness vast amounts of underutilized storage that is
unreliable in its raw form. Moreover, only truly important and otherwise
unrecoverable data
must be stored in a high-durability Glacier store and is thus subject
to large storage overhead. Data of lesser importance and data that can
be regenerated after a catastrophic failure can be stored with far less
overhead in a separate instance of Glacier that is configured with a
less stringent durability requirement.
On the other hand, our experiments show that Glacier is able to manage
this large amount of data with a surprisingly low maintenance overhead
and that it is scalable both with respect to load and system
size. Thus, it fulfills all the requirements for a cooperative storage
system that can leverage unused disk space and provide hard,
analytical durability guarantees, even under pessimistic failure
assumptions. Moreover, our experience with the
ePOST deployment shows that the system is practical, and that it can
effectively protect user data from large-scale correlated
failures. The ever-increasing number of virus and worm attacks
strongly suggests that this property is crucial for cooperative storage
system.
8 Conclusions
We have presented the design and evaluation of Glacier, a system that
ensures durability of unrecoverable data in a cooperative,
decentralized storage system, despite large-scale, correlated,
Byzantine failures of storage nodes. Glacier's approach is `extreme'
in the sense that it does not rely on introspection, which has inherent
limitations in its ability to capture all sources of correlated failures;
instead, it uses massive redundancy to mask the effects of
large-scale correlated failures such as worm attacks. The system
uses erasure codes and garbage collection to mitigate the
storage cost of redundancy and relies on aggregation and a
loosely coupled fragment maintenance protocol to reduce the
message costs. Our experience with a real-world deployment shows that
the message overhead for maintaining the erasure coded fragments is
low. The storage overheads can be substantial when the availability
requirements are high and a large fraction of nodes is assumed to
suffer correlated failures. However, cooperative storage systems
harness a potentially huge amount of storage. Glacier uses this raw,
unreliable storage to provide hard durability guarantees, which is
required for important and otherwise unrecoverable data.
This paper has benefited considerably from the comments of the
anonymous NSDI reviewers and our shepherd, Mike Dahlin.
This research was supported in part by Texas ATP (003604-0079-2001),
by NSF (ANI-0225660, https://project-iris.net) and by gifts from
Microsoft Research and from Intel Research.
- 1
-
A. Adya, W. J. Bolosky, M. Castro, G. Cermak, R. Chaiken, J. R. Douceur,
J. Howell, J. R. Lorch, M. Theimer, and R. P. Wattenhofer.
FARSITE: Federated, available, and reliable storage for an
incompletely trusted environment.
In Proc. OSDI, Boston, MA, Dec 2002.
- 2
-
N. Alon, H. Kaplan, M. Krivelevich, D. Malkhi, and J. Stern.
Scalable secure storage when half the system is faulty.
In Proc. ICALP, 2000.
- 3
-
Y. Amir and A. Wool.
Evaluating quorum systems over the internet.
In Proc. 26th Annual Intl. Symposium on Fault-Tolerant Computing
(FTCS '96), page 26. IEEE Computer Society, 1996.
- 4
-
M. Bakkaloglu, J. J. Wylie, C. Wang, and G. R. Ganger.
On correlated failures in survivable storage systems.
Technical Report Carnegie Mellon CMU-CS-02-129, May 2002.
- 5
-
R. Bhagwan, K. Tati, Y. Cheng, S. Savage, and G. M. Voelker.
TotalRecall: System support for automated availability management.
In Proc. NSDI, San Francisco, CA, Mar 2004.
- 6
-
C. Blake and R. Rodrigues.
High availability, scalable storage, dynamic peer networks: Pick two.
In Proc. HotOS, pages 1-6, Lihue, HI, May 2003.
- 7
-
J. Bloemer, M. Kalfane, M. Karpinski, R. Karp, M. Luby, and D. Zuckerman.
An XOR-based erasure-resilient coding scheme.
Technical Report ICSI TR-95-048, August 1995.
- 8
-
W. J. Bolosky, J. R. Douceur, D. Ely, and M. Theimer.
Feasibility of a serverless distributed file system deployed on an
existing set of desktop PCs.
In Proc. Intl. Conference on Measurement and Modeling of
Computer Systems, Santa Clara, CA, June 2000.
- 9
-
A. R. Butt, T. A. Johnson, Y. Zheng, and Y. C. Hu.
Hoard: A peer-to-peer enhancement for the network file system.
Technical Report Purdue University ECE-03-08, 2003.
- 10
-
M. Castro, P. Druschel, A. Ganesh, A. Rowstron, and D. S. Wallach.
Secure routing for structured peer-to-peer overlay networks.
In Proc. OSDI, Boston, MA, Dec 2002.
- 11
-
M. Castro, P. Druschel, A.-M. Kermarrec, and A. Rowstron.
SCRIBE: A large-scale and decentralized application-level multicast
infrastructure.
IEEE JSAC, 20(8), Oct. 2002.
- 12
-
J. Cates.
Robust and efficient data management for a distributed hash table.
Master's thesis, Massachusetts Institute of Technology, May 2003.
- 13
-
F. W. Chang, M. Ji, S.-T. A. Leung, J. MacCormick, S. E. Perl, and L. Zhang.
Myriad: Cost-effective disaster tolerance.
In Proc. FAST, pages 103-116. USENIX Association, 2002.
- 14
-
Y. Chen, J. Edler, A. Goldberg, A. Gottlieb, S. Sobti, and P. Yianilos.
A prototype implementation of archival intermemory.
In Proc. 4th ACM Conference on Digital Libraries (DL'99), 1999.
- 15
-
L. P. Cox, C. D. Murray, and B. D. Noble.
Pastiche: Making backup cheap and easy.
In Proc. OSDI, Boston, MA, Dec 2002.
- 16
-
F. Dabek, E. Brunskill, M. F. Kaashoek, D. Karger, R. Morris, I. Stoica, and
H. Balakrishnan.
Building peer-to-peer systems with chord, a distributed lookup
service.
In Proc. HotOS, Schloss Elmau, Germany, May 2001.
- 17
-
F. Dabek, M. F. Kaashoek, D. Karger, R. Morris, and I. Stoica.
Wide-area cooperative storage with CFS.
In Proc. SOSP, Banff, Canada, Oct 2001.
- 18
-
R. Dingledine, M. J. Freedman, and D. Molnar.
The Free Haven project: Distributed anonymous storage service.
In Proc. Workshop on Design Issues in Anonymity and
Unobservability (LNCS 2009), July 2000.
- 19
-
J. R. Douceur.
The Sybil attack.
In Proc. of IPTPS, March 2002.
- 20
-
P. Druschel and A. Rowstron.
PAST: a large-scale, persistent peer-to-peer storage utility.
In Proc. HotOS, Schloss Elmau, Germany, May 2001.
- 21
-
The FreePastry web site.
https://freepastry.rice.edu/.
- 22
-
E. Grochowski.
Emerging trends in data storage on magnetic hard disk drives.
Datatech, pages 11-16, Sep 1998.
- 23
-
F. Junqueira, R. Bhagwan, A. Hevia, K. Marzullo, and G. M. Voelker.
Surviving internet catastrophes.
In Proc. 2005 Usenix Annual Technical Conference, Apr 2005.
- 24
-
F. Junqueira, R. Bhagwan, K. Marzullo, S. Savage, and G. M. Voelker.
The Phoenix recovery system: Rebuilding from the ashes of an
internet catastrophe.
In Proc. HotOS, Lihue, HI, May 2003.
- 25
-
F. Junqueira and K. Marzullo.
Designing algorithms for dependent process failures.
In Proc. Intl. Workshop on Future Directions in Distributed
Computing (FuDiCo), 2002.
- 26
-
K. Keeton, C. Santos, D. Beyer, J. Chase, and J. Wilkes.
Designing for disasters.
In Proc. FAST, Mar 2004.
- 27
-
J. Kubiatowicz, D. Bindel, Y. Chen, S. Czerwinski, P. Eaton, D. Geels,
R. Gummadi, S. Rhea, H. Weatherspoon, W. Weimer, C. Wells, and B. Zhao.
OceanStore: An architecture for global-scale persistent storage.
In Proc. ASPLOS, Nov 2000.
- 28
-
A. Mislove, A. Post, C. Reis, P. Willmann, P. Druschel, D. S. Wallach,
X. Bonnaire, P. Sens, J.-M. Busca, and L. Arantes-Bezerra.
POST: A secure, resilient, cooperative messaging system.
In Proc. HotOS, Lihue, HI, May 2003.
- 29
-
D. Moore, V. Paxson, S. Savage, C. Shannon, S. Staniford, and N. Weaver.
Inside the Slammer worm.
IEEE Security and Privacy, 1(4):33-39, Jul 2003.
- 30
-
D. Moore, C. Shannon, and J. Brown.
Code-Red: A case study on the spread and victims of an internet
worm.
In Proc. 2nd ACM Internet Measurement Workshop, 2002.
- 31
-
A. Muthitacharoen, R. Morris, T. Gil, and B. Chen.
Ivy: A read/write peer-to-peer file system.
In Proc. OSDI, Boston, MA, December 2002.
- 32
-
T.-W. Ngan, D. S. Wallach, and P. Druschel.
Enforcing fair sharing of peer-to-peer resources.
In Proc. IPTPS, Berkeley, CA, Feb 2003.
- 33
-
Network time protocol (version 3) specification, implementation and analysis.
RFC 1305.
- 34
-
Onestat.com.
https://www.onestat.com/.
- 35
-
M. O. Rabin.
Efficient dispersal of information for security, load balancing, and
fault tolerance.
J. ACM, 36(2):335-348, 1989.
- 36
-
M. Rosenblum and J. K. Ousterhout.
The design and implementation of a log-structured file system.
In Proc. SOSP, pages 1-15. ACM Press, 1991.
- 37
-
A. Rowstron and P. Druschel.
Pastry: Scalable, distributed object location and routing for
large-scale peer-to-peer systems.
In Proc. Middleware, pages 329-350, Heidelberg, Germany, Nov
2001.
- 38
-
E. H. Spafford.
The internet worm incident.
Technical Report Purdue CSD-TR-933, West Lafayette, IN 47907-2004,
1991.
- 39
-
S. Staniford, V. Paxson, and N. Weaver.
How to 0wn the internet in your spare time.
In Proc. USENIX Security, Aug 2002.
- 40
-
I. Stoica, R. Morris, D. Karger, M. F. Kaashoek, and H. Balakrishnan.
Chord: A scalable peer-to-peer lookup service for internet
applications.
In Proc. ACM SIGCOMM, pages 149-160, San Diego, CA, August
2001.
- 41
-
D. Tang and R. K. Iyer.
Analysis and modeling of correlated failures in multicomputer
systems.
IEEE Trans. Comput., 41(5):567-577, 1992.
- 42
-
H. Weatherspoon and J. Kubiatowicz.
Erasure coding vs. replication: A quantitative comparison.
In Proc. IPTPS, MIT Faculty Club, Cambridge, MA, Mar 2002.
- 43
-
H. Weatherspoon, T. Moscovitz, and J. Kubiatowicz.
Introspective failure analysis: Avoiding correlated failures in
peer-to-peer systems.
In Proc. International Workshop on Reliable Peer-to-Peer
Distributed Systems, Oct 2002.
- 44
-
C. Wells.
The OceanStore archive: Goals, structures, and self-repair.
U.C. Berkeley Masters Report, May 2002.
- 45
-
J. J. Wylie, M. W. Bigrigg, J. D. Strunk, G. R. Ganger, H. Kiliccote, and P. K.
Khosla.
Survivable information storage systems.
IEEE Computer, 33(8):61-68, Aug 2000.
- 46
-
B. Y. Zhao, J. D. Kubiatowicz, and A. D. Joseph.
Tapestry: An infrastructure for fault-tolerant wide-area location and
routing.
Technical Report U.C. Berkeley UCB//CSD-01-1141, Apr 2001.
- 47
-
C. C. Zou, W. Gong, and D. Towsley.
Code red worm propagation modeling and analysis.
In Proc. 9th ACM Conference on Computer and Communication
Security (CCS'02), Washington, DC, Nov 2002.
|


![]() fragment holders are online during insertion. In
this case, the inserting node sends additional probe messages, which
are answered by one of the owners' neighbors. These neighbors then
act as temporary fragment holders. When an owner rejoins the overlay,
its neighbors learn about it using the standard overlay mechanisms and
then deliver their fragments to the final destination.
fragment holders are online during insertion. In
this case, the inserting node sends additional probe messages, which
are answered by one of the owners' neighbors. These neighbors then
act as temporary fragment holders. When an owner rejoins the overlay,
its neighbors learn about it using the standard overlay mechanisms and
then deliver their fragments to the final destination.
![]() , while the message overhead is determined
by the number of fragments N that have to be maintained per object.
Both depend on the guaranteed durability Pmin
and the maximal correlated failure fraction fmax,
which are configurable.
, while the message overhead is determined
by the number of fragments N that have to be maintained per object.
Both depend on the guaranteed durability Pmin
and the maximal correlated failure fraction fmax,
which are configurable.