


Next: Incremental State Processing
Up: Handling Large States
Previous: Managing Memory Resources
Time Taken for a Transition
The basic step of CMC consists of a transition, which generates a
single successor from a particular state. A transition consists of the
following steps.
- State Restoring: First, CMC restores the system to the
desired start state of the transition.
- Executing the Transition: After restoring the state,
CMC transfers control to one of the enabled threads in the system.
The thread executes the TCP code to process a specific input
event such as a packet reception or a timeout.
- Computing the Hash: When the thread yields control back to
CMC, the implementation state, as modified by the thread, represents the
successor state of the transition. To store this state in the hash
table, CMC computes a signature and a hash value (that determines the
location of the signature in the hash table) for the state. Additionally,
CMC might perform state transformations (§5.1)
before this hash computation.
- State Storing: If the successor state is not present in
the hash table, CMC queues a copy of the successor state for further
exploration.
Thus, each transition requires at least three traversals of the state
contents. When the state is hundreds of kilobytes, naively performing
these traversals leads to a poor memory cache performance, considerably
slowing the model checker. Table 2 shows the time taken
for a transition when CMC processes the entire state contents during the
transition. In this case, each transition takes around 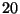 milliseconds.
At this rate, CMC can run for weeks without running out of memory. (A
gigabyte hash table can easily store
milliseconds.
At this rate, CMC can run for weeks without running out of memory. (A
gigabyte hash table can easily store 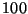 million states, and for the TCP
model, only one in five transitions generate a new state.)
million states, and for the TCP
model, only one in five transitions generate a new state.)
From Table 2, we can see that the hash computation is the
most expensive step in a transition; CMC spends more than 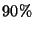 of its
time computing the signature and the hash value of the state. While saving
and restoring states involve simple memory copies, hash computation
requires performing a few arithmetic operations for
every byte of the state.
of its
time computing the signature and the hash value of the state. While saving
and restoring states involve simple memory copies, hash computation
requires performing a few arithmetic operations for
every byte of the state.


Next: Incremental State Processing
Up: Handling Large States
Previous: Managing Memory Resources
Madanlal Musuvathi
2004-03-03

![]() milliseconds.
At this rate, CMC can run for weeks without running out of memory. (A
gigabyte hash table can easily store
milliseconds.
At this rate, CMC can run for weeks without running out of memory. (A
gigabyte hash table can easily store ![]() million states, and for the TCP
model, only one in five transitions generate a new state.)
million states, and for the TCP
model, only one in five transitions generate a new state.)
![]() of its
time computing the signature and the hash value of the state. While saving
and restoring states involve simple memory copies, hash computation
requires performing a few arithmetic operations for
every byte of the state.
of its
time computing the signature and the hash value of the state. While saving
and restoring states involve simple memory copies, hash computation
requires performing a few arithmetic operations for
every byte of the state.