|
NSDI '04 Paper
[NSDI '04 Technical Program]
Efficient Routing for Peer-to-Peer Overlays
Anjali Gupta, Barbara Liskov, and Rodrigo Rodrigues
MIT Computer Science and Artificial Intelligence Laboratory
{anjali,liskov,rodrigo}@csail.mit.edu
Abstract:
Most current peer-to-peer lookup schemes keep a small amount of
routing state per node, typically logarithmic in the number of overlay
nodes. This design assumes that routing information at each member
node must be kept small, so that the bookkeeping required to respond
to system membership changes is also small, given that aggressive
membership dynamics are expected. As a consequence, lookups have high latency as
each lookup requires contacting several nodes in sequence.
In this paper, we question these assumptions by presenting two peer-to-peer
routing algorithms with small lookup paths. First, we present a
one-hop routing scheme. We show how to disseminate information about
membership changes quickly enough so that nodes maintain accurate
routing tables with complete membership information. We also deduce
analytic bandwidth requirements for our scheme that demonstrate
its feasibility.
We also propose a two-hop routing scheme for large scale systems of
more than a few million nodes, where the bandwidth requirements of
one-hop routing can become too large.
This scheme keeps a fixed
fraction of the total routing state on each node, chosen such that
the first hop has low latency, and thus the additional delay is
small.
We validate our analytic model using simulation results that show
that our algorithms can maintain routing information sufficiently
up-to-date such that a large fraction (e.g., 99%) of the queries
will succeed without being re-routed.
Introduction
Structured peer-to-peer overlays like
Chord [15], CAN [11],
Pastry [13], and Tapestry [18] provide a
substrate for building large-scale distributed applications. These
overlays allow applications to locate objects stored in the system in
a limited number of overlay hops.
Peer-to-peer lookup algorithms strive to maintain a small amount of
per-node routing state - typically 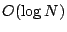 - because their
designers expect
that system membership changes frequently. This expectation has been
confirmed for successfully deployed systems. A recent
study [14] shows that the average session time in
Gnutella is only - because their
designers expect
that system membership changes frequently. This expectation has been
confirmed for successfully deployed systems. A recent
study [14] shows that the average session time in
Gnutella is only 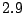 hours. This is equivalent to saying that in a
system with hours. This is equivalent to saying that in a
system with 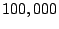 nodes, there are about nodes, there are about 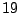 membership change
events per second. membership change
events per second.
Maintaining small tables helps keep the amount of bookkeeping required
to deal with membership changes small. However, there is a price to
pay for having only a small amount of routing state per node: lookups
have high latency since each lookup requires contacting several nodes
in sequence.
This paper questions the need to keep routing state small. We take
the position that maintaining full routing state (i.e., a complete
description of system membership) is viable even in a very large
system, e.g., containing a million nodes. We present techniques that
show that in systems of this size, nodes can maintain membership
information accurately yet the communication costs are low. The
results imply that a peer-to-peer system can route very efficiently
even though the system is large and membership is changing rapidly.
We present a novel peer-to-peer lookup system that maintains complete
membership information at each node. We show analytic results that
prove that the system meets our goals of reasonable accuracy and
bandwidth usage. It is, of course, easy to achieve these goals for
small systems. Our algorithm is designed to scale to large
systems. Our analysis shows that we can use one-hop routing for
systems of up to a few millions of nodes.
Our analysis also shows that beyond a few million nodes, the bandwidth
requirements of the one-hop scheme become too large. We present
the design of a two-hop lookup scheme that overcomes this problem,
and still provides faster lookups than existing peer-to-peer routing
algorithms. We also present an analytic model of the two-hop system
and conclude that its bandwidth requirements are reasonable, even for
systems with tens of millions of nodes.
Finally, the paper presents simulation results that corroborate what
our analytic models predict. We also show that performance does not
degrade significantly as the system becomes larger or smaller than
due to aggressive system dynamics.
The rest of the paper is organized as follows. Section 2
presents our system model. Sections 3
and 4 describe our one-hop and two-hop routing schemes,
respectively. Section 5 evaluates our
system. We conclude
with a discussion of what we have accomplished.
System Model
We consider a system of 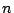 nodes, where nodes, where 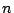 is a large number like is a large number like
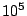 or or 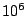 . We assume dynamic membership behavior as in
Gnutella, which is representative of an open Internet
environment. From the study of Gnutella and
Napster [14], we deduce that systems of . We assume dynamic membership behavior as in
Gnutella, which is representative of an open Internet
environment. From the study of Gnutella and
Napster [14], we deduce that systems of 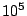 and and
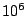 nodes would show around 20 and 200 membership changes per
second, respectively. We call this rate nodes would show around 20 and 200 membership changes per
second, respectively. We call this rate 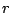 . We refer to membership changes
as events in the rest of the paper. . We refer to membership changes
as events in the rest of the paper.
Every node in the overlay is assigned a random 128-bit node
identifier. Identifiers are ordered in an identifier ring
modulo 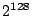 . We assume that identifiers are generated such that
the resulting set is uniformly distributed in the identifier space,
for example, by setting a node's identifier to be the cryptographic
hash of its network address. Every node has a predecessor and a
successor in the identifier ring, and it periodically sends keep-alive
messages to these nodes. . We assume that identifiers are generated such that
the resulting set is uniformly distributed in the identifier space,
for example, by setting a node's identifier to be the cryptographic
hash of its network address. Every node has a predecessor and a
successor in the identifier ring, and it periodically sends keep-alive
messages to these nodes.
Similarly, each item has a 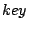 , which is also an identifier in the
ring. Responsibility for an item (e.g., providing storage for it)
rests with its successor; this is the first node in the identifier ring
clockwise from , which is also an identifier in the
ring. Responsibility for an item (e.g., providing storage for it)
rests with its successor; this is the first node in the identifier ring
clockwise from 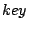 . This mapping from keys to nodes is based on the
one used in Chord [15], but changing our system to
use other mappings is straightforward. . This mapping from keys to nodes is based on the
one used in Chord [15], but changing our system to
use other mappings is straightforward.
Clients issue queries that try to reach the successor node of a
particular identifier. We intend our system to satisfy a large
fraction, 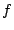 , of the queries correctly on the first attempt
(where each attempt requires one or two hops, depending on which
scheme we use). Our goal is to support high values of , of the queries correctly on the first attempt
(where each attempt requires one or two hops, depending on which
scheme we use). Our goal is to support high values of 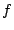 , e.g., , e.g.,
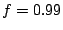 . A query may fail in its first attempt due to a membership
change, if the notification of the change has not reached the querying
node. In such a case, the query can still be rerouted and succeed in a
higher number of hops. Nevertheless, we define failed queries as
those that are not answered correctly in the first attempt, as
our objective is to have one- or two-hop lookups, depending on which
algorithm we use. . A query may fail in its first attempt due to a membership
change, if the notification of the change has not reached the querying
node. In such a case, the query can still be rerouted and succeed in a
higher number of hops. Nevertheless, we define failed queries as
those that are not answered correctly in the first attempt, as
our objective is to have one- or two-hop lookups, depending on which
algorithm we use.
One Hop Lookups
This section presents the design and analysis of our one-hop scheme.
In this scheme, every node maintains a full routing table containing
information about every other node in the overlay. The actual query
success rate depends on the accuracy of this information.
Section 3.1 describes how the algorithm handles
membership changes, namely how to convey information about these
changes to all the nodes in the ring. Section 3.2
explains how the algorithm reacts to node failures and presents an
informal correctness argument for our approach.
Section 3.3 discusses issues about asymmetry in the load of
individual nodes. Section 3.4 presents an analysis of the
bandwidth requirements of this scheme.
Membership Changes
Membership changes (i.e., nodes joining and leaving the ring) raise
two important issues that our algorithm must address. First, we must
update local information about the membership change, in order for
each node in the system to determine precisely which interval in the
id space it is responsible for. The second issue is conveying information
about the change to all the nodes in the ring so that these nodes will
maintain correct information about the system membership and consequently
manage to route in a single hop.
To maintain correct local information (i.e., information about each
node's successor and predecessor node), every node 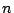 runs a
stabilization routine periodically, wherein it sends keep-alive
messages to its successor runs a
stabilization routine periodically, wherein it sends keep-alive
messages to its successor 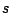 and predecessor and predecessor 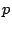 . Node . Node 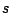 checks if checks if
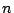 is indeed its predecessor, and if not, it notifies is indeed its predecessor, and if not, it notifies 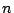 of the
existence of another node between them. Similarly of the
existence of another node between them. Similarly 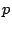 checks if checks if 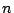 is
indeed its successor, and if not it notifies is
indeed its successor, and if not it notifies 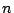 . If either of . If either of 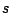 or or
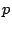 does not respond, does not respond, 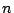 pings it repeatedly until a time-out period
when it decides that the node is unreachable or dead. pings it repeatedly until a time-out period
when it decides that the node is unreachable or dead.
A joining node
contacts another system node to get its view of the current
membership; this protocol is similar to the Chord
protocol [15,16]. The membership
information enables it to get in touch with its predecessor and
successor, thus informing them of its presence.
To maintain correct full routing tables, notifications of membership
change events, i.e., joins and leaves, must reach every node in the
system within a specified amount of time (depending on what fraction
of failed queries, i.e., 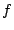 , is deemed acceptable). Our goal is to do
this in a way that has low notification delay yet reasonable bandwidth
consumption, since bandwidth is likely to be the scarcest resource in
the system. , is deemed acceptable). Our goal is to do
this in a way that has low notification delay yet reasonable bandwidth
consumption, since bandwidth is likely to be the scarcest resource in
the system.
We achieve this goal by superimposing a well-defined hierarchy on
the system. This hierarchy is used to form dissemination trees, which
are used to propagate event information.
We impose this hierarchy on a system with dynamic membership by
dividing the 128-bit circular identifier space into 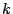 equal contiguous
intervals called slices. The equal contiguous
intervals called slices. The 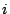 th slice contains all
nodes currently in the overlay whose node identifiers lie in the range th slice contains all
nodes currently in the overlay whose node identifiers lie in the range
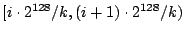 . Since nodes have
uniformly distributed random identifiers, these slices will have about
the same number of nodes at any time. Each slice has a slice
leader, which is chosen dynamically as the node that is the successor
of the mid-point of the slice identifier space. For example, the slice
leader of the . Since nodes have
uniformly distributed random identifiers, these slices will have about
the same number of nodes at any time. Each slice has a slice
leader, which is chosen dynamically as the node that is the successor
of the mid-point of the slice identifier space. For example, the slice
leader of the 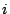 th slice is the successor node of the key th slice is the successor node of the key
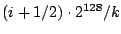 . When a new node joins the system it learns about
the slice leader from one of its neighbors along with other
information like the data it is responsible for and its routing table. . When a new node joins the system it learns about
the slice leader from one of its neighbors along with other
information like the data it is responsible for and its routing table.
Similarly, each slice is divided into equal-sized intervals called
units. Each unit has a unit leader, which is dynamically chosen
as the successor of the mid-point of the unit identifier space.
Figure 1:
Flow of event notifications in the system
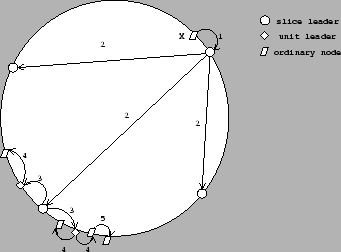 |
Figure 1 depicts how information flows in the system.
When a node (labeled X in Figure 1) detects a
change in membership (its successor failed or it has a new successor),
it sends an event notification message to its slice leader (1). The slice leader collects all event notifications it receives
from its own slice and aggregates them for 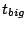 seconds before
sending a message to other slice leaders (2). To spread out
bandwidth utilization, communication with different slice leaders
is not synchronized: the slice leader ensures only that it communicates with
each individual slice leader once every seconds before
sending a message to other slice leaders (2). To spread out
bandwidth utilization, communication with different slice leaders
is not synchronized: the slice leader ensures only that it communicates with
each individual slice leader once every 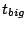 seconds.
Therefore, messages to different slice leaders are sent
at different points in time and contain different sets of events. seconds.
Therefore, messages to different slice leaders are sent
at different points in time and contain different sets of events.
The slice
leaders aggregate messages
they receive for a short time period 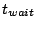 and then dispatch the
aggregate message to all unit leaders of their respective slices (3). A unit leader piggybacks this information on its keep-alive
messages to its successor and predecessor (4). and then dispatch the
aggregate message to all unit leaders of their respective slices (3). A unit leader piggybacks this information on its keep-alive
messages to its successor and predecessor (4).
Other nodes
propagate this information
in one direction: if they receive information from their predecessors,
they send it to their successors and vice versa.
The information is piggy-backed on keep-alive messages. In this way, all nodes in the system receive notification
of all events, but within a unit information is always
flowing from the unit leader to the ends of the unit. Nodes at unit
boundaries do not send information to their neighboring nodes outside
their unit. As a result, there is no redundancy in the
communications: a node will get information only from its neighbor
that is one step closer to its unit leader.
We get several benefits from choosing this design.
First, it imposes a structure on the system, with well-defined event
dissemination trees. This structure helps us ensure that there is no
redundancy in communications, which leads to efficient bandwidth usage.
Second, aggregation of several events into one message allows us to
avoid small messages. Small messages are a problem since the
protocol overhead becomes significant relative to the message size,
leading to higher bandwidth usage. This effect will be analyzed in
more detail in Section 3.4.
Our scheme is a three-level hierarchy. The choice of the number of
levels in the hierarchy involves a tradeoff: A large number of levels
implies a larger delay in propagating the information, whereas a small
number of levels generates a large load at the nodes in the upper
levels. We chose a three level hierarchy because it has low delay,
yet bandwidth consumption at top level nodes is reasonable.
Fault Tolerance
If a query fails on its first attempt it does not
return an error to an application. Instead, queries can be rerouted.
If a
lookup query from node 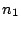 to node to node 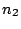 fails because fails because 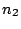 is no
longer in the system, is no
longer in the system, 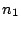 can retry the query by sending it to can retry the query by sending it to
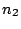 's successor.
If the query failed because a recently
joined node, 's successor.
If the query failed because a recently
joined node, 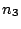 , is the new successor for the key that , is the new successor for the key that 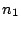 is
looking up, is
looking up, 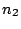 can reply with the identity of can reply with the identity of 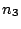 (if it
knows about (if it
knows about 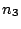 ), and ), and 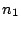 can contact can contact 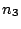 in a second routing step. in a second routing step.
Since our scheme is dependent on the correct functioning of
slice leaders, we need to recover from their failure.
Since there are relatively few slice leaders,
their failures are infrequent. Therefore, we do not have to be very
aggressive about replacing them in order to maintain our query success
target. When a slice or unit leader fails,
its successor soon detects the failure and
becomes the new leader.
Between the time a slice or unit leader fails, and
a new node takes over, some event notification messages may be lost,
and the information about those membership changes will not be
reflected in the system nodes' membership tables. This is not an
issue for routing correctness, since each node maintains correct
information about its predecessor and successor. It will, however, lead
to more routing hops and if we allowed these errors to accumulate, it
would eventually lead to a degradation of the one hop lookup success
rate.
To avoid this accumulation, we use the lookups themselves to detect
and propagate these inaccuracies. When a node performs a lookup and
detects that its routing entry is incorrect (i.e., the lookup
timed out, or was re-routed to a new successor), this new information
is then pushed to all the system nodes via the normal channels: it notifies
its slice leader about the event.
The correctness of our protocols is based on the fact that successor
and predecessor pointers are correct. This ensures that, even if the
remainder of the membership information contains errors, the query
will eventually succeed after re-routing. In other words, our complete
membership description can be seen as an optimization to
following successor pointers, in the same way as Chord fingers are
an optimization to successors (or similarly for other
peer-to-peer routing schemes).
Furthermore, we can argue that our successor
and predecessor pointers are correct due to the fact that we essentially
follow the same protocol as Chord to maintain these, and this has already
been proven correct [16].
Scalability
Slice leaders have more work to do than other nodes, and this might be
a problem for a poorly provisioned node with a low bandwidth
connection to the Internet. To overcome this problem we can identify
well connected and well provisioned nodes as ``supernodes'' on entry
into the system (as in [17]). There can be a parallel ring of supernodes, and the successor (in the
supernode ring) of the midpoint of the slice identifier space becomes
the slice leader. We do require a sufficient number of supernodes
to ensure that there are at least a few per slice.
As we will show in Section 3.4, bandwidth requirements are
small enough to make most participants in the system potential
supernodes in a 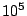 sized system (in such a
system, slice leaders will require 35
kbps upstream bandwidth). In a million-node system we may require
supernodes to be well-connected academic or corporate users (the
bandwidth requirements increase to 350 kbps). Section 4
presents the two-hop scheme that may be required when we wish the
system to accommodate even larger memberships. sized system (in such a
system, slice leaders will require 35
kbps upstream bandwidth). In a million-node system we may require
supernodes to be well-connected academic or corporate users (the
bandwidth requirements increase to 350 kbps). Section 4
presents the two-hop scheme that may be required when we wish the
system to accommodate even larger memberships.
Analysis
This section presents an analysis of how to parameterize the system to
satisfy our goal of fast propagation. To achieve our desired success
rate, we need to propagate information about events within some
time period 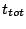 ; we begin this section by showing how to compute
this quantity. Yet we also require good performance, especially with
respect to bandwidth utilization. Later in the section we show how
we satisfy this requirement by controlling the number of slices and
units. ; we begin this section by showing how to compute
this quantity. Yet we also require good performance, especially with
respect to bandwidth utilization. Later in the section we show how
we satisfy this requirement by controlling the number of slices and
units.
Our analysis considers only non-failure situations.
It does not take into account overheads of
slice and unit leader failure because these events are rare.
It also ignores message loss and
delay since this simplifies the presentation, and the overhead introduced
by message delays and retransmissions is small compared to other
costs in the system.
Our analysis assumes that query targets are distributed uniformly
throughout the ring.
It is based on a worst case pattern
of events, queries, and notifications: we assume all events
happen just after the last slice-leader notifications, and all queries
happen immediately after that, so that none of the affected routing
table entries has been corrected and all queries targeted at
those nodes (i.e., the nodes causing the events) fail. In a real
deployment, queries would be interleaved with events and
notifications, so fewer of them would fail.
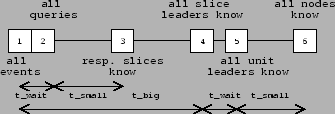
This scenario is illustrated by the timeline in
Figure 2. Here 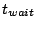 is the frequency with which
slice leaders communicate with their unit leaders, is the frequency with which
slice leaders communicate with their unit leaders, 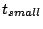 is the
time it takes to propagate information throughout a unit, and is the
time it takes to propagate information throughout a unit, and
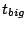 is the time a slice leader waits between communications to
some other slice leader. Within is the time a slice leader waits between communications to
some other slice leader. Within
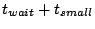 seconds (point
3), slices in which the events occurred all have correct entries for
nodes affected by the respective events. After seconds (point
3), slices in which the events occurred all have correct entries for
nodes affected by the respective events. After 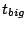 seconds of
the events (point 4), slice leaders notify other slice leaders. Within
a further seconds of
the events (point 4), slice leaders notify other slice leaders. Within
a further
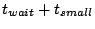 seconds (point 6), all nodes in the
system receive notification about all events. seconds (point 6), all nodes in the
system receive notification about all events.
Thus,
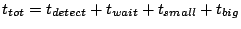 .
The quantity .
The quantity 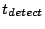 represents the delay between the time
an event occurs and when the leader of that slice first learns about
it. represents the delay between the time
an event occurs and when the leader of that slice first learns about
it.
Figure 2:
Timeline of the worst case situation
 |
Configuration Parameters
The following parameters characterize a system deployment:
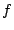 is the acceptable fraction of queries that fail
in the first routing attempt is the acceptable fraction of queries that fail
in the first routing attempt
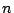 is the expected number of nodes in the
system is the expected number of nodes in the
system
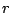 is the expected rate of membership changes in the system is the expected rate of membership changes in the system
Given these parameters, we can compute 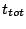 . Our assumption that
query targets are distributed uniformly around the ring implies that
the fraction of failed queries is proportional to the expected number of
incorrect entries in a querying node's routing table.
Given our worst case assumption, all the entries concerning events
that occurred in the last . Our assumption that
query targets are distributed uniformly around the ring implies that
the fraction of failed queries is proportional to the expected number of
incorrect entries in a querying node's routing table.
Given our worst case assumption, all the entries concerning events
that occurred in the last 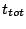 seconds are incorrect and
therefore the fraction of failed queries is seconds are incorrect and
therefore the fraction of failed queries is
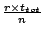 . Therefore, to ensure that no more than a fraction . Therefore, to ensure that no more than a fraction 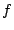 of
queries fail we need: of
queries fail we need:
For a system with 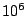 nodes, with a rate of nodes, with a rate of 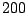 events events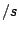 , and , and
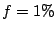 , we get a time interval as large as , we get a time interval as large as 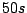 to propagate all
information. Note also that if to propagate all
information. Note also that if 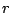 is linearly proportional to is linearly proportional to 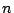 ,
then ,
then 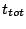 is independent of is independent of 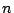 . It is only a function of the
desired success rate. . It is only a function of the
desired success rate.
Slices and Units
Our system performance depends on the number of slices and units:
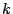 is the number of slices the ring is divided into. is the number of slices the ring is divided into.
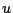 is the number of units in a slice. is the number of units in a slice.
Parameters 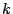 and and 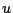 determine the expected unit size.
This in turn determines determine the expected unit size.
This in turn determines
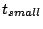 , the time it takes for information to propagate
from a unit leader to all members of a unit, given
an assumption about , the time it takes for information to propagate
from a unit leader to all members of a unit, given
an assumption about 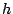 , the frequency of keep-alive probes.
From , the frequency of keep-alive probes.
From 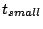 we can determine we can determine 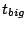 from our calculated
value for from our calculated
value for 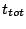 , given choices of values for , given choices of values for 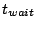 and and 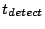 .
(Recall that .
(Recall that
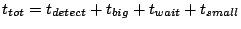 .) .)
To simplify the analysis we will choose values for 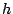 , , 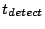 , and , and
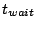 . As a result our analysis will be concerned with just two
independent variables, . As a result our analysis will be concerned with just two
independent variables, 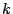 and and 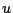 , given a particular choice of
values for , given a particular choice of
values for 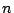 , , 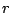 , and , and 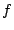 . We will use one second for both . We will use one second for both
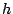 and and 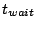 . This is a reasonable decision since the amount of
data being sent in probes and messages to unit leaders is large enough to
make the overhead in these messages small (e.g., information about 20
events will be sent in a system with . This is a reasonable decision since the amount of
data being sent in probes and messages to unit leaders is large enough to
make the overhead in these messages small (e.g., information about 20
events will be sent in a system with 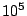 nodes). Note that with
this choice of nodes). Note that with
this choice of 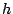 , , 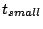 will be half the unit size. We will use
three seconds for will be half the unit size. We will use
three seconds for 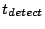 to account for the delay in detecting
a missed keep-alive message and a few probes to confirm the event. to account for the delay in detecting
a missed keep-alive message and a few probes to confirm the event.
Cost Analysis
Our goal is to choose values for 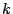 and and 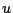 in a way that
reduces bandwidth utilization. In particular we are concerned
with minimizing bandwidth use at the slice leaders,
since they have the most work to do in our approach. in a way that
reduces bandwidth utilization. In particular we are concerned
with minimizing bandwidth use at the slice leaders,
since they have the most work to do in our approach.
Bandwidth is consumed both to propagate the actual data, and
because of the message overhead. 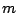 bytes will be required to
describe an event, and the overhead per message will be bytes will be required to
describe an event, and the overhead per message will be 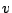 . .
There are four types of communication in our system.
- Keep-alive messages: Keep-alive
messages form the base level communication between a node and its
predecessor and successor. These messages include information about
recent events. As described in Section 3.1, our
system avoids sending redundant information in these messages by
controlling the direction of information flow (from unit leader to
unit members) and by not sending information across unit boundaries.
Since keep-alive messages are sent every second, every node that is not on the
edge of a unit will send and acknowledge an aggregate message containing,
on average, 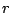 events. The size of this message is therefore events. The size of this message is therefore 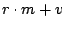 and
the size of the acknowledgment is and
the size of the acknowledgment is 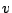 . .
- Event notification to slice leaders:
Whenever a node detects an event, it sends a notification to its slice
leader. The expected number of events per second
in a slice is
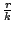 .
The downstream bandwidth utilization on slice
leaders is therefore .
The downstream bandwidth utilization on slice
leaders is therefore
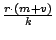 . Since each message
must be acknowledged, the upstream utilization is . Since each message
must be acknowledged, the upstream utilization is
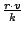 . .
- Messages exchanged between slice leaders:
Each message sent from one slice leader to another batches together
events that occurred in the last
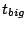 seconds in the slice. The
typical message size is, therefore, seconds in the slice. The
typical message size is, therefore,
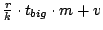 bytes. During any bytes. During any 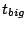 period, a slice leader sends this
message to all other slice leaders ( period, a slice leader sends this
message to all other slice leaders (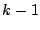 of them), and receives an
acknowledgment from each of them. Since each slice leader receives as
much as it gets on average, the upstream and downstream use of
bandwidth is symmetric. Therefore, the bandwidth utilization (both
upstream and downstream) is of them), and receives an
acknowledgment from each of them. Since each slice leader receives as
much as it gets on average, the upstream and downstream use of
bandwidth is symmetric. Therefore, the bandwidth utilization (both
upstream and downstream) is
- Messages from slice leaders to unit leaders:
Messages received by a slice leader are batched for one second and
then forwarded to unit leaders. In one second,
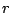 events happen and
therefore the aggregate message size is events happen and
therefore the aggregate message size is
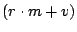 and the
bandwidth utilization is and the
bandwidth utilization is
Table 1 summarizes the net bandwidth use on each
node. To clarify the presentation, we have removed insignificant terms
from the expressions.
Table 1:
Summary of bandwidth use
| |
Upstream |
Downstream |
| Slice Leader |
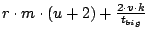 |
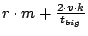 |
| Unit Leader |
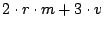 |
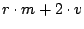 |
| Other nodes |
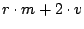 |
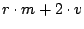 |
|
Figure 3:
Bandwidth use on a slice leader with 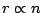
 |
Using these formulas we can compute the load on non-slice leaders in a
particular configuration. In this computations we use 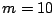 bytes and bytes and
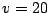 bytes. In a system with bytes. In a system with 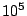 nodes, we see that the load on an
ordinary node is 3.84 kbps and the load on a unit leader is 7.36 kbps
upstream and 3.84 kbps downstream. For a system with nodes, we see that the load on an
ordinary node is 3.84 kbps and the load on a unit leader is 7.36 kbps
upstream and 3.84 kbps downstream. For a system with 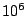 nodes, these
numbers become 38.4 kbps, 73.6 kbps, and 38.4 kbps respectively. nodes, these
numbers become 38.4 kbps, 73.6 kbps, and 38.4 kbps respectively.
From the table it is clear that the upstream bandwidth
required for a slice leader is likely to be the dominating and limiting
term. Therefore, we shall choose parameters that minimize this bandwidth.
By simplifying the expression and using the interrelationship between
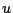 and and 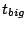 (explained in Section 3.4.2) we get a function that depends on
two independent variables (explained in Section 3.4.2) we get a function that depends on
two independent variables 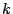 and and 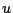 .
By analyzing the function, we deduce that
the minimum is achieved for
the following values: .
By analyzing the function, we deduce that
the minimum is achieved for
the following values:
These formulas allow us to compute values for 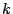 and and 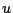 .
For example in a system of .
For example in a system of 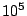 nodes we want roughly 500 slices
each containing 5 units. In a system of nodes we want roughly 500 slices
each containing 5 units. In a system of 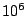 nodes, we still have
5 units per slice, but now there are 5000 slices. nodes, we still have
5 units per slice, but now there are 5000 slices.
Given values for 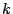 and and 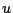 we can compute the unit size and
this in turn allows us to compute we can compute the unit size and
this in turn allows us to compute 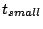 and and 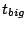 . We find
that we use least bandwidth when . We find
that we use least bandwidth when
Thus, we choose 23 seconds for 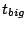 and 23 seconds for and 23 seconds for
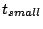 . .
Figure 4:
Aggregate bandwidth overhead of the scheme as a percentage of the theoretical optimum
 |
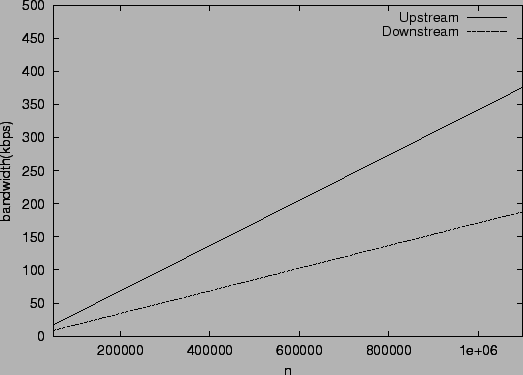
Given these values and the formulas in Table 1, we can plot the
bandwidth usage per slice leader in systems of various sizes. The results of this calculation
are shown in
Figure 3. Note that the load increases only
linearly with the size of the system. The load is quite modest in a
system with 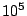 nodes (35 kbps upstream bandwidth), and therefore
even nodes behind cable modems can act as slice leaders in such a
system. In a system with nodes (35 kbps upstream bandwidth), and therefore
even nodes behind cable modems can act as slice leaders in such a
system. In a system with 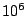 nodes the upstream bandwidth required
at a slice leader is approximately 350 kbps. Here it would be more
appropriate to limit slice leaders to being machines on reasonably
provisioned local area networks.
For larger networks, the bandwidth increases to a point where a slice
leader would need to be a well-provisioned node. nodes the upstream bandwidth required
at a slice leader is approximately 350 kbps. Here it would be more
appropriate to limit slice leaders to being machines on reasonably
provisioned local area networks.
For larger networks, the bandwidth increases to a point where a slice
leader would need to be a well-provisioned node.
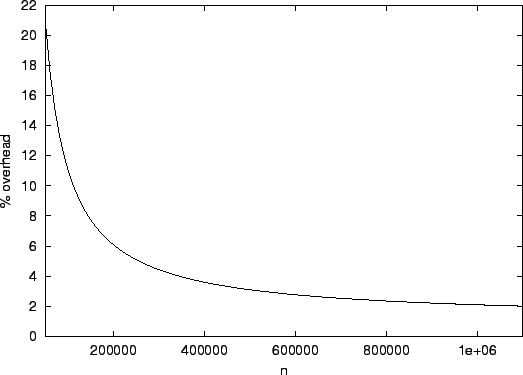
Figure 4 shows the percentage overhead of this
scheme in terms of aggregate bandwidth used in the system with respect
to the hypothetical optimum scheme with zero overhead. In such a
scheme scheme, the cost is just the total bandwidth used in sending
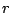 events to every node in the system every second, i.e., events to every node in the system every second, i.e.,
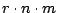 . Note that the overhead in our system comes from the
per-message protocol overhead. The scheme itself does not propagate
any redundant information. We note that the overhead is approximately
20% for a system containing . Note that the overhead in our system comes from the
per-message protocol overhead. The scheme itself does not propagate
any redundant information. We note that the overhead is approximately
20% for a system containing 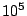 nodes and goes down to 2% for a system
containing nodes and goes down to 2% for a system
containing 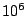 nodes. This result is reasonable because messages get
larger and the overhead becomes less significant as system size
increases. nodes. This result is reasonable because messages get
larger and the overhead becomes less significant as system size
increases.
Two Hop Lookups
The scheme that was presented in the previous section works well for
systems as large as a few million nodes. For systems of larger size,
the bandwidth requirements of this scheme may become too large for a
significant fraction of nodes. In this section, we propose a two-hop
scheme. This scheme keeps a fixed fraction of the total routing state
on each node and consumes much less bandwidth, and thus scales to a
larger system size. We begin by presenting the algorithm design
in Section 4.1. Section 4.2 analyzes
the bandwidth requirements of this scheme.
System Design
Our design for a routing algorithm that routes in two hops is based
on a structure like that used in the one-hop scheme, with slices, units, and
their respective leaders, as described previously.
In addition, every slice leader chooses a group of its own nodes for
each other slice; thus there are 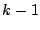 such groups. Each group is of
size such groups. Each group is of
size 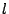 . The groups may be
chosen randomly or they may be based on proximity metrics, i.e., each
group may be chosen so that its members are dispersed (in terms of
network location) in a way that approximates the network spread among
all members of the slice. . The groups may be
chosen randomly or they may be based on proximity metrics, i.e., each
group may be chosen so that its members are dispersed (in terms of
network location) in a way that approximates the network spread among
all members of the slice.
The slice leader sends routing information about one group to
exactly one other slice leader. The information about the group is
then disseminated to all members of that slice as in the one hop
scheme. Therefore, each node has routing information for exactly 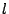 nodes in every other slice. Each node maintains an ordering (e.g., by
sending probes) for the
nodes in every other slice. Each node maintains an ordering (e.g., by
sending probes) for the 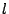 nodes based on network distance to itself.
It maintains such an ordering for every slice and thus builds a table
of nodes based on network distance to itself.
It maintains such an ordering for every slice and thus builds a table
of 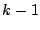 nodes that are close to it, one from every other slice. In
addition, every node keeps full routing information about nodes in its
own slice. nodes that are close to it, one from every other slice. In
addition, every node keeps full routing information about nodes in its
own slice.
When a node wants to query the successor of a key, it sends a lookup
request to its chosen node in the slice containing the key. The chosen
node then examines its own routing table to identify the successor of
the key and forwards the request to that node. For the rest of the
paper, we shall refer to the chosen intermediate nodes as forwarding
nodes.
The information flow in the system is similar to what we saw for
the one-hop lookup algorithm in Figure 1. The only
difference occurs in what a slice leader sends to other
slice leaders in step (2). The message it sends to the 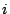 th
slice leader is empty unless one or more of the th
slice leader is empty unless one or more of the 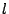 nodes it previously sent
to that slice leader have left the system. In that case, it sends
information about the nodes that have left the system and the nodes
that it chooses to replace them. nodes it previously sent
to that slice leader have left the system. In that case, it sends
information about the nodes that have left the system and the nodes
that it chooses to replace them.
When a node learns of different membership for some other slice,
it probes the nodes it just heard about and updates its proximity information
for that slice.
Tolerating slice and unit leader failure works similarly to the one
hop case.
Analysis
This section presents an analysis of how to parameterize the system to
satisfy our goal of fast propagation. As before, our analysis does
not take into account overheads of slice and unit leader failure
because these events are rare. It also ignores message loss and delay
and proximity probes since this simplifies the presentation, and the
overhead introduced by probes and by message delays and
retransmissions is small compared to other time constants in the
system.
As before, our analysis assumes that query targets are located
uniformly at random around the ring. It is based on a worst case
pattern of queries and notifications. There are two ways in which a
query can fail. First, the forwarding node has failed and the querying
node is not yet aware of the event. Second, the successor of the key
being queried has changed and the forwarding node is not yet aware of
the event. The probability of a query failing depends on these events,
which may not be independent. Therefore, we assume the upper bound
for the failure
probability is the sum of the probabilities of these events.
The time taken to spread information about an event within a slice
depends on the unit size, and as before, we call it 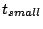 . Then the time
taken to spread information about an event to all nodes in the system
is . Then the time
taken to spread information about an event to all nodes in the system
is
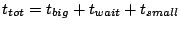 . Therefore, the average (over locations in the
ring) probability of query failure because of leave of forwarding node
is approximately . Therefore, the average (over locations in the
ring) probability of query failure because of leave of forwarding node
is approximately
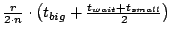 .
The average probability of query failure because of change of key's
successor is .
The average probability of query failure because of change of key's
successor is
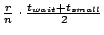 . Therefore, the expected fraction of failed
queries is upper bounded by . Therefore, the expected fraction of failed
queries is upper bounded by
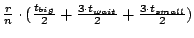 . Therefore, to ensure that no
more than a fraction . Therefore, to ensure that no
more than a fraction 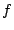 of queries fail, we need: of queries fail, we need:
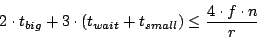
For example, for a system with 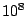 nodes, with a rate of nodes, with a rate of 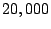 events
events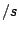 , and , and 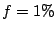 , we require that , we require that
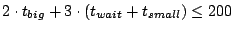 seconds. Note that if seconds. Note that if 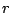 is linearly proportional
to is linearly proportional
to 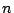 , this inequality is independent of , this inequality is independent of 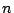 . It is only a function
of the desired success rate. We choose . It is only a function
of the desired success rate. We choose 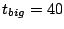 seconds, seconds, 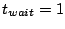 seconds and
seconds and
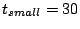 seconds. This choice leaves an interval of
around 4 seconds for detection of a join or leave event. Given that
keep-alive messages are exchanged every second, this implies that the
expected size of a unit must be seconds. This choice leaves an interval of
around 4 seconds for detection of a join or leave event. Given that
keep-alive messages are exchanged every second, this implies that the
expected size of a unit must be 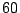 . To control upstream bandwidth
utilization on slice leaders, we fix the number of units in a slice to
25. This implies that the expected size of a slice should be 1500 and
the ring should be divided into . To control upstream bandwidth
utilization on slice leaders, we fix the number of units in a slice to
25. This implies that the expected size of a slice should be 1500 and
the ring should be divided into 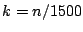 slices. slices.
In terms of bandwidth costs, we need to have into account the fact
that we are dealing with small messages, so we need to consider protocol
overheads. Assume that 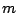 bytes will be required to
describe an event, and the overhead per message will be bytes will be required to
describe an event, and the overhead per message will be 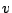 . .
There are four types of communication in our system:
- Keep-alive messages: Keep-alives
comprise the base level communication between a node and its
predecessor and successor. These messages include information about
recent events in the node's slice and about exported nodes in other
slices. As described in Section 4.1, our system
avoids sending redundant information in these messages by controlling
the direction of information flow (from unit leader to unit members)
and by not sending information across unit boundaries.
Since keep-alive messages are sent every second, every node that is not on the
edge of a unit will send and acknowledge an aggregate message containing,
on average,
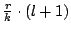 events. The size of this message is
therefore events. The size of this message is
therefore
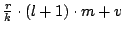 and
the size of the acknowledgment is and
the size of the acknowledgment is 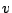 . .
- Event notification to slice leaders:
This is identical to the one-hop case.
Whenever a node detects an event, it sends a notification to its slice
leader. The expected number of events per second
in a slice is
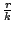 .
The downstream bandwidth utilization on slice
leaders is therefore .
The downstream bandwidth utilization on slice
leaders is therefore
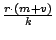 . Since each message
must be acknowledged, the upstream utilization is . Since each message
must be acknowledged, the upstream utilization is
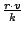 . .
- Messages between slice leaders:
Each message sent from one slice leader to another
contains information about changes in exported nodes, if any. The
expected message size is, therefore,
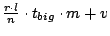 bytes. During any bytes. During any 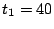 seconds period, a slice leader sends this
message to all other slice leaders, and receives an
acknowledgment from each of them. Since each slice leader receives as
much as it gets on average, the upstream and downstream use of
bandwidth is symmetric. Therefore, the bandwidth utilization (both
upstream and downstream) is seconds period, a slice leader sends this
message to all other slice leaders, and receives an
acknowledgment from each of them. Since each slice leader receives as
much as it gets on average, the upstream and downstream use of
bandwidth is symmetric. Therefore, the bandwidth utilization (both
upstream and downstream) is
- Messages from slice leaders to unit leaders:
Messages received by a slice leader are batched for one second and
then forwarded to unit leaders. In one second,
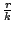 events happen within
the slice and events happen within
the slice and
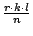 events are exported. There
are 25 units per slice, and therefore, the bandwidth utilization is events are exported. There
are 25 units per slice, and therefore, the bandwidth utilization is
Using these formulas we can compute the load on all nodes for a system
of any size and an appropriate choice of 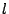 . For a system of size . For a system of size
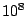 , we may choose , we may choose 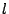 to be approximately to be approximately 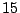 . Since slices are
large, we expect that this group size will allow each node to be able
to find at least one node (in every slice) which is close to it in
terms of network proximity even if the groups are populated
randomly. This will make the first hop in the lookup a low latency
hop, bringing down the total routing delay. If algorithms for
clustering nodes on the basis of network proximity are used, then . Since slices are
large, we expect that this group size will allow each node to be able
to find at least one node (in every slice) which is close to it in
terms of network proximity even if the groups are populated
randomly. This will make the first hop in the lookup a low latency
hop, bringing down the total routing delay. If algorithms for
clustering nodes on the basis of network proximity are used, then 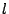 may be fixed depending on the size and the number of clusters. In
this computations we use
may be fixed depending on the size and the number of clusters. In
this computations we use 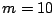 bytes and bytes and 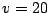 bytes. Table 2 summarizes the net bandwidth use on
each node in a system of size
bytes. Table 2 summarizes the net bandwidth use on
each node in a system of size 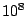 having having 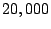 events per
second, and with events per
second, and with 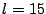 . The load on slice leaders increases
linearly with the size of the system. Therefore, this scheme would
scale up to a system of around half a billion nodes. . The load on slice leaders increases
linearly with the size of the system. Therefore, this scheme would
scale up to a system of around half a billion nodes.
Table 2:
Summary of bandwidth use for a system of size 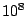
| |
Upstream |
Downstream |
| Slice Leader |
1.6 Mbps |
800 kbps |
| Unit Leader |
1 kbps |
530 bps |
| Ordinary node |
530 bps |
530 bps |
|
Evaluation
In this section, we present experimental results obtained with
simulations of the one hop and two hop schemes. In the first set of
experiments, we used a coarse-grained simulator to understand the
overall behavior of the one and two hop systems with tens of thousands
of nodes. This simulation scales to approximately 20,000 nodes. In
the second set of experiments we use a more fine-grained simulation of
the one hop system where the simulation environment could not support
more than 2000 nodes.
In both experiments we derived inter-host latencies from Internet
measurements among a set of 1024 DNS servers [5]. Note
that our experimental results are largely independent of topology
since we did not measure lookup latency (this would be influenced by
the distance to the forwarding node in the two-hop scheme), and the
impact of inter-node latency on query failure rates is minimal,
since the latencies are over an order of magnitude smaller than
the timeouts used for propagating information.
The experiments using the coarse-grained simulator were aimed at
validating our analytic results concerning query success rate. The
coarse-grained simulator is based on some simplifying assumptions that
allow it to scale to larger network sizes. First, it is synchronous:
the simulation proceeds in a series of rounds (each representing one
second of processing), where all nodes receive messages, perform local
processing of the messages, and send messages to other nodes. Second,
in this case we did not simulate slice leader failures. Packet losses
are also not simulated.
Figure 5:
Query Failure Rate in a one hop system of size 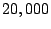 with changing
inter-slice communication frequency with changing
inter-slice communication frequency
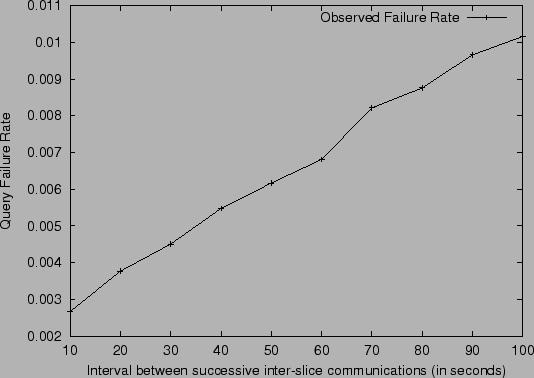 |
The first set of experiments shows the fraction of successful queries
as a function of interslice communication rate. The expected number of
nodes in the system is 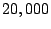 , the mean join rate is 2 nodes per
second, and the mean leave rate is 2 nodes per second. Node lifetime is
exponentially distributed. New nodes and queries are distributed
uniformly in the ID space. The query rate is 1 query per node per
second. , the mean join rate is 2 nodes per
second, and the mean leave rate is 2 nodes per second. Node lifetime is
exponentially distributed. New nodes and queries are distributed
uniformly in the ID space. The query rate is 1 query per node per
second.
For the one hop scheme, the number of slices is chosen to be 50 and
there are 5 units in every slice (these are good choices
according to our analysis). The
frequency of inter-slice communication varied from 1 every 10 seconds
to 1 every 100 seconds.
The results are shown in Figure 5. We can see that
the query failure rate grows steadily with the time between
inter-slice communication. Note, however, that even with a relatively
infrequent communication of once every 100 seconds, we still obtain an
average of about a 1% failure rate.
This simulation confirms our expectation that the failed query rate we
computed analytically was conservative. We can see that when the
inter-slice communication is set to 23 s (the value suggested by our
analysis), the query failure rate is about 0.4%, and not 1% as we
conservatively predicted in Section 3. The reason why
the actual failure rate is lower is because our analysis assumed
the worse case where all queries are issued right after membership
events occur, and before any events were propagated.
In reality, queries are distributed through the time
interval that it takes to propagate the information, and by
the time some queries are issued, some nodes already have received
the most up-to-date information.
Figure 6:
Query Failure Rate in a two hop system of size 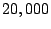 with changing
inter-slice communication frequency with changing
inter-slice communication frequency
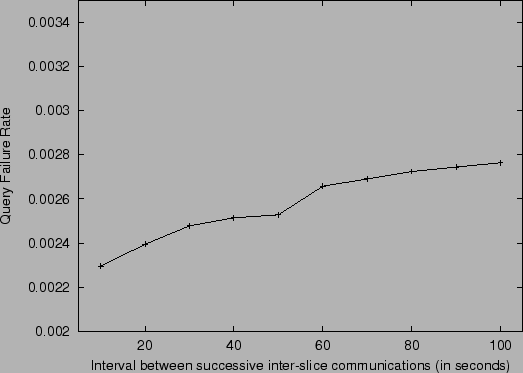 |
Figure 6 shows a similar experiment for the
simulation of the two hop scheme. Here the expected number of slices
in the system is chosen to be the bandwidth-optimal slice count of
7. Similarly, the number of units per slice is chosen to be 60 (again
this choice comes from our analysis). By comparing
Figures 5 and 6, we can see
that the two hop scheme causes a lower fraction of failed queries than
the one hop scheme. This happens for two reasons. In the two hop
scheme, the first hop fails only if the forwarding node fails;
node joins do not cause routing failures in this case. Also the
second hop is more likely to succeed than the single hop in the one
hop case, since the choice of target node is made by the forwarding
node, which has very up-to-date information about its own slice.
These points also explain why the two hop system has much lower
sensitivity to change in frequency of inter-slice communications than
the one hop system.
Figure 7:
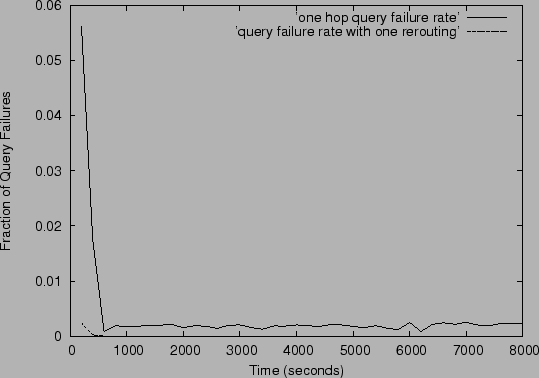
Query Failure Rate in a one hop system of size 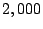
 |
In this section we report on simulations of the one hop routing algorithm using
p2psim [4], a peer-to-peer protocol simulator where we could
implement the complete functionality of the one hop protocol.
Using this simulator we are able to explore bandwidth utilization
and also the impact of slice and unit leader failures.
In the first experiment we measure the evolution of the query failure
rate of a system that grows very fast initially, and then stabilizes
to ``typical'' membership dynamics.
We simulate a system with 2000 dynamic nodes with 10 slices and 5
units per slice. The results are shown in
Figure 7. In the first 300 seconds of the
simulation, all nodes join rapidly. After that the system shows
Gnutella-like churn [14] with 24 events per
minute. All nodes join by obtaining a routing table from another node;
the routing tables then continue to grow as new nodes come in.
After approximately the first 10 minutes, the query failure rate
stayed consistently at around 0.2%. We also did experiments to
determine the failure rate observed after the query is re-routed once.
In this case the failure
rate settles down to approximately one failure in 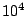 queries, or
0.01%. This is because the local information about a slice,
especially knowledge of predecessors and successors gets transmitted
very rapidly. Thus, 99.99% of the queries are correctly satisfied by
two or fewer hops. queries, or
0.01%. This is because the local information about a slice,
especially knowledge of predecessors and successors gets transmitted
very rapidly. Thus, 99.99% of the queries are correctly satisfied by
two or fewer hops.
Next, we examine the behavior of the system in the presence of a burst
of membership departures. Again we simulated a system with 2000
nodes, with 10 slices and 5 units per slice. The query rate was 1
lookup per second per node. At time instant t=8000 seconds, 45% of
the nodes in the system were made to crash. These nodes are chosen
randomly. Figure 8 shows the fraction of lookups that
failed subsequent to the crash. It takes the system about 50 seconds
to return to a reasonable query success rate, but it doesn't stabilize
at the same query success rate that it had prior to the crash for
another 350 seconds. What is happening in this interval is recovery
from slice leader failures. The query rate has an important role in
slice leader recovery; queries help in restoring stale state by
regenerating event notifications that are lost because of slice-leader
failures. For example, with a query rate of 1 lookup every 10 seconds,
the system did not stabilize below 2% for the length of the
simulation (50,000 seconds) while for a query rate of 2 lookups per
second, the system stabilized within 300 seconds. This indicates that
it may be useful to artificially insert queries in the system during
periods of inactivity.
Figure 8:
Query Failure Rate in a one hop system of size 2000 after 45% of the nodes crash at t=8000s
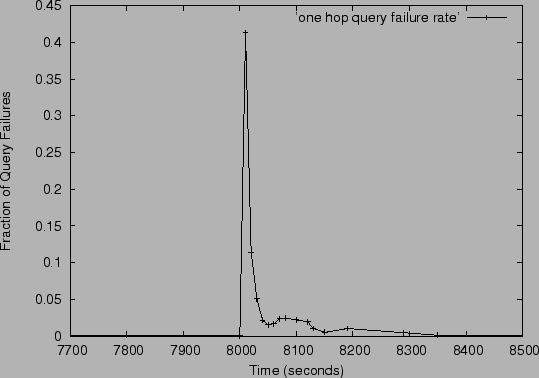 |
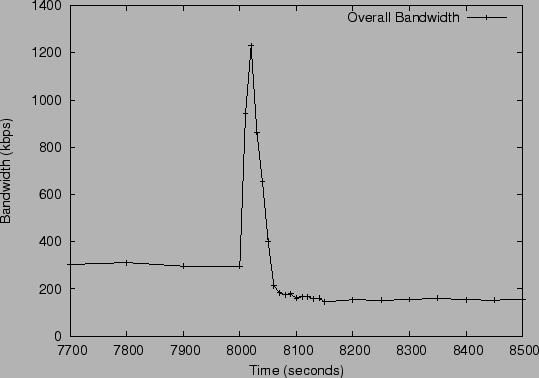
Figure 9 shows the overall bandwidth used in the
system in this period. The aggregate bandwidth used in the entire
system is around 300 kbps before the crash and settles into around 180
kbps after approximately 150 seconds. (The steady-state bandwidth
decreases due to the decrease in the system size.) We can see that
while the duration of the spike is similar to that of the spike
in query failure rate, bandwidth settles down to
expected levels faster than successful lookups. This happens because
lookups continue to fail on routing table entries whose notifications
are lost in slice leader failures. These failures have to be
``re-discovered'' by lookups, and then fixed slice-by-slice, which
takes longer. While each failed lookup generates notifications and
thus increases maintenance bandwidth, at the system size of around
2000 most messages (after the spike settles down) are dominated by the
UDP/IP packet overhead. Thus, the overall effect on bandwidth is
significantly lower.
Figure 9:
Bandwidth used in a one hop system of size 2000 after 45% of the nodes crash at t=8000s
 |
We also ran experiments in which we simulated bursts of crashes of
different fractions of nodes. We observed that the time periods taken
for the lookups and bandwidth to settle down were almost the same in
all cases. We expect this to happen because the time taken to
stabilize in the system is dependent on the system size, and chosen
parameters of unit size and 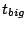 which remain the same in all
cases. which remain the same in all
cases.
We also computed the average spike bandwidth. This was measured by
computing the average bandwidth used by the entire system in the 50
seconds it took for the system to settle down in all cases. From
Figure 10 we see that the bandwidth use grows
approximately linearly with the size of the crash. In all cases,
the bandwidth consumption is reasonable, given the fact that this
bandwidth is split among over a thousand nodes.
Figure 10:
Average spike bandwidth after a fraction of the nodes crash in a burst
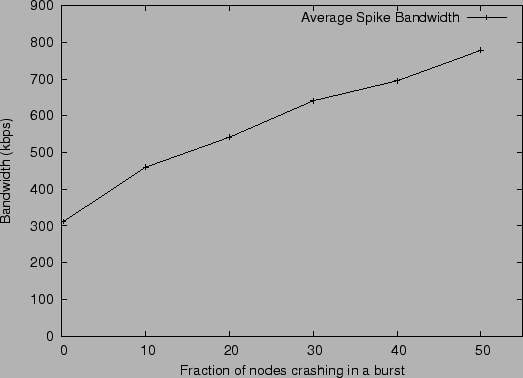 |
Discussion
In this section we discuss features that we did not incorporate into
our algorithms, but that may be of use in the future.
Existing peer-to-peer routing algorithms like Pastry [13] and
Tapestry [18]
carefully exploit inter-node
proximity when choosing a node's routing table entries. By trying
to populate a node's routing tables with nearby nodes, the routing
process is simplified, as shorter routing hops become more likely.
Our one hop scheme does not require proximity for routing, as
proximity information is of no use in practice in this scheme. For our
two hop scheme, we mentioned in Section 4.1 how
proximity can be exploited to improve routing.
However, we can also improve our algorithms by using proximity
information when forming our dissemination trees (which in our case
are formed by randomly chosen slice and unit leaders). The main
improvement comes from improving the dissemination of information
within a slice. We think that inter-slice communication is a small part
of the overall load, and since the slice leaders are chosen to be
well-connected nodes, there is not much point in trying to improve
this situation.
For disseminating information within a slice, however, we could
improve our current scheme by using an application-level multicast
technique that takes proximity into account.
Either a
peer-to-peer technique (e.g., Scribe [1] or
Bayeux [19]) or a traditional technique (e.g., SRM [3]
or RMTP [8]) might be appropriate.
Previous peer-to-peer systems exploited the fact that queries for the
same key from different clients have lookup paths that overlap in the
final segments, to perform caching of the objects that were returned
on the nodes contacted in the lookup path. This provided a natural way
to perform load balancing -- popular content was cached longer, and
thus it was more likely that a client would obtain that content from a
cached copy on the lookup path.
Our two hop scheme can use a similar scheme to provide load-balancing
and caching. This will lead to popular items being cached at the forwarders,
where they can be accessed in one hop; note that an added benefit
is the the querying node will usually have good proximity to the
forwarder.
Since the one hop scheme doesn't have extra routing steps we can't use
them for load balancing. But one-hop routing can be combined with caching
schemes to achieve load balancing (and nearby access) if
desired. In addition, load balancing might be achieved at the
application level by taking advantage of replication. In a
peer-to-peer system data must be replicated in order to avoid loss
when nodes depart. A query can take advantage of replication to
retrieve an item from the replica most proximate to the querying node.
Related Work
Rodrigues et al. [12] proposed a single hop
distributed hash table but they assumed a much smaller peer dynamics,
like that in a corporate environment, and therefore did not have to
deal with the difficulties of rapidly handling a large number of membership
changes with efficient bandwidth usage. Douceur
et al. [2] present a system
that routes in a constant number of hops, but that design assumes
smaller peer dynamics and searches can be lossy.
Kelips [6] uses 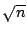 sized tables per node and a gossip mechanism to
propagate event notifications to provide constant time lookups.
Their lookups, however, are constant time only when the routing
table entries are reasonably accurate. As seen before, these systems
are highly dynamic and the accuracy of the tables depends on how
long it takes for the system to converge after an event.
The expected convergence time for an event
in Kelips is sized tables per node and a gossip mechanism to
propagate event notifications to provide constant time lookups.
Their lookups, however, are constant time only when the routing
table entries are reasonably accurate. As seen before, these systems
are highly dynamic and the accuracy of the tables depends on how
long it takes for the system to converge after an event.
The expected convergence time for an event
in Kelips is
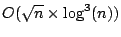 . While this will
be tens of seconds for small systems of around a 1000 nodes,
for systems having . While this will
be tens of seconds for small systems of around a 1000 nodes,
for systems having 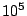 to to 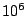 nodes, it takes
over an hour for an event to be propagated through the system.
At this rate, a large fraction of the routing entries in each table are likely
to be stale, and a correspondingly large fraction of queries would
fail on their first attempt. nodes, it takes
over an hour for an event to be propagated through the system.
At this rate, a large fraction of the routing entries in each table are likely
to be stale, and a correspondingly large fraction of queries would
fail on their first attempt.
Mahajan et al. [9] also derive analytic models for the
cost of maintaining reliability in the Pastry [13]
peer-to-peer routing algorithm in a dynamic setting. This work differs substantially from ours
in that the nature of the routing algorithms is quite
different - Pastry uses only 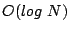 state but requires state but requires 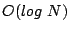 hops per lookup - and they focus their work on techniques to reduce
their (already low) maintenance cost.
hops per lookup - and they focus their work on techniques to reduce
their (already low) maintenance cost.
Liben-Nowell et al. [7] provide a lower-bound on
the cost of maintaining routing information in peer-to-peer networks that try
to maintain topological structure. We are designing
a system that requires significantly larger bandwidth than in the lower bound
because we aim to achieve a much lower
lookup latency.
Mizrak et al. [10] present an alternative two-hop routing scheme.
In this scheme, all queries are routed through (their equivalent
of) slice leaders and ordinary nodes do not exchange state.
Our two hop scheme gives the querying node different possibilities
for the forwarding node, which allows us to employ clever techniques
to decide which forwarding node to use (e.g., based on proximity).
Conclusions
This paper questions the necessity of multi-hop lookups in
peer-to-peer routing algorithms. We introduce the design of two novel
peer-to-peer lookup algorithms. These algorithms route in one and two
hops, respectively, unless the lookup fails and other routes need to
be attempted. We designed our algorithms to provide a small fraction
of lookup failures (e.g., 1%).
We present analytic results that show how we can parameterize the system
to obtain reasonable bandwidth consumption, despite the fact that
we are dealing with a highly dynamic membership. We present simulation
results that support our analysis that the system delivers a large
fraction of lookups within one or two hops, depending on the algorithm.
Previous peer-to-peer systems exploited the fact that queries for the
same id from different clients have lookup paths that overlap in the
final segments, to perform caching of the objects that were returned
on the nodes contacted in the lookup path. This provided a natural way
to perform load balancing -- popular content was cached longer and
more often, and it became
more likely that a client would obtain that content from a cached copy
on the lookup path.
Our two hop algorithm can use a similar scheme to provide load-balancing
and caching. We are investigating ways to obtain similar advantages
in the one hop scheme.
Currently peer-to-peer systems have high lookup latency and are
therefore only well-suited for applications that do not mind
high-latency store and retrieve operations (e.g., backups) or that
store and retrieve massive amounts of data (e.g., a source tree
distribution). Moving to more efficient routing removes this
constraint. This way we can enable a much larger class of
applications for peer-to-peer systems.
We would like to thank our shepherd Ion Stoica, and the anonymous
referees for their helpful comments on drafts of this paper.
This research is supported by DARPA under contract F30602-98-1-0237
and by the NSF under Cooperative Agreement ANI-0225660. R.
Rodrigues was supported by a fellowship from the Calouste Gulbenkian
Foundation, and was previously supported by a Praxis XXI fellowship.
- 1
-
M. Castro, P. Druschel, A.-M. Kermarrec, and A. Rowstron.
SCRIBE: A large-scale and decentralised application-level multicast
infrastructure.
IEEE Journal on Selected Areas in Communications (JSAC),
2002.
- 2
-
J. R. Douceur, A. Adya, W. J. Bolosky, D. Simon, and M. Theimer.
Reclaiming space from duplicate files in a serverless distributed
file system.
In Proceedings of the 22nd IEEE International Conference on
Distributed Computing Systems, July 2002.
- 3
-
S. Floyd, V. Jacobson, C.-G. Liu, S. McCanne, and L. Zhang.
A reliable multicast framework for light-weight sessions and
application level framing.
IEEEACM Transactions on Networking, 5(6):784-803, 1997.
- 4
-
T. Gil, F. Kaashoek, J. Li, R. Morris, and J. Stribling.
p2psim: A simulator for peer-to-peer protocols.
https://www.pdos.lcs.mit.edu/p2psim/.
- 5
-
K. P. Gummadi, S. Saroiu, and S. D. Gribble.
King: Estimating latency between arbitrary internet end hosts.
In Proceedings of the SIGCOMM Internet Measurement Workshop
(IMW 2002), Marseille, France, November 2002.
- 6
-
I. Gupta, K. Birman, P. Linga, A. Demers, and R. van Renesse.
Kelips: Building an efficient and stable P2P DHT through increased
memory and background overhead.
In Proceedings of the 2nd International Workshop on Peer-to-Peer
Systems (IPTPS '03), Feb. 2003.
- 7
-
D. Liben-Nowell, H. Balakrishnan, and D. Karger.
Analysis of the evolution of peer-to-peer systems.
In Proceedings of the Twenty-First Annual ACM Symposium on
Principles of Distributed Computing (PODC 2002), 2002.
- 8
-
J. C. Lin and S. Paul.
RMTP: A reliable multicast transport protocol.
In Proceedings IEEE INFOCOM '96, pages 1414-1424, San
Francisco, CA, Mar. 1996.
- 9
-
R. Mahajan, M. Castro, and A. Rowstron.
Controlling the cost of reliability in peer-to-peer overlays.
In Proceedings of the 2nd International Workshop on Peer-to-Peer
Systems (IPTPS '03), Feb. 2003.
- 10
-
A. Mizrak, Y. Cheng, V. Kumar, and S. Savage.
Structured superpeers: Leveraging heterogeneity to provide
constant-time lookup.
In IEEE Workshop on Internet Applications, 2003.
- 11
-
S. Ratnasamy, P. Francis, M. Handley, R. Karp, and S. Shenker.
A scalable content-addressable network.
In ACM SIGCOMM, Aug. 2001.
- 12
-
R. Rodrigues, B. Liskov, and L. Shrira.
The design of a robust peer-to-peer system.
In Proceedings of the 10th SIGOPS European Workshop, Sept.
2002.
- 13
-
A. Rowstron and P. Druschel.
Pastry: Scalable, decentralized object location, and routing for
large-scale peer-to-peer systems.
In IFIP/ACM Middleware, Nov. 2001.
- 14
-
S. Saroiu, P. K. Gummadi, and S. D. Gribble.
A measurement study of peer-to-peer file sharing systems.
In Proceedings of Multimedia Computing and Networking 2002
(MMCN'02), Jan. 2002.
- 15
-
I. Stoica, R. Morris, D. Karger, F. Kaashoek, and H. Balakrishnan.
Chord: A scalable Peer-To-Peer lookup service for internet
applications.
In ACM SIGCOMM, Aug. 2001.
- 16
-
I. Stoica, R. Morris, D. Karger, M. F. Kaashoeki, and H. Balakrishnan.
Chord: A scalable peer-to-peer lookup service for internet
applications.
Technical Report MIT-LCS-TR-819, MIT, Mar. 2001.
- 17
-
B. Zhao, Y. Duan, L. Huang, A. Joseph, and J. Kubiatowicz.
Brocade: Landmark routing on overlay networks.
In Proceedings of 1st International Workshop on Peer-to-Peer
Systems (IPTPS), Cambridge, MA, USA, Mar. 2002.
- 18
-
B. Y. Zhao, J. D. Kubiatowicz, and A. D. Joseph.
Tapestry: An infrastructure for fault-tolerant wide-area location and
routing.
Technical Report UCB/CSD-01-1141, UC Berkeley, Apr. 2001.
- 19
-
S. Q. Zhuang, B. Y. Zhao, A. D. Joseph, R. H. Katz, and J. D. Kubiatowicz.
Bayeux: An architecture for scalable and fault-tolerant wide-area
data dissemination.
In Network and Operating System Support for Digital Audio and
Video, 11th International Workshop, NOSSDAV 2001, June 2001.
Efficient Routing for Peer-to-Peer Overlays
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 onehop.tex
The translation was initiated by Anjali Gupta on 2004-02-10
|


![]() , the mean join rate is 2 nodes per
second, and the mean leave rate is 2 nodes per second. Node lifetime is
exponentially distributed. New nodes and queries are distributed
uniformly in the ID space. The query rate is 1 query per node per
second.
, the mean join rate is 2 nodes per
second, and the mean leave rate is 2 nodes per second. Node lifetime is
exponentially distributed. New nodes and queries are distributed
uniformly in the ID space. The query rate is 1 query per node per
second.

![]() queries, or
0.01%. This is because the local information about a slice,
especially knowledge of predecessors and successors gets transmitted
very rapidly. Thus, 99.99% of the queries are correctly satisfied by
two or fewer hops.
queries, or
0.01%. This is because the local information about a slice,
especially knowledge of predecessors and successors gets transmitted
very rapidly. Thus, 99.99% of the queries are correctly satisfied by
two or fewer hops.

![]() which remain the same in all
cases.
which remain the same in all
cases.
![]() sized tables per node and a gossip mechanism to
propagate event notifications to provide constant time lookups.
Their lookups, however, are constant time only when the routing
table entries are reasonably accurate. As seen before, these systems
are highly dynamic and the accuracy of the tables depends on how
long it takes for the system to converge after an event.
The expected convergence time for an event
in Kelips is
sized tables per node and a gossip mechanism to
propagate event notifications to provide constant time lookups.
Their lookups, however, are constant time only when the routing
table entries are reasonably accurate. As seen before, these systems
are highly dynamic and the accuracy of the tables depends on how
long it takes for the system to converge after an event.
The expected convergence time for an event
in Kelips is
![]() . While this will
be tens of seconds for small systems of around a 1000 nodes,
for systems having
. While this will
be tens of seconds for small systems of around a 1000 nodes,
for systems having ![]() to
to ![]() nodes, it takes
over an hour for an event to be propagated through the system.
At this rate, a large fraction of the routing entries in each table are likely
to be stale, and a correspondingly large fraction of queries would
fail on their first attempt.
nodes, it takes
over an hour for an event to be propagated through the system.
At this rate, a large fraction of the routing entries in each table are likely
to be stale, and a correspondingly large fraction of queries would
fail on their first attempt.
![]() state but requires
state but requires ![]() hops per lookup - and they focus their work on techniques to reduce
their (already low) maintenance cost.
hops per lookup - and they focus their work on techniques to reduce
their (already low) maintenance cost.