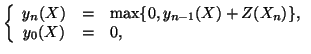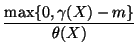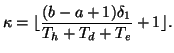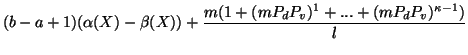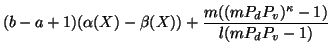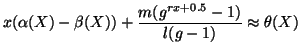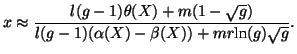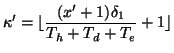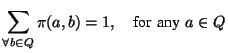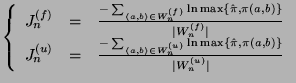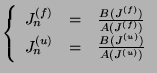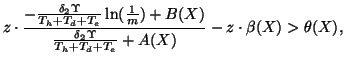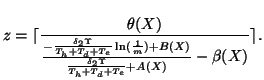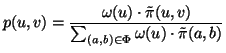Catching Instant Messaging Worms with Change-Point Detection Techniques
Guanhua Yan![[*]](footnote.png)
Information Sciences (CCS-3)
Los Alamos National Laboratory
Los Alamos, NM 87545, USA
ghyan@lanl.gov
Zhen Xiao
School of Electronics Engineering and Computer Science
Peking University
Beijing, P. R. China
xiaozhen@net.pku.edu.cn
Stephan Eidenbenz
Information Sciences (CCS-3)
Los Alamos National Laboratory
Los Alamos, NM 87545, USA
eidenben@lanl.gov
Abstract:
Instant messaging (IM) systems have gained a lot of popularity in
recent years. The increasing number of IM users has lured malware
authors to develop more worms and viruses that spread in IM
networks. In response to such growing security threat to IM systems,
it is imperative to develop a fast and responsive IM worm detection
system. In this paper, we apply change-point detection techniques to
catch two families of IM worms, one aimed at infecting all
vulnerable machines as quickly as possible and the other aimed at
spreading slowly in a stealthy fashion to evade
detection. Experimental results demonstrate that the proposed
solutions are very effective in detecting both families of IM worms.
Instant messaging (IM) systems have grown tremendously in the past few
years. It is estimated that the total number of active IM accounts
will increase from 867 million by the end of 2005 to 1.2 billion by
2009 [5] and the number of enterprise IM users
will increase from 67 million in 2007 to 127 million in 2011
[6]. Accompanied with such
increasing popularity of IM systems is the growing security threat
that IM malware poses to both residential and enterprise IM users. For
instance, from January 1, 2005 through September 2005, more than 360
new IM worms have surfaced [8]. According to a
report from Akonix Systems Inc., there have been 346 IM attacks in
2007 [4]. In 2005, Reuters was even forced to shut down
its instant messaging service temporarily due to the Kelvir IM worm
[16].
IM worms have posed significant challenges to security protection for
enterprise-like networks. IM worms can be leveraged to implant
rootkits or bots onto victim machines inside an enterprise network
after traditional perimeter protections such as firewalls have been
bypassed. The two major propagation vectors of IM worms are file
transfers and URL-embedded chat messages. An IM worm using the
first approach (e.g., Sumom.a [19]) requests transferring
a file, which contains the worm code, to an online buddy; in the
second approach, an IM worm (e.g., Kelvir.k [7]) sends a
hyperlink, which is embedded in a text chat message, to an online
buddy. If the receiver accepts the file transfer request or clicks the
embedded URL, a malicious file will be downloaded onto her machine and
its execution creates a new infection.
Outbreaks of traditional Internet worms such as Code Red tell us that
any effective defense scheme against an epidemic spreading requires a
fast and responsive alert system [18]. Motivated by
this, we propose to apply change-point detection techniques to detect
two families of IM worms quickly. The first family of IM worms aim to
infect all vulnerable machines as quickly as possible by aggressively
hunting for new victims. We detect this type of IM worms by monitoring
abrupt increase of file transfer requests or URL-embedded chat
messages in the IM system. The second family of IM worms allow only a
limited number of infection attempts within a certain period of
time. Although spreading more slowly, this type of IM worms do not
trigger a large number of file transfer requests or URL-embedded chat
messages. Our detection scheme relies on the observation that
different degrees of social online intimacy among IM buddies lead to
uneven communication messages exchanged among them. An IM worm that
randomly chooses online buddies as infection victims can, very likely,
generate file transfer requests or URL-embedded chat messages between
IM buddies that barely chat in the past. To detect this type of IM
worms, we measure the average log-likelihood of file transfer requests
or URL-embedded chat messages in the IM system; its abrupt decrease is
a good indication of stealthy IM worm propagation. We evaluate our
detection schemes with an IM dataset collected from a large enterprise
network and experimental results show that they are very effective in
detecting both families of IM worms.
The remainder of this paper is organized as follows. Section
II presents some background knowledge about IM
architecture and IM worms. Section III
discusses IM worms that aggressively scan for new victims and their
detection. Section IV discusses how an
intelligent IM worm evades the detection scheme described in Section
III. In this section, we also provide an
algorithm that detects this type of IM worms. In Section
V, we evaluate the effectiveness of the proposed
solutions with an IM dataset collected from a large corporate
network. We present some related work in Section
VI and conclude this paper in Section
VII.
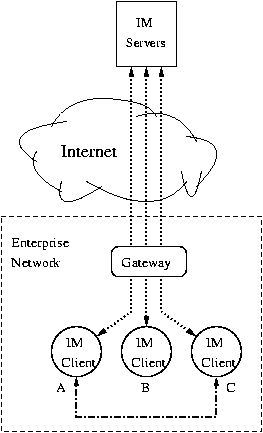
2 IM Architectures and IM Worms
IM architectures. Popular IM systems include MSN messenger, AIM,
Yahoo Messenger, IRC, ICQ, and Google Talk. Although these systems are
built on different protocols, they bear little difference in their
basic client-server structures. The general framework of an IM system
in an enterprise-like network is depicted in
Fig. 1. IM servers form the backbone of an IM
system and their typical functionalities include account management,
user authentication, presence notification, text-based chat message
relaying, file transfer establishment, and group chatting. Albeit
major IM systems provide similar functionalities, their server
architectures may differ from each other. For instance, a text-based
chat message in the AIM system has to go through two BOS (Basic Oscar
Services) servers before it is delivered to the receiver, but a
similar message in the MSN system traverses only one SB (switchboard)
server [23].
Figure 1:
Architecture of a typical IM system
|
In our work, we focus on schemes that detect IM worm propagation in a
centralized fashion. More specifically, we consider approaches that
can be directly deployed at the IM servers, or at the enterprise
gateway if the goal is to protect an enterprise network. The
feasibility of such a solution requires further
explanation. Encryption is rarely used in existing major IM systems,
suggesting IM servers or enterprise gateways can see most text-based
chat messages delivered through them. Hence, if an IM worm uses the
URL-embedded chat messages to spread itself, the IM servers or the
enterprise gateway can parse unencrypted chat messages and derive the
URL information. However, the IM servers or the enterprise gateway can
not capture the file being transferred between two IM clients, unless
the sender and receiver are both protected by a firewall or NAT router
[23]. Hence, if an IM worm propagates through file
transfers, we may not be able to detect IM worm propagation through
binary malware code analysis at the enterprise gateway or the IM
servers. Nevertheless, any file transfer between two IM clients must
involve some IM servers to set up their initial connection, so we can
still infer that a file transfer is going to take place between two IM
clients by analyzing IM command traffic at the enterprise gateway or
the IM servers.
IM worms. An infection attempt through an IM network consists of
two processes: handshaking and downloading. In the
handshaking step, an infected machine with IM account  requests a
file transfer or sends a URL-embedded chat message to
requests a
file transfer or sends a URL-embedded chat message to 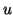 's online
buddy
's online
buddy 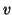 . When IM user
. When IM user 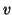 receives the file transfer request or the
URL-embedded chat message, she decides whether to accept the request
or click on the URL. Only if she does so will the next step take
place: the recipient machine downloads the worm code body from the
machine that
receives the file transfer request or the
URL-embedded chat message, she decides whether to accept the request
or click on the URL. Only if she does so will the next step take
place: the recipient machine downloads the worm code body from the
machine that 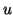 is using if the file transfer scheme is used, or from
the host specified by the URL if the worm spreads by URL-embedded chat
messages. Once the second step finishes, the recipient machine gets
infected if it is vulnerable to the worm infection; otherwise, the
infection attempt fails.
is using if the file transfer scheme is used, or from
the host specified by the URL if the worm spreads by URL-embedded chat
messages. Once the second step finishes, the recipient machine gets
infected if it is vulnerable to the worm infection; otherwise, the
infection attempt fails.
We use 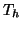 and
and 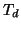 to denote the durations of the handshaking
step and the downloading step, respectively. We also use
to denote the durations of the handshaking
step and the downloading step, respectively. We also use 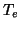 to
denote the time needed to execute the worm code on a victim machine,
e.g., modifying the registry on a Windows machine. Let
to
denote the time needed to execute the worm code on a victim machine,
e.g., modifying the registry on a Windows machine. Let 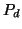 be the
probability that a node accepts a file transfer request or clicks on
the embedded URL.
be the
probability that a node accepts a file transfer request or clicks on
the embedded URL. 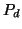 essentially reflects the probability that the
worm spreading attempt succeeds in each hop. We also use
essentially reflects the probability that the
worm spreading attempt succeeds in each hop. We also use 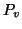 to
denote the probability that a node is vulnerable to the worm infection
after the worm code body is downloaded.
to
denote the probability that a node is vulnerable to the worm infection
after the worm code body is downloaded.
3 Fast Scanning IM Worms
Many existing IM worms adopt the fast scanning strategy, that is,
they, after infecting a new host, immediately iterate the online buddy
list and attempt to infect each contact on it either by requesting a
file transfer or sending out a URL-embedded chat message. Such IM
worms include Bropia and Kelvir that have been observed spreading on
the MSN IM network. The common objective of fast scanning IM worms is
to infect all vulnerable machines as quickly as possible. Experiences
with traditional Internet worms such as Code Red and Slammer suggest
that an effective defense scheme against a fast scanning worm must
detect it at its early propagation stage [18].
Algorithm description. The aggressive spreading strategy used
by fast scanning IM worms, although accelerating their propagation,
inevitably increases the number of file transfer requests or
URL-embedded chat messages in the IM systems, depending on their
infection vectors. Moreover, these file transfer requests or
URL-embedded text messages introduced by fast scanning IM worms bear
different source-destination pairs. Such a distinguishing feature of
fast scanning IM worms motivates us to apply sequential change
detection theory for their detection. The key idea of sequential
change detection theory is to locate the point of change, if it
occurs, within an observed time series by checking whether it is
statistically homogeneous in an online fashion. Further explanation
requires more notations. We discretize time into measurement windows
of equal length 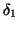 , denoted by
, denoted by
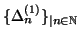 . We use random sequence
. We use random sequence
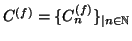 and
and
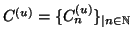 to
denote the total number of file transfer requests and URL-embedded
chat messages with different source-destination pairs that have been
observed within the
to
denote the total number of file transfer requests and URL-embedded
chat messages with different source-destination pairs that have been
observed within the 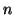 -th measurement window, respectively.
-th measurement window, respectively.
To detect fast scanning IM worms, we use the CUSUM algorithm
[14], which is a standard tool in statistical process
control. Particularly, we apply its non-parametric version
[1] as it does not demand any a
priori information on distributions of the random sequence before
and/or after the change point. Let
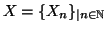 be a random sequence with mean
be a random sequence with mean 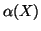 under normal operation. Our
goal is to detect whether there is an abrupt change of mean in
under normal operation. Our
goal is to detect whether there is an abrupt change of mean in 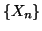 . As the non-parametric CUSUM algorithm only works on random
sequences with negative means before the change point and positive
means after the change point, we transform
. As the non-parametric CUSUM algorithm only works on random
sequences with negative means before the change point and positive
means after the change point, we transform
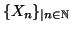 into a new random sequence
into a new random sequence
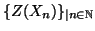 , where
, where
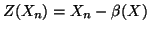 ,
, 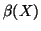 is a
constant depending on random process
is a
constant depending on random process 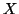 , and
, and
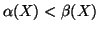 .
.
The non-parametric CUSUM algorithm works as follows. First we define
sequence
 :
:
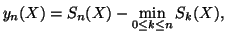 |
(1) |
where
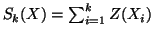 and
and
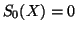 . We can calculate
. We can calculate 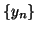 more efficiently in a recursive manner:
more efficiently in a recursive manner:
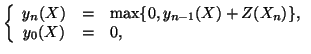 |
(2) |
In this way, 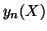 can be immediately computed based on
can be immediately computed based on
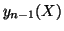 once measurement
once measurement 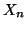 is available. Thereafter, we
decide whether there is an abrupt change at time
is available. Thereafter, we
decide whether there is an abrupt change at time 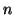 by comparing
by comparing
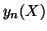 against a predefined threshold
against a predefined threshold 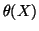 : if
: if
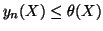 , there is no abrupt change of mean in random sequence
, there is no abrupt change of mean in random sequence 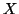 ;
otherwise, there is.
;
otherwise, there is.
One might suggest that we apply the CUSUM algorithm directly on random
sequence
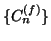 or
or
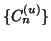 to detect fast scanning
IM worms spreading by file transfers or URL-embedded chat messages. A
basic assumption of the CUSUM algorithm, however, is that the process
before the change point should be stationary. It is easy to see that
both random sequences
to detect fast scanning
IM worms spreading by file transfers or URL-embedded chat messages. A
basic assumption of the CUSUM algorithm, however, is that the process
before the change point should be stationary. It is easy to see that
both random sequences
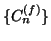 are
are
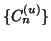 vary with
the number of online users, which typically changes over the time in a
day. For instance, measurements of IM traffic in a large corporate
network reveal that the peak times of user login and user logout are
around 9AM and 5PM, respectively, which are strongly correlated with
employees' working hours [23]. If we attempt to
detect a fast scanning IM worm quickly by selecting a measurement
window
vary with
the number of online users, which typically changes over the time in a
day. For instance, measurements of IM traffic in a large corporate
network reveal that the peak times of user login and user logout are
around 9AM and 5PM, respectively, which are strongly correlated with
employees' working hours [23]. If we attempt to
detect a fast scanning IM worm quickly by selecting a measurement
window
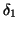 much smaller than a day, applying the CUSUM
algorithm directly on random sequence
much smaller than a day, applying the CUSUM
algorithm directly on random sequence
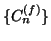 or
or
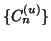 may lead to high false alarm rates.
may lead to high false alarm rates.
To circumvent this problem, we measure another random process
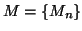 , in which
, in which 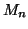 is the number of online IM users within the
is the number of online IM users within the
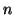 -th measurement window
-th measurement window
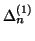 . Instead of detecting
abrupt changes on
. Instead of detecting
abrupt changes on
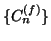 or
or
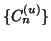 directly, we
normalize them by
directly, we
normalize them by 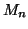 first before applying the CUSUM
algorithm. Algorithm 1 provides a brief
overview of our solution to detecting fast scanning IM worms:
first before applying the CUSUM
algorithm. Algorithm 1 provides a brief
overview of our solution to detecting fast scanning IM worms:

When implementing Algorithm 1, if there
are no online IM users (i.e., 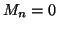 ), we ignore this measurement
window, which means that the next measurement window is still the
), we ignore this measurement
window, which means that the next measurement window is still the
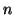 -th measurement window.
-th measurement window.
Parameter configuration. We set the model parameters in a
similar way as in [21]. First,
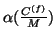 and
and
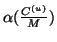 can be
estimated from training data. Define:
can be
estimated from training data. Define:
where 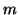 is the time when the worm starts to propagate,
is the time when the worm starts to propagate, 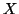 is
either
is
either
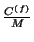 or
or
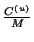 ,
, 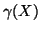 denotes
the time of the change point, and
denotes
the time of the change point, and 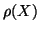 is the normalized
detection time after the change point. Let
is the normalized
detection time after the change point. Let 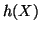 be the increase of
mean after the IM worm starts to propagate. We then have:
be the increase of
mean after the IM worm starts to propagate. We then have:
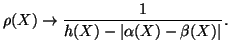 |
(5) |
By choosing 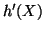 , which is a lower bound of
, which is a lower bound of 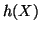 , to replace
, to replace
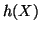 , we can set
, we can set 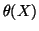 as follows:
as follows:
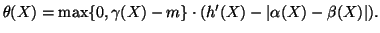 |
(6) |
Similar to [21], we let 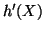 be
be
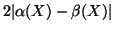 . Recall that
. Recall that 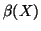 is an upper bound of
is an upper bound of
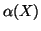 ; hence, we can choose
; hence, we can choose 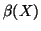 to be
to be
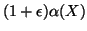 , where
, where 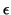 is a positive number. We also
specify
is a positive number. We also
specify
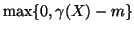 as the target detection delay
as the target detection delay
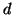 . We thus have:
. We thus have:
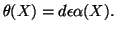 |
(7) |
Algorithm analysis. We now analyze how effective the CUSUM
algorithm is in detecting fast scanning IM worms. We assume that a
machine attempts to spread the worm onto its online IM buddies
immediately after it gets infected. For simplicity, we also assume
that at the initial propagation stage, the number of buddies that have
already been infected can be ignored. Let 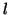 be the average number of
online users and
be the average number of
online users and 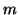 be the average number of online buddies of each
online user in the IM network when the IM worm is spreading. When an
infected machine attempts to spread the worm onto
be the average number of online buddies of each
online user in the IM network when the IM worm is spreading. When an
infected machine attempts to spread the worm onto 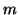 online buddies,
online buddies,
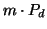 of them actually download the worm code. We assume that
the worm downloading time is
of them actually download the worm code. We assume that
the worm downloading time is 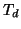
![[*]](footnote.png) . Hence, if an
infected machine initiates a successful infection attempt to an online
buddy at time
. Hence, if an
infected machine initiates a successful infection attempt to an online
buddy at time 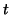 , the victim machine is infected at time
, the victim machine is infected at time
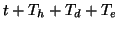 . Among the
. Among the 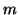 online buddies, an infected machine can
only infect
online buddies, an infected machine can
only infect 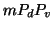 of them successfully. Let
of them successfully. Let 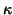 be the number
of worm generations before the worm is detected by the CUSUM
algorithm. The number of infected machines in the
be the number
of worm generations before the worm is detected by the CUSUM
algorithm. The number of infected machines in the 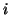 -th worm
generation, where
-th worm
generation, where
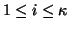 , is
, is
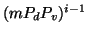 . Suppose
that the IM worm starts to spread at the beginning of measurement
window
. Suppose
that the IM worm starts to spread at the beginning of measurement
window
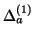 and the IM worm is detected at the end of
measurement window
and the IM worm is detected at the end of
measurement window
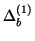 . We then have:
. We then have:
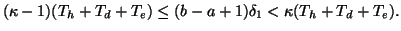 |
(8) |
Therefore, 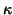 can be represented as:
can be represented as:
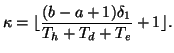 |
(9) |
Moreover, 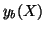 , where
, where 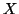 is
is
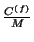 or
or
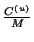 , can be approximated as follows:
, can be approximated as follows:
As we have
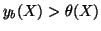 and
and
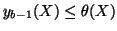 , we can
estimate
, we can
estimate  , which is the number of measurement windows required
to detect the fast scanning IM worm. First, suppose that
, which is the number of measurement windows required
to detect the fast scanning IM worm. First, suppose that
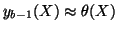 and
and
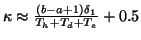 . Let
. Let 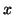 be
be 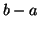 ,
, 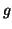 be
be
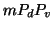 , and
, and 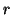 be
be
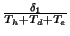 . We then have:
. We then have:
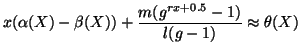 |
(10) |
As it is difficult to solve the above equation analytically, we use
Taylor approximation for 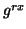 . Although it is possible to use
Taylor series of orders higher than one, the solution becomes
lengthy. Hence, we use the first-order Taylor series at point 0, i.e.,
. Although it is possible to use
Taylor series of orders higher than one, the solution becomes
lengthy. Hence, we use the first-order Taylor series at point 0, i.e.,
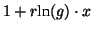 , to approximate it. Finally, we have:
, to approximate it. Finally, we have:
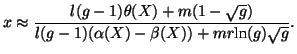 |
(11) |
We can thus establish the following theorem:
Theorem 1
Given the assumptions we have made, Algo.
1 needs approximately
![$ [x]+1$](img97.png)
measurement windows to detect the fast scanning IM worm, where
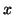
is given in Eq. (
11).
From Eq. (11), we observe that if 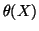 is
high, or
is
high, or 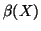 is chosen much larger than
is chosen much larger than 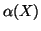 , it takes a
longer time to detect the fast scanning IM worm, which is consistent
with our intuition.
, it takes a
longer time to detect the fast scanning IM worm, which is consistent
with our intuition.
Implementation. If Algorithm 1 is
implemented by the IM servers, it needs to know the online status of
each IM user. Such information is already available because the IM
servers need to notify an IM user of each buddy's presence status when
she just logs into the IM system. If Algorithm
1 is implemented at the enterprise
gateway, there are two ways of keeping the online status of each
internal IM user. One is to intercept every IM command that carries
the presence information of an IM user. The second approach is to
monitor the persistent TCP connections between the IM user and some IM
servers, such as the BOS server in the AIM system and the notification
server in the MSN system [23]: if such TCP
connections are still alive, the corresponding IM user is online.
4 Self-Restraining IM Worms
Security by obscurity is never a good practice. If an adversary knows
that Algorithm 1 has been deployed to
detect IM worms, can he design an intelligent IM worm that spreads
without being caught? We demonstrate its possibility in the following
discussion. Note that the CUSUM algorithm triggers an alarm only when
the cumulative sum reaches threshold 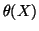 ; this allows an IM
worm to ramp up its infection coverage using the fast scanning
strategy to a certain point without being detected. After that, the
difference between
; this allows an IM
worm to ramp up its infection coverage using the fast scanning
strategy to a certain point without being detected. After that, the
difference between 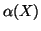 and
and 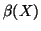 allows the IM worm to
spread at a constant speed without increasing
allows the IM worm to
spread at a constant speed without increasing 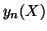 . Following the
scenario analyzed in Section III, an
adversary estimates
. Following the
scenario analyzed in Section III, an
adversary estimates 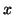 according to Eq. (11) and
predicts that a fast scanning IM is detected after
according to Eq. (11) and
predicts that a fast scanning IM is detected after ![$ [x]+1$](img97.png) measurement
windows. To avoid detection, the IM worm is designed to stop
propagating in a fast scanning mode after
measurement
windows. To avoid detection, the IM worm is designed to stop
propagating in a fast scanning mode after 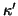 generations,
where:
generations,
where:
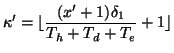 |
(12) |
and 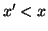 .
.
Since 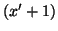 -th measurement window, the worm spreads in a
self-restraining manner. If the number of file transfer requests or
URL-embedded chat messages per measurement window generated by the
worm does not exceed
-th measurement window, the worm spreads in a
self-restraining manner. If the number of file transfer requests or
URL-embedded chat messages per measurement window generated by the
worm does not exceed
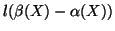 , it is highly likely
that the worm propagates without triggering an alarm. We now show how
an intelligent IM worm can achieve this using a token-based
approach. Note that the number of infected machines in the
, it is highly likely
that the worm propagates without triggering an alarm. We now show how
an intelligent IM worm can achieve this using a token-based
approach. Note that the number of infected machines in the
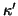 -th generation is
-th generation is
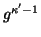 , where we recall
, where we recall
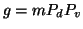 . Let
. Let 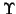 be
be
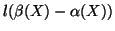 . After a
. After a
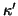 -th worm instance is created,
-th worm instance is created,
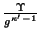 tokens are generated for
it
tokens are generated for
it![[*]](footnote.png) .
.
The color of a token can be green or red. Initially, we
set the colors of all tokens to green. The protocol works as follows:
(1) If the color of a token changes to green, the holding worm
instance randomly chooses a new victim that it has never tried to
infect from the online IM buddy list and then attempts to infect
it. If the holding worm instance cannot find an online buddy contact
that has never been tried, it passes the green token to a random
online buddy that it knows has already been infected, or to the
machine from which it gets infected![[*]](footnote.png) ; otherwise, it changes the color of the
token to red, inscribes the current time onto the token, and
schedules an activation timer which fires after
; otherwise, it changes the color of the
token to red, inscribes the current time onto the token, and
schedules an activation timer which fires after 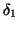 time
units since the timestamp on the token. (2) When an activation
timer fires, the associated token changes to green and the holding
worm instance proceeds as in (1). (3) If a worm instance
successfully infects a new machine, it cancels any of its red tokens,
if it has such one, and passes it to the new machine without altering
its inscribed timestamp. (4) When a worm instance receives a red
token with time stamp
time
units since the timestamp on the token. (2) When an activation
timer fires, the associated token changes to green and the holding
worm instance proceeds as in (1). (3) If a worm instance
successfully infects a new machine, it cancels any of its red tokens,
if it has such one, and passes it to the new machine without altering
its inscribed timestamp. (4) When a worm instance receives a red
token with time stamp 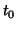 , it schedules an activation timer after
time
, it schedules an activation timer after
time
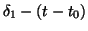 , where
, where 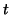 is the current time. (5) When
a worm instance receives a green token, it proceeds in the same way as
in (1). We can easily establish the following property of the
token-based protocol (proof omitted due to space limitation):
is the current time. (5) When
a worm instance receives a green token, it proceeds in the same way as
in (1). We can easily establish the following property of the
token-based protocol (proof omitted due to space limitation):
Theorem 2
The token-based protocol guarantees that within any time interval of
length
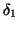
since the last
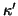
-th generation worm
instance has been installed, the total number of file transfer
requests or URL-embedded chat messages generated by the worm is at
most
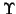
.
Algorithm description. We call intelligent IM worms that use
rate limiting methods such as the token-based protocol
self-restraining IM worms. To detect such type of IM worms,
monitoring surges of file transfer requests or URL-embedded chat
messages in the IM system is not sufficient. Instead, we measure
likelihoods of file transfers or URL-embedded chat messages between IM
clients and use them to decide whether a self-restraining IM worm is
spreading. This idea is based on the measurements on IM messages in a
large corporate network: on average, an AIM user chats with only 1.9
buddies, about 7% on her buddy list, and an MSN user chats with 5.5
buddies, 25% on her buddy list, in a month
[23]. Such an observation suggests that an IM user
tends to chat more often with a small set of her online buddies, which
reflects her online social intimacy. However, self-restraining IM
worms as described do not have that knowledge about social
relationships between IM users. Hence, when an IM worm instance
chooses a victim from the online buddy list, it randomly picks one
from those that have not been attempted before. As such randomness may
not reflect real-world online social intimacy, it offers a weakness
for their detection.
Similar to Algorithm 1, we discretize
time into measurement windows of equal length 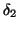 , denoted by
, denoted by
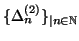 .
. 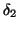 is not
necessarily equal to
is not
necessarily equal to 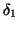 . Let
. Let 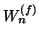 and
and 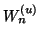 denote the set of IM user pairs
denote the set of IM user pairs
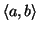 , where IM user
, where IM user
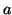 sends at least one file transfer request and at least one
URL-embedded chat message to IM user
sends at least one file transfer request and at least one
URL-embedded chat message to IM user 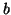 within measurement window
within measurement window
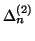 , respectively. We also use
, respectively. We also use 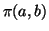 to denote the
metric that reflects how close IM user
to denote the
metric that reflects how close IM user 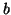 is to IM user
is to IM user 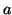 in the IM
world. Essentially,
in the IM
world. Essentially, 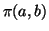 is the probability that IM user
is the probability that IM user 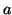 sends a chat message or a file transfer request to
sends a chat message or a file transfer request to 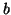 in the
history. Let
in the
history. Let 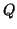 be the whole set of IM users. We have:
be the whole set of IM users. We have:
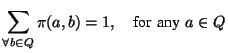 |
(13) |
We use the EWMA (exponentially weighted moving average) approach to
update 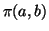 . First, we discretize time into intervals of the
same length. A time interval here can represent, for instance, a
week. Let
. First, we discretize time into intervals of the
same length. A time interval here can represent, for instance, a
week. Let
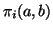 denote the
denote the 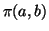 value estimated after the
value estimated after the
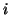 -th time interval and
-th time interval and
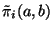 denote the fraction of
chat messages or file transfer requests that are sent from
denote the fraction of
chat messages or file transfer requests that are sent from 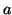 to
to 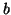 during the
during the 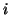 -th time interval. We then update
-th time interval. We then update
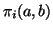 as
follows:
as
follows:
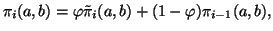 |
(14) |
where
![$ \varphi \in [0,1]$](img124.png) is the weighting factor. It is trivial to
verify that Eq. (13) must be true for any
is the weighting factor. It is trivial to
verify that Eq. (13) must be true for any 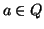 and
and
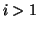 if initially
if initially
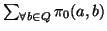 is equal to
1.
is equal to
1.
We define sequences
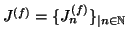 and
and
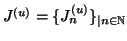 as follows:
as follows:
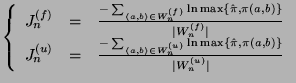 |
(15) |
where
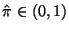 .
.
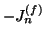 and
and
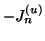 give
the average log-likelihood of file transfer requests and URL-embedded
chat messages within measurement window
give
the average log-likelihood of file transfer requests and URL-embedded
chat messages within measurement window
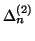 ,
respectively. In Eq. (15), we use the minimum of
,
respectively. In Eq. (15), we use the minimum of
 and
and 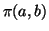 in case that the latter is 0.
in case that the latter is 0.
We then monitor abrupt change of
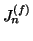 and
and
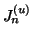 to
detect self-restraining IM worms:
to
detect self-restraining IM worms:

Parameters in Algorithm 2 are specified
in a similar manner as in Algorithm
1. For brevity, we do not replicate it
here.
Algorithm analysis. We consider the self-restraining IM worm
that uses the token-based scheme to control its propagation speed. The
total number of tokens is 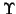 . We assume that at the initial
stage of worm propagation, each worm instance has received at most one
token
. We assume that at the initial
stage of worm propagation, each worm instance has received at most one
token![[*]](footnote.png) . Also
let the number of online buddies per user be
. Also
let the number of online buddies per user be 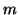 . To ease analysis, we
further assume that under normal conditions, the nominators and
denominators in Eq. (15) are constant. That is,
. To ease analysis, we
further assume that under normal conditions, the nominators and
denominators in Eq. (15) are constant. That is,
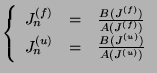 |
(16) |
where
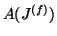 ,
,
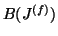 ,
,
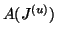 , and
, and
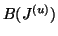 are
constants. Suppose that the self-restraining IM worm starts
propagating at the beginning of the
are
constants. Suppose that the self-restraining IM worm starts
propagating at the beginning of the 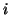 -th measurement window and
Algorithm 2 detects it after
-th measurement window and
Algorithm 2 detects it after 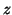 measurement windows. We ignore the cases in which the worm sends a
file transfer request or a URL-embedded chat message from
measurement windows. We ignore the cases in which the worm sends a
file transfer request or a URL-embedded chat message from 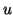 to
to 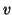 but there is also a normal file transfer request or URL-embedded chat
message from
but there is also a normal file transfer request or URL-embedded chat
message from 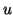 and
and 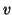 . This is a reasonable assumption because the
infection attempts by a self-restraining IM worm are usually small
(otherwise, Algorithm 1 can detect it). Suppose that we choose a small
. This is a reasonable assumption because the
infection attempts by a self-restraining IM worm are usually small
(otherwise, Algorithm 1 can detect it). Suppose that we choose a small
 such that it is smaller than
such that it is smaller than 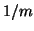 . We then have:
. We then have:
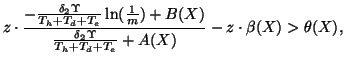 |
(17) |
where 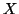 is
is 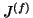 or
or 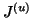 , depending on the spreading vector
of the IM worm. Hence, the CUSUM algorithm is able to detect the
self-restraining IM worm after
, depending on the spreading vector
of the IM worm. Hence, the CUSUM algorithm is able to detect the
self-restraining IM worm after 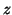 measurement windows, where
measurement windows, where
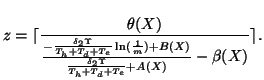 |
(18) |
We can thus establish the following theorem:
Theorem 3
Given the assumptions we have made, Algorithm
2 needs approximately
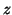
measurement
windows to detect the self-restraining IM worm, where
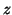
is given
in Eq. (
18).
From Eq. (18), it is clear that a too large
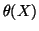 or
or 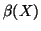 extends the detection period. But in
reality,
extends the detection period. But in
reality, 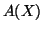 and
and 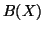 change over time. Hence, making
change over time. Hence, making 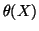 or
or 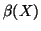 too small can introduce high false alarm rates.
too small can introduce high false alarm rates.
Implementation. One implementation issue with the
aforementioned algorithm is the complexity of collecting 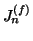 and
and 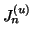 . The algorithm requires knowledge of buddy
relationships in the IM system. If the algorithm is implemented at the
IM servers, such knowledge is already available, as the IM servers
need it to notify an IM client of the presence statuses of her buddies
if they change. For instance, in the AIM system, when an IM user logs
in, the client software sends a list of her IM buddies in screen names
to the message server; these names will be monitored for login/logout
events. If the detection algorithm is implemented at the enterprise
gateway, we need to parse IM command messages to derive buddy
relationships. For instance, the detection algorithm designed for the
AIM system can capture the ``oncoming buddy'' commands at the
enterprise gateway that appear in the following three cases: first,
the AIM messenger server notifies each user of the statuses of her
buddies when she is logging into the system; second, whenever one of
the buddies comes online after a user logged in, she gets a
notification from the servers; third, the IM servers regularly use
these commands to update the buddy list of each user [13].
. The algorithm requires knowledge of buddy
relationships in the IM system. If the algorithm is implemented at the
IM servers, such knowledge is already available, as the IM servers
need it to notify an IM client of the presence statuses of her buddies
if they change. For instance, in the AIM system, when an IM user logs
in, the client software sends a list of her IM buddies in screen names
to the message server; these names will be monitored for login/logout
events. If the detection algorithm is implemented at the enterprise
gateway, we need to parse IM command messages to derive buddy
relationships. For instance, the detection algorithm designed for the
AIM system can capture the ``oncoming buddy'' commands at the
enterprise gateway that appear in the following three cases: first,
the AIM messenger server notifies each user of the statuses of her
buddies when she is logging into the system; second, whenever one of
the buddies comes online after a user logged in, she gets a
notification from the servers; third, the IM servers regularly use
these commands to update the buddy list of each user [13].
Algorithm 2 also requires knowledge of
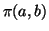 from each online IM user
from each online IM user 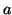 to each of her buddies
to each of her buddies 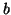 . As
text-based chat messages and file transfer requests go through IM
servers, we can calculate
. As
text-based chat messages and file transfer requests go through IM
servers, we can calculate 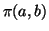 by parsing IM chat messages or IM
command messages for setting up file transfers at the IM servers or
the enterprise gateway.
by parsing IM chat messages or IM
command messages for setting up file transfers at the IM servers or
the enterprise gateway.
5 Experimental Evaluation
We use a realistic MSN IM messaging dataset to evaluate the
effectiveness of our algorithms in detecting IM worms. This dataset,
collected from a large corporate network, records chat messages of
internal IM users and their online durations within a year. Our
experiments are based on part of this dataset that has ten weeks'
records. This subset has 193 internal IM users; on average, each of
them has 22 IM buddies. In total, 3851 external IM contacts appear on
the buddy lists of these 193 internal IM users. Unfortunately, we
cannot get the buddy lists of these external IM users. As observed in
[12,17], IM networks tend
to have power-law structures. We use the Power-Law Out-Degree
Algorithm [15] to generate power-law
graphs with 3581 nodes, whose average outdegree is 22. The power law
exponent is set to be 1.7, based on measurement results from
[12,17]. For simplicity, we
let the buddy relationships in the external graph be
symmetric. Furthermore, if an external user is on the buddy list of an
internal user, she also has that internal user on her own buddy list.
In our experiments, we consider only IM worms that are based on file
transfers. Due to some technical problems, we are not able to obtain
sufficient data on normal file transfers between internal IM users or
between internal IM users and external IM users as of writing. We thus
use measurement results from [10]: on average
an online IM user sends out 1.84 file transfer requests per 24
hours. Similarly, we assume that the average number of file transfer
requires an IM user receives is also 1.84. For each file transfer
request, the probability that it falls into a time interval is
proportional to the number of online internal IM users; once the time
interval is chosen, its exact appearance time at the enterprise
gateway is uniformly distributed within that time interval.
Now we introduce how to generate the sender and receiver of a file
transfer request if it is issued by an internal IM user. For each of
the 193 internal IM users, we build a buddy relationship table, an
entry in which indicates the probability that a chat message is sent
from her to the corresponding contact on her buddy list within the
current week (i.e., not history based). These probabilities are
empirically measured from the IM dataset. Let
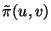 denote the probability that a chat message goes from internal IM user
denote the probability that a chat message goes from internal IM user
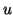 to another IM user
to another IM user 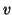 . Also, we measure the probability that an
outbound chat message (i.e., it is generated from an internal IM user)
comes from a specific internal IM user
. Also, we measure the probability that an
outbound chat message (i.e., it is generated from an internal IM user)
comes from a specific internal IM user 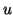 , denoted by
, denoted by
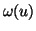 . Then, when a file transfer request sent by an internal IM
user is generated within a time interval, we first collect the entire
set of IM user pairs
. Then, when a file transfer request sent by an internal IM
user is generated within a time interval, we first collect the entire
set of IM user pairs 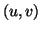 , where
, where 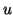 is an internal IM user and
both IM users
is an internal IM user and
both IM users 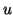 and
and 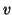 are online during that time interval. Let
are online during that time interval. Let
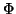 be this set. Then, IM user pair
be this set. Then, IM user pair 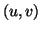 is chosen with
probability
is chosen with
probability 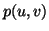 :
:
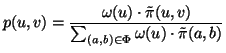 |
(19) |
In the experiments, we assume that the delay in seconds from one IM
user to another obeys normal distribution
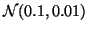 in
seconds. The time that a recipient of a file transfer request spends
on deciding whether to accept the request is exponentially distributed
with mean 5 seconds. The downloading time is generated from normal
distribution
in
seconds. The time that a recipient of a file transfer request spends
on deciding whether to accept the request is exponentially distributed
with mean 5 seconds. The downloading time is generated from normal
distribution
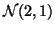 . We ignore the execution time of
downloaded malware in our experiments. We vary the acceptance ratio of
a file transfer request (i.e.,
. We ignore the execution time of
downloaded malware in our experiments. We vary the acceptance ratio of
a file transfer request (i.e., 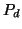 ) among 0.25, 0.5, 0.75, and
1.0. We also vary the vulnerable probability of a machine (i.e.,
) among 0.25, 0.5, 0.75, and
1.0. We also vary the vulnerable probability of a machine (i.e.,
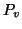 ) among 0.25, 0.5, 0.75, and 1.0.
) among 0.25, 0.5, 0.75, and 1.0.
For each simulation scenario, we randomly pick an IM node, either
internal or external, as the initial infection. The first infection
takes place at simulation time 42000 seconds![[*]](footnote.png) . For each simulation
scenario, we run it 10 times with different random number generation
seeds. In our experiments, IM worm detection is performed at the
enterprise gateway.
. For each simulation
scenario, we run it 10 times with different random number generation
seeds. In our experiments, IM worm detection is performed at the
enterprise gateway.
1 Detection of Fast Scanning IM Worms
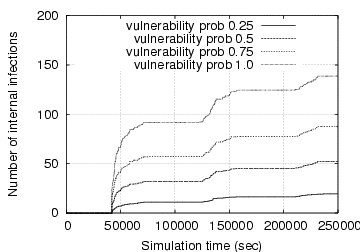
Figure 2:
Growth curves of internal infections when the IM worm uses
the fast scanning spreading strategy
 |
 |
| (1) Acceptance ratio = 0.5 |
(2) Vulnerable prob = 0.5 |
|
In Fig. 2, we present the growth
curves of internal infections (i.e., infected machines that are behind
the enterprise gateway) when the IM worm uses the fast scanning
spreading strategy. Obviously, when the acceptance ratio (i.e., 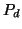 )
is fixed, a higher percentage of vulnerable IM contacts leads to
faster IM worm spreading; similarly, when a fixed portion of IM
contacts is vulnerable, a higher acceptance ratio also accelerates IM
worm propagation. Both observations agree with our
intuition. Moreover, the maximum number of infected internal IM
contacts is bounded by the number of internal vulnerable
machines. This is confirmed in the right graph: the number of internal
infections is always less than 97 (recall that there are 193 internal
IM users in our dataset). However, this is not true when the
acceptance ratio is fixed at 50% and the vulnerable probability is
100%. It is because an IM user can receive multiple file transfer
requests from different buddies and accepting any one of them leads to
a new infection.
)
is fixed, a higher percentage of vulnerable IM contacts leads to
faster IM worm spreading; similarly, when a fixed portion of IM
contacts is vulnerable, a higher acceptance ratio also accelerates IM
worm propagation. Both observations agree with our
intuition. Moreover, the maximum number of infected internal IM
contacts is bounded by the number of internal vulnerable
machines. This is confirmed in the right graph: the number of internal
infections is always less than 97 (recall that there are 193 internal
IM users in our dataset). However, this is not true when the
acceptance ratio is fixed at 50% and the vulnerable probability is
100%. It is because an IM user can receive multiple file transfer
requests from different buddies and accepting any one of them leads to
a new infection.
We now investigate how effective Algorithm
1 is in detecting these fast scanning IM
worms. We let the measurement window size be 300 seconds. The
threshold parameter is computed based on Eq. (7), in
which we let 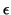 be 3 and
be 3 and 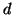 be 3. Here, we choose a
relatively large
be 3. Here, we choose a
relatively large 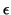 so that effects of white noise (e.g.,
bursts of normal file transfer requests) can be offset. We first test
the algorithm when there is no IM worm spreading. No false positives
have been observed. We then test 160 sample runs with 16 different
combinations of vulnerable probabilities and acceptance ratios. We
find that there are eight false negatives. A closer examination at the
eight false negatives reveals that in all of them either one (the
initial infection point) or two have been infected before simulation
time 250,000 seconds. Due to no widespread worm propagation, Algorithm
1 cannot detect it based on the number
of file transfer requests observed.
so that effects of white noise (e.g.,
bursts of normal file transfer requests) can be offset. We first test
the algorithm when there is no IM worm spreading. No false positives
have been observed. We then test 160 sample runs with 16 different
combinations of vulnerable probabilities and acceptance ratios. We
find that there are eight false negatives. A closer examination at the
eight false negatives reveals that in all of them either one (the
initial infection point) or two have been infected before simulation
time 250,000 seconds. Due to no widespread worm propagation, Algorithm
1 cannot detect it based on the number
of file transfer requests observed.
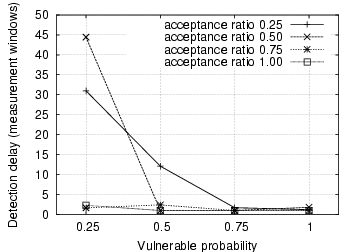
Figure 3:
Detection delay in measurement windows for fast scanning IM worms
|
|
Figure 4:
Fraction of internal infections at detection time for fast scanning IM worms
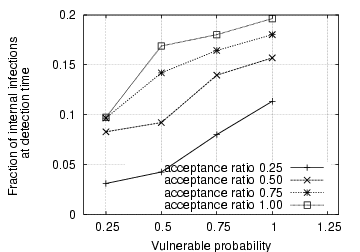
|
|
Fig. 3 depicts the detection delay in terms of
measurement windows. For most of the scenarios, it takes between one
and three measurement windows to detect the IM worm propagation. We,
however, observe that when both the acceptance ratio and vulnerable
probability are low, it takes a significant number of measurement
windows to detect the IM worm. This is because in these cases the IM
worm propagates very slowly and thus does not generate a large number
of file transfer requests within a single measurement window. This is
further confirmed in Fig. 4, which
demonstrates the fraction of internal IM contacts that are infected
among all internal vulnerable machines when the IM worm is
detected. It is observed that for those cases with large detection
delays, the fraction of internal infections is below 10%. On the
other hand, when the vulnerable probability is 1.0, the fraction of
internal infections reaches between 15% and 20% when the IM worm is
detected, even though it takes only one measurement window. In these
cases, we can accelerate IM worm detection by decreasing the
measurement window size.
We now consider a self-restraining IM worm that limits its spreading
speed to evade detection by Algorithm
1. This worm allows only three infection
attempts (i.e., file transfer requests in our experiments) every 300
seconds. It uses the token-based protocol, as described in Section
IV, to control its propagation
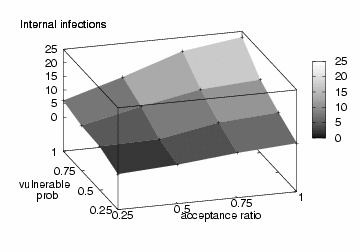
speed. Fig. 5 depicts the number of
internal infections at simulation time 250,000 seconds as a function
of acceptance ratio and vulnerable probability. Compared against the
fast scanning IM worm, the self-restraining IM worm propagates much
more slowly. For instance, when the acceptance ratio is 50% and the
vulnerable probability is 75%, the number of internal infections is
only 9 after simulation time 250,000 seconds, as opposed to 88
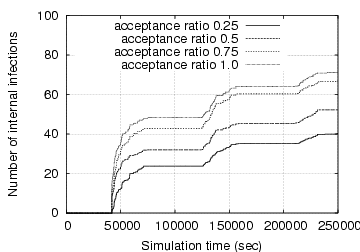
internal infections with the fast scanning spreading strategy.
Figure 5:
Number of internal infections with the self-restraining spreading strategy
|
|
Figure 6:
Detection ratio of self-restraining IM worms with Algorithm 1
|
|
Figure 7:
Detection delay of self-restraining IM worms with Algorithm 2
|
|
Figure 8:
Fraction of internal infections at detection time with Algorithm 2
|
|
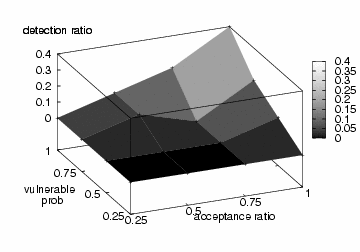
Fig. 6 presents the successful detection ratio
of the self-restraining IM worm by Algorithm
1. Among 160 sample runs, Algorithm
1 can only catch 11 of them before
simulation time 250,000 seconds. This leads to a poor average
detection ratio of 7%. The result is not surprising because Algorithm
1 relies on the abrupt increase of file
transfer requests for detection but the self-restraining IM worm
generates only a limited number of file transfer requests per
measurement window.
We now evaluate the effectiveness of Algorithm
2 in detecting self-restraining IM
worms. The measurement window 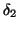 used in this algorithm is
also set to be 300 seconds. We let the weighting factor
used in this algorithm is
also set to be 300 seconds. We let the weighting factor 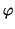 be
0.25 in Eq. (14) and parameter
be
0.25 in Eq. (14) and parameter  be
be
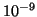 in Eq. (15). The
in Eq. (15). The 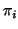 parameter in
Eq. (14) is updated every week. Similar to the
experiments in Section V-A, we let both
parameter in
Eq. (14) is updated every week. Similar to the
experiments in Section V-A, we let both
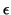 and
and 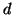 be 3.
be 3.
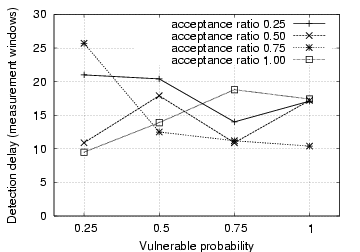
The experimental results show that Algorithm
2 is able to detect the propagation of
the self-restraining IM worm in all the 160 sample
runs. Fig. 7 depicts the
number of measurement windows that are needed to detect the IM worm
under different combinations of acceptance ratios and vulnerable
probabilities. The average detection delay is 16 measurement windows,
which is equivalent to one hour and 20
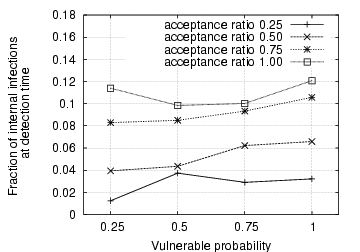
minutes. Fig. 8 gives the
fraction of internal infections among all internal vulnerable machines
when the IM worm is detected. Obviously, only a small fraction of
internal IM contacts has been infected before the IM worm is detected,
suggesting that Algorithm 2 is effective
in detecting self-restraining IM worms at their early stages.
6 Related Work
IM malware has posed significant security threats to both residential
and enterprise IM users. Mannan et al. presented a survey on secure
public instant messaging in [9]. They later
proposed to use limited throttling and CAPTCHA-based
challenge-response schemes to defend against IM worms
[10]; they also developed a cryptographic
protocol to further enhance authentication and secure communications
in public IM systems [11]. Smith analyzed a
French language IM system and after observing the IM network is
scale-free, he suggested that IM worms can be effectively mitigated by
disabling the top few most connected IM accounts
[17]. In [22], Williamson
et al. demonstrated the effectiveness of a virus throttling algorithm
against IM worm propagation. Xie et al. proposed a framework called
HoneyIM that uses decoy IM accounts in normal users' buddy lists to
detect IM propagation in enterprise-like networks
[24]. Compared with previous solutions, our work
focuses on a centralized approach that leverages statistical metrics
collected from IM systems. As our solution does not require
involvement of IM clients, it can be more easily deployed than those
distributed detection schemes such as HoneyIM.
Applying change-point detection techniques to detect network attacks
is not a new idea. Wang et al. applied the non-parametric CUSUM
algorithm to detect TCP SYN flooding attacks
[21]. The CUSUM algorithm has also been used
to detect Internet worms in [2,3]. IM worms differ from traditional Internet
worms such as Code Red II and Slammer because they propagate in social
IM networks. In our work, we demonstrate that the change-point
detection techniques are effective in catching IM worms with different
spreading strategies.
7 Conclusions And Future Work
In this paper, we have proposed to apply change-point detection
techniques to detect both fast scanning and self-restraining IM
worms. We monitor abrupt increase of file transfer requests or
URL-embedded chat messages to detect fast scanning IM worms; we
leverage social intimacy of IM users to detect stealthy IM worms that
spread slowly. Experimental results show that the proposed solutions
are effective in detecting both families of IM worms. We are
currently developing algorithms for detecting another type of stealthy
IM worms, which spread themselves between two online users only after
they observe some ongoing conversations between them. In the future,
we plan to evaluate the detection schemes proposed in this paper
against more realistic IM datasets.
- 1
-
B. E. Brodsky and B. S. Darkhovsky.
Nonparametric Methods in Change Point Problems.
Kluwer Academic Publishers, 1993.
- 2
-
T. Bu, A. Chen, S. V. Wiel, and T. Woo.
Design and evaluation of a fast and robust worm detection algorithm.
In Proceedings of IEEE Infocom'06, 2006.
- 3
-
J. Chan, C. Leckie, and T. Peng.
Hitlist worm detection using source ip address history.
In Proceedings of Australian Telecommunication Networks and
Applications Conference, 2006.
- 4
-
IM security exploits explode in 2007.
https://esj.com/news/article.aspx?EditorialsID=2945.
- 5
-
https://www.internetnews.com/stats/article.php/3521456.
- 6
-
https://software.tekrati.com/research/9512/.
- 7
-
https://www.viruslist.com/en/viruses/encyclopedia?virusid=78581.
- 8
-
M. Landesman.
Kelvir worm overview.
https://antivirus.about.com/od/virusdescriptions/a/kelvirfam.htm.
- 9
-
M. Mannan and P.C.v. Oorschot.
Secure public instant messaging: A survey.
In Proceedings of Privacy, Security and Trust (PST'04), 2004.
- 10
-
M. Mannan and P.C.v. Oorschot.
On instanct messaging worms, analysis, and countermeasures.
In Proceedings of WORM'05, November 2005.
- 11
-
M. Mannan and P.C.v. Oorschot.
A protocol for secure public instant messaging. financial
cryptography and data security.
In Proceedings of Financial Cryptography and Data Security 2006
(FC'06), 2006.
- 12
-
C. D. Morse and H. Wang.
The structure of an instance messenger network and its vulnerability
to malicious codes.
In Proceedings of ACM SIGCOMM 2005 Poster Session, August 2005.
- 13
-
AIM/Oscar Protocol Specification.
https://www.oilcan.org/oscar/.
- 14
-
E. S. Page.
Continuous inspection schemes.
Biometrika, 41, 1954.
- 15
-
C. R. Palmer and J. G. Steffan.
Generating network topologies that obey power laws.
In Proceedings of GLOBECOM'00, 2000.
- 16
-
https://www.theregister.co.uk/2005/04/15/im_worm_runs_amok/.
- 17
-
R. D. Smith.
Instant messaging as a scale-free network.
https://arxiv.org/abs/cond-mat/0206378v2, 2002.
- 18
-
S. Staniford, V. Paxson, and N. Weaver.
How to 0wn the internet in your spare time.
In Proceedings of the 11th USENIX Security Symposium (Security
'02), 2002.
- 19
-
https://www.viruslist.com/en/viruses/encyclopedia?virusid=75305.
- 20
-
https://www.viruslist.com/en/virusesdescribed?chapter=153312410.
- 21
-
H. Wang, D. Zhang, and K. G. Shin.
Detecting SYN flodding attacks.
In Proceedings of IEEE INFOCOM'02, June 2002.
- 22
-
M. Williamson, A. Parry, and A. Byde.
Virus throttling for instant messaging.
In Virus Bulletin Conference, September 2004.
- 23
-
Z. Xiao, L. Guo, and J. Tracey.
Understanding instant messaging traffic characteristics.
In Proceedings of ICDCS'07, 2007.
- 24
-
M. Xie, Z. Wu, and H. Wang.
HoneyIM: Fast detection and suppression of instant messaging
malware in enterprise-like networks.
In Proceedings of ACSAC'07, 2007.
Catching Instant Messaging Worms with Change-Point Detection Techniques
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation leet-im-worm.tex
The translation was initiated by Guanhua Yan on 2008-03-26
Footnotes
- ... Yan
![[*]](footnote.png)
- Los Alamos National Laboratory Publication No. LA-UR-08-1010
- ...
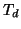
![[*]](footnote.png)
- Here, we ignore the
network-level interaction among multiple sessions that download worm
code from the same infected host. This is because typical IM worms
have small sizes, especially after packing themselves when
spreading. For instance, the code size of Kelvir IM worm is about
24KB, if unpacked, or 9KB if packed
[20]. Hence, using TCP, typical IM worm code
can be downloaded within only a few round trip times and thus less
than one second. Moreover, receivers of file transfer requests think
for different time before they decide to download the worm code. Such
stochasticity also reduces the synchrony among worm code downloading
processes that are initiated by the same worm instance.
- ...
it
![[*]](footnote.png)
- In one implementation,
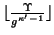 tokens are created
deterministically and another one is created with probability
tokens are created
deterministically and another one is created with probability
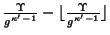 . If the protocol is
implemented as such, the following Theorem
2 may not strictly follow due to
randomness.
. If the protocol is
implemented as such, the following Theorem
2 may not strictly follow due to
randomness.
- ... infected
![[*]](footnote.png)
- We suppose that once a
new machine is infected, it reports to the machine that infects it. If
the worm spreads by file transfers, the sender and the receiver know
each other's IP address. But if the worm spreads by URL-embedded chat
messages, the sender and the receiver may not know each other's IP
address. But such information can be relayed by the remote server
where the worm code resides.
- ...
token
![[*]](footnote.png)
- If a worm instance has received more than one token,
the worm instance will not attempt to infect the buddies that it has
already tried. This may not hold for the
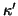 -th generation worm
instances if
-th generation worm
instances if
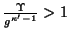 , but after that, it
is very likely that tokens are passed onto different IM users.
, but after that, it
is very likely that tokens are passed onto different IM users.
- ... seconds
![[*]](footnote.png)
- This initial
infection time is carefully chosen so that there are a significant
number of online IM users at that point.
Guanhua Yan
2008-03-26
![[*]](footnote.png)