JVM '02 Paper [JVM '02 Tech Program Index]

Pp. 41–50 of the Proceedings

Optimizing Precision Overhead for x86 Processors

Takeshi Ogasawara Hideaki Komatsu Toshio Nakatani

IBM Japan, Tokyo Research Laboratory
1623-14 Shimotsuruma, Yamato-Shi, Kanagawa, Japan 242-8502
{takeshi,komatsu,nakatani}@jp.ibm.com

Abstract:

It is a major challenge for a Java JIT compiler to perform single-precision floating-point operations efficiently for the x86 processors. In previous research, the double-precision mode is set as the default precision mode when methods are invoked. This introduces redundant mode switches to preserve the default precision mode across method boundaries. Furthermore, the precision mode is switched only at the start and end points of a given method to reduce the overhead of rounding double-precision results to single-precision ones. Therefore, methods that include both single- and double-precision operations cannot switch the mode and have to suffer from the overhead of rounding using this convention, even if single-precision operations are dominant.

We propose a new approach to these problems. We eliminate redundant mode switches by ignoring the default precision mode and calling a method in the same precision mode as the caller. For methods that include both single- and double-precision methods, we reduce the overhead of rounding by isolating code segments of a given method that should be executed in the single-precision mode. We implemented our approach in IBM's production-quality Just-in-Time compiler, and obtained experimental results, showing that, in SPECjvm98, it consistently shows the best performance in any configuration of benchmark programs, inline policies, and processor architectures compared to previous research.

1 Introduction

The Java language [4] has unique specifications that enable programmers to create highly portable programs. In particular, it requires floating-point operations that conform to the IEEE 754 standard [5]. Under these specifications, Java programs running on a different platform can calculate the same result for a given floating-point operation. FP-strictness [21] as introduced by Java 2 has relaxed the specification with respect to overflow and underflow, but it still calls for strict precision.

A Just-in-Time (JIT) compiler for Java [15,3,17,19,16,2] is critical for high-performance Java virtual machines. It must follow the language specification, while it is also expected to generate efficient code. A JIT compiler for the x86 processors faces several performance challenges unique to the x86 architecture.

In particular, it is a major challenge for a Java JIT compiler to perform single-precision floating-point operations efficiently for the x86 processors. Unlike other processors, the x86 processor has a precision mode that determines whether the floating-point unit executes the same instruction in either single or double precision. In general, the double precision mode is usually set as the default precision mode throughout the program execution, and the single-precision floating-point operations are emulated in the double-precision mode. This is true even for recent processors that support a new instruction set, the Streaming Single-instruction-multiple-data Extensions 2 (SSE2) [8], since the original instruction set can perform some operations more efficiently.

There are two approaches to performing single-precision floating-point operations for Java programs in the double-precision mode of the x86 processors. One [12] is to emulate the single-precision floating-point operations in the double-precision mode by rounding a double-precision result to the single-precision value. This can be accomplished by storing it from the register to a single-precision memory and loading it back again to the register. This store-reload for rounding is required for each single-precision floating-point operation, because Java doesn't allow the double-precision values to be accumulated for the conversion to a single-precision value once at the end. Obviously the drawback of this store-reload approach is the latency of store-to-load forwarding [13] for each single-precision floating-point operation.

The other approach is to switch the mode from the double precision to the single precision mode at the start point of the method and perform all the floating-point operations in the single-precision mode without emulation. The drawback of this mode-switch approach is the penalty of mode switches at every point of the code where the control is transferred from and to another code block. Furthermore, this approach is not applicable to those methods that include both double-precision and single-precision floating-point operations, since obviously a double-precision operation cannot be performed in the single-precision mode.

Recently Paleczny et al. [17] proposed a mixed approach in which the mode switch is used whenever it gains performance over the store-reload approach. This eliminates the overhead of some cases for the store-reload approach, but it still suffers from the overhead of the mode switch and a high overhead for those methods that include both double-precision and single-precision floating-point operations.

In this paper, we propose a new approach called precision-aware invocation, in which we ignore the default precision mode and call a method in the same precision mode as the caller whenever appropriate. We add a property called floating-point precision type (FPPT) to each compiled code block. In our approach, we eliminate the overhead of redundant switching between the single-precision mode and the default precision mode (that is, double-precision mode) by preserving the default precision mode across the method boundaries. Only when we call a method of a different precision mode must we switch the precision mode at the start and end points of the method.

We further propose a technique called precision region analysis to reduce the number of operations to emulate single-precision floating-point operations in the double-precision mode using the store-reload approach. In this technique, our JIT compiler analyzes the bytecode of the given methods, and locates the places at which it should switch the precision mode at a finer granularity without switching the mode only at the start and end points of the method.

In summary, the contributions of our paper are the following:

We minimize the number of redundant mode switches in the JIT compiled code by eliminating the default precision mode and introducing precision-aware invocation based on the floating-point precision type of each method.
We reduce the number of operations to emulate single-precision floating-point operations in the double-precision mode by doing precision region analysis in the JIT compiler.

The rest of this paper is organized as follows. Section 2 describes the portability of Java floating-point types and the overhead of executing single-precision floating-point operations on the x86 processors. Section 3 describes our new techniques to minimize the redundant mode switches and the number of operations to emulate them in the double-precision mode. Section 4 presents our experimental results. Section 5 discusses related work. Finally, Section 6 concludes the paper.

2 Portability and Overhead of the Java Floating-Point Types

This section describes the Java specification for floating-point operations and how single-precision floating-point operations are performed in conforming to it on the x86 processors. The section then describes what problems previous JIT compilers for the x86 face in order to perform these operations efficiently.

2.1 Java Floating-Point Operations and the IEEE 754 Standard

Java has two floating-point types: float and double. Floating-point values of these types and operations on them should conform to the IEEE 754 standard [5,22]. The standard defines the binary floating-point format, which consists of three components: sign, exponent, and significand. The Java floating-point types, float and double, are associated with the single and double precision formats of the standard, respectively. Therefore, all the Java virtual machines should generate the same result for a given floating-point expression at the bitwise level in their binary formats.

Java 2 has introduced a new semantic category, FP-strict [21]. The semantics of FP-strict code are the same as that of the original specifications. On the other hand, non-FP-strict code still performs a floating-point operation with the same size of significand as that of FP-strict code, but it extends the exponent. Regardless of FP-strictness, it is not permissible to perform a single-precision operation in double precision.

2.2 Floating-Point Unit and Precision Mode on the x86

The x86 has a floating-point unit that supports the IEEE 754 standard [9]. The floating-point unit does not have separate instructions for each type of floating-point precision. Instead, it executes an instruction in either single or double precision by switching the precision mode. There is a special instruction, fldcw, which modifies the hardware flags that switch the mode. However, since the overhead of fldcw is quite large, frequent switching of the precision mode degrades the performance of a program. Although the overhead of fldcw is optimized in the NetBurst [6], it is still a significant penalty.

There is a way to perform a single-precision operation so that a program does not suffer from the penalty of switching the precision mode. First, perform the operation in double precision. Second, store the calculated result in the register into a memory location of single-precision size. This translates the result to the single-precision value. Third, load it back into the register. However this rounding store-reload operation [12] inserts additional latency in the data flow, even though the store-to-load forwarding feature enables the load to receive the stored value from the store buffer without accessing memory.

**Figure 1:** Examples of x86 single-precision operations
$\begin{figure}\scriptsize\begin{verbatim}; start in double-precision mode fld... ...ecision mode\end{verbatim}\small (b) The rounding store-load method \end{figure}$

Figure 1 shows two versions of x86 instructions for these two methods, which perform the same single-precision operations,

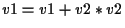2.3 Problems of Previous JIT Compilers

For Java Just-in-Time (JIT) compilers for x86-based processors [3,17,19], it is critical to reduce the precision-related overhead to optimize a Java program that frequently executes floating-point operations. In previous research, double precision is used as the default mode for compiled code [17]. This default precision mode was required because the interpreter usually runs in the double precision mode and selectively compiled code can be called by an interpreted method or by a method that will be dynamically loaded in the future.

If a traditional compiler analyzes a method and the analysis shows that the improvement by eliminating the rounding store-reloads exceeds the overhead of executing fldcw [17], it inserts an fldcw instruction to start the code in the single precision mode. It also inserts an fldcw to restore the default mode at each exit point. If this method invokes another method that is also analyzed to switch to the single precision mode, the compiler inserts an fldcw to restore the default mode before the invocation and another fldcw to switch to the single precision mode after the invocation. There are variations of this approach with different thresholds for determining whether or not to switch the mode. This approach balances the cost of fldcw and the latency caused by the rounding store-reload, while it minimizes the total penalty for supporting Java's floating-point specification. However, it still suffers from the following two forms of overhead.

The first overhead is redundant switches of the precision mode during method invocations. Consider the case when a method runs in single precision and invokes another method that prefers to run in single precision. Since the default mode is double and every method assumes that it is invoked in double precision, the caller method executes an fldcw to switch the precision mode from single to double before the invocation. Then the callee method immediately executes a second fldcw to switch from double to single. A similar redundant switch occurs when the callee method returns to the caller.

The second overhead is the rounding store-reloads caused by the convention of the mode switch required at the start and end points. Since default-precision operations must be performed in the double-precision mode, this convention makes the entire code run in the double-precision mode if the code includes double-precision operations as well as single-precision operations. As a result, these single-operations require rounding store-reloads. Another case is when a compiler determines that the penalty of these rounding store-reloads is less costly than that of the mode switch at the start and end points even if the code includes single-precision operations but not double-precision operations. The problem is that, if these rounding store-reloads are executed frequently at runtime, the cumulative overhead significantly degrades the performance of the program.

These overheads for a program that performs single-precision operations are caused by the default precision mode and the ordinary mode-switch convention. To minimize these overheads, we need to analyze the entire call graph of methods to determine where the precision mode changes. However, it is difficult for a JIT compiler to do such an analysis because it does not compile all the methods at one time. In particular, JIT compilers cannot analyze interpreted methods when they perform selective compilation to reduce the time and resources for compilation [17,19]. Our goal is to remove these overheads to conform to the IEEE 754 standard without analyzing the entire program.

3 Precision Region Optimization (PRO)

This section describes our new techniques to minimize redundant mode switches and reduce store-reload operations for rounding in those methods which include both single- and double-precision operations.

3.1 Tracking the Floating-Point Precision Type of Code Blocks

To eliminate redundant mode switches and reduce the memory latency of rounding store-reloads, our JIT-compiled code has an attribute called floating-point precision type (FPPT). The FPPT of code shows the precision mode in which the code is called. When a method calls another method, it calls the code with the same FPPT as the current precision of the call site.

**Figure 2:** Precision-aware method invocations and code generation.
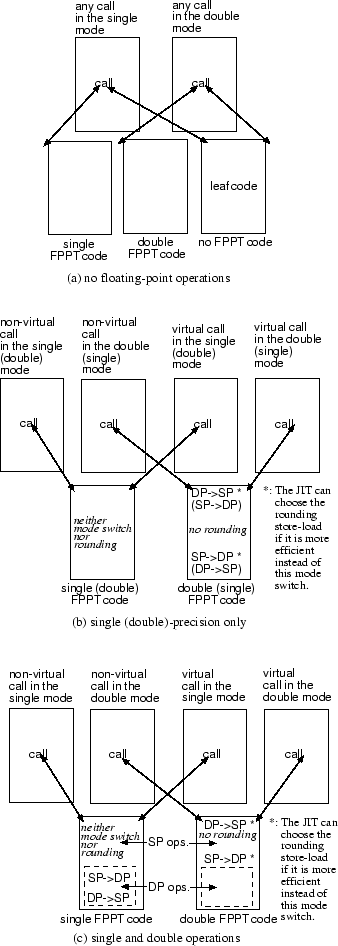$\begin{figure}\centering\ifnum \pdfoutput>0 \hfill\pdfximage width 7.5cm {FPPT.p... ...tximage\hfill\mbox{} \else \epsfig{file=FPPT.eps, width=7.5cm}\fi\end{figure}$

Figure 2 shows all of the combinations of caller's precision (single or double), the type of invocations (virtual or non-virtual), callee's FPPT (single or double), and the type of floating-point operations included in the code (none, single, double, or both). Each rectangle shows a code segment. DP and SP denote double and single precision, respectively. Each arrow shows a method invocation. The code for an FPPT is generated only if a method invocation that points to it actually occurs.

We explain how we generate the code for an FPPT for three different cases using Figure 2. The first case is when calling a method whose bytecode does not include any floating-point operations (Figure 2a). If it includes call sites, the compiled code has a specific FPPT since it had to determine the FPPT for the callee code. The body of the single-FPPT code block and that of the double-FPPT are the same. If the method is a leaf method, the FPPT is not used. The second case is when calling a method whose bytecode includes floating-point operations of either single or double precision (Figure 2b). There is no mode switch if the caller's precision is the same as the precision of these operations. Otherwise, the compiler analyzes the bytecode to determine whether the mode switch is required, considering the tradeoff. For the mode switch, it is performed only once across the method boundary. In addition, since the code bodies for the same-precision and different-precision cases are the same, the compiler can easily generate one by duplicating the other. The third case is when calling a method whose bytecode includes single and double operations (Figure 2c). This case is the same as the second one except that switching to double occurs to perform double-precision operations in the single-FPPT code.

The binary translation from the code of one FPPT to that of the other FPPT is done simply by inserting or removing instructions for the mode switch and the rounding store-reload. Since this is much faster than the compiler's optimizations for the original code, the overhead of introducing the FPPT is negligible at compilation time. However, in general, a method tends to be called from either single or double precision. Therefore, it is expected that the majority of methods have either a single- or a double-FPPT version of the code and the degree of code expansion is quite low.

3.2 Precision Region Analysis

If a method includes both single- and double-precision operations (the case of Figure 2c), the approach of previous research makes the compiled code run in the double-precision mode because double-precision operations must be performed in the double-precision mode. However, this introduces the penalty of extra rounding store-reloads for the single-precision operations. In particular, this problem incurs a significant penalty when a method includes many single-precision operations but only a few double-precision operations.

The JIT compiler can determine which code segments perform single-precision operations in the single-precision mode rather than making the entire code block run in the double-precision mode. The basic idea is to shrink wrap program regions that run in the double-precision mode. Since there is a performance trade-off between the mode switch method and the rounding store-reload method, this shrink-wrapping is relaxed for a double-precision region and single-precision operations adjacent to the region may be included in the region to minimize the overhead of calculating single-precision results.

**Figure 3:** The algorithm of precision region analysis
$\begin{figure}\small\renewedcommand{baselinestretch}{0.75}\begin{verbatim}/* S... ... pendingSpSectionOpCount = 0; } }\end{verbatim}%%included in html \end{figure}$

Figure 3 shows the algorithm of our precision region analysis. The first step of the algorithm is the intra basic block analysis. The JIT compiler sections each basic block so that each code section includes either single- or double-precision operations. It also counts the number of floating-point operations for each section. The second step is the inter basic block analysis. The JIT compiler arranges basic blocks in depth-first-search order based on the control flow graph, considering the history of the branches recorded while the interpreter executed the method. The algorithm processes basic blocks in this order. The result is that it prioritizes the optimization of a control path that has been frequently executed by the interpreter, since the target basic block of a frequently taken branch appears earlier than that of a rarely taken branch in this order. The JIT compiler traverses basic blocks in this order and checks the precision of each section. For contiguous single-precision sections, it records entering them and counts the number of operations. This recording of single-precision sections continues until the JIT compiler encounters a double-precision section, the head of a loop, or a basic block that is not a target of the previous basic block. When there are enough single-precision operations to justify switching the mode, the precision of these sections remains as single. Otherwise, they are modified to be double-precision sections, so that the code of these sections runs in the double-precision mode. For the basic blocks of exception handlers, the JIT compiler can propagate the precision of an exception-throwing point to its handler, although this process is not shown in Figure 3.

**Figure 4:** An example of shrink-wrapping double-precision regions
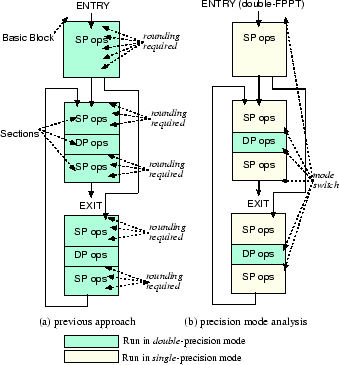$\begin{figure}\centering\ifnum \pdfoutput>0 \hfill\pdfximage width 7.5cm {PMA.pd... ...stximage\hfill\mbox{} \else \epsfig{file=PMA.eps, width=7.5cm}\fi\end{figure}$

Figure 4 illustrates how floating-point operations are performed when a method includes both single- and double-precision operations by using an example. Figures 4a and 4b show the results of the previous approach and our precision region analysis, respectively. In Figure 4a, all of the sections are in a double-precision region. By applying the precision region analysis, only double-precision sections are shrink-wrapped with mode-switch instructions in Figure 4b. In this example, the algorithm finds out that the overhead of rounding store-reloads required in the first and second sections is higher than the cost of two mode switches. As a result, these sections are marked as single-precision so that the code generation generates mode-switch instructions. Similarly, it determines that the fourth, fifth, and eighth sections should run in the single-precision mode.

3.3 Precision-Aware Invocation

For each call site within the method, the JIT compiler uses the precision mode at the call site and generates instructions that call the target code of the FPPT that matches that precision mode. The method block that maintains the information for a method has two entries for code pointers, one for single-FPPT and another for double-FPPT. The generated instructions use one of these pointers, depending on the precision mode at the call site.

4 Measurements

In this section, we evaluate precision-aware invocation using our system. We used the modules of SPECjvm98 as benchmark programs. Subsection 4.1 explains the methodology of our evaluation. Subsection 4.2 explains the system used in our experiments. Subsection 4.3 explains the details of the benchmark programs used in our experiments, focusing on the floating-point operations. Subsection 4.4 presents the results and discusses them.

4.1 Experimental Methodology

For practicality, we used the SPECjvm98 benchmark suite [23] in the test mode throughout our experiments. SPECjvm98 is a suite of benchmark programs and is currently accepted as one of the major Java benchmarks for evaluating Java VMs [16,19,2,3].

We compare the rounding store-reload (denoted as Rounding), the mode-switch method (denoted as Switch), previous research [17] (denoted as HSS), and our precision region optimization (denoted as PRO) with each other. We use Roundign and Switch to emulate the two extreme conventions with respect to controlling the precision mode. In Rounding, single-precision operations are always performed in the default precision mode, or double. This emulates the ordinary approach of ignoring the penalty of rounding store-reloads. Therefore, it can be used to measure the maximum number of possible rounding store-reloads. In Switch, single-precision operations are always performed in the single-precision mode by switching the mode at the start and end points if the method includes only single-precision operations. Code that includes a double-precision operation always runs in the double-precision mode. This emulates the ordinary approach of ignoring the effects of the numbers of call sites. Therefore, this can be used to measure the maximum number of possible mode switches. In HSS, the Switch approach is applied for methods that include enough single-precision operations (at least 32 and more than 10 times of the number of call sites), but not any double-precision operations, and the Rounding approach is applied for other methods.

4.2 Environment

We implemented precision region optimization on our production quality Java Just-In-Time (JIT) compiler [18,11,10,14,19], which is part of the IBM Developer Kit for Windows, Java 2 Technology Edition [7], Version 1.3.1.

Throughout the measurements, we used the same parameters for the Java VM and SPECjvm98. The initial and maximum amounts of Java heap space were 128 MB, specified with the parameters -Xms128m -Xmx128m. The SPECjvm98 parameter string -m5 -M5 -s100 causes each benchmark program to be executed five times using a problem size of 100.

The measurements were performed on an Intel Pentium-III 1GHz CPU with 512 MB physical memory running Microsoft Windows NT Workstation Version 4.0 with Service Pack 6. For measurements of the execution time with other examples of the x86 architecture, we used an AMD Athlon MP 1.2GHz processor and an Intel Pentium 4 2.0GHz processor.

4.3 Characteristics of the Benchmark Programs

Table 1: The dynamic counts of floating-point operations

benchmark	XPO¹	SP arith	DP arith	Compare	Global ld/st	Prec Conv	Int Conv
_227_mtrt	off	114,575,305	193,540	52,202,408	230,989,486	386,490	132,001
	on	114,768,845	0	52,202,408	230,989,486	8	132,001
_222_mpegaudio	off	1,091,260,405	1,549,221	40,112,640	781,219,540	1,549,221	20,065,036
	on	1,092,809,573	53	40,112,640	781,219,540	53	20,065,036

Table 2: The dynamic counts of method invocations

		no inlining			tiny inlining			aggressive inlining
		total	w/SP		total	w/SP		total	w/SP
benchmarks	XPO		w/o DP	w/DP		w/o DP	w/DP		w/o DP	w/DP
_227_mtrt	off	310,344,583	5.11%	0.04%	22,810,014	52.11%	1.26%	11,738,192	38.98%	2.31%
_227_mtrt	on	310,344,583	5.19%	0.02%	22,810,016	53.15%	0.23%	11,738,192	40.85%	0.44%
_222_mpegaudio	off	117,631,096	3.95%	1.30%	36,768,517	12.64%	4.16%	21,874,285	19.54%	7.00%
_222_mpegaudio	on	117,631,096	4.61%	0.64%	36,768,517	14.75%	2.06%	21,874,285	23.08%	3.46%

Table 3: The dynamic characteristics of single-precision operations performed by methods that include both single- and double-precision operations

benchmark	XPO	no inlining	tiny inlining	aggressive inlining
_227_mtrt	off	0.262% (4)	2.057% (8)	3.589% (9)
	on	0.071% (1)	0.071% (1)	0.084% (1)
_222_mpegaudio	off	3.226% (2)	3.226% (2)	3.226% (2)
	on	0.812% (1)	0.812% (1)	0.812% (1)

Table 4: The dynamic counts of mode switches and rounding store-reloads

		no inlining		tiny method inling		aggressive inling
benchmarks		switch	store-reload	switch	store-reload	switch	store-reload
_227_mtrt	Rounding	0	82,591,461	0	81,921,296	0	73,964,450
	Switch	435,817,517	102,613	30,328,119	102,597	8,921,599	102,597
	HSS	0	82,591,461	0	81,921,296	1,894,731	36,379,374
	PRO	108,901	51,437	108,901	51,437	108,901	51,437
_222_mpegaudio	Rounding	0	983,089,608	0	983,072,178	0	983,072,178
	Switch	50,667,740	17,484	10,485,380	54	10,169,023	54
	HSS	9,322,377	642,969,130	9,322,377	642,951,700	9,322,377	642,951,700
	PRO	3,649,659	17,484	3,649,659	54	9,760	54

This section gives an overview of the characteristics of the benchmark programs. We focus on two benchmark programs of SPECjvm98 that are floating-point intensive. The other programs are not. Table 1 shows the number for each category of floating-point operations for each benchmark program of SPECjvm98 during the fifth run, by which time all of the major methods have been selectively compiled by the JIT compiler. Since these numbers are counted at the intermediate-language level but not at the machine-instruction level, they are independent of machine architectures. The XPO column is explained in the next paragraph. The SP arith and DP arith columns of Table 1 show the numbers of single- and double-precision arithmetic operations such as addition, respectively. The Compare column shows the number of compare operations ². The Global ld/st column shows the number of memory operations for the global area such as static fields and object fields. This does not include memory operations that required by spilling registers in and out for the local frame. The Prec Conv column shows the number of operations that convert a value of one precision to the other. The last column shows the number of operations that convert a floating-point value to the corresponding integer value.

The XPO column shows whether excessive-precision operations are optimized or not. In some cases, source operands for a double-precision operation have only single precision and the result of the operation is immediately converted into single precision. If the corresponding operation in single precision can calculate the same value as the double-precision operation does for these single-precision values, we can translate this excessive-precision operation into a single-precision one. As shown in Table 1, this excessive-precision optimization reduced the dynamic counts of double-precision operations.

The problem caused by a default precision mode across the method boundaries has been discussed in Section 2.3. The resulting performance degradation is proportional to the number of method invocations. Table 2 shows the number of method invocations during the fifth run for each level of method inlining. We applied three policies of inlining: no inlining, tiny method inlining, and aggressive inlining. In tiny method inlining, only tiny methods are inlined into the target code. In aggressive inlining, methods are inlined unless their calling depths and the code expansion reach the pre-defined thresholds. For each inlining policy, the invocation count of all the methods, that of the methods that include single-precision but not double-precision operations, and that of the methods that include both single- and double-precision operations during the fifth run are shown in Table 2. The number of redundant mode-switches is proportional to the invocation count of the methods that include single-precision but not double-precision operations.

We have also discussed the problem of the ordinary mode-switch convention in the case of methods that include both single- and double-precision operations in Section 2.3. Table 3 shows the dynamic count of single-precision operations performed by these methods and the ratio for the total floating-point operations in each benchmark program. In previous research, these single-precision operations have to be performed in double precision, so this table shows the maximum numbers of single-precision operations that precision region analysis can optimize with respect to the overhead of rounding store-reloads. For these benchmark programs, excessive-precision optimization reduces the number of methods that include both single- and double-precision operations by translating the double-precision operations into the single-precision ones. However, there still remains a small number of single-precision operations that require rounding store-reloads.

4.4 Results and discussion

In this section, we assume that excessive-precision optimization has been applied.

4.4.1 Dynamic counts of mode switches and rounding store-reloads

Table 4 shows the number of mode switches and rounding store-reloads during the fifth run for each method-inlining policy. Overall, PRO significantly improve these dynamic counts for each policy of inlining. The store-reload columns for PRO show the numbers of the type conversion operations performed in every configuration. In addition to them, a method that has to run in double precision because of including both single- and double-precision operations performs rounding store-reloads for single-precision operations in Switch for _227_mtrt.

4.4.2 Execution time

Table 5: The execution times on Pentium III

benchmarks		no inlining	tiny method inlining	aggressive inlining
_227_mtrt	Rounding	4.313	2.719	2.406
	Switch	10.578	3.140	2.391
	HSS	4.312	2.703	2.250
	PRO	3.969	2.375	2.062
_222_mpegaudio	Rounding	7.687	7.203	7.062
	Switch	6.734	5.563	5.421
	HSS	7.234	6.750	6.625
	PRO	5.826	5.453	5.219

Table 6: The execution times on Pentium 4

benchmarks		no inlining	tiny method inlining	aggressive inlining
_227_mtrt	Rounding	3.105	2.193	2.063
	Switch	4.527	1.942	1.732
	HSS	3.164	2.193	1.843
	PRO	2.774	1.793	1.663
_222_mpegaudio	Rounding	5.809	5.377	5.408
	Switch	3.665	3.155	3.175
	HSS	4.977	4.536	4.537
	PRO	3.565	3.134	3.034

Table 7: The execution times on Athlon MP

benchmarks		no inlining	tiny method inling	aggressive inlining
_227_mtrt	Rounding	3.535	2.503	2.273
	Switch	6.149	2.473	2.133
	HSS	3.545	2.483	2.153
	PRO	3.175	2.213	1.983
	Rounding	6.319	5.818	5.828
_222_mpegaudio	Switch	4.586	3.895	3.906
	HSS	5.598	5.087	5.107
	PRO	4.296	3.835	3.765

Tables 5 through 7 show the execution time of the benchmark programs in seconds using Rounding, Switch, HSS, and PRO for each method-inlining policy. Overall, PRO consistently shows the best performance in any configuration of inline policies and processor architectures. On the other hand, the best performer among Rounding, Switch, and HSS changes depending on benchmark programs, inline policies, and processor architectures. For instance, in _227_mtrt, Switch shows the worst performance without inlining, though it is the best of the three with tiny and aggressive inlining on Pentium 4 and Athlon MP. In _222_mpegaudio, Switch shows the best performance of the three even without inlining. Most importantly, PRO with tiny inlining shows performance comparable to the best performance of the others with aggressive inlining in every configuration of benchmark programs and processor architectures. This means that PRO can greatly improve the performance of the compiled code during the code optimization stage without incuring the heavy compilation overhead caused by aggressive inlining [20].

5 Related Work

A report of the Java Grande Forum [12] discusses the problems that arise when making Java programs that frequently perform floating-point operations run efficiently on the x86 processors while conforming to the Java specification. It describes a technique for another x86-specific problem, or double rounding, as well as the rounding store-reload technique. We did not address this problem in this paper.

Another previous research report [17] presents a heuristic for determining when to insert fldcw instructions by using the number of single-precision operations, the number of double-precision operations, and the number of call sites. This approach suffers from the overhead of redundant mode switches across the method boundaries. In addition, there are problems from the overhead of rounding store-reloads performed by methods that include both single- and double-precision operations.

Streaming SIMD Extensions 2 (SSE2) [6] introduced a new set of floating-point instructions to the x86. It has new instructions that operate on separate floating-point registers. There are some differences between the SSE2 and the original instruction set. The SSE2 instructions do not completely correspond to the original instructions, and some instructions do not exist in SSE2. In addition, the size of single-precision registers is half of that of the double-precision registers, while the original registers can contain both single- and double-precision values. Furthermore, the original instruction set can perform more efficiently than SSE2 for some Java floating-point operations. Thus, since SSE2 has different characteristics from the original instruction set, there are situations where one or the other system is superior.

6 Conclusions

This paper has presented a novel approach to optimization of Java floating-point operations for the x86. It consists of tracking the floating-point precision type of code blocks, precision region analysis, and precision-aware invocation. By generating the code blocks with the appropriate floating point precision types, the default precision mode can be ignored. Precision region analysis investigates the code and finds appropriate code points where mode switch instructions can be inserted to minimize the overhead of rounding store-reloads. Finally, since the compiled code calls the target code with the same floating-point precision type as the call site, there is no redundant mode switch across the method boundaries. Our new approach does not sacrifice the strictness of the precision, while it minimizes the x86-specific overhead to preserve the strictness.

We have presented experimental data about the dynamic characteristics of floating-point operations, using floating-point intensive programs from a widely used benchmark suite. Using that data, we have shown that these programs perform many rounding store-reloads and mode switches, as well as the floating-point operations. We have presented experimental results with a modified version of IBM's production-level Just-in-Time compiler and discussed the effectiveness of our approach. Experimental results show that, in floating-point intensive programs, our approach greatly reduced rounding store-reloads and redundant mode switches and consistently shows the best performance in any configuration of benchmark programs, inline policies, and x86 processor implementation.

Bibliography

1: Proceedings of the ACM SIGPLAN Conference on Object-Oriented Programming Systems, Languages and Applications (OOPSLA-2000) (New York, NY, USA, 2000), ACM Press.
2: ARNOLD, M., FINK, S., GROVE, D., HIND, M., AND SWEENEY, P. F.
Adaptive optimization in the Jalapeño JVM.
In ACM [1], pp. 47-65.
3: CIERNIAK, M., LUEH, G., AND STICHNOTH, J. M.
Practicing JUDO: Java under dynamic optimizations.
In ACM SIGPLAN '00 Conference on Programming language design and implementation (New York, NY, USA, May 2000), ACM Press, pp. 18-21.
4: GOSLING, J., JOY, B., AND STEELE, G.
The Java Language Specification.
The Java Series. Addison-Wesley, Reading, Massachusetts, Aug. 1996.
5: GOSLING, J., JOY, B., AND STEELE, G.
The Java Language Specification.
In The Java Series [4], Aug. 1996, ch. 4.2.3.
6: HINTON, G., SAGER, D., UPTON, M., BOGGS, D., CARMEAN, D., KYKER, A., AND ROUSSEL, P.
The microarchitecture of the pentium 4 processor.
Intel Technology Journal Q1 (2001).
7: The IBM Developer Kit, Java 2 Technology Edition.
https://www.ibm.com/developerworks/java/jdk/.
8: INTEL CORPORATION.
P6 Family of Processors Hardware Developer's Manual.
Intel Corporation, Sept. 1998.
9: INTEL CORPORATION.
IA-32 Intel Architecture Software Developer's Manual, Volume 1: Basic Architecture.
Intel Corporation, Mt. Prospect, IL, 2001.
10: ISHIZAKI, K., KAWAHITO, M., YASUE, T., KOMATSU, H., AND NAKATANI, T.
A study of devirtualization techniques for a Java Just-In-Time compiler.
In ACM [1], pp. 294-310.
11: ISHIZAKI, K., KAWAHITO, M., YASUE, T., TAKEUCHI, M., OGASAWARA, T., SUGANUMA, T., ONODERA, T., KOMATSU, H., AND NAKATANI, T.
Design, implementation, and evaluation of optimizations in a Java Just-In-Time compiler.
Concurrency: Practice and Experience 12, 6 (2000), 457-475.
12: Java Grande Forum Report: Making Java Work for High-End Computing.
https://www.javagrande.org/sc98/sc98grande.pdf.
13: JOHNSON, M.
Superscalar Microprocessor Design.
Prentice Hall Series in Innovative Technology. Prentice Hall, Englewood Cliffs, NJ, Jan. 1991.
14: KAWAHITO, M., KOMATSU, H., AND NAKATANI, T.
Effective null pointer check elimination utilizing hardware trap.
In Proceedings of the 9th international conference on Architectural support for programming languages and operating systems (ASPLOS-IX) (New York, NY, USA, Nov. 2000), ACM Press, pp. 118-127.
15: KRALL, A., AND PROBST, M.
Monitors and exceptions: How to implement Java efficiently.
In ACM 1998 Workshop on Java for High-Performance Network Computing (New York, NY, USA, 1998), ACM Press, pp. 15-24.
Also published as Concurrency: Practice and Experience, 10(11-13), September 1998, CODEN CPEXEI, ISSN 1040-3108.
16: LEE, S., YANG, B.-S., KIM, S., PARK, S., MOON, S.-M., AND EBCIOSGLU, K.
Efficient Java exception handling in Just-in-Time compilation.
In Proceedings of the ACM 2000 Conference on Java Grande (New York, NY, USA, June 2000), ACM Press, pp. 1-8.
17: PALECZNY, M., VICK, C., AND CLICK, C.
The Java HotSpot server compiler.
In Proceedings of the Java Virtual Machine Research and Technology Symposium (Apr. 2001), USENIX Association, pp. 1-12.
18: SUGANUMA, T., OGASAWARA, T., TAKEUCHI, M., YASUE, T., KAWAHITO, M., ISHIZAKI, K., KOMATSU, H., AND NAKATANI, T.
Overview of the IBM Java Just-In-Time compiler.
IBM Syst. J. 39, 1 (2000), 175-193.
19: SUGANUMA, T., YASUE, T., KAWAHITO, M., KOMATSU, H., AND NAKATANI, T.
A dynamic optimization framework for a Java Just-In-Time compiler.
In Proceedings of the ACM SIGPLAN Conference on Object-Oriented Programming Systems, Languages and Applications (OOPSLA-2001) (New York, NY, USA, 2001), ACM Press, pp. 180-194.
20: SUGANUMA, T., YASUE, T., AND NAKATANI, T.
An empirical study of method inlining for a Java a Just-In-Time compiler.
In Proceedings of the Java Virtual Machine Research and Technology Symposium (Aug. 2002), USENIX Association.
21: SUN.
Updates to the Java language specification for JDK release 1.2 floating point.
https://java.sun.com/docs/books/jls/strictfp-changes.pdf, Dec. 1998.
22: THE INSTITUTE OF ELECTRICAL AND ELECTRONICS ENGINEERS, INC.
IEEE standard for binary floating-point arithmetic, Oct. 1985.
23: THE STANDARD PERFORMANCE EVALUATION CORPORATION (SPEC).
JVM Client98 (SPECjvm98).
https://www.spec.org/osg/jvm98/, 1998.

About this document ...

Optimizing Precision Overhead for x86 Processors

This document was generated using the LaTeX2HTML translator Version 2002 (1.63)

The command line arguments were:
latex2html -split 0 -show_section_numbers -white -no_navigation draft.tex

The translation was initiated by takeshi on 2002-05-29

Footnotes

... XPO ¹: XPO = excessive-precision optimization
... ²: The x86 compares all of the 80 bits of floating-point values in the registers regardless of the precision mode.

takeshi 2002-05-29

This paper was originally published in the Proceedings of the 2nd Java^TM Virtual Machine Research and Technology Symposium, San Francisco, California, USA August 1-2, 2002
Last changed: 22 July 2002 ml

Technical Program

JVM '02 Home

USENIX home