


Next: Comparison with Adaptive NetFlow
Up: Experimental evaluation
Previous: Experimental evaluation
Accuracy of core flow slicing algorithm
In this section, we evaluate the core flow slicing algorithm against the
``full-state'' approach. These experiments provide more insight into the
efficacy of the flow slicing algorithm and the effect of changing various
variables such as flow slicing probability and slice length on the memory usage
and the mean relative error of results.
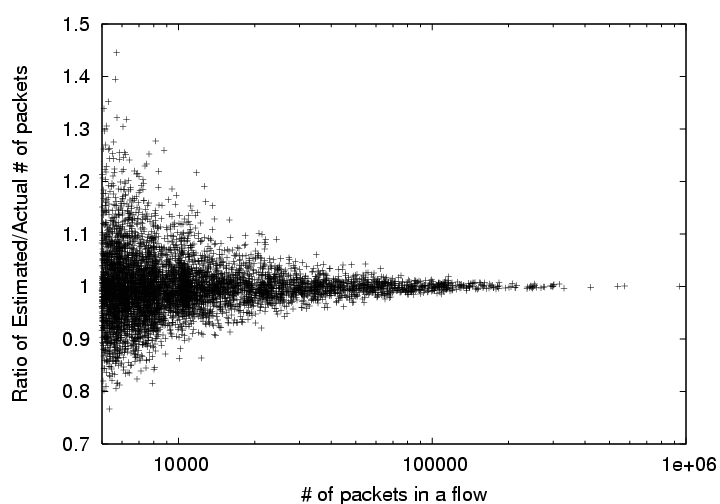
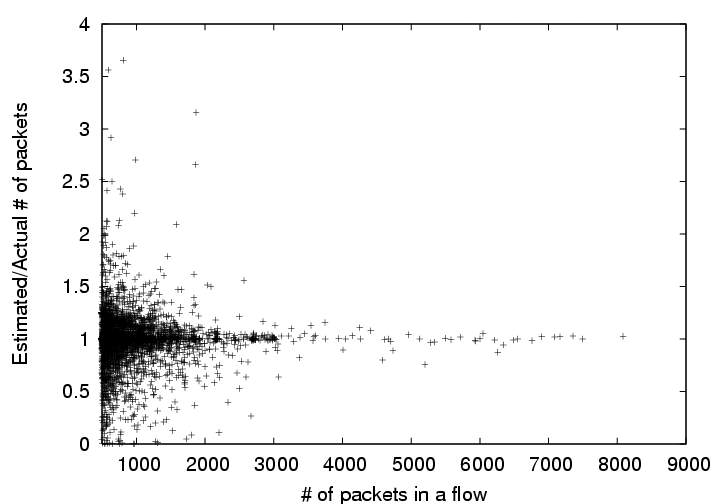
Figure 2:
Scatter plot depicting the accuracy of packet count estimates based on
flow slices.
|
Are estimates unbiased? For this experiment, we fix the flow slicing
probability 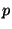 to 0.8% (1 in 125) and the slice duration to 60 seconds.
Figure 2 shows the scatter plot of ratio of the estimated and
true flow sizes (in number of packets) on the y-axis with increasing true flow
size on the x-axis. Note that the plot only shows flows that have more than
5,000 packets throughout the duration of the trace (1 hour). From this scatter
plot, we can see that most of the flows have been accurately estimated (within
10%). The estimates converge to the true values as the flow
size increases. The presence of two-sided errors empirically
confirms the unbiasedness of estimates based on flow slicing.
to 0.8% (1 in 125) and the slice duration to 60 seconds.
Figure 2 shows the scatter plot of ratio of the estimated and
true flow sizes (in number of packets) on the y-axis with increasing true flow
size on the x-axis. Note that the plot only shows flows that have more than
5,000 packets throughout the duration of the trace (1 hour). From this scatter
plot, we can see that most of the flows have been accurately estimated (within
10%). The estimates converge to the true values as the flow
size increases. The presence of two-sided errors empirically
confirms the unbiasedness of estimates based on flow slicing.
Figure 3:
Trade-off between the mean relative error and memory usage as we increase
flow slicing probability.
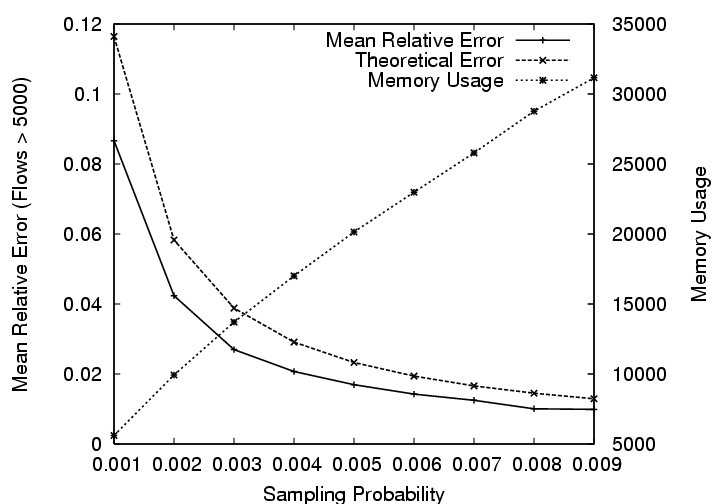 |
What is the effect of flow slicing probability on the accuracy of these
estimates ? According to , increasing flow slicing
probability increases the accuracy of estimated flow sizes.
Besides, the
memory usage should increase as the slicing probability increases. In
Figure 6.1, the mean relative error for flows larger
than 5,000 and the corresponding memory usage have been plotted with varying
slicing probability on the x-axis. Apart from the empirical value of the mean
relative error, we also plot the theoretical value based on
. Figure 6.1 confirms that
increasing slicing probability decreases the mean relative error while
increasing the memory usage. It can also be observed from the figure that the
theoretical and empirical values of mean relative errors are in close agreement
thus validating the analysis in .
Figure:
Scatter plot depicting the errors introduced in interpolating bin
measures from slices.
 |
What kinds of errors do we introduce by interpolating the number of packets
in time bins? The goal of this experiment is to study the errors introduced
when interpolating the number of packets in various time bins from flow slices
that do not use bins (they only store the timestamps of the first and last
packet). In , the y-axis has the ratio of estimated to actual
size of the flow in a given bin and the x-axis has the actual flow size (in
packets). For this experiment, we used a slice length of 90 seconds and divided
it up equally into 10 bins of size 9 seconds each. Two conclusions can be drawn
from the results in . First, for large flows, the error in
the estimates obtained by interpolating bins from slices is insignificant. On
the other hand, for relatively small flows, interpolating from flow slices
results in much higher error. This is because we divide the entire volume of
traffic for a particular flow among the bins it covers (see
for more details); the error depends on the timing of
bursts of traffic. Of course, to capture the fine grained traffic information,
the extension proposed in could be used, but it would result
in higher memory requirements. Second, we can observe the presence two-sided
errors indicates lack of bias.
Table 4:
Comparison of the error introduced by multifactor smart sampling and
smart sampling into estimates of traffic of various applications (average of 10
runs with different seeds). Both algorithms were configured to reduce the number
of flow records from 1,700,000 to around 190,000.
| Port number used as |
Multifactor s. s. error |
Smart sampling error |
Actual traffic |
|
|
| aggregation key |
Pkts |
Bytes |
SYNs |
Pkts |
Bytes |
SYNs |
Pkts |
Bytes |
SYNs |
|
|
| Web (80) |
0.4% |
0.7% |
0.8% |
0.3% |
0.1% |
1.6% |
17.5M |
1582M |
1852K |
|
|
| Kazaa (1214) |
0.4% |
0.2% |
2.4% |
0.6% |
0.1% |
12.4% |
2.67M |
1527M |
44.9K |
|
|
| eDonkey (4662) |
0.5% |
0.7% |
1.5% |
1.0% |
0.2% |
4.5% |
2.96M |
1075M |
344K |
|
|
| telnet (23) |
0.6% |
0.8% |
4.9% |
0.9% |
1.0% |
39.2% |
1.84M |
79.1M |
12.0K |
|
|
| SMB (445) |
1.3% |
1.6% |
1.1% |
2.5% |
1.8% |
3.1% |
1.50M |
93.3M |
1380K |
|
|
| SMTP (25) |
1.9% |
1.0% |
1.4% |
2.7% |
0.9% |
6.4% |
0.43M |
130M |
86.9K |
|
|
| DNS (53) |
1.8% |
2.4% |
3.6% |
2.7% |
1.7% |
16.8% |
0.45M |
34.8M |
6.02K |
|
|
|
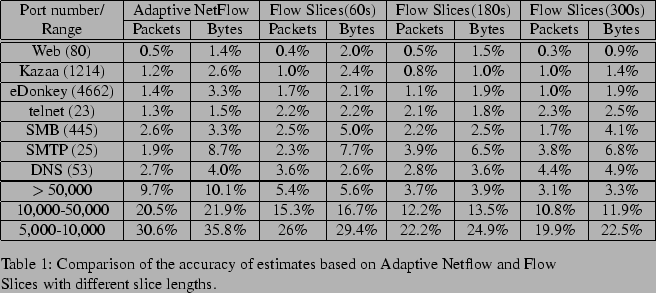
What is the effect of multi-factor smartsampling on the accuracy of estimates? In , we
proposed a modification to smart sampling to improve the accuracy of the
estimates for the number of flow arrivals. Table 4 summarizes
the results of our experiment comparing multi-factor smart sampling with smart
sampling. Before we discuss the details of this experiment, we want to note that
we found that , that only the first packet of a flow can have the
SYN flag set, is often violated in our trace. For some applications, the average
number of packets with the SYN flag set per flow is almost 2 (due to SYN
retransmissions).
This affects all estimators of flow arrivals based on SYN counts. In this
experiment, we do not aim to evaluate the accuracy of estimators based on SYN
counts, but the effect of smart sampling on their estimates. Therefore, we do
not measure the error relative to the actual number of flow arrivals, but to the
estimate of flow arrivals based on the input to the two smart sampling
algorithms. The input we used is the result of Flow Slices with a packet
sampling probability of 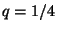 and flow slicing probability of
and flow slicing probability of 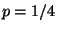 , using a
slice length of 60 seconds and an inactivity timeout of 15 seconds. The
threshold used for smart sampling is
, using a
slice length of 60 seconds and an inactivity timeout of 15 seconds. The
threshold used for smart sampling is 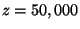 bytes. The thresholds used for
multi-factor smart sampling,
bytes. The thresholds used for
multi-factor smart sampling,  packets,
packets,
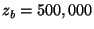 bytes and
bytes and
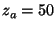 flows, have been selected so that it produces approximately same number
of records as smart sampling (from 1,700,000 down to roughly 190,000).
Table 4 shows the error introduced by the two variants of smart
sampling into estimates of the traffic of various applications identified by
destination port numbers. While smart sampling introduces very large errors in
the flow arrival estimates, multi-factor smart sampling ensures that the errors
are comparable to packet and byte count estimates. For example, smart sampling
incurs an error of 39.2% for telnet because it's small flows (approximately
6,600 bytes per flow on average compared to 34,000 for Kazaa) are discriminated
against by smart sampling. Multi-factor smart sampling, on the other hand,
achieves more accurate flow arrival counts by biasing its sampling towards
records with non-zero flow arrivals. This typically results in only a slight
reduction in the accuracy of packet and byte count estimates.
flows, have been selected so that it produces approximately same number
of records as smart sampling (from 1,700,000 down to roughly 190,000).
Table 4 shows the error introduced by the two variants of smart
sampling into estimates of the traffic of various applications identified by
destination port numbers. While smart sampling introduces very large errors in
the flow arrival estimates, multi-factor smart sampling ensures that the errors
are comparable to packet and byte count estimates. For example, smart sampling
incurs an error of 39.2% for telnet because it's small flows (approximately
6,600 bytes per flow on average compared to 34,000 for Kazaa) are discriminated
against by smart sampling. Multi-factor smart sampling, on the other hand,
achieves more accurate flow arrival counts by biasing its sampling towards
records with non-zero flow arrivals. This typically results in only a slight
reduction in the accuracy of packet and byte count estimates.


Next: Comparison with Adaptive NetFlow
Up: Experimental evaluation
Previous: Experimental evaluation
Ramana Rao Kompella
2005-08-12


![]() to 0.8% (1 in 125) and the slice duration to 60 seconds.
Figure 2 shows the scatter plot of ratio of the estimated and
true flow sizes (in number of packets) on the y-axis with increasing true flow
size on the x-axis. Note that the plot only shows flows that have more than
5,000 packets throughout the duration of the trace (1 hour). From this scatter
plot, we can see that most of the flows have been accurately estimated (within
10%). The estimates converge to the true values as the flow
size increases. The presence of two-sided errors empirically
confirms the unbiasedness of estimates based on flow slicing.
to 0.8% (1 in 125) and the slice duration to 60 seconds.
Figure 2 shows the scatter plot of ratio of the estimated and
true flow sizes (in number of packets) on the y-axis with increasing true flow
size on the x-axis. Note that the plot only shows flows that have more than
5,000 packets throughout the duration of the trace (1 hour). From this scatter
plot, we can see that most of the flows have been accurately estimated (within
10%). The estimates converge to the true values as the flow
size increases. The presence of two-sided errors empirically
confirms the unbiasedness of estimates based on flow slicing.

