TaP: Table-based Prefetching for Storage Caches

Mingju Li
University of New Hampshire
mingjul@cs.unh.edu
Elizabeth Varki
University of New Hampshire
varki@cs.unh.edu
Swapnil Bhatia
University of New Hampshire
sbhatia@cs.unh.edu
Arif Merchant
Hewlett-Packard Labs
arif@hpl.hp.com

Abstract:

TaP is a storage cache sequential prefetching and caching technique to improve the read-ahead cache hit rate and system response time. A unique feature of TaP is the use of a table to detect sequential access patterns in the I/O workload and to dynamically determine the optimum prefetch cache size. When compared to some popular prefetching techniques, TaP gives a better hit rate and response time while using a read cache that is often an order of magnitude smaller than that needed by other techniques. TaP is especially efficient when the I/O workload consists of interleaved requests from various applications, where only some of the applications are accessing their data sequentially. For example, TaP achieves the same hit rate as the other techniques with a cache length that is 100 times smaller than the cache needed by other techniques when the interleaved workload consists of 10% sequential application data and 90% random application data.

Index Terms: RAID, prefetch cache, sequential stream detection, read caches, read-ahead hit rate, I/O performance evaluation, disk array.

1 Introduction

Storage devices have evolved from disks directly attached to a host computer and controlled by the host's operating system into independent and self-managed devices containing tens-to-hundreds of disks accessed by several computer systems via a network. Large and mid-size storage devices have sophisticated controllers that control when and how disk data are stored, retrieved, and transmitted. In addition to the disks and controllers, storage devices have high-speed cache memory. The most effective way of speeding up storage systems is to ensure that required data are already loaded in the cache from the disks when read I/O requests for this data arrive, and to ensure that there is sufficient cache space for all write I/O requests to be written to cache immediately.

The storage caching technique determines how the storage cache space is allocated between read and write request data. The read request data stored in a cache are further classified as re-reference data, prefetch data, and old request data. The re-reference data are prior read I/O request data that are accessed often. The prefetch data are prefetched from the disks into the cache by the caching technique before I/O requests for these data arrive. The old request data are prior read I/O request data that have not yet been re-referenced. The caching technique makes decisions on how much space to allocate to re-reference, prefetch, and old request data.

A key factor underlying the success of a prefetching technique is the effectiveness of the technique that identifies sequential streams in the I/O workload, where a stream refers to the sequence of I/O requests corresponding to a particular application that are submitted by the application over a period of time. A stream is said to be sequential if the corresponding data are being read sequentially. Sequential stream detection is a difficult task since a storage system has no knowledge of the file systems or of the applications accessing its data. Consequently, a storage system has to identify sequential streams in its workload based solely on the addresses of I/O requests. Unfortunately, I/O requests from various streams are interleaved, so the outstanding I/O workload at any point in time shows little sequentiality, even when each stream accessing the storage device is sequential. As a result, a storage sequential stream detection technique must search past request addresses to see if an incoming I/O request is contiguous to any past I/O request. Thus, in addition to enabling re-reference hits, old I/O requests that remain in the cache facilitate sequential stream detection.

The key disadvantage of using the cache to detect sequential streams is that valuable cache space must be used to store old request data. Previous studies have shown that only a small percentage of the total I/O workload displays a high degree of re-reference hits [33,40] since storage caches are at the bottom of the cache hierarchy in computer systems. However, even when the locality-of-reference in the workload is too low to justify a large read cache, it is still needed to store the large number of old I/O requests required to detect sequential streams. This is an inefficient use of scarce cache memory, which typically constitutes 0.1% to 0.3% of the available disk space [16,24].

We propose using a separate data structure, namely, a table of request addresses, to detect sequential streams and to adapt the prefetch cache size efficiently based on the I/O workload. We refer to the our proposed prefetching technique as Table-based Prefetching (TaP). The TaP table is used to record request addresses and determine the optimum prefetch cache size for TaP. We define the optimum prefetch cache size of TaP as the cache size that is sufficient and necessary to obtain TaP's best achievable read-ahead hit rate for a given I/O workload. When an arriving I/O request misses in the prefetch cache, the TaP technique searches the TaP table to check if this new request's address is contiguous to any prior request addresses. If so, TaP flags this I/O request as belonging to a sequential stream and activates prefetching, else the TaP technique inserts the address of this request into the TaP table. TaP dynamically adapts the size of the prefetch cache depending on the fraction of sequential streams in the I/O workload. When the prefetch cache gets full and requests are thrown out, the request's address is inserted into the TaP table. In addition, a flag is set in the corresponding entry of the TaP table. This information is used by TaP to determine whether the size of the prefetch cache is too small for the current workload.

The key advantages of the TaP technique are as follows:

1. The optimum prefetch cache size can be determined efficiently.
2. Old I/O request data need not be stored, so the cache space can be judiciously shared between the write data, the prefetched data, and the re-reference data. (Note that the TaP table could also be used to identify missed re-references. This approach is not discussed here since it is not the focus of this paper.) Having a larger prefetch cache can improve the overall efficiency of a prefetching technique by permitting more data to be prefetched with a lower probability of the data getting evicted before being used.
3. The address tracking mechanism is not limited by the size of the cache, so more of history can be stored. As a result, there is a higher probability that the TaP technique would be able to identify sequential streams when the overall I/O workload contains a mix of requests from several random and sequential streams.
4. The TaP technique is simple but effective, and has low implementation complexity--its simplicity is one of its strengths.

Our simulation study shows that the TaP technique gives the same or better hit rate and response time as the other prefetching techniques used for comparison, while using a smaller read cache.

The rest of the paper is organized as follows. Section 2 presents a classification of existing cache prefetch techniques and the related work. The motivation and design of TaP technique are explained in Section 3. Section 4 presents the experimental evaluation of the TaP technique. Section 5 presents the conclusion.

2 Sequential prefetching techniques and related work

A sequential prefetching technique consists of three modules. The sequential detection module deals with the detection of sequential streams in the I/O workload; the prefetching module deals with data prefetching details like how much data to prefetch and when to trigger the prefetch; the cache management module deals with preserving useful prefetched data until I/O requests for the data arrive. It is the cache management module that determines the size of the prefetch cache and the prefetch cache replacement policy.

Sequential detection module: The sequential detection module determines whether a missed I/O request is part of a sequential stream. It is an optional module in prefetching techniques. Some prefetching techniques use access patterns that are not based on sequentiality to predict what data to prefetch [10,17,27,41], while other prefetching techniques prefetch sequential data without any analysis of access patterns [37,38]. For example, the Prefetch-On-Miss technique activates sequential prefetching whenever an I/O request misses in the read cache without checking for sequentiality [35].

If the sequential detection module is present in a prefetching technique, then it is activated when an I/O request misses in the cache. Most current prefetching techniques use the cache to track addresses [18,19] or predict future accesses based on previous access patterns [6,12,20] in the cache. Some techniques use offline information [23,25,26] and need to know future data access patterns for prefetching. Every I/O request that misses in the cache activates the sequential detection module which searches the read cache for contiguous data. If contiguous data are found in the cache, then a sequential stream is detected and prefetching is activated for the detected stream. Henceforth, we shall refer to these Cache based Prefetching techniques as CaP techniques. There are several variations of the CaP technique. For example, instead of detecting a sequential stream the first time contiguous data are found in the cache on a miss, the detection technique could treat the missed I/O request as a potential start of a sequential stream. In this case, prefetching is not triggered immediately. Instead, a flag is set in the cache line where the missed I/O request is loaded. If this flagged cache line is found to be contiguous to yet another incoming missed request, a sequential stream is detected and prefetch is triggered.

There is very limited prior work on table based sequential prefetching techniques in storage devices. A table has been used in main memory hardware caches to keep track of data access patterns [8]. Mohan et al. [32] developed an algorithm with a stream table for processor caches which determines the spatial locality in an application's memory reference. The table saves stream information that has been detected. A table has been used in disk caches to predict sequential accesses [21]. The table stores time stamps associated with each entry in the cache and these time stamps are used in making prefetching decisions. A prefetching technique for networked storage systems called STEP  [29] has been proposed in a most recent study. It uses a table for sequential access detection and prefetching. The table is maintained as a balanced tree and each entry records information for a recognized sequential stream or a new stream. While TaP also has a table, unlike these techniques, TaP uses the table to store different information (for example, the TaP table does not store time stamps and does not record information for recognized sequential streams).

While a lot of work has been done on workload prediction and prefetching in numerous areas such as processors [8,9], web architecture [15], databases [12,36], and file systems [7,28], the characteristics of their workload are different from those of a storage system workload. In addition, access pattern prediction in those fields requires application or file system information while such information is not available to an independent storage system. For example, ZFS uses semantic information about file system to detect sequential streams [1].

Prefetching module:

The prefetching module of a prefetching technique is activated when an I/O request hits in the prefetch cache or when the sequential detection module identifies a new sequential stream. The prefetching module determines how much data to prefetch. If data corresponding to several I/O requests are prefetched at a time, then prefetching is not triggered every time there is a hit. The prefetching module determines when to trigger a prefetch. Therefore, the prefetching module determines the efficiency of a cache prefetching technique once sequential streams are detected. For example, it would be sufficient to prefetch only one request at a time for a sequential stream with a low arrival rate, but the technique would have to prefetch more requests for a sequential stream with a high arrival rate. However, other factors must be considered too. For example, if the traffic at the disks is high, then prefetching should be triggered early enough for the prefetched data to arrive at the cache in time to result in hits. Gill and Bathen [18] developed a technique that determines the prefetching trigger point and the prefetching degree (i.e., amount of data to prefetch) based on the workload intensity and storage system load. Several other papers have analyzed the prefetching degree based on various factors [11,13,35,37,38].

Cache management module:

The cache management module determines the cache replacement policy and the prefetch cache size. Typically, the prefetch cache is managed along with the rest of the read cache as a single unit. There is no separate space or replacement policy allocated for the prefetch cache. Instead, prefetched data are loaded into the single cache and treated just like regular data. When the cache is full, prefetched data are thrown out like the rest of the data depending on the cache replacement policy. Treating prefetched data like the rest of cache data is not necessarily a good idea. Patterson et al. [34] developed a cache module which contains three partitions based on hint information from the applications. Pendse and Bhagavathula [35] divided the read cache into fixed-size prefetch and random (including re-reference and old I/O request data) caches, and analyzed the prefetch cache replacement scheme.

ACME [4] and ARC [31] are two techniques that have different replacement policies for different cache portions. They use a virtual cache to manage their cache replacement policies. ACME maintains data in caches as objects and a set of virtual caches (i.e., tables) is designed to keep past object header information for the distributed caches. Thus header information in each virtual cache is used to make decisions regarding replacement policies for the corresponding real cache. ARC separates the cache into two portions, one dedicated to the most recently-used and the other to the most frequently-used data. A cache directory (or table) is used for tracking the ``recency" and ``frequency" of past requests to change the size of both cache portions. The virtual caches in these two techniques are used neither for detection nor prefetching of sequential streams. SARC [19] divides the read cache into prefetch and random cache lists and compares the relative hits in the bottom of the two lists to adapt the size of the lists dynamically. However, their sequential detection module is based on CaP, so they store some old data (although in two lists) for sequential stream detection (and re-reference hits). Compared to the techniques above, TaP is designed to use a table for lower level storage sequential detection, prefetching, and cache sizing in low level storage.

2.1 Prefetching technique classification

As mentioned earlier, the sequential detection module is an optional component of prefetching techniques. Based on the existence or lack of the sequentiality detection module and on when prefetching is triggered, the sequential prefetching techniques can be classified as follows.

1. Always Prefetch (AP): There is no sequential detection module and this technique always triggers a prefetch regardless of whether an I/O request hits or misses in the cache.
   

2. Never Prefetch (NP): There is no sequential detection module and this technique does no prefetching.
   

3. Prefetch on Miss (PoM): There is no sequential detection module and this technique prefetches every time an I/O request misses in the read cache.
   

4. Prefetch on Hit (PoH): Prefetch is triggered by a cache miss with some detection schemes, and then every I/O request that hits in the read cache causes a prefetch. This is the only class of prefetch techniques that has a sequential detection module. If the degree of prefetch is high (i.e., data equivalent to several I/O requests are prefetched), then prefetching is not triggered upon every hit.

   Based upon whether the sequential detection module is cache based or table based, the PoH techniques are further classified as follows.
   

   1. CaP: The set of prior I/O request data stored in the read cache are searched to identify the start of a sequential stream. Most existing storage system prefetch techniques belong to this category.

   2. TaP: The set of prior I/O request addresses stored in the TaP table are searched to identify the start of a sequential stream and to determine the optimum prefetch cache size. Both TaP in this paper and STEP [29] are newly developed techniques that belong to this category.

3 Design of the TaP technique

3.1 Motivation and goal

The design of the TaP technique is motivated by the following observations of lower levels of storage systems:

1. There is little value in caching old request data because the proportion of this data that will be re-referenced is small [33].
2. Most I/O workloads contain some sequential access patterns because file systems and storage systems try to manage data layout on disk devices such that data that are sequential in the application and file system space are also sequential in the disk address space. However, individual sequential patterns are interleaved with each other and therefore the aggregate I/O workload displays little sequentiality.
3. Although current middle or large storage systems have big caches and powerful controllers, their prefetching performance is poor. The study in [39] shows that the prefetching technique does not benefit the performance of the evaluated storage system when there are more than four sequential I/O streams since the prefetching technique does not recognize the interleaved sequential pattern in the workload. In addition, most well-studied prefetching techniques with advanced sequential detection schemes are designed for higher levels of computer systems. These are not suitable for storage systems because they need information from file systems or applications which is not available to storage systems.

4. Performance of a sequential prefetching technique is degraded if it uses an inefficient sequential detection module because of the following reasons:
   1. False positive detection errors generate unnecessary I/O traffic at the disks and increase the response time by considering random data as sequential. Moreover, valuable cache space is used to store useless data, thereby displacing correctly prefetched data that get evicted from the prefetch cache before they are used. The AP and PoM techniques are both likely to cause this problem if the I/O workload contains random streams or partly sequential streams.

   2. False negative detection errors decrease the hit rate and increase the response time by failing to identify sequential streams in the workload. The NP technique always faces this problem since it never prefetches. The CaP technique faces this problem when the workload consists of a mix of random and sequential streams because, in this case, the history of request addresses is too short to record sequential patterns.

   3. Correctly prefetched data from sequential streams could be evicted before the data can be used. This can occur if the prefetch cache gets full. For a given read cache size, AP, PoM and the CaP techniques are more susceptible to this problem since either they prefetch too much useless data (as in AP and PoM) or they store data from past I/O requests (as in CaP).

With the above observations in view, TaP is designed to detect, prefetch, and cache only sequential streams into its prefetch cache. Consequently, TaP is capable of identifying the minimal amount of data that should be prefetched and cached, and can therefore maintain the cache size at an optimal level. We consider a workload solely consisting of reads--the write workload is handled by the write cache.

At the heart of the TaP technique is the TaP table. TaP uses this table for two crucial functions: sequential stream detection and cache size management. The address of a request that is not found in the prefetch cache, is searched in this table. If it is not found in the table either, then assuming that the address is part of a new sequential stream, the address of the next expected request in this stream is recorded in the table. If the assumption turns out to be correct, then the address recorded in the table will be seen in the workload in the near future, and TaP will begin prefetching that stream when this occurs. As the table is populated with new addresses of potentially sequential streams, old addresses that have not led to a stream detection so far, are evicted on a FIFO basis. In this way, the table plays a key role in TaP's ability to detect sequential streams.

The TaP table also plays a central role in maintaining the prefetch cache size at an optimal level. In addition to addresses of cache misses, addresses of requests that are evicted from the cache before they are hit are also inserted into the TaP table. These addresses are marked with a special flag, replaceFlag, in the table. TaP exploits the possibility that such pre-hit evictions may be the result of a smaller than optimal cache in the following way. If such flagged, evicted streams are soon re-detected by the detection method discussed above, then TaP rightly concludes that the cache is undersized and initiates a cache size increment. This upward movement of the cache size is balanced by the TaP Decrement Module (discussed below), which maintains a downward pressure on the cache size to prevent cache inflation.

In summary, an address that ends up in the table does so in one of exactly two ways. A request that misses in the cache and the table is inserted into the table. The address of a pre-hit eviction from the prefetch cache is also inserted into the table. Data that are cached do not have entries in the table.

3.2 TaP pseudocode

Figure 1: TaP pseudocode

Table 1: Important constants in TaP

Variables/constants	Usage
prefetchDegree	prefetch size
triggerOffset	when to prefetch
strideRange	sequential stream detection range
incrAmount	how much to increase prefetch cache size
decrAmount	how much to decrease prefetch cache size
measurementWindow	time window for hit rate measurement

The TaP pseudocode is listed in Figure 1. The important constants used in the pseudocode are listed in Table 1. The first three constants are the inputs to the TaP algorithm provided by the system administrator. These affect the detection and the prefetching module. The variables prefetchDegree and trigOffset relate to the prefetching module, and determine how much data to prefetch and when to trigger a prefetch. The prefetching module is separate from the sequential detection module and is not the focus of TaP, so the current version of TaP uses constant values. However, a more versatile prefetching module can be incorporated into TaP and will improve the overall performance of TaP. The constant strideRange is used to specify the sequential stream detection range. When the TaP Table is searched, a hit within a stride range is considered (TableHit(req, strideRange)). The reason for searching within a stride range is that operating systems sometimes submit requests out of sequence. The last three parameters affect the cache management module. They should be chosen carefully by the administrator because they determine the tradeoff between performance and cache size economy. While the pseudocode implements the TaP table as a queue for ease of explanation, a hash table is a more appropriate data structure for the table. In addition, the TaP table bound derived below (Equation 4) justifies that the growth rate of the table size is sufficiently small. Therefore, the table search time is likely to be negligible. Moreover, the short table search time also guarantees that the controller-CPU cost is small since searching the TaP table is the CPU's biggest cost.

As shown in the pseudocode, when a new request arrives, it is handled by the TaPCacheManage() function. The TaP cache manager decides whether the request is part of an already detected sequential stream or if it should be recorded for future detection.

ProcessCacheHit()

If the request generates a cache hit, TaP serves the request from the cache. TaP interprets this request as being part of an already recognized sequential stream and prefetches the next request in the stream. The previous request is evicted from the cache.

ProcessCacheMiss()

If the request is not found to be in the cache, then its address is searched in the TaP table. If the request's address is found in the table, then this implies that two ``consecutive'' requests have been detected. TaP takes this as an indication of the start of a sequential stream and begins prefetching this stream. In addition, if the replaceFlag field of the request's entry in the table is set, then this entry must be the result of a pre-hit eviction from the cache. Therefore, TaP increments the cache size by incrAmount. (The Increment Module is discussed in further detail below.) If a request is not found to be in the table, then the address of the expected succeeding request is recorded in the table for detection in the future.

The TaP cache manager periodically monitors the cache size for inflation. During every period of time where measurementWindow requests arrive, the TaP cache manager maintains a count of the total number of cache hits accrued.

HitRateStable()

At the end of this measurement period, the cache manager compares the short term hit rate in the current window to its value in the previous window. We define the short term hit rate as the ratio of hits to total requests in a measurement window. If the current and previous values are within some small additive constant $\delta$ of each other, then the cache manager concludes that the hit rate has been fairly stable. It takes this as an indication that the cache is adequately sized and might even be inflated. Therefore, it decreases the cache size by a preset amount equal to the decrAmount.

We next describe the rationale behind the TaP Increment and Decrement modules.

3.3 TaP cache size management modules

The degree of sequentiality of the I/O workload changes over a time period. The TaP table is a useful tool for determining whether the prefetch cache size is too small for the current workload. The replaceFlag field of an entry in the TaP table is used for this purpose. The default value of the replaceFlag variable is false. When a prefetched request is evicted before a hit by the replacement scheme, the request's address is inserted into the TaP table with the replaceFlag set to true. Whenever there is a table hit, the replaceFlag is checked. If the flag is true, then the prefetch cache size is increased. Thus, entries that are reinstated into the TaP table from the cache are used to detect whether the cache size is too small.

While reinstated entries are a reliable indicator of cache space scarcity, a perfect indicator of cache size inflation is not obvious. The TaP cache manager uses a ``downward pressure'' approach to cache size deflation using the measured short term hit rate. The basic idea is that whenever the TaP cache manager observes the hit rate measured over some short term window of time to be stable (measurementWindow), it (pessimistically) assumes that the cache is slightly inflated and begins a gradual decrease of the cache size. The decrease continues so long as the hit rate remains stable. If the cache size falls below the optimal value, then the hit rate changes and this change prevents the TaP cache manager from decreasing the cache size any further. Moreover, a smaller than optimal cache size will lead to pre-hit evictions from the cache into the TaP table and re-insertions from the TaP table into the cache, which will quickly trigger an increase in the cache size back to the optimal value. Thus, as a result of the downward pressure from the decrement module, the cache size always rides close to the optimal value.

While the cache size oscillates around the optimal value when the workload is stable, the extent of these oscillations is small as seen in Figure 3. For example, at time 50000, the optimal value for the cache size is 50. The TaP cache manager maintains the cache size close to this value with an oscillation of less than five cache lines independent of the optimal cache size. In addition, these oscillations do not burden the CPU much, because there are only a few more operations (such as increasing or decreasing the cache size) added in each of the measurementWindows where the oscillations occur.

3.4 Bounding cache and table size

The table size, T, refers to the number of request addresses that can be stored in the TaP table. The table replacement scheme is a FIFO policy. When a request address gets a hit, it is removed from the TaP table. The cache size, C, refers to the number of cache lines assuming that exactly 1 prefetch request is stored in each line. Without loss of generality, it is assumed that the prefetch degree is 1 request and prefetch is triggered upon every hit in the prefetch cache.

Below we derive a simple optimum bound for the cache size and simple pessimistic bounds for the cache and table size. The TaP technique initializes the prefetch cache size to the optimum bound, since TaP continually adapts the size of the prefetch cache size to match the sequential degree of the workload. The TaP table size is set to the pessimistic bound since the memory space used by a table could be orders of magnitude smaller than the cache size (i.e., a cache line is an order of magnitude larger than a table entry).

The prefetch cache size must be large enough to hold prefetched data from each of the sequential streams. Suppose there are S sequential or partly sequential streams accessing the storage device. Then the cache size must contain at least S lines.

$${\sf C}\ge {\sf S}$$ (1)

We now derive a pessimistic bound for C (and T). For real storage systems, it is difficult to get information about the degree of sequentiality of each workload stream or the variance in the inter-arrival rate of each stream. So, we derive worst-case bounds using only the number of (sequential + random) workload streams M and the number of sequential streams S. The bounds are derived as a function of a parameter $\epsilon$ which represents the acceptable percentage of reduction in the read-ahead hit rate. That is, if the acceptable percentage reduction in the hit rate is given, then a pessimistic bound for C and T can be computed.

Consider a workload consisting of M interleaved streams. A prefetching technique tries to ensure that a request prefetched for stream $i$ survives in the cache until the next I/O request from stream $i$ arrives. Between two requests from stream $i$, there can be several requests from the ${\sf M}-1$ other streams. Of these ${\sf M}-1$ streams, there can be at most ${\sf S}-1$ sequential streams. A prefetching technique should ensure that the request from stream $i$ is not evicted from the cache due to cache insertions resulting from these sequential stream arrivals. Let seqarrival# represent the number of requests that arrive from other sequential streams between two requests from stream $i$.

Consider a synthetic workload in which (a) future request arrivals are independent of past arrivals, and (b) there is equal probability that the next arrival is from any of the M streams. Then,

$$Pr({\sf seqarrival\char93 }= n) = \left(\frac{{\sf S}-1}{{\sf S}}\right)^{n} \times \frac{1}{{\sf S}}$$

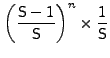Some of these seqarrival# arrivals could be from recognized sequential streams and would hit in the cache. Therefore, the prefetches initiated by these requests would not need new insertions into the cache. The sequential arrivals that miss in the cache (and hit in the TaP table) are the only arrivals that cause new insertions into the cache. Let insertions# represent the number of requests that result in new insertions into the prefetch cache between two arrivals from a stream $i$. Hence, ${\sf insertions\char93 }\le {\sf seqarrival\char93 }.$

Since the cache replacement scheme is a FIFO, a new prefetched request is stored at location 0 of the cache. For this prefetched data to be useful, its corresponding I/O request must arrive within C or fewer requests. The probability that the number of cache insertions in the worst case are no more than can fit in the cache (without evicting the prefetched request) is:

$$Pr({\sf insertions\char93 }< {\sf C}) = \sum_{k=0}^{{\sf C}-1}\left(\frac{{\sf S}-1}{{\sf S}}\right)^{k} \times \frac{1}{{\sf S}}$$

$$= 1 - \left(\frac{{\sf S}-1}{{\sf S}}\right)^{{\sf C}}$$

Therefore,

$$Pr({\sf insertions\char93 }\ge {\sf C}) = \left(\frac{{\sf S}-1}{{\sf S}}\right)^{{\sf C}}$$ (2)

Equation (2) provides the probability that a prefetched request is evicted from the cache before it is used. We bound this probability of eviction to some small value $\epsilon > 0$.

$$\left(\frac{{\sf S}-1}{{\sf S}}\right)^{{\sf C}} \leq \epsilon.$$

This implies that the cache size

$${\sf C}\ge \frac{\log(\epsilon)}{\log\left(\frac{{\sf S}-1}{{\sf S}}\right)}.$$ (3)

Following an approach analogous to the one taken for the cache size, we can obtain a bound on the TaP table size

$${\sf T}\ge \frac{\log(\epsilon)}{\log\left(\frac{M-1}{M}\right)}.$$ (4)

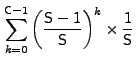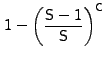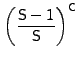Although these bounds are derived and used for synthetic workloads, they are also a guide for evaluating TaP's performance on real workloads. The bound in Equation (4) allows us to choose the tradeoff between maximizing the hit rate and minimizing the table size in inverse relation to the value chosen for $\epsilon$. The CPU cost incurred by TaP is dominated by the size of the table that is searched for hits. Since this cost is only logarithmically related to the miss probability and inverse-logarithmically related to the fraction of interleaving streams, it is not prohibitively large.

4 Experimental evaluation

We evaluate the TaP technique using the Disksim 3.0 simulator [5]. Table 2 gives the setup used for our experiments. We configured four Cheetah9LP 9GB disks as a RAID-5 system. The cache is divided into cache lines of size 8 blocks with 512 bytes per block. The cache size and the I/O workload are varied in our experiments. We use both synthetic workloads and realistic workloads. The synthetic workload uses several possible combinations of random and sequential streams in order to evaluate the technique under different conditions. It should be noted that due to memory and computing constraints, our simulation storage setup is much smaller than real storage systems, so the workload is also scaled down appropriately.

We compare the TaP technique against the CaP, AP, PoM, and NP techniques. The storage system's mean response time and the cache's prefetch hit rate are measured for the various prefetch techniques. Parameters such as prefetching degree and prefetching trigger are set at similar values for each of the techniques. The prefetching degree is set at 1 (i.e., only 1 request is prefetched), so prefetching is triggered upon every hit in the prefetch cache. The TaP table length is set at the upper limit for the workload (Equation 4). The memory space utilized by TaP in our experiments is negligible compared to the cache size--the maximum space used by the TaP table in all our experiments is 4KB. To ensure fairness, we compare the performances of the various techniques under similar workloads and cache sizes. Note that the cache size for compared techniques is set to the sum of the cache and table size used by TaP. Both TaP and CaP initiate prefetch under similar conditions--for TaP, prefetch is initiated upon the first hit in the table, and for CaP, prefetch is initiated when an incoming request is found to be contiguous to an old request stored in the read cache.

Table 2: Storage simulator setup

Disksim parameter	Value
storage cache line	8 blocks
prefetch cache replacement policy	FIFO
storage RAID organization	RAID 5
stripe unit size	8 blocks
number of disks	4
disk type	cheetah9LP
disk capacity	17783240 blocks
mean disk read seek time	5.4 msec
maximum disk read seek time	10.63 msec
disk revolutions per minute	10045 rpm

4.1 TaP cache size manager in action

The first experiment evaluates the performance of TaP's cache size manager as the workload changes. Figure 3 shows the result of a simulation of the TaP cache manager when the synthetic workload illustrated in Figure 2 is used. The workload starts with 10 streams with a sequentiality of 10%. These short-lived streams can be seen as a dense band of mostly random points from time 0 to 10000 in Figure 2. At time 8000, 50 completely sequential streams arrive. These appear as almost horizontal lines from time 8000 to time about 140000 in Figure 2. The TaP cache manager reacts to the influx of sequential streams by increasing the cache size. When the 10% sequential streams finish, the TaP cache manager decrements the cache size, without opposition from the increment module, until the optimal size of 50 is reached. This size is optimal because there are only 50 sequential streams in the workload at this point. Approximately at time 80000, 100 completely sequential streams are added to the workload which prompts the TaP cache manager to increment the cache size to the new optimal value of 150. At time 140000, the first 50 sequential streams finish. Again, the downward pressure meets no resistance and the cache size settles to the optimal value of 100. At time 200000, 50 streams with sequentiality 70% arrive and the cache size is incremented to accommodate them. The increase is larger than 50 because more cache space is required to get hits on streams with lower sequentiality: this is because of the single unavoidable extra prefetch at the end of a sequential run in a partially sequential stream. The sequential streams that arrived at time 80000 finish at time close to 220000 and the 50 streams with 70% sequentiality finish a little after time 250000. Both of these events allow the decrement module to gradually decrease the cache size. The workload changes again at times 250000 and 280000 when 10 streams with sequentiality 90% and 20 streams with sequentiality 100% are added, respectively. The cache is still inflated when these streams arrive, and so the gradual decrease of the cache size continues. At time 300000, the cache stabilizes to a value optimal for the 90% sequential streams. When these end, the cache size finally decrements to the optimal value of around 20 for the last remaining 20 completely sequential streams. Figure 4 shows that on average, a hit rate close to the maximum achievable with the current workload, is maintained throughout the simulation.

In summary, this experiment illustrates that the TaP cache manager is appropriately responsive to the changes in a non-stationary workload. The increment module, using the pre-hit eviction information from the table, is highly effective in quickly incrementing the cache size to a value that is optimal for the current workload. The decrement module, by maintaining a downward pressure on the cache size, prevents cache size inflation. Together, the two modules force the cache size to ride close to a value optimal for the current workload.

Figure 2: A visualization of the workload used for the TaP cache management simulation

Figure 3: A sample of the behavior of the TaP cache manager

Figure 4: Short and long term hit rate obtained using the TaP cache manager

4.2 A comparison of TaP and CaP

Figure 5 shows the results of a comparison of the TaP and CaP techniques on the basis of the cache size required by each to achieve the best possible hit rate on a given workload. In this experiment, we generated a synthetic workload of the following type. The workload is composed of a total of 50 streams, each of which arrives at an instant chosen uniformly at random in the simulation. Each stream in the workload is either completely sequential or completely random and is of a fixed finite duration much smaller than the length of the simulation. The number of completely sequential streams is varied from 1 to 50 (X axis of Figure 5), the remainder of the streams are random. First, the workload is run through a cache managed by the TaP technique with a table length of 1000 entries, and the hit rate achieved by TaP is recorded. Next, in order to find the cache size at which the CaP technique achieves the same hit rate as TaP, a series of experiments are conducted using the same workload as offered to TaP. We define the hit rate achieved by CaP to be the same as TaP when the relative difference between the two rates is no more than 5%.

Figure 5: A comparison of cache sizes required by TaP and CaP to achieve matching hit rates as a function of the number of sequential streams (from 1 to 50).

Clearly, the cache size required by CaP to achieve the same hit rate as TaP is almost an order of magnitude larger when the number of sequential streams is small. This underscores the effectiveness of TaP's table-based techniques in two ways. First, it shows that TaP can detect and exploit sequentiality with a small prefetch cache size even when the sequentiality is latent and interleaved in a large amount of random data. This improvement in detection provides a significant reduction in the response time for individual sequential streams, even when the average hit rate of the workload is arbitrarily low. Thus, TaP succeeds in ``connecting the dots'' while using a minimal amount of cache resource. The additional resource used by TaP, the table, is only a fraction (2-10 cache blocks) of the size of the cache. Second, as a result of the superior detection capability, the TaP cache manager's table-based cache inadequacy indicator can accurately and promptly respond to changes in a non-stationary workload.

4.3 SPC2-like workload

SPC2 [3,18] is a popular benchmark that simulates workloads generated by applications that access their workload sequentially. Since we do not have access to the official SPC2 workload generator, we generated the workload using SPC2 published specifications [3]. The SPC2 workload is an interleaved mixture of highly sequential streams. Hence, all prefetched data would eventually result in hits if the data remain in the cache until their corresponding I/O requests arrive. In our experimental evaluation, we measure the mean hit rate and the response time as a function of some control variable such as the number of sequential streams or the cache size. However, in each experimental run, the cache size must be held constant for two reasons. First, the competing algorithms (AP, PoM, CaP) require a constant cache size. Second, we are interested in measuring performance given a fixed cache size. Therefore, TaP's dynamic cache sizing function is disabled for all the experiments in the sequel. We compare the performances of the various techniques under similar workloads and cache (+ table) sizes. A side-effect of turning off the prefetch cache sizing function is that the replaceFlag has no impact. That is, when a prefetch request is thrown out of the prefetch cache by the replacement scheme, its address is not put in the TaP table.

In our experiments, the number of streams is varied from 1 to 500. Depending on the cache size and prefetching technique, some of the prefetched data may get thrown out before they are used. PoM and NP perform far worse than the other techniques for obvious reasons, so below we analyze the results for TaP, CaP, and AP. From Figure 6 (a) one can see that when there is sufficient cache space to store at least one request from each of the streams, the cache hit rate is close to 1 for AP, TaP, and CaP (while PoM has a hit rate of 0.5 and NP has a hit rate of 0). As the number of sequential streams increases (beyond 40), the cache is no longer large enough to hold data from all the streams. Therefore, the hit rate gradually decreases.

We first compare the TaP with the CaP technique as the number of streams increases. TaP performs better than CaP since the small cache size makes it difficult for CaP to identify sequential streams. As a result, the total number of prefetches for CaP are far fewer than for TaP as shown in Figure 6 (c). We define the useful prefetch ratio as the total number of prefetched requests that result in hits divided by the total number of prefetched requests. CaP stores random data for sequentiality detection thereby increasing the probability that prefetched data are thrown out before being used. Therefore, CaP has a lower useful prefetch ratio than TaP as shown in Figure 6 (d). Overall, TaP has a higher hit rate and a lower response time (Figure 6 (a) and (b)) than CaP.

We now compare the TaP and the AP techniques. TaP and AP perform similarly when the cache size is large enough to store data from all the streams. As the number of streams increases, the performance of AP is worse than that of TaP (Figure 6 (a) and (b)), and the reason can be seen by studying Figure 6 (c) and (d). As the number of streams increases relative to the cache size, AP continues to prefetch more than TaP. When a prefetched request is thrown out by the replacement scheme, TaP treats the next request from this stream as a random request and does not prefetch. (The address of the replaced request is not inserted into the TaP table since the cache size is not dynamically increased in this experimental evaluation.) AP prefetches on hits/misses while TaP only prefetches on hits. When the cache is too small for the workload, AP's useful prefetch ratio is much smaller than TaP's useful ratio, and as a result AP performs worse than TaP. The comparison between AP and TaP shows the negative impact of prefetching for this highly sequential workload when the cache size is too small to hold data from all the sequential streams. Figure 7 underscores this point: here, the cache size is very small. The performance of AP is comparable to CaP up to a certain point, but as the number of streams continues to increase, the performance of AP becomes worse than NP. Thus, for really small caches, never prefetch is better than always prefetch even when all the streams are highly sequential. TaP outperforms all the techniques evaluated for this cache size and workload. The mean response time for TaP is 20% lower than that of the other techniques.

Figure 6: Performance of prefetching techniques with a cache of 4MB, table of 4KB, and the SPC2-like workload.

Figure 7: Performance of prefetching techniques with a cache of 240KB, table less than 0.8KB, and the SPC2-like workload.

4.4 Mix of 100% sequential streams and 100% random streams

Figure 8: Performance of prefetching techniques with a cache of 4MB, table of 4KB, on a workload consisting of 300 streams of which $m$ (X axis) are completely sequential and all others are completely random.

In this set of experiments, a synthetic workload is used. The cache size and the total number of streams is fixed. Figure 8 shows the performance of the various techniques as the number of sequential streams is increased. The hit rate of all techniques (except NP) increases as the number of sequential streams increases. TaP consistently performs better than the other techniques and shows more improvement than the other techniques as the number of sequential streams increases. CaP performs worse that TaP, AP, and PoM as the number of sequential streams increases since CaP's sequential detection module is inefficient for this workload. AP and PoM have higher response time than NP when there are few sequential streams, but this changes as the fraction of sequential streams increases.

4.5 Varying cache sizes

Figure 9: Impact of the cache size on the performance of prefetching techniques, total 80 streams, 60 completely sequential

Figure 10: Impact of the cache size on the performance of prefetching techniques, total 80 streams, 20 completely sequential

Figure 11: Performance of prefetching techniques as the number of BSUs (streams) in the SPC-1 workload is varied with cache size of 240KB

This set of experiments demonstrates the efficient use of cache space by the TaP technique. In the first set of experiments (Figure 9), the workload is fixed at 20 random streams and 60 sequential streams. Regardless of the cache size, TaP consistently performs better than the other techniques because of TaP's efficient sequentiality detection module. In most cases, TaP uses less than half the cache space that CaP uses to get the same performance. For example, Figure 9 (b) shows that in order to keep response time under 4ms, TaP needs only 2MB while CaP and AP need more than 4MB . (PoM and NP are never able to achieve a response time of 4ms in this set of experiments.)

In the second set of experiments (Figure 10), the workload is fixed at 60 random streams and 20 sequential streams (i.e., the number of sequential streams is decreased making the workload more random). With just 25% of the workload consisting of sequential streams, TaP is still able to detect the small degree of sequential streams with very small cache sizes. Both AP and CaP perform poorly for different reasons: AP's failure results from prefetching both random and sequential stream data into a small cache, so prefetched data from sequential streams get thrown out before they result in hits. CaP's failure results from its dependence on the cache size for sequentiality detection; the small cache fills quickly with random data, so sequential stream data are thrown out before they can be used for sequentiality detection. The efficient use of the cache by TaP is highlighted by this experiment. For example, when the prefetch cache is about 1MB, TaP's hit rate is about 4 times higher than all other techniques; and to achieve a response time of 6ms, TaP uses only 1 MB while CaP uses 4MB.

4.6 SPC1-like-read workload

SPC1 [2,22,30] is a popular benchmark that simulates workloads generated by business applications. Since we do not have access to the official SPC1 workload generator, we use a freely available alternative SPC1 workload generator [14]. We modified the workload by ignoring all write requests. Thus, the final workload is a SPC1-like-read workload. The number of Business Scaling Units (BSUs) roughly corresponds to the number of users generating the workload [14]. Therefore, the number of BSUs roughly corresponds to the number of workload streams.

We fix the cache size and then study the effect of increasing the number of BSUs. Figure 11 shows that the hit rate of the cache is small even with 1 BSU (hit rate < 0.3). This implies that the SPC1 workload has low degree of sequentiality. As the number of BSUs increase, the hit rate of all the prefetching strategies decreases. This implies that the cache is too small and that the degree of sequentiality per stream is low. Even for a workload with such low sequentiality, TaP gives the best hit rate and the lowest response time.

5 Conclusion

The TaP technique belongs to the class of Prefetch-on-Hit (PoH) techniques. Unlike existing PoH techniques that use the read cache to detect sequential streams in the I/O workload, the TaP technique uses a table to detect sequential streams. The use of a table by TaP ensures that a longer history of request access patterns can be tracked by the sequential detection module. This feature is very useful since I/O workloads consist of interleaved requests from various applications.

A unique feature of TaP is that the prefetch cache size is adjusted dynamically based on cache usage information from the TaP table. When the I/O workload has few sequential streams, the prefetch cache size is decreased and vice-versa. Our evaluation shows that for most workloads, TaP performs better than the other techniques for the smallest sized prefetch cache. TaP is superior to cache based PoH (CaP) techniques when the workload intensity is high and there is a mixture of sequential, partly sequential, and random workloads. At this point, the cache and disks are heavily utilized. The CaP technique wastes valuable cache space storing old data for sequential stream detection, particularly when the re-reference rate is low, as is often the case.

As future work, we plan to develop an integrated table-based technique that extracts both re-reference and sequential stream information from the I/O workload. Currently, re-reference data are detected when old I/O request data in the cache are hit. Prior studies have shown that most of the I/O workload is not re-referenced. However, a small fraction of the I/O workload gets many re-reference hits [33,40]. The use of a table shows promise in detecting this small fraction of highly re-referenced data and managing the size of the re-reference cache.

Acknowledgments

We thank our anonymous reviewers for their helpful comments. We also thank Randal Burns, our shepherd, for directing the camera-ready version of this paper. This work was supported in part by the US National Science Foundation under CAREER grant CCR-0093111.

Bibliography

1

ZFS performance.
online, 2007.
https://www.solarisinternals.com/wiki/index.php/ZFS_Performance.

2

SPC Benchmark-1(SPC-1) Official Specification, revision 1.10.1.
Tech. rep., Effective 27 Sept. 2006.
https://www.storageperformance.org/specs.

3

SPC Benchmark-2(SPC-2) Official Specification, vesion 1.2.1.
Tech. rep., Effective 27 Sept. 2006.
https://www.storageperformance.org/specs.

4

ARI, I., AMER, A., GRAMACY, R., MILLER, E. L., BRANDT, S. A., AND LONG, D. D. E.
ACME: adaptive caching using multiple experts.
In Proceedings of the 2002 Workshop on Distributed Data and Structures (WDAS) (2002), Carleton Scientific.
Extended version of the WDAS 2002 workshop paper.

5

BUCY, J. S., AND GANGER, G. R.
The DiskSim simulation environment version 3.0 reference manual.
Tech. Rep. CMU-CS-03-102, Carnegie Mellon University, School of Computer Science, January 2003.

6

CAO, P., FELTEN, E. W., KARLIN, A. R., AND LI, K.
A study of integrated prefetching and caching strategies.
In SIGMETRICS '95/PERFORMANCE '95: Proceedings of the 1995 ACM SIGMETRICS Joint International Conference on Measurement and Modeling of Computer Systems (1995), ACM Press, pp. 188-197.

7

CAO, P., FELTEN, E. W., KARLIN, A. R., AND LI, K.
Implementation and performance of integrated application-controlled file caching, prefetching, and disk scheduling.
ACM Transactions on Computer Systems 14, 4 (1996), 311-343.

8

CHEN, T.-F., AND BAER, J.-L.
Effective hardware based data prefetching for high-performance processors.
IEEE Trans. computers 44, 5 (1995), 609-623.

9

CHI, C.-H., AND CHEUNG, C.-M.
Hardware-driven prefetching for pointer data references.
In Proceedings of the 12th international conference on Supercomputing ICS (1998), ACM.

10

CHRYSOS, G. Z., AND EMER, J. S.
Memory dependence prediction using store sets.
In Proceedings of the 25th Annual International Symposium (1998), Computer Architecture, 1998, pp. 142-153.

11

CORTES, T., AND LABARTA, J.
Linear aggressive prefetching: A way to increase the performance of cooperative caches.
In Proceedings of the Joint International Parallel Processing Symposium and IEEE Symposium on Parallel and Distributed Processing (1999), pp. 45-54.

12

CUREWITZ, K. M., KRISHNAN, P., AND VITTER, J. S.
Practical prefetching via data compression.
In Proceedings of the ACM SIGMOD (1993), International Conference on Management of Data archive, pp. 257 - 266.

13

DAHLGREN, F., DUBOIS, M., AND STENSTROM, P.
Fixed and adaptive sequential prefetching in shared memory multiprocessors.
In International Conference on Parallel Processing (1993), IEEE Computer Society, pp. 56-63.

14

DANIEL, S., AND FAITH, R. E.
A portable, open-source implementation of the SPC-1 workload.
In Proceedings of the IEEE International Workload Characterization (2005).

15

DOMENECH, J., SAHUQUILLO, J., GIL, J. A., AND PONT, A.
The impact of the web prefetching architecture on the limits of reducing user's perceived latency.
In Proceedings of the 2006 IEEE/WIC/ACM International Conference on Web Intelligence (2006), IEEE Computer Society, pp. 740-744.

16

FARLEY, M.
Storage Networking Fundamentals: An Introduction to Storage Devices, Subsystems, Applications, Management, and Filing Systems.
Cisco Press, 2004.

17

FU, J. W. C., AND PATEL, J. H.
Data prefetching in multiprocessor vector cache memories.
In Proceedings of the 18th annual international symposium on computer architecture (1991), Computer Architecture, pp. 54-63.

18

GILL, B. S., AND BATHEN, L. A. D.
AMP: Adaptive multi-stream prefetching in a shared cache.
In Proc. of USENIX 2007 Annual Technical Conference (Feb 2007), 5th USENIX Conference on File and Storage Technologies.

19

GILL, B. S., AND MODHA, D. S.
SARC: Sequential prefetching in adaptive replacement cache.
In Proc. of USENIX 2005 Annual Technical Conference (2005), pp. 293-308.

20

GRIFFIOEN, J., AND APPLETON, R.
Reducing file system latency using a predictive approach.
In Proceedings of the USENIX Summer 1994 Technical Conference on USENIX Summer 1994 Technical Conference (1994), vol. 1, USENIX Association Berkeley, CA, USA, pp. 197-208.

21

GRIMSRUD, K. S., ARCHIBALD, J. K., AND NELSON, B. E.
Multiple prefetch adaptive disk caching.
IEEE Trans. Knowl. Data Eng. 5, 1 (1993), 88-103.

22

JOHNSON, S., MCNUTT, B., AND REITH, R.
The making of a standard benchmark for open system storage.
In J. Comput. Resouce Management (Winter 2001), no. 101, pp. 26-32.

23

KALLAHALLA, M., AND VARMAN, P. J.
Optimal prefetching and caching for parallel I/O sytems.
In SPAA '01: Proceedings of the Thirteenth Annual ACM Symposium on Parallel Algorithms and Architectures (New York, NY, USA, 2001), ACM Press, pp. 219-228.

24

KAREDLA, R., LOVE, J. S., AND WHERRY, B. G.
Caching strategies to improve disk system performance.
Computer 27, 3 (1994), 38-46.

25

KIMBREL, T., AND KARLIN, A. R.
Near-optimal parallel prefetching and caching.
In SIAM Journal on Computing Archive (2000), vol. 29, Society for Industrial and Applied Mathematics, pp. 1051 - 1082.

26

KIMBREL, T., TOMKINS, A., PATTERSON, R. H., CAO, B. B. P., FELTEN, E. W., GIBSON, G. A., KARLIN, A. R., AND LI, K.
A trace-driven comparison of algorithms for parallel prefetching and caching.
In USENIX 2nd Symposium on OS Design and Implementation (OSDI '96) (1996), pp. 19-34.

27

LEE, R. L., YEW, P. C., AND LAWRIE, D. H.
Data prefetching in shared memory multiprocessors.
In International Conference on Parallel Processing (1987), IEEE Computer Society, pp. 28-31.

28

LEI, H., AND DUCHAMP, D.
An analytical approach to file prefetching.
In Proceedings of the USENIX 1997 Annual Technical Conference (1997), pp. 275-288.

29

LIANG, S., JIANG, S., AND ZHANG, X.
STEP: Sequentiality and thrashing detection based prefetching to improve performance of networked storage servers.
In Distributed Computing Systems, 2007. ICDCS '07. 27th International Conference on (2007), pp. 64-.

30

MCNUTT, B., AND JOHNSON, S.
A standard test of I/O cache.
In Proceedings on Computer Measurement Group's 2001 International Conference (2001).

31

MEGIDDO, N., AND MODHA, D. S.
ARC: A self-tuning, low overhead replacement cache.
In USENIX Conference on File and Storage Technologies (FAST '03) (2003), pp. 115-130.

32

MOHAN, T., DE SUPINSKI, B. R., MCKEE, S. A., MUELLER, F., AND YOO, A.
A quantitative measure of memory reference regularity.
In International Parellel and Distributed Processing Symposium (April 2002).

33

MUNTZ, D., AND HONEYMAN, P.
Multi-level caching in distributed file systems - or - your cache ain't nuthin' but trash.
In Proceedings of the USENIX Winter 1992 Technical Conference (San Fransisco, CA, USA, 1992), pp. 305-313.

34

PATTERSON, R. H., GIBSON, G. A., GINTING, E., STODOLSKY, D., AND ZELENKA, J.
Informed prefetching and caching.
In Proc. SOSP Conf. December, 1995.

35

PENDSE, R., AND BHAGAVATHULA, R.
Pre-fetching with the segmented LRU algorithm.
Circuits and Systems, 1999. 42nd Midwest Symposium on 2, 3 (1999), 862-865.

36

SMITH, A. J.
Sequentiality and prefetching in database systems.
ACM Transactions on Database Systems 3, 3 (1978), 223-247.

37

SMITH, A. J.
Cache memories.
ACM Computing Surveys 14, 3 (1982), 473-530.

38

TCHEUN, M. K., YOON, H., AND MAENG, S. R.
An adaptive sequential prefetching scheme in shared-memory multiprocessors.
In International Conference on Parallel Processing (1997), IEEE Computer Society, pp. 306 - 313.

39

VARKI, E., MERCHANT, A., XU, J., AND QIU, X.
Issues and challenges in the performance analysis of real disk arrays.
IEEE Transactions on Parallel and Distributed Systems 15, 6 (2004), 559-574.

40

WONG, T. M., AND WILKES, J.
My cache or yours? making storage more exclusive.
In Proceedings of the General Track: 2002 USENIX Annual Technical Conference (Berkeley, CA, USA, 2002), USENIX Association, pp. 161-175.

41

ZILLES, C., AND SOHI, G.
Execution-based prediction using speculative slices.
In Proceedings of the 28th annual international symposium on Computer architecture (2001), pp. 1-13.

About this document ...

TaP: Table-based Prefetching for Storage Caches

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.62)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation doc.tex

The translation was initiated by root on 2008-01-04