Note that we intend to compute a theoretical upper bound which is necessarily
achievable.
Proof.
By Eqn.
3 the aggregate hits for the set of caches
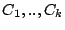
is
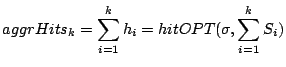 |
(4) |
By the definition of
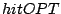
, this is the same as that obtained by Belady's OPT on a
cache of the aggregate size.
Since Belady's OPT is known to deliver the maximum possible hit ratio,
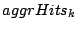
is maximized for all
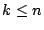
.

Proof.
Inter-cache traffic is the sum of misses and demotions between two adjacent caches (by Eqn.
2).
Since, OPT-UB is defined to
have no demotions and maximizes the aggregate hits at all levels of the cache (Lemma
II.1),
no other policy can have lower inter-cache traffic than OPT-UB.

Proof.
We prove by contradiction. Let a better performing policy achieve a lower average response time (equivalently, lower total response time) for a workload than OPT-UB, by providing
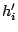
hits
at each corresponding cache
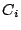
, and
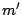
overall misses, as compared to
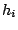
hits and
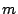
misses for OPT-UB.
(a) follows as the sum of all hits and misses is the same for both policies (
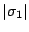
) and the second term on both sides of the inequality can be removed.
The second term on the right hand side of (b) is non-negative because
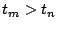
and by Lemma
II.1, no policy can have more aggregate hits (up to any cache level) than OPT-UB.
(c) follows by removing the non-negative second term in inequality (b). (d) follows as the
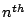
term in the summation is zero.
Note that between step (a) and step (d), the superscript of the summation has dropped from
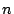
to
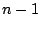
. Steps (a) through (d) can be repeated until
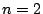
(as, for all
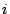
,
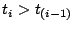
). We will then arrive at
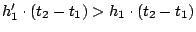
.
As
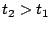
, it implies that
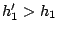
, which contradicts Lemma
II.1,
which states that OPT-UB maximizes
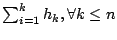
(including
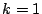
).


![]() ,
exhibits for each cache
,
exhibits for each cache ![]() ,
, ![]() number of hits,
while requiring no demotions or reloads from disks, where,
number of hits,
while requiring no demotions or reloads from disks, where,
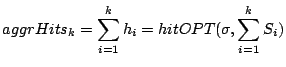
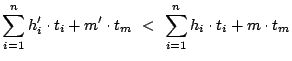
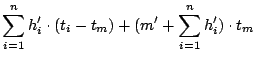
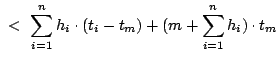
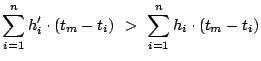
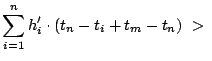
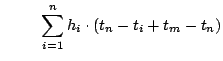
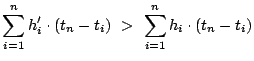
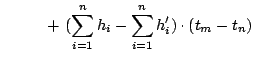
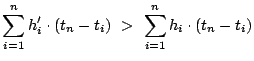
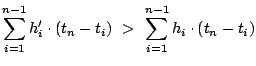
![]()