
Next: Optimal Upper Bound: OPT-UB
Up: Offline Optimal
Previous: Offline Optimal
The offline optimal performance, which is the best possible performance given
full knowledge of the future requests, is a critical guide for
cache algorithm development. The offline optimal algorithm for single-level
caches is the classic Belady's MIN or OPT [4] which simply
evicts the page with the furthest re-reference time.
For four decades, the quest for a similar algorithm for multi-level caches has
remained unfulfilled. Hit ratio, the performance metric that served us so well
in single-level caches, loses its fidelity to performance in multi-level caches,
where the benefit of a
hit depends on which level it occurred in (e.g. two hits on a higher
cache could be better than three hits on a lower cache.)
The average read response time is a much better performance metric, but is
complicated in the presence of demotions and/or eviction-based reloading from
disks. The inter-cache bandwidth usage is another important metric since
many scenarios are bottle-necked by network resources [33].
It does appear that different policies would be optimal depending on which
performance metric we use.
We now prove universal bounds for the single-path scenario as depicted in
Figure 3 that simultaneously apply to both the average response
time and inter-cache bandwidth metrics.
The bounds apply to all algorithms irrespective of whether demotions,
inclusion, or hints are used.
Later, we explain extensions to compute the bounds for the multi-path scenarios as well.
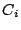 |
Cache at level 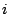 , ,
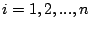 |
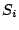 |
Size of the cache 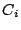 |
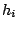 |
Number of hits at 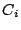 |
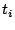 |
Avg. round-trip response time from 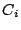 |
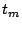 |
Avg. round-trip response time from disks |
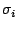 |
Sequence of reads seen by 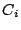 |
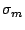 |
Sequence of reads (misses) seen by disks |
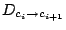 |
Number of demotions from 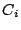 to to 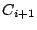 |
From Figure 3 and definitions above, the total response time is
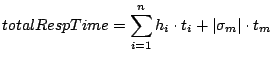 |
(1) |
and the inter-cache traffic between caches 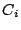 and
and 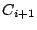 is
is
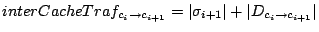 |
(2) |
We define
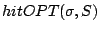 to be the number of hits produced by Belady's offline OPT
policy on the request sequence
to be the number of hits produced by Belady's offline OPT
policy on the request sequence 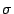 and a single-level cache of size
and a single-level cache of size 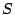 .
.


Next: Optimal Upper Bound: OPT-UB
Up: Offline Optimal
Previous: Offline Optimal
root
2008-01-08