
5th USENIX Conference on File and Storage Technologies - Paper
Pp. 47–60 of the Proceedings
Proportional-Share Scheduling for Distributed Storage Systems
Yin Wang1
University of Michigan
yinw@eecs.umich.edu
Arif Merchant
HP Laboratories
arif@hpl.hp.com
Abstract:
Fully distributed storage systems have gained popularity in the past
few years because of their ability to use cheap commodity hardware
and their high scalability. While there are a number of algorithms
for providing differentiated quality of service to clients of a
centralized storage system, the problem has not been solved for
distributed storage systems. Providing performance guarantees in
distributed storage systems is more complex because clients may have
different data layouts and access their data through different
coordinators (access nodes), yet the performance guarantees required
are global.
This paper presents a distributed scheduling framework. It is an
adaptation of fair queuing algorithms for distributed servers.
Specifically, upon scheduling each request, it enforces an extra
delay (possibly zero) that corresponds to the amount of service the
client gets on other servers. Different performance goals, e.g., per
storage node proportional sharing, total service proportional
sharing or mixed, can be met by different delay functions. The delay
functions can be calculated at coordinators locally so excess
communication is avoided. The analysis and experimental results show
that the framework can enforce performance goals under different
data layouts and workloads.
The storage requirements of commercial and institutional
organizations are growing rapidly. A popular approach for reducing
the resulting cost and complexity of management is to consolidate
the separate computing and storage resources of various applications
into a common pool. The common resources can then be managed
together and shared more efficiently. Distributed storage systems,
such as Federated Array of Bricks (FAB) [20],
Petal [16], and IceCube [27], are designed to serve as
large storage pools. They are built from a number of individual
storage nodes, or bricks, but present a single, highly-available
store to users. High scalability is another advantage of distributed
storage systems. The system can grow smoothly from small to
large-scale installations because it is not limited by the capacity
of an array or mainframe chassis. This satisfies the needs of
service providers to continuously add application workloads onto
storage resources.
Figure 1:
A distributed storage system
|
A data center serving a large enterprise may support thousands of
applications. Inevitably, some of these applications will have
higher storage performance requirements than others. Traditionally,
these requirements have been met by allocating separate storage for
such applications; for example, applications with high write rates
may be allocated storage on high-end disk arrays with large caches,
while other applications live on less expensive, lower-end storage.
However, maintaining separate storage hardware in a data center can
be a management nightmare. It would be preferable to provide each
application with the service level it requires while sharing
storage. However, storage systems typically treat all I/O requests
equally, which makes differentiated service difficult. Additionally,
a bursty I/O workload from one application can cause other
applications sharing the same storage to suffer.
One solution to this problem is to specify the performance
requirement of each application's storage workload and enable the
storage system to ensure that it is met. Thus applications are
insulated from the impact of workload surges in other applications.
This can be achieved by ordering the requests from the applications
appropriately, usually through a centralized scheduler, to
coordinate access to the shared resources
[5,6,24]. The scheduler can be
implemented in the server or as a separate interposed request
scheduler [2,12,17,29] that treats the
storage server as a black box and applies the resource control
externally.
Centralized scheduling methods, however, fit poorly with distributed
storage systems. To see this, consider the typical distributed
storage system shown in Figure 1. The system is
composed of bricks; each brick is a computer with a CPU, memory,
networking, and storage. In a symmetric system, each brick runs the
same software. Data stored by the system is distributed across the
bricks. Typically, a client accesses the data through a
coordinator, which locates the bricks where the data resides and
performs the I/O operation. A brick may act both as a storage node
and a coordinator. Different requests, even from the same client,
may be coordinated by different bricks. Two features in this
distributed architecture prevent us from applying any existing
request scheduling algorithm directly. First, the coordinators are
distributed. A coordinator schedules requests possibly without the
knowledge of requests processed by other coordinators. Second, the
data corresponding to requests from a client could be distributed
over many bricks, since a logical volume in a distributed storage
system may be striped, replicated, or erasure-coded across many
bricks [7]. Our goal is to design a distributed
scheduler that can provide service guarantees regardless of the data
layout.
This paper proposes a distributed algorithm to enforce
proportional sharing of storage resources among streams of
requests. Each stream has an assigned weight, and the
algorithm reserves for it a minimum share of the system capacity
proportional to its weight. Surplus resources are shared among
streams with outstanding requests, also in proportion to their
weights. System capacity, in this context, can be defined in a
variety of ways: for example, the number of I/Os per second, the
number of bytes read or written per second, etc. The algorithm is
work-conserving: no resource is left idle if there is any request
waiting for it. However, it can be shown easily that a
work-conserving scheduling algorithm for multiple resources (bricks
in our system) cannot achieve proportional sharing in all cases. We
present an extension to the basic algorithm that allows per-brick
proportional sharing in such cases, or a method that provides a
hybrid between system-wide proportional sharing and per-brick
proportional sharing. This method allows total proportional sharing
when possible while ensuring a minimum level of service on each
brick for all streams.
The contribution of this paper includes a novel distributed
scheduling framework that can incorporate many existing centralized
fair queuing algorithms. Within the framework, several algorithms
that are extensions to Start-time Fair Queuing [8] are
developed for different system settings and performance goals. To
the best of our knowledge, this is the first algorithm that can
achieve total service proportional sharing for distributed storage
resources with distributed schedulers. We evaluate the proposed
algorithms both analytically and experimentally on a FAB system, but
the results are applicable to most distributed storage systems. The
results confirm that the algorithms allocate resources fairly under
various settings
-- different data layouts, clients accessing the data through
multiple coordinators, and fluctuating service demands.
This paper is organized as follows. Section 2
presents an overview of the problem, the background, and the related
work. Section 3 describes our distributed fair
queueing framework, two instantiations of it, and their properties.
Section 4 presents the experimental evaluation of
the algorithms. Section 5 concludes.
2 Overview and background
We describe here the distributed storage system that our framework
is designed for, the proportional sharing properties it is intended
to enforce, the centralized algorithm that we base our work upon,
and other related work.
Figure 2 shows the configuration of a typical
distributed storage system. The system includes a collection of
storage bricks, which might be built from commodity disks,
CPUs, and NVRAM. Bricks are connected by a standard network such as
gigabit Ethernet. Access to the data on the bricks is handled by the
coordinators, which present a virtual disk or logical
volume interface to the clients. In the FAB distributed storage
system [20], a client may access data through an arbitrary
coordinator or a set of coordinators at the same time to balance its
load. Coordinators also handle data layout and volume management
tasks, such as volume creation, deletion, extension and migration.
In FAB, the coordinators reside on the bricks, but this is not
required. We consider local area distributed storage systems where
the network latencies are small compared with disk latencies. We
assume that the network bandwidths are sufficiently large that the
I/O throughput is limited by the bricks rather than the network.
Figure 2:
Data access model of a
distributed storage system. Different clients may have different
data layouts spreading across different sets of bricks. However,
coordinators know all data layouts and can handle requests from any
client.
|
The data layout is usually designed to optimize properties such as
load balance, availability, and reliability. In FAB, a logical
volume is divided into a number of segments, which may be
distributed across bricks using a replicated or erasure-coded
layout. The choice of brick-set for each segment is determined by
the storage system. Generally, the layout is opaque to the clients.
The scheduling algorithm we present is designed for such a
distributed system, making a minimum of assumptions. The data for a
client may be laid out in an arbitrary manner. Clients may request
data located on an arbitrary set of bricks at arbitrary and even
fluctuating rates, possibly through an arbitrary set of
coordinators.
2.2 Proportional Sharing
Table 1:
Some symbols used in this paper.
| SYMBOLS |
DESCRIPTION |
 |
Weight of stream  |
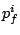 |
Stream  's 's 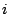 -th request -th request |
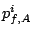 |
Stream  's 's 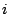 -th request to brick -th request to brick  |
 |
Cost of a single request |
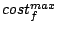 |
Max request cost of stream  |
 |
Max cost on brick  of of  |
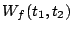 |
Aggregate cost of requests served from  during interval during interval ![$[t_1, t_2]$](img20.gif) |
 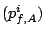 |
Total cost of requests in between and and 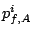 , including , including 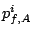 |
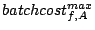 |
Max value of
 |
 |
Arrival time of a request |
 |
Start tag of a request |
 |
Finish tag of a request |
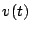 |
Virtual time at time  |
 |
Delay value of a request |
|
The algorithms in this paper support proportional sharing of
resources for clients with queued requests. Each client is assigned
a weight by the user and, in every time interval, the algorithms try
to ensure that clients with requests pending during that interval
receive service proportional to their weights.
More precisely, I/O requests are grouped into service classes called
streams, each with a weight assigned; e.g., all requests from
a client could form a single stream. A stream is backlogged if
it has requests queued. A stream  consists a sequence of requests consists a sequence of requests
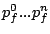 . Each request has an associated service cost . Each request has an associated service cost
 . For example, with bandwidth performance goals, the
cost might be the size of the requested data; with service time
goals, request processing time might be the cost. The maximum
request cost of stream . For example, with bandwidth performance goals, the
cost might be the size of the requested data; with service time
goals, request processing time might be the cost. The maximum
request cost of stream  is denoted is denoted 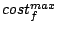 . The weight
assigned to stream . The weight
assigned to stream  is denoted is denoted  ; only the relative values
of the weights matter for proportional sharing. ; only the relative values
of the weights matter for proportional sharing.
Formally, if 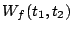 is the aggregate cost of the requests
from stream is the aggregate cost of the requests
from stream  served in the time interval served in the time interval ![$[t_1, t_2]$](img20.gif) , then the
unfairness between two continuously backlogged streams , then the
unfairness between two continuously backlogged streams  and and  is defined to be:
is defined to be:
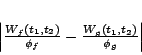 |
(1) |
A fair proportional sharing algorithm should guarantee that
(1) is bounded by a constant. The constant usually
depends on the stream characteristics, e.g., 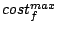 . The
time interval . The
time interval ![$[t_1, t_2]$](img20.gif) in (1) may be any time
duration. This corresponds to a ``use it or lose it" policy, i.e., a
stream will not suffer during one time interval for consuming
surplus resources in another interval, nor will it benefit later
from under-utilizing resources. in (1) may be any time
duration. This corresponds to a ``use it or lose it" policy, i.e., a
stream will not suffer during one time interval for consuming
surplus resources in another interval, nor will it benefit later
from under-utilizing resources.
In the case of distributed data storage, we need to define what is
to be proportionally shared. Let us first look at the following
example.
There are two alternatives for the above example, which induce two
different meanings for proportional sharing. The first is
single brick proportional sharing, i.e., service capacity of brick
 will be proportionally shared. Many existing proportional
sharing algorithms fall into this category. However, stream will be proportionally shared. Many existing proportional
sharing algorithms fall into this category. However, stream  also
receives service at brick also
receives service at brick 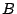 , thus receiving higher overall
service. While this appears fair because stream , thus receiving higher overall
service. While this appears fair because stream  does a better
job of balancing its load over the bricks than stream does a better
job of balancing its load over the bricks than stream  , note that
the data layout may be managed by the storage system and opaque to
the clients; thus the quality of load balancing is merely an
accident. From the clients' point of view, stream , note that
the data layout may be managed by the storage system and opaque to
the clients; thus the quality of load balancing is merely an
accident. From the clients' point of view, stream  unfairly
receives less service than stream unfairly
receives less service than stream  . The other alternative is
total service proportional sharing. In this case, the share of the
service stream . The other alternative is
total service proportional sharing. In this case, the share of the
service stream  receives on brick receives on brick  can be increased to
compensate for the fact that stream can be increased to
compensate for the fact that stream  receives service on brick receives service on brick
 , while , while  does not. This problem is more intricate and little
work has been done on it. does not. This problem is more intricate and little
work has been done on it.
It is not always possible to guarantee total service proportional
sharing with a work-conserving scheduler, i.e., where the server is
never left idle when there is a request queued. Consider the
following extreme case.
Example 2
Stream  requests service from brick  only, while equally
weighted stream  is sending requests to  and many other
bricks. The amount of service  obtains from the other bricks is
larger than the capacity of  . With a work-conserving scheduler,
it is impossible to equalize the total service of the two streams.

If the scheduler tries to make the total service received by  and and
 as close to equal as possible, as close to equal as possible,  will be blocked at brick will be blocked at brick  ,
which may not be desirable. Inspired by the example, we would like
to guarantee some minimum service on each brick for each stream, yet
satisfy total service proportional sharing whenever possible. ,
which may not be desirable. Inspired by the example, we would like
to guarantee some minimum service on each brick for each stream, yet
satisfy total service proportional sharing whenever possible.
In this paper, we propose a distributed algorithm framework under
which single brick proportional sharing, total service proportional
sharing, and total service proportional sharing with a minimum
service guarantee are all possible. We note that, although we focus
on distributed storage systems, the algorithms we propose may be
more broadly applicable to other distributed systems.
In selecting an approach towards a distributed proportional sharing
scheduler, we must take four requirements into account: i) the
scheduler must be work-conserving: resources that backlogged streams
are waiting for should never be idle; ii) ``use it or lose it'', as
described in the previous section; iii) the scheduler should
accommodate fluctuating service capacity since the service times of
IOs can vary unpredictably due to the effects of caching,
sequentiality, and interference by other streams; and iv) reasonable
computational complexity--there might be thousands of bricks and
clients in a distributed storage system, hence the computational and
communication costs must be considered.
There are many centralized scheduling algorithms that could be
extended to distributed systems
[3,4,8,28,30,17,14,9].
We chose to focus on the Start-time Fair
Queuing (SFQ) [8] and its extension SFQ( ) [12]
because they come closest to meeting the requirements above. We
present a brief discussion of the SFQ and SFQ( ) [12]
because they come closest to meeting the requirements above. We
present a brief discussion of the SFQ and SFQ( ) algorithms in the
remainder of this section. ) algorithms in the
remainder of this section.
SFQ is a proportional sharing scheduler for a single server;
intuitively, it works as follows. SFQ assigns a start time tag
and a finish time tag to each request corresponding to the
normalized times at which the request should start and complete
according to a system notion of virtual time. For each stream,
a new request is assigned a start time based on the assigned finish
time of the previous request, or the current virtual time, whichever
is greater. The finish time is assigned as the start time plus the
normalized cost of the request. The virtual time is set to be the
start time of the currently executing request, or the finish time of
the last completed request if there is none currently executing.
Requests are scheduled in the order of their start tags. It can be
shown that, in any time interval, the service received by two
backlogged workloads is approximately proportionate to their
weights.
More formally, the request 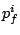 is assigned the start tag is assigned the start tag
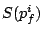 and the finish tag and the finish tag 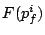 as follows: as follows:
where 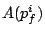 is the arrival time of request is the arrival time of request 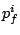 , and , and 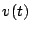 is the virtual time at
is the virtual time at  ; ;
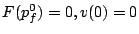 . .
SFQ cannot be directly applied to storage systems, since storage
servers are concurrent, serving multiple requests at a time, and the
virtual time 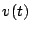 is not defined. Jin et al. [12]
extended SFQ to concurrent servers by defining the virtual time as
the maximum start tag of requests in service (the last request
dispatched). The resulting algorithm is called
depth-controlled start-time fair queuing and abbreviated to
SFQ( is not defined. Jin et al. [12]
extended SFQ to concurrent servers by defining the virtual time as
the maximum start tag of requests in service (the last request
dispatched). The resulting algorithm is called
depth-controlled start-time fair queuing and abbreviated to
SFQ( ), where ), where  is the queue depth of the storage device. As
with SFQ, the following theorem [12] shows that SFQ( is the queue depth of the storage device. As
with SFQ, the following theorem [12] shows that SFQ( )
provides backlogged workloads with proportionate service, albeit
with a looser bound on the unfairness. )
provides backlogged workloads with proportionate service, albeit
with a looser bound on the unfairness.
While there are more complex variations of SFQ [12] that can
reduce the unfairness of SFQ( ), for simplicity, we use SFQ( ), for simplicity, we use SFQ( )
as the basis for our distributed scheduling algorithms. Since the
original SFQ algorithm cannot be directly applied to storage
systems, for the sake of readability, we will use ``SFQ'' to refer
to SFQ( )
as the basis for our distributed scheduling algorithms. Since the
original SFQ algorithm cannot be directly applied to storage
systems, for the sake of readability, we will use ``SFQ'' to refer
to SFQ( ) in the remainder of the paper. ) in the remainder of the paper.
Extensive research in scheduling for packet switching networks has
yielded a series of fair queuing algorithms; see
[19,28,8,3]. These algorithms have
been adapted to storage systems for service proportional sharing.
For example, YFQ [1], SFQ( ) and FSFQ( ) and FSFQ( ) [12]
are based on start-time fair queueing [8];
SLEDS [2] and SARC [29] use leaky buckets;
CVC [11] employs the virtual clock [30]. Fair
queuing algorithms are popular for two reasons: 1) they provide
theoretically proven strong fairness, even under fluctuating service
capacity, and 2) they are work-conserving. ) [12]
are based on start-time fair queueing [8];
SLEDS [2] and SARC [29] use leaky buckets;
CVC [11] employs the virtual clock [30]. Fair
queuing algorithms are popular for two reasons: 1) they provide
theoretically proven strong fairness, even under fluctuating service
capacity, and 2) they are work-conserving.
However, fair queuing algorithms are not convenient for real-time
performance goals, such as latencies. To address this issue, one
approach is based on real-time schedulers; e.g.,
Façade [17] implements an Earliest Deadline First (EDF)
queue with the proportional feedback for adjusting the disk queue
length. Another method is feedback control, a classical engineering
technique that has recently been applied to many computing
systems [10]. These generally require at least a
rudimentary model of the system being controlled. In the case of
storage systems, whose performance is notoriously difficult to
model [22,25], Triage [14] adopts an
adaptive controller that can automatically adjust the system model
based on input-output observations.
There are some frameworks [11,29] combining the above
two objectives (proportional sharing and latency guarantees) in a
two-level architecture. Usually, the first level guarantees
proportional sharing by fair queueing methods, such as
CVC [11] and SARC [29]. The second level tries
to meet the latency goal with a real-time scheduler, such as EDF.
Some feedback from the second level to the first level scheduler is
helpful to balance the two objectives [29].
All of the above methods are designed for use in a centralized
scheduler and cannot be directly applied to our distributed scheduling
problem.
Existing methods for providing quality of service in distributed
systems can be put into two categories. The first category is the
distributed scheduling of a single resource. The main problem here
is to maintain information at each scheduler regarding the amount of
resource each stream has so far received. For example, in fair
queuing algorithms, where there is usually a system virtual time
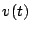 representing the normalized fair amount of service that all
backlogged clients should have received by time representing the normalized fair amount of service that all
backlogged clients should have received by time  , the problem is
how to synchronize the virtual time among all distributed
schedulers. This can be solved in a number or ways; for example, in
high capacity crossbar switches, in order to fairly allocate the
bandwidth of the output link, the virtual time of different input
ports can be synchronized by the access buffer inside the
crossbar [21]. In wireless networks, the communication
medium is shared. When a node can overhear packages from neighboring
nodes for synchronization, distributed priority backoff schemes
closely approximate a single global fair
queue [18,13,23]. In the context of storage
scheduling, Request Window [12] is a distributed scheduler
that is similar to a leaky bucket scheduler. Services for different
clients are balanced by the windows issued by the storage server. It
is not fully work-conserving under light workloads. , the problem is
how to synchronize the virtual time among all distributed
schedulers. This can be solved in a number or ways; for example, in
high capacity crossbar switches, in order to fairly allocate the
bandwidth of the output link, the virtual time of different input
ports can be synchronized by the access buffer inside the
crossbar [21]. In wireless networks, the communication
medium is shared. When a node can overhear packages from neighboring
nodes for synchronization, distributed priority backoff schemes
closely approximate a single global fair
queue [18,13,23]. In the context of storage
scheduling, Request Window [12] is a distributed scheduler
that is similar to a leaky bucket scheduler. Services for different
clients are balanced by the windows issued by the storage server. It
is not fully work-conserving under light workloads.
The second category is centralized scheduling of multiple resources.
Gulati and Varman [9] address the problem of allocating
disk bandwidth fairly among concurrent competing flows in a parallel
I/O system with multiple disks and a centralized scheduler. They aim
at the optimization problem of minimizing the unfairness among
different clients with concurrent requests. I/O requests are
scheduled in batches, and a combinatorial optimization problem is
solved in each round, which makes the method computationally
expensive. The centralized controller makes it unsuitable for use in
fully distributed high-performance systems, such as FAB.
To the best of our knowledge, the problem of fair scheduling in
distributed storage systems that involve both distributed schedulers
and distributed data has not been previously addressed.
3 Proportional Sharing in Distributed Storage Systems
We describe a framework for proportional
sharing in distributed storage systems, beginning with the
intuition, followed by a detailed description, and two
instantiations of the method exhibiting different sharing
properties.
3.1 An intuitive explanation
First, let us consider the simplified problem where
the data is centralized at one brick, but the coordinators may be
distributed. An SFQ scheduler could be placed either at coordinators
or at the storage brick. As fair scheduling requires the information
for all backlogged streams, direct or indirect communication among
coordinators may be necessary if the scheduler is implemented at
coordinators. Placing the scheduler at bricks avoids the problem. In
fact, SFQ( ) can be used without modification in this case,
provided that coordinators attach a stream ID to each request so
that the scheduler at the brick can assign the start tag
accordingly. ) can be used without modification in this case,
provided that coordinators attach a stream ID to each request so
that the scheduler at the brick can assign the start tag
accordingly.
Now consider the case where the data is distributed over multiple
bricks as well. In this case, SFQ schedulers at each brick can guarantee
only single brick proportional sharing, but not necessarily
total service proportional sharing because the scheduler at each
brick sees only the requests directed to it and cannot account for
the service rendered at other bricks.
Suppose, however, that each coordinator broadcasts all requests to
all bricks. Clearly, in this case, each brick has complete knowledge
of all requests for each stream. Each brick responds only to the
requests for which it is the correct destination. The remaining
requests are treated as virtual requests, and we call the
combined stream of real and virtual request a virtual stream;
see Fig. 4.
A virtual request takes zero processing time but does account for
the service share allocated to its source stream. Then the SFQ
scheduler at the brick guarantees service proportional sharing of
backlogged virtual streams. As the aggregate service cost of a
virtual stream equals the aggregate service cost of the original
stream, total service proportional sharing can be achieved.
Figure 4:
The naive approach. The
coordinator broadcasts every request to all bricks. Requests to
incorrect destination bricks are virtual and take zero
processing time. Proportional scheduling at each local brick
guarantees total service proportional sharing.
|
The above approach is simple and straightforward, but with
large-scale distributed storage systems, broadcasting is not
acceptable. We observe, however, that the SFQ scheduler requires
only knowledge of the cost of each virtual request, the coordinators
may therefore broadcast the cost value instead of the request
itself. In addition, the coordinator may combine the cost of
consecutive virtual requests and piggyback the total cost
information onto the next real request; see
Fig. 5. The communication overhead is
negligible because, in general, read/write data rather than requests
dominate the communication and the local area network connecting
bricks usually has enough bandwidth for this small overhead.
Figure 5:
The improved approach. Only
the aggregate cost of virtual requests is communicated, indicated by
the number before each request (assuming unit cost of each request).
Broadcasting is avoided yet total service proportional sharing can
be achieved.
|
The piggyback cost information on each real request is called the
delay of the request, because the modified SFQ scheduler will
delay processing the request according to this value. Different
delay values may be used for different performance goals, which
greatly extends the ability of SFQ schedulers. This flexibility is
captured in the framework presented next.
3.2 Distributed Fair Queuing Framework
We propose the distributed fair queuing framework displayed in
Fig. 6; as we show later, it can be used for total
proportional sharing, single-brick proportional sharing, or a hybrid
between the two. Assume there are streams 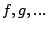 and bricks and bricks 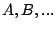 . The fair queueing scheduler is placed at each brick as just
discussed. The scheduler has a priority queue for all streams and
orders all requests by some priority, e.g., start time tags in the
case of an SFQ scheduler. On the other hand, each coordinator has a
separate queue for each stream, where the requests in a queue may
have different destinations. . The fair queueing scheduler is placed at each brick as just
discussed. The scheduler has a priority queue for all streams and
orders all requests by some priority, e.g., start time tags in the
case of an SFQ scheduler. On the other hand, each coordinator has a
separate queue for each stream, where the requests in a queue may
have different destinations.
When we apply SFQ to the framework, each request has a start tag and
a finish tag. To incorporate the idea presented in the previous
section, we modify the computation of the tags as follows:
The only difference between SFQ
formulae (2-3) and those above is the new
delay function for each request, which is calculated at coordinators
and carried by the request. The normalized delay value translates
into the amount of time by which the start tag should be shifted.
How the delay is computed depends upon the proportional sharing
properties we wish to achieve, and we will discuss several delay
functions and the resulting sharing properties in the sections that
follow. We will refer to the modified Start-time Fair Queuing
algorithm as Distributed Start-time Fair Queuing (DSFQ).
In DSFQ, as in SFQ( ), ), 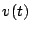 is defined to be the start tag of
the last request dispatched to the disk before or at time is defined to be the start tag of
the last request dispatched to the disk before or at time  . There
is no global virtual time in the system. Each brick maintains its
own virtual time, which varies at different bricks depending on the
workload and the service capacity of the brick. . There
is no global virtual time in the system. Each brick maintains its
own virtual time, which varies at different bricks depending on the
workload and the service capacity of the brick.
We note that the framework we propose works with other fair
scheduling algorithms [28] as long as each stream has its
own clock such that the delay can be applied; for example, a similar
extension could be made to the Virtual Clock
algorithm [30] if we desire proportional service over an
extended time period (time-averaged fairness) rather than the ``use
it or lose it'' property (instantaneous fairness) supported by SFQ.
Other options between these two extreme cases could be implemented
in this framework, as well. For example, the scheduler can constrain
each stream's time tag to be within some window of the global
virtual time. Thus, a stream that under-utilizes its share can get
extra service later, but only to a limited extent.
If the delay value is set to always be zero, DSFQ reduces to SFQ and
achieves single brick proportional sharing. We next consider other
performance goals.
Figure 6:
The distributed fair queuing
framework
|
3.3 Total Service Proportional Sharing
We describe how the distributed fair queueing framework can be used
for total proportional sharing when each stream uses one coordinator,
and then argue that the same method also engenders total proportional
sharing with multiple coordinators per stream.
We first assume that requests from one stream are always processed
by one coordinator; different streams may or may not have different
coordinators. We will later extend this to the multiple coordinator
case. The performance goal, as before, is that the total amount of
service each client receives must be proportional to its weight.
As described in Section 3.1, the following delay function
for a request from stream  to brick to brick  represents the total cost
of requests sent to other bricks since the previous request to brick represents the total cost
of requests sent to other bricks since the previous request to brick
 . .
When this delay function is used with the distributed scheduling
framework defined by formulae (5-7),
we call the resulting algorithm TOTAL-DSFQ. The delay function
(7) is the total service cost of requests sent to
other bricks since the last request on the brick. Intuitively, it
implies that, if the brick is otherwise busy, a request should wait
an extra time corresponding to the aggregate service requirements of
the preceding requests from the same stream that were sent to other
bricks, normalized by the stream's weight.
Why TOTAL-DSFQ engenders proportional sharing of the total
service received by the streams can be explained using virtual
streams. According to the formulae
(5-7), TOTAL-DSFQ is exactly
equivalent to the architecture where coordinators send virtual
streams to the bricks and bricks are controlled by the standard SFQ.
This virtual stream contains all the requests in  , but the
requests that are not destined for , but the
requests that are not destined for  are served at are served at  in zero
time. Note that SFQ holds its fairness property even when the
service capacity varies [8]. In our case, the server
capacity (processing speed) varies from normal, if the request is to
be serviced on the same brick, to infinity if the request is virtual
and is to be serviced elsewhere. Intuitively, since the brick in zero
time. Note that SFQ holds its fairness property even when the
service capacity varies [8]. In our case, the server
capacity (processing speed) varies from normal, if the request is to
be serviced on the same brick, to infinity if the request is virtual
and is to be serviced elsewhere. Intuitively, since the brick  sees all the requests in
sees all the requests in  (and their costs) as a part of the
virtual stream, the SFQ scheduler at (and their costs) as a part of the
virtual stream, the SFQ scheduler at  factors in the costs of the
virtual requests served elsewhere in its scheduling, even though
they consume no service time at factors in the costs of the
virtual requests served elsewhere in its scheduling, even though
they consume no service time at  . This will lead to proportional
sharing of the total service. The theorem below formalizes the
bounds on unfairness using TOTAL-DSFQ. . This will lead to proportional
sharing of the total service. The theorem below formalizes the
bounds on unfairness using TOTAL-DSFQ.

The bound in Formula (8) has two parts. The first part
is similar to the bound of SFQ( ) in (4), the
unfairness due to server queues. The second part is new and
contributed by the distributed data. If the majority of requests of
stream ) in (4), the
unfairness due to server queues. The second part is new and
contributed by the distributed data. If the majority of requests of
stream  is processed at the backlogged server, the is processed at the backlogged server, the
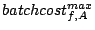 is small and the bound is tight. Otherwise,
if is small and the bound is tight. Otherwise,
if  gets a lot of service at other bricks, the bound is loose. gets a lot of service at other bricks, the bound is loose.
As we showed in Example 2, however, there are
situations in which total proportional sharing is impossible with
work conserving schedulers. In the theorem above, this corresponds
to the case with an infinite
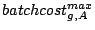 , and hence the
bound is infinite. To delineate more precisely when total
proportional sharing is possible under TOTAL-DSFQ, we
characterize when the total service rates of the streams are
proportional to their weights. The theorem below says that, under
TOTAL-DSFQ, if a set of streams are backlogged together at a
set of bricks, then either their normalized total service rates over
all bricks are equal (thus satisfying the total proportionality
requirement), or there are some streams whose normalized service
rates are equal and the remainder receive no service at the
backlogged bricks because they already receive more service
elsewhere. , and hence the
bound is infinite. To delineate more precisely when total
proportional sharing is possible under TOTAL-DSFQ, we
characterize when the total service rates of the streams are
proportional to their weights. The theorem below says that, under
TOTAL-DSFQ, if a set of streams are backlogged together at a
set of bricks, then either their normalized total service rates over
all bricks are equal (thus satisfying the total proportionality
requirement), or there are some streams whose normalized service
rates are equal and the remainder receive no service at the
backlogged bricks because they already receive more service
elsewhere.
Let
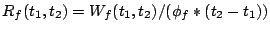 be the
normalized service rate of stream be the
normalized service rate of stream  in the duration in the duration  .
If the total service rates of streams are proportional to their
weights, then their normalized service rates should be equal as the
time interval .
If the total service rates of streams are proportional to their
weights, then their normalized service rates should be equal as the
time interval  goes to infinity. Suppose stream goes to infinity. Suppose stream  is
backlogged at a set of bricks, denoted as set is
backlogged at a set of bricks, denoted as set 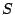 , its normalized
service rate at , its normalized
service rate at 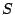 is denoted as is denoted as
 , and , and
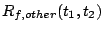 denotes its normalized total service rate at
all other bricks. denotes its normalized total service rate at
all other bricks.
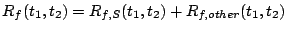 . We drop . We drop  hereafter as we always consider interval hereafter as we always consider interval
 . .
Theorem 3
Under TOTAL-DSFQ, if during 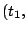 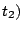 , streams , streams
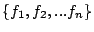 are backlogged at a set of bricks are backlogged at a set of bricks 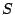 , in the order , in the order
  , as , as
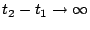 , either , either
 or or
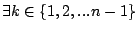 , such that , such that
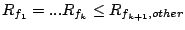 and and
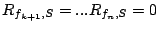 . .
The intuition of Theorem 3 is as follows. At
brick set 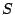 , let us first set , let us first set
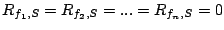 and try to allocate the
resources of and try to allocate the
resources of 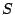 . Stream . Stream 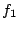 has the highest priority since its
delay is the smallest. Thus the SFQ scheduler will increase has the highest priority since its
delay is the smallest. Thus the SFQ scheduler will increase
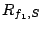 until until
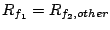 . Now both . Now both 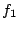 and and 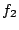 have the same total service rate and the same highest priority.
Brick set
have the same total service rate and the same highest priority.
Brick set 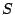 will then increase will then increase 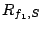 and and 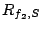 equally
until equally
until
 . In the end, either all the
streams have the same total service rate, or it is impossible to
balance all streams due to the limited service capacity of all
bricks in . In the end, either all the
streams have the same total service rate, or it is impossible to
balance all streams due to the limited service capacity of all
bricks in 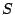 . In the latter case, the first . In the latter case, the first  streams have equal
total service rates, while the remaining streams are blocked for
service at streams have equal
total service rates, while the remaining streams are blocked for
service at 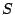 . Intuitively, this is the best we can do with a
work-conserving scheduler to equalize normalized service rates. . Intuitively, this is the best we can do with a
work-conserving scheduler to equalize normalized service rates.
In Section 3.4 we propose a modification to TOTAL-DSFQ that ensures no stream is blocked at any brick.
3.3.2 Single-client Multi-coordinator
So far we have assumed that a stream requests service through one
coordinator only. In many high-end systems, however, it is
preferable for high-load clients to distribute their requests among
multiple coordinators in order to balance the load on the
coordinators. In this section, we discuss the single-client
multi-coordinator setting and the corresponding fairness analysis
for TOTAL-DSFQ. In summary, we find that TOTAL-DSFQ
does engender total proportional sharing in this setting, except in
some unusual cases.
We motivate the analysis with an example. First, let us assume that
a stream accesses two coordinators in round-robin order and examine
the effect on the delay function (7) through the
example stream in Fig. 5. The result is
displayed in Fig. 7. Odd-numbered requests are
processed by the first coordinator and even-numbered requests are
processed by the second coordinator. With one coordinator, the three
requests to brick  have delay values 0, 2 and 0. With two
round-robin coordinators, the delay values of the two requests
dispatched by the first coordinator are now 0 and 1; the delay value
of the request dispatched by the second coordinator is 1. Thus,
although individual request may have delay value different from the
case of single coordinator, the total amount of delay remains the
same. This is because every virtual request (to other bricks)
is counted exactly once. have delay values 0, 2 and 0. With two
round-robin coordinators, the delay values of the two requests
dispatched by the first coordinator are now 0 and 1; the delay value
of the request dispatched by the second coordinator is 1. Thus,
although individual request may have delay value different from the
case of single coordinator, the total amount of delay remains the
same. This is because every virtual request (to other bricks)
is counted exactly once.
Figure 7:
Effect of multiple
coordinators under TOTAL-DSFQ. Delay value of an
individual request is different from
Fig. 5, but the total amount of delay
remains the same.
|
We formalize this result in Theorem 4 below,
which says, essentially, that streams backlogged at a brick receive
total proportional service so long as each stream uses a consistent
set of coordinators (i.e., the same set of coordinators for each
brick it accesses).
Formally, assume stream  sends requests through sends requests through 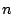 coordinators coordinators
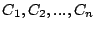 , and coordinator , and coordinator  receives a substream of receives a substream of
 denoted as denoted as 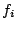 . With respect to brick . With respect to brick  , each substream , each substream
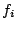 has its has its
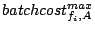 . Let us first assume that . Let us first assume that
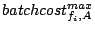 is finite for all substreams, i.e.,
requests to is finite for all substreams, i.e.,
requests to  are distributed among all coordinators. are distributed among all coordinators.
An anomalous case arises if a stream partitions the bricks into
disjoint subsets and accesses each partition through separate
coordinators. In this case, the requests served in one partition
will never be counted in the delay of any request to the other
partition, and the total service may no longer be proportional to
the weight. For example,
requests to 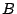 in Fig. 7 have smaller delay
values than the ones in Fig. 5. This case
is unlikely to occur with most load balancing schemes such as
round-robin or uniformly random selection of coordinators. Note that
the algorithm will still guarantee total proportional sharing if
different streams use separate coordinators. in Fig. 7 have smaller delay
values than the ones in Fig. 5. This case
is unlikely to occur with most load balancing schemes such as
round-robin or uniformly random selection of coordinators. Note that
the algorithm will still guarantee total proportional sharing if
different streams use separate coordinators.
More interestingly, selecting randomly among multiple coordinators
may smooth out the stream, and result in more uniform delay values.
For example, if
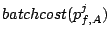 in the original stream is a sequence of
i.i.d. (independent, identically distributed) random variables with large variance such that in the original stream is a sequence of
i.i.d. (independent, identically distributed) random variables with large variance such that
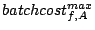 might be large, it is not difficult to show
that with independently random mapping of each request to a
coordinator, might be large, it is not difficult to show
that with independently random mapping of each request to a
coordinator,
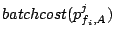 is also a sequence of i.i.d. random variables
with the same mean, but the variance decreases as number of
coordinators increases. This means that under random selection of
coordinators, while the average delay is still the same (thus
service rate is the same), the variance in the delay value is
reduced and therefore the unfairness bound is tighter. We test this
observation through an empirical study later. is also a sequence of i.i.d. random variables
with the same mean, but the variance decreases as number of
coordinators increases. This means that under random selection of
coordinators, while the average delay is still the same (thus
service rate is the same), the variance in the delay value is
reduced and therefore the unfairness bound is tighter. We test this
observation through an empirical study later.
3.4 Hybrid Proportional Sharing
Under TOTAL-DSFQ, Theorem 3 tells us that
a stream may be blocked at a brick if it gets too much service at
other bricks. This is not desirable in many cases. We would like to
guarantee a minimum service rate for each stream on every brick so
the client program can always make progress. Under the DSFQ
framework, i.e., formulae (5-6), this
means that the delay must be bounded, using a different delay
function than the one used in TOTAL-DSFQ. We next develop a
delay function that guarantees a minimum service share to backlogged
streams on each brick.
Let us assume that the weights assigned to streams are normalized,
i.e.
 and and
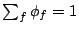 . Suppose that, in
addition to the weight . Suppose that, in
addition to the weight  , each stream , each stream  is assigned a
brick-minimum weight is assigned a
brick-minimum weight 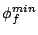 , corresponding to the minimum
service share per brick for the stream.3 We can then show that
the following delay function will guarantee the required minimum
service share on each brick for each stream.
2pt , corresponding to the minimum
service share per brick for the stream.3 We can then show that
the following delay function will guarantee the required minimum
service share on each brick for each stream.
2pt
We can see, for example, that setting
 yields a
delay of zero, and the algorithm then reduces to single brick
proportional sharing that guarantees minimum share yields a
delay of zero, and the algorithm then reduces to single brick
proportional sharing that guarantees minimum share  for
stream for
stream  , as expected. , as expected.
By combining delay function (11) with the delay
function (7) for TOTAL-DSFQ, we can achieve an
algorithm that approaches total proportional sharing while
guaranteeing a minimum service level for each stream per brick, as
follows.
2pt
The DSFQ algorithm using the delay function (12)
defines a new algorithm called HYBRID-DSFQ. Since the delay
under HYBRID-DSFQ is no greater than the delay in
(11), the service rate at every brick is no less
than the rate under (11), thus the minimum per
brick service share 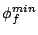 is still guaranteed. On the other
hand, if the amount of service a stream is still guaranteed. On the other
hand, if the amount of service a stream  receives on other bricks
between requests to brick receives on other bricks
between requests to brick  is lower than is lower than
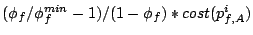 , the delay
function behaves similarly to equation (7), and hence
the sharing properties in this case should be similar to TOTAL-DSFQ, i.e., total proportional sharing. , the delay
function behaves similarly to equation (7), and hence
the sharing properties in this case should be similar to TOTAL-DSFQ, i.e., total proportional sharing.
Empirical evidence (in Section 4.3) indicates that
HYBRID-DSFQ works as expected for various workloads. However,
there are pathological workloads that can violate the total service
proportional sharing property. For example, if a stream using two
bricks knows its data layout, it can alternate bursts to one brick
and then the other. Under TOTAL-DSFQ, the first request in
each burst would have received a large delay, corresponding to the
service the stream had received on the other brick during the
preceding burst, but in HYBRID-DSFQ, the delay is truncated by
the minimum share term in the delay function. As a result, the
stream receives more service than its weight entitles it to. We
believe that this can be resolved by including more history in the
minimum share term, but the design and evaluation of such a delay
function is reserved to future work.
4 Experimental Evaluation
We evaluate our distributed proportional sharing algorithm in a
prototype FAB system [20], which consists of six bricks.
Each brick is an identically configured HP ProLiant DL380 server
with 2x 2.8GHz Xeon CPU, 1.5GB RAM, 2x Gigabit NIC, and an
integrated Smart Array 6i storage controller with four 18G
Ultral320, 15K rpm SCSI disks configured as RAID 0. All bricks are
running SUSE 9.2 Linux, kernel 2.6.8-24.10-smp. Each brick runs a
coordinator. To simplify performance comparisons, FAB caching was
turned off, except at the disk level.4
The workload generator consists of a number of clients (streams),
each running several Postmark [15] instances. We chose
Postmark as the workload generator because its independent,
randomly-distributed requests give us the flexibility to configure
different workloads for demonstration and for testing extreme cases.
Each Postmark thread has exactly one outstanding request in the
system at any time, accessing its isolated 256MB logical volume.
Unless otherwise specified, each volume resides on a single brick
and each thread generates random read/write requests with file sizes
from 1KB to 16KB. The number of transactions per thread is
sufficiently large so the thread is always active when it is on.
Other parameters of Postmark are set to the default values.
With our work-conserving schedulers, until a stream is backlogged,
its IO throughput increases as the number of threads increases. When
it is backlogged, on the other hand, the actual service amount
depends on the scheduling algorithm. To simplify calculation, we
target throughput (MB/sec) proportional sharing, and define the cost
of a request to be its size. Other cost functions such as IO/sec or
estimated disk service time could be used as well.
We first demonstrate the effect of TOTAL-DSFQ on two streams
reading from one brick. Stream  consistently has 30 Postmark
threads, while the number of Postmark threads for stream consistently has 30 Postmark
threads, while the number of Postmark threads for stream  is
increased from 0 to 20. The ratio of weights between is
increased from 0 to 20. The ratio of weights between  and and  is at
1:2. As the data is not distributed, the delay value is always zero
and this is essentially the same as SFQ( is at
1:2. As the data is not distributed, the delay value is always zero
and this is essentially the same as SFQ( ) [12]. ) [12].
Figure 8:
Proportional sharing on one brick.  : : =1:2; legend in (a) also applies to (b). =1:2; legend in (a) also applies to (b).
![\includegraphics[scale=.6 keepaspectratio=true]{test1a.eps}](test1a.png)
throughputs for two streams
![\includegraphics[scale=.6 keepaspectratio=true]{test1b.eps}](test1b.png)
latencies for two streams
|
Figure 8 shows the performance isolation between the
two clients. The throughput of stream  is increasing and its
latency is fixed until is increasing and its
latency is fixed until  acquires its proportional share at around 13
threads. After that, additional threads do not give any more
bandwidth but increase the latency. On the other hand, the throughput and
latency of stream acquires its proportional share at around 13
threads. After that, additional threads do not give any more
bandwidth but increase the latency. On the other hand, the throughput and
latency of stream  are both affected by are both affected by  . Once . Once  gets its
share, it has no further impact on gets its
share, it has no further impact on  . .
4.2 Total Service Proportional Sharing
Figure 9 demonstrates the effectiveness of TOTAL-DSFQ for two clients. The workload streams have access
patterns shown in Fig. 3. We arranged the data
layout so that each Postmark thread accesses only one brick. Stream
 and stream and stream  both have 30 threads on brick both have 30 threads on brick  throughout the
experiment, meanwhile, an increasing number of threads from throughout the
experiment, meanwhile, an increasing number of threads from  is
processed at brick is
processed at brick 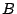 . Postmark allows us to specify the maximum
size of the random files generated, and we tested the algorithm with
workloads using two different maximum random file sizes, 16KB and
1MB. . Postmark allows us to specify the maximum
size of the random files generated, and we tested the algorithm with
workloads using two different maximum random file sizes, 16KB and
1MB.
Figure 9(a) shows that as the number of Postmark threads
from stream  directed to brick directed to brick 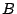 increases, its throughput from
brick increases, its throughput from
brick 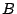 increases, and the share it receives at brick increases, and the share it receives at brick  decreases to compensate. The total throughputs received by streams
decreases to compensate. The total throughputs received by streams
 and and  stay roughly equal throughout. As the stream stay roughly equal throughout. As the stream  becomes
more unbalanced between bricks becomes
more unbalanced between bricks  and and 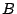 , however, the throughput
difference between streams , however, the throughput
difference between streams  and and  varies more. This can be
related to the fairness bound in Theorem 2: as the
imbalance increases, so does varies more. This can be
related to the fairness bound in Theorem 2: as the
imbalance increases, so does
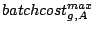 , and the bound
becomes a little looser. Figure 9(b) uses the same data
layout but with a different file size and weight ratio. As , and the bound
becomes a little looser. Figure 9(b) uses the same data
layout but with a different file size and weight ratio. As  gets
more service on gets
more service on  , its throughput rises on , its throughput rises on  from 0 to 175 MB/s.
As a result, the algorithm increases from 0 to 175 MB/s.
As a result, the algorithm increases  's share on the shared brick 's share on the shared brick
 , and its throughput rises from 40 MB/s to 75 MB/s, while , and its throughput rises from 40 MB/s to 75 MB/s, while  's
throughput on 's
throughput on  drops from 160 MB/s to 125 MB/s. In combination
the throughput of both streams increases, whole maintaining a 1:4
ratio. drops from 160 MB/s to 125 MB/s. In combination
the throughput of both streams increases, whole maintaining a 1:4
ratio.
Figure 9:
Total service proportional sharing.
 's data is on brick 's data is on brick  only; only;  has data on both bricks has data on both bricks  and and
 . As . As  gets more service on the bricks it does not share with gets more service on the bricks it does not share with
 , the algorithm increases , the algorithm increases  's share on the brick they do share;
thus the total throughputs of both streams
increase. 's share on the brick they do share;
thus the total throughputs of both streams
increase.
|
The experiment in Figure 10 has a data layout with
dependencies among requests. Each thread in  accesses all three
bricks, while stream accesses all three
bricks, while stream  accesses one brick only. The resource
allocation is balanced when stream accesses one brick only. The resource
allocation is balanced when stream  has three or more threads on
the shared brick. As has three or more threads on
the shared brick. As  has a RAID-0 data layout, the service rates
on the other two bricks are limited by the rate on the shared brick.
This experiment shows that TOTAL-DSFQ correctly controls the
total share in the case where requests on different bricks are
dependent. We note that in this example, the scheduler could
allocate more bandwidth on the shared brick to stream has a RAID-0 data layout, the service rates
on the other two bricks are limited by the rate on the shared brick.
This experiment shows that TOTAL-DSFQ correctly controls the
total share in the case where requests on different bricks are
dependent. We note that in this example, the scheduler could
allocate more bandwidth on the shared brick to stream  in order
to improve the total system throughput instead of maintaining
proportional service; however, this is not our goal. in order
to improve the total system throughput instead of maintaining
proportional service; however, this is not our goal.
Figure 10:
Total service proportional sharing with striped data.
 : : =1:1. =1:1.  has RAID-0 logical volume striping on
three bricks; has RAID-0 logical volume striping on
three bricks;  's data is on one brick only. 's data is on one brick only.
| |
Figure 11 is the result with multiple coordinators. The
data layouts and workloads are the same as in the experiment shown
in Figures 3 and 9: two bricks,
stream  accesses only one, and stream accesses only one, and stream  accesses both. The only
difference is that stream accesses both. The only
difference is that stream  accesses both bricks accesses both bricks  and and  through two or four coordinators in round-robin order.
through two or four coordinators in round-robin order.
Figure 11:
Total service proportional sharing with multi-coordinator,
 : : =1:1 =1:1
![\includegraphics[scale=.6 keepaspectratio=true]{test6a.eps}](test6a.png)
Two coordinators
![\includegraphics[scale=.6 keepaspectratio=true]{test6b.eps}](test6b.png)
Four coordinators
|
Using multiple coordinators still guarantees proportional sharing of
the total throughput. Furthermore, a comparison of
Fig. 9, 11(a), and 11(b)
indicates that as the number of coordinators increases, the match
between the total throughputs received by  and and  is closer,
i.e., the unfairness bound is tighter. This confirms the observation
in Section 3.3.2 that multiple coordinators may
smooth out a stream and reduce the unfairness. is closer,
i.e., the unfairness bound is tighter. This confirms the observation
in Section 3.3.2 that multiple coordinators may
smooth out a stream and reduce the unfairness.
4.3 Hybrid Proportional Sharing
The result of HYBRID-DSFQ is presented in
Fig. 12. The workload is the same as in the experiment
shown in Figures 3 and 9: stream  accesses brick
accesses brick  only, and stream only, and stream  accesses both accesses both  and and 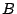 .
Streams .
Streams  and and  both have 20 Postmark threads on both have 20 Postmark threads on  , and , and  has an increasing number of Postmark threads on
has an increasing number of Postmark threads on 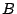 . We wish to give
stream . We wish to give
stream  a minimum share of a minimum share of 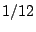 on brick on brick  when it is
backlogged.
This corresponds to when it is
backlogged.
This corresponds to
 ; based on
Equation 12, the delay function for ; based on
Equation 12, the delay function for  is
2pt is
2pt
Stream  is served on is served on  only and thus the delay is always zero. only and thus the delay is always zero.
Figure 12:
Two-brick experiment using HYBRID-DSFQ
![\includegraphics[scale=.6 keepaspectratio=true]{test5a.eps}](test5a.png)
throughputs with HYBRID-DSFQ
![\includegraphics[scale=.6 keepaspectratio=true]{test5b.eps}](test5b.png)
throughputs with HYBRID-DSFQ, two coordinators
|
With HYBRID-DSFQ, the algorithm reserves a minimum share for
each stream, and tries to make the total throughput as close as
possible without reallocating the reserved share. For this workload,
the service capacity of a brick is approximately 6MB/sec. We can see
in Fig. 12(a) that if the throughput of stream  on
brick on
brick 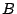 is less than 4MB, HYBRID-DSFQ can balance the total
throughputs of the two streams. As is less than 4MB, HYBRID-DSFQ can balance the total
throughputs of the two streams. As  receives more service on
brick receives more service on
brick  , the maximum delay part in HYBRID-DSFQ takes effect
and , the maximum delay part in HYBRID-DSFQ takes effect
and  gets its minimum share on brick gets its minimum share on brick  . The total throughputs
are no longer proportional to the assigned weights, but is still
reasonably close. Figure 12(b) repeats the experiment
with the streams selecting between two coordinators alternately; the
workload and data layout are otherwise identical to the single
coordinator experiment. The results indicate that HYBRID-DSFQ
works as designed with multiple coordinators too. . The total throughputs
are no longer proportional to the assigned weights, but is still
reasonably close. Figure 12(b) repeats the experiment
with the streams selecting between two coordinators alternately; the
workload and data layout are otherwise identical to the single
coordinator experiment. The results indicate that HYBRID-DSFQ
works as designed with multiple coordinators too.
First we investigate how TOTAL-DSFQ responds to sudden changes
in load by using an on/off fluctuating workload.
Figure 13 shows the total throughputs of the three
streams. Steams  and and  are continuously backlogged at brick are continuously backlogged at brick  and thus the total throughputs are the same. When stream
and thus the total throughputs are the same. When stream  is on,
some bandwidth on brick is on,
some bandwidth on brick  is occupied by is occupied by  ( ( 's service is not
proportional to its weight because of insufficient threads it has
and thus it is not backlogged on brick 's service is not
proportional to its weight because of insufficient threads it has
and thus it is not backlogged on brick  ). As a result, ). As a result,  's
throughput drops. Then 's
throughput drops. Then  's throughput follows closely after a
second, because part of 's throughput follows closely after a
second, because part of  's share on 's share on  is reallocated to is reallocated to  to
compensate its loss on to
compensate its loss on  . Detailed throughputs of . Detailed throughputs of  on each
brick is not shown on the picture. We also see that as the number of
threads (and hence the SFQ depth) increases, the sharp drop in on each
brick is not shown on the picture. We also see that as the number of
threads (and hence the SFQ depth) increases, the sharp drop in  's
throughput is more significant. These experimental observations
agree with the unfairness bounds on TOTAL-DSFQ shown in
Theorem 2, which increase with the queue depth. 's
throughput is more significant. These experimental observations
agree with the unfairness bounds on TOTAL-DSFQ shown in
Theorem 2, which increase with the queue depth.
Figure 13:
Fluctuating workloads. Streams  and and  both have the same number
of Postmark threads on brick both have the same number
of Postmark threads on brick  , and stream , and stream  has 10 additional
Postmark threads on brick has 10 additional
Postmark threads on brick  . In addition, there is a stream . In addition, there is a stream  that has 10 on/off threads on brick
that has 10 on/off threads on brick  that are repeatedly on
together for 10 seconds and then off for 10 seconds. The weights are
equal: that are repeatedly on
together for 10 seconds and then off for 10 seconds. The weights are
equal:
 . .
|
Next we examine the effectiveness of different proportional sharing
algorithms through sinusoidal workloads. Both streams  and and  access three bricks and overlap on one brick only, brick
access three bricks and overlap on one brick only, brick  . The
number of Postmark threads for each stream on each brick is
approximately a sinusoidal function with different frequency; see
Fig. 14(a). To demonstrate the effectiveness of
proportional sharing, we try to saturate brick . The
number of Postmark threads for each stream on each brick is
approximately a sinusoidal function with different frequency; see
Fig. 14(a). To demonstrate the effectiveness of
proportional sharing, we try to saturate brick  by setting the
number of threads on it to a sinusoidal function varying from 15 to
35, while thread numbers on other bricks take values from 0 to 10
(not shown in Fig. 14(a)). The result confirms several
hypotheses. Figure 14(b) is the result on a standard
FAB without any fair scheduling. Not surprisingly, the throughput
curves are similar to the thread curves in Fig. 14(a)
except when the server is saturated. Figure 14(c) shows
that single brick proportional sharing provides proportional service
on brick by setting the
number of threads on it to a sinusoidal function varying from 15 to
35, while thread numbers on other bricks take values from 0 to 10
(not shown in Fig. 14(a)). The result confirms several
hypotheses. Figure 14(b) is the result on a standard
FAB without any fair scheduling. Not surprisingly, the throughput
curves are similar to the thread curves in Fig. 14(a)
except when the server is saturated. Figure 14(c) shows
that single brick proportional sharing provides proportional service
on brick  but not necessarily the total service. At time 250, the
service on but not necessarily the total service. At time 250, the
service on  is not proportional because is not proportional because  has minimum threads
on has minimum threads
on  and is not backlogged. Figure 14(d) displays the
effect of total service proportional sharing. The total service
rates match well in general. At times around 65, 100, 150, and 210,
the rates deviate because one stream gets too much service on other
bricks, and its service on and is not backlogged. Figure 14(d) displays the
effect of total service proportional sharing. The total service
rates match well in general. At times around 65, 100, 150, and 210,
the rates deviate because one stream gets too much service on other
bricks, and its service on  drops close to zero. Thus TOTAL-DSFQ cannot balance the total service. At time around
230-260, the service rates are not close because stream drops close to zero. Thus TOTAL-DSFQ cannot balance the total service. At time around
230-260, the service rates are not close because stream  is not
backlogged, as was the case in Fig. 14(c). Finally,
Fig. 14(e) confirms the effect of hybrid proportional
sharing. Comparing with Fig. 14(d), HYBRID-DSFQ
proportional sharing guarantees minimum share when TOTAL-DSFQ
does not, at the cost of slightly greater deviation from total
proportional sharing during some periods. is not
backlogged, as was the case in Fig. 14(c). Finally,
Fig. 14(e) confirms the effect of hybrid proportional
sharing. Comparing with Fig. 14(d), HYBRID-DSFQ
proportional sharing guarantees minimum share when TOTAL-DSFQ
does not, at the cost of slightly greater deviation from total
proportional sharing during some periods.
Figure 14:
Sinusoidal workloads,  : : =1:1. The legend in (a) applies to all the figures. =1:1. The legend in (a) applies to all the figures.
![\includegraphics[scale=.6 keepaspectratio=true]{testsint.eps}](testsint.png)
Number of Postmark threads
![\includegraphics[scale=.6 keepaspectratio=true]{testsina.eps}](testsina.png)
Without any proportional sharing scheduling
![\includegraphics[scale=.6 keepaspectratio=true]{testsinc.eps}](testsinc.png)
Single brick proportional sharing
![\includegraphics[scale=.6 keepaspectratio=true]{testsinb.eps}](testsinb.png)
Total service proportional sharing
![\includegraphics[scale=.6 keepaspectratio=true]{testsind.eps}](testsind.png)
Hybrid proportional sharing
|
5 Conclusions
In this paper, we presented a proportional-service scheduling
framework suitable for use in a distributed storage system. We use
it to devise a distributed scheduler that enforces proportional
sharing of total service between streams to the degree possible
given the workloads. Enforcing proportional total service in a
distributed storage system is hard because different clients can
access data from multiple storage nodes (bricks) using different,
and possibly multiple, access points (coordinators). Thus, there is
no single entity that knows the state of all the streams and the
service they have received. Our scheduler extends the
SFQ( ) [12] algorithm, which was designed as a centralized
scheduler. Our scheduler is fully distributed, adds very little
communication overhead, has low computational requirements, and is
work-conserving. We prove the fairness properties of this scheduler
analytically and also show experimental results from an
implementation on the FAB distributed storage system that illustrate
these properties. ) [12] algorithm, which was designed as a centralized
scheduler. Our scheduler is fully distributed, adds very little
communication overhead, has low computational requirements, and is
work-conserving. We prove the fairness properties of this scheduler
analytically and also show experimental results from an
implementation on the FAB distributed storage system that illustrate
these properties.
We also present examples of unbalanced workloads for which no
work-conserving scheduler can provide proportional sharing of the
total throughput, and attempting to come close can block some
clients on some bricks. We demonstrate a hybrid scheduler that
attempts to provide total proportional sharing where possible, while
guaranteeing a minimum share per brick for every client.
Experimental evidence indicates that it works well.
Our work leaves several issues open. First, we assumed that clients
using multiple coordinators load those coordinators equally or
randomly; while this is a reasonable assumption in most cases, there
may be cases when it does not hold -- for example, when some
coordinators have an affinity to data on particular bricks. Some
degree of communication between coordinators may be required in
order to provide total proportional sharing in this case. Second,
more work is needed to design and evaluate better hybrid delay
functions that can deal robustly with pathological workloads.
Finally, our algorithms are designed for enforcing proportional
service guarantees, but in many cases, requirements may be based
partially on absolute service levels, such as a specified minimum
throughput, or maximum response time. We plan to address how this
may be combined with proportional sharing in future work.
Antonio Hondroulis and Hernan Laffitte assisted with experimental
setup. Marcos Aguilera, Eric Anderson, Christos Karamanolis, Magnus
Karlsson, Kimberly Keeton, Terence Kelly, Mustafa Uysal, Alistair
Veitch and John Wilkes provided valuable comments. We also thank the
anonymous reviewers for their comments, and Carl Waldspurger for
shepherding the paper.
-
- 1
- J. L. Bruno, J. C. Brustoloni, E. Gabber, B. Ozden, and A. Silberschatz.
Disk scheduling with quality of service guarantees.
In Proceedings of the IEEE International Conference on Multimedia Computing and Systems (ICMCS), June 1999.
- 2
- D. D. Chambliss, G. A. Alvarez, P. Pandey, and D. Jadav.
Performance virtualization for large-scale storage systems.
In Proceedings of the 22nd International Symposium on Reliable Distributed Systems (SRDS). IEEE Computer Society, Oct. 2003.
- 3
- H. M. Chaskar and U. Madhow.
Fair scheduling with tunable latency: A round-robin approach.
Proceedings of the IEEE, 83(10):1374-96, 1995.
- 4
- A. Demers, S. Keshav, and S. Shenker.
Analysis and simulation of a fair queueing algorithm.
In SIGCOMM: Symposium proceedings on Communications architectures & protocols, Sept. 1989.
- 5
- Z. Dimitrijevic and R. Rangaswami.
Quality of service support for real-time storage systems.
In International IPSI-2003 Conference, Oct. 2003.
- 6
- B. Dragovic, K. Fraser, S. Hand, T. Harris, A. Ho, I. Pratt, A. Warfield, P. Barham, and R. Neugebauer.
Xen and the art of virtualization.
In Proceedings of the ACM Symposium on Operating Systems Principles, Oct. 2003.
- 7
- S. Frølund, A. Merchant, Y. Saito, S. Spence, and A. Veitch.
A decentralized algorithm for erasure-coded virtual disks.
In Int. Conf. on Dependable Systems and Networks, June 2004.
- 8
- P. Goyal, M. Vin, and H. Cheng.
Start-time fair queueing: A scheduling algorithm for integrated services packet switching networks.
ACM Transactions on Networking, 5(5):690-704, 1997.
- 9
- A. Gulati and P. Varman.
Lexicographic QoS scheduling for parallel I/O.
In Proceedings of the 17th ACM Symposium on Parallelism in Algorithms and Architectures, July 2005.
- 10
- J. L. Hellerstein, Y. Diao, S. Parekh, and D. M. Tilbury.
Feedback Control of Computing Systems.
Wiley-IEEE Press, 2004.
- 11
- L. Huang, G. Peng, and T. cker Chiueh.
Multi-dimensional storage virtualization.
In Proceedings of the International Conference on Measurement and Modeling of Computer Systems (SIGMETRICS), June 2004.
- 12
- W. Jin, J. S. Chase, and J. Kaur.
Interposed proportional sharing for a storage service utility.
In Proceedings of the International Conference on Measurement and Modeling of Computer Systems (SIGMETRICS), June 2004.
- 13
- V. Kanodia, C. Li, A. Sabharwal, B. Sadeghi, and E. Knightly.
Distributed priority scheduling and medium access in ad hoc networks.
Wireless Networks, 8(5):455-466, Nov. 2002.
- 14
- M. Karlsson, C. Karamanolis, and X. Zhu.
Triage: Performance isolation and differentiation for storage systems.
In Proceedings of the 12th International Workshop on Quality of Service (IWQoS). IEEE, June 2004.
- 15
- J. Katcher.
Postmark: A new file system benchmark.
Technical Report 3022, Network Appliance, Oct. 1997.
- 16
- E. K. Lee and C. A. Thekkath.
Petal: Distributed virtual disks.
In Proceedings of ASPLOS. ACM, Oct. 1996.
- 17
- C. R. Lumb, A. Merchant, and G. A. Alvarez.
Façade: virtual storage devices with performance guarantees.
In Proceedings of the 2nd USENIX Conference on File and Storage Technologies (FAST), Mar. 2003.
- 18
- H. Luo, S. Lu, V. Bharghavan, J. Cheng, and G. Zhong.
A packet scheduling approach to QoS support in multihop wireless networks.
Mob. Netw. Appl., 9(3):193-206, 2004.
- 19
- A. K. Parekh and R. G. Gallager.
A generalized processor sharing approach to flow control in integrated services networks: The single node case.
IEEE/ACM Transactions on Networking, 1(3):344-357, 1993.
- 20
- Y. Saito, S. Frølund, A. Veitch, A. Merchant, and S. Spence.
Fab: Building distributed enterprise disk arrays from commodity components.
In Proceedings of ASPLOS. ACM, Oct. 2004.
- 21
- D. C. Stephens and H. Zhang.
Implementing distributed packet fair queueing in a scalable switch architecture.
In Proceedings of INFOCOM, Mar. 1998.
- 22
- M. Uysal, G. A. Alvarez, and A. Merchant.
A modular, analytical throughput model for modern disk arrays.
In Proc. of the 9th Intl. Symp. on Modeling, Analysis and Simulation on Computer and Telecommunications Systems (MASCOTS). IEEE, Aug. 2001.
- 23
- N. H. Vaidya, P. Bahl, and S. Gupta.
Distributed fair scheduling in a wireless lan.
In MobiCom: Proceedings of the 6th annual international conference on Mobile computing and networking, Aug. 2000.
- 24
- C. A. Waldspurger.
Memory resource management in VMware ESX server.
In Proceedings of the USENIX Symposium on Operating Systems Design and Implementation, Dec. 2002.
- 25
- M. Wang, K. Au, A. Ailamaki, A. Brockwell, C. Faloutsos, and G. R. Ganger.
Storage device performance prediction with cart models.
In Proceedings of the International Conference on Measurement and Modeling of Computer Systems (SIGMETRICS), June 2004.
- 26
- Y. Wang and A. Merchant.
Proportional service allocation in distributed storage systems.
Technical Report HPL-2006-184, HP Laboratories, Dec. 2006.
- 27
- W. Wilcke et al.
IBM intelligent bricks project--petabytes and beyond.
IBM Journal of Research and Development, 50(2/3):181-197, Mar. 2006.
- 28
- H. Zhang.
Service disciplines for guaranteed performance service in packet-switching networks.
Proceedings of the IEEE, 83(10):1374-96, 1995.
- 29
- J. Zhang, A. Sivasubramaniam, A. Riska, Q. Wang, and E. Riedel.
An interposed 2-level I/O scheduling framework for performance virtualization.
In Proceedings of the International Conference on Measurement and Modeling of Computer Systems (SIGMETRICS), June 2005.
- 30
- L. Zhang.
Virtualclock: A new traffic control algorithm for packet-switched networks.
ACM Transactions on Computer Systems, 9(2):101-124, 1991.
Footnotes
- ... Wang1
- This work was done during an internship at HP Laboratories.
- ... disk2
- If there are
multiple disks (the normal case),
 is the sum of the queue depths of the disks. is the sum of the queue depths of the disks.
- ... stream.3
- Setting the
brick-minimum weights requires knowledge of the client data layouts.
We do not discuss this further in the paper.
- ... level.4
- Our algorithms focus
on the management of storage bandwidth; a full exploration of the
management of multiple resources (including cache and network
bandwidth) to control end-to-end performance is beyond the scope of
this paper.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Yin Wang
2006-12-18
|
