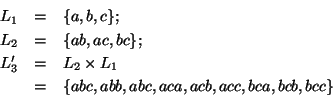C-Miner: Mining Block Correlations
in Storage Systems
Zhenmin Li, Zhifeng Chen, Sudarshan M.
Srinivasan and Yuanyuan Zhou
Department of Computer Science
University of Illinois at
Urbana-Champaign, Urbana, IL 61801
{zli4,zchen9,smsriniv,yyzhou}@cs.uiuc.edu
Abstract:
Block correlations are common semantic patterns in storage systems. These
correlations can be exploited for improving the effectiveness of storage
caching, prefetching, data layout and disk scheduling. Unfortunately,
information about block correlations is not available at the storage system
level. Previous approaches for discovering file correlations in file systems do
not scale well enough to be used for discovering block correlations in storage
systems. In this paper, we propose C-Miner, an algorithm which uses a
data mining technique called frequent sequence mining to discover block
correlations in storage systems. C-Miner runs reasonably fast with
feasible space requirement, indicating that it is a practical tool for
dynamically inferring correlations in a storage system. Moreover, we have also
evaluated the benefits of block correlation-directed prefetching and data layout
through experiments. Our results using real system workloads show that
correlation-directed prefetching and data layout can reduce average I/O response
time by 12-25% compared to the base case, and 7-20% compared to the commonly
used sequential prefetching scheme.
Introduction
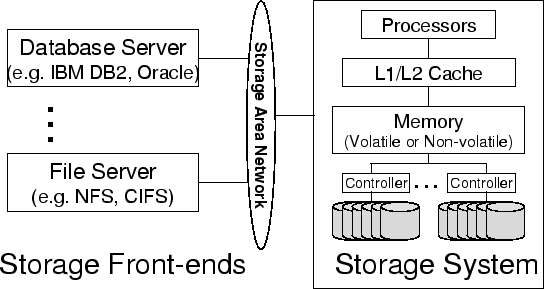
To satisfy the growing demand for storage, modern storage systems are becoming
increasingly intelligent. For example, the IBM Storage Tank system [29] consists of a cluster of storage nodes
connected using a storage area network. Each storage node includes processors,
memory and disk arrays. An EMC Symmetric server contains up to eighty 333
MHz microprocessors with up to 4-64 GB of memory as the storage cache [19]. Figure 1
gives an example architecture of modern storage systems. Many storage systems
also provide virtualization capabilities to hide disk layout and configurations
from storage clients [36,3]. Unfortunately, it is not an easy
task to exploit the increasing intelligence in storage systems. One primary
reason is the narrow I/O interface between storage applications and storage
systems. In such a simple interface, storage applications perform only block
read or write operations without any indication of access patterns or data
semantics. As a result, storage systems can only manage data at the block level
without knowing any semantic information such as the semantic correlations
between blocks. Therefore, much previous work had to rely on simple patterns
such as temporal locality, sequentiality, and loop references to improve storage
system performance, without fully exploiting its intelligence. This motivates a
more powerful analysis tool to discover more complex patterns, especially
semantic patterns, in storage systems.
Figure 1: Example of modern storage
architecture
 |
Block correlations are common semantic patterns in storage systems. Many blocks
are correlated by semantics. For example, in a database that uses index trees
such as B-trees to speed up query performance, a tree node is correlated to its
parent node and its ancestor nodes. Similarly, in a file server-backend storage
system, a file block is correlated to its inode block. Correlated blocks tend to
be accessed relatively close to each other in an access stream. Exploring these
correlations is very useful for improving the effectiveness of storage caching,
prefetching, data layout and disk scheduling. For example, at each access, a
storage system can prefetch correlated blocks into its storage cache so that
subsequent accesses to these blocks do not need to access disks, which is
several orders of magnitude slower than accessing directly from a storage cache.
As self-managing systems are becoming ever so important, capturing block
correlations would enhance the storage system's knowledge about its workloads, a
necessary step toward providing self-tuning capability. Unfortunately,
information about block correlations are unavailable at a storage system because
a storage system exports only block interfaces. Since databases or file systems
are typically provided by vendors different from those of storage systems, it is
quite difficult and complex to extend the block I/O interface to allow upper
levels to inform a storage system about block correlations. Recently,
Arpaci-Dusseau et al. proposed a very interesting approach called
semantically-smart disk systems (SDS) [54] by using a ``gray-box'' technology to
infer data structure and categorize data in storage systems. However, this
approach requires probing in the front-end and assumes that the front-ends
conform to the FFS-like file system layout. An alternative approach is to infer
block correlations fully transparently inside a storage system by only observing
access sequences. This approach does not require any probing from a front-end
and also makes no assumption about the type of the front-ends. Therefore, this
approach is more general and can be applied to storage systems with any
front-end file systems or database servers. Semantic distances [34,35] and probability graphs [24,25] are such ``black-box''
approaches. They are quite useful in discovering file correlations in file
systems (see section 2.3 for more
details). This paper proposes C-Miner, a method which applies a data
mining technique called frequent sequence mining to discover block
correlations in storage systems. Specifically, we have modified a recently
proposed data mining algorithm called CloSpan [66] to find block correlations in
several storage traces collected in real systems. To the best of our knowledge,
C-Miner is the first approach to infer block correlations involving
multiple blocks. Furthermore, C-Miner is more scalable and
space-efficient than previous approaches. It runs reasonably fast with
reasonable space overhead, indicating that it is a practical tool for
dynamically inferring correlations in a storage system. Moreover, we have also
evaluated the benefits of block correlation-directed prefetching and disk data
layout using the real system workloads. Compared to the base case, this scheme
reduces the average response time by 12% to 25%. Compared to the sequential
prefetching scheme, it also reduces the average response time by 7% to 20%. The
paper is organized as follows. In the next section, we briefly describe block
correlations, the benefits of exploiting block correlations, and approaches to
discover block correlations. In section 3,
we present our data mining method to discover block correlations. Section 4
discusses how to take advantage of block correlations in the storage cache for
prefetching and disk layout. Section 5
presents our experimental results. Section 6
discusses the related work and section 7
concludes the paper.
Block Correlations
What are Block Correlations?
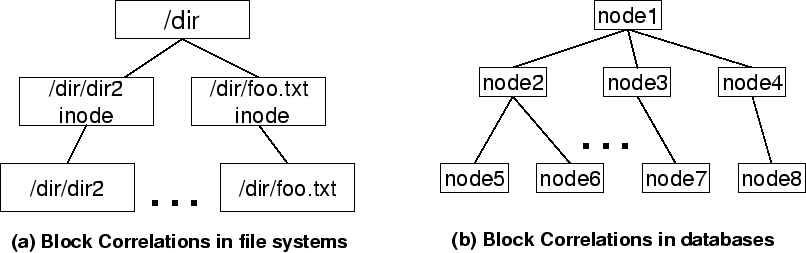
Block correlations commonly exist in storage systems. Two or more blocks are
correlated if they are ``linked'' together semantically. For example, Figure 2(a)
shows some block correlations in a storage system which manages data for an NFS
server. In this example, a directory block ``/dir'' is directly correlated to
the inode block of ``/dir/foo.txt'', which is also directly correlated to the
file block of ``/dir/foo.txt''. Besides direct correlations, blocks can also be
correlated indirectly through another block. For example, the directory block
``/dir'' is indirectly correlated to the file block of ``/dir/foo.txt''. Figure 2(b)
shows block correlations in a database-backend storage system. Databases
commonly use a tree structure such as B-tree or B*-tree to store data. In such a
data structure, a node is directly correlated to its parent and children, and
also indirectly correlated to its ancestor and descendant nodes.
Figure 2: Examples of block
correlations
 |
Unlike other access patterns such as temporal locality, block correlations are
inherent in the data managed by a storage system. Access patterns such as
temporal locality or sequentiality depend on workloads and can therefore change
dynamically, whereas block correlations are relatively more stable and do not
depend on workloads, but rather on data semantics. When block semantics are
changed (for example, a block is reallocated to store other data), some block
correlations may be affected. In general, block semantics are more stable than
workloads, especially in systems that do not have very bursty deletion and
insertion operations that can significantly change block semantics. As we will
show in section 5.3, block correlations
can remain stable for several days in file systems. Correlated blocks are
usually accessed very close to each other. This is because most storage
front-ends (database servers or file servers) usually follow semantic ``links''
to access blocks. For example, an NFS server needs to access an inode block
before accessing a file block. Similarly, a database server first needs to
access a parent node before accessing its children. Due to the interleaving of
requests and transactions, these I/O requests may not be always consecutive in
the access stream received by a storage system. But they should be relatively
close within a short distance from each other. Spatial locality is a simple case
of block correlations. An access stream exhibits spatial locality if, after a
block is accessed, other blocks that are near it are likely to be accessed in
the near future. This is based on the observation that a block is usually
semantically correlated to its neighboring blocks. For example, if a file's
blocks are allocated in disks consecutively, these blocks are correlated to each
other. Therefore, in some workloads, these blocks are likely accessed one after
another. However, many correlations are more complex than spatial locality. For
example, in an NFS server, an inode block is usually allocated separately from
its file blocks and a directory block is allocated separately from the inode
blocks of the files in this directory. Therefore, although accesses to these
correlated blocks are close to each other in the access stream, they do not
exhibit good spatial locality because these blocks are far away from each other
in the disk layout and even on different disks. In some cases, a block
correlation may involve more than two blocks. For example, a three-block
correlation might be: if
both 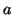 and
and 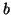 are accessed recently,
are accessed recently, 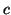 is very likely to be accessed in a short period of time. Basically,
is very likely to be accessed in a short period of time. Basically, 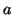 and
and 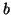 are correlated to
are correlated to 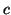 , but
, but 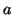 or
or 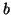 alone may not be correlated to
alone may not be correlated to
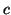 . To give a real instance of this multi-block correlation, let us
consider a B* tree which also links all the leaf nodes together.
. To give a real instance of this multi-block correlation, let us
consider a B* tree which also links all the leaf nodes together. 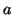 ,
,
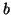 and
and 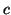 are all leaf nodes. If
are all leaf nodes. If 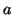 is accessed, the system cannot predict that
is accessed, the system cannot predict that 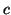 is going to be accessed soon. However, if
is going to be accessed soon. However, if 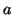 and
and 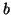 are accessed one after another, it is likely that
are accessed one after another, it is likely that 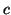 will be accessed soon because it is likely that the front-end is
doing a sequence scan of all the leaf nodes, which is very common in
decision-support system (DSS) workloads [7,68].
Block correlations can be exploited to improve storage system performance.
First, correlations can be used to direct prefetching. For example, if a strong
correlation exists between blocks
will be accessed soon because it is likely that the front-end is
doing a sequence scan of all the leaf nodes, which is very common in
decision-support system (DSS) workloads [7,68].
Block correlations can be exploited to improve storage system performance.
First, correlations can be used to direct prefetching. For example, if a strong
correlation exists between blocks 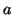 and
and
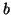 , these two blocks can be fetched together from disks whenever one of
them is accessed. The disk read-ahead optimization is an example of exploiting
the simple sequential block correlations by prefetching subsequent disk blocks
ahead of time. Several studies [55,14,31] have shown that using even
these simple sequential correlations can significantly improve the storage
system performance. Our results in section 5.5
demonstrate that prefetching based on block correlations can improve the
performance much better than such simple sequential prefetching in most cases. A
storage system can also lay out data in disks according to block correlations.
For example, a block can be collocated with its correlated blocks so that they
can be fetched together using just one disk access. This optimization can reduce
the number of disk seeks and rotations, which dominate the average disk access
latency. With correlation-directed disk layouts, the system only needs to pay a
one-time seek and rotational delay to get multiple blocks that are likely to be
accessed soon. Previous studies [52,54] have shown promising results in allocating
correlated file blocks on the same track to avoid track-switching costs.
Correlations can also be used to direct storage caching. For example, a storage
cache can ``promote'' or ``demote'' a block after its correlated block is
accessed or evicted. After an access to block
, these two blocks can be fetched together from disks whenever one of
them is accessed. The disk read-ahead optimization is an example of exploiting
the simple sequential block correlations by prefetching subsequent disk blocks
ahead of time. Several studies [55,14,31] have shown that using even
these simple sequential correlations can significantly improve the storage
system performance. Our results in section 5.5
demonstrate that prefetching based on block correlations can improve the
performance much better than such simple sequential prefetching in most cases. A
storage system can also lay out data in disks according to block correlations.
For example, a block can be collocated with its correlated blocks so that they
can be fetched together using just one disk access. This optimization can reduce
the number of disk seeks and rotations, which dominate the average disk access
latency. With correlation-directed disk layouts, the system only needs to pay a
one-time seek and rotational delay to get multiple blocks that are likely to be
accessed soon. Previous studies [52,54] have shown promising results in allocating
correlated file blocks on the same track to avoid track-switching costs.
Correlations can also be used to direct storage caching. For example, a storage
cache can ``promote'' or ``demote'' a block after its correlated block is
accessed or evicted. After an access to block
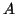 , blocks that are correlated to
, blocks that are correlated to 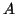 are likely to be accessed very soon. Therefore, a cache replacement
algorithm can specially ``mark'' these blocks to avoid being evicted. Similarly,
after a block
are likely to be accessed very soon. Therefore, a cache replacement
algorithm can specially ``mark'' these blocks to avoid being evicted. Similarly,
after a block 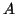 is evicted, blocks that are correlated to
is evicted, blocks that are correlated to 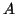 are not very likely to be accessed soon so it might be OK to also
evict these blocks in subsequent replacement decisions. The storage cache can
also give higher priority to those blocks that are correlated to many other
blocks. Therefore, for databases that use tree structures, it would achieve a
similar effect as the DBMIN cache replacement algorithm that is specially
designed for database workloads [15]. This algorithm gives higher priority to root
blocks or high-level index blocks to stay in a database buffer cache. Besides
performance, block correlations can also be used to improve storage system
security, reliability and energy-efficiency. For example, malicious clients
accesses the storage system in a very different pattern from the normal clients.
By catching abnormal block correlations in an access stream, the storage system
can detect such kind of malicious users. When a file block is archived to a
tertiary storage, its correlated blocks may also need to be backed up in order
to provide consistency. In addition, storage power management schemes can also
take advantage of block correlations by clustering correlated blocks in the same
disk so it is possible for other disks to transition into standby mode [11]. The experiments in this study focus on
demonstrating the benefits of exploiting block correlations in improving storage
system performance. The usages for security, reliability and energy-efficiency
remain as our future work.
are not very likely to be accessed soon so it might be OK to also
evict these blocks in subsequent replacement decisions. The storage cache can
also give higher priority to those blocks that are correlated to many other
blocks. Therefore, for databases that use tree structures, it would achieve a
similar effect as the DBMIN cache replacement algorithm that is specially
designed for database workloads [15]. This algorithm gives higher priority to root
blocks or high-level index blocks to stay in a database buffer cache. Besides
performance, block correlations can also be used to improve storage system
security, reliability and energy-efficiency. For example, malicious clients
accesses the storage system in a very different pattern from the normal clients.
By catching abnormal block correlations in an access stream, the storage system
can detect such kind of malicious users. When a file block is archived to a
tertiary storage, its correlated blocks may also need to be backed up in order
to provide consistency. In addition, storage power management schemes can also
take advantage of block correlations by clustering correlated blocks in the same
disk so it is possible for other disks to transition into standby mode [11]. The experiments in this study focus on
demonstrating the benefits of exploiting block correlations in improving storage
system performance. The usages for security, reliability and energy-efficiency
remain as our future work.
Obtaining Block Correlations
There can be three possible approaches to obtain block correlations in storage
systems. These approaches trade transparency and generality for accuracy at
different degrees. The ``black box'' approach is most transparent and general
because it infers block correlations without any assumption or modification to
storage front-ends. The ``gray box'' approach does not need modifications to
front-end software but makes certain assumptions about front-ends and also
requires probing from front-ends. The ``white box'' approach completely relies
on front-ends to provide information and therefore has the most accurate
information but is least transparent.
infer block correlations completely inside a storage system, without any
assumption on the storage front-ends. One commonly used method of this approach
is to infer block correlations based on accesses. The observation is that
correlated blocks are usually accessed relatively close to each other.
Therefore, if two blocks are almost always accessed together within a short
access distance, it is very likely that these two blocks are correlated to each
other. In other words, it is possible to automatically infer block correlations
in a storage system by dynamically analyzing the access stream. In the field of
networked or mobile file systems, researchers have proposed semantic distance
(SD) [34,35] or probability graphs [24,25] to capture file correlations in
file systems. The main idea is to use a graph to record the number of times two
items are accessed within a specified access distance. In an SD graph, a node
represents an accessed item 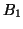 with edges linking to other items. The weight of each edge
with edges linking to other items. The weight of each edge 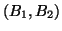 is the number of times that
is the number of times that 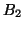 is accessed within the specified lookahead window of
is accessed within the specified lookahead window of 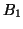 's access. So if the weight for an edge is large, the corresponding
items are probably correlated. The algorithm to build the SD graph from an
access stream works like this: Suppose the specified lookahead window size is
100, i.e., accesses that are less than 100 accesses apart are considered to be
``close'' accesses. Initially the probability graph is empty. The algorithm
processes each access one after another. The algorithm always keeps track of the
items of most recent 100 accesses in the current sliding window. When an item
's access. So if the weight for an edge is large, the corresponding
items are probably correlated. The algorithm to build the SD graph from an
access stream works like this: Suppose the specified lookahead window size is
100, i.e., accesses that are less than 100 accesses apart are considered to be
``close'' accesses. Initially the probability graph is empty. The algorithm
processes each access one after another. The algorithm always keeps track of the
items of most recent 100 accesses in the current sliding window. When an item 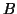 is accessed, it adds node
is accessed, it adds node
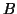 into the graph if it is not in the graph yet. It also increments the
weight of the edge
into the graph if it is not in the graph yet. It also increments the
weight of the edge 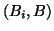 for any
for any 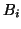 accessed during the current window. If such an edge is not in the
graph, it adds this edge and sets the initial weight to be 1. After the entire
access stream is processed, the algorithm rescans the SD graph and only records
those correlations with weights larger than a given threshold. Even though
probability graphs or SD graphs work well for inferring file correlations in a
file system, they, unfortunately, are not practical for inferring block
correlations in storage systems because of two reasons. (1) Scalability
problem: a semantic distance graph requires one node to represent each
accessed item and also one edge to capture each non-zero-weight correlation.
When the system has a huge number of items as in a storage system, an SD graph
is too big to be practical. For instance, if we assume the specified window size
is 100, it may require more than 100 edges associated with each node. Therefore,
one node would occupy at least
accessed during the current window. If such an edge is not in the
graph, it adds this edge and sets the initial weight to be 1. After the entire
access stream is processed, the algorithm rescans the SD graph and only records
those correlations with weights larger than a given threshold. Even though
probability graphs or SD graphs work well for inferring file correlations in a
file system, they, unfortunately, are not practical for inferring block
correlations in storage systems because of two reasons. (1) Scalability
problem: a semantic distance graph requires one node to represent each
accessed item and also one edge to capture each non-zero-weight correlation.
When the system has a huge number of items as in a storage system, an SD graph
is too big to be practical. For instance, if we assume the specified window size
is 100, it may require more than 100 edges associated with each node. Therefore,
one node would occupy at least
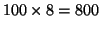 (assuming each edge requires 8 bytes to store the
weight and the disk block number of
(assuming each edge requires 8 bytes to store the
weight and the disk block number of 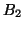 ). For a small storage system with only 80 GB and a block size of 8
KB, the probability graph would occupy 8 GB, 10% of the storage capacity.
Besides space overheads, building and searching such a large graph would also
take a significantly large amount of time. (2) Multi-block correlation
problem: these graphs cannot represent correlations that involve more than
two blocks. For example, the block correlations described at the end of the
Section 2.1 cannot be conveniently represented
in a semantic distance graph. Therefore, these techniques can lose some
important block correlations. In this paper, we present a practical black box
approach that uses a data mining method to automatically infer both dual-block
and multi-block correlations in storage systems. In Section 3,
we describe our approach in detail.
). For a small storage system with only 80 GB and a block size of 8
KB, the probability graph would occupy 8 GB, 10% of the storage capacity.
Besides space overheads, building and searching such a large graph would also
take a significantly large amount of time. (2) Multi-block correlation
problem: these graphs cannot represent correlations that involve more than
two blocks. For example, the block correlations described at the end of the
Section 2.1 cannot be conveniently represented
in a semantic distance graph. Therefore, these techniques can lose some
important block correlations. In this paper, we present a practical black box
approach that uses a data mining method to automatically infer both dual-block
and multi-block correlations in storage systems. In Section 3,
we describe our approach in detail.
are investigated by Arpaci-Dusseau et al in [5]. They
developed three gray-box information and control layers between a client and the
OS, and combined algorithmic knowledge, observations and inferences to collect
information. The gray-box idea has been explored by Sivathanu et al in storage
systems to automatically obtain file-system knowledge [54]. The main idea is to probe from a storage
front-end by performing some standard operations and then observing the
triggered I/O accesses to the storage system. It works very well for file
systems that conform to FFS-like structure (if the front-end security is not a
concern). The advantage of this approach is that it does not require any
modification to the storage front-end software. The tradeoff is that it requires
the front-end to conform to specific disk layouts such as FFS-like structure.
rely on storage front-ends to directly pass semantic information to obtain
block correlations in a storage system. For example, the storage I/O interface
can be modified using a higher-level, object-like interface [23] so that correlations can be easily expressed
using the object interface. The advantage with this approach is that it can
obtain very accurate information about block correlations from storage
front-ends. However, it requires modifying storage front-end software, some of
which, such as database servers, are too large to be easily ported to
object-based storage interface.
Mining for Block Correlations
Data mining, also known as knowledge discovery in databases (KDD), has developed
quickly in recent years due to the wide availability of voluminous data and the
imminent need for extracting useful information and knowledge from them.
Traditional methods of data analysis dependent on human handling cannot scale
well to huge sizes of data sets. In this section, we first introduce some
fundamental data mining concepts and analysis methods used in our paper and then
describe C-Miner, our algorithm for inferring block correlations in
storage systems.
Frequent Sequence Mining
Different patterns can be discovered by different data mining techniques,
including association analysis, classification and prediction, cluster analysis,
outlier analysis, and evolution analysis [27]. Among these techniques, association
analysis can help discover correlations between two or more sets of events or
attributes. Suppose there exists a strong association between events 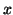 and
and 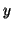 , it means that if event
, it means that if event 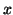 happens, event
happens, event
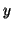 is also very likely to happen. We use the association rule
is also very likely to happen. We use the association rule
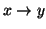 to describe such a correlation between these two events.
Frequent sequence mining is one type of association analysis to discover
frequent subsequences in a sequence database [1]. A subsequence is considered
frequent when it occurs in at least a specified number of sequences
(called min_support) in the sequence database. A subsequence is not
necessarily contiguous in an original sequence. For example, a sequence database
to describe such a correlation between these two events.
Frequent sequence mining is one type of association analysis to discover
frequent subsequences in a sequence database [1]. A subsequence is considered
frequent when it occurs in at least a specified number of sequences
(called min_support) in the sequence database. A subsequence is not
necessarily contiguous in an original sequence. For example, a sequence database 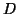 has five sequences:
has five sequences:
The number of occurrences of subsequence 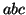 is 4. We denote the number of occurrences of a subsequence as its
is 4. We denote the number of occurrences of a subsequence as its 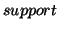 . Obviously, the smaller
. Obviously, the smaller 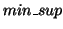 is, the more frequent subsequences the database contains. In
the above example, if
is, the more frequent subsequences the database contains. In
the above example, if 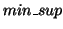 is specified as 5, only the subsequence
is specified as 5, only the subsequence 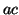 is frequent; if
is frequent; if 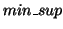 is specified as 4, the frequent subsequences are
is specified as 4, the frequent subsequences are
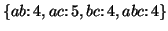 , where the numbers are the supports of the subsequences.
Frequent sequence mining is an active research topic in data mining [67,46,6] with broad applications,
such as mining motifs in DNA sequences, analysis of customer shopping sequences
etc. To the best of our knowledge, our study is the first one that uses frequent
sequence mining to discover patterns in storage systems.
C-Miner is based on a recently proposed frequent sequence mining
algorithm called CloSpan (Closed Sequential Pattern mining)[66]. The main idea of CloSpan is to
find only closed frequent subsequences. A closed sequence is a
subsequence whose support is different from that of its super-sequences. In the
above example, subsequence
, where the numbers are the supports of the subsequences.
Frequent sequence mining is an active research topic in data mining [67,46,6] with broad applications,
such as mining motifs in DNA sequences, analysis of customer shopping sequences
etc. To the best of our knowledge, our study is the first one that uses frequent
sequence mining to discover patterns in storage systems.
C-Miner is based on a recently proposed frequent sequence mining
algorithm called CloSpan (Closed Sequential Pattern mining)[66]. The main idea of CloSpan is to
find only closed frequent subsequences. A closed sequence is a
subsequence whose support is different from that of its super-sequences. In the
above example, subsequence 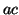 is closed because its support is 5, and the support of any one of
its super-sequences (for example,
is closed because its support is 5, and the support of any one of
its super-sequences (for example, 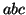 and
and 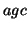 , etc.) is no more than 4; on the other hand, subsequence
, etc.) is no more than 4; on the other hand, subsequence 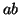 is not closed because its support is the same as that of one of its
super-sequences,
is not closed because its support is the same as that of one of its
super-sequences, 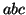 . CloSpan only produces the closed frequent subsequences rather
than all frequent subsequences since any non-closed subsequences can be
indicated by their super-sequences with the same support. In the above example,
the frequent subsequences are
. CloSpan only produces the closed frequent subsequences rather
than all frequent subsequences since any non-closed subsequences can be
indicated by their super-sequences with the same support. In the above example,
the frequent subsequences are
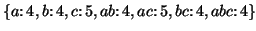 , but we
only need to produce the closed subsequences
, but we
only need to produce the closed subsequences
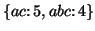 . This feature significantly reduces the number of patterns
generated, especially for long frequent subsequences. More details can be found
in [46,66].
. This feature significantly reduces the number of patterns
generated, especially for long frequent subsequences. More details can be found
in [46,66].
C-Miner: Our Mining Algorithm
Frequent sequence mining is a good candidate for inferring block correlations in
storage systems. One can map a block to an item, and an access sequence to a
sequence in the sequence database. Using frequent sequence mining, we can obtain
all the frequent subsequences in an access stream. A frequent subsequence
indicates that the involved blocks are frequently accessed together. In other
words, frequent subsequences are good indications of block correlations in a
storage system. One limitation with the basic mining algorithm is that it does
not consider the gap of a frequent subsequence. If a frequent sequence contains
two accesses that are very far from each other in terms of access time, such a
correlation is not interesting for our application. From the system's point of
view, it is much more interesting to consider frequent access subsequences that
are not far apart. For example, if a frequent subsequence 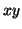 always appears in the original sequence with a distance of more
than 1000 accesses, it is not a very interesting pattern because it is hard for
storage systems to exploit it. Further, such correlations are generally less
accurate. To address this issue, C-Miner restricts access distances. In
order to describe how far apart two accesses are in the access stream, the
access distance between them is denoted as
always appears in the original sequence with a distance of more
than 1000 accesses, it is not a very interesting pattern because it is hard for
storage systems to exploit it. Further, such correlations are generally less
accurate. To address this issue, C-Miner restricts access distances. In
order to describe how far apart two accesses are in the access stream, the
access distance between them is denoted as 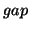 , measured by the number of accesses between these two accesses. We
specify a maximum distance threshold, denoted as
, measured by the number of accesses between these two accesses. We
specify a maximum distance threshold, denoted as 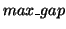 . All the uninteresting frequent sequences whose gaps are
larger than the threshold are filtered out. This is similar to the lookahead
window used in the semantic distance algorithms.
. All the uninteresting frequent sequences whose gaps are
larger than the threshold are filtered out. This is similar to the lookahead
window used in the semantic distance algorithms.
Existing frequent sequence mining algorithms including CloSpan are designed to
discover patterns for a sequence database rather than a single long sequence of
time-series information as in storage systems. To overcome this limitation,
C-Miner preprocesses the access sequence (that is, the history access
trace) by breaking it into fixed-size short sequences. The size of each short
sequence is called
cutting window size. There are two ways to cut the long access stream
into short sequences - overlapped cutting and non-overlapped cutting. The
overlapped cutting divides an entire access stream into many short sequences and
leaves some overlapped regions between any two consecutive sequences.
Non-overlapped cutting is straightforward; it simply splits the access stream
into access sequences of equal size. Figure 3
illustrates how these two methods cut the access stream 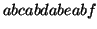 into short sequences with length of 4. Overlapped cutting
may increase the number of occurrences for some subsequences if it falls in the
overlapped region. In the example shown in Figure
3, using overlapped cutting results in 5 short sequences:
into short sequences with length of 4. Overlapped cutting
may increase the number of occurrences for some subsequences if it falls in the
overlapped region. In the example shown in Figure
3, using overlapped cutting results in 5 short sequences:
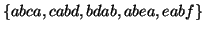 . The subsequences
. The subsequences 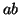 in
in 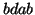 and
and  occurs only once in the original access stream, but now is
counted twice since the short sequences,
occurs only once in the original access stream, but now is
counted twice since the short sequences, 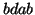 and
and 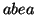 , overlap with each other. It is quite difficult to determine how
many redundant occurrences there are due to overlapping. Another drawback is
that the overlapped cutting generates more sequences than non-overlapped
cutting. Therefore it takes the mining algorithm a longer time to infer frequent
subsequences.
, overlap with each other. It is quite difficult to determine how
many redundant occurrences there are due to overlapping. Another drawback is
that the overlapped cutting generates more sequences than non-overlapped
cutting. Therefore it takes the mining algorithm a longer time to infer frequent
subsequences.
Figure 3: Overlapping and
non-overlapping window
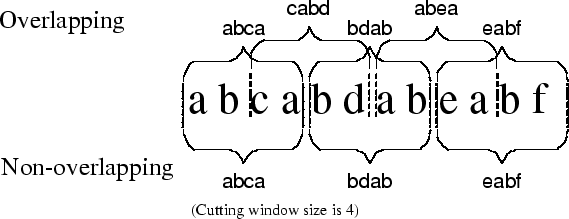 |
Using non-overlapped cutting can, however, lead to loss of frequent subsequences
that are split into two or more sequences, and therefore can decrease the
support values of some frequent subsequences because some of their occurrences
are split into two sequences. In the example shown in figure
3, the non-overlapped cutting results in only 3 sequences:
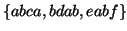 . The support for
. The support for 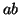 is 3, but the actual support in the original long sequence is 4.
The lost support is because the second occurrence is broken across two windows
and is therefore not counted. But we believe that the amount of lost information
in the non-overlapped cutting scheme is quite small, especially if the cutting
window size is relatively large. Since C-Miner restricts the access
distance of a frequent subsequence, only a few frequent subsequences may be
split across multiple windows. Suppose the instances of a frequent subsequence
are distributed uniformly in the access stream, the cutting windows size is
is 3, but the actual support in the original long sequence is 4.
The lost support is because the second occurrence is broken across two windows
and is therefore not counted. But we believe that the amount of lost information
in the non-overlapped cutting scheme is quite small, especially if the cutting
window size is relatively large. Since C-Miner restricts the access
distance of a frequent subsequence, only a few frequent subsequences may be
split across multiple windows. Suppose the instances of a frequent subsequence
are distributed uniformly in the access stream, the cutting windows size is 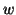 and the maximum access distance for frequent sequences is
and the maximum access distance for frequent sequences is 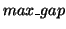 (
(
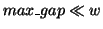 ). Then, in the worst case, the probability that an
instance of a frequent subsequence is split across two sequences is
). Then, in the worst case, the probability that an
instance of a frequent subsequence is split across two sequences is 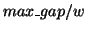 . For example, if the access distance is limited within
50, and the cutting window size is 500 accesses, the support value is lost by at
most 10% in the worst case. Therefore, most frequent subsequences would still be
considered frequent after non-overlapped cutting. Based on this analysis, we use
non-overlapped cutting in our experiments.
. For example, if the access distance is limited within
50, and the cutting window size is 500 accesses, the support value is lost by at
most 10% in the worst case. Therefore, most frequent subsequences would still be
considered frequent after non-overlapped cutting. Based on this analysis, we use
non-overlapped cutting in our experiments.
Once it has a database of short sequences, C-Miner
mines the database and produces frequent subsequences, which can then be used to
derive block correlations. C-Miner mainly consists of two stages: (1)
generating a candidate set of frequent subsequences that includes all the closed
frequent subsequences; and (2) pruning the non-closed subsequences from the
candidate set. In the first stage, C-Miner generates a candidate set of
frequent sequences using a depth-first search procedure. The following
pseudo-code shows the mining algorithm. In the algorithm, 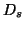 is a suffix database which contains all the maximum suffixes of
the sequences that contain the frequent subsequence
is a suffix database which contains all the maximum suffixes of
the sequences that contain the frequent subsequence  . For example, in the previous sequence database
. For example, in the previous sequence database 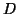 , the suffix database of frequent subsequences
, the suffix database of frequent subsequences 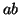 is
is
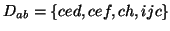 .
.
![\begin{boxedminipage}[thb]{3in}
\renewcommand {1.09}{1}\begin{tabbing}\hspace{...
...amond \alpha$\ means to concatenate $s$\ with $\alpha$.)}
\end{boxedminipage}](img50.png)
There are two main ideas in C-Miner to improve the mining efficiency.
The first idea is based on an obvious observation that if a sequence is
frequent, then all of its subsequences are frequent. For example, if a sequence 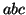 is frequent, all of its subsequences
is frequent, all of its subsequences
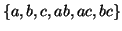 are frequent. Based on this observation, C-Miner recursively
produces a longer frequent subsequence by concatenating every frequent item to a
shorter frequent subsequence that has already been obtained in the previous
iterations. To better explain this idea, let us consider an example. In order to
get the set
are frequent. Based on this observation, C-Miner recursively
produces a longer frequent subsequence by concatenating every frequent item to a
shorter frequent subsequence that has already been obtained in the previous
iterations. To better explain this idea, let us consider an example. In order to
get the set 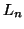 of frequent subsequences with length
of frequent subsequences with length 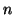 , we can join the set
, we can join the set 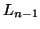 of frequent subsequences with length
of frequent subsequences with length 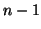 and the set
and the set 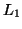 of frequent subsequences with length 1. For example, suppose we
have already computed
of frequent subsequences with length 1. For example, suppose we
have already computed 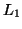 and
and 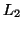 as shown below. In order to compute
as shown below. In order to compute 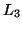 , we can first compute
, we can first compute 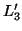 by concatenating a subsequence from
by concatenating a subsequence from 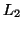 and an item from
and an item from 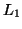 :
:
For greater efficiency, C-Miner does not join the sequences in set 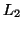 with all the items in
with all the items in 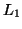 . Instead, each sequence in
. Instead, each sequence in 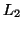 is concatenated with only the frequent items in its suffix
database. In our example, for the frequent sequence
is concatenated with only the frequent items in its suffix
database. In our example, for the frequent sequence 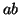 in
in 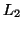 , its suffix database is
, its suffix database is
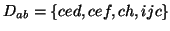 , and only
, and only 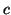 is the frequent item, so
is the frequent item, so 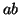 is only concatenated with
is only concatenated with 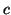 and then we get a longer sequence
and then we get a longer sequence 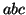 that belongs to
that belongs to 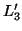 . The second idea is used for efficiently evaluating whether a
concatenated subsequence is frequent or not. It tries to avoid searching through
the whole database. Instead, it only checks with certain suffixes. In the above
example, for each sequence
. The second idea is used for efficiently evaluating whether a
concatenated subsequence is frequent or not. It tries to avoid searching through
the whole database. Instead, it only checks with certain suffixes. In the above
example, for each sequence 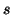 in
in
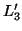 , C-Miner checks whether it is frequent or not by
searching the suffix database
, C-Miner checks whether it is frequent or not by
searching the suffix database 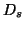 . If the number of its occurrences is greater than
. If the number of its occurrences is greater than 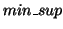 ,
, 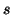 is added into
is added into 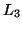 , which is the set of frequent subsequences of length 3.
C-Miner continues computing
, which is the set of frequent subsequences of length 3.
C-Miner continues computing 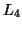 from
from 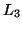 ,
,
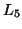 from
from 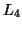 , and so on until no more subsequences can be added into the set of
frequent subsequences. In order to mine frequent sequences more efficiently,
C-Miner uses a technique that can efficiently determine whether there are
new closed patterns in search subspaces and stop checking those unpromising
subspaces. The basic idea is based on the following observation about a closed
sequence property. In the algorithm step 2, among all the sequences in
, and so on until no more subsequences can be added into the set of
frequent subsequences. In order to mine frequent sequences more efficiently,
C-Miner uses a technique that can efficiently determine whether there are
new closed patterns in search subspaces and stop checking those unpromising
subspaces. The basic idea is based on the following observation about a closed
sequence property. In the algorithm step 2, among all the sequences in 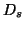 , if an item
, if an item 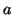 always occurs before another item
always occurs before another item
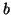 , C-Miner does not need to search any sequences with prefix
, C-Miner does not need to search any sequences with prefix 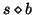 . The reason is that
. The reason is that
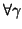 ,
,
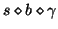 is not closed under this condition. Take the previous
sequence database as an example.
is not closed under this condition. Take the previous
sequence database as an example. 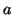 always occurs before
always occurs before
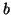 , so any subsequence with prefix
, so any subsequence with prefix 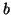 is not closed because it is also a subsequence with prefix
is not closed because it is also a subsequence with prefix 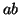 . Therefore, C-Miner does not need to search the frequent
sequences with prefix
. Therefore, C-Miner does not need to search the frequent
sequences with prefix 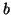 because all these frequent sequences are included in the frequent
sequences with prefix
because all these frequent sequences are included in the frequent
sequences with prefix
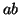 (e.g.,
(e.g., 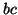 is included in
is included in 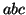 with support 4). Without searching these unpromising branches,
C-Miner can generate the candidate frequent sequences much more
efficiently.
with support 4). Without searching these unpromising branches,
C-Miner can generate the candidate frequent sequences much more
efficiently.
C-Miner produces frequent sequences that indicate block correlations,
but it does not directly generate the association rules in the form of
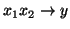 , which is much easier to use in storage systems.
In order to convert the frequent sequences into association rules, C-Miner
breaks each sequence into several rules. In order to limit the number of rules,
C-Miner constrains the length of a rule (the number of items on the left
side of a rule). For example, a frequent sequence
, which is much easier to use in storage systems.
In order to convert the frequent sequences into association rules, C-Miner
breaks each sequence into several rules. In order to limit the number of rules,
C-Miner constrains the length of a rule (the number of items on the left
side of a rule). For example, a frequent sequence 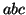 may be broken into the following set of rules with the same
support of
may be broken into the following set of rules with the same
support of
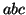 :
:
Different closed frequent sequences can be broken into the same rules. For
example, both 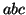 and
and 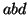 can be broken into the same rule
can be broken into the same rule
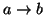 , but they may have different support values. The
support of a rule is the maximum support of all corresponding closed
frequent sequences.
, but they may have different support values. The
support of a rule is the maximum support of all corresponding closed
frequent sequences.
For each association rule, we also need to evaluate its accuracy . In order to
describe the reliability of a rule, we introduce 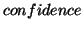 to measure the accuracy. For example, in the above example,
to measure the accuracy. For example, in the above example, 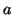 occurs 5 times, but
occurs 5 times, but 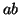 only occurs 4 times; this means that when
only occurs 4 times; this means that when 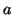 is accessed,
is accessed, 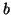 is also accessed in the near future (within
is also accessed in the near future (within
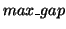 distance) with probability 80%. We call this probability the
confidence of the rule. When we use an association rule to predict future
accesses, its confidence indicates the expected prediction accuracy. Predictions
based on low-confidence rules are likely to be wrong and may not be able to
improve system performance. Worse still, they may hurt the system performance
due to overheads and side-effects. Because of this, we use confidence to
restrict rules and filter out those with low probability. The
distance) with probability 80%. We call this probability the
confidence of the rule. When we use an association rule to predict future
accesses, its confidence indicates the expected prediction accuracy. Predictions
based on low-confidence rules are likely to be wrong and may not be able to
improve system performance. Worse still, they may hurt the system performance
due to overheads and side-effects. Because of this, we use confidence to
restrict rules and filter out those with low probability. The 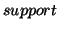 metric is different from
metric is different from 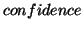 . For example, suppose
. For example, suppose 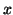 and
and 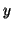 are accessed only once in the entire access stream and their
accesses are within the
are accessed only once in the entire access stream and their
accesses are within the 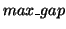 distance, the confidence of the association rule
distance, the confidence of the association rule
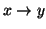 is 100% whereas its support is only 1. This rule is not very
interesting because it happens rarely. On the other hand, if a rule has high
support but very low confidence (e.g. 5%), it may not be useful because it is
too inaccurate to be used for prediction. Therefore, in practice, we usually
specify a minimum support threshold
is 100% whereas its support is only 1. This rule is not very
interesting because it happens rarely. On the other hand, if a rule has high
support but very low confidence (e.g. 5%), it may not be useful because it is
too inaccurate to be used for prediction. Therefore, in practice, we usually
specify a minimum support threshold 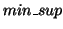 and a minimum confidence threshold
and a minimum confidence threshold 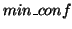 in order to filter low-quality association rules. We can
estimate the confidence for each rule in a simple way. Suppose we need to
compute the confidence for rule
in order to filter low-quality association rules. We can
estimate the confidence for each rule in a simple way. Suppose we need to
compute the confidence for rule
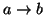 . Assume that the supports for
. Assume that the supports for 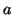 and
and 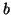 are
are 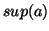 and
and 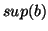 , respectively. Then the confidence for this rule is
, respectively. Then the confidence for this rule is
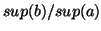 . Since both sides of each rule are frequent sequences
(or frequent items) and the supports for all the frequent sequences are already
obtained from post-processing,
. Since both sides of each rule are frequent sequences
(or frequent items) and the supports for all the frequent sequences are already
obtained from post-processing, 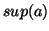 and
and 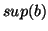 are ready to be used for computing the confidence of the rule.
Compared with other methods such as probability graphs or SD graphs,
C-Miner can find more correlations, especially those multi-block
correlations. From our experiments, we find that these multi-block correlations
are very useful for systems. For dual-block correlations, which can also be
inferred using previous approaches, C-Miner is more efficient. First,
C-Miner is much more space efficient than SD graphs because it does not
need to maintain the information for non-frequent sequences, whereas SD graphs
need to keep the information for every block during the graph building process.
Second, in terms of time complexity, C-Miner is the same (
are ready to be used for computing the confidence of the rule.
Compared with other methods such as probability graphs or SD graphs,
C-Miner can find more correlations, especially those multi-block
correlations. From our experiments, we find that these multi-block correlations
are very useful for systems. For dual-block correlations, which can also be
inferred using previous approaches, C-Miner is more efficient. First,
C-Miner is much more space efficient than SD graphs because it does not
need to maintain the information for non-frequent sequences, whereas SD graphs
need to keep the information for every block during the graph building process.
Second, in terms of time complexity, C-Miner is the same (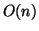 ) as SD. But in practice, since C-Miner has much smaller
memory footprint size, it is more efficient and can run in a cheap uniprocessor
machine with moderate memory size as used in our experiments. Other frequent
sequence mining algorithms such as PrefixSpan[46] can also find long frequent
sequences. Compared with these frequent sequence mining algorithms,
C-Miner is more efficient for discovering long frequent sequences
because it not only avoids searching the non-frequent sequences while generating
longer sequences, but also prunes all the unpromising searching branches
according to the closed sequence property as we have discussed. C-Miner
can outperform PrefixSpan by an order of magnitude for some datasets.
) as SD. But in practice, since C-Miner has much smaller
memory footprint size, it is more efficient and can run in a cheap uniprocessor
machine with moderate memory size as used in our experiments. Other frequent
sequence mining algorithms such as PrefixSpan[46] can also find long frequent
sequences. Compared with these frequent sequence mining algorithms,
C-Miner is more efficient for discovering long frequent sequences
because it not only avoids searching the non-frequent sequences while generating
longer sequences, but also prunes all the unpromising searching branches
according to the closed sequence property as we have discussed. C-Miner
can outperform PrefixSpan by an order of magnitude for some datasets.
Case Studies
The block correlation information inferred by C-Miner can be used to
prefetch more intelligently. Assume that C-Miner has obtained a block
correlation rule: if block 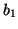 is accessed, block
is accessed, block 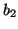 will also be accessed soon within a short distance ( of length
will also be accessed soon within a short distance ( of length 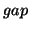 ) with a certain confidence (probability). Based on this rule, when
there is an access to block
) with a certain confidence (probability). Based on this rule, when
there is an access to block 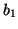 , we can prefetch block
, we can prefetch block 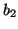 into the storage cache since it will probably be accessed soon.
Doing such can avoid future accesses to disks to fetch these blocks. Several
design issues should be considered while using block correlations for
prefetching. One of the most important issues is how to effectively share the
limited size cache for both caching and prefetching. If prefetching is too
aggressive, it can pollute the storage cache and may even degrade the cache hit
ratio and system performance. This problem has been investigated thoroughly by
previous work [9,10,45]. We therefore do not investigate
it further in our paper. In our simulation experiments, we simply fix the cache
size for prefetched data so it does not compete with non-prefetching requests.
However, the total cache size is fixed at the same value for the system with and
without prefetching in order to have a fair comparison. Another design issue is
the extra disk load imposed by prefetch requests. If the disk load is too heavy,
the disk utilization is close to 100%. In this case, prefetching can add
significant overheads to demand requests, canceling out the benefits of improved
storage cache hit ratio. Two methods can be used to alleviate this problem. The
first method is to differentiate between demand requests and prefetch requests
by using a priority-based disk scheduling scheme. In particular, the system uses
two waiting queues in the disk scheduler: critical and non-critical. All the
demand requests are issued to the critical queue, while the prefetch requests
are issued to the non-critical queue which has lower priority. The other method
is to throttle the prefetch requests to a disk if the disk is heavily utilized.
Since the correlation rules have different confidences, we can set a confidence
threshold to limit the number of rules that are used for prefetching. All the
rules with confidence lower than the threshold are ignored. Obviously, the
higher the confidence threshold is, the fewer the rules are used. Therefore, CDP
acts less aggressively. In order to adjust the threshold to make prefetching
adapt to the current disk workload, we keep track of the current load on each
disk. When the workload is too high, say the disk utilization is more than 80%,
we increase the confidence threshold for correlation rules that direct the
issuing of prefetch requests to this disk. Once the disk load drops down to a
low level, say the utilization is less than 50%, we decrease the confidence
threshold for correlation rules so that more rules can be used for prefetching.
By doing this, the overhead on disk bandwidth caused by prefetches is kept
within an acceptable range.
Block correlations can help lay out data on disks to improve performance. The
dominant latencies in a disk access are the seek time and rotation delay. So if
correlated blocks can be allocated together on a disk and can be fetched using
one disk access, the total seek time and rotation delay for all these blocks can
be reduced. Thereafter, both of the throughput and the response time can be
improved. But CDP is more effective than disk layout for improving response time
as shown in section 5.5. We can lay out
the blocks on disks based on block correlatoins like that: if we know a
correlation
into the storage cache since it will probably be accessed soon.
Doing such can avoid future accesses to disks to fetch these blocks. Several
design issues should be considered while using block correlations for
prefetching. One of the most important issues is how to effectively share the
limited size cache for both caching and prefetching. If prefetching is too
aggressive, it can pollute the storage cache and may even degrade the cache hit
ratio and system performance. This problem has been investigated thoroughly by
previous work [9,10,45]. We therefore do not investigate
it further in our paper. In our simulation experiments, we simply fix the cache
size for prefetched data so it does not compete with non-prefetching requests.
However, the total cache size is fixed at the same value for the system with and
without prefetching in order to have a fair comparison. Another design issue is
the extra disk load imposed by prefetch requests. If the disk load is too heavy,
the disk utilization is close to 100%. In this case, prefetching can add
significant overheads to demand requests, canceling out the benefits of improved
storage cache hit ratio. Two methods can be used to alleviate this problem. The
first method is to differentiate between demand requests and prefetch requests
by using a priority-based disk scheduling scheme. In particular, the system uses
two waiting queues in the disk scheduler: critical and non-critical. All the
demand requests are issued to the critical queue, while the prefetch requests
are issued to the non-critical queue which has lower priority. The other method
is to throttle the prefetch requests to a disk if the disk is heavily utilized.
Since the correlation rules have different confidences, we can set a confidence
threshold to limit the number of rules that are used for prefetching. All the
rules with confidence lower than the threshold are ignored. Obviously, the
higher the confidence threshold is, the fewer the rules are used. Therefore, CDP
acts less aggressively. In order to adjust the threshold to make prefetching
adapt to the current disk workload, we keep track of the current load on each
disk. When the workload is too high, say the disk utilization is more than 80%,
we increase the confidence threshold for correlation rules that direct the
issuing of prefetch requests to this disk. Once the disk load drops down to a
low level, say the utilization is less than 50%, we decrease the confidence
threshold for correlation rules so that more rules can be used for prefetching.
By doing this, the overhead on disk bandwidth caused by prefetches is kept
within an acceptable range.
Block correlations can help lay out data on disks to improve performance. The
dominant latencies in a disk access are the seek time and rotation delay. So if
correlated blocks can be allocated together on a disk and can be fetched using
one disk access, the total seek time and rotation delay for all these blocks can
be reduced. Thereafter, both of the throughput and the response time can be
improved. But CDP is more effective than disk layout for improving response time
as shown in section 5.5. We can lay out
the blocks on disks based on block correlatoins like that: if we know a
correlation 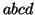 from C-Miner, we can try to allocate them contiguously
in a disk. Whenever any one of these blocks is read, all four blocks are fetched
together into the storage cache using one disk access. Since some blocks may
appear in several patterns, we allocate the block based on the rules with
highest support value. One of the main design issues is how to maintain the
directory information and reorganize data without an impact on the foreground
workload. After reorganizing disk layouts, we need to map logical block numbers
to new physical block numbers. The mapping table might become very large. Some
previous work has studied these issues and shown that disk layout reorganization
is feasible to implement [50]. They proposed a
two-tiered software architecture to combine multiple disk layout heuristics so
that it adapts to different environments. Block correlation-directed disk layout
can be one of the heuristics in their framework. Due to space limitation, we do
not discuss this issue further.
from C-Miner, we can try to allocate them contiguously
in a disk. Whenever any one of these blocks is read, all four blocks are fetched
together into the storage cache using one disk access. Since some blocks may
appear in several patterns, we allocate the block based on the rules with
highest support value. One of the main design issues is how to maintain the
directory information and reorganize data without an impact on the foreground
workload. After reorganizing disk layouts, we need to map logical block numbers
to new physical block numbers. The mapping table might become very large. Some
previous work has studied these issues and shown that disk layout reorganization
is feasible to implement [50]. They proposed a
two-tiered software architecture to combine multiple disk layout heuristics so
that it adapts to different environments. Block correlation-directed disk layout
can be one of the heuristics in their framework. Due to space limitation, we do
not discuss this issue further.
Simulation Results
Evaluation Methodology
To evaluate the benefits of exploiting block correlations in block prefetching
and disk data layout, we use trace-driven simulations with several large disk
traces collected in real systems. Our simulator combines the widely used DiskSim
simulator [20] with a storage cache simulator,
CacheSim, to simulate a complete storage system. CacheSim implements the Least
Recently Used (LRU) replacement policy. Accesses to the simulated storage system
first go through a storage cache and only read misses or writes access physical
disks. The simulated disk specification is similar to that of the 10000 RPM IBM
Ultrastar 36Z15. The parameters are taken from the disk's data sheet [28,11]. Our experiments use the following four real
system traces:
- TPC-C Trace is an I/O trace collected on a storage system connected
to a Microsoft SQL Server via storage area network. The Microsoft Server SQL
clients connect to the Microsoft SQL Server via Ethernet and run the TPC-C
benchmark [39] for 2 hours. The database consists of 256
warehouses and the footprint is 60GB, and the storage system employs a RAID of 4
disks. A more detailed description of this trace can be found in [69,13].
- Cello-92 was collected at Hewlett-Packard Laboratories in 1992 [49,48]. It captured all low-level disk I/O
performed by the system. We used the trace gathered on Cello, which is a
timesharing system used by a group of researchers at HP Labs to do simulations,
compilation, editing and email. The trace includes the accesses to 8 disks. We
have also tried other HP disk trace files, and the results are similar.
- Cello-96 is similar to Cello-92. The only difference is that this
trace was collected in 1996 and thereby contains more modern workloads. It
includes the accesses to 20 disks from multiple users and miscellaneous
applications. It contains a lot of sequential access patterns, so the simple
sequential prefetching approaches can significantly benefit from them.
- OLTP is a trace of an OLTP application running at a large financial
institution. It was made available by the Storage Performance Council [58]. The disk subsystem is composed of 19
disks.
All the traces are collected after filtering through a first-level buffer cache
such as the database server cache. Fortunately, unlike other access patterns
such temporal locality that can be filtered by large first-level buffer caches,
most block correlations can still be discovered at the second-level. Only those
correlations involving ``hot'' blocks that always stay at the first-level can be
lost at the second-level. However, these correlations are not useful to exploit
anyway since ``hot'' blocks are kept at the first-level and therefore are rarely
accessed at the second-level. In our experiments, we use only the first half
part of the trace to mine block correlations using C-Miner. Using these
correlation rules, we evaluate the performance of correlation-directed
prefetching and data layout using the rest of the traces. The correlation rules
are kept unchanged during the evaluation phase. For example, in Cello-92, we use
the first 3-days' trace to mine block correlations and use the following 4 days
to evaluate the correlation-directed prefetching and data layout. The reason for
doing this is to show the stable characteristic of block correlations and
predictive powers of our method. To provide a more fair comparison, we also
implement the commonly used sequential prefetching scheme. At non-consecutive
misses to disks, the system also issues a prefetch request to load 16
consecutive blocks. We have also tried prefetching more or fewer blocks, but the
results are similar or worse.
Visualization of Block Correlations
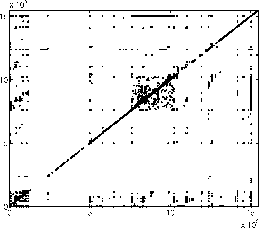
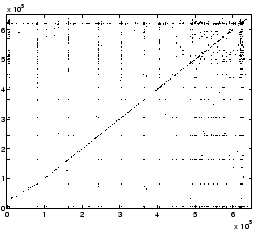
Figure 4 plots the block
correlations discovered by C-Miner from the Cello-96 and TPC-C traces.
Since multi-block correlations are difficult to visualize, we plot only
dual-block correlations. If there is an association rule
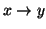 , we plot a corresponding point at
, we plot a corresponding point at 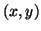 . Therefore, each point
. Therefore, each point 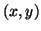 in the graphs indicates a correlation between blocks
in the graphs indicates a correlation between blocks 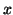 and
and 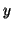 . Since the traces contain multiple disks' accesses, we plot the disk
block address using a unified continuous address space by plotting one disk
address space after another.
. Since the traces contain multiple disks' accesses, we plot the disk
block address using a unified continuous address space by plotting one disk
address space after another.
Figure 4: Block correlations mined from
traces
(a) Cello-96 trace
|
(b) TPC-C trace
|
|
Simple patterns such as spatial locality can be demonstrated in such a
correlation graph. It is indicated by dark areas around the diagonal line. This
is because the spatial locality can be represented by an association rule
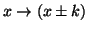 where
where 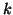 is a small number, which means that if block
is a small number, which means that if block 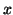 accessed, its neighbor blocks are likely to be accessed soon. Since
accessed, its neighbor blocks are likely to be accessed soon. Since 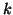 is small, the points
is small, the points 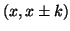 are around the diagonal line, as shown on the Cello-96 traces (Figure 4a).
The graph for the TPC-C trace does not have such apparent characteristic,
indicating TPC-C does not have strong spatial locality. Some more complex
patterns can also be seen from correlation graphs. For example, in figure 4b,
there are many horizontal or vertical lines, indicating some blocks are
correlated to many other blocks. Because this is a database I/O trace, these hot
blocks with many correlations are likely to be the root of trees or subtrees. In
the next subsection, we visualize block correlations specifically for tree
structures.
In order to demonstrate the capability of C-Miner to discover semantics
in a tree structure, we use a synthetic trace that simulates a client that
searches data in a B-tree data structure, which is commonly used in databases.
The B-tree maintains the indices for 5000 data items, each block has space for
four search-key values and five pointers. We perform 1000 searches. To simulate
a real-world situation where some ``hot'' data items are searched more
frequently than others, searches are not uniformly distributed. Instead, we use
a Zipf distribution and 80% of searches are to 100 ``hot'' data items. The block
correlations mined from the B-tree trace are visualized in figures 5.
Note here constructing this tree does not take any semantic information from the
application (the synthetic trace generator). The edges between nodes are
reconstructed purely based on block correlations. Due to the space limitation,
we only show part of the correlations. Each rule
are around the diagonal line, as shown on the Cello-96 traces (Figure 4a).
The graph for the TPC-C trace does not have such apparent characteristic,
indicating TPC-C does not have strong spatial locality. Some more complex
patterns can also be seen from correlation graphs. For example, in figure 4b,
there are many horizontal or vertical lines, indicating some blocks are
correlated to many other blocks. Because this is a database I/O trace, these hot
blocks with many correlations are likely to be the root of trees or subtrees. In
the next subsection, we visualize block correlations specifically for tree
structures.
In order to demonstrate the capability of C-Miner to discover semantics
in a tree structure, we use a synthetic trace that simulates a client that
searches data in a B-tree data structure, which is commonly used in databases.
The B-tree maintains the indices for 5000 data items, each block has space for
four search-key values and five pointers. We perform 1000 searches. To simulate
a real-world situation where some ``hot'' data items are searched more
frequently than others, searches are not uniformly distributed. Instead, we use
a Zipf distribution and 80% of searches are to 100 ``hot'' data items. The block
correlations mined from the B-tree trace are visualized in figures 5.
Note here constructing this tree does not take any semantic information from the
application (the synthetic trace generator). The edges between nodes are
reconstructed purely based on block correlations. Due to the space limitation,
we only show part of the correlations. Each rule
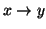 is denoted as a directed edge with support as its weight. The
figure illustrates that the block correlations implicate a tree-like structure.
Also note that our approach to obtain block correlations is fully transparent
without any assumption on storage front-ends.
is denoted as a directed edge with support as its weight. The
figure illustrates that the block correlations implicate a tree-like structure.
Also note that our approach to obtain block correlations is fully transparent
without any assumption on storage front-ends.
Stability of Block Correlations
In order to show that block correlations are relatively stable, we use the
correlation rules mined from the first 3 days of the Cello-92 trace. Our
simulator applies these rules to the next 4 days' trace without updating any
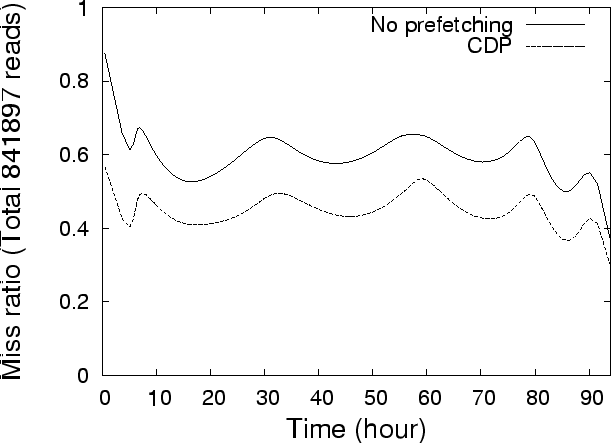
rules. Figure 6 shows the miss ratio for
the next 4 days' trace using correlated-directed prefetching (CDP). The
miss ratios in the figure are calculated by aggregating every 10000 read
operations. This figure shows that CDP is always better than the base case. This
implies that correlations mined from the first 3 days are still effective for
the next 4 days. In other words, block correlations are relatively stable for a
relative long period of time. Therefore, there is no need to run C-Miner
continuously in the background to update block correlations. This also shows
that, as long as the mining algorithm is reasonably efficient, the mining
overhead is not a big issue.
Figure 6: Miss ratio for Cello-92
(64MB; 4MB)
 |
Data Mining Overhead
Table 1 shows the running time and space
overheads for mining different traces. C-Miner is running on an Intel
Xeon 2.4GHz machine and Windows 2000 Server. The time and space overhead does
not depend on the confidence of rules as we discussed in section 3.2
but the number of rules does. The results show that C-Miner can
effectively and practically discover block correlations for different workloads.
For example, it takes less than 1 hour to discover half a million association
rules from the Cello-96 trace that contains a full-day's disk requests. For the
TPC-C trace, although it takes about 1 hour to mine 1 hour's trace, it is still
practical for storage systems. Because block correlations are relatively stable,
it is unnecessary to keep mining for correlations in the background. Instead, it
might be acceptable to spend one hour every week on running C-Miner to
update correlation rules. In our experiments, we only use parts of the traces to
mine correlations, and use the remaining traces to evaluate correlation-directed
prefetching and disk layout. Our experimental results indicate that correlations
are relative stable and are useful for accesses made much later after the
training period.
Table 1: Mining Overhead (
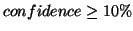 )
)
| Training Trace |
# of rules |
time |
space |
| |
(K) |
(sec) |
(MB) |
| Cello-92 (3 days) |
228 |
7800 |
3.1 |
| Cello-96 (1 day) |
514 |
2089 |
4.6 |
| TPC-C (1 hour) |
235 |
3355 |
9.2 |
| OLTP (2.5 hours) |
186 |
174 |
172.6 |
|
C-Miner is also efficient in terms of space overhead for most of
traces. It takes less than 10 MB to mine the Cello and TPC-C traces. With such a
small requirement, the data mining can run on the same machine as the storage
system without causing too much memory overhead. A uniprocessor PC with 512MB
memory would do the work. In the future, we will investigate using stream mining
algorithms to effectively mine continuous information with much less time and
space overhead. The stream mining algorithm could be embedded in the storage
controllers using their spare CPU power.
Correlation-directed Prefetching and Disk Layout
The bar graphs in figures 7a-d compare the read
miss ratios and response times using the four different schemes: base-line (no-prefetching),
sequential prefetching, correlation-directed prefetching (CDP), and
correlation-directed prefetching and disk layout (CDP+layout). For the last
three schemes with prefetching, the prefetch cache size is set to be the same.
All four settings use the same total size of storage cache in order to make a
fair comparison. In other words, the
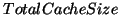 , which equals to the sum of
, which equals to the sum of
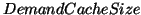 and
and
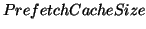 , is the same for all four schemes. CDP can improve
the average I/O response time for the base-line case by up to 25%. For instance,
in Cello-92, CDP has 24.4% lower storage cache hit ratios than the base-line
case. This translates into 24.75% improvement in the average I/O response time.
These improvements are due to the fact that prefetching reduces the number of
capacity misses as well as the number of cold misses. When the cache size is
small, some blocks are evicted and need to be fetched again for disks upon
subsequent accesses. Prefetching can avoid misses at some of these accesses. The
improvement by CDP is much more significant than that by the commonly used
sequential prefetching scheme, especially in the case of TPC-C and Cello-92. For
example, for the TPC-C trace, sequential prefetching only slightly reduces the
cache miss ratio (by only 2%), which is then completely cancelled out by the
prefetching overheads. Therefore, sequential prefetching has even worse response
time than the base case. For the other two traces (Cello-92 and OLTP trace), the
improvement of the sequential prefetching scheme is very small, almost invisible
in terms of the average response time. However, in Cello-96, sequential
prefetching has a lower miss ratio and slightly better response time than CDP.
This is because this trace has a lot of sequential accesses. But these
sequential accesses are not frequent enough in the access stream so it is not
caught by C-Miner. Fortunately, our patterns obtained by C-Miner
can be complementary and combined with the existing online sequential
prefetching algorithms that can detect non-frequent sequential access patterns.
CDP+layout has only small improvement over CDP. Obviously, CDP+layout should not
affect cache miss ratio at all. It only matters to average I/O response time
when the disk is heavily utilized. Its benefits are only visible in the Cello-96
trace, where CDP+layout has 4% better average response time than CDP. This small
improvement indicates that our optimization for hiding prefetching overheads
using priority-based disk scheduling is already good enough. Therefore, disk
layout does not provide significant benefits. However, when the disk is too
heavily utilized for the disk scheduling scheme to hide most of the prefetching
overheads, we expect the benefit of correlation-directed disk layout will be
larger.
A parameter that might affect the benefits of correlation directed prefetching
is the confidence threshold. Figure 8 shows
the effects of varying the confidence threshold from 0% to 90% . A lower
confidence threshold corresponds to a more aggressive prefetching policy. The
figure shows that the miss ratio is minimum when prefetching is most aggressive
and all the rules are used. We can see that the line is flat when the confidence
is smaller than 30%, which indicates that the rules with small confidence are
useless.
, is the same for all four schemes. CDP can improve
the average I/O response time for the base-line case by up to 25%. For instance,
in Cello-92, CDP has 24.4% lower storage cache hit ratios than the base-line
case. This translates into 24.75% improvement in the average I/O response time.
These improvements are due to the fact that prefetching reduces the number of
capacity misses as well as the number of cold misses. When the cache size is
small, some blocks are evicted and need to be fetched again for disks upon
subsequent accesses. Prefetching can avoid misses at some of these accesses. The
improvement by CDP is much more significant than that by the commonly used
sequential prefetching scheme, especially in the case of TPC-C and Cello-92. For
example, for the TPC-C trace, sequential prefetching only slightly reduces the
cache miss ratio (by only 2%), which is then completely cancelled out by the
prefetching overheads. Therefore, sequential prefetching has even worse response
time than the base case. For the other two traces (Cello-92 and OLTP trace), the
improvement of the sequential prefetching scheme is very small, almost invisible
in terms of the average response time. However, in Cello-96, sequential
prefetching has a lower miss ratio and slightly better response time than CDP.
This is because this trace has a lot of sequential accesses. But these
sequential accesses are not frequent enough in the access stream so it is not
caught by C-Miner. Fortunately, our patterns obtained by C-Miner
can be complementary and combined with the existing online sequential
prefetching algorithms that can detect non-frequent sequential access patterns.
CDP+layout has only small improvement over CDP. Obviously, CDP+layout should not
affect cache miss ratio at all. It only matters to average I/O response time
when the disk is heavily utilized. Its benefits are only visible in the Cello-96
trace, where CDP+layout has 4% better average response time than CDP. This small
improvement indicates that our optimization for hiding prefetching overheads
using priority-based disk scheduling is already good enough. Therefore, disk
layout does not provide significant benefits. However, when the disk is too
heavily utilized for the disk scheduling scheme to hide most of the prefetching
overheads, we expect the benefit of correlation-directed disk layout will be
larger.
A parameter that might affect the benefits of correlation directed prefetching
is the confidence threshold. Figure 8 shows
the effects of varying the confidence threshold from 0% to 90% . A lower
confidence threshold corresponds to a more aggressive prefetching policy. The
figure shows that the miss ratio is minimum when prefetching is most aggressive
and all the rules are used. We can see that the line is flat when the confidence
is smaller than 30%, which indicates that the rules with small confidence are
useless.
Figure 8: Effect of the confidence
threshold (Cello-92)
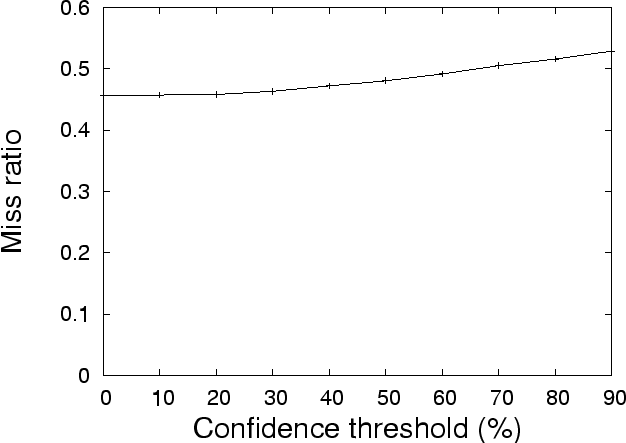 |
If the cache size is comparable to the footprint of a trace, the system simply
caches all accesses. Because of this, the read misses in the case of no
prefetching are predominantly cold misses since subsequent accesses will be
cache hits and will not go to the disk. Therefore, the prefetching schemes do
not yield much improvement in performance. We study the effects of the cache
size by varying the cache size for TPC-C exponentially from 256 MB to 1024 MB.
In this experiment, we keep the prefetch cache fixed at 128 MB and vary the size
of the demand cache. As expected, when the cache size is set at 256 MB,
CDP+layout shows an improvement of 14.62% in miss ratio while with 512 MB, the
improvement is only 10.58%. It is important to note that our workloads have
relatively small working set sizes. In large real systems, it is usually not the
case that the entire working set can fit into main memory.
Figure 9: Effect of varying the total
cache size for TPC-C
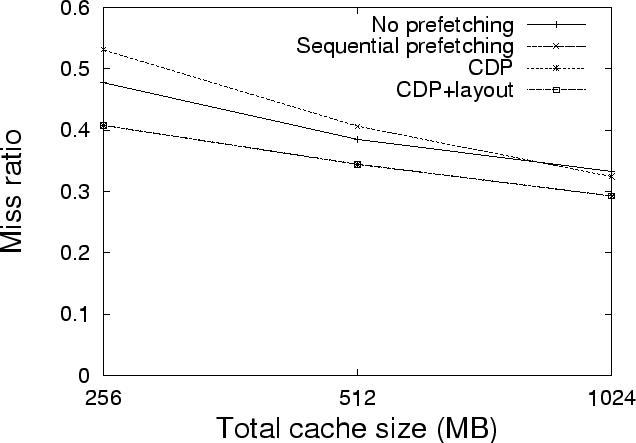 |
Figure 10: Effect of varying the
prefetch cache size (Note: the total cache size is fixed. Therefore, the demand
cache size is also changing with the prefetch cache size. In the base-line case,
there is no prefetch cache)
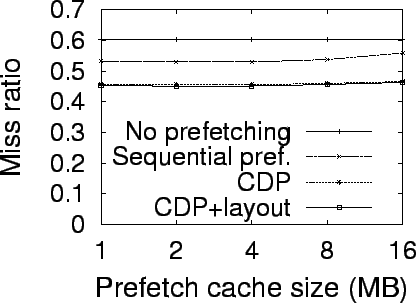
(a) Cello-92 - miss ratio
|
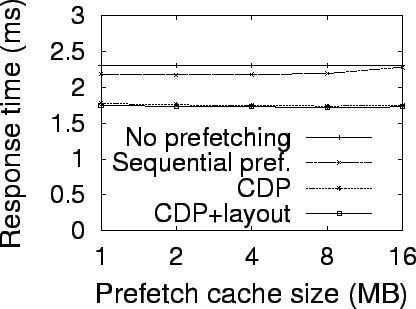
(b) Cello-92 - response time
|

(c) TPC-C - miss ratio
|
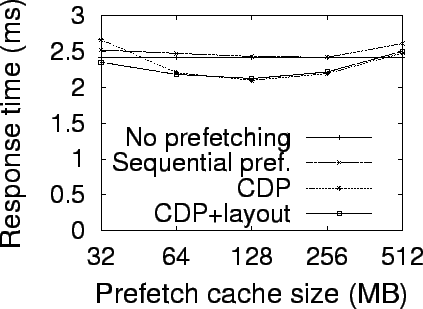
(d) TPC-C - response time
|
|
Figures 10a-d show the effects of
varying the prefetch cache size while the total cache size is fixed. In TPC-C,
for instance, the storage cache miss ratio with CDP initially decreases as the
prefetch cache size increases. It reaches the minimum when the prefetch cache
size is set to 128 MB. Beyond that point the miss ratio increases again with the
prefetch cache size. This phenomenon is also true for the sequential prefetching,
even though it performs worse than CDP with almost all prefetch cache sizes. The
above phenomenon can be quite expected. When the prefetch cache size is very
small, prefetched blocks may be replaced even before they are used. Even though
the demand cache size is increased correspondingly, its benefit is not large
enough to offset the loss in unused prefetches. Even worse, the overhead imposed
by CDP causes an increase in the response time compared to the base case, as
shown on Figure 10d. Fortunately, in
this case, the CDP+layout starts to show the benefits of correlation-directed
disk layout. It is still able to provide some small improvement over the base
line case. As the prefetch cache size increases, blocks can be retained longer
in the prefetch cache and subsequently be used to handle block requests.
However, the increase in prefetch cache size corresponds to a reduced demand
cache size, but the benefit of prefetching in reducing misses outweighs the loss
in the demand cache. Beyond 128 MB, increasing the prefetch cache size no longer
has benefits for increasing hit ratio. So the loss due to the reduced demand
cache size starts to dominate. Therefore, the overall miss ratio increases.
Related Work
In this section, we briefly discuss some representative work that is closely
related to our work. Section 2 has
discussed various approaches to capture data semantics. Thus, we do not repeat
them here. Data prefetching has also been studied extensively in databases, file
systems and parallel applications with intensive I/Os. Most of previous
prefetching work either relies on applications to pass hints or is based on
simple heuristics such as sequential accesses. Examples of prefetching studies
for databases include [56,63,44,22,21] as well some recent work [53] for mobile data delivery environments.
Prefetching for file I/Os include application-controlled prefetching [9,10] and informed prefetching [60,32,45], just to name a few. [57] is an example of prefetching in disk
caches. I/O prefetching for out-of-core applications include compiler-assisted
prefetching [43,8] and prefetching through
speculative execution [12]. In the spectrum of sophisticated
prefetching schemes, research has been conducted for semantic distance-based
file prefetching for mobile or networked file servers. Besides the probability
graph-based approach described in Section 2,
the SEER project from UCLA [34,35] groups related files into clusters by keeping
track of semantic distances between files and downloading as many complete
clusters as possible onto the mobile station. The CLUMP project tries to
leverage the concept of semantic distance to prefetch file clusters [18]. Kroeger extends the probability graph to
a trie with each node representing the sequence of consecutive file accesses
from the root to the node [33]. Lei and Duchamp also use a similar
structure by building a probability tree [59,38]. Vellanki and Chervenak combine
Patterson's cost-benefit analysis with probabilistic prefetching for high
performance parallel file systems [61]. Similar to the probability graph, most
of these approaches may be feasible for prefetching at file granularity, but are
impractical to track block correlations in a storage system (see Section 2).
Some studies used data compression techniques for prefetching. It was first
proposed by Vitter and Krishnan [62]. The basic idea is to encode the data
expected with higher probability using fewer bits. The prefetchers based on any
optimal character-by-character data compressor were theoretically proven to be
optimal in page fault rate. Later, [17] analyzed some practical issues of
such a technique, and proposed three practical data compressors for prefetching.
Data mining methods have been mostly used to discover patterns in sales, finance
or bio-informatics databases [27,26]. Only a few studies have applied them in
systems. A well-known example is using data mining for intrusion detection [37,16]. Data mining has recently been used in
performance evaluation [40] to model bursty traffic. Data
mining and machine learning have been used in web environments to predict HTTP
requests. Schechter et al. introduced path profiling to predict HTTP requests in
web environments [51]. Pitkow and Pirolli have used longest
repeating subsequences to perform path matching for predicting web accesses from
a client [47]. These schemes predict the next
HTTP request by matching the surfer's current sequence against the path profile
database. While path-based prediction may work very well for web environments,
it is very difficult to capture block correlations in storage systems. This is
because web browser/server workloads are different from storage workloads. Each
web client usually only browses one page at a time, whereas a storage front-end
such as database server can have hundreds of outstanding requests. Since the
path-matching schemes do not allow any gaps in the subsequence or path, they
cannot be used easily to capture block correlations in a storage system. To
support gaps or lookahead distances in these work will suffer the same problem
as the probability graph-based approach. Our work is also related to various
adaptive approaches using learning techniques [41,4], intelligent storage cache management [69,65,42,13], and autonomic storage systems [64,2,30]
Conclusions and Future Work
This paper proposes C-Miner, a novel approach that uses data mining
techniques to systematically mine access sequences in a storage system to infer
block correlations. More specifically, we have designed a frequent sequence
mining algorithm to find correlations among blocks. Using several large real
system disk traces, our experiments show that
C-Miner is reasonably fast with small space requirement and is
therefore practical to be used on-line in an autonomic storage system. We have
also evaluated correlation-directed prefetching and data layout. Our
experimental results with real-system traces have shown that
correlation-directed prefetching and data layout can improve I/O average
response time by 12-25% compared to no-prefetching, and 7-20% compared to the
commonly used sequential prefetching. Our study has several limitations. First,
even though this paper focuses on how to obtain block correlations, our
evaluation of the block correlation-directed prefetching and disk layout was
conducted using only simulations. We are in the process of implementing
correlation-directed prefetching and disk layout in our previously built storage
system. Second, we have only evaluated four real-system workloads, it would be
interesting to evaluate other workloads such as those with substantially
sequential accesses. Third, we do not compare with the semantic-distance graph
approach. The main reason is that our preliminary experiment indicates that the
SD graphs significantly exceed the memory space, making it extremely slow and
almost infeasible to build such graphs. Currently, C-Miner does not
consider the recency factor, that is, some recent frequent subsequences may be
more important than other ``ancient'' frequent subsequences. To mine time-series
data, our algorithm needs to be modified to change the support or confidence
value of a rule dynamically as time progresses. Currently, we are designing
efficient stream data mining algorithms specifically for mining access sequences
for storage systems and any other similar situations.
The authors would like to thank the shepherd, Jeff Chase, and the anonymous
reviewers for their invaluable feedback. We appreciate Kimberly Keeton of HP
labs for the constructive discussion and thank HP storage system labs for
providing us cello traces. We are also grateful to Professor Jiawei Han and his
student Xifeng Yan for their help with the CloSpan algorithm and insightful
discussions. This research is supported by the NSF CCR-0305854 grant and IBM CAS
Fellowship. Our experiments were conducted on equipment provided through the IBM
SUR grant.
- 1
-
R. Agrawal and R. Srikant.
Mining sequential patterns.
In Eleventh International Conference on Data Engineering, 1995.
- 2
-
E. Anderson, M. Hobbs, K. Keeton, S. Spence, M. Uysal, and A. Veitch.
Hippodrome: running circles around storage administration.
In Proceedings of the First USENIX Conference on File and Storage
Technologies, 2002.
- 3
-
G. H. Anthes.
Storage virtualization: The next step.
Computerworld, January 28, 2002.
- 4
-
I. Ari, A. Amer, E. Miller, S. Brandt, and D. Long.
Who is more adaptive? ACME: adaptive caching using multiple experts.
In Workshop on Distributed Data and Structures (WDAS), 2002.
- 5
-
A. C. Arpaci-Dusseau and R. H. Arpaci-Dusseau.
Information and control in gray-box systems.
In Proceedings of the eighteenth ACM symposium on Operating systems
principles, 2001.
- 6
-
J. Ayres, J. E. Gehrke, T. Yiu, and J. Flannick.
Sequential pattern mining using bitmaps.
In Proc. 2002 ACM SIGKDD Int. Conf. Knowledge Discovery in Databases
(KDD'02), pages 429-435, Edmonton, Canada, July 2002.
- 7
-
L. A. Barroso, K. Gharachorloo, and E. Bugnion.
Memory system characterization of commercial workloads.
In Proceedings of the 25th annual international symposium on Computer
architecture, pages 3-14. IEEE Press, 1998.
- 8
-
A. D. Brown, T. C. Mowry, and O. Krieger.
Compiler-based I/O prefetching for out-of-core applications.
ACM Transactions on Computer Systems, 19(2):111-170, 2001.
- 9
-
P. Cao, E. Felten, and K. Li.
Application-controlled file caching policies.
In USENIX Summer 1994 Technical Conference, pages 171-182, June
1994.
- 10
-
P. Cao, E. W. Felten, A. Karlin, and K. Li.
A study of integrated prefetching and caching strategies.
In Proceedings of ACM SIGMETRICS, May 1995.
- 11
-
E. V. Carrera, E. Pinheiro, and R. Bianchini.
Conserving disk energy in network servers.
In Proceedings of the 17th International Conference on Supercomputing,
June 2003.
- 12
-
F. W. Chang and G. A. Gibson.
Automatic I/O hint generation through speculative execution.
In Operating Systems Design and Implementation, pages 1-14, 1999.
- 13
-
Z. Chen, Y. Zhou, and K. Li.
Eviction-based cache placement for storage caches.
In USENIX, 2003.
- 14
-
J. Choi, S. H. Noh, S. L. Min, and Y. Cho.
Towards application/file-level characterization of block references: a case
for fine-grained buffer management.
In Proceedings of the 2000 ACM SIGMETRICS international conference on
Measurement and modeling of computer systems, 2000.
- 15
-
H. Chou and D. DeWitt.
An evaluation of buffer management strategies for relational database
systems.
In Proceedings of the 19th International Conference on Very Large Data
Bases, pages 127-141, Dublin, Ireland, 1993.
- 16
-
C. Clifton and G. Gengo.
Developing custom intrusion detection filters using data mining.
In 2000 Military Communications International Symposium (MILCOM2000),
Los Angeles, California, Oct. 2000.
- 17
-
K. M. Curewitz, P. Krishnan, and J. S. Vitter.
Practical prefetching via data compression.
In Proc. 1993 ACM-SIGMOD Conference on Management of Data, pages
257-266, May 1993.
- 18
-
P. R. Eaton, D. Geels, and G. Mori.
Clump: Improving file system performance through adaptive optimizations.
- 19
-
EMC Corporation.
Symmetrix 3000 and 5000 Enterprise Storage Systems product description
guide., 1999.
- 20
-
G. Ganger.
Systemoriented evaluation of I/O subsystem performance.
Technical Report CSE-TR-243-95, University of Michigan, June 1995.
- 21
-
C. A. Gerlhof and A. Kemper.
A multi-threaded architecture for prefetching in object bases.
In M. Jarke, J. A. B. Jr., and K. G. Jeffery, editors, Advances in
Database Technology - EDBT'94. 4th International Conference on Extending
Database Technology, Cambridge, United Kingdom, March 28-31, 1994, Proceedings,
volume 779 of Lecture Notes in Computer Science, pages 351-364.
Springer, 1994.
- 22
-
C. A. Gerlhof and A. Kemper.
Prefetch support relations in object bases.
In M. P. Atkinson, D. Maier, and V. Benzaken, editors, Persistent
Object Systems, Proceedings of the Sixth International Workshop on Persistent
Object Systems, Tarascon, Provence, France, 5-9 September 1994, Workshops
in Computing, pages 115-126. Springer and British Computer Society, 1994.
- 23
-
G. A. Gibson, D. F. Nagle, K. Amiri, J. Butler, F. W. Chang, H. Gobioff,
C. Hardin, E. Riedel, D. Rochberg, and J. Zelenka.
A cost-effective, high-bandwidth storage architecture.
In the 8th International Conference on Architectural Support for
Programming Languages and Operating Systems (ASPLOS), 1998.
- 24
-
J. Griffioen and R. Appleton.
Reducing file system latency using a predictive approach.
In In Proceedings of the 1994 Summer USENIX Conference, 1994.
- 25
-
J. Griffioen and R. Appleton.
Performance measurements of automatic prefetching.
In In Proceedings of the International Conference on Parallel and
Distributed Computing Systems, 1995.
- 26
-
J. Han.
How can data mining help bio-data analysis?
In Proc. 2002 Workshop on Data Mining in Bioinformatics (BIOKDD'02),
pages 1-4, Edmonton, Canada, July 2002.
- 27
-
J. Han and M. Kamber.
Data Mining: Concepts and Techniques.
Morgan Kaufmann Publishers, 2001.
- 28
-
IBM hard disk drive - Ultrastar 36Z15.
- 29
-
IBM.
Storage Tank, a distributed storage system.
IBM White Paper, https://www.almaden.ibm.com/StorageSystems/file_systems/
storage_tank/papers.shtml.
- 30
-
K. Keeton and J. Wilkes.
Automating data dependability.
Proceedings of the 10th ACM-SIGOPS European Workshop, 2002.
- 31
-
J. Kim, J. Choi, J. Kim, S. Noh, S. Min, Y. Cho, and C. Kim.
A low-overhead high-performance unified buffer management scheme that
exploits sequential and looping references.
In Proceedings of the 4th Symposium on Operating Systems Design and
Implementation (OSDI), pages 119-134, San Diego, CA, Oct. 2000.
- 32
-
T. Kimbrel, A. Tomkins, R. H. Patterson, B. Bershad, P. Cao, E. Felten,
G. Gibson, A. R. Karlin, and K. Li.
A trace-driven comparison of algorithms for parallel prefetching and
caching.
In Proceedings of the 1996 Symposium on Operating Systems Design and
Implementation, pages 19-34. USENIX Association, 1996.
- 33
-
T. M. Kroeger and D. D. E. Long.
Predicting file-system actions from prior events.
In 1996 USENIX Annual Technical Conference, pages 319-328, 1996.
- 34
-
G. Kuenning.
Design of the SEER predictive caching scheme.
In Workshop on Mobile Computing Systems and Applications, 1994.
- 35
-
G. H. Kuenning and G. J. Popek.
Automated hoarding for mobile computers.
In Proceedings of the 15th Symposium on Operating Systems Principles,
pages 264-275, St. Malo, France, Oct. 1997. ACM.
- 36
-
E. K. Lee and C. A. Thekkath.
Petal: distributed virtual disks.
In Proceedings of the seventh international conference on Architectural
support for programming languages and operating systems, pages 84-92. ACM
Press, 1996.
- 37
-
W. Lee and S. Stolfo.
Data mining approaches for intrusion detection.
In Proceedings of the 7th USENIX Security Symposium, San Antonio,
TX, 1998.
- 38
-
H. Lei and D. Duchamp.
An analytical approach to file prefetching.
In 1997 USENIX Annual Technical Conference, Anaheim, California,
USA, 1997.
- 39
-
S. T. Leutenegger and D. Dias.
A modeling study of the TPC-C benchmark.
SIGMOD Record, 22(2):22-31, June 1993.
- 40
-
T. M. M. Wang, N. Chan, S. Papadimitriou, and C. Faloutsos.
Data mining meets performance evaluation: Fast algorithms for modeling
bursty traffic.
18th Internal Conference on Data Engineering, 2002.
- 41
-
T. M. Madhyastha, G. A. Gibson, and C. Faloutsos.
Informed prefetching of collective input/output requests.
Proceedings of SC99.
- 42
-
N. Megiddo and D. S. Modha.
Arc: A self-tuning, low overhead replacement cache.
In Proc. 2nd USENIX Conference on File and Storage Technologies (FAST
03), San Franciso, CA, 2003.
- 43
-
T. C. Mowry, A. K. Demke, and O. Krieger.
Automatic compiler-inserted I/O prefetching for out-of-core applications.
In Proceedings of the 1996 Symposium on Operating Systems Design and
Implementation, pages 3-17. USENIX Association, Oct. 1996.
- 44
-
M. Palmer and S. B. Zdonik.
Fido: A cache that learns to fetch.
In G. M. Lohman, A. Sernadas, and R. Camps, editors, 17th International
Conference on Very Large Data Bases, September 3-6, 1991, Barcelona, Catalonia,
Spain, Proceedings, pages 255-264. Morgan Kaufmann, 1991.
- 45
-
R. H. Patterson, G. A. Gibson, E. Ginting, D. Stodolsky, and J. Zelenka.
Informed prefetching and caching.
In the 15th ACM Symposium on Operating System Principles, 1995.
- 46
-
J. Pei, J. Han, B. Mortazavi-Asl, H. Pinto, Q. Chen, U. Dayal, and M.-C. Hsu.
PrefixSpan: Mining sequential patterns efficiently by prefix-projected
pattern growth.
In Proc. 2001 Int. Conf. Data Engineering (ICDE'01), pages 215-224,
Heidelberg, Germany, April 2001.
- 47
-
J. E. Pitkow and P. Pirolli.
Mining longest repeating subsequences to predict world wide web surfing.
In USENIX Symposium on Internet Technologies and Systems, 1999.
- 48
-
C. Ruemmler and J. Wilkes.
A trace-driven analysis of disk working set sizes.
Technical Report HPL-OSR-93-23, Hewlett-Packard Laboratories, Palo Alto, CA,
USA, Apr. 5 1993.
- 49
-
C. Ruemmler and J. Wilkes.
UNIX disk access patterns.
In Proceedings of the Winter 1993 USENIX Conference, 1993.
- 50
-
B. Salmon, E. Thereska, C. A. Soules, and G. R. Ganger.
A two-tiered software architecture for automated tuning of disk layouts.
In First Workshop on Algorithms and Architectures for Self-Managing
Systems, June 2003.
- 51
-
S. Schechter, M. Krishnan, and M. D. Smith.
Using path profiles to predict http requests.
In Seventh Intl World Wide Web Conference, Apr 1998.
- 52
-
J. Schindler, J. Griffin, C. Lumb, and G. Ganger.
Track-aligned extents: matching access patterns to disk drive
characteristics.
In Proceedings of the First USENIX Conference on File and Storage
Technologies, 2002.
- 53
-
A. Seifert and M. H. Scholl.
A multi-version cache replacement and prefetching policy for hybrid data
delivery environments.
In 28th International Conference on Very Large Data Bases (VLDB),
2002.
- 54
-
M. Sivathanu, V. Prabhakaran, F. Popovici, T. E. Denehy, A. C. Arpaci-Dusseau,
and R. H. Arpaci-Dusseau.
Semantically-Smart Disk Systems.
In Proceedings of the Second USENIX Conference on File and Storage
Technologies, 2003.
- 55
-
A. J. Smith.
Sequentiality and prefetching in database systems.
ACM Transactions on Database Systems, 3(3):223-247, Sept. 1978.
- 56
-
B. J. Smith.
A pipelined, shared resource MIMD computer.
In Proceedings of International Conference on Parallel Proc essing,
pages 6-8, 1978.
- 57
-
V. Soloviev.
Prefetching in segmented disk cache for multi-disk systems.
In Proceedings of the fourth workshop on I/O in parallel and distributed
systems, pages 69-82. ACM Press, 1996.
- 58
-
Storage Performance Council.
SPC I/O traces.
https://www.storageperformance.org/.
- 59
-
C. D. Tait, H. Lei, S. Acharya, and H. Chang.
Intelligent file hoarding for mobile computers.
In Mobile Computing and Networking, pages 119-125, 1995.
- 60
-
A. Tomkins, R. H. Patterson, and G. Gibson.
Informed multi-process prefetching and caching.
In Proceedings of the 1997 ACM SIGMETRICS Conference on Measurement and
Modeling of Computer Systems, pages 100-114. ACM Press, 1997.
- 61
-
V. Vellanki and A. Chervenak.
A cost-benefit scheme for high performance predictive prefetching.
In Proceedings of SC99: High Performance Networking and Computing,
Portland, OR, 1999. ACM Press and IEEE Computer Society Press.
- 62
-
J. S. Vitter and P. Krishnan.
Optimal prefetching via data compression.
In Proceedings of the 32nd Annual IEEE Symposium on Foundations of
Computer Science, Oct 1991.
- 63
-
H. Wedekind and G. Zoerntlein.
Prefetching in realtime database applications.
In Proceedings of the 1986 ACM SIGMOD international conference on
Management of data, pages 215-226. ACM Press, 1986.
- 64
-
J. Wilkes, R. Golding, C. Staelin, and T. Sullivan.
The HP AutoRAID hierarchical storage system.
Proc. of the 15th Symp. on Operating Systems Principles, 1995.
- 65
-
T. Wong and J. Wilkes.
My cache or yours? making storage more exclusive.
In USENIX, 2002.
- 66
-
X. Yan, J. Han, and R. Afshar.
CloSpan: Mining closed sequential patterns in large datasets.
In Proc. 2003 SIAM Int. Conf. Data Mining (SDM'03), San Fransisco,
CA, May 2003.
- 67
-
M. Zaki.
SPADE: An efficient algorithm for mining frequent sequences.
Machine Learning, 40:31-60, 2001.
- 68
-
Y. Zhang, J. Zhang, A. Sivasubramaniam, C. Liu, and H. Franke.
Decision-support workload characteristics on clustered database server from
the OS perspective.
In Proceedings of the International Conference on Distributed Conputing
Systems(ICDCS), May 2003.
- 69
-
Y. Zhou, J. F. Philbin, and K. Li.
The multi-queue replacement algorithm for second level buffer caches.
In Proceedings of the Usenix Technical Conference, June 2001.
Department of Computer Science
University of Illinois at Urbana-Champaign
Urbana, IL 61801


![]() is a suffix database which contains all the maximum suffixes of
the sequences that contain the frequent subsequence
is a suffix database which contains all the maximum suffixes of
the sequences that contain the frequent subsequence ![]() . For example, in the previous sequence database
. For example, in the previous sequence database ![]() , the suffix database of frequent subsequences
, the suffix database of frequent subsequences ![]() is
is
![]() .
. ![\begin{boxedminipage}[thb]{3in}
\renewcommand {1.09}{1}\begin{tabbing}\hspace{...
...amond \alpha$\ means to concatenate $s$\ with $\alpha$.)}
\end{boxedminipage}](img50.png)
![]() is frequent, all of its subsequences
is frequent, all of its subsequences
![]() are frequent. Based on this observation, C-Miner recursively
produces a longer frequent subsequence by concatenating every frequent item to a
shorter frequent subsequence that has already been obtained in the previous
iterations. To better explain this idea, let us consider an example. In order to
get the set
are frequent. Based on this observation, C-Miner recursively
produces a longer frequent subsequence by concatenating every frequent item to a
shorter frequent subsequence that has already been obtained in the previous
iterations. To better explain this idea, let us consider an example. In order to
get the set ![]() of frequent subsequences with length
of frequent subsequences with length ![]() , we can join the set
, we can join the set ![]() of frequent subsequences with length
of frequent subsequences with length ![]() and the set
and the set ![]() of frequent subsequences with length 1. For example, suppose we
have already computed
of frequent subsequences with length 1. For example, suppose we
have already computed ![]() and
and ![]() as shown below. In order to compute
as shown below. In order to compute ![]() , we can first compute
, we can first compute ![]() by concatenating a subsequence from
by concatenating a subsequence from ![]() and an item from
and an item from ![]() :
: