2. Overview and Motivation

We first define the file download problem more formally, and then outline the goals and motivation for our work. Consider a content server with a network link of bandwidth R_nbytes/s and a population of N clients concurrently downloading shared files. We use the term file to mean a unique ordered set of data blocks; thus it could refer to any segment of a larger data set. Suppose that each client i can receive data at a sustained rate $R_c^i \leq R_n$, with an average client rate R_c bytes/s. The goal is to schedule block reads from disks and block transfers to clients in order to maximize X(N), the system throughput for N concurrent requests, or the number of download requests completed per time unit. Unless it is saturated, the server should be fair and it should complete each request in the minimum time that the network allows: a request from client i to download a file of length L bytes should complete after approximate delay L/R_cⁱ.

Since this paper focuses on the design of the server and its storage system, we will claim success when the server is network-limited, i.e., it consumes all of its available network bandwidth. Suppose the average file length is L bytes. For low client loads, the server may be limited by the aggregate network bandwidth to its clients: $X(N) \le R_cN/L$. If the client population is large, or if the clients have high-speed links, then the server may be limited by its own network link: $X(N) \le R_n/L$ (with unicast). We assume without loss of generality that the server's CPU and memory system are able to sustain the peak data rate R_nwhen serving large files.

Our objective, then, is to minimize the memory and storage resources needed to feed content to the network at the peak rate R_n for a sufficiently large client population: $N \ge R_n/R_c$. Suppose the content server has a memory of size M and D disks delivering a peak bandwidth of R_d byte/s each. Our purpose is to explore how block reordering can reduce the number of disks D needed for a given M, and/or reduce the M needed for a given D and R_d. Equivalently, we may view the objective as maximizing the network speed R_n or client population size N that a given configuration (M,D) can support. The problem is uninteresting for small R_n, e.g., in serverless P2P systems that distribute server functions across many slow clients. The problem is most interesting for servers in data centers with high-capacity network links, serving large client populations with slow transfer rates R_c. N may be quite large for commercial content servers with a large bandwidth disparity relative to their clients: IP network bandwidth prices are dropping [13], while broadband deployments for the ``last mile'' to clients continue to lag behind. Although our approach does not require multicast support, it is compatible with multicast and N may be even larger when it exists.

 

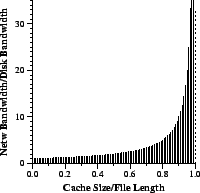Figure 1: The maximum ratio of network bandwidth to disk bandwidth, as a function of the portion of the data set size that fits in the cache. The system is heavily disk-limited unless the bulk of the data set fits in memory. though.

2.1 Caching

The server's memory of size M consists of a common pool of shared buffers. A server uses these buffers for some combination of disk buffering, network buffering, and data caching. For example, suppose the server fetches data from storage in blocks of size Bbytes. A typical server would buffer each fetched block until all client transmits of the block to clients have completed; the surplus memory acts as a cache over blocks recently fetched for some client i that are deemed likely to be needed soon for another client j requesting the same file. Caching is effective for small files that can reside in the cache in their entirety until the next request [6]. However, if j's request arrives t time units after i's, then the server has already fetched up to tR_cⁱ bytes of the file into memory and delivered them to i. The memory needed to cache the segment until j is ready to receive it grows with the inter-arrival time t. If R_cⁱ > R_c^j then the required cache space continues to grow as the transfers progress--when the system is constrained to deliver the data in order to both clients, as for conventional file servers.

Since each file request accesses each block of the file exactly once, block accesses are uniformly distributed over the entire file length. As the number of clients increases, and as client rates and arrival times vary, the block access request stream shows less temporal locality and becomes effectively random. Of course, there is spatial locality when the server delivers each block in sequence; the system may exploit this by using a larger block size B, as discussed below (or, equivalently, by prefetching more deeply). Suppose without loss of generality that the content consists of a single file of length L >> M, or any number of equally popular files with aggregate size L. Then the probability of any block access being a cache hit is P_hit = M/L, and P_miss = 1 - M/L is the probability that the access requires a disk fetch. Then the server's storage system must be capable of sustaining block fetches at rate (R_n/B)(1 - M/L). Figure 1 shows the role of cache size in determining the number of disks required to sustain this rate.

  

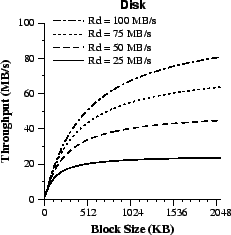
Figure 2: Disk throughput with random block accesses in a disk with positioning time T_pos = 0.005s across different transfer block sizes, and sequential disk transfer rates R_d. We show that as R_d increases, block size must exceed one megabyte to achieve peak disk throughput.

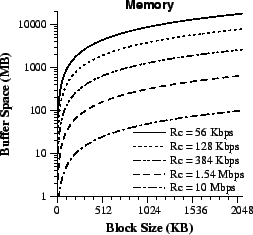
Figure 3: Minimum buffer space required to support clients at different rates in a server with a 1 Gbps network link. The minimum buffer space can reach several gigabytes for large populations of clients with bandwidth less than 1 Mbps.

2.2 Storage Throughput

The areal density of magnetic storage has been doubling every year, and disks today spin several times faster than ten years ago [13]. While these trends increase sequential disk bandwidth, throughput for random block accesses (IOPS) has not kept pace. Seek costs tend to dominate random accesses, and these costs are limited by mechanical movement and are not improving as rapidly. Unfortunately, the block miss stream for a content server degrades to random access as the client population N increases, for the same reasons outlined above.

One solution is to increase the block size B. This reduces the rate of disk operations required to sustain a given effective bandwidth, which is inversely proportional to B. This technique can significantly reduce the number of disks required. Suppose each disk has an average head positioning time per access of T_pos seconds (seek plus half-rotation). Every disk access moves a block of size B bytes, and takes time T_pos + B/R_d. Thus, each disk supports $\frac{1}{T_{pos} + B/R_d}$ random accesses per time unit, and the aggregate peak disk bandwidth for D disks becomes $X_d = \frac{B\times D}{T_{pos} + B/R_d}$bytes/s. The server needs $D=\frac{R_n}{B/(T_{pos} + B/R_d)}$disks to fully pipeline the network. For example, Figure 2 illustrates the disk random access throughput when T_pos = 0.005 s, a typical value. With block size B = 256 KB, and disks of R_d = 50 MB/s, the disk throughput X_d becomes roughly 25 MB/s. We need about D=5 such disks to feed a server network link of R_n = 1 Gb/s.

However, Figure 3 shows that this approach consumes large amounts of memory with large client populations. Depending on the buffering scheme the minimum memory size M for N active clients is $NB/2 \leq M \leq 2NB$. The 1 Gb/s server can support N = 664 T1 (1.544 Mbps = 193 KB/s) client connections, consuming a minimum M = 87 MB just for device buffering with B = 256 KB. If we increase the block size to B = 1 MB then disk throughput becomes X_d = 40MB/s, the number of disks drops to D=4, and the minimum memory grows to M = 325 MB. If instead, we assume slower clients with R_c = 56 Kbps, the server needs a minimum M = 2.18 GB and M = 8.7 GB for block size B = 256 KB and B = 1 MB, respectively. In media servers using large block sizes it is common to eliminate the cache and partition memory into separate buffer regions for each client; each region is sufficient to hold any blocks in transit between the disk and the network for that client [4].

2.3 Summary

In this section we explained why accesses at the block level appear increasingly random as the client population Ngrows. This minimizes the benefit of conventional caching and weakens the locality of the disk accesses from the cache miss stream. The combination of these effects increases server cost, since more disks and/or more memory are needed to fill any given network link. For example, the experiments in this paper use disks with average sequential throughput of R_d = 33 MByte/s, but a conventional FTP server under even modest load delivers a per-disk throughput of roughly 10 MB/s, including cache hits. Thus we need about a dozen such disks to feed a network link of 1 Gb/s.