|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
FAST 2002 Paper
[FAST Tech Program Index]
Enabling the Archival Storage of Signed DocumentsPetros Maniatis Mary Baker
Abstract: Documents in digital formats are increasingly becoming a common form
of expression for anything from rants and opinions to transaction records
and contracts. Archiving such documents for the long term, particularly
when their only form is digital, can be very important. Sadly, the principal
digital expression of an author's intent, the digital signature, is not fit
for long-term archives of documents; signing keys can expire or become compromised,
rendering the documents they signed indistinguishable from illicit forgeries.
We propose KASTS, an extension of traditional archival storage systems that
enables the long-term storage of signed documents. KASTS combines time stamping
of signed documents with storage of past signature verification keys. We
argue that such an extended archival storage system is feasible and describe
one possible design for it.
|

|
As a first step, Jane needs a digital signing facility to sign her manifesto. In public-key cryptography, on which most commercial digital signature schemes rely, signatures are generated and verified with a signing key pair . This key pair consists of a secret signing key, used to generate digital signatures, and a public signature verification key , used to verify signatures produced by the corresponding signing key. To be able to sign digital documents, Jane must first generate such a signing key pair, and then she must publish the signature verification key from her key pair, so that anyone can verify her signatures.
Signature verification keys are published encapsulated within identity certificates. An identity certificate is issued by a Certification Authority (CA), such as Verisign, Thawte or Entrust, and certifies the association between an identity name (i.e., an identifier for a signer) and the signature verification key that should be used to verify signatures by that identity. Identity certificates also contain the time at which they are issued and the maximum duration of their validity period. Figure 1 shows a simplified identity certificate for Jane. It indicates that "AB25 E90F ..." is Jane's signature verification key for at most a year starting July 9th of 2001. Jane acquires this certificate by contacting the CA securely and sending it her signature verification key. Jane does not, of course, send her secret signing key to the CA or to anyone else; she keeps it hidden and well protected.
To indicate the official character of the certificate, and to protect its integrity, the CA signs every identity certificate it issues using its own signing key pair, also called the master signing key pair. Since the CA lies at the top of the certification totem pole and there is no one to certify the validity of its signature verification keys, identity certificates for the CA are different from those issued to Jane: they are signed by the CA itself. CA certificates bootstrap the certification process, which is why they are sometimes referred to as bootstrapping, or root CA certificates. Because a CA client cannot verify the validity of a bootstrapping certificate since it is self-signed, the CA publishes its certificates via secure channels, for example by postal mail or bundled within store-purchased software, such as web browsers and email clients.
Once Jane has finished proofreading her manifesto, she uses her secret signing key to sign it, producing the signed manifesto of Figure 2 . Anyone in possession of the signed manifesto can use the verify operation of the digital signing facility and Jane's verification key to check that the document was in fact signed by Jane's signing key.
Jane can now publish her signed manifesto online. As long as her identity certificate is available to readers of the manifesto and there are no security breaches, her authorship of the document is indisputable.
The validity of Jane's signature on the document relies on a ``validation chain'' consisting of two links. The first link is between Jane and her signing key pair. Unless a verifier knows for a fact that "AB25 E90F ..." is Jane's signature verification key, he has no reason to believe that the signature on the manifesto identifies Jane as the signer, even if it is a mathematically correct signature. The second link is between the CA and its master signing key pair. Again, unless a verifier knows for a fact the master verification key, he has no reason to believe that a correct signature on Jane's identity certificate comes from the CA.

|
Unfortunately, the validation chain can break in two ways (refer to Figure 3 for the relevant timeline). First, any one of the links may become compromised ; in this scenario, a burglar enters the headquarters of the CA, stealing backup tapes that contain the master signing key, on November 28th, 2001. The break-in is discovered on the following day, so the CA promptly publicizes the event on November 29th. On the same day, a new master signing key pair is generated, and published widely. This burglary breaks the validation chain on Jane's document since, once the CA's key pair is compromised, it is not clear to a verifier of Jane's signatures whether her certificate was signed by the CA's master signing key before or after November 28th. The burglar could have easily issued new certificates on November 28th, claiming an earlier issuance date; there is nothing anyone can do to distinguish such illicit certificates from legitimate ones.
A second way the validation chain for Jane's manifesto can break is when any one of the links expires; in our scenario, Jane's key expires on July 9th, 2002 and the CA's original key would have expired, if it had not been compromised, at the end of its two-year validity period, on January 1st, 2002. One of the reasons that expiration dates are set on identity certificates is to limit the possible amount of damage (i.e., illegitimate signatures produced) that a compromised key can cause, especially if the compromise goes unnoticed. Certificate lifetimes can be set according to the importance of the enclosed key (a master CA key versus the key of a relatively unimportant individual), expected key usage (more signatures mean more fodder for cryptanalysis), and other factors [19].
Sadly, key expiration only compounds the problem for Jane's documents. Once a key expires, all verifiers are expected to assume the key is compromised or ``compromisable,'' and should no longer trust it. In this scenario, Split Infinitives Inc. (SII), a powerful organization favoring the avid use of split infinitives, has devoted large computational resources to discovering Jane's signing key. Since Jane was careful when requesting her certificate, her key expires before SII can possibly recover it. Yet even if SII recovers Jane's signing key after July 9th, 2002, they can still write a contradictory manifesto, sign it with the expired recovered signing key and publish it. After Jane's key expires, it is not easy to determine whether the new, illicit manifesto was signed before Jane's key expired or after. Therefore a verifier has no reason to believe as authentic any document signed by that key, whether Jane's original manifesto, or the counterfeit one.
This makes it hard for Jane to publish her manifesto for posterity. Unless Jane is available and willing to keep resigning and republishing her manifesto every time its validation chain is broken through compromise or expiration, there is nothing she can do to have her document archived meaningfully for long periods of time.
In this section we explain how combining time stamping and the storage of old signature verification keys helps solve the problem described above.
Time stamping allows a signer to create a proof of when he signed a particular item. In general, the purpose of time stamping is to build a timeline of documents. This is done by a Time Stamping Service (TSS), a trusted but accountable third party whose function is to maintain and be able to prove temporal ordering relationships among submitted documents. A time stamp for a document contains the time when the document was stamped and a proof that the document was in fact stamped then. A verifier can check the veracity of a time stamp on a document with the help of the TSS, by checking that the included proof matches the claimed time. Accountability means that, although the service is generally trusted, it can be caught if it ``cheats.'' Cheating in the case of a time stamping service amounts to post-dating, pre-dating, or forgetting about a document. We present how time stamping services are designed in more detail in Section 6.1 .
The main idea that helps us solve the problem described in the previous section is to time stamp a signature at the time it is produced [15]. Now a verifier can know whether a signature was generated before or after the event that breaks the validation chain of that signature, such as a discovered compromise or a certificate expiration.
However, time stamping by itself is not sufficient. A verifier who seeks to check the authorship of Jane's manifesto, long after the signing key pair she used has changed, needs to find the appropriate signature verification key. Consequently, we also need some method to archive and retrieve old signature verification keys to enable the long-term archival storage of signed documents.
Two types of keys must be archived. The first type consists of CA-certified keys, that is, keys whose association with a particular identity is vouched for by the signature of the CA on an identity certificate. This is the case with Jane's identity certificate: In July 2001, the CA vouched with its signature that the signature verification key "AB25 E90F ..." belongs to Jane. In this respect, Jane's certificate is just a special case of a signed document, and as such, it can be archived in a manner similar to how Jane's manifesto is archived (except for the complications described in Section 7.2 ).
The second type of key consists of bootstrapping keys, which are traditionally self-certified by the very entity to which they are issued. The master verification key of the CA belongs to this type. A verifier must acquire this key through a secure distribution channel, perhaps by picking it up in person or by receiving it as part of a software distribution. Though this kind of procedure might be practical for obtaining the current master verification key of a unique CA, it can be impractical and unscalable for archived old master keys of perhaps multiple CAs.
For this reason, the need for a Key Archival Service (KAS) becomes clear. This is a trusted, accountable service intended for archiving specifically bootstrapping keys. Nothing precludes conventional, CA-certified keys from being archived at the KAS, but this is not necessary, since conventional keys, encapsulated in identity certificates, can be archived as regular documents.
The system presented in this work, KASTS, extends traditional archival storage systems to accommodate signed documents, using accountable key archival storage and time stamping services.
Here we present a high-level view of KASTS. Besides the conventional archival storage service it extends, KASTS consists of a TSS, a KAS, and a small client-side library. All certificates are issued by a CA.
The storage service is untrusted, and maintains arbitrary documents submitted to it. KASTS submits signed, time stamped documents, including certificates issued by the CA, to the storage service for long-term storage.
The TSS maintains a timeline of all the documents that it time stamps. It is trusted by everyone within its scope to maintain a unique, tamper-proof timeline, although it remains accountable (see Section 6.1 ). Anyone who verifies the validity of a time stamp on a document can be convinced that the document was signed no later than the time indicated in the time stamp.
The KAS maintains an archive primarily of CA master certificates, but also of any other identity certificates submitted to it. Furthermore, it maintains time stamped snapshots of its archive, with the help of the TSS; in that respect, it is a client of the TSS. It is trusted to maintain a unique, tamper-proof archive, although it remains as accountable as the TSS (see Section 6.2 ). Anyone who verifies the existence of a certificate in a particular timed snapshot of the KAS can be convinced that the certificate was current and not revoked at the time indicated in the archive snapshot.
Although not a part of KASTS, the CA is an important entity for the system, since it is the issuer of all certificates. It is trusted to maintain a unique, tamper-proof name space at any one time, mapping names to identity certificates.
Clients make use of KASTS via a small client-side library. The interface presented by the library includes the following operations:
In the interest of clarity, we assume the existence of a single TSS, KAS and CA in the remainder of this paper. However, in parallel ongoing work [20], we explore how this design can be ported to a more complex setting where multiple competing TSSes, KASes and CAs coexist. Some of our design decisions are biased by our experiences in that more realistic setting.
In this section we demonstrate how to use this system, both for publication of signed documents and for later verification of those documents. We explain each of the following steps:
The primary objective of this task is to allow the storage of the different master signature verification keys used to verify the CA's signature on individual identity certificates. Every time the CA changes master keys, it updates the key archive, as shown in Figure 4 .
First the CA generates a new master signing key pair for itself. It keeps the secret master signing key away from prying eyes, but publishes widely the master verification key (VCA).
The CA also submits VCA, along with its maximum validity period to the KAS for storage (step 1). Once the storage of the key at the KAS has been completed, the CA may request an optional proof of storage from it. The proof consists of a time stamp of the entire KAS archive after the insertion, and a proof of inclusion of the new key in the archive (step 2). This only serves as an enforcement of the accountability of the KAS. We explain the details of such proofs and the reasoning behind them in Section 6.2 .
Jane goes through this process to create and archive her signature verification key. The process is illustrated in Figure 5 .
First, Jane generates a new signing key pair. She keeps the secret signing key SJ safe, but submits the public verification key, VJ (or "AB25 E90F ...") to the CA for registration (step 1). The CA returns a new signed identity certificate (marked J:VJ in the figure) to Jane (step 2). This is the certificate shown in Figure 1 .
Jane then submits the CA's signature on her newly acquired certificate to the TSS for time stamping (step 3). The TSS responds with a time stamp on the CA's signature (step 4).
Finally, Jane bundles together her certificate along with the time stamp and publishes them both in the archival storage system (step 5).
It is worth pointing out that, although Jane time stamped the signature of her certificate instead of the entire signed certificate, the result is the same. This is because signatures are cryptographically dependent on the documents for which they are generated, by means of a one-way hash function. Therefore, by time stamping the signature, the TSS effectively also time stamps the entire signed certificate as well.
Now Jane follows a publication process to place her manifesto in the extended archival storage system. See Figure 6 for an illustration.
First, Jane signs the manifesto (shown as M in the figure) with her secret signing key SJ (steps 1 and 2). She submits the resulting signature to the TSS for time stamping (step 3). Once she receives the time stamp back from the TSS (step 4), Jane submits the bundle consisting of her manifesto, her signature on it, and the time stamp on her signature to the archival storage system (step 5). Again, time stamping the signature is equivalent to time stamping the signed document.
To verify the authenticity and authorship of the manifesto, a reader first needs to find the applicable master verification key, i.e., the CA signature verification key that was current at the time at which the manifesto claims to have been signed. See Figure 7 for an illustration.
Given the time indicated in the time stamp of the manifesto (step 1), the reader requests a CA verification key from the KAS (step 2).
The KAS returns the applicable master verification key if one is found, along with a proof of its (non)existence there (step 3).
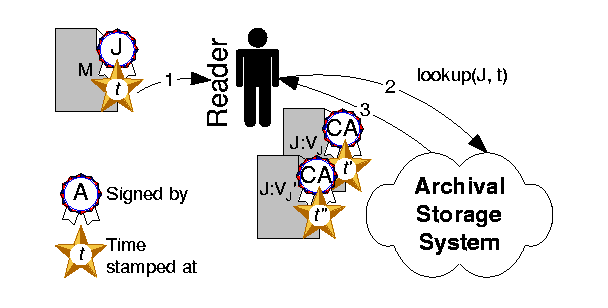
Finally, the reader must retrieve the appropriate identity certificate for Jane, given the time at which the manifesto was time stamped, as shown in Figure 8 .
|
The reader searches the archival storage system for identity certificates for Jane around the time at which the manifesto was stamped (step 1). The certificates whose time stamps come immediately before and after the point in time shown in the manifesto time stamp are sought (step 2).
The earlier certificate (J:VJ) is the one whose key is applicable to the signature on the manifesto, and its validity extends until the date of issuance of the later certificate (J:VJ ') (step 3). If no certificate is returned that was time stamped after the manifesto, then the verifier presumes that the maximum duration of the earlier certificate has been used up in full, i.e., he presumes that the key in the certificate was not compromised before the expiration time of that certificate. Section 7.2 discusses some potential complications with this approach and ways to avoid them.
In this section we explore the design of the two KASTS components in more detail and we evaluate their viability.
Centralized TSSes have existed and operated for many years [3,16,27]. Their basic functionality allows clients to submit document digests for time stamping at a preset granularity called a round (typically one second long) and to submit a time stamped document for subsequent verification. In this section we describe how a TSS works. We use this information to describe how we extend the time stamping model to build a timed archive of keys, in Section 6.2 .
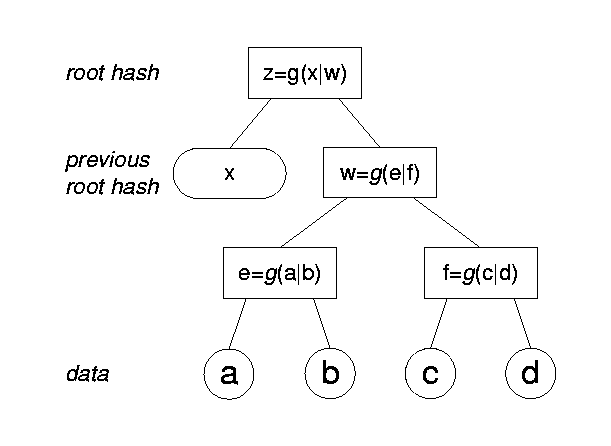
The prevalent design for TSSes is based on collision-resistant hash functions [9]. A linking data structure is used to aggregate all document digests submitted for time stamping during the same round. The data structure traditionally used is the Merkle tree [22]. A Merkle tree is a regular k-ary tree, whose contents are all stored in the leaves, sorted using a predetermined total order. Every internal tree node is labeled by concatenating in order the labels of its k children (or nil values for missing children) and applying to the result a one-way, collision-resistant hash function. The label of the root is sometimes called the root hash of the tree. The root hash ``represents'' exactly the ordered set of the leaves of the tree. No digest may be added into or removed from the tree without altering the value of the root hash, unless a k-way collision for the hash function can be found, which is believed to be computationally intractable (see Section 7.3 for more details). Figure 9 shows a binary Merkle tree, where g(.) is the hash function, a, b, c and d are the linked data and z the root hash.
|
A time stamp for a digest consists of the time at which its round was created and a proof of inclusion of the digest in the associated linking data structure. This proof allows a verifier to determine definitively whether a digest is contained within a linking data structure given the root hash of the structure. Therefore, verifying a time stamp on a document amounts to requesting from the TSS the root hash for the time at which a document claims to have been time stamped and then verifying that the time stamp proves the inclusion of the document digest in the associated linking data structure.
In Merkle trees, the proof of inclusion for a digest consists of all those values that can help recompute the root hash of the tree from that digest. Those values are the labels and locations of the sibling nodes of the digest and of all of its ancestors in the tree. In Figure 9 , the proof of inclusion for c consists of the values d, e and x and their locations right, left and left , respectively. Using these, a verifier can compute z=g(x|g(e|g(c|d))) , and then compare z to the root hash reported by the TSS for the linking data structure. Assuming that the tree in the figure is created by the TSS at time t, the time stamp for c looks like [t; right/d, left/e, left/x].
A newly created linking data structure depends on the data structure created during the previous second. This dependency is effected by including the root hash of the previous round into the newly created tree. Consequently, a document digest in previous linking data structures cannot change, be added or removed, since that would result in a changed root hash for the associated data structure, which transitively results in a changed root hash for subsequent data structures. In the example of Figure 9 , value x is the root hash from the previous time stamping round.
Chaining together linking data structures from older to more recent ones allows TSSes to claim the property of accountability. A TSS is accountable if it cannot cheat, by back- or post-dating a document. This is accomplished by periodically--usually, once a week--widely publishing the root hash created during normal time stamping operations on a newspaper or other paper journal with wide distribution. A skeptical TSS client can verify the honesty of the TSS by requesting all intervening root hashes between a given, unpublished root hash and the closest published one. If the hash link is verified, then it is extremely unlikely that the TSS has inserted, modified or deleted digests in its data structures after it published its root hashes.
The feasibility of practical time stamping is no longer questionable. Current commercial services time stamp a few million digests per hour in second-long rounds (and can be configured to do much more), using under 10 conventional, off-the-shelf PC-grade computers [7]. The archive of root hashes for continuous operations of almost a decade so far do not surpass 50 GB, which bodes well for the scalability of the service over time.
The Key Archival Service maintains the timed history of signature verification keys, most notably the master verification keys used and published by the CA, as well as other keys submitted to it for storage. Maintaining this history and making it widely available is essential to the orderly operation of the system we describe here. The functionality of the KAS can be bundled together with the CA or the TSS, although we present it here separately for clarity.
Although the KAS is absolutely necessary only for the storage of the master verification keys of the CA, we have designed it with a much larger data set in mind, for two reasons. First, we want our design to be usable in a more complex setting, where multiple CAs (in the thousands) coexist. Second, we expect that storing non-root keys in the KAS may be advisable, especially given the concerns described in Section 7.2 .
In the next three sections we detail the basic data structures used in the KAS, the actual design of the service and, finally, its expected storage complexity.
|
|
Similarly to the TSS, the KAS accumulates key updates--arriving to KASTS client libraries via rekey(identity, new certificate) requests--for a predetermined time period called the key storage round. At the end of the key storage round, the archive is modified and time stamped to reflect the updates that arrived since the previous round, as well as any expirations of previously archived keys. Based on common frequency of key change policies and anticipating the use of the KAS by not only the CA, we currently set the duration of a KAS round to two weeks. Note that durations of TSS and KAS rounds differ by several orders of magnitude.
The simplest design for the KAS would employ a centralized--or centrally administered--database of tuples of the form <time, identity, verification key, maximum validity period>. However, to provide the same level of accountability that is offered by the TSS, as seen in Section 6.1 , we rely heavily for the design of our KAS on Merkle trees. By using a linking data structure, the KAS can return a proof of storage of the result every time it handles a lookup or rekey request. The first part of that proof is a time stamp on the particular key storage round of the KAS. The latter part of the proof is a linking tree existence proof of the result in the KAS, similar to proofs described in the previous section.
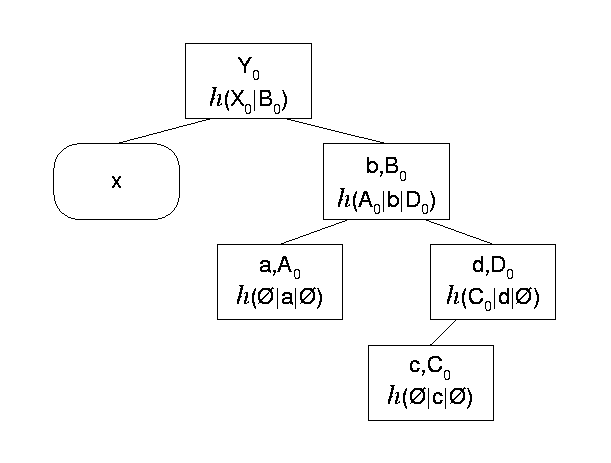
For the KAS we use a variation of Merkle trees proposed by Buldas et al. [4], called authenticated search trees. Buldas et al. suggest this modification to thwart attempts by the maintaining party to keep an inconsistent, unsorted tree linking structure. In authenticated search trees, data occupy not only leaf nodes, but also internal tree nodes. Furthermore, the computation of a node label takes as input the search key of the node in addition to the labels of the node's children. The principal contribution of authenticated search trees is that they allow clients who receive an existence or non-existence proof from the tree maintainer to verify that the maintainer is keeping the tree sorted. Figure 10 shows an authenticated search tree containing the same data as the Merkle tree of Figure 9 . Again, the root hash of the previous round is x.
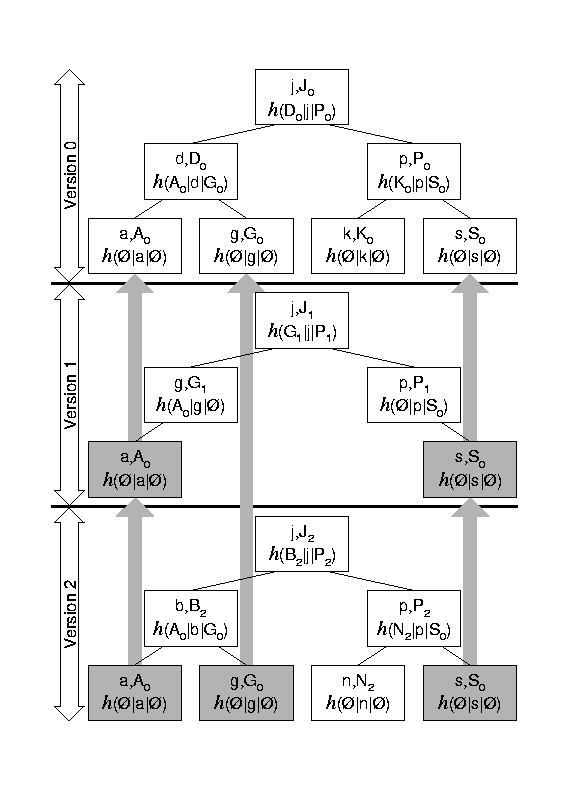
Authenticated search trees, like all trees, can be efficiently versioned, so as to preserve different snapshots of the set of stored data without excessive redundancy. Figure 11 shows an example of that. The top tree shows the initial version (version 0) of an authenticated search tree. The middle tree shows version 1, resulting from removing the nodes containing d and k from the tree of version 0. The bottom tree is version 2, which results from inserting nodes containing b and n into the tree of version 1. The grayed out nodes are merely references to the original nodes in version 0, and need not be copied for each subsequent snapshot, unless they change in content or label. Versioning is not useful in the Merkle trees used in time stamping, since in that case all contents of the tree change entirely from version to version.
Note that in Figure 11 , tree operations are balanced. This is another welcome property of trees that we use in archiving. Since existence and non-existence proofs have maximum length proportional to the height of the tree, balancing the tree helps such proofs to remain short in the worst case. Balanced trees in our preliminary prototype of the KAS are on-disk B-trees, and are similar to those introduced by Naor et al. [23]. However, no balancing is applied to the topmost level of the tree, so that the previous round hash is always one hash operation away from the new round hash. In Figure 10 , only the subtree rooted at the node labeled B0 is balanced.
There are two kinds of authenticated search trees used in the KAS, Archive Snapshots and Time Trees. Archive Snapshots store one node for each tuple of the type <time, identity, verification key, maximum validity period>, ordered by the identity attribute. There is an Archive Snapshot tree for each distinct version of the KAS archive, i.e., one for each round. Therefore, a single Archive Snapshot contains all the valid keys known to the KAS at the end of the associated round.
Every Archive Snapshot has a distinct root node, as long as it has at least one node difference from the preceding round (we do not alter the archive during rounds with no key updates). This is because inserting, modifying or removing a node results in creating a new version of its parent node, and the changes iteratively percolate up to the root.
The roots of every Archive Snapshot ever built by the KAS are archived in a Time Tree, which is also an authenticated search tree based on B-trees. Time Tree nodes store tuples of the form <round time, snapshot root> , ordered by the round time attribute. There is only one current Time Tree within a KAS. At the end of a round, after the new Archive Snapshot is created, a new node for the root of that snapshot is inserted into the Time Tree. See Figure 12 for an illustration of the different trees used in the KAS.
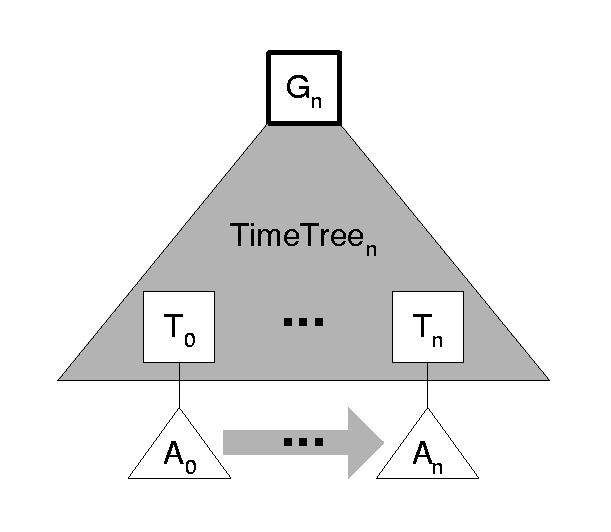
|
The root Gn of the current Time Tree can be seen as a digest of the history of operations of the KAS up to the end of the previous round, since no Archive Snapshot can change without causing a change to the latest Time Tree root. At the end of round n , Gn is submitted to the TSS for time stamping.
To respond to a lookup(identity, time) request, the KAS first locates the appropriate Archive Snapshot in the Time Tree, searching on the time entry of the request. The appropriate snapshot is the one whose round time immediately precedes the time in the lookup request. Then, the KAS locates the appropriate key entry in the Archive Snapshot, searching on the identity entry of the request. The result (found or not found) is returned along with a proof of storage that consists of the time stamp on the current Time Tree root hash, a proof of existence of the snapshot in the Time Tree and the proof of (non)existence of the returned key in the selected snapshot tree.
Storage and computation costs incurred by the operation of the KAS are reasonable, even if we anticipate heavy storage of keys other than those of the CA, or even if there are many CAs. Tree operations on Archive Snapshot trees create O(logN) new tree nodes for each identity certificate event (insertion, modification or removal), if the previous snapshot had N total nodes. This is the worst case space increase per certificate, since it only occurs if an insertion, modification or removal affects a node at the bottom of the balanced tree, thereby requiring copy-on-modify changes along every tree level to the root. Therefore, the storage required for all Archive Snapshots should be in the worst case on the order of NlogN if a total of N identity certificates are archived. All balanced tree operations take time logM in the number M of keys in the current snapshot, which is much smaller than the total number N of archived keys. Even if every one of the clients of the extended archival storage system uses the KAS to store their signature verification keys, as opposed to storing their identity certificates in the storage substrate, the size of the KAS would still remain in achievable orders of magnitude. An archive of 1 billion verification keys would require roughly 300 TB (assuming minimal disk block fragmentation within B-tree nodes), which is not astronomical for a high-performance service today.
The size of the Time Tree is exactly K nodes, if the KAS contains archives for K distinct snapshots. This, of course, is dependent on the length of the KAS round. Tree operations in the Time Tree take time on the order of logK.
We expect the KAS to receive significantly less traffic than a CA would, for two reasons. First, KAS responses are immutable during a single KAS round, and only change slightly after the passage of each subsequent round in an incremental fashion, to accommodate the increasing size of the Time Tree. Therefore they can be cached very efficiently away from the KAS. In contrast, traffic to CAs usually includes ``repeat customers'' who check for online certificate revocations. In summary, we expect the long term deployment and operation of a KAS to be at least as feasible as a CA--if not more so.
In describing KASTS so far we have assumed that a valid signature is one that was time stamped during the validity period of the associated identity certificate. Section 7.1 touches on the distinction between a valid signature and a valid indication of the purported signer's intent.
In Section 7.2 we explain how the use of a conventional storage substrate to store identity certificates can, in some cases, lead to forgery attacks against our system, and we propose a solution.
Finally, in Section 7.3 we describe why we consider time stamping ``stronger'' than digital signatures.
A fundamental issue that affects what KASTS guarantees and what it does not is the semantic content of a digital signature.
Although real-world, paper-and-pen signatures have enjoyed for centuries often unwarranted absolute trust, digital signatures do not establish beyond doubt the identity of the signer. Instead, digital signatures establish beyond doubt whether or not the signer had in his possession a particular secret signing key. The link from a digital signature to the intent of its purported signer is strong only as long as the key used to produce the signature is known exclusively to the individual with whom that key is associated by the CA. The strength of this link has long been considered significantly weaker than that between a paper signature and its signer.
However, digital signatures are slowly becoming legally binding [11]. Although the legal guidelines for their use are fairly specific [1], they have yet to face a significant challenge in court. In the meantime, assuming that the party to whom a signing key is issued bears the liability for anything signed by that key during its validity period, proactive key changes seem to be the only measure against unnoticed key compromise. By changing signing keys frequently and making them short-lived, a signer limits the amount of damage that can be done with any single compromised key.
In KASTS, all regular identity certificates and other signed documents coexist independently in the same archival storage system. The reason for decoupling a signed document from the identity certificate necessary to verify the signature on that document is efficiency, especially in the case of very short documents. Otherwise redundancy would be unavoidable, since, in general, many documents are signed by the same key.
This means that each complete retrieval and verification of a signed document requires the retrieval of at least two pieces of information from the untrusted storage substrate: the document itself and the corresponding identity certificate needed to verify it. The corresponding identity certificate to a signed document is that whose validity period contains the signing time of the document. This validity period is the minimum of the nominal validity period indicated on the certificate itself and the time difference until a newer certificate for the same identity is registered. In other words, a verifier ascribes a validity period shorter than the nominal to Jane's year-long certificate issued on 7/9/2001 once he finds a newer certificate for Jane issued before 7/9/2002.
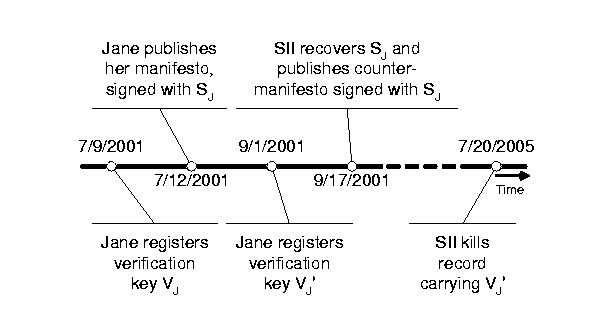
|
However, if an adversary has a non-negligible probability of causing individual documents--and therefore individual identity certificates--in the storage system to disappear or be delayed during retrieval, then he can cause a verifier to consider a signature verification key valid at a time when it was not. Figure 13 illustrates a modification of the earlier scenario from Figure 3 . In this scenario, Jane decides to get a new signing key pair on 9/1/2001, long before her old one expires on 7/9/2002. By installing a new identity certificate for herself, Jane essentially revokes the validity of her previous verification key VJ, which would otherwise remain valid until 7/9/2002. Between the issuance of her replacement key pair and the expiration of the old key pair, evil Split Infinitives Inc. successfully recovers her old, now revoked signing key SJ, and uses it to sign and publish a contradicting manifesto. Clearly, this contradicting manifesto should not be considered valid by a verifier, since it is signed after the signing key has been revoked.
Assume now that long into the future, on 7/20/2005, SII manages to kill Jane's newer certificate or temporarily hamper its retrieval. An unaware verifier who retrieves SII's counter manifesto after this time is forced to consider it valid, since he can only find the year-long certificate for VJ whose uncontested validity period contains the signing time of the counter-manifesto.
This attack is dependent on the properties of the archival storage substrate used in the particular implementation. Some systems (e.g., Freenet [6]), while not ``trusted'' in theory, do have measures to combat directed attacks against specific documents. In the absence of such a storage substrate though, identity certificates should either be stored at a separate storage system offering stronger safeguards against denial of service, be bundled with the associated document at some storage cost, or be decapsulated and stored at the KAS. Given our expected performance characteristics of the KAS, the third option seems attractive.
Time stamping digital signatures to extend their lifetime relies on a fundamental premise: that it is harder to break a time stamp than it is to break a digital signature. In fact, this is not trivially true. Time stamping and digital signatures rely on similar cryptographic constructs that build on the conjectured intractability of certain mathematical problems (e.g., discrete logarithms in cyclical groups, factorization of large numbers) or on the conjectured irreversibility of complex one-way algorithms (e.g., the SHA1 hash function [24]). None of these basic building blocks is proven to be secure against arbitrary computational attacks in all realistic settings, even though their security is supported by overwhelmingly strong evidence [21, p. 87].
The difference, however, lies in that digital signatures employ a secret component, a signing key, which can be stolen, leaked, or (with great difficulty) recovered via brute computational force. Instead, the hashing schemes used in most time stamping systems have no such vulnerability, since they do not have a secret key component (also called a trapdoor). The only possible attack against such schemes is finding an algorithmic way to annul their computational intractability assumptions.
One technique used to safeguard TSSes against even such groundbreaking attacks is best described as ``hedging.'' Surety, Inc. [27] has patented the practice of concurrently using two different, independent hashing schemes. The hope is that if one of the two hashing schemes is found to have debilitating vulnerabilities, the strength of the other hashing scheme will last until the TSS can take counter-measures, e.g., reissue all time stamps using a new pair of hashing schemes that are still considered impenetrable. The low rate at which computational advances occur against state-of-the-art hashing schemes seems to support the adequacy of this technique.
Although the basic idea on which KASTS is founded is simple [15], we are not aware of a system design that actually takes advantage of it and works out the details, incorporating both time stamping of signatures and timed storage of old verification keys. The secure archival storage work we are aware of (for example, OceanStore [18], Cooper et al. [8], SFS-RO [12]) addresses mostly issues of data survivability, format redundancy, confidentiality on-the-wire or on disk, and authentication/authorization of clients and servers. Rosenthal et al. [26] describe a system for preservation of online scientific journals against malicious destruction. The authors voice their concern over the storage of signed documents, but give no definite solutions. We believe that the increasing preference of the business world towards electronic transaction records will only compound the necessity for a design such as ours.
Time stamping seems to be essential to conduct secure transactions with lasting effects in the digital world of the Internet. However, the number of researchers exploring this topic is surprisingly small. Haber and Stornetta [16] introduced the time stamping problem and suggested ways to build linking data structures among documents. Benaloh and de Mare [3], Buldas et al. [5], Goodrich et al. [14] and Naor et al. [23] explored more efficient linking schemes, in the time stamping setting or in that of authenticated dictionaries. A very detailed specification of a time stamping service was produced in the TIMESEC project [25].
Our KAS shares characteristics with earlier work using authenticated data structures, such as Merkle trees and their derivatives. Most notably, the work done by Kocher on the distribution of certificate revocation records [17] relies on this basic idea to distribute certificate revocation records inexpensively. A trusted server creates a binary linking data structure (a Certificate Revocation Tree or CRT) out of all current certificate revocation records. Then, the digest of the tree is distributed securely by that trusted server, but the tree itself is distributed insecurely by untrusted servers. A verifier can always check the validity of a revocation record, as long as a proof of that record's existence in the tree is available and the signed digest of the tree can be retrieved securely. The KAS is more general than the CRT mechanism, in that it maintains timed snapshots of certificates and their revocation or expiration status, to allow the validation of old signatures produced with now-defunct signing keys.
The system we propose is complementary to the basic idea of the Eternity Service [2], for a survivable, incorruptible archive of documents, though intended for a much ``tamer'' environment. We approach the more hostile environment foreseen by Anderson [2] in future work.
The basic assumptions throughout this paper are that only one TSS and CA exist, that they are both trusted by everyone, and that they are expected to live forever, as far as the stored documents are concerned. This, unfortunately, is neither practical nor realistic.
Many distinct, competing Certification Authorities exist at the time of this writing. They make revenue out of issuing certificates to their clients and remaining online so as to verify those certificates at a later time. They also capitalize on reputation, how much they are trusted to do their job well, and by how many people.
However, CAs are also corporate entities, which may not be trusted by everyone. They must abide by the laws of the land in which they are incorporated and they are staffed by humans who may abide by the same or different laws and who may be coerced to act in ways that do not necessarily parallel the common good, or the good of every single potential client. In that sense, a single CA is not bound to be trusted by everyone in the world. As long as all the participants in a transaction requiring identity certification trust the same CA, all is well. However, in the increasing diversity of electronic transactions, expecting all participants in all transactions to trust the same third party might be considered utopistic. Although fewer commercial TSSes than CAs are in operation today, we expect the same argument to hold for time stamping.
Finally, both CAs and TSSes must obey the laws of business, under which companies come, and very frequently, go. In light of the big market upheaval of the late 1990's and the early 2000's, it would be unreasonably optimistic to assume that any single CA or TSS is going to exist with certainty for a long period of time.
Without the assumptions of CA and TSS uniqueness, global trust and immortality, building a system equivalent to KASTS as described in this paper becomes significantly less straightforward. We motivate, describe and design such a system in [ 20], using randomized Byzantine fault-tolerant agreement protocols. However, it remains future work to build, evaluate and prove correct a system of such complexity.
In this paper we motivate, design and argue for the use of time stamping and timed storage of signature verification keys to enable the long-term archival storage of signed documents.
The need for time stamping and storage of signature verification keys arises from the inherently short life of digital signatures, especially compared to long-lived documents such as contracts, property titles, transaction records or even works of art.
We design KASTS, an extension to conventional archival storage systems for signed documents, using a Time Stamping Service, and a Key Archival Service that maintains timed snapshots of valid signature verification keys at different times in the past.
We argue that building and operating KASTS is feasible, based on experience with existing TSSes, CAs and archival storage services. In addition, the KAS has low storage requirements (on the order of NlogN, N is the number of different key records being archived) and has expected request rates similar to those of a CA or TSS.
This work is supported by the Stanford Networking Research Center, by DARPA (contract N66001-00-C-8015) and by Sonera Corporation. Petros Maniatis is supported by a USENIX Scholar Fellowship. We would like to thank Ed Swierk for several close reads of our drafts, Mema Roussopoulos, Henry Tirri and the anonymous reviewers for their helpful comments on this paper, as well as Mahadev Satyanarayanan, our paper shepherd, for his guidance.
|
This paper was originally published in the
Proceedings of the FAST '02 Conference on File and Storage Technologies, January 28-30, 2002, Doubletree Hotel, Monterey, California, USA.
Last changed: 27 Dec. 2001 ml |
|