On Auditing Elections When Precincts Have Different Sizes

Javed A. Aslam
College of Computer and Information Science
Northeastern University
Boston, MA 02115
jaa@ccs.neu.edu

Raluca A. Popa and Ronald L. Rivest
Computer Science and Artificial Intelligence Laboratory
Massachusetts Institute of Technology
Cambridge, MA 02139
ralucap,rivest@mit.edu

Abstract

We address the problem of auditing an election when precincts may have different sizes. Prior work in this field has emphasized the simpler case when all precincts have the same size. Using auditing methods developed for use with equal-sized precincts can, however, be inefficient or result in loss of statistical confidence when applied to elections with variable-sized precincts.

We survey, evaluate, and compare a variety of approaches to the variable-sized precinct auditing problem, including the SAFE method [11] which is based on theory developed for equal-sized precincts. We introduce new methods such as the negative-exponential method ``NEGEXP'' that select precincts independently for auditing with predetermined probabilities, and the ``PPEBWR'' method that uses a sequence of rounds to select precincts with replacement according to some predetermined probability distribution that may depend on error bounds for each precinct (hence the name PPEBWR: probability proportional to error bounds, with replacement), where the error bounds may depend on the sizes of the precincts, or on how the votes were cast in each precinct.

We give experimental results showing that NEGEXP and PPEBWR can dramatically reduce (by a factor or two or three) the cost of auditing compared to methods such as SAFE that depend on the use of uniform sampling. Sampling so that larger precincts are audited with appropriately larger probability can yield large reductions in expected number of votes counted in an audit.

We also present the optimal auditing strategy, which is nicely representable as a linear programming problem but only efficiently computable for small elections (fewer than a dozen precincts). We conclude with some recommendations for practice.

1 Introduction

Post-election audits are an essential tool for ensuring the integrity of election outcomes. They can detect, with high probability, both errors due to machine mis-programming and errors due to malicious manipulation of electronic vote totals. By using statistical samples, they are quite efficient and economical. This paper explores auditing approaches that achieve improved efficiency (sometimes by a factor of two or three, measured in terms of the number of votes counted) over previous methods.

Suppose we have an election with $n$ precincts, $P_1$, ..., $P_n$. Let $v_i$ denote the number of voters who voted in precinct $P_i$; we call $v_i$ the ``size'' of the precinct $P_i$. Let the total number of such voters be $V=\sum_i v_i$. Assume without loss of generality that $v_1 \ge v_2 \ge \cdots \ge v_n$.

We focus on auditing precincts as opposed to votes because this is the common form of auditing encountered in practice. If one is interested in sampling votes, then the results in Aslam et al. [1] apply because the votes can be modeled as precincts of equal size (in particular, of size one). In this paper, we are interested in the more general problem, that is, when precincts have different sizes.

Precinct sizes can vary dramatically, sometimes by an order of magnitude or more. See Figure 2.

Methods for auditing elections must, if they are to be efficient and effective, take such precinct size variations into account.

Suppose further that in precinct $P_i$ we have both electronic records and paper records for each voter. The electronic records are easy to tally. For the purposes of this paper, the paper records are used only as a source of authoritative information when the electronic records are audited. They may be considered more authoritative since the voters may have verified them directly. In practice, more care is needed, since the electronic records could reasonably be judged as more authoritative in situations where the paper records were obviously damaged or lost and the electronic records appear undamaged.

Auditing is desirable since a malicious party, the ``adversary,'' may have manipulated some of the electronic tallies so that a favored candidate appears to have won the election. It is also possible for a simple software bug caused the electronic tallies to be inaccurate. However, we focus on detecting malicious adversarial behavior because it is the more challenging task.

A precinct can be ``audited'' by re-counting by hand the paper records of that precinct to confirm that they match the electronic totals for that precinct. We ignore here the important fact that hand-counting may be inaccurate, and assume that any discrepancies are due to fraud on the part of the adversary. In practice, the discrepancy might have to be larger than some prespecified threshold to trigger a conclusion of fraud in that precinct.

See the overviews [8,13,6] for information about current election auditing procedures. In this paper we ignore many of the complexities of real elections; these complexities are addressed in other papers. We do so in order to focus on our central issue: how to select a sample of precincts to audit when the precincts have different sizes. See Neff [12], Cordero et al. [5], Saltman [17], Dopp et al. [7], and Aslam et al. [1], for additional discussion of the mathematics of auditing, and additional references to the literature.

1.1 Outline

We begin with an overview of the auditor's general approach in Section 2. In Section 3 we review the adversary's objectives and capabilities. Section 4 then reviews the auditor's strategy. Some known results for auditing when all precincts have equal size are discussed in Section 5. We next review in Section 6 the ``SAFE'' method, which deals with variable-sized precincts using the mathematics developed for equal-sized precincts, by first deriving a lower bound on the number of precincts that must have been corrupted, if the election outcome was changed. Section 7 introduces basic auditing methods, where each precinct is chosen independently according to a precomputed probability distribution. A particularly attractive basic auditing method is introduced in Section 8; this method is called the ``negative-exponential'' (NEGEXP) auditing method. We then consider audits where precincts are not chosen independently. Section 9 introduces the method of sampling with probability proportional to error bounds, with replacement (PPEBWR); a special case of this procedure is PPSWR, ``sampling with probability proportional to size, with replacement.'' Section 10 discusses vote-dependent auditing, where the probability of auditing a precinct depends on the actual vote counts for each candidate. Section 11 gives experimental results using data from Ohio and Minnesota. Section 12 presents a method based on linear programming for determining an optimal auditing procedure, which unfortunately appears to be computationally too expensive for practical use. Section 13 closes with discussion and recommendations for practice.

2 Auditing Objectives and Costs

We assume here that the election is a winner-take-all (plurality) election from a field of $k$ candidates.

After the election, the auditor randomly selects a sample of precincts for the post-election audit. In each selected precinct the paper ballots are counted by hand; the totals obtained in this manner are then compared with the electronic tallies. We assume that the paper ballots are maintained securely and that they can be accurately counted during the post-election audit.

The auditor wishes to assure himself (and everyone else) that the level of error and/or fraud in the election is likely to be low or nonexistent, or at least insufficient to have changed the election outcome. If the audit finds no (significant) discrepancies between the electronic and paper tallies, the auditor announces that no fraud was discovered, and the election results may be certified by the appropriate election official.

However, if significant discrepancies are found between the electronic and paper tallies, additional investigations may be appropriate. For example, state law may require a full recount of the paper ballots. Stark [19] gives procedures for incrementally auditing larger and larger samples when discrepancies are found, until the desired level of confidence in the election outcome is achieved.

When planning the audit, the auditor knows the number $r_{ij}$ of reported (electronic) votes for each candidate $j$ in precinct $i$, and the total size $v_i$ (total number of votes cast) of each precinct $P_i$. The auditor also knows the reported margin of victory, denoted $M^{(r)}$ of the winning candidate over the runner-up--this is the difference between the number of votes reported for the apparently victorious candidate and the number of votes reported for the runner-up. Larger audits are appropriate when the margins of victory are smaller (see, e.g., Norden et al. [13]).

2.1 Auditing objective

We believe that the audit should be designed to achieve a pre-specified level of confidence in the election outcome, i.e., when an election is ultimately certified, one should be confident, in a statistically quantifiable manner, that the election outcome is correct. It is the correct (and efficient) approach. Naive methods that audit a fixed fraction of precincts tend to waste money when the margin of victory is large, and provide poor confidence in the election outcome when the margin of victory is small. See McCarthy et al. [11].

In order to ensure that an election outcome is correct, one must be able to detect levels of fraud sufficient to change the outcome of the election. We thus assume the auditor desires to test at a certain significance level $\alpha$ that error or fraud is unlikely to have affected the election outcome. A well-designed audit can reduce the likelihood that significant fraud or error has gone undetected. A significance level of $\alpha=0.05$ means that the chance that error large enough to have changed the election outcome will go undetected is one in twenty.

Let $c$ denote the ``confidence level'' of the audit, where $c = 1-\alpha .$ Thus, a test at significance level $\alpha=5\%$ provides a confidence level of $c=95\%$. This is independent of the way fraud was committed (at the level of the machine, precinct, vote or other) because we only model the overall fraud in our formulas. We follow Stark [19] in adopting as our null hypothesis ``the (electronic) election outcome is incorrect'', so that $\alpha$ is an upper bound on the probability that the null hypothesis will be rejected (i.e. that the electronic outcome will be accepted) when the null hypothesis is true (the electronic outcome is wrong).

2.2 Choosing a sample

Depending on the precinct sizes, the reported votes for each candidate, and thus the reported margin of victory, the auditor determines how to select an appropriately-sized random sample of precincts for auditing.

We explore three methods by which the auditor chooses a sample:

• [BASIC] The auditor determines a probability for each precinct that it will be audited, based on the precinct's size and on the overall margin of victory, and then independently selects each precinct with its specified probability. Such basic auditing strategies are discussed in Sections 7-8.

• [WITH REPLACEMENT] The auditor determines a probability for each precinct that it will be selected during a round, and does $t$ rounds of drawing with replacement to select the precincts to be audited. With ``sampling with replacement,'' a selected precinct is placed back into the collection of precincts and thus may be drawn more than once. Any precinct drawn at least once will be audited. Examples of this approach are the PPEBWR (sampling with probability proportional to error bounds with replacement) method of Section 9 and the PPSWR method: sampling ``with probability proportional to size, with replacement.''

• [OPTIMAL] The auditor determines a probability for each subset of precincts specifying the probability that that subset will be audited. This includes the optimal auditing strategy of Section 12.

2.3 Auditing cost

If all precincts have the same size, one may measure the cost of performing an audit in terms of the (expected) number of precincts audited. If precincts have a variety of sizes, the (expected) number of votes counted appears to be a better measure of auditing cost. The auditing cost is most reasonably measured in person-hours, which will be proportional to the number of votes recounted. The overall cost may have a constant additive term for each precinct (a setup cost), but this should be small compared to the cost to audit the votes.

3 Adversarial Objectives

We assume the adversary wishes to corrupt enough of the electronic tallies so that his favored candidate wins the most votes according to the reported electronic tallies. Without loss of generality, we'll let candidate $1$ be the adversary's favored candidate. The adversary tries to do his manipulations in such a way as to minimize the chance that his changes to the electronic tallies will be caught during the post-election audit.

Let $a_{ij}$ denote the actual number of (paper) votes for candidate $j$ in precinct $i$, and let $r_{ij}$ denote the reported number of (electronic) votes for candidate $j$ in precinct $i$. With no adversarial manipulation, we will have $r_{ij}=a_{ij}$ for all $i$ and $j$. We ignore in this paper small explainable discrepancies that can be handled by slight modifications to the procedures discussed here.

We thus have for all $i$: $\sum_j a_{ij} = \sum_j r_{ij} = v_i ;$ the total number of paper votes cast in precinct $i$ is equal to the number of electronic votes cast in precinct $i$; this number is $v_i$, the ``size'' of precinct $i$. (Our techniques can perhaps be extended to handle situations where such reconciliation is not done; we have not yet examined this question closely.)

Let $A_j$ denote the total actual number of votes for candidate $j$: $A_j = \sum_i a_{ij} ,$ and let $R_j$ denote the total number of votes reported for candidate $j$: $R_j = \sum_i r_{ij} .$ The adversary's favored candidate, candidate $1$, will be the winner of the electronic report totals if $R_1 > \max(R_2, R_3, \ldots, R_k) .$

We assume for now that the election is really between candidate $1$ and candidate $2$, so that the adversary's objective is to ensure that candidate $1$ is reported to win the election and that candidate $2$ is not. There may be other candidates in the race, but for the moment we'll assume that they are minor candidates. It is also convenient to consider ``invalid'' and ``undervote'' to be such ``minor candidates'' when doing the tallying.

The adversary can manipulate the election in favor of his or her desired candidate by shifting the electronic tallies from one candidate to another. He or she might move votes from some candidate to candidate $1$. Or move votes from candidate $2$ to some other candidate. These manipulations can change the election outcome, and yield a false ``margin of victory.'' The margin of victory plays a key role in our analysis.

Let $M^{(a)}$ denote the ``actual margin of victory'' (in votes) of candidate $1$ over candidate $2$: $M^{(a)} = A_1 - A_2 .$ Let $M = M^{(r)}$ denote the ``reported margin of victory'' (in votes) for candidate $1$ over candidate $2$: $M = M^{(r)} = R_1 - R_2 .$ Note that $M = M^{(r)}$ will be known to the auditor at the beginning of the audit, but that $M^{(a)}$ will not.

The adversary may be in a situation initially where $M^{(a)}<0$ (i.e. $A_1<A_2$); that is, his or her favored candidate, candidate $1$, has lost to candidate $2$. The adversary must, in order to change the election outcome, manipulate the (electronic) votes so that $M^{(r)}>0$ (i.e. so that $R_1 > R_2$) and do so in a way that goes undetected.

The ``error'' $e_i^*$ in favor of candidate $1$ introduced in the margin of victory computation in precinct $i$ by the adversary's manipulations is (in votes):

$$e^*_i = (r_{i1}-r_{i2}) - (a_{i1} - a_{i2}) ;$$

Here $(r_{i1}-r_{i2})$ is the reported margin of victory for candidate $1$, while $(a_{i1}-a_{i2})$ is his actual margin of victory, so their difference is the amount of error introduced by the adversary in the margin of victory.

An upper bound on the amount by which the adversary can improve the margin of victory in favor of his candidate in precinct $1$ is:

$$e^*_i \leq 2a_{i2} + \sum_{j>2} a_{ij} = v_i - a_{i1} + a_{i2} .$$ (1)

Each vote moved from candidate $2$ to candidate $1$ improves the margin by $2$ votes, and each vote moved from candidate $j$ ($j>2$) to candidate $1$ improves the margin by $1$ vote. (See also Stark [19].)

Let $E^*$ denote the total error (in votes, from all precincts) introduced in the margin of victory computation by the adversary: $E^* = \sum_i e^*_i .$ Clearly, $M^{(r)} = M^{(a)} + E^* .$ That is, the reported margin of victory is equal to the actual margin of victory, plus the error introduced by the adversary.

The adversary has to introduce enough error $E^*$ so that the reported margin of victory $M^{(r)}$ becomes positive, even though the initial (actual) margin of victory $M^{(a)}$ is negative. Thus, the amount of error introduced satisfies both of the inequalities: $E^* > -M^{(a)}$ and $E^* > M^{(r)} .$ The second inequality is of most interest to the auditor, since at the beginning of the audit the auditor knows $M^{(r)}$ but not $M^{(a)}$. For convenience, we shall use $M = M^{(r)}$ in the sequel, and let $m$ denote the fraction of votes represented by the margin of victory: $m = M / V\$ (recall that $V$ denotes the total number of votes cast: $V=\sum_i v_i$).

We assume here that the adversary wishes to change the election outcome while minimizing the probability of detection--that is, while minimizing the chance that one or more of the precincts chosen have been corrupted. If the post-election audit fails to find any error, the adversary's candidate might be declared the winner, while in fact some other candidate (e.g. candidate $2$) actually should have won.

The adversary might not be willing to corrupt all available votes in a precinct; this would generate too much suspicion. Dopp and Stenger [7] suggest that the adversary might not dare to flip more than a fraction $s=0.20$ of the votes in a precinct. The value $s$ is also denoted WPM in the literature, and called the Within-Precinct-Miscount.

Our auditing methods in this paper depend heavily on the use of such upper bounds on $e^*_i$, that is, on the maximum amount by which the adversary can change the margin of victory in each precinct. We use $e_i$ to denote such an upper bound on $e^*_i$. Following Dopp and Stenger, we would have as an upper bound $e_i$ for $e_i^*$:

$$e_i = 2 s v_i .$$ (2)

We call this the ``Linear Error Bound Assumption''. The factor of $2$ occurs since we assume that the adversary is able to switch $s v_i$ votes from candidate $2$ to candidate $1$.

We may also presume that the adversary knows the general form of the auditing method. Indeed, the auditing method may be mandated by law, or described in public documents. While the adversary may not know which specific precincts will be chosen for auditing, because they are determined by rolls of the dice or other random means, the adversary is assumed to know the method by which those precincts will be chosen, and thus to know the probability that any particular precinct will be chosen for auditing.

We let $Q$ denote the set of corrupted precincts, and let $b$ denote the number $\left\vert Q\right\vert$ of corrupted precincts. In this discussion, we assumed that ``reconciliation'' is performed when the election is over, confirming that the number of votes recorded electronically is equal to the number of votes recorded on paper; an adversary would presumably not try to make these totals differ, but only shift the electronic tallies to favor his candidate at the expense of other candidates. If ``reconciliation'' is not performed and an adversary reduces the number of votes cast in a precinct that is, say, known to be favorable to the opponent, our techniques can still discover the fraud within the desired confidence level. This happens if the resulting change in the margin of victory (expressed in votes) is at most the error bound $e_i$ of the resulting precinct. This condition holds when the adversary decreases the total number of votes cast in the precinct by at most a factor of $1+2s$ ($\approx -30\%$ for $s = 20\%$). Arguably, if the final number of votes cast is reduced even more, such a dramatic corruption should be detected.

4 Auditing Method

4.1 Types of audits

There are many different ways to perform an audit; see Norden et al. [13] for discussion. In this paper we focus on how the sample is selected; an auditing method is one of following five types:

A fixed audit determines the amount of auditing to do by fiat--e.g., it selects a fixed number of precincts (or votes) to be counted (or perhaps a fixed percentage, instead of a fixed number). It does not pay attention to the precinct sizes, the reported margin of victory, or the reported vote counts. Fixed audits are simple to understand, but are frequently very costly or statistically weak.

If an audit is not a fixed audit, it is an adjustable audit--the size of the audit is adjustable according to various parameters of the election. There are four types of adjustable audits, in order of increasing utilization of available parameter information.

The first (and simplest) type of adjustable audit is a margin-dependent audit. Here the selection of precincts to be audited depends only on the reported margin of victory $M$. An election that is a landslide (with a very large margin of victory) results in smaller audit sample sizes than an election that is tight.

In order for an audit to provide a guaranteed level of confidence in the election outcome while still being efficient (it does not audit significantly more votes/precincts than needed), it must be margin-dependent (or better). The remaining three types of adjustable audits are refinements of the margin-dependent audit. Margin-dependent audits have been proposed by Saltman [17], Lobdill [10], Dopp and Stenger [7], McCarthy et al. [11], among others.

The second type of adjustable audit is a size-dependent audit. Here the selection of precincts to be audited depends not only on the reported margin of victory $M$ but also on the precinct sizes $\{v_i\}$. A size-dependent audit audits larger precincts with higher probability and audits small precincts with smaller probability. This reflects the fact that the larger precincts are ``juicier targets'' for the adversary. Overall, the total amount of auditing work performed may easily be less than for an audit that does not take precinct sizes into account.

The third type of adjustable audit is a vote-dependent audit. Here the selection of precincts to be audited depends not only on the reported margin of victory $M$ and the precinct sizes $\{v_i\}$, but also on the reported vote counts $\{r_{ij}\}$. A vote-dependent audit can reflect the intuition that if precinct $A$ reports more votes for candidate $1$ (the reported winner) than precinct $B$ reports, then precinct $A$ should perhaps be audited with higher probability, since it may have experienced a larger amount of fraud. See Section 10; also see Calandrino et al. [3].

The fourth type of adjustable audit is a history-dependent audit. Here the selection of precincts to be audited depends not only on the reported margin of victory $M$, the precinct sizes $\{v_i\}$, and the reported vote counts $\{r_{ij}\}$, but also on records of similar data for previous elections. A precinct whose reported vote counts are at odds with those from previous similar elections becomes more likely to be audited.

Here we consider what we call an error-bound-dependent audit, where the auditor computes for each precinct $P_i$ an error bound $e_i$ on the error (change in margin of victory) that the adversary could have made in that precinct. An error-dependent audit is a special case of a size-dependent audit, if the error bound for precinct $P_i$ depends only the size $v_i$ of the precinct, as in the Linear Error Bound Assumption of equation (2) where the error bound is simply proportional to the precinct size. The linear error bound assumption leads, for example, to sampling strategies of the form ``probability proportional size,'' as we shall see, since our ``probability proportional to error bound'' strategy becomes ``probability proportional to size'' when ``error bound is proportional to size.''

However, the error-dependent audit could be a special case of a vote-dependent audit, if the error bound $e_i$ depends on the votes cast in precinct $P_i$. We explore this possibility in Section 10. In any case, it is useful to formally ``decouple'' the error bound from the precinct size; we let $E = \sum_i e_i$ denote the sum of these error bounds.

4.2 High-level structure of an audit

The post-election audit involves the following steps.

1. Determine the relevant parameters of the election (margin of victory $M$, precinct sizes $\{v_i\}$, reported vote counts $\{r_{ij}\}$, and error bounds $\{e_i\}$).

2. Select a sample $\cal S$ of precincts to be audited.

3. Count by hand all the paper ballots for every precinct in the sample. If precinct $P_i$ is audited, then the actual vote counts $a_{ij}$ and the votes that were changed become known to the auditor. If no discrepancy is observed, precinct $P_i$ is deemed to be good (i.e. uncorrupted); otherwise precinct $P_i$ is detected as being bad (i.e. corrupted).

4. If no errors are found in any audited precinct, announce that candidate $1$ (the reported winner of the electronic totals) is the winner of the election. Otherwise, trigger some enlarged examination (escalate the audit).

We do not discuss triggers and escalation in this paper, although such discussion is very important and needs to be included in any complete treatment of post-election auditing (see Stark [19]).

4.3 Selecting a sample

How should the auditor select precincts to audit? The auditor wishes to maximize the probability of detection: the probability that the auditor audits at least one bad precinct (with nonzero error $e^*_i$), if there is sufficient error to have changed the election outcome. The auditor's method should be randomized, as is usual in game theory; this unpredictability prevents the adversary from knowing in advance which precincts will be audited.

We first review auditing procedures to use when all precincts have the same size. We then proceed to discuss the case of interest in this paper, that is, when precincts have a variety of sizes.

5 Equal-sized Precincts

This section briefly reviews the situation when all $n$ of the precincts have the same size $v$ (so $V = nv$). We adopt the Linear Error Bound Assumption ($e_i\le 2sv_i$) of equation (2) in this section. Let $b$ denote the number of precincts that have been corrupted. Since an adversary who changed the election outcome must have introduced sufficient error, $2 b s v \ge M ,$ so that (see Dopp et al. [7]) $b = M / 2 s v$ is the minimum number of precincts the adversary could have corrupted.

When all precincts have the same size, the auditor should pick an appropriate number $u$ of distinct precincts uniformly at random to audit. See Neff [12], Saltman [17], or Aslam et al. [1] for discussion and procedures for calculating appropriate audit sample sizes.

The probability of detecting at least one corrupted precinct in a sample of size $u$ is $1 - {{n-b}\choose{u}} / {{n}\choose{u}} .$ By choosing $u$ so that

$$u \ge (n - (b-1)/2)(1-\alpha^{1/b})$$ (3)

one has a test at significance level $\alpha$ (i.e., at ``confidence level'' $c=1-\alpha$): with probability at least $c=1-\alpha$ one or more corrupted precincts will be detected, if there are at least $b$ corrupted precincts (for detailed explanation see Aslam et al. [1].)

Rivest [16] suggests approximating equation (3) by a ``Rule of Thumb'': $u \ge 1/m ;$ one over the (fractional) margin of victory $m = M / V\$. For equal-sized precincts (with $s=0.20$), this gives remarkably good results, corresponding to a confidence level of at least $c=92\%$.

6 The SAFE Auditing Method

The ``SAFE'' auditing method by McCarthy et al. [11] is perhaps the best-known approach to auditing elections; it adapts the approach for handling equal-sized precincts discussed above to handle variable-sized precincts.

In 2006 Stanislevic [18] presented a conservative way of handling precincts of different sizes; this approach was also developed independently by Dopp et al. [7]. This method is the basis for the SAFE auditing procedure.

It assumes that the adversary corrupts the larger precincts first, yielding a lower bound on the number $b_{min}$ of precincts that must have been corrupted if the election outcome was changed. The auditor can then use $b_{min}$ in an auditing method that samples precincts uniformly. More precisely, the auditor knows that if the adversary changed the election outcome, he or she must have corrupted at least $b_{min}$ precincts, where $b_{min}$ is the least integer such that $2s \sum_{1\le i\le b_{min}} v_i \ge M .$ (Recall our assumption that $v_1\ge v_2 \ge \cdots v_n$.) Then the auditor draws a sample of size $u$ precincts uniformly, where $u$ satisfies (3); this ensures a probability of at least $1-\alpha$ that a corrupted precinct will be sampled, if the adversary produced enough fraud to have changed the election outcome.

7 Basic Auditing Methods

This section reviews ``basic'' auditing methods, where each precinct is audited independently with a precinct-specific probability determined by the auditor. Many interesting auditing procedures are basic auditing procedures. We try restricting our attention to ``basic'' methods in an effort to make some of the math simpler; although we shall see in Section 9 that the math is actually fairly simple for some non-basic methods.

This section assumes that the auditor will audit each precinct $P_i$ independently with some probability $p_i$, where $0\le p_i\le 1$. The auditing method is thus determined by the vector ${\bf p} = (p_1, p_2, \ldots, p_n)$. The probabilities $p_i$ sum to the expected number of precincts audited; they do not normally sum to $1$ because commonly we audit more than one precinct. The expected workload (i.e., the expected number of votes to be counted) is

$$v({\bf p}) = \sum_i p_i v_i\$$ (4)

because we audit each set of $v_i$ votes with probability $p_i$. We assume that vectors ${\bf p} = (p_1, p_2, \ldots, p_n)$, ${\bf v} = (v_1, v_2, \ldots, v_n)$, and ${\bf e} = (e_1,e_2,\ldots,e_n)$, are public knowledge and known to everyone, including the adversary. (We ignore the fact that in practice, it might be difficult for the adversary to obtain some of this information, in which case the auditor's success at detecting fraud might even be somewhat greater than we calculate here.)

In the basic auditing procedures we describe in this paper, the chance of auditing a precinct is independent of the error introduced into that precinct by the adversary. Thus, we can assume that the adversary makes the maximum change possible in each corrupted precinct: $e^*_i = e_i$. This helps the adversary reduce the number of precincts corrupted and reduces the chance of him being caught during an audit.

A basic auditing method is not difficult to implement in practice in an open and transparent way. A table is printed giving for each precinct $P_i$ its corresponding probability $p_i$ of being audited. For each precinct $P_i$, four ten-sided dice are rolled to give a four-digit decimal number $x_i=0.d_1d_2d_3d_4$. Here $d_j$ is the digit from the $j$-th dice roll. If $x_i < p_i$, then precinct $P_i$ is audited; otherwise it is not. The probability table and a video-tape of the dice-rolling are published. See [5] for more discussion on the use of dice.

One very nice aspect of basic auditing methods is that we can easily compute the exact significance level for ${\bf p}$. Given ${\bf p}$, one can use a dynamic programming algorithm to compute the probability of detecting an adversary who changes the margin by $M$ votes or more. This algorithm, and applications of it to heuristically compute optimal basic auditing strategies, are given by Rivest [15].

8 Negative-exponential Auditing Method (NEGEXP)

This section presents the ``negative exponential'' auditing method NEGEXP, which appears to have near-optimal efficiency, and which is quite simple and elegant. Depending on the details of the audit being performed, either NEGEXP or the PPEBWR of the next section may be the better practical choice.

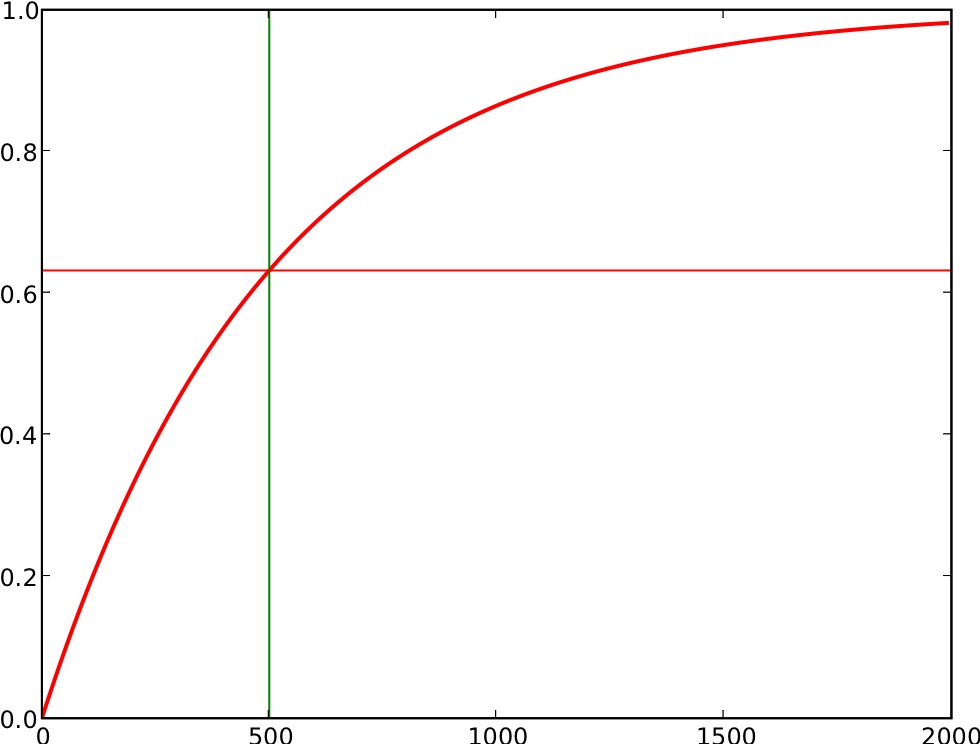
The ``negative-exponential'' auditing method (NEGEXP) is a heuristic basic auditing method. Intuitively, the probability that a precinct is audited is one minus a negative exponential function of the error bound for a precinct. See Figure 1.

The ``value'' to the adversary of corrupting precinct $i$ is assumed to be $e_i$, the known upper bound on the amount of error (in the margin of victory) that can be introduced in precinct $i$. In a typical situation $e_i$ might be proportional to $v_i$; this is the Linear Error Bound Assumption.

Intuitively, the auditor wants to make the adversary's risk of detection grow with the ``value'' a precinct has to the adversary; this motivates the adversary to leave untouched those precincts with large error bounds. The adversary thus ends up having to corrupt a larger number of smaller precincts, which increases his or her chance of being caught in a random sample.

The motivation for the NEGEXP method is the following strategy for the auditor: determine auditing probabilities so that the chance of auditing at least one precinct from the set of corrupted precincts depends only on the total error bound of that set of precincts. For example, the adversary will then be indifferent between corrupting a single precinct with error bound $e_\ell = (e_i+e_j)$ or corrupting two precincts with respective error bounds $e_i$ and $e_j$. The chance of being caught on $P_\ell$ or being caught on at least one of $P_i$ and $P_j$ should be the same.

This implies that the auditor does not audit each $P_i$ with probability $q_i=1-p_i$, where

$$q_i = \exp(-e_i/w),$$ (5)

and where $w$ is some fixed constant. Thus, if $e_\ell = e_i + e_j$, we have

$$\begin{eqnarray*} q_\ell & = & \exp(-e_\ell / w) \;\; = \;\; \exp(-(e_i + e_j) / w) \\ & = & \exp(-e_i/w) \cdot \exp(-e_j/w), \end{eqnarray*}$$

from which we can conclude that $q_\ell = q_i q_j$ as desired. Since $w$ is constant, $q_i^{1/e_i}$ is constant.

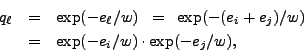
Our NEGEXP auditing method thus yields, from (5),

$$p_i = 1 - \exp(-e_i/w) ;$$ (6)

see Figure 1. The name ``negative exponential'' refers to the negative exponential appearing in this formula.

With the NEGEXP method, as the error bound $e_i$ increases, the probability of auditing $P_i$ increases, starting off at $0$ for $e_i = 0$ and increasing as $e_i$ increases, and levelling off approaching $1$ asymptotically for large $e_i$. The chance of auditing $P_i$ passes $(1-1/e) \approx 63\%$ as $e_i$ exceeds $w$.

Figure: The negative exponential function $p_i = 1-\exp(-e_i/w)$ for $w=500$. The horizontal axis is the error bound $e_i$; the vertical axis is the audit probability $p_i$. Here $w$ is a arbitrary positive parameter set to achieve a given overall confidence level. Precincts with error bounds larger than $w$ have at least a 63% chance of being audited.

The value $w$ can be thought of as approximating a ``threshold'' value: precincts with $e_i$ larger than $w$ have a fairly high probability of being audited, while those smaller than $w$ have a smaller chance of being audited. As $w$ decreases, the auditing gets more stringent: more precincts are likely to be audited.

An auditor may choose to use the NEGEXP auditing method of equation (6), and choose $w$ to achieve an audit with a given significance level.

The design of NEGEXP makes this easy, since NEGEXP has the property that for any set $Q$ of precincts that the adversary may choose to corrupt satisfying $\sum_{i\in Q} e_i \ge M ,$ the chance of detection is at least

$$1 - \prod_{i\in Q} \exp(-e_i/w) \ge 1 - \exp(-M/w) .$$ (7)

The reason is that the probability of detecting at least one corrupted precinct is one minus the probability of not detecting any of the corrupt precincts in $Q$. The latter is the product of the probability of not detecting any precinct in $Q$, that is $\prod_{i\in Q} q_i$, yielding the desired chance of detection $1 - \prod_{i\in Q} q_i$.

This holds no matter what set of precincts, $Q$, the adversary chooses.

How can an auditor audit enough to achieve a given significance level? The relationship of equation (7) gives a very nice way for the auditor to choose $w$: by choosing

$$w = \frac{M}{-\ln(\alpha)}$$ (8)

the auditor achieves a test with significance at least $\alpha$: there is probability at least $1-\alpha$ of catching an error of at least $M$, no matter what set of precincts $Q$ the adversary uses. For example, by choosing $w \approx M/3$, the auditor tests at significance level $5\%$ for margin-shift error of size $M$ or greater. If we use equation (8) to determine $w$, then we have

$$p_i = 1 - \alpha^{e_i/M} .$$ (9)

With the Linear Error Bound Assumption, this becomes

$$p_i = 1 - \alpha^{2sv_i / M} .$$ (10)

However, an auditor may want to adjust the probabilities $p_i$ to achieve a desired expected number of precincts audited or a desired expected number of votes counted. He or she can use any of several standard packages for root-finding to find a value of $w$ that meets the given constraints. In any case, it is easy to print out a table of the precinct probabilities $p_i$, so that one can utilize a suitable dice-based protocol for actually picking the precincts. We also note that if $e_i = \hbox{const}*v_i$,

$$p_i = 1 - \exp(-e_i/w) \approx e_i/w \approx \hbox{const}*v_i/w$$

when $e_i$ is small relative to $w$, so that the NEGEXP method can be viewed as an approximation to a method whereby precincts are selected with probability proportional to their size (PPS).

This completes our description of the NEGEXP auditing method. Section 11 presents experimental results for this method. In the next section, we describe a different method (PPEBWR), which turns out to be nearly identical (but slightly better) in efficiency to the NEGEXP method, and which in some circumstances may be easier to work with, although it is somewhat less flexible.

9 Sampling with Probability Proportional to Error Bound with Replacement
(PPEBWR)

This section presents the ``PPEBWR'' (sampling with probability proportional to error bound, with replacement) auditing strategy. It is simple to implement, and does at least as well as the NEGEXP method. Indeed, the PPEBWR is an excellent method in many respects, and we recommend its use, although the NEGEXP may be more useful when additional flexibility is required (e.g. having multiple races with overlapping jurisdictions).

Consider auditing an election with non-uniform error bounds ${\bf e} = (e_1,e_2,\ldots,e_n)$ where $E = \sum_i e_i$. Let $M$ be the (minimum) level of error one wishes to detect; $M$ is the margin of victory. Consider the following sampling-with-replacement procedure. Form a sampling distribution ${\bf p}$ over the precincts:

$${\bf p} = (e_1/E, e_2/E, \ldots, e_n/E),$$ (11)

and draw $t$ samples with replacement according to ${\bf p}$. Eliminate duplicates, and audit the set of precincts obtained. It is easy to use dice to select the precincts to be audited in a public and transparent manner. The probabilities $p_i = e_i/E$ of equation (11) can be computed, and then their cumulative values are computed: $\hat{p_i} = \sum_{1\le j \le i} p_j$ and printed out. For each of $t$ rounds, four decimal dice are rolled, and the four digits $d_1$, $d_2$, $d_3$, and $d_4$ are combined to yield a four-digit decimal number $x=0.d_1d_2d_3d_4$. Then $P_i$ is marked for auditing if $\hat{p}_{i-1} \le x < \hat{p}_i .$ The printed tables and a videotape of the dice-rolling are made publicly available. This approach only requires rolling $t$ random numbers, whereas the basic methods of Sections 7-8 require rolling $n$ random numbers. When the Linear Error Bound Assumption holds, the PPEBWR method performs sampling with probability proportional to size within each round. We call the overall method sampling with probability proportional to size, with replacement, or ``PPSWR''. The use of sampling with probability proportional to size (PPS) is well-known in a number of fields, including statistics and survey-sampling (see Hansen and Hurwitz [9] and Cochran [4, Ch. 9A]) and financial auditing, where dollar-unit sampling (DUS) samples accounts with probability proportional to their book value (see [14]). Some results from this literature may also be useful or relevant to auditing elections. Indeed, Stark has suggested that some of our results may be alternatively derivable from results (such as the Stringer bound [21]) in this literature. We introduce notation to distinguish the per-round selection probabilities (denoted by $p_i$) from the overall selection probabilities (denoted by $\pi_i$). The probability of selecting precinct $i$ at least once in $t$ rounds is one minus the probability of not selecting it in any round. The probability of not selecting precinct $i$ in one round is $1-p_i$ and over $t$ rounds is $(1-p_i)^t$. Hence, the probability of selecting precinct $i$ at least once in $t$ rounds is

$$\pi_i = 1 - (1-p_i)^t.$$ (12)

Precinct $P_i$ is audited if and only if it is not missed during each of the $t$ selection rounds, and $\pi_i$ denotes this overall probability that precinct $P_i$ is audited.

While the per-round probabilities $p_i$ are proportional to size, the overall probabilities $\pi_i$ are generally not: note that as $t$ gets large the overall probability of selection of each precinct approaches $1$. Actually, the overall probabilities $\pi_i$ turn out to be nearly identical (but slightly less) than those computed by the NEGEXP method.

We now show how to determine the number $t$ of rounds for a desired audit significance level $\alpha$. Any set of precincts whose total error bound is at least $M$ will have probability weight at least $M/E$. Similar to the derivation in (12) where we replace $p_i$ by $M/E$ , the probability that at least one such precinct is detected is at least

$$1 - (1 - M/E)^t.$$

We want this to be at least $1-\alpha$ for the desired confidence level of $1-\alpha$; solving

$$1 - (1 - M/E)^t \geq 1 - \alpha$$

for $t$, we obtain that

$$t_* = \frac{\ln(\alpha)}{\ln(1-M/E)}$$ (13)

is the minimum sufficient sample size. Thus, drawing at least $t_*$ samples, with replacement, will guarantee catching fraud of size sufficient to have changed the election outcome, with probability at least $1-\alpha$.

We can show that the probability $\pi_i$ with which any given precinct $P_i$ is audited is slightly smaller than the negative-exponential audit probability leading to a slightly more efficient sample size. Our experimental results have shown that the difference in audit sizes of the two methods is nevertheless small.

The costs of the PPEBWR strategy are easy to compute.

The expected number of precincts audited is $\sum_i \pi_i,$ and the expected number of votes audited is $\sum_i v_i \pi_i.$

Note that in both NEGEXP and PPEBWR the confidence level achieved is at least $c=1-\alpha$ no matters what strategy the adversary follows (within the assumptions made). This includes the best possible strategy in which the adversary is aware of our auditing scheme and minimizes his detection probability; he/she still cannot lower this probability beyond $c=1-\alpha$.

10 Vote-dependent Auditing

This section drops the assumption that error bounds are proportional to precinct size, i.e., that $e_i = 2s v_i .$ How else can the auditor obtain a bound on the error? Instead of having a size-dependent audit, he or she may have a vote-dependent audit, using the fact that $e_i^* \le e_i$ if

$$e_i = 2r_{i1} + \sum_{j>2} r_{ij} = v_i + r_{i1} - r_{i2} ;$$

here we are measuring the margin of victory between candidate 1 and candidate 2.

If we are unsure who the ``runner-up'' is, we can take the maximum bound over any such ``runner-up'': $e_i = v_i + r_{i1} - \min_j r_{ij} .$ Note that the ``candidates'' used for the ``invalid'' or ``undervote'' tallies should be excluded--they cannot be winners or runners-up. These bounds $e_i$ will usually be larger than those obtained via a within-shift bound $2sv_i$, thus giving worse results. However, in a two-candidate race if a precinct votes almost entirely for the electronic runner-up, the new bound may be smaller.

Stark [19, Section 3.1] suggests ``pooling'' several obviously losing candidates to create an obviously losing ``pseudo-candidate'' to reduce the error bounds; this can also be applied here.

11 Experimental Results

We illustrate and compare the previously described methods for handling variable-sized precincts using data from Ohio. These results show that taking precinct size into account (e.g. by using NEGEXP or PPSWR) can result in dramatic reductions in auditing cost, compared to methods (such as SAFE) that do not.

11.1 Ohio 2004 CD-5

Mark Lindeman kindly supplied a dataset of precinct vote counts (sizes) for the Ohio congressional district 5 race (OH-05) in 2004. A total of $V=315540$ votes were cast in 640 precincts, whose sizes ranged from 1637 (largest) to 132 (smallest), a difference by a factor of more than 12. See Figure 2.

Figure 2: The first graph shows the distribution of 640 precinct sizes for Ohio 2004 Congressional District 5. A total of 315,540 votes were cast. The maximum precinct size was 1637, the average was 493, and the minimum was 132. The second graph shows the probability distribution for picking precincts in this example, using the NEGEXP method.

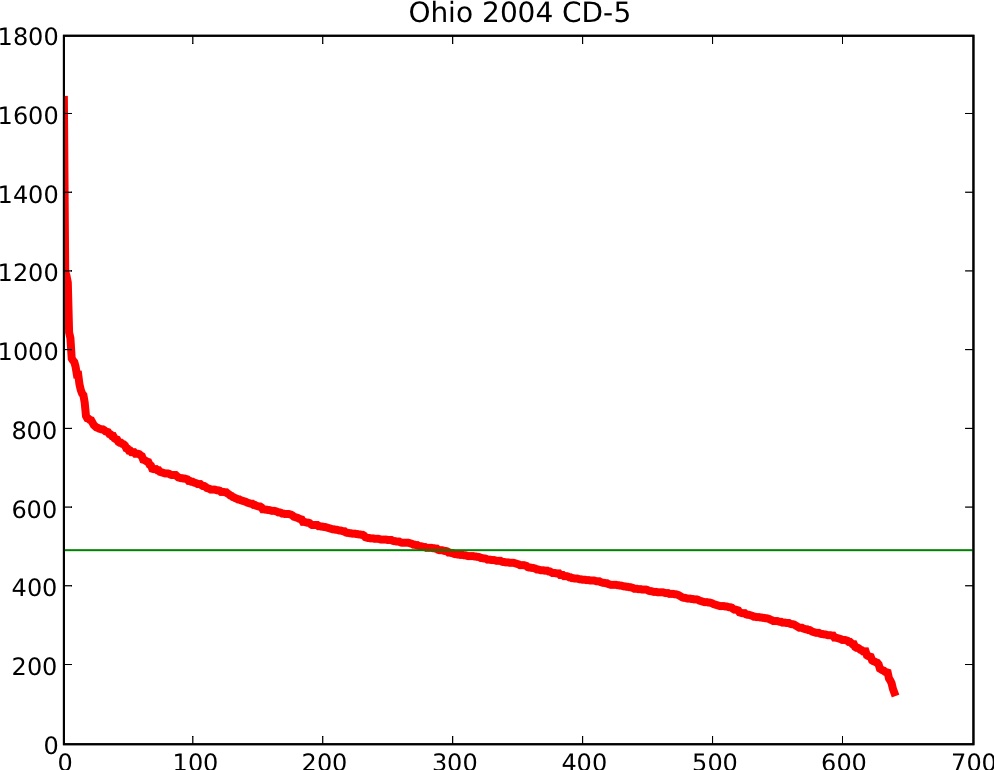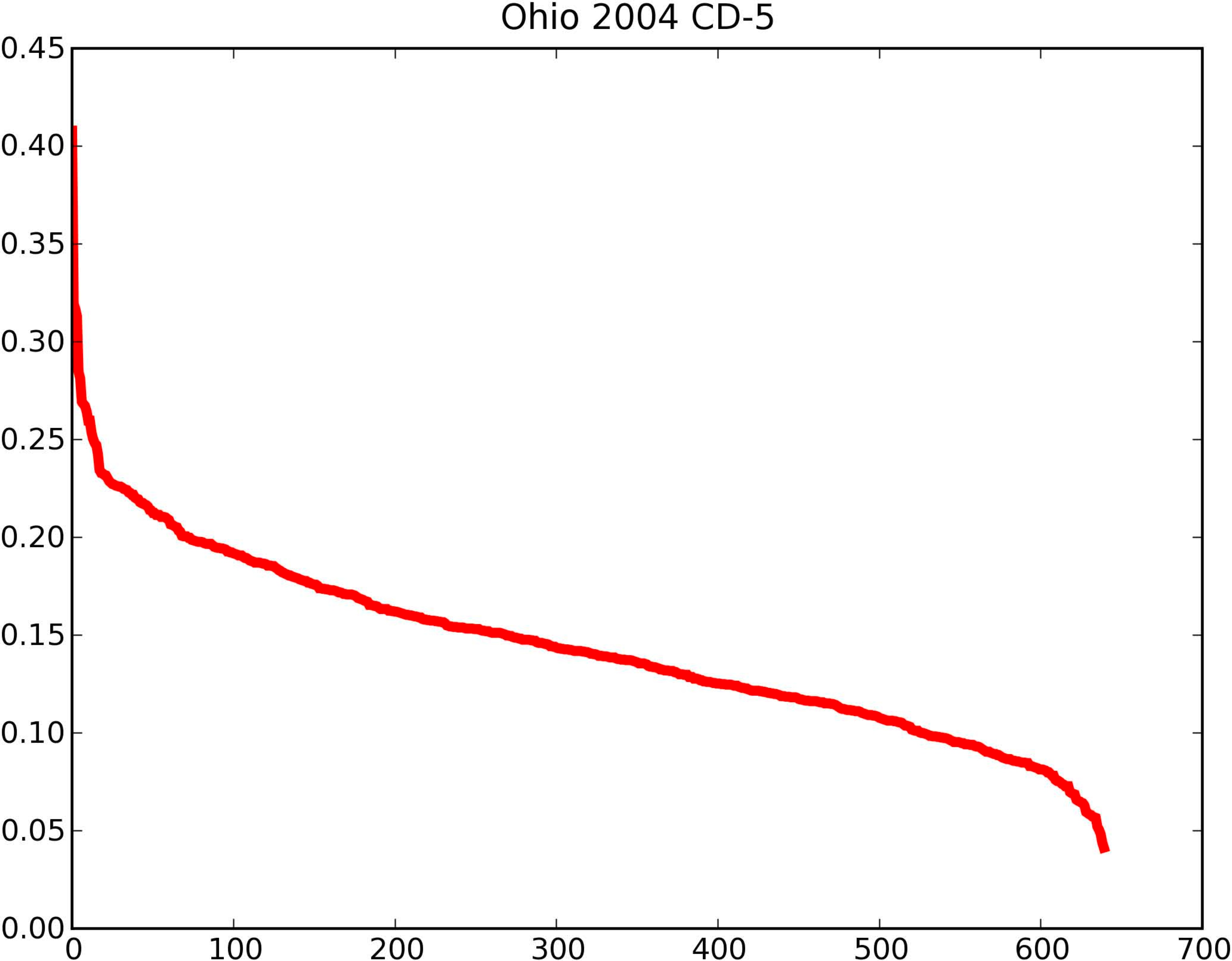
Let us assume a margin of victory of $m = 1\%$: $M=0.01V = 3155$. Assume the adversary changes at most $s = 20\%$ of a precinct's votes, and assume a confidence level of $92\%$ ($\alpha=0.08$).

If the precincts were equal-sized, the Rule of Thumb [16] would suggest auditing $1/m=100$ precincts. The more accurate APR formula (3) suggests auditing 93 precincts (here $b=M/2sv=16$ precincts). The expected workload would be 45852 votes counted. But the precincts are quite far from being equal-sized. If we sample 93 precincts uniformly (using the APR recommendation inappropriately here, since the precincts are variable-sized), we now only achieve a 67% confidence of detecting at least one corrupted precinct, when the adversary has changed enough votes to change the election outcome. The reason is that all of the corruption can fit in the 7 largest precincts now.

The SAFE auditing method [11] would determine that $b_{min} = 7$ (reduced from $b=16$ for the uniform case, since now the adversary need only corrupt the 7 largest precincts to change the election outcome). Using a uniform sampling procedure to have at least a 92% chance of picking one of those 7 precincts (or any corrupted precinct) requires a sample size of 193 precincts (chosen uniformly), and an expected workload of 95,155 votes to recount.

With the NEGEXP method, larger precincts are sampled with greater probability. The adversary is thus prodded to disperse his corruption more broadly, and thus needs to use more precincts, which makes detecting the corruption easier for the auditor. The NEGEXP method computes $w = -M/\ln(\alpha) = 1249$, and audits a precinct of size $v_i$ with probability $p_i=1-\exp(-0.4v_i/w)$. The largest precinct is audited with probability 0.408, while the smallest is audited with probability 0.041. The expected number of precincts selected for auditing is only 92.6, and the expected workload is only 50,937 votes counted.

The PPEBWR method gave results almost identical to those for the NEGEXP method. The expected number of distinct precincts sampled was 91.6, and the expected workload was 50402 votes counted. Each precinct was sampled with a probability within 0.0031 of the corresponding probability for the NEGEXP method.

We see that for this example the NEGEXP method (or the PPEBWR method) is approximately twice as efficient (in terms of votes counted) as the SAFE method, for the same confidence level.

The program and datasets for our experiments are available at https://people.csail.mit.edu/rivest/pps/varsize.py, https://people.csail.mit.edu/rivest/pps/oh5votesonly.txt (Ohio).

The SAFE method may often be a poor choice when there are variable-precinct-sizes, particularly when there are a few very large precincts. One really needs a method that is tuned to variable-sized precincts by using variable auditing probabilities, rather than a method that uses uniform sampling probabilities.

12 Optimal Auditing Method

The optimal auditing method can be represented as a probability distribution assigning a probability $p_S$ to each subset $S$, where $p_S$ indicates the probability that the auditor will choose the subset of precincts, $S$, for auditing. Since there are $2^n$ such subsets, representing these probabilities explicitly takes space exponential in $n$.

The optimal strategy can be found with linear programming, if the number $n$ of precincts is not too large (say a dozen at most). The linear programming formulation requires that for each subset $B$ of total error bound $M$ or more votes, the sum of the probabilities of the subsets $S$ having nonnegative intersection with $B$ needs to be at least $1-\alpha$.

$$(\forall B)\left[ \left(\sum_{i\in B}e_i \ge M\right) ... ...t(\sum_{S:S\cap B \neq \phi}p_S \ge 1-\alpha\right) \right]$$

In addition to these constraints, the probabilities $p_S$ must form a distribution; i.e., they each must be nonnegative, and their sum must be 1.

Finally, the objective function to be minimized is the expected number of votes to be recounted:

$$\sum_S p_S \sum_{i\in S} v_i .$$

For example, suppose we have $n=3$ precincts $A,B,C$ with sizes ${\bf v} = (60,40,20)$ and error bounds ${\bf e} = (30,20,10)$, an adversarial corruption target of $M=30$ votes, and a target significance level of $\alpha=5\%$. Then an optimal auditing strategy, when the auditor is charged on a per-vote-recounted basis, is:

$$\begin{eqnarray*} p_{\phi} & = & 0.013746 \\ p_{A} & = & 0.036253 \\ p_{C} & = & 0.036253 \\ p_{AC} & = & 0.913746 \end{eqnarray*}$$

Here $\phi$ denotes the empty subset; subsets not shown have zero auditing probability. The expected cost of this optimal auditing strategy is 76 votes recounted. (The above strategy also optimizes (at 1.9) the expected number of precincts recounted; however, it is not always the case that the same probability distribution optimizes for both precincts counted and votes counted: a small counterexample occurs for ${\bf v}={\bf e}=(20,20,10,10)$ and $M=30$.)

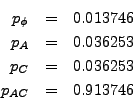
This approach is the ``gold standard'' for auditing with variable-sized precincts, in the sense that it definitely provides the most efficient procedure in terms of the stated optimization criterion. (We note that it is easy to refine this approach to handle the following variations: (1) an optimization criterion that is some linear combination of precincts counted and ballots counted and (2) a requirement that exactly (or at least, or at most) a certain number of precincts be audited.)

However, as noted, it may yield an auditing strategy with as many as $2^n$ potential actions (subsets to be audited) for the auditor, and so is not efficient enough for real use, except for very small elections.

13 Discussion and Recommendations

13.1 Recommendations for practice-PPEBWR

We recommend the use of the PPEBWR method for use in an audit in a simple election. It gives the most efficient audit, for a given confidence level, of the audit methods studied here (other than the optimal method, which is too inefficient for practical use). Figure 3 summarizes the PPEBWR audit procedure recommended for use.

Figure 3: Auditing with the recommended PPEBWR method.

In an election containing multiple races (possibly with overlapping jurisdictions), the NEGEXP method is the more flexible. See Section 13.2 for discussion.

If the error bounds are computed using only the Linear Error Bound Assumption, so that $e_i=2sv_i$, then the probability of picking precinct $P_i$ is just $v_i/V$, so that we are picking with ``probability proportional to size''--this is then the PPSWR procedure. When the Linear Error Bound Assumption is used, one is assuming that errors larger than $2sv_i$ in a precinct will be noticed and caught ``by other means''; one should ensure that this indeed happens. (Letting runners-up pick precincts to audit could be such a mechanism.)

Other considerations may result in interesting and reasonable modifications. Letting runners-up pick precincts to audit is probably helpful, although these precincts should then be ignored during the PPEBWR portion of the audit.

The ``escalation'' procedure for enlarging the audit when significant discrepancies are found is (intentionally) left rather unspecified here. We recommend reading Stark [19] for guidance. At one extreme, one can perform a full recount of all votes cast. More reasonably, one can utilize a staged procedure, where the error budget $\alpha$ is allocated among the stages; only if enough new discrepancies are discovered in one stage does auditing proceed to the next.

13.2 Recommendations for practice-NEGEXP

Figure 4 summarizes the NEGEXP audit procedure recommended for use. The NEGEXP method seems intrinsically more flexible than the PPEBWR method.

Figure 4: Auditing with the recommended NEGEXP method.

NEGEXP can handle multiple races with overlapping jurisdictions such that each precinct is audited at most once even when it is marked for auditing in multiple races. As with any basic auditing method, each precinct is audited independently with a precinct-specific probability. Assume that when a precinct is audited, we audit all races voted on in that precinct. Since the results for each race may imply a different auditing probability for the precinct, it suffices to audit the precinct with the maximum of the probabilities corresponding to the different races.

In a similar manner, the NEGEXP method can be used when the auditing probabilities need to be changed (e.g. because of the effect of late-reporting jurisdictions). Assume that the auditing probability changes from $p$ to $p'$. If the precinct was audited in the first audit, nothing additional needs to be done. If the precinct was not audited and $p \ge p'$, nothing needs to be done because we already audited the precinct with a larger probability than we need to. Otherwise (when $p < p'$), a dice-roll with probability $(p'-p)/(1-p)$ should be used to determine if the precinct should now be audited. The additional dice-roll ensures that the overall probability of auditing the precinct in discussion is $p'$, the final auditing probability.

13.3 Discussion

If the election is not a plurality (winner-take-all), little changes except that the notion of a ``margin of victory'' needs to be appropriately modified, so that the notion of a ``candidate'' is replaced by that of an ``election outcome''. (Elaboration omitted here.) Our auditing problem is closely related to the classic notion of an ``inspection game'', with an ``inspector'' (the auditor) and an ``inspectee'' (the adversary). Inspection games fit within the standard framework of game theory. With optimal play, both auditor and adversary use randomized strategies. See Avenhaus et al. [2] for discussion.

It would be preferable in general, rather than having to deal with precincts of widely differing sizes, if one could somehow group the records for the larger precincts into ``bins'' for ``pseudo-precincts'' of some smaller standard size. (One can do this for say paper absentee ballots, by dividing the paper ballots into nominal standard precinct-sized batches before scanning them.) It is harder to do this if you have DRE's with wide disparities between the number of voters voting on each such machine. See Neff [12] and Wand [22] for further discussion.

14 Conclusions

We have presented two useful post-election auditing procedures: a powerful and flexible ``negative-exponential'' (NEGEXP) method, and a slightly more efficient ``sampling with probability proportional to size, with replacement'' (PPEBWR) method.

Acknowledgments

Thanks to Mark Lindeman for helpful discussions and the Ohio dataset. Thanks also to Kathy Dopp, Andy Drucker, Silvio Micali, Howard Stanislevic, Christos Papadimitriou, and Jerry Lobdill for constructive suggestions. Thanks to Phil Stark for his detailed feedback and pointers to the financial auditing literature.

Bibliography

1

ASLAM, J., POPA, R., AND RIVEST, R. L.
On estimating the size and confidence of a statistical audit.
In Proceedings EVT'07 (2007).
https://www.usenix.org/events/evt07/tech/full_papers/aslam/aslam.pdfhttps://www.usenix.org/events/evt07/tech/full_papers/aslam/ aslam.pdf.

2

AVENHAUS, R., STENGEL, B. V., AND ZAMIR, S.
Inspection games.
In Handbook of Game Theory, R. J. Aumann and S. Hart, Eds., vol. III. Elsevier, January 30 1998.
https://citeseer.ist.psu.edu/212144.html.

3

CALANDRINO, J. A., HALDERMAN, J. A., AND FELTEN, E. W.
Machine-assisted election auditing.
In Proc. EVT'07 (2007).
https://www.usenix.org/event/evt07/tech/full_papers/calandrino/calandrino.pdfhttps://www.usenix.org/event/evt07/tech/full_papers/calandrino/ calandrino.pdf.

4

COCHRAN, W. G.
Sampling Techniques (3rd ed.).
Wiley, 1977.

5

CORDERO, A., WAGNER, D., AND DILL, D.
The role of dice in election audits -- extended abstract, June 16 2006.
IAVoSS Workshop on Trustworthy Elections (WOTE 2006). https://www.cs.berkeley.edu/ daw/papers/dice-wote06.pdfhttps://www.cs.berkeley.edu/~daw/papers/dice-wote06.pdf.

6

DOPP, K.
History of confidence election auditing development (1975 to 2007) and overview of election auditing fundamentals, 2007.
https://electionarchive.org/ucvAnalysis/US/paper-audits/History-of-Election-Auditing-Development.pdfhttps://electionarchive.org/ucvAnalysis/US/paper-audits/History-of-Election-Auditing-Development.pdf.

7

DOPP, K., AND STENGER, F.
The election integrity audit, 2006.
https://electionarchive.org/ucvAnalysis/US/paper-audits/ElectionIntegrityAudit.pdfhttps://electionarchive.org/ucvAnalysis/US/paper-audits/ElectionIntegrityAudit.pdf.

8

ELECTIONLINE.ORG.
Case study: Auditing the vote, March 2007.
https://electionline.org/Portals/1/Publications/EB17.pdfhttps://electionline.org/Portals/1/Publications/EB17.pdf.

9

HANSEN, M. H., AND HURWITZ, W. N.
On the theory of sampling from finite populations.
Ann. Math. Stat. 14 (1943), 333-362.

10

LOBDILL, J.
Considering vote count distributions in designing election audits, Oct 9 (rev. 11/26/2006) 2006.
https://vote.nist.gov/Considering-Vote-Count-Distribution-in-Designing-Election-Audits-Rev-2-11-26-06.pdfhttps://vote.nist.gov/Considering-Vote-Count-Distribution-in-Designing-Election-Audits-Rev-2-11-26-06.pdf.

11

MCCARTHY, J., STANISLEVIC, H., LINDEMAN, M., ASH, A., ADDONA, V., AND BATCHER, M.
Percentage-based versus SAFE vote tabulation auditing: a graphic comparison.
The American Statistician 62, 1 (February 2008), 11-16.
Full version: https://verifiedvoting.org/downloads/TAS_paper.pdfhttps://verifiedvoting.org/downloads/TAS_paper.pdf.

12

NEFF, C. A.
Election confidence--a comparison of methodologies and their relative effectiveness at achieving it (revision 6), December 17, 2003.
https://www.votehere.com/papers/ElectionConfidence.pdfhttps://www.votehere.com/papers/ElectionConfidence.pdf.

13

NORDEN, L., BURSTEIN, A., HALL, J. L., AND CHEN, M.
Post-election audits: Restoring trust in elections, 2007.
Brennan Center for Justice at New York University [School of Law and Samuelson Law, Technology and Public Policy Clinic at UC Berkeley School of Law], https://www.brennancenter.org/dynamic/subpages/download_file_50089.pdfhttps://www.brennancenter.org/dynamic/subpages/
download_file_50089.pdf.

14

ON NONSTANDARD MIXTURES OF DISTRIBUTIONS, P.
Statistical models and analysis in auditing: A study of statistical models and methods for analyzing nonstandard mixtures of distributions in auditing.
National Academy Press, Washington, D.C., 1988.

15

RIVEST, R. L.
On auditing elections when precincts have different sizes, 2007.
https://people.csail.mit.edu/rivest/OnAuditingElectionsWhenPrecinctsHaveDifferentSizes.pdfhttps://people.csail.mit.edu/rivest/OnAuditing ElectionsWhenPrecinctsHaveDifferentSizes.pdf.

16

RIVEST, R. L.
A simple rule of thumb for election audit size determination, 2007.
https://people.csail.mit.edu/rivest/Rivest-ASimpleRuleOfThumbForElectionAuditSizeDetermination.pdfhttps://people.csail.mit.edu/rivest/Rivest-ASimpleRuleOfThumbForElectionAuditSizeDetermination.pdf.

17

SALTMAN, R. G.
Effective use of computing technology in vote-tallying.
Tech. Rep. NBSIR 75-687, National Bureau of Standards (Information Technology Division), March 1975.
https://csrc.nist.gov/publications/nistpubs/NBS_SP_500-30.pdfhttps://csrc.nist.gov/publications/nistpubs/NBS_SP_500-30.pdf.

18

STANISLEVIC, H.
Random auditing of e-voting systems: How much is enough?, Revision August 16, 2006.
https://www.votetrustusa.org/pdfs/VTTF/EVEPAuditing.pdfhttps://www.votetrustusa.org/pdfs/VTTF/EVEPAuditing.pdf.

19

STARK, P. B.
Conservative statistical post-election audits, Nov 15 2007.
https://statistics.berkeley.edu/ stark/Preprints/conservativeElectionAudits07.pdfhttps://statistics.berkeley.edu/~stark/ Preprints/conservativeElectionAudits07.pdf.

20

STARK, P. B.
Election audits by sampling with probability proportional to an error bbound: Dealing with discrepancies, Feb 20 2008.
https://www.stat.berkeley.edu/ stark/Preprints/ppebwrwd08.pdfhttps://www.stat.berkeley.edu/~stark/Preprints/ppebwrwd08.pdf.

21

STRINGER, K.
Practical aspects of statistical sampling in auditing.
In Proceedings of the Business and Economic Statistics Section (Washington, D.C., 1963), American Statistical Association, pp. 405-411.

22

WAND, J.
Auditing an election using sampling: The impact of bin size on the probability of detecting manipulation, Feb 2004.
https://wand.stanford.edu/elections/probability.pdfhttps://wand.stanford.edu/elections/probability.pdf.

About this document ...

On Auditing Elections When Precincts Have Different Sizes

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation varsize.tex

The translation was initiated by Raluca Ada Popa on 2008-06-30