 |

Joseph R. Kiniry, Dermot Cochran, and Patrick E. Tierney
School of Computer Science and Informatics
University College Dublin
Activist computer scientists, including some of the authors of this paper, have been working against the adoption by governments of commercial, proprietary, insecure, poorly designed and implemented voting systems the world-over. And, while we mainly work to accomplish our goals by educating citizens and communicating with the press, we also must propose solutions to the problems of trustworthy e-voting. If a computer-based voting system is to ever be adopted, that system must be demonstrably of extremely high quality. This paper discusses a methodology and a set of tools we have used to implement a vote counting plugin, for an experimental computer-based voting system using applied formal methods.
Regardless of the concerns raised by experts and activists, governments are adopting computer-based technology for e-voting. Researchers and activists concerned about this situation fall in two overlapping camps: researchers that are struggling against the adoption of poor process, technology, and implementation in computer-based voting, and researchers that are proposing new techniques, theories, technologies to solve some of the computer-based voting challenges. Our work falls broadly into both of these camps, but this work in particular focuses on the latter, as we propose a concrete software platform and software engineering process for trustworthy e-voting research.
Computer-based voting, from a mathematical and computer science point-of-view, is full of interesting algorithmic challenges--challenges that are sometimes radically different than those that we understand in other domains. For example, in many voting systems the anonymity of the voter must be preserved, but we must guarantee that the legitimate ballot of the voter is counted.
If a computer-based technology is used in trustworthy voting, then the software system must be of extremely high quality. There are a variety of techniques for constructing a very high quality system, e.g., model-based design, rigorous unit testing, and formal verification, to name a few. Therefore, usable, practical best-practices in rigorous software development, especially as applied to a real, concrete, trustworthy computer-based voting system, are very relevant today.
The work described in this article is useful to researchers because it provides a concrete foundation for future trustworthy voting experimentation. On the other hand, this research is useful to governments and their experts because it provides concrete evidence that modern verification-centric software development with formal methods is achievable without significant cost or time.
The KOA system, originally developed for and released by the Dutch government, can be used as both a standard kiosk-based computer-based voting system as well as a remote telephone and Internet-based voting system. It has a general-purpose voting system-independent core and a ``plugin'' model for supporting various voting systems like the list-based system of Holland or Ireland's Proportional Representation - Single Transferable Vote (PR-STV) based system [7].
As mentioned previously, this software system is only meant to provide a very high-quality, extensible research platform for computer-based voting -- it is not meant to be used in any governmental elections. To highlight this extensibility, as well as to provide evidence that a verification-centric software engineering methodology results in a software system of very high quality, the Irish voting system has been formally specified and verified.
The following summary is organized from a process-centric point-of-view. Each stage in the (mostly linear) development process is described. After describing the various aspects of our verification-centric process, we discuss the Irish voting case study that uses this methodology.
The first stage of our process is to perform domain analysis. The distinct core concepts of the domain that we are trying to model are identified, usually while interacting as a group, and sometimes with domain experts present. Considering input from several parties elucidates different perspectives on the system and helps the group find agreement on which concepts are core, how to define these concepts, and how these concepts relate to one another.
We use a language called ``Extended Business Object Notation'' (or EBON for short) to describe our system at this early stage [15]. EBON is a system specification language akin to UML that differs in several key respects [8,9]. Contrary to UML, EBON has a relatively small number of charts and diagrams, a simple semantics, a graphical and human-readable textual syntax, and it is easy to maintain consistency between an EBON specification and a concrete realization of that specification.
After high-level analysis is complete, we move on to defining medium-level contracts using EBON. During this design stage, we identify inheritance relationships between classes, client-supplier relationships between classes, specify the formal semantics of features and constraints, and identify interesting scenarios in which classes interact.
Because we specify classes with invariants and assertions like pre- and postconditions, we are following a strict design-by-contract approach to program construction. This methodology is further emphasized below when we discuss our implementation strategy.
Scenarios, which are similar to UML's use cases, identify interesting interactions between classes. Scenarios are used to concretely identify and create module- and subsystem-level unit tests during implementation and testing.
Next, our medium-level specifications are made concrete in a popular specification language called the Java Modeling Language (JML).
The Java Modeling Language (JML) is a formal behavioral specification language for Java [11,12]. Effectively, it is a small extension to the Java programming language that uses annotations embedded in special comments to formally express properties of a Java class or interface.
JML is used at two levels. At a high level one uses JML to describe a mathematical model-based specification (the ``Modeling'' of JML) of a software system system. JML models are functional, executable, formally specified and verified constructs like sets, sequences, bags, maps, etc. At a lower level JML is used to describe a concrete software architecture with familiar constructs like invariants, preconditions, postconditions, etc.
To connect these two levels, a specifier describes a functional or relational refinement relating the high level model-based specification and the low level, contract-based, description of the implementation.
We use JML not just because of our local expertise and involvement in the JML community, but because there is a large range of powerful tools that understand JML, some of which we discuss below [1,13].
For example, we compile JML specification into runtime checks, we generate (tens of thousands of) unit tests from JML specifications, and we formally verify that Java method implementations fulfill their contracts expressed in JML.
At the present time we initially refine from EBON specifications to JML by hand, translating EBON classes into concrete Java primitive types, pre-provided JML model classes, new JML models, and concrete Java modules (classes and interfaces). We maintain the connection between the specification layers by using a combination of simple scripts and a development process that emphasizes manual inspection and specification conformance checking.
During this refinement phase concrete choices of data representation are made by identifying which EBON classes should be full-fledged Java types, and how these Java types should relate to each other. E.g, if two classes inherit from each other in EBON, then they must inherit from each other in the JML/Java architecture.
After a model-based specification is written in JML and medium-level EBON contracts are refined into JML contracts on a Java modules, the implementation of the system commences. Because we use JML, our specifications are formal and executable, and our implementation is testable against, and verifiable with respect to, the JML specification using tools such as the JML tool suite and ESC/Java2 [2,10] (discussed below). This combination of tools and techniques provides a high level of confidence that the software system implements the requirements correctly.
Our implementation strategy is, generally, to implement the constructors, factories, and initializers first, as these features let one focus on invariants and the initial state of objects. Next, we focus on the easiest/smallest ``leaf'' methods--methods like basic getters and setters, overridden base methods from java.lang.Object, etc. We then move up the chain of methods, aiming to tackle less complex methods before more complex ones, implementing methods deeper in the expected call stack of the application.
It is important to note that we do not need to implement the whole system, or even a whole class, before checking the correctness of method implementations. Firstly, we unit test methods early and independently as soon as we have constructors and factories implemented. And secondly, extended static checking is modular, as each method body is checked independently of any other method body. Thus, unit tests and ESC/Java2 are run very frequently, typically after only a few new lines of code are written.
Testing includes manual development of automated tests at the method, class, component, and subsystem levels, and automatic generation of tests at the method and constructor level.
The JML-JUnit tool is used to generate test cases from the JML specification [3]. This testing methodology uses method specifications as test oracles and focuses on unit testing methods and constructors independently. Test data generators are written for all types in the system by manually identifying ``interesting'' data values in the whole system-under-test.
In addition to the testing, the implementation is verified with respect to the JML specifications. Whereas testing covers a finite number of data values, verification is used to prove check the logical correctness of the implementation.
ESC/Java2 is a modular static verification tool that checks for common runtime errors and verifies that a Java method implementation conforms to its JML specification. ESC/Java2 translates program source and its specifications into verification conditions that are passed to one of several automated and interactive theorem prover, which in turn either verify that no problems are found or generate a counterexample indicating a potential bug. The tool and its built-in provers operate automatically with reasonable performance--most methods are checked in less than a handful of seconds.
Now that we have reviewed the our verification-centric process and methodology, a case study focusing on the Irish voting system is discussed.
The Irish voting system represents an interesting case study for applied formal methods because Ireland's PR-STV voting system is non-trivial and, given we are working in an Irish university, it has local relevance.
A voting system consists of several interrelated concepts. There is either one or more positions to be filled by election, or an outcome to be decided by referendum. This case study is concerned with the voting system for Irish general elections.
In Irish elections, there are a number of seats to be filled in each constituency. There are almost always more candidates than seats, and there are a large number of registered voters. Each voter casts a ballot using the PR-STV system, and those ballot papers are counted using an process (an algorithm) that is defined by Irish law. The voting algorithm is iterative, requiring that a decision is made at each iteration either to deem a candidate elected, or to eliminate a candidate with lowest votes received.
These concepts are represented by EBON classes or Java types in the specification: Ballot, Ballot Box, Candidate, Decision, Election Algorithm, Election Details, and Election Results.
Votáil is the Irish word for Voting. The Votáil specification is a JML specification for the Irish vote counting system [4]. This formal specification is derived from the complete functional specification for the Dáil election count algorithm [5,6].
Thirty nine formal assertions are identified in the Commentary on Count Rules published by the Irish Department of Environment and Local Government. Each assertion expressed in JML is identified by a Javadoc comment. In addition, a state machine is specified so as to link all of the assertions together. Java classes are specified for the vote counting algorithm, e.g., to represent the ballot papers and to represent the candidates. Concrete examples of how the methodology was applied will clarify this work.
We summarize a detailed example of specification of a Java method in Votáil. Each method is specified with English by using both an extended version of Javadoc, used to encode the EBON informal specifications, and JML to express detailed formal specifications. JML specification encode not only functional behavior, but also safety and progress properties of the voting system.
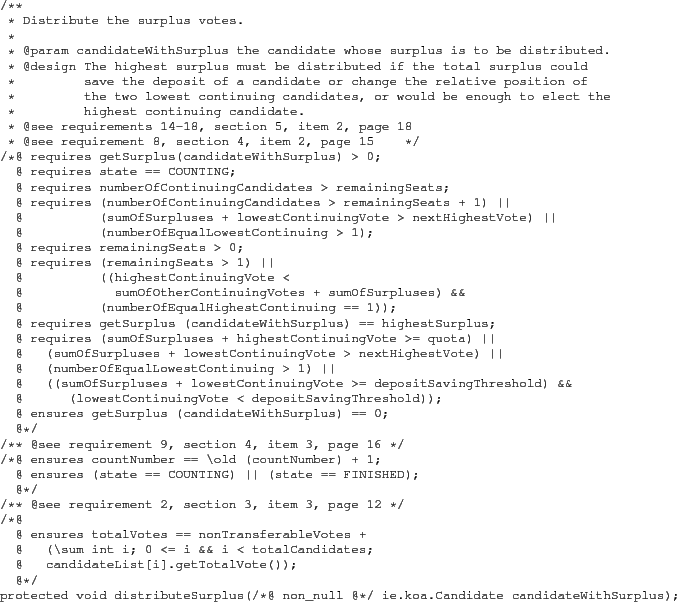
For an example of a formal requirement, we look to Section 5, item 2 on page 18 of the Count Requirements and Commentary on Count Rules [5] which states:
The distribution of the only or the largest available surplus is mandatory if it - or, where there is more than one surplus, the sum of the surpluses - could possibly do any of the following:-
Elect a continuing candidate. This condition is satisfied if the (sum of the) surplus(es) and the votes of the highest continuing candidate equals or exceeds the quota;
Save the lowest candidate from exclusion. This condition is satisfied if the (sum of the) surplus(es), together with the sum of the votes of the lowest continuing candidate, is equal to or greater than the number of votes credited to the second lowest continuing candidate; ...
The requirement is translated into EBON as follows:
If the number of continuing candidates is equal to the number of seats remaining unfilled, or the number of continuing candidates exceeds by one the number of unfilled seats or there is one unfilled seat, then do not distribute any surplus unless it could allow one or more candidates with at least one vote to save their deposits.
Finally, this requirement is formally specified in the architecture as JML pre/postconditions for the distributeSurplus method shown in Figure 1.
Note again how each high-level requirement or constraint is specified both in formal natural language (akin to ``legal English") and in one or more formal assertions.
The Votáil specification is type checked and checked for consistency using ESC/Java2.
As is already obvious, we follow a strict design-by-contract approach to system design and development [14]. Thus, we have a fairly strict set of programming style standards and a process that restricts a programmer's ability to make changes to the system that are not tested, verified, and properly specified.
ESC/Java2 is used to ensure that the specifications for each class, method, and field were strictly adhered to. Recall that ESC/Java2 is reasoning about all code paths simultaneously, modularly, and statically.
As discussed earlier, JML-JUnit automatically generates an extensive unit test suite.
Many of the ``interesting'' data values necessary for testing are
identified quickly due to the fact that arrays are used frequently in
the system. Therefore, values like ![]() ,
, ![]() and the length of each
array were very useful. Other values that were used were already
specified in the contracts, such as maximum possible rounds of
counting. Some other values identified are the maximum values of
Java primitive types like integers and longs.
and the length of each
array were very useful. Other values that were used were already
specified in the contracts, such as maximum possible rounds of
counting. Some other values identified are the maximum values of
Java primitive types like integers and longs.
For each value added to the test data, the number of tests increases by between 100 to 1000 tests depending on the complexity and size method being tested. For example, by adding one extra data value while testing the method Ballot.load(), the number of tests increased by over 700 tests.
JML-JUnit has been very useful and provided extensive information about how the system works and performs. The fact that the JML specifications are also tested adds precision to the testing and helps us identify problems with both the implementation and the specifications. By continually adding particular data values, we aim to have 100% test coverage of the system.
The main errors in specifications that have been discovered are concentrated on arrays that had no upper bounds specified for them. Also, we discover that some specifications are too weak to verify the class invariants. To solve these problems we correct and strengthen the specifications, and use helper methods (methods that need not maintain class invariants).
One of the invariants in the system specifies that random numbers must be unique e.g. to simulate random shuffling of ballot papers. This invariant which is part of both the Candidate and Ballot classes, is the source of many errors reported by ESC/Java2.
//@ public constraint //@ \old(lastSetAddedCountNumber) < //@ lastSetAddedCountNumber;
For example, there is a bug in this constraint assertion, as it must hold for all methods (pure or otherwise), and the JML reference manual indicates that constraints generally are reflexive and transitive, and `<' is not reflexive. To correct this constraint, the `<' operator is replaced by `<='.
As another example, the addVote() and removeVote() methods need to have the following precondition:
//@ requires 0 <= numberOfVotes;This precondition is added to set a lower bound on the variable numberOfVotes to ensure that the invariant
//@ public invariant //@ (\forall int i; 0 < i && i < MAXCOUNT; //@ 0 <= votesAdded[i]);is always valid.
Because computer-based voting (a) is full of interesting algorithmic and security challenges, (b) is an application area ripe for the use of formal methods, and (c) is having a dramatic broad impact on society today, we have chosen to work with governments and independently on a computer-based voting system. We believe that governments should use our work as a benchmark against which to compare other trustworthy voting system. We offer researchers a well-documented verification-centric process, a set of techniques and tools for rigorously developing quality software, and, as a case study and foundation for future research, an open source trustworthy voting system developed with these tools and techniques.
While integrating the Votáil subsystem into the KOA system, and prior to/during the new full FLOSS foundation release of KOA, a number of new pieces of English documentation and functional specification must be written. We hope that the availability of such documentation and specifications will provide additional motivation for electronic and remote voting researchers and developers to seriously consider the KOA system as a foundation for their work. While some practitioners cringe at the ``look-and-feel'' of formal specifications, they are necessary for obtaining full-blown verification. In response to this challenge, exploratory research is underway to bridge the gap between detailed specifications and higher-level, more readable domain specific languages for voting.
We intend for KOA to be the first formally specified and verified remote and local voting system available in the world, and furthermore it is available under the GPL license. It is unclear how to compare such a system to the current commercial and FLOSS voting systems being proposed by others, given that none of them, to our knowledge, even write formal specifications, let alone perform verification. We hope that this work will inspire and challenge other groups working on trustworthy voting.
This work is being supported by the European Project Mobius within the IST 6th Framework. This paper reflects only the authors' views and the Community is not liable for any use that may be made of the information contained therein.
The KOA system's home page is found at secure.ucd.ie/products/opensource/KOA
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons paper.tex
The translation was initiated by DermotCochran on 2007-06-29