A Hierarchical Semantic Overlay Approach to P2P Similarity Search

Duc A. Tran
Computer Science Department
University of Dayton
Dayton, OH 45469
duc.tran@notes.udayton.edu

1 Introduction

One of the most important problems in information retrieval is similarity search. Informally, the problem is: given a similarity query, which can be a point query or a range query, we need to return a set of contents that are most relevant to the search criteria according to some semantic distance function. We propose EZSearch, a decentralized solution to this problem in the context of Peer-to-Peer (P2P) networks. EZSearch features the following for a network of $N$ users. First, queries can be answered with $O(log_kN)$ worst-case search time and low search overhead. Second, to maintain the hierarchy, a node keeps track of only $O(k)$ other nodes and failure recovery requires no more than $O(k)$ reconnections; these overheads are independent of the network size. Last but not least, the number of objects whose indices are stored at remote nodes is small and, therefore, so are the costs of index migration, storage, and validity.

2 Peer-to-Peer Similarity Search

We consider a P2P network where each node has a set of data objects to share with other nodes in the network. These data objects are described based on the vector space model used in information retrieval theory [1]. Each data object $x$ is represented as a $d$-term semantic vector $T_x$ $=$ ($w_{1x}$, $w_{2x}$, .., $w_{dx}$), where each dimension $t_{i}$ reflects the keyword, concept, or term associated with $x$ and $w_{ix}$ the weight to reflect the significance of $t_{i}$ in representing the semantic of $x$. Without loss of generality, we assume that all the weight values belong to the interval [0, 1].

We employ the commonly used Cosine distance function to measure the semantic similarity between two objects $x$ and $y$: $simdist(x, y) = \cos^{-1} \frac{T_x \cdot T_y}{\Vert T_x\Vert _2\Vert T_y\Vert _2}$ where $T_x \cdot T_y$ is the dot product between vectors $T_x$ and $T_y$ and $\Vert.\Vert _2$ is the Euclidean vector norm. The smaller $simdist(x,y)$ is, the more semantically similar are $X$ and $Y$ to each other.

We consider two types of queries: point queries and range queries. A point query is described by a term vector $Q$ $=$ ($w_{1Q}$, $w_{2Q}$, .., $w_{dQ}$). We expect to return those data objects $x$ such that $simdist(x, Q)$ is minimum. In some applications, the user may also specify a small constant $\epsilon$ to find those objects such that $simdist(x, Q) < \epsilon$. There are two types of range query, namely simple and composite. A simple range query is described by a hyperrectangular region $Q$ $=$ [$min_{1Q}$, $max_{1Q}$] $\times$ [$min_{2Q}$, $max_{2Q}$] $\times$ .. $\times$ [$min_{dQ}$, $max_{dQ}$]. A composite range query is a set of simple range queries. For a range query $Q$, we expect to return those data objects that belong to the region $Q$. While the system is aimed to be fully decentralized, we assume that a new user knows at least one existing user before the former can join the network.

3 Proposed Solution: EZSearch

The basic idea behind EZSearch is as follows. Peers (i.e., user nodes) are partitioned into clusters. Each cluster contains nodes having similar contents and manages a subspace of indices (peer_location $P$, term_vector $T_x$), or an index zone. For a search, the simplest solution is to scan all the clusters, which, however, would incur a linear search time. Alternatively, similar to using search trees for logarithmic runtime search, we can build a decision hierarchical overlay on top of these clusters such that the search scope will be reduced by some factor if the query is forwarded from a layer of the hierarchy to a lower layer.

For building the cluster overlay, we propose to use the Zigzag hierarchy, which we originally devised for streaming multimedia [2,3]. The main advantage of Zigzag is its capability to handle the dynamics of P2P networks. We first present Zigzag and then propose how similarity search can be fulfilled efficiently using this hierarchy.

3.1 Zigzag Hierarchy

Definition 1   [Zigzag hierarchy] A Zigzag-$k$ hierarchy of $N$ nodes is a multi-layer hierarchy of clusters recursively defined below: ($k$ $>$ 3 is a constant):

1. Layer 0 contains all peers.
2. If the number of peers at layer $j$ is greater than $3k$, they are partitioned into clusters whose size is in [$k$, $3k$]. Otherwise, we reach the highest layer, where peers form only a single cluster. The size of this highest-layer cluster is in [2, $3k$].
3. A layer-$j$ cluster designates two member peers as its head and associate-head. The head automatically appears at layer ($j+1$). The cluster partition at layer ($j+1$) is the same as at layer $j$. An exception applies to the highest-layer cluster in which only the head role is needed but the associate-head role is not necessary.

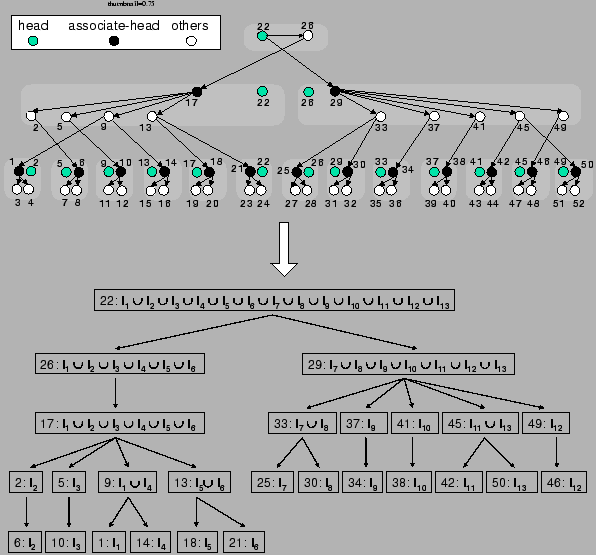
An illustration is given in the top diagram of Figure 1, where 52 nodes are organized into a Zigzag-4 hierarchy. Hereafter, we denote by $head(.)$ and $ahead(.)$ the head and associate-head, respectively, of a cluster or a peer. Since a peer may have different associate-heads at different layers, we use the notation $ahead_i(P)$ to refer to the associate-head of $P$ at layer $i$. For instance, in Figure 1, $ahead_0(22)$ = 21, $ahead_1(22)$ = 17. Below are the terms we use for the rest of the paper:

• Foreign head: A non-head non-associate-head clustermate $Y$ of a peer $X$ at layer $j>0$ is called a ``foreign head" of layer-($j-1$) clustermates of $X$.
• Super cluster: A layer-$j$ ($j>0$) cluster is the super cluster of any layer-$(j-1)$ cluster whose head appears in the layer-$j$ cluster.

Figure 1: Top diagram: Connectivity in a zigzag-4 hierarchy of 52 nodes; Bottom diagram: Corresponding index zone assignments

Definition 2   [Connectivity in Zigzag hierarchy] (illustrated by the top diagram of Figure 1)

• Intra-cluster connectivity: In a cluster, the associate-head has a link to every other non-head peer. E.g., in Figure 1 (top diagram), associate-head 17 of its layer-1 cluster has a link to all of its layer-1 non-head clustermates (peers 2, 5, 9, 13). An exception applies to the highest-layer cluster in which all peers have a link from its head (because there is no associate-head for this layer).
• Inter-cluster connectivity: The associate-head of a cluster has a link from one of its foreign heads. E.g., in Figure 1 (top diagram), associate-head 18 at layer 0 has a link from peer 13, which is one of peer 18's foreign heads. There is an exception: for a second-highest-layer cluster, if its associate-head does not have a foreign head, the associate-head has a link from the head of the highest-layer cluster. For instance, associate-head 17 at layer 1 has a link from peer 26 which is the head of the highest-layer cluster.

The above rules guarantee a tree structure including all the peers; we call this tree the Zigzag tree. A Zigzag-$k$ hierarchy of $N$ peers provides the following desirable properties: (see [3] for complete proofs): (1) The maximum nodal degree in the Zigzag tree is $6k-3$, (2) The maximum height of the Zigzag tree is 2$log_kN+1$, (3) Recovery of a peer failure requires at most $6k-2$ peer reconnections, and (4) As peers join and leave, a cluster may be split or merged with another cluster to satisfy the [$k$, $3k$] cluster size constraint. The worst-case number of peer reconnections due to a split or merger is $O(k)$.

3.2 Index Zone Assignment Policy

We propose to organize peers into a Zigzag hierarchy. Each cluster of this hierarchy is assigned a zone of the entire index space. Zone assignment is important to searching and follows the policy described below.

Definition 3   [Zone Assignment Policy]

1. At layer 0: Each layer-0 cluster owns a non-overlapped index zone, which is a set of hyperrectangles $\{[\alpha_1, \beta_1] \times [\alpha_2, \beta_2] \times ... \times [\alpha_d, \beta_d]\}$, such that the union of all the zones of layer-0 clusters is $I=[0,1]^d$. This zone is known to both the head and associate-head of the cluster, and also said to be ``covered by", or ``owned by", the associate-head. The head will store the indices of those objects that belong to peers outside this cluster but lie inside its index zone.
2. At layer $j>0$: Each peer $P$ keeps a list of pairs $(child_i, zone(child_i))$ where $child_i$ is a child node of $P$ in the Zigzag tree and $zone(child_i)$ the index zone covered by $child_i$. The index zone covered by peer $P$, denoted by $zone(P)$, is the union of these child zones. The index zone owned by a cluster is that covered by the associate-head of this cluster.

As an example, we consider the hierarchy in Figure 1 and suppose that the index zones owned by the 13 layer-0 clusters are $I_1$, $I_2$, .., $I_{13}$ (respectively, from left to right). Thus, $zone(1)$ $=$ $I_1$, $zone(5)$ $=$ $I_2$, $zone(9)$ $=$ $I_3$, etc. Because peer 9 has two children (peer 1 and peer 14), peer 9 keeps the value {(1, $I_{1}$), (14, $I_{4}$)} and $zone(9)$ $=$ $I_{1} \cup I_{4}$. The index zone assignments are similar for other peers and shown in Figure 1 (bottom diagram). Since peers other than the heads and associate-heads at layer 0 do not own any index zone, they are not present in this index zone tree.

The advantage of the zone assignment policy is its support for efficient search. A search query just follows the links in the Zigzag tree to branches that lead to the smallest index zone(s) containing the query. The next subsection details the search algorithm.

3.3 Search Algorithms

We assume that peers are already organized into a Zigzag hierarchy and index zones are assigned to peers and clusters according to the zone assignment policy. We present here only the algorithm for range-query search. Algorithms for point queries can be generalized from this algorithm and can be found in [4]. Supposing that a peer $P$ submits a range query $Q$, there are two scenarios:

Case 1: $P$ is a leaf in the Zigzag tree (e.g., peers 15, 36, 40 in Figure 1) and $P$ needs to process query $Q$. Since $P$ does not have any index zone information, it sends the query to its associate-head $ahead_0(P)$. $ahead_0(P)$ computes $Q_1$ $=$ $Q \cap zone(P)$. If $Q_1$ $\neq \emptyset$, some results of $Q$, that correspond to $Q_1$, can be found locally. Indeed, $ahead_0(P)$ just needs to broadcast query $Q_1$ to all layer-0 clustermates asking them to return to peer $P$ the objects inside $Q_1$. Furthermore, when $head(P)$ receives $Q_1$, if it stores any index (peer_location $P'$, term_vector $T_x$) such that $T_x \in Q_1$, $head(P)$ asks peer $P'$ to send object $x$ to peer $P$. We must also return the results that correspond to query $Q - Q_1$ if $Q - Q_1 \neq \emptyset$ because these results are not in the local cluster. In this case, $ahead_0(P)$ creates a new query $Q_2$ $=$ $Q - Q_1$. How $ahead_0(P)$ processes query $Q_2$ is similar to the case below.

Case 2: $P$ is a non-leaf node in the Z-tree (e.g., peers 22, 37, 42 in Figure 1) and $P$ needs to process query $Q$. In this case, $P$ must own a zone $zone(P)$. Query $Q$ is broken into two subqueries $Q_1$ $=$ $Q \cap zone(P)$ and $Q_2$ $=$ $Q - Q_1$, which will be handled in parallel as follows.

• Query $Q_1$: If $Q_1$ $=$ $\emptyset$, nothing needs to be done. Else, the results of $Q_1$ can be found in a layer-0 cluster reachable from peer $P$. By looking at the list $(child_i, zone(child_i))$ for every child, $P$ breaks $Q_1$ further into subqueries $Q_{11}$, $Q_{12}$, ... where $Q_{1i} = Q_1 \cap zone(child_i)$. (It is easy to prove that $Q_{1i} \cap Q_{1j} = \emptyset$ for every $i \neq j$.) The results for $Q_{1i}$ can be found in a layer-0 cluster reachable from $child_i$. Hence, peer $P$ just needs to forward these subqueries to the corresponding child peers. The handling of such a subquery at the corresponding child resembles that at peer $P$.
• Query $Q_2$: If $Q_2$ $=$ $\emptyset$, nothing needs to be done. Else, the results satisfying $Q_2$ cannot be found in any cluster reachable from $P$. In this case, $P$ just needs to forwards $Q_2$ to the parent of $P$ in the Zigzag tree. The handling of query $Q_2$ at this parent resembles the way $P$ handles the original query $Q$.

Eventually, all the subqueries, created when necessary as above, will reach layer-0 clusters where the corresponding results can be found locally (like in Case 1). The collection of all these results is the final result for the original query $Q$ initiated by peer $P$.

The search path length is at most the maximum distance in hops between two peers in the Zigzag tree, or $4log_kN+2$. The search overhead is proportional to the total number of peers contacted for all the subqueries, which depends on the range of the original query. In our performance study, we found that this overhead is indeed very small.

3.4 Hierarchy Construction

Initially, there is only one peer in the network. It is the head of its self-formed cluster $C$, which grows larger as subsequent peers join. The index zone owned by this cluster is $I$ $=$ $[0, 1]^d$ and the ID of this zone is kept at the head node. When the cluster size exceeds $3k$, we need to partition $C$ into two smaller clusters, $C_0$ and $C_1$, whose sizes are in the interval [$k$, $3k$]. We propose to partition $I$ along a selected dimension $t_{l}$ into two halves $I_{0l}$ $=$ $[0, 1]^{l-1}$ $\times$ [0, 1/2) $\times$ $[0, 1]^{d-l}$ and $I_{1l}$ $=$ $[0, 1]^{l-1}$ $\times$ [1/2, 1] $\times$ $[0, 1]^{d-l}$, each to be owned by $C_0$ and $C_1$. It is possible that a peer in cluster $C_0$ has an object in $I_{1l}$ (similarly, a peer in cluster $C_1$ may have an object in $I_{0l}$). In this case, we store the index of this object in the other cluster. The number of such objects is called the index migration overhead. We want to minimize this overhead so that (1) the communication overhead due to index relocation is low, and (2) peers in the same cluster have highly similar objects. This is equivalent to minimizing $F = \sum_{P \in C_0}{n^P_{1l}} + \sum_{P \in C_1}{n^P_{0l}}$ where $n^P_{il} = cardinality(\{object x \in P \mid T_x \in I_{il}\})$. The algorithm for this purpose is run by $head(C)$ - the head of cluster $C$. Upon a request sent by $head(C)$, each peer $P$ in $C$ submits to $head(C)$ a set of tuples ($t_l$, $n^P_{1l}$, $n^P_{0l}$), for all $l$ $\in$ [1, $d$]. Upon receipt of those sets from all the member peers, we can devise a simple greedy but optimal algorithm for $head(C)$ to find the best $C_0$, $C_1$, and dimension $t_l$. The complexity of this algorithm is $O(dklog_2k)$.

Each cluster $C_i$ randomly selects two nodes as its head $head(C_i)$ and associate-head $ahead(C_i)$ (the old head of cluster $C$, however, is preferred to remain head of the newly created cluster it belongs to). The heads will automatically belong to layer 1 and form a new cluster. Since layer 1 now is the highest layer, only the head needs to be designated; this head is randomly chosen between the two member peers. The index zone owned by this cluster is the union of the zones owned by its child clusters; in this case, it is $I_{0l}+I_{1l}$.

Having the Zigzag hierarchy initially constructed, we need maintain it under network dynamics such as when a peer publishes or removes objects, and joins or quits the network. The detailed solutions to these sub-problems are presented in [4], which shows that removal of a peer requires $O(k)$ peer reconnections, addition of a peer requires $O(log_kN)$ peer contacts, and addition or removal of an object also requires $O(log_kN)$ peer contacts.

4 Simulation Results and Future Work

We conducted simulation for EZSearch. Peers arrived at rate 2 peers per second and might quit the network randomly at anytime. Thus the contents and indices stored in the network changed dynamically. The results were promising. For instance, Figure 2 shows the effect of the constant $k$ used in the Zigzag-$k$ hierarchy. In all scenarios, the query and any of its subqueries do not travel more than 12 nodes (among 10,003 nodes) before knowing the locations of the answers. Normalized search overhead is computed as $\frac{n}{N\times V}$, where $n$ is the number of nodes a query and its subqueries visit during the search, $N$ the number of nodes currently in the system, and $V$ the volume of the query. For a query of volume 0.2, the broadcast-based search would incur a normalized search overhead of $10003/(0.2 \times 10003)$ $=$ 5. EZSearch has a normalized search overhead always less than 0.6 (on average) and 1.8 (worst-case), and much smaller when $k$ is larger. EZSearch therefore is fast and highly efficient. Our future work includes (1) refining the current algorithms for stronger index locality preservation within each cluster, and (2) considering various distributions of objects over peers.

Figure 2: After the system runs for 5000 seconds, 10003 nodes are active. Each node has up to 10 2-d objects. 2000 queries are generated with ranges following a Zipf distribution in which about 80% of the queries have a volume of approximately 20% of the unit hypercube

Bibliography

1

M. Berry, Z. Drmac, and E. Jessup.
Matrices, vector spaces, and information retrieval.
SIAM Review, 41(2):335-362, 1999.

2

D. A. Tran, K. A. Hua, and T. T. Do.
Zigzag: An efficient peer-to-peer scheme for media streaming.
In IEEE INFOCOM, San Francisco, CA, March-April 2003.

3

D. A. Tran, K. A. Hua, and T. T. Do.
A peer-to-peer architecture for media streaming.
IEEE Journal on Selected Areas in Communications, 22(1), January 2004.

4

D. A. Tran and H. Nguyen.
EZSearch: Fast and scalable similarity search in peer-to-peer networks.
Unpublished, January 2005.

About this document ...

A Hierarchical Semantic Overlay Approach to P2P Similarity Search

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons main.tex

The translation was initiated by on 2005-02-14