Check out the new USENIX Web site.

Home About USENIX Events Membership Publications Students
OSDI '02 Paper    [OSDI '02 Tech Program Index]

Pp. 299-314 of the Proceedings


Secure routing for structured peer-to-peer overlay networks

To appear in the Fifth Symposium on Operating Systems Design and Implementation (OSDI 2002)


Miguel Castro1, Peter Druschel2, Ayalvadi Ganesh1, Antony Rowstron1 and Dan S. Wallach2

1Microsoft Research Ltd., 7 J J Thomson Avenue, Cambridge, CB3 0FB, UK
{mcastro,ajg,antr}@microsoft.com
2Rice University, 6100 Main Street, MS 132, Houston, TX 77005-1892, USA
{druschel,dwallach}@cs.rice.edu

Abstract:

Structured peer-to-peer overlay networks provide a substrate for the construction of large-scale, decentralized applications, including distributed storage, group communication, and content distribution. These overlays are highly resilient; they can route messages correctly even when a large fraction of the nodes crash or the network partitions. But current overlays are not secure; even a small fraction of malicious nodes can prevent correct message delivery throughout the overlay. This problem is particularly serious in open peer-to-peer systems, where many diverse, autonomous parties without pre-existing trust relationships wish to pool their resources. This paper studies attacks aimed at preventing correct message delivery in structured peer-to-peer overlays and presents defenses to these attacks. We describe and evaluate techniques that allow nodes to join the overlay, to maintain routing state, and to forward messages securely in the presence of malicious nodes.


1 Introduction

Structured peer-to-peer (p2p) overlays like CAN [16], Chord [20], Pastry [17] and Tapestry [21] provide a self-organizing substrate for large-scale peer-to-peer applications. These systems provide a powerful platform for the construction of a variety of decentralized services, including network storage, content distribution, and application-level multicast. Structured overlays allow applications to locate any object in a probabilistically bounded, small number of network hops, while requiring per-node routing tables with only a small number of entries. Moreover, the systems are scalable, fault-tolerant and provide effective load balancing.

However, to fully realize the potential of the p2p paradigm, such overlay networks must be able to support an open environment where mutually distrusting parties with conflicting interests are allowed to join. Even in a closed system of sufficiently large scale, it may be unrealistic to assume that none of the participating nodes have been compromised by attackers. Thus, structured overlays must be robust to a variety of security attacks, including the case where a fraction of the participating nodes act maliciously. Such nodes may mis-route, corrupt, or drop messages and routing information. Additionally, they may attempt to assume the identity of other nodes and corrupt or delete objects they are supposed to store on behalf of the system.

In this paper, we consider security issues in structured p2p overlay networks. We describe attacks that can be mounted against such overlays and the applications they support, and present the design of secure techniques that can thwart such attacks. In particular, we identify secure routing as a key building block that can be combined with existing, application-specific security techniques to construct secure, decentralized applications upon structured overlays. Secure routing requires (1) a secure assignment of node identifiers, (2) secure routing table maintenance, and (3) secure message forwarding. We present techniques for each of these problems, and show how using these techniques, secure routing can be maintained efficiently despite up to 25% of malicious participating nodes. Moreover, we show that the overhead of secure routing is acceptable and proportional to the fraction of malicious nodes.

The rest of this paper is organized as follows. Section 2 gives some background on structured p2p overlays, specifies models and assumptions, and defines secure routing. Sections 3, 4 and 5 present attacks on and solutions for assignment of identifiers to nodes, routing table maintenance and message forwarding, respectively. Section 6 explains how the overhead of secure routing can be minimized by using self-certifying data. Finally, Section 7 discusses related work and Section 8 provides conclusions.


2 Background, models and solution

In this section, we present some background on structured p2p overlay protocols like CAN, Chord, Tapestry and Pastry. Space limitations prevent us from giving a detailed overview of each protocol. Instead, we describe an abstract model of structured p2p overlay networks that we use to keep the discussion independent of any particular protocol. For concreteness, we also give an overview of Pastry and point out relevant differences with the other protocols. Next, we describe models and assumptions used later in the paper about how faulty nodes may behave. Finally, we define secure routing and outline our solution.

Throughout this paper, most of the analyses and techniques are presented in terms of our abstract model, and should apply to other structured overlays except when otherwise noted. However, the security and performance of our techniques was fully evaluated only in the context of Pastry; a full evaluation of the techniques in other protocols is future work.


2.1 Routing overlay model

We define an abstract model of a structured p2p routing overlay, designed to capture the key concepts common to overlays like CAN, Chord, Tapestry and Pastry.

In our model, participating nodes are assigned uniform random identifiers, nodeIds, from a large id space (e.g., the set of 128-bit unsigned integers). Application-specific objects are assigned unique identifiers, called keys, selected from the same id space. Each key is mapped by the overlay to a unique live node, called the key's root. The protocol routes messages with a given key to its associated root.

To route messages efficiently, each node maintains a routing table with nodeIds of other nodes and their associated IP addresses. Moreover, each node maintains a neighbor set, consisting of some number of nodes with nodeIds near the current node in the id space. Since nodeId assignment is random, any neighbor set represents a random sample of all participating nodes.

For fault tolerance, application objects are stored at more than one node in the overlay. A replica function maps an object's key to a set of replica keys, such that the set of replica roots associated with the replica keys represents a random sample of participating nodes in the overlay. Each replica root stores a copy of the object.

Next, we discuss existing structured p2p overlay protocols and how they relate to our abstract model.

Figure 1: Routing table of a Pastry node with nodeId $ 65a1x$, $ b=4$. Digits are in base 16, $ x$ represents an arbitrary suffix.
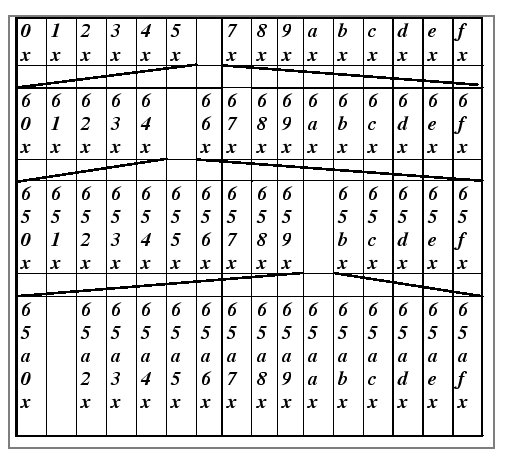
\psfig{file=table.eps,width=1.0\textwidth}
Figure 2: Routing a message from node $ 65a1fc$ with key $ d46a1c$. The dots depict live nodes in Pastry's circular namespace.
\psfig{file=ring.eps,width=1.0\textwidth}


2.2 Pastry

Pastry nodeIds are assigned randomly with uniform distribution from a circular 128-bit id space. Given a 128-bit key, Pastry routes an associated message toward the live node whose nodeId is numerically closest to the key. Each Pastry node keeps track of its neighbor set and notifies applications of changes in the set.

Node state: For the purpose of routing, nodeIds and keys are thought of as a sequence of digits in base $ 2^b$ ($ b$ is a configuration parameter with typical value 4). A node's routing table is organized into $ 128/2^b$ rows and $ 2^b$ columns. The $ 2^b$ entries in row $ r$ of the routing table contain the IP addresses of nodes whose nodeIds share the first $ r$ digits with the present node's nodeId; the $ r + 1$th nodeId digit of the node in column $ c$ of row $ r$ equals $ c$. The column in row $ r$ that corresponds to the value of the $ r + 1$th digit of the local node's nodeId remains empty. A routing table entry is left empty if no node with the appropriate nodeId prefix is known. Figure 1 depicts an example routing table.

Each node also maintains a neighbor set (called a ``leaf set''). The leaf set is the set of $ l$ nodes with nodeIds that are numerically closest to the present node's nodeId, with $ l/2$ larger and $ l/2$ smaller nodeIds than the current node's id. The value of $ l$ is constant for all nodes in the overlay, with a typical value of approximately $ \lceil 8*log_{2^b} N \rceil$, where $ N$ is the number of expected nodes in the overlay. The leaf set ensures reliable message delivery and is used to store replicas of application objects.

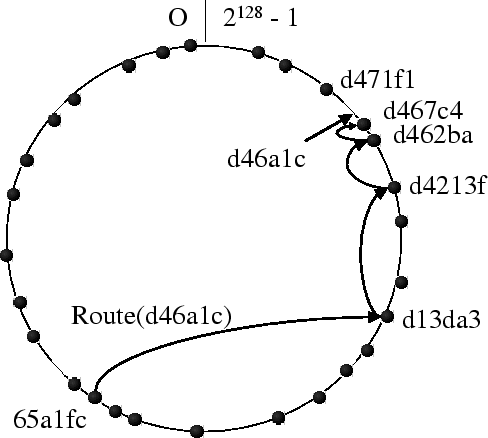
Message routing: At each routing step, a node seeks to forward the message to a node in the routing table whose nodeId shares with the key a prefix that is at least one digit (or $ b$ bits) longer than the prefix that the key shares with the present node's id. If no such node can be found, the message is forwarded to a node whose nodeId shares a prefix with the key as long as the current node, but is numerically closer to the key than the present node's id. If no appropriate node exists in either the routing table or neighbor set, then the current node or its immediate neighbor is the message's final destination.

Figure 2 shows the path of an example message. Analysis shows that the expected number of routing hops is slightly below $ log_{2^b} N$, with a distribution that is tight around the mean. Moreover, simulation shows that the routing is highly resilient to crash failures.

To achieve self-organization, Pastry nodes must dynamically maintain their node state, i.e., the routing table and neighbor set, in the presence of node arrivals and node failures. A newly arriving node with the new nodeId $ X$ can initialize its state by asking any existing Pastry node $ A$ to route a special message using $ X$ as the key. The message is routed to the existing node $ Z$ with nodeId numerically closest to $ X$. $ X$ then obtains the neighbor set from $ Z$ and constructs its routing table by copying rows from the routing tables of the nodes it encountered on the original route from $ A$ to $ Z$. Finally, $ X$ announces its presence to the initial members of its neighbor set, which in turn update their own neighbor sets and routing tables. Similarly, the overlay can adapt to abrupt node failure by exchanging a small number of messages ( $ O(log_{2^b} N)$) among a small number of nodes.


2.3 CAN, Chord, Tapestry

Next, we briefly describe CAN, Chord and Tapestry, with an emphasis on the differences relative to Pastry.

Tapestry is very similar to Pastry but differs in its approach to mapping keys to nodes and in how it manages replication. In Tapestry, neighboring nodes in the namespace are not aware of each other. When a node's routing table does not have an entry for a node that matches a key's $ n$th digit, the message is forwarded to the node with the next higher value in the $ n$th digit, modulo $ 2^b$, found in the routing table. This procedure, called surrogate routing, maps keys to a unique live node if the node routing tables are consistent. Tapestry does not have a direct analog to a neighbor set, although one can think of the lowest populated level of the Tapestry routing table as a neighbor set. For fault tolerance, Tapestry's replica function produces a set of random keys, yielding a set of replica roots at random points in the id space. The expected number of routing hops in Tapestry is $ log_{2^b} N$.

Chord uses a 160-bit circular id space. Unlike Pastry, Chord forwards messages only in clockwise direction in the circular id space. Instead of the prefix-based routing table in Pastry, Chord nodes maintain a routing table consisting of up to $ 160$ pointers to other live nodes (called a ``finger table''). The $ i$th entry in the finger table of node $ n$ refers to the live node with the smallest nodeId clockwise from $ n + 2^{i-1}$. The first entry points to $ n$'s successor, and subsequent entries refer to nodes at repeatedly doubling distances from $ n$. Each node in Chord also maintains pointers to its predecessor and to its $ n$ successors in the nodeId space (this successor list represents the neighbor set in our model). Like Pastry, Chord's replica function maps an object's key to the nodeIds in the neighbor set of the key's root, i.e., replicas are stored in the neighbor set of the key's root for fault tolerance. The expected number of routing hops in Chord is $ \frac{1}{2} log_2 N$.

CAN routes messages in a $ d$-dimensional space, where each node maintains a routing table with $ O(d)$ entries and any node can be reached in $ (d/4)(N^{1/d})$ routing hops on average. The entries in a node's routing table refer to its neighbors in the $ d$-dimensional space. CAN's neighbor table duals as both the routing table and the neighbor set in our model. Like Tapestry, CAN's replica function produces random keys for storing replicas at diverse locations. Unlike Pastry, Tapestry and Chord, CAN's routing table does not grow with the network size, but the number of routing hops grows faster than $ log N$ in this case.

Tapestry and Pastry construct their overlay in a Internet topology-aware manner to reduce routing delays and network utilization. In these protocols, routing table entries can be chosen arbitrarily from an entire segment of the nodeId space without increasing the expected number of routing hops. The protocols exploit this by initializing the routing table to refer to nodes that are nearby in the network topology and have the appropriate nodeId prefix. This greatly facilitates proximity routing [17]. However, it also makes these systems vulnerable to certain attacks, as shown in Section 4.

The choice of entries in CAN's and Chord's routing tables is tightly constrained. The CAN routing table entries refer to specific neighboring nodes in each dimension, while the Chord finger table entries refer to specific points in the nodeId space. This makes proximity routing harder but it protects nodes from attacks that exploit attacking nodes' proximity to their victims.

2.4 System model

The system runs on a set of $ N$ nodes that form an overlay using one of the protocols described in the previous section. We assume a bound $ f$ ( $ 0 \leq f < 1$) on the fraction of nodes that may be faulty. Faults are modeled using a constrained-collusion Byzantine failure model, i.e., faulty nodes can behave arbitrarily and they may not all necessarily be operating as a single conspiracy. The set of faulty nodes is partitioned into independent coalitions, which are disjoint sets with size bounded by $ cN$ ( $ 1/N \leq c \leq f$). When $ c = f$, all faulty nodes may collude with each other to cause the most damage to the system. We model the case where nodes are grouped into multiple independent coalitions by setting $ c < f$. Members of a coalition can work together to corrupt the overlay but are unaware of nodes in other coalitions. We studied the behavior of the system with $ c$ ranging from $ 1/N$ to $ f$ to model different failure scenarios.

We assume that every node in the p2p overlay has a static IP address at which it can be contacted. In this paper, we ignore nodes with dynamically assigned IP addresses, and nodes behind network address translation boxes or firewalls. While p2p overlays can be extended to address these concerns, this paper focuses on more traditional network hosts.

The nodes communicate over normal Internet connections. We distinguish between two types of communication: network-level, where nodes communicate directly without routing through the overlay, and overlay-level, where messages are routed through the overlay using one of the protocols discussed in the previous section. We use cryptographic techniques to prevent adversaries from observing or modifying network-level communication between correct nodes. An adversary has complete control over network-level communication to and from nodes that it controls. This can compromise overlay-level communication that is routed through a faulty node. Adversaries may delay messages between correct nodes but we assume that any message sent by a correct node to a correct destination over an overlay route with no faulty nodes is delivered within time $ D$ with probability $ P_{D}$.


2.5 Secure routing

Next, we define a secure routing primitive that can be combined with existing techniques to construct secure applications on structured p2p overlays. Subsequent sections show how to implement the secure routing primitive under the fault and network models that we described in the previous section.

The routing primitives implemented by current structured p2p overlays provide a best-effort service to deliver a message to a replica root associated with a given key. With malicious overlay nodes, the message may be dropped or corrupted, or it may be delivered to a malicious node instead of a legitimate replica root. Therefore, these primitives cannot be used to construct secure applications. For example, when inserting an object, an application cannot ensure that the replicas are placed on legitimate, diverse replica roots as opposed to faulty nodes that impersonate replica roots. Even if applications use cryptographic methods to authenticate objects, malicious nodes may still corrupt, delete, deny access to or supply stale copies of all replicas of an object.

To address this problem, we define a secure routing primitive. The secure routing primitive ensures that when a non-faulty node sends a message to a key $ k$, the message reaches all non-faulty members in the set of replica roots $ R_k$ with very high probability. $ R_k$ is defined as the set of nodes that contains, for each member of the set of replica keys associated with $ k$, a live root node that is responsible for that replica key. In Pastry, for instance, $ R_k$ is simply a set of live nodes with nodeIds numerically closest to the key. Secure routing ensures that (1) the message is eventually delivered, despite nodes that may corrupt, drop or misroute the message; and (2) the message is delivered to all legitimate replica roots for the key, despite nodes that may attempt to impersonate a replica root.

Secure routing can be combined with existing security techniques to safely maintain state in a structured p2p overlay. For instance, self-certifying data can be stored on the replica roots, or a Byzantine-fault-tolerant replication algorithm like BFT [4] can be used to maintain the replicated state. Secure routing guarantees that the replicas are initially placed on legitimate replica roots, and that a lookup message reaches a replica if one exists. Similarly, secure routing can be used to build other secure services, such as maintaining file metadata and user quotas in a distributed storage utility. The details of such services are beyond the scope of this paper.

Implementing the secure routing primitive requires the solution of three problems: securely assigning nodeIds to nodes, securely maintaining the routing tables, and securely forwarding messages. Secure nodeId assignment ensures that an attacker cannot choose the value of nodeIds assigned to the nodes that the attacker controls. Without it, the attacker could arrange to control all replicas of a given object, or to mediate all traffic to and from a victim node.

Secure routing table maintenance ensures that the fraction of faulty nodes that appear in the routing tables of correct nodes does not exceed, on average, the fraction of faulty nodes in the entire overlay. Without it, an attacker could prevent correct message delivery, given only a relatively small number of faulty nodes. Finally, secure message forwarding ensures that at least one copy of a message sent to a key reaches each correct replica root for the key with high probability. Sections 3, 4 and 5 describe solutions to each of these problems.


3 Secure nodeId assignment

The performance and security of structured p2p overlay networks depend on the fundamental assumption that there is a uniform random distribution of nodeIds that cannot be controlled by an attacker. This section discusses what goes wrong when the attacker violates this assumption, and how this problem can be addressed.

3.1 Attacks

Attackers who can choose nodeIds can compromise the integrity of a structured p2p overlay, without needing to control a particularly large fraction of the nodes. For example, an attacker may partition a Pastry or Chord overlay if she controls two complete and disjoint neighbor sets. Such attackers may also target particular victim nodes by carefully choosing nodeIds. For example, they may arrange for every entry in a victim's routing table and neighbor set to point to a hostile node in a Chord overlay. At that point, the victim's access to the overlay network is completely mediated by the attacker.

Attackers who can choose nodeIds can also control access to target objects. The attacker can choose the closest nodeIds to all replica keys for a particular target object, thus controlling all replica roots. As a result, the attacker could delete, corrupt, or deny access to the object. Even when attackers cannot choose nodeIds, they may still be able to mount all the attacks above (and more) if they can obtain a large number of legitimate nodeIds easily. This is known as a Sybil attack [10].

Previous approaches to nodeId assignment have either assumed nodeIds are chosen randomly by the new node [5] or compute nodeIds by hashing the IP address of the node [20]. Neither approach is secure because an attacker has the opportunity either to choose nodeIds that are not necessarily random, or to choose an IP address that hashes to a desired interval in the nodeId space. Particularly as IPv6 is deployed, even modest attackers will have more potential IP addresses at their disposal than there are likely to be nodes in a given p2p network.


3.2 Solution: certified nodeIds

One solution to securing the assignment of nodeIds is to delegate the problem to a central, trusted authority. We use a set of trusted certification authorities (CAs) to assign nodeIds to principals and to sign nodeId certificates, which bind a random nodeId to the public key that speaks for its principal and an IP address. The CAs ensure that nodeIds are chosen randomly from the id space, and prevent nodes from forging nodeIds. Furthermore, these certificates give the overlay a public key infrastructure, suitable for establishing encrypted and authenticated channels between nodes.

Like conventional CAs, ours can be offline to reduce the risk of exposing certificate signing keys. They are not involved in the regular operation of the overlay. Nodes with valid nodeId certificates can join the overlay, route messages, and leave repeatedly without involvement of the CAs. As with any CA infrastructure, the CA's public keys must be well known, and can be installed as part of the node software itself, as is done with current Web browsers.

The inclusion of an IP address in the certificate deserves some explanation. Some p2p protocols, such as Tapestry and Pastry, measure the network delay between nodes and choose routing table entries that minimize delay. If an attacker with multiple legitimate nodeId certificates could freely swap certificates among nodes it controls, it might be able to increase the fraction of attacker's nodes in a target node's routing table. By binding the nodeId to an IP address, it becomes harder for an attacker to move nodeIds across nodes. We allow multiple nodeId certificates per IP address because the IP addresses of nodes may change and because otherwise, attackers could deny service by hijacking victim's IP addresses.

A downside of binding nodeIds to IP addresses is that, if a node's IP address changes, either as a result of dynamic address assignment, host mobility, or organizational network changes, then the node's old certificate and nodeId become invalid. In p2p systems where IP addresses are allowed to change dynamically, nodeId swapping attacks may be unavoidable.

Certified nodeIds work well when nodes have fixed nodeIds, which is the case in Chord, Pastry, and Tapestry. However, it might be harder to secure nodeId assignment in CAN. CAN nodeIds represent a zone in a $ d$-dimensional space that is split in half when a new node joins [16]. Both the nodeId of the original node and the nodeId of the joining node change during this process.

3.2.1 Sybil attacks

While nodeId assignment by a CA ensures that nodeIds are chosen randomly, it is also important to prevent an attacker from easily obtaining a large number of nodeId certificates. One solution is to require an attacker to pay money for certificates, via credit card or any other suitable mechanism. With this solution, the cost of an attack grows naturally with the size of the network. For example, if nodeId certificates cost $20, controlling 10% of an overlay with 1,000 nodes costs $2,000 and the cost rises to $2,000,000 with 1,000,000 nodes. The cost of targeted attacks is even higher; it costs an expected $20,000 to obtain the closest nodeId to a particular point in the id space in an overlay with 1,000 nodes. Apart from making attacks economically expensive, these fees can also fund the operation of the CAs.

Another solution is to bind nodeIds to real-world identities instead of charging money. In practice, different forms of CAs are suitable in different situations. The identity-based CA is the preferred solution in ``virtual private'' overlays run by an organization that already maintains employment or membership records with strong identity checks. In an open Internet deployment, a money-only CA may be more suitable because it avoids the complexities of authenticating real-world identities.

None of the known solutions to nodeId assignment are effective when the overlay network is very small. For small overlay networks, we must require that all members of the network are trusted not to cheat. Only when a network reaches a critical mass, where it becomes sufficiently hard for an attacker to muster enough resources to control a significant fraction of the overlay, should untrusted nodes be allowed to join.

3.3 Rejected: distributed nodeId generation

The CAs represent points of failure, vulnerable to both technical and legal attacks. Also, for some p2p networks, it may be cumbersome to require users to spend money or prove their real-world identities. Therefore, it would be desirable to construct secure p2p overlays without requiring centralized authorities, fees or identity checks. Unfortunately, fully decentralized nodeId assignment appears to have fundamental security limitations [10]. None of the methods we are aware of can ultimately prevent a determined attacker from acquiring a large collection of nodeIds.

However, several techniques may be able to, at a minimum, moderate the rate at which an attacker can acquire nodeIds. One possible solution is to require prospective nodes to solve crypto puzzles [15] to gain the right to use a nodeId, an approach that has been taken to address a number of denial of service attacks [13,8]. Unfortunately, the cost of solving a crypto puzzle must be acceptable to the slowest legitimate node, yet the puzzle must be hard enough to sufficiently slow down an attacker with access to many fast machines. This conflict limits the effectiveness of any such technique.

For completeness, we briefly describe here one relatively simple approach to generate certified nodeIds in a completely distributed fashion using crypto puzzles. The idea is to require new nodes to generate a key pair with the property that the SHA-1 hash of the public key has the first $ p$ bits zero. The expected number of operations required to generate such a key pair is $ 2^p$. The properties of public-key cryptography allow the nodes to use a secure hash of the public key as their nodeId. This hash should be computed using SHA-1 with a different initialization vector or MD5 to avoid reducing the number of random bits in nodeIds. Nodes can prove that they performed the required amount of work to use a nodeId without revealing information that would allow others to reuse their work. The value of $ p$ can be set to achieve the desired level of security.

It is also possible to bind IP addresses with nodeIds to avoid attacks on overlays that exploit network locality. The idea is to require nodes to consume resources in order to be able to use a given nodeId with an IP address. We do this by requiring nodes to find a string $ x$ such that SHA-1(SHA-1(ipaddr,x),nodeId) has $ p'$ bits equal to zero. Nodes would be required to present such an $ x$ for the pair (nodeId,ipaddr) to be accepted by others.

Finally, it is possible to periodically invalidate nodeIds by having some trusted entity broadcast to the overlay a message supplying a different initialization vector for the hash computations. This makes it harder for an attacker to accumulate many nodeIds over time and to reuse nodeIds computed for one overlay in another overlay. However, it requires legitimate nodes to periodically spend additional time and communication to maintain their membership in the overlay.


4 Secure routing table maintenance

We now turn our attention to the problem of secure routing table maintenance. The routing table maintenance mechanisms are used to create routing tables and neighbor sets for joining nodes, and to maintain them after creation. Ideally, each routing table and neighbor set should have an average fraction of only $ f$ random entries that point to nodes controlled by the attacker (called ``bad entries''). But attackers can increase the fraction of bad entries by supplying bad routing updates, which reduces the probability of routing successfully to replica roots.

Preventing attackers from choosing nodeIds is necessary to avoid this problem but it is not sufficient as illustrated by the two attacks discussed next. We also discuss solutions to this problem.

4.1 Attacks

The first attack is aimed at routing algorithms that use network proximity information to improve routing efficiency: attackers may fake proximity to increase the fraction of bad routing table entries. For example, the network model that we assumed allows an attacker to control communication to and from faulty nodes that it controls. When a correct node $ p$ sends a probe to estimate delay to a faulty node with a certain nodeId, an attacker can intercept the probe and have the faulty node closest to $ p$ reply to it. If the attacker controls enough faulty nodes spread over the Internet, it can make nodes that it controls appear close to correct nodes to increase the probability that they are used for routing. The attack is harder when $ c$ (the maximal fraction of colluding nodes) is small even if $ f$ is large.

This attack can be ruled out by a more restrictive communication model, since nodeId certificates bind IP addresses to nodeIds (see Section 3.2). For example, if faulty nodes can only observe messages that are sent to their own IP address [19], this attack is prevented. But note that a rogue ISP or corporation with several offices around the world could easily perform this attack by configuring their routers appropriately. The attack is also possible if there is any other form of indirection that the attacker can control, e.g., mobile IPv6.

The second attack does not manipulate proximity information. Instead, it exploits the fact that it is hard to determine whether routing updates are legitimate in overlay protocols like Tapestry and Pastry. Nodes receive routing updates when they join the overlay and when other nodes join, and they fetch routing table rows from other nodes in their routing table periodically to patch holes and reduce hop delays. In these systems, attackers can more easily supply routing updates that always point to faulty nodes. This simple attack causes the fraction of bad routing table entries to increase toward one as the bad routing updates are propagated. More precisely, routing updates from correct nodes point to a faulty node with probability at least $ f$ whereas this probability can be as high as one for routing updates from faulty nodes. Correct nodes receive updates from other correct nodes with probability at most $ 1-f$ and from faulty nodes with probability at least $ f$. Therefore, the probability that a routing table entry is faulty after an update is at least $ (1-f) \times f + f \times 1$, which is greater than $ f$. This effect cascades with each subsequent update, causing the fraction of faulty entries to tend towards one.

Systems without strong constraints on the set of nodeIds that can fill each routing table slot are more vulnerable to this attack. Pastry and Tapestry impose very weak constraints at the top levels of routing tables. This flexibility makes it hard to determine if routing updates are unbiased but it allows these systems to effectively exploit network proximity to improve routing performance. CAN and Chord impose strong constraints on nodeIds in routing table entries: they need to be the closest nodeIds to some point in the id space. This makes it hard to exploit network proximity to improve performance but it is good for security; if attackers cannot choose the nodeIds they control, the probability that an attacker controls the nodeId closest to a point in the id space is $ f$.


4.2 Solution: constrained routing table

To enable secure routing table maintenance, it is important to impose strong constraints on the set of nodeIds that can fill each slot in a routing table. For example, the entry in each slot can be constrained to be the closest nodeId to some point in the id space as in Chord. This constraint can be verified and it is independent of network proximity information, which can be manipulated by attackers.

The solution that we propose uses two routing tables: one that exploits network proximity information for efficient routing (as in Pastry and Tapestry), and one that constrains routing table entries (as in Chord). In normal operation, the first routing table is used to forward messages to achieve good performance. The second one is used only when the efficient routing technique fails. We use the test in Section 5.2 to detect when routing fails.

We modified Pastry to use this solution. We use the normal locality-aware Pastry routing table and an additional constrained Pastry routing table. In the locality-aware routing table of a node with identifier $ i$, the slot at level $ l$ and domain $ d$ can contain any nodeId that shares the first $ l$ digits with $ i$ and has the value $ d$ in the $ l+1$st digit. In the constrained routing table, the entry is further constrained to point to the closest nodeId to a point $ p$ in the domain. We define $ p$ as follows: it shares the first $ l$ digits with $ i$, it has the value $ d$ in the $ l+1$st digit, and it has the same remaining digits as $ i$.

Pastry's message forwarding works with the constrained routing table without modifications. The same would be true with Tapestry. But the algorithms to initialize and maintain the routing table were modified as follows.

All overlay routing algorithms rely on a bootstrap node to initialize the routing state of a newly joining node. The bootstrap node is responsible for routing a message using the nodeId of the joining node as the key. If the bootstrap node is faulty, it can completely corrupt the view of the overlay network as seen by the new node. Therefore, it is necessary to use a set of diverse bootstrap nodes large enough to ensure that with very high probability, at least one of them is correct. The use of nodeId certificates makes the task of choosing such a set easier because the attacker cannot forge nodeIds.

A newly joining node, $ n$, picks a set of bootstrap nodes and asks all of them to route using its nodeId as the key. Then, non-faulty bootstrap nodes use secure forwarding techniques (described in Section 5.2) to obtain the neighbor set for the joining node. Node $ n$ collects the proposed neighbor sets from each of the bootstrap nodes, and picks the ``closest'' live nodeIds from each proposed set to be its neighbor set (where the definition of closest is protocol specific).

The locality-aware routing table is initialized as before by collecting rows from the nodes along the route to the nodeId. The difference is that there are several routes; $ n$ picks the entry with minimal network delay from the set of candidates it receives for each routing table slot.

Each entry in the constrained routing table can be initialized by using secure forwarding to obtain the live nodeId closest to the desired point $ p$ in the id space. This is similar to what is done in Chord. The problem is that it is quite expensive with $ b > 1$ (recall that $ b$ controls the number of columns in the routing table of Tapestry and Pastry). To reduce the overhead, we can take advantage of the fact that, by induction, the constrained routing tables of the nodes in $ n$'s neighbor set point to entries that are close to the desired point $ p$. Therefore, $ n$ can collect routing tables from the nodes in its neighbor set and use them to initialize its constrained routing table. From the set of candidates that it receives for each entry, it picks the nodeId that is closest to the desired point for that entry. As a side effect of this process, $ n$ informs the nodes in its neighbor set of its arrival.

We exploit the symmetry in the constrained routing table to inform nodes that need to update their routing tables to reflect $ n$'s arrival: $ n$ checks its neighbor set and the set of candidates for each entry to determine which candidates should update routing table entries to point to $ n$. It informs those candidates of its arrival.

To ensure neighbor set stabilization in the absence of new joins and leaves, $ n$ informs the members of its neighbor set whenever it changes and it periodically retransmits this information until its receipt is acknowledged.


5 Secure message forwarding

The use of certified nodeIds and secure routing table maintenance ensure that each constrained routing table (and neighbor set) has an average fraction of only $ f$ random entries that point to nodes controlled by the attacker. But routing with the constrained routing table is not sufficient because the attacker can reduce the probability of successful delivery by simply not forwarding messages according to the algorithm. The attack is effective even when $ f$ is small, as we will show. This section describes an efficient solution to this problem.

5.1 Attacks

All structured p2p overlays provide a primitive to send a message to a key. In the absence of faults, the message is delivered to the root node for the key after an average of $ h$ routing hops. But routing may fail if any of the $ h-1$ nodes along the route between the sender and the root are faulty; faulty nodes may simply drop the message, route the message to the wrong place, or pretend to be the key's root. Therefore, the probability of routing successfully between two correct nodes when a fraction $ f$ of the nodes is faulty is only: $ (1-f)^{h-1}$, which is independent of $ c$.

The root node for a key may itself be faulty. As discussed before, applications can tolerate root faults by replicating the information associated with the key on several nodes -- the replica roots. Therefore, the probability of routing successfully to a correct replica root is only: $ \sigma = (1-f)^{h}$. The value of $ h$ depends on the overlay: it is $ (d/4)(N^{1/d})$ in CAN, $ log_2(N)/2$ in Chord, and $ log_{2^b}(N)$ in Pastry and Tapestry.

We ran simulations of Pastry to validate this model. The model predicts a probability of success slightly lower than the probability that we observed in the simulations (because the number of Pastry hops is slightly less than $ log_{2^b}(N)$ on average [3]) but the error was below 2%.

Figure 3 plots the probability of routing to a correct replica in Pastry (computed using the model) for different values of $ f$, $ N$, and $ b=4$. The probability drops quite fast when $ f$ or $ N$ increase. Even with only 10% of the nodes compromised, the probability of successful routing is only 65% when there are 100,000 nodes in a Pastry overlay.

Figure 3: Probability of routing to a correct replica.
\begin{figure}\centering \psfig{file=prob-route-succ.eps,height=0.45\textwidth,angle=-90}\end{figure}

In CAN, Pastry, and Tapestry, applications can reduce the number of hops by increasing the value of $ d$ or $ b$. Fewer hops increase the probability of routing correctly. For example, the probability of successful delivery with $ f=0.1$ and 100,000 nodes is 65% in Pastry when $ b=4$ and 75% when $ b=6$. But increasing $ b$ also increases the cost of routing table maintenance; a high probability of routing success requires an impractically large value of $ b$. Chord currently uses a fixed $ b=1$, which results in a low probability of success, e.g., the probability is only 42% under the same conditions.


5.2 Solution: detect faults, use diverse routes

The results in Figure 3 show that it is important to devise mechanisms to route securely. We want a secure routing primitive that takes a message and a destination key and ensures that with very high probability at least one copy of the message reaches each correct replica root for the key. The question is how to do this efficiently.

Our approach is to route a message efficiently and to apply a failure test to determine if routing worked. We only use more expensive redundant routing when the failure test returns positive. In more detail, our secure routing primitive routes a message efficiently to the root of the destination key using the locality-aware routing table. Then, it collects the prospective set of replica roots from the prospective root node and applies the failure test to the set. If the test is negative, the prospective replica roots are accepted as the correct ones. If it is positive, message copies are sent over diverse routes toward the various replica roots such that with high probability each correct replica root is reached. We start by describing how to implement the failure test. Then we explain redundant routing and why we rejected an alternate approach called iterative routing.

5.2.1 Routing failure test

The failure test takes a key and a set of prospective replica roots for the key. It returns negative if the set of roots is likely to be correct for the key. Otherwise, it returns positive. Of course, routing can fail without the sender ever receiving a set of prospective replica roots. The sender detects this by starting a timer when it sends a message. If it does not receive a response before the timer expires, the failure test returns positive triggering the use of redundant routing.

Detecting routing failures is difficult because a coalition of faulty nodes can pretend to be the legitimate replica roots for a given key. Since the replica roots are determined by the structure of the overlay, a node whose nodeId is far from the key must rely on overlay routing to determine the correct set of replica roots. But if a message is routed by a faulty node, the adversary can fabricate a credible route and replica root set that contain only nodes it controls. Furthermore, it might be the case that the adversary just happens to legitimately control one of the actual replica roots. This problem is common to all structured p2p overlay protocols.

The routing failure test is based on the observation that the average density of nodeIds per unit of ``volume'' in the id space is greater than the average density of faulty nodeIds. The test works by comparing the density of nodeIds in the neighbor set of the sender with the density of nodeIds close to the replica roots of the destination key. We describe the test in detail only in the context of Pastry to simplify the presentation; the generalization to other overlays is straightforward. Overlays that distribute replica keys for a key uniformly over the id space can still use this check by comparing the density at the sender with the average distance between each replica key and its root's nodeId.

In Pastry, the set of replica roots for a key is a subset of the neighbor set of the key's root node, called the key's root neigbor set. Each correct node $ p$ computes the average numerical distance, $ \mu_p$, between consecutive nodeIds in its neighbor set. The neighbor set of $ p$ contains $ l+1$ live nodes: $ p$, the $ l/2$ nodes with the closest nodeIds less than $ p$'s, and the $ l/2$ nodes with the closest nodeIds greater than $ p$'s. To test a prospective root neighbor set, $ rn = id_0,...,id_{l+1}$, for a key $ x$, $ p$ checks that:

  1. all nodeIds in $ rn$ have a valid nodeId certificate, the closest nodeId to the key is the middle one, and the nodeIds satisfy the definition of a neighbor set

  2. the average numerical distance, $ \mu_{rn}$, between consecutive nodeIds in $ rn$ satisfies: $ \mu_{rn} < \mu_p \times \gamma$

If $ rn$ satisfies both conditions, the test returns negative; otherwise, it returns positive. The test can be inaccurate in one of two ways: it can return a false positive when the prospective root neighbor set is correct, or it can return a false negative when the prospective set is incorrect. We call the probability of false positives $ \alpha $ and the probability of false negatives $ \beta $. The parameter $ \gamma$ controls the tradeoff between $ \alpha $ and $ \beta $. Intuitively, increasing $ \gamma$ decreases $ \alpha $ but it also increases $ \beta $.

Assuming that there are $ N$ live nodes with nodeIds uniformly distributed over the id space (which has length $ D=2^{128}$), the distances between consecutive nodeIds are approximately independent exponential random variables with mean $ D/N$ for large $ N$. The same holds for the distances between consecutive nodeIds of faulty nodes that can collude together but the mean is $ D/(c \times N)$. It is interesting to note that $ \alpha $ and $ \beta $ are independent of $ f$. They only depend on the upper bound, $ c$, on the fraction of colluding nodes because faulty nodes only know the identities of faulty nodes that they collude with.

Under these assumptions, we have derived the following expressions to compute $ \alpha $ and $ \beta $ (see detailed derivation in the Appendix):

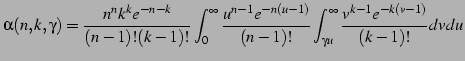$\displaystyle \alpha(n,k,\gamma) = \frac{n^n k^k e^{-n-k}}{(n-1)!(k-1)!} \int_0... ...u-1)}}{(n-1)!} \int_{\gamma u}^{\infty} \frac{v^{k-1}e^{-k(v-1)}}{(k-1)!} dv du$    

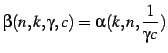$\displaystyle \beta(n,k,\gamma,c) = \alpha(k,n, \frac{1}{\gamma c})$    

These expressions can be used to compute $ \alpha $ and $ \beta $ numerically. We also computed the following closed-form upper bounds for $ \alpha $ and $ \beta $:

$\displaystyle \alpha \leq \exp \left\{ -k \Bigl[ (r+1)\log \frac{r+\gamma}{r+1} - \log \gamma \Bigr] \right\}$    

$\displaystyle \beta \leq \exp \left\{ -k \Bigl[ (r+1)\log \frac{r+\gamma c}{r+1} + \log (\gamma c) \Bigr] \right\}$    

where $ n$ is the number of distance samples used to compute $ \mu_p$, $ k$ is the number of distance samples used to compute $ \mu_{rn}$, and $ r = n/k$. The test above used $ n = k = l$.

The analysis shows that $ \alpha $ and $ \beta $ are independent of $ N$ (provided $ k \ll N$), and that the test's accuracy can be improved by increasing the number of distance samples used to compute the means. It is easy to increase the number of samples $ n$ used to compute $ \mu_p$ by augmenting the mechanism that is already in place to stabilize neighbor sets. This mechanism propagates nodeIds that are added and removed from a neighbor set to the other members of the set; it can be extended to propagate nodeIds further but we omit the details due to lack of space. It is hard to increase the number of samples used to compute $ \mu_{rn}$ because of some attacks that we describe below. Therefore, we keep $ k = l$.

Figure 4: Routing failure test: probability of false positives ($ \alpha $) and negatives ($ \beta $). The predicted curves are almost indistinguishable from the simulation measurements but the upper bounds are not tight.
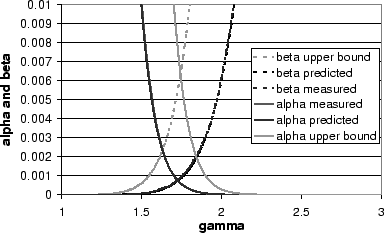\begin{figure}\centering \psfig{file=leafdensity1a.eps,height=0.45\textwidth,angle=-90}\end{figure}

We ran several simulations to evaluate the effectiveness of our routing failure test. The simulations ran in a system with 100,000 random nodeIds. Figure 4 plots values of $ \alpha $ and $ \beta $ for different values of $ \gamma$ with $ f=c=0.3$, the number of samples at the sender is $ n=256$, and the number of root neighbors is $ k=l=32$. The figure shows predicted values computed numerically, the upper bounds, and values measured in the simulations. The predicted curves match the measured curves almost exactly but the upper bounds are not very tight. The minimum error is obtained when $ \alpha = \beta$, which is equal to $ 0.0008$ with $ \gamma = 1.72$ in this case.

5.2.1.1 Attacks:

There are several attacks that could invalidate the analysis and weaken our routing failure test. First, the attacker can collect nodeId certificates of nodes that have left the overlay, and use them to increase the density of a prospective root neighbor set. Second, the attacker can include both nodeIds of nodes it controls and nodeIds of correct nodes in a prospective root neighbor set. Both attacks can reduce the probability that messages reach all correct replica roots. The second attack is harder to counter in overlays that distribute replica keys over the id space because replica roots have no detailed knowledge about the nodeIds close to other replica keys.

These attacks can be avoided by having the sender contact all the prospective root neighbors to determine if they are live and if they have a nodeId certificate that was omitted from the prospective root neighbor set. To implement this efficiently, the prospective root returns to the sender a message with the list of nodeId certificates, a list with the secure hashes of the neighbor sets reported by each of the prospective root neighbors, and the set of nodeIds (not in the prospective root neighbor set) that are used to compute the hashes in this list. The sender checks that the hashes are consistent with the identifiers of the prospective root neighbors. Then, it sends each prospective root neigbor the corresponding neighbor set hash for confirmation.

In the absence of faults, the root neighbors will confirm the hashes and the sender can perform the density comparison immediately. For a sufficiently large timeout, this happens with probability $ \tau = binom(0; k, f)$, where binom is the binomial distribution [6] and $ k$ is the number of root neighbors. With faulty nodes in the prospective root neighbor set, the routing failure test may require more communication before the density check can be run. We are still studying the best strategy to deal with this case. Currently, we consider the test failed when the prospective root neighbors don't agree and use redundant routing. But, it may be worthwhile investing some additional communication before reverting to redundant routing.

In addition to these attacks, there is a nodeId suppression attack that seems to be unavoidable and significantly decreases the accuracy of this test. The attacker can suppress nodeIds close to the sender by leaving the overlay, which increases $ \beta $. Similarly, the attacker can suppress nodeIds in the root neighbor set, which increases $ \alpha $. Furthermore, the attacker can alternate between the two modes and honest nodes have no way of detecting in which mode they are operating.

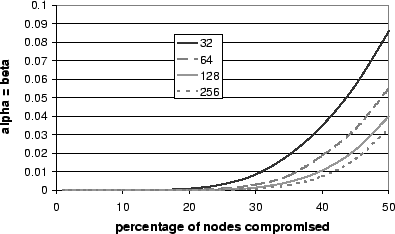
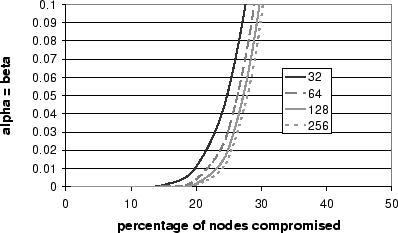
We ran simulations to compute the minimum error probability ( $ \alpha = \beta$) with and without nodeId suppression attacks for different values of $ c = f$. The probability of error increases fast with $ c$ and it is higher than $ 0.001$ for $ c \geq 0.35$ even with 256 samples at the sender. The nodeId suppression attack increases the minimum probability of error for large percentages of compromised nodes, e.g., the probability of error is higher than 0.001 for $ c \geq 0.2$ even with 256 samples at the sender. Figures 5 and 6 show the results without and with nodeId suppression attacks, respectively.

Figure 5: Routing failure test: minimum error probability without nodeId suppression attacks and varying number of samples.
\begin{figure}\centering \psfig{file=leafdensity3.eps,height=0.45\textwidth,angle=-90}\end{figure}

Figure 6: Routing failure test: minimum error probability with nodeId suppression attacks and varying number of samples.
\begin{figure}\centering \psfig{file=leafdensity2.eps,height=0.45\textwidth,angle=-90} \end{figure}

These results indicate that our routing failure test is not very accurate. But, fortunately we can trade off an increase in $ \alpha $ to achieve a target $ \beta $ and use redundant routing to disambiguate false positives. We ran simulations to determine the minimum $ \alpha $ that can be achieved for a target $ \beta = 0.001$ with different values of $ c = f$, and different numbers of samples at the sender. Figure 7 shows the results with nodeId suppression attacks.

Figure 7: Routing failure test: probability of false positives for a false negative rate of 0.001 with nodeId suppression attacks and varying number of samples.
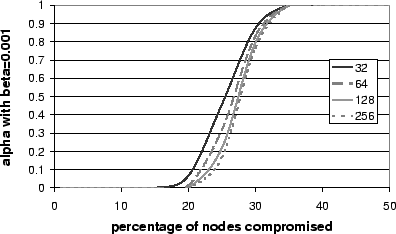\begin{figure}\centering \psfig{file=leafdensity4.eps,height=0.45\textwidth,angle=-90}\end{figure}

The results show that the test is not meaningful for this target $ \beta $ and $ c > 0.3$ with nodeId suppression attacks. However, setting $ \gamma = 1.23$ with 256 samples at the sender enables the routing failure test to achieve the target $ \beta $ for $ c \leq 0.3$. For this value of $ \gamma$ and with $ c=0.3$, nodeId suppression attacks can increase $ \alpha $ to 0.77. But without nodeId suppression attacks the value of $ \alpha $ is only 0.12, i.e., redundant routing is required 12% of the time.

5.2.2 Redundant routing

The redundant routing technique is invoked when the routing failure test is positive. The idea is simply to route copies of the message over multiple routes toward each of the destination key's replica roots. If enough copies of the message are sent along diverse routes to each replica key, all correct replica roots will receive at least one copy of the message with high probability.

The issue is how to ensure that routes are diverse. One approach is to ask the members of the sender's neighbor set to forward the copies of the message to the replica keys. This technique is sufficient in overlays that distribute the replica keys uniformly over the id space (e.g., CAN and Tapestry). But it is not sufficient in overlays that choose replica roots in the neighbor set of the key's root (e.g., Chord and Pastry) because the routes all converge on the key's root, which might be faulty. For these overlays, we developed a technique called neighbor set anycast that sends copies of the message toward the destination key until they reach a node with the key's root in its neighbor set. Then it uses the detailed knowledge that such a node has about the portion of the id space around the destination key to ensure that all correct replica roots receive a copy of the message.

To simplify the presentation, we only describe in detail how redundant routing works in Pastry. If a correct node $ p$ sends a message to a destination key $ x$ and the routing failure test is positive, it does the following:

(1) $ p$ sends $ r$ messages to the destination key $ x$. Each message is forwarded via a different member of $ p$'s neighbor set; this causes the messages to use diverse routes. All messages are forwarded using the constrained routing table and they include a nonce.

(2) Any correct node that receives one of the messages and has $ x$'s root in its neighbor set returns its nodeId certificate and the nonce, signed with its private key, to $ p$.

(3) $ p$ collects in a set $ \cal N$ the $ l/2+1$ nodeId certificates numerically closest to $ x$ on the left, and the $ l/2+1$ closest to $ x$ on the right. Only certificates with valid signed nonces are added to $ \cal N$ and they are first marked pending.

(4) After a timeout or after all $ r$ replies are received, $ p$ sends a list with the nodeIds in $ \cal N$ to each node marked pending in $ \cal N$ and marks the nodes done.

(5) Any correct node that receives this list forwards $ p$'s original message to the nodes in its neighbor set that are not in the list, or it sends a confirmation to $ p$ if there are no such nodes. This may cause steps 2 to 4 to be repeated.

(6) Once $ p$ has received a confirmation from each of the nodes in $ \cal N$, or step 4 was executed three times, it computes the set of replica roots for $ x$ from $ \cal N$.

If the timeout is sufficiently large and correct nodes have another correct node in each half of their neighbor set1, the probability of reaching all correct replica roots of $ x$ is approximately equal to the probability that at least one of the anycast messages is forwarded over a route with no faults to a correct node with the key's root in its neighbor set. Assuming independent routes, this probability is:

$\displaystyle 1 - binom(0; r, (1-f)^{1+log_{2^b}N}) $

where binom is the binomial distribution [6] with 0 successful routes, $ r$ trials, and the probability of routing successfully in each trial is $ (1-f)^{1+log_{2^b}N}$. The $ +1$ counts the extra hop for messages routed through a neighbor set member. The probability of success for this technique depends on $ f$ and is independent of $ c$.

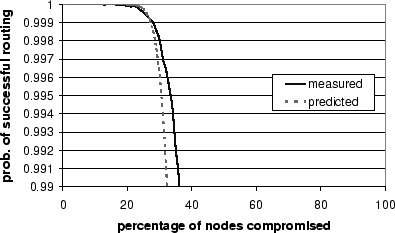
We also ran simulations to determine the probability of reaching all correct replica roots with our redundant routing technique. Figure 8 plots the predicted probability and the probability measured in the simulator for 100,000 nodes, $ b=4$, and $ l=r=32$. The analytic model matches the results well for high success probabilities. The results show that the probability of success is greater than 0.999 for $ f < 0.3$. Therefore, this technique combined with our routing failure test can achieve a reliability of approximately 0.999 for $ f < 0.3$.

Figure 8: Model and simulation results for the probability of reaching all correct replica roots using redundant routing with neighbor set anycast.
\begin{figure}\centering \psfig{file=leafanycast.eps,height=0.45\textwidth,angle=-90}\end{figure}

We studied several versions of redundant routing that achieve the same probability of success but perform differently. For example, the signed nonces are used to ensure that the nodeId certificates in $ \cal N$ belong to live nodes. But nodes can avoid signing nonces by periodically signing their clock reading in a system with loosely synchronized clocks, and no signatures are necessary if the attacker cannot forge IP source addresses. We are still exploring the design space. For example, it should be possible to improve performance significantly by sending the anycast messages one at a time and using a version of the routing failure test after each one. This approach would also work well when reading self-certifying data.

5.2.3 Putting it all together: performance

The performance of Pastry's secure routing primitive depends on the cost of the routing failure test, the cost of redundant routing, and on the probability that redundant routing can be avoided. This section presents an analysis of these costs and probability. For simplicity, we assume that all faulty nodes can collude ($ c = f$), the number of probes used by redundant routing is equal to the neighbor set size ($ r=l$), the number of samples at the source for routing failure tests is $ n=256$, and the number of nodes in the overlay is $ N=100,000$.

The cost of the routing failure test when it returns negative is an extra round-trip delay and $ 2l+1$ messages. The total number of bytes in all messages is:


$\displaystyle l \times ($IdSize$\displaystyle +2$HashSize$\displaystyle )+(l+1) \times$   IdCertSize$\displaystyle +(2l+1) \times$   HdrSize    


Using PSS-R [1] for signing nodeId certificates with 1024-bit modulus and 512-bit modulus for the node public keys, the nodeId certificate size is 128B. Therefore, the extra bandwidth consumed by the routing failure test is approximately 5.6 KB with $ l=32$ and 2.9 KB with $ l=16$ (plus the space used up by message headers). When the test returns positive, it adds the same number of messages and bytes but the extra delay is the timeout period.

The cost of redundant routing depends on the value of $ f$. The best case occurs when all of the root's neighbor set is added to $ \cal N$ in the first iteration. In this case, redundant routing adds $ \log_{2^b}N+3$ extra message delays and $ l \times (\log_{2^b}N+3)$ messages. The total number of bytes in these messages is:


$\displaystyle l \times (l \times$   IdSize$\displaystyle +$IdCertSize$\displaystyle +$SigSize$\displaystyle )+l \times (\log_{2^b}N+3) \times$   HdrSize    


Using PSS-R for signing nonces, the signed nonce size is 64B. Therefore, the extra bandwidth consumed in this case is 22 KB with $ l=32$ and 7 KB with $ l=16$ (plus the space used up by message headers).

Under attack redundant routing adds a delay of at most three timeout periods and the expected number of extra messages is less than $ l \times (\log_{2^b}N+2)+ (l-g) \times (3+g)$, where $ g=l \times (1-f)^{log_{2^b}N+1}$ is the expected number of correct nodes in the root's neighbor set that is added to $ \cal N$ in the first iteration. The expected number of messages is less than 451 with $ l=32$ and $ f = 0.25$ and less than 188 with $ l=16$ and $ f = 0.18$. The total number of bytes sent under attack is similar to the best case value except that the sender sends an additional $ l(l-g) \times$   IdSize bytes in nodeId lists and the number of messages increases. This is an additional 12 KB with $ l=32$ and $ f = 0.25$ and 1 KB with $ l=16$ and $ f = 0.18$ (plus the space used up by message headers).

The probability of avoiding redundant routing is given by $ \sigma \times \tau \times (1-\alpha)$, where $ \sigma$ is the probability that the overlay routes the message to the correct replica root, $ \tau$ is the probability that there are no faulty nodes in the neighbor set of the root, and $ \alpha $ is the false positive rate of the routing failure test. We use $ \sigma = (1-f)^{log_{2^b}N}$, which assumes that routing tables have an average of $ f$ random bad entries. This assumption holds for the locality-aware routing table in the absence of the attacks discussed in Section 4 and it holds for the constrained routing table even with these attacks. We do not have a good model of the effect of these attacks on the locality aware routing table but we believe that they are very hard to mount for small values of $ f$ ($ \le 0.1$).

The parameters $ \gamma$ and $ l$, should be set based on the desired security level, which can be expressed as the probability $ \Sigma$ that all correct replica roots receive a copy of the message. The overlay size and the assignment of values to the parameters implicitly define a bound on $ f$. If this bound is exceeded, $ \Sigma$ will drop. For example, we saw that $ f \le 0.3 \Rightarrow \Sigma \ge 0.999$ with $ \gamma = 1.23$ and $ l=32$. But redundant routing is invoked 12% of the time for this value of $ \gamma$ even with no faults.

One can trade off security for improved performance by increasing $ \gamma$ to reduce $ \alpha $, and by decreasing $ l$ to reduce the cost of the routing failure test and redundant routing and to increase $ \tau$. For example, consider the following two scenarios: (1) $ f \le 0.18 \Rightarrow \Sigma \ge 0.999$ with $ \gamma = 1.8$ and $ l=16$, and (2) $ f \le 0.25 \Rightarrow \Sigma \ge 0.999$ with $ \gamma = 1.58$ and $ l=32$. Figure 9 plots the probability of avoiding redundant routing in these two scenarios for different values of $ f$. Without faults, redundant routing is invoked only 0.5% of the time in scenario (1) and 0.4% in (2). In the common case when the fraction of faulty nodes is small, the routing failure test improves performance significantly by avoiding the cost of redundant routing.

Figure 9: Probability of avoiding redundant routing in two scenarios: (1) $ f \le 0.18 \Rightarrow \Sigma \ge 0.999$ with $ \gamma = 1.8$ and $ l=16$, and (2) $ f \le 0.25 \Rightarrow \Sigma \ge 0.999$ with $ \gamma = 1.58$ and $ l=32$.
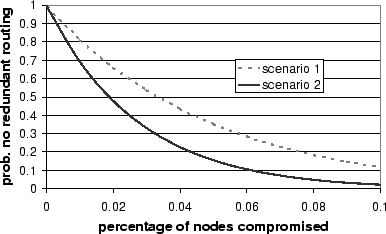\begin{figure}\centering \psfig{file=figperf.eps,height=0.45\textwidth,angle=-90}\end{figure}

5.2.4 Rejected: checked iterative routing

An alternative to redundant routing is iterative routing, as suggested in Sit and Morris [19]: the sender starts by looking up the next hop in its routing table and setting a variable $ n$ to point to this node; then, the sender asks $ n$ for the next hop and updates $ n$ to point to the returned value. The process is repeated until this value is the root of the destination key.

Iterative routing doubles the cost relative to the more traditional recursive solution but it may increase the probability of routing successfully because it allows the sender to pick an alternative next hop when it fails to receive an entry from a node. This is not a strong defense against an attacker who can provide a faulty node as the next hop. However, iterative routing can be augmented with hop tests to check whether the next hop in a route is correct.

Hop tests are effective in systems like Chord or Pastry with the constrained routing table because each routing table entry should contain the nodeId closest to a specific point $ p$ in the id space. One can use a mechanism identical to the nodeId density checking that we used for the routing failure test. The only difference is that the average distance between consecutive nodeIds close to the sender is compared to the distance between the nodeId in the routing table entry and the desired point $ p$. We ran simulations to compute the false positive and false negative rates for this approach with different values of $ c$ (these rates are independent of $ f$). For example, the minimum error for this hop test ( $ \alpha = \beta$) is equal to approximately 0.35 with $ c=0.3$ and 256 samples to compute the mean at the sender.

The error is high because there is a single sample at the destination hop. However, our simulations indicate that iterative lookups using Pastry's constrained routing table with this hop check improve the probability of routing successfully. For example, the probability of routing successfully with $ c=0.3$, $ N=100,000$, $ b=4$, $ l=32$, and 256 samples to compute the mean at the sender, improves from below 0.3 to 0.4. But it adds an extra 2.7 hops to each route on average because of false positives.

We tried to increase the number of samples by having the sender fetch an entire routing table row during each iterative routing step without revealing the index of the required slot. Unfortunately, this performs worse than obtaining a single sample because the attacker can combine good and bad routing table entries to obtain a high average density.

We also tried to combine checked iterative routing with the redundant routing technique that we described before. We used checked iterative routing for the neighbor set anycast messages in the hope that the improved success probability for the iterative routes would result in an improvement over redundant routing with recursive routes. But there was no visible improvement, most likely because the iterative routes are less independent than the recursive routes. We conclude that the routing failure test combined with redundant routing is the most effective solution for implementing secure routing.


6 Self-certifying data

The secure routing primitive adds significant overhead over conventional routing. In this section, we describe how the use of secure routing can be minimized by using self-certifying data.

The reliance on secure routing can be reduced by storing self-certifying data in the overlay, i.e., data whose integrity can be verified by the client. This allows clients to use efficient routing to request a copy of an object. If a client receives a copy of the object, it can check its integrity and resort to secure routing only when the integrity check fails or there was no response within a timeout period.

Self-certifying data does not help when inserting new objects in the overlay or when verifying that an object is not stored in the overlay. In these cases, we use the secure routing primitive to ensure that all correct replica roots are reached. Similarly, node joining requires secure routing. Nevertheless, self-certifying data can eliminate the overhead of secure routing in common cases.

Self-certifying data has been used in several systems. For example, CFS [7] uses a cryptographic hash of a file's contents as the key during insertion and lookup of the file, and PAST [18] inserts signed files into the overlay.

The technique can be extended to support mutable objects with strong consistency guarantees. One can use a system like PAST to store self-certifying group descriptors that identify the set of hosts responsible for replicating the object. Group descriptors can be used as follows. At object creation time, the owner of the object uses secure routing to insert a group descriptor into the overlay under a key that identifies the object. The descriptor contains the public keys and IP addresses of the object's replica holders and it is signed by the owner.

The replica group can run a Byzantine-fault-tolerant replication algorithm like BFT [4] and the initial group membership is the set of replica roots associated with the key. In this setting, read and write operations can be performed as follows: the client uses efficient routing to retrieve a group descriptor from the overlay and checks the descriptor's signature; if correct, it uses the information in the descriptor to authenticate the replica holders and to invoke a replicated operation. If the client fails to retrieve a valid descriptor or if it fails to authenticate the replica holders, it uses the secure routing primitive to obtain a correct group descriptor or to assert that the object does not exist. This procedure provides strong consistency guarantees (linearizability [11]) for reads and writes while avoiding the routing failure test in the common case.

Changing the membership of the group that is responsible for replicating an object is not trivial; it requires securely inserting a new group descriptor in the overlay and ensuring that clients can reliably detect stale group descriptors. The following technique allows groups to change membership while retaining strong consistency guarantees. Each group of hosts that stores replicas of a given object maintains a private/public key pair associated with the group. When the group membership changes, each host in the new membership generates a new key pair for the group, the hosts in the old membership use their old keys to sign a new group descriptor containing the new keys, and then delete the old keys.

If this operation is performed by a quorum of replica holders before the bound on the number of faulty group members is exceeded [4], old replica holders that fail will not be able to collude to pretend they are the current group because they cannot form the quorum necessary to authenticate themselves to a client.

Group descriptors can be authenticated by following a signature chain that starts with an owner signature and has signatures of a quorum of replicas for each subsequent membership change. The chain can be shortened by a new signature from the owner or, alternatively, replicas can use proactive signature sharing [12] to avoid the need for chaining signatures.


7 Related work

Sit and Morris [19] present a framework for performing security analyses of p2p networks. Their adversarial model allows for nodes to generate packets with arbitrary contents, but assumes that nodes cannot intercept arbitrary traffic. They then present a taxonomy of possible attacks. At the routing layer, they identify node lookup, routing table maintenance, and network partitioning / virtualization as security risks. They also discuss issues in higher-level protocols, such as file storage, where nodes may not necessarily maintain the necessary invariants, such as storage replication. Finally, they discuss various classes of denial-of-service attacks, including rapidly joining and leaving the network, or arranging for other nodes to send bulk volumes of data to overload a victim's network connection (i.e., distributed denial of service attacks).

Dingledine et al. [9] and Douceur [10] discuss address spoofing attacks. With a large number of potentially malicious nodes in the system and without a trusted central authority to certify node identities, it becomes very difficult to know whether you can trust the claimed identity of somebody to whom you have never before communicated. Dingledine proposes to address this with various schemes, including the use of micro-cash, that allow nodes to build up reputations.

Bellovin [2] identifies a number of issues with Napster and Gnutella. He discusses how difficult it might be to limit Napster and Gnutella use via firewalls, and how they can leak information that users might consider private, such as the search queries they issue to the network. Bellovin also expresses concern over Gnutella's ``push'' feature, intended to work around firewalls, which might be useful for distributed denial of service attacks. He considers Napster's centralized architecture to be more secure against such attacks, although it requires all users to trust the central server.

It is worthwhile mentioning a very elegant alternative solution for secure routing table maintenance and forwarding that we rejected. This solution replaces each node by a group of diverse replicas as suggested by Lynch et al. [14]. The replicas are coordinated using a state machine replication algorithm like BFT [4] that can tolerate Byzantine faults. BFT can replicate arbitrary state machines and, therefore, it can replicate Pastry's routing table maintenance and forwarding protocols. Additionally, the algorithm in [14] provides strong consistency guarantees for overlay routing and maintenance.

However, there are two disadvantages: the solution is expensive even without faults, and it is less resilient than the solution that we propose. Each routing step is expensive because it requires an agreement protocol between the replicas. Since the replicas should be geographically dispersed to reduce the probability of correlated faults, agreement latency will be high. Additionally, each group of replicas must have less than $ 1/3$ of its nodes faulty. This bound on the number of faulty replicas per group results in a relatively low probability of successful routing. The probability that a replica group with $ r$ replicas is correct when a fraction $ f$ of the nodes in the Pastry overlay is compromised is $ \sum_{i=0}^{\lfloor r/3 \rfloor}binom(i;r,f)$, where binom denotes the binomial distribution with $ i$ successes, $ r$ trials, and probability of success $ f$. For example, the probability that a replica group is correct with 20% of the nodes compromised and 32 replicas is less than 93%. In this example, the probability of routing correctly with 100,000 nodes in the overlay is only 72%.


8 Conclusions

Structured peer-to-peer overlay networks have previously assumed a fail-stop model for nodes; any node accessible in the network was assumed to correctly follow the protocol. However, if nodes are malicious and conspire with each other, it is possible for a small number of nodes to compromise the overlay and the applications built upon it. This paper has presented the design and analysis of techniques for secure node joining, routing table maintenance, and message forwarding in structured p2p overlays. These techniques provide secure routing, which can be combined with existing techniques to construct applications that are robust in the presence of malicious participants. A routing failure test allows the use of efficient proximity-aware routing in the common case, resorting to the more costly redundant routing technique only when the test indicates possible interference by an attacker. Moreover, we show how the use of secure routing can be reduced by using self-certifying application data. These techniques allow us to tolerate up to 25% malicious nodes while providing good performance when the fraction of compromised nodes is small.

Acknowledgments

We wish to thank Robert Morris, Rodrigo Rodrigues, Fabien Petitcolas, our shepherd David Wetherall and the anonymous referees for their helpful comments. We also wish to thank Adam Stubblefield for many discussions on the nodeId assignment problem. This work was supported in part by grants from Texas ATP (003604-0079-2001) and NSF (CCR-9985332).

Bibliography

1
M. Bellare and P. Rogaway.
The exact security of digital signatures- How to sign with RSA and Rabin.
In Advances in Cryptology - EUROCRYPT 96, Lecture Notes in Computer Science, Vol. 1070. Springer-Verlag, 1996.

2
Steve Bellovin.
Security aspects of Napster and Gnutella.
In 2001 Usenix Annual Technical Conference, Boston, Massachusetts, June 2001.
Invited talk.

3
Miguel Castro, Peter Druschel, Y. Charlie Hu, and Antony Rowstron.
Exploiting network proximity in peer-to-peer overlay networks.
Technical Report MSR-TR-2002-82, Microsoft Research, May 2002.

4
Miguel Castro and Barbara Liskov.
Practical byzantine fault tolerance.
In Proceedings of the Third Symposium on Operating Systems Design and Implementation (OSDI'99), New Orleans, Louisiana, February 1999.

5
Ian Clarke, Oskar Sandberg, Brandon Wiley, and Theodore W. Hong.
Freenet: A distributed anonymous information storage and retrieval system.
In Workshop on Design Issues in Anonymity and Unobservability, pages 311-320, July 2000.
ICSI, Berkeley, California.

6
Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest.
Introduction to Algorithms.
MIT Electrical Engineering and Computer Science Series. MIT Press, 1990.

7
Frank Dabek, M. Frans Kaashoek, David Karger, Robert Morris, and Ion Stoica.
Wide-area cooperative storage with CFS.
In Proc. ACM SOSP'01, Banff, Canada, October 2001.

8
Drew Dean and Adam Stubblefield.
Using client puzzles to protect TLS.
In 10th Usenix Security Symposium, pages 1-8, Washington, D.C., August 2001.

9
Roger Dingledine, Michael J. Freedman, and David Molnar.
Accountability measures for peer-to-peer systems.
In Peer-to-Peer: Harnessing the Power of Disruptive Technologies. O'Reilly and Associates, November 2000.

10
John R. Douceur.
The Sybil attack.
In Proceedings for the 1st International Workshop on Peer-to-Peer Systems (IPTPS '02), Cambridge, Massachusetts, March 2002.

11
M. P. Herlihy and J. M. Wing.
Axioms for Concurrent Objects.
In Proceedings of 14th ACM Symposium on Principles of Programming Languages, pages 13-26, January 1987.

12
A. Herzberg, M. Jakobsson, S. Jarecki, H. Krawczyk, and M. Yung.
Proactive public key and signature systems.
In Proc. of the 1997 ACM Conference on Computers and Communication Security, 1997.

13
Ari Juels and John Brainard.
Client puzzles: A cryptographic defense against connection depletion attacks.
In Internet Society Symposium on Network and Distributed System Security (NDSS '99), pages 151-165, San Diego, California, February 1999.

14
Nancy Lynch, Dahlia Malkhi, and David Ratajczak.
Atomic data access in content addressable networks.
In Proceedings for the 1st International Workshop on Peer-to-Peer Systems (IPTPS '02), Cambridge, Massachusetts, March 2002.

15
Ralph C. Merkle.
Secure communications over insecure channels.
Communications of the ACM, 21(4):294-299, April 1978.

16
Sylvia Ratnasamy, Paul Francis, Mark Handley, Richard Karp, and Scott Shenker.
A scalable content-addressable network.
In Proc. ACM SIGCOMM'01, San Diego, California, August 2001.

17
Antony Rowstron and Peter Druschel.
Pastry: Scalable, distributed object location and routing for large-scale peer-to-peer systems.
In Proc. IFIP/ACM Middleware 2001, Heidelberg, Germany, November 2001.

18
Antony Rowstron and Peter Druschel.
Storage management and caching in PAST, a large-scale, persistent peer-to-peer storage utility.
In Proc. ACM SOSP'01, Banff, Canada, October 2001.

19
Emil Sit and Robert Morris.
Security considerations for peer-to-peer distributed hash tables.
In Proceedings for the 1st International Workshop on Peer-to-Peer Systems (IPTPS '02), Cambridge, Massachusetts, March 2002.

20
Ion Stoica, Robert Morris, David Karger, M. Frans Kaashoek, and Hari Balakrishnan.
Chord: A scalable peer-to-peer lookup service for Internet applications.
In Proc. ACM SIGCOMM'01, San Diego, California, August 2001.

21
Ben Y. Zhao, John D. Kubiatowicz, and Anthony D. Joseph.
Tapestry: An infrastructure for fault-resilient wide-area location and routing.
Technical Report UCB//CSD-01-1141, U. C. Berkeley, April 2001.

Appendix

This appendix describes an analytic model for the probability of false positives and negatives in the routing failure test.

We assume that there exist $ N$ nodeIds distributed uniformly at random on an interval of length $ D=2^{128}$. If $ N$ is large and we look at the $ K$ nodeIds closest to an arbitrarily chosen location on this interval (for some $ K \ll N$), the location of these $ K$ nodeIds is well approximated in distribution by a Poisson process of rate $ N/D$. In particular, the inter-point distances are approximately independent exponential random variables with mean $ D/N$.

Let $ F_1$ denote the exponential distribution with mean $ \mu_1 = D/N$ and $ F_2$ the exponential distribution with mean $ \mu_2 = D/Nf$, where $ f$ is the fraction of faulty nodes. Suppose $ y_1, \ldots, y_k$ are independent identically distributed (iid) and are drawn from one of these two distributions and we are required to identify which distribution they are drawn from, e.g., $ y_1, \ldots, y_k$ can be a prospective set of replica roots in Pastry and we are trying to determine if the set is correct or if it contains only faulty nodes. An optimal hypothesis test is based on comparing the likelihood ratio to a threshold; by writing down the likelihood ratio, we see that this is equivalent to comparing the sample mean, denoted $ \mu_y$, to a threshold $ T$.

We are in a situation where $ N$ is unknown but we have samples $ x_1, \ldots, x_n$ from $ F_1$ (i.e., the samples that we collect from the nodeIds close to the sender in the id space). We propose the following hypothesis test: choose a threshold of the form $ \gamma \mu_x$, for some constant $ \gamma \in (1, 1/f)$, and accept/reject the hypothesis that $ Y_i$ are iid $ F_1$ by comparing $ \mu_y$ to this threshold. We now compute the false positive probability, $ \alpha $, and the false negative probability, $ \beta $, for this test.

Denote $ n/k$ by $ r$ and assume without loss of generality that $ r$ is an integer. For $ i=1,\ldots,k$, define

$\displaystyle Z_i = Y_i - \frac{\gamma}{r} (X_{(i-1)r+1} + \ldots + X_{ir}), $

and note that the $ Z_i$ are iid random variables. Let $ S_j$ denote the sum of $ j$ iid exponential random variables with mean $ \mu_1 = D/N$. The event that $ \mu_Y > \gamma \mu_X$ is then the event that $ \sum_{i=1}^k Z_i > 0$. Thus,

$\displaystyle \alpha(n,k,\gamma) = P_1 (\sum_{i=1}^k Z_i > 0) = P(\frac{1}{k} S_k > \frac{\gamma}{n} S_n),$ (1)

where we write $ P_1$ to denote probabilities when the $ Y_i$ have distribution $ F_1$. Recalling that $ S_j$ has the gamma distribution with shape parameter $ j$ and scale parameter $ 1/\mu_1$, we can rewrite the above as
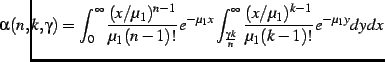    $\displaystyle \negthickspace\negthickspace\negthickspace\negthickspace\negthins... ...c{\gamma k}{n}}^{\infty} \frac{(x/\mu_1)^{k-1}}{\mu_1(k-1)!} e^{-\mu_1 y} dy dx$  
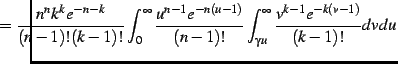    $\displaystyle \negthickspace\negthickspace\negthickspace\negthickspace\negthins... ...u-1)}}{(n-1)!} \int_{\gamma u}^{\infty} \frac{v^{k-1}e^{-k(v-1)}}{(k-1)!} dv du$  

where we used the change of variables $ u=x/(n\mu_1)$ and $ v=y/(k\mu_1)$ to obtain the last equality. This expression can be used to compute $ \alpha $ numerically.

We now derive a simple closed-form expression for an upper bound on $ \alpha $. The bound shows that $ \alpha $ decays exponentially in the sample size, $ k$, and in fact captures the exact exponential rate of decay. For arbitrary $ \theta \ge 0$, we have by Chernoff's bound that

$\displaystyle \alpha \le E[\exp (\theta \sum_{i=1}^k Z_i)] = \left( E[e^{\theta Y_1}] \right)^k \left( E[\exp(-\frac{\gamma \theta}{r} X_1)] \right)^{rk} $

Now, if $ X$ has an exponential distribution with mean $ \mu$, then $ E[e^{\theta X}]$ is $ 1/(1-\theta \mu)$ for $ \theta<1/\mu$ and $ +\infty$ for $ \theta \ge 1/\mu$. Thus, for all $ \theta \in [0,1/\mu_1)$, we have

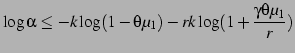
$\displaystyle \log \alpha \le -k\log (1-\theta \mu_1) - rk\log (1+\frac{\gamma \theta \mu_1}{r}) $

The tightest upper bound is obtained by minimising the expression on the right over $ \theta \in [0,1/\mu_1)$. The minimum is attained at $ \theta = \frac{r}{r+1}\frac{\gamma-1}{\gamma \mu_1}$. Substituting this above yields the bound,

$\displaystyle \alpha \le \exp \left\{ -k \Bigl[ (r+1)\log \frac{r+\gamma}{r+1} - \log \gamma \Bigr] \right\}$ (2)

We can derive an expression for the false negative probability, $ \beta $, along similar lines. Now, the $ Y_i$ are iid with distribution $ F_2$, i.e., they are exponentially distributed with mean $ \mu_2 = \mu_1/f$, and we are interested in the event that $ \mu_Y \le \gamma \mu_X$. If this happens, then we fail to reject the hypothesis that the $ Y_i$ have distribution $ F_1$. Thus

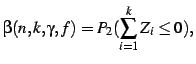
$\displaystyle \beta(n,k,\gamma,f) = P_2 (\sum_{i=1}^k Z_i \le 0), $

where we write $ P_2$ to denote probabilities when the $ Y_i$ are exponential with mean $ \mu_1/f$. In this case, $ Y_1$ has the same distribution as $ X_1/f$, so $ \sum_{i=1}^k Y_i$ has the same distribution as $ (\sum_{i=1}^k X_i)/f$, and we obtain using (1) that

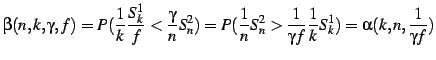
$\displaystyle \beta(n,k,\gamma,f) = P(\frac{1}{k} \frac{S^1_k}{f} < \frac{\gam... ...^2_n > \frac{1}{\gamma f} \frac{1}{k} S^1_k) = \alpha(k,n, \frac{1}{\gamma f}) $

This allows us to compute $ \beta $ numerically and by combining this with (2), we obtain the following closed-form upper bound

$\displaystyle \beta \le \exp \left\{ -k \Bigl[ (r+1)\log \frac{r+\gamma f}{r+1} - \log (\gamma f) \Bigr] \right\}$    


Footnotes

... set1
The neighbor set size $ l$ should be chosen to ensure this with high probability

Generated by Sitaram Iyer (ssiyer@cs.rice.edu)
This paper was originally published in the Proceedings of the 5th Symposium on Operating Systems Design and Implementation, December 9–11, Boston, MA, US
Last changed: 6 Nov. 2002 aw
Technical Program
OSDI '02 Home
USENIX home