
Cliff C. Zou![]() , Nick Duffield
, Nick Duffield![]() , Don Towsley
, Don Towsley![]() , Weibo
Gong
, Weibo
Gong![]()
![]() University of Massachusetts, Amherst, MA
University of Massachusetts, Amherst, MA
![]() AT&T Labs Research, Florham Park, NJ
AT&T Labs Research, Florham Park, NJ
The current Internet is constantly under network attacks. Many defense methods and systems have been proposed to deal with these attacks. These systems typically first detect the on-going attack traffic, then block (filter) the attack traffic accordingly. Attack detection is of crucial importance in such defense systems. An imperfect detection algorithm will inevitably generate detection errors in terms of ``false positives" and ``false negatives". A ``false positive" means incorrectly identifying a normal packet (or connection, or host, etc) as an attack whereas a ``false negative" means incorrectly identifying an attack as a normal one.
Most research has focused on stationary network operation with fixed configurations. However in reality, attack detection systems have to face rapidly changing network conditions and various attack intensities. Therefore, besides finding a good detection algorithm, it is equally or more important to design an ``intelligent" defense system that can automatically adjust its detection and filtering parameters to achieve the best performance possible under every possible attack situation.
We introduce an ``adaptive defense principle" based on ``cost minimization" -- a defense system adaptively adjusts its configurations according to network conditions and ``attack severity" in order to minimize the combined cost introduced by false positives and false negatives at any time. We call such a defense system as an ``adaptive defense system". Compared to a traditional non-adaptive defense system, an adaptive defense system generates fewer false alarms in normal situations (or under light attacks) while protecting a network or a server more vigorously under severe attacks.
Denote by ![]() the ``attack severity" at time
the ``attack severity" at time ![]() , which can be the fraction or volume of attack
traffic, or other metrics determined by the types of attacks. Denote by
, which can be the fraction or volume of attack
traffic, or other metrics determined by the types of attacks. Denote by ![]() the set of configuration
parameters used in the detection algorithm. A defense system's false positive cost and false negative cost at
time
the set of configuration
parameters used in the detection algorithm. A defense system's false positive cost and false negative cost at
time ![]() , denoted by
, denoted by
![]() and
and
![]() respectively, are functions of
respectively, are functions of
![]() and
and ![]() . Whenever the attack severity
. Whenever the attack severity ![]() changes, the adaptive defense system will
choose the up-to-date optimal configurations
changes, the adaptive defense system will
choose the up-to-date optimal configurations ![]() by minimizing the combined cost:
by minimizing the combined cost:
We present concrete adaptive defense systems for defending against two major network attacks: SYN flood DDoS attack, and Internet worm infection. The adaptive defense is a high-level system design that can be built on top of various non-adaptive detection and filtering algorithms, which makes it applicable for a wide range of security defenses.
The rest of the paper is organized as follows. Section 2 surveys related work. We present the system design for defending against DDoS attack and Internet worm infection in Section 3 and Section 4, respectively. In Section 5 we evaluate the performance of these two adaptive defense systems. Finally Section 6 concludes this paper.
Mirkovic et al. [10] presented a comprehensive taxonomy of DDoS attack and defense mechanisms. Many DDoS detection approaches, such as the ``IP traceback" [12], or the ``MULTOPS" [2], try to find the identities of the real attacking sources. Hussain et al. [6] presented a framework to classify DDoS attacks into single-source and multi-source attacks. However, these methods cannot be used directly to block attack DDoS traffic. In order to detect and filter SYN flood packets at the victim end, Kim et al. [8] provided a general anomaly detection framework. Jin et al. [3] provided a concrete ``Hop-Count Filtering" algorithm to filter out spoofed attack SYN packets based on packets' TTL values.
For Internet worm defense, Williamson [16] proposed a rate-limiting ``throttling" method to constrain infection traffic. ``EarlyBird" in [13] and ``Autograph" in [7] detect and block worm spreading through identifying the common bit-strings among all infection network traffic of a worm. To prevent internal infection, Staniford [14] presented the segmentation idea to separate an enterprise network into many isolated subnetworks. Jung et al. [4][5] presented ``Threshold Random Walk (TRW)" detection algorithms to detect and block worm infection based on the excessive number of unsuccessful scans sent by a worm. Weaver et al. [15] presented a simplified version of TRW algorithm that is suitable for both hardware and software implementation. Pang et al. [11] provided a comprehensive study of the characteristics of the abnormal traffic in the Internet.
Lee et al. [9] considered various cost factors, including false positive/negative cost, in the process of developing Intrusion Detection System (IDS). However, such a cost-sensitive design is a static system design method, which does not consider how to dynamically adjust an IDS's configurations according to the attack condition. Our previous paper [17] only briefly mentioned the adaptive defense principle, but never explored it.
``SYN flood" attack is a denial-of-service attack by sending a large amount of SYN packets to a network or a server [10]. The attack packets usually have spoofed source addresses to hide the real attacking sources and also make defense much harder. For simplicity, we refer to the victim of a SYN flood attack as a server.
The ``Hop-Count Filtering" (HCF) algorithm presented in [3] is a concrete and promising approach for SYN flood DDoS attack. In a nutshell, HCF infers the hop-length of a connection request source to a server based on the Time-to-Live (TTL) value in the incoming SYN packet IP header, then compares this value with the real hop-length of the client, which is derived from the client's previous successful connections. If these two values are different, HCF determines that the incoming SYN packet is a spoofed attack packet. Since attackers do not know the real hop-counts from their spoofed source addresses to the victim, spoofing the initial TTL values cannot help attack packets to avoid HCF detection as proved in [3]. Due to space constraint, please refer to [3] for the detail of the HCF detection.
Denote the ``false positive probability" as ![]() , the probability of incorrectly dropping a normal
packet (or a normal connection, or a normal host for other types of attacks); denote the ``false
negative probability" as
, the probability of incorrectly dropping a normal
packet (or a normal connection, or a normal host for other types of attacks); denote the ``false
negative probability" as ![]() , the probability of incorrectly treating an attack as a normal one. Due to
memory constraint and Internet routing path changes, the HCF can change its detection strictness by allowing
curtain deviation of the observed hop-count value from the value saved in its hop-count table. We run the HCF
detection on the simulated normal SYN traffic and spoofed SYN flood traffic, respectively. From the
simulation, we derive the detection performance in terms of
, the probability of incorrectly treating an attack as a normal one. Due to
memory constraint and Internet routing path changes, the HCF can change its detection strictness by allowing
curtain deviation of the observed hop-count value from the value saved in its hop-count table. We run the HCF
detection on the simulated normal SYN traffic and spoofed SYN flood traffic, respectively. From the
simulation, we derive the detection performance in terms of ![]() and
and ![]() under different detection
configurations. Fig. 1 shows the detection performance trade-off for the server
``net.yahoo.com", whose hop-count data is provided to us by authors in [3]. Nine small circles
in the figure from the left to the right represent the detection performance under different configurations.
We define a detection sensitivity parameter
under different detection
configurations. Fig. 1 shows the detection performance trade-off for the server
``net.yahoo.com", whose hop-count data is provided to us by authors in [3]. Nine small circles
in the figure from the left to the right represent the detection performance under different configurations.
We define a detection sensitivity parameter ![]() (
(
![]() ): each small circle in
Fig. 1 from the left to the right corresponds to
): each small circle in
Fig. 1 from the left to the right corresponds to ![]() to
to ![]() , respectively.
, respectively.
We extend this discrete HCF to a continuous HCF based on ``probabilistic dropping". Suppose the continuous
HCF uses a real number ![]() as its detection parameter,
as its detection parameter,
![]() . Denote an integer
. Denote an integer
![]() and a real value
and a real value
![]() . Then, this continuous HCF will accept all packets
acceptable by the discrete HCF with
. Then, this continuous HCF will accept all packets
acceptable by the discrete HCF with
![]() while drop all packets that should be dropped by the
discrete HCF with
while drop all packets that should be dropped by the
discrete HCF with
![]() . For the remaining packets that should be dropped by the
. For the remaining packets that should be dropped by the ![]() HCF but
accepted by the
HCF but
accepted by the ![]() HCF, the continuous HCF accepts them with the probability
HCF, the continuous HCF accepts them with the probability ![]() . In this continuous
HCF, both
. In this continuous
HCF, both ![]() and
and ![]() are piece-wise linear functions of
are piece-wise linear functions of ![]() . Therefore,
. Therefore, ![]() is also a piece-wise
linear function of
is also a piece-wise
linear function of ![]() as shown in Fig. 1.
as shown in Fig. 1.
Denote by ![]() the fraction of attack packets among all incoming SYN packets.
the fraction of attack packets among all incoming SYN packets. ![]() naturally exhibits the
relative attack intensity compared to the normal payload of a server, and hence, we use
naturally exhibits the
relative attack intensity compared to the normal payload of a server, and hence, we use ![]() to represent
the ``attack severity" of a SYN flood DDoS attack.
to represent
the ``attack severity" of a SYN flood DDoS attack.
The adaptive defense system updates its HCF detection parameter ![]() periodically at each discrete time
denoted by
periodically at each discrete time
denoted by ![]()
![]() . During the time interval from
. During the time interval from ![]() to
to ![]() , the HCF implements
, the HCF implements ![]() ,
which corresponds to the pair of
,
which corresponds to the pair of ![]() and
and ![]() . During this time period, the fraction of incoming
packets identified by the defense system as attack packets is denoted by
. During this time period, the fraction of incoming
packets identified by the defense system as attack packets is denoted by ![]() , while the real attack
fraction is denoted by
, while the real attack
fraction is denoted by ![]() .
.
![]() differs from the observed value
differs from the observed value ![]() because: (1) the limited samples within a discrete time
interval introduce an observation statistical error; and (2) some attack packets are not counted in
because: (1) the limited samples within a discrete time
interval introduce an observation statistical error; and (2) some attack packets are not counted in ![]() due to false negatives whereas some normal packets are counted in
due to false negatives whereas some normal packets are counted in ![]() due to false positives.
due to false positives.
In the following we derive an unbiased estimate of the real attack severity, denoted by
![]() .
Suppose during the time interval from
.
Suppose during the time interval from ![]() to
to ![]() , the attack severity
, the attack severity ![]() does not change and the
defense system receives
does not change and the
defense system receives ![]() SYN packets. Then,
SYN packets. Then,
![]() packets are attack packets while the remaining
packets are attack packets while the remaining
![]() are normal ones. The defense system drops
are normal ones. The defense system drops
![]() packets, among which
packets, among which
![]() are real attack packets and the remaining
are real attack packets and the remaining
![]() are falsely dropped
normal packets. Therefore, we have
are falsely dropped
normal packets. Therefore, we have
Through statistical analysis, we find
![]() ; hence
; hence
![]() is an unbiased estimate.
is an unbiased estimate.
Fig. 2 illustrates the architecture of the adaptive defense system. At the end of time
![]() , the adaptive defense system first uses (3) to derive an estimate
, the adaptive defense system first uses (3) to derive an estimate
![]() of
the real attack severity, then finds the ``optimal" detection parameters
of
the real attack severity, then finds the ``optimal" detection parameters ![]() ,
, ![]() (i.e.,
(i.e.,
![]() ) for use in the next time interval. The ``optimization" module tries to minimize the combined
cost of false positives and false negatives by minimizing:
) for use in the next time interval. The ``optimization" module tries to minimize the combined
cost of false positives and false negatives by minimizing:
Those two cost factors, ![]() and
and ![]() , have concrete physical meanings: they represent the cost of
incorrectly dropping (accepting) a normal (attack) SYN packet, respectively. In some cases, they can be
chosen as constants whereas in other cases they should be functions of the attack severity. For example,
while a server can tolerate a small number of false negatives, beyond some point, the received attack traffic
will severely consume the system's resources. Whether to choose constant or functional cost factors should be
determined by the specific defense requirement and experiences from security staffs.
, have concrete physical meanings: they represent the cost of
incorrectly dropping (accepting) a normal (attack) SYN packet, respectively. In some cases, they can be
chosen as constants whereas in other cases they should be functions of the attack severity. For example,
while a server can tolerate a small number of false negatives, beyond some point, the received attack traffic
will severely consume the system's resources. Whether to choose constant or functional cost factors should be
determined by the specific defense requirement and experiences from security staffs.
The general cost function (4) is suitable for a wide range of security defense systems. If a server has a specific requirement, however, an object-oriented performance function would achieve a better defense performance.
A server usually has two separate buffers for incoming TCP connections: one for pending connections called ``pending buffer"; another for connections that have been established. The pending buffer is susceptible to SYN flood DDoS attack. Suppose the server's performance is not affected by the number of pending connections in the pending buffer so long as the buffer is not overflowed. Such a server has a specific performance objective: to accept as many as possible normal connection requests.
Define ``sojourn time" to be the time period a SYN packet resides in the pending buffer. Denote the average
sojourn time of a normal SYN packet as ![]() and the average sojourn time of an attack SYN packet as
and the average sojourn time of an attack SYN packet as ![]() .
The adaptive defense system updates its parameters periodically at each discrete time
.
The adaptive defense system updates its parameters periodically at each discrete time ![]() and the time
interval is denoted by
and the time
interval is denoted by ![]() . The defense system still has the same architecture as shown in
Fig. 2. Suppose the server has a pending buffer that can hold
. The defense system still has the same architecture as shown in
Fig. 2. Suppose the server has a pending buffer that can hold ![]() pending TCP connections
at the same time. At the end of discrete time
pending TCP connections
at the same time. At the end of discrete time ![]() , denote the number of incoming packets during the last time
interval as
, denote the number of incoming packets during the last time
interval as ![]() .
.
If the defense system deactivates its filtering functionality and allows all ![]() packets to pass through,
the buffer size requirement, denoted by
packets to pass through,
the buffer size requirement, denoted by ![]() , is:
, is:
If the defense system activates its filtering functionality with parameters ![]() ,
, ![]() , then
, then
![]() attack packets and
attack packets and
![]() normal packets will pass through the
detection/filtering module to reach the server. Thus the buffer size requirement, denoted by
normal packets will pass through the
detection/filtering module to reach the server. Thus the buffer size requirement, denoted by ![]() , is:
, is:
Therefore, at time ![]() , the adaptive defense system should choose its defense parameters
, the adaptive defense system should choose its defense parameters
![]() for the next time interval according to:
for the next time interval according to:
Basically, (7) tries to minimize the cost caused by over-filtering (![]() ) or
under-filtering (
) or
under-filtering (![]() ).
).
In this section, we study how to design an adaptive defense system for defending against a fast spreading Internet worm, such as Code Red, Slammer and Blaster [1].
Because a scanning worm blindly scans IP space to find targets, a worm-infected host has a much lower probability to set up successful connections than a benign host. ``Threshold Random Walk (TRW)" [4][5] detection is based on the fact that a worm-infected host sends out many more failed connection requests than successful requests. Weaver et al. [15] further simplified the TRW algorithm for hardware implementation. We deploy a modified version of the worm detector presented in [15] as the underlying detection algorithm.
Our modified TRW detector works in the following way: each source host that initiates a connection is
assigned a non-negative ``counter" with the initial value of zero. This counter (if not equals to zero)
decreases by one if the source host initiates a successful connection, and increases by one if the source
initiates a failed connection. Multiple connection attempts from a source targeting the same destination are
treated as one connection attempt (e.g., TCP/SYN retransmission before the timeout). A source host is
determined to be infectious when its counter reaches a threshold ![]() .
.
The next step is to represent the Internet worm ``attack severity". An enterprise network has a fraction of
unused IP addresses. All connection attempts to these addresses, which are called ``illegal scans", will
always fail. We use the number of illegal scans observed in a discrete time interval, denoted by ![]() , to
represent the attack severity.
, to
represent the attack severity.
Fig. 3 illustrates the architecture of the adaptive defense system. Whenever the
``detector" detects an infected host, it sends the host IP to the ``filter" where further scanning traffic
from the host will be blocked. Denote by ![]() the number of illegal scans observed from time
the number of illegal scans observed from time ![]() to
to ![]() and
and ![]() the detection parameter used from
the detection parameter used from ![]() to
to ![]() . Fig. 3 shows that at the end
of time
. Fig. 3 shows that at the end
of time ![]() , the system derives the optimal
, the system derives the optimal ![]() to use for the next time interval based on the current
attack severity
to use for the next time interval based on the current
attack severity ![]() . The ``optimization" module derives
. The ``optimization" module derives ![]() based on the performance function:
based on the performance function:
In this section, we evaluate the defense performance of the above two adaptive defense systems based on either simulation experiments or real attack traces.
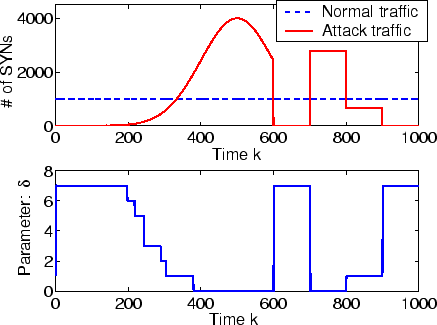 |
To verify the attack severity estimation (3), we plot the real value ![]() , the
observed value
, the
observed value ![]() and the estimated value
and the estimated value
![]() as functions of time
as functions of time ![]() in
Fig. 5. This figure clearly shows that Eq. (3) provides accurate
estimation results at any time.
in
Fig. 5. This figure clearly shows that Eq. (3) provides accurate
estimation results at any time.
Next, we study the adaptive defense system based on the buffer-aware function (7).
![]() seconds as used in previous experiment. We assume that normal SYN packets have the average
sojourn time
seconds as used in previous experiment. We assume that normal SYN packets have the average
sojourn time ![]() seconds in the pending buffer; attack packets have
seconds in the pending buffer; attack packets have ![]() seconds (since most attack
packets will stay in the buffer until time-out). The pending buffer is assumed to be able to support
seconds (since most attack
packets will stay in the buffer until time-out). The pending buffer is assumed to be able to support ![]() connection requests at the same time.
connection requests at the same time.
|
The SYN flood attack follows the same dynamics as the experiment shown in Fig. 5.
Fig. 6 shows how the defense system adjusts its parameter ![]() .
.
![]() means the
defense system deactivates its filtering functionality. This figure and previous Fig. 4
show that both adaptive defense systems have the similar responses. The difference is that the adaptive
defense system here has a continuously changing optimal
means the
defense system deactivates its filtering functionality. This figure and previous Fig. 4
show that both adaptive defense systems have the similar responses. The difference is that the adaptive
defense system here has a continuously changing optimal ![]() since (7) is a non-linear
function of
since (7) is a non-linear
function of ![]() (while (4) is a linear function of
(while (4) is a linear function of ![]() ).
).
In the above two experiments, we also obtain the information of accepted normal packets. To see the adaptive
defense performance, we also conduct a baseline experiment where a fixed-parameter HCF with ![]() is
deployed, which is the recommended setting in [3]. Fig. 7(a) and
Fig. 7(b) show the defense performance in terms of the number of accepted normal SYNs for
these two adaptive defense systems, respectively.
is
deployed, which is the recommended setting in [3]. Fig. 7(a) and
Fig. 7(b) show the defense performance in terms of the number of accepted normal SYNs for
these two adaptive defense systems, respectively.
Compared with the fixed-parameter defense, both adaptive defense systems accept more normal connection requests either under very light attacks or under heavy attacks. The fixed-parameter defense system uses a set of settings that is optimal only for a specific attack condition, which is not suitable for a real implementation where people expect a defense system to work well under various network conditions.
Fig. 7 also shows that we do not need to design a very accurate adaptive defense system
in order to improve the performance of an underlying non-adaptive detection algorithm. As long as we use the
adaptive defense principle to adjust a system's settings, the defense performance will be improved more or
less. In fact, we run the experiment shown in Fig. 4 many times with different values of
![]() and
and ![]() , the adaptive defense system always improves its performance compared with the
fixed-parameter system in terms of the number of accepted normal requests (similar results as shown in
Fig. 7).
, the adaptive defense system always improves its performance compared with the
fixed-parameter system in terms of the number of accepted normal requests (similar results as shown in
Fig. 7).
In the following experiments, we use a monitored Slammer propagation trace to study the performance of the
adaptive defense system. The trace is a tcpdump data containing all UDP packets (targeting at port 1434)
received by a /16 network. The top graph of Fig. 8 shows the number of Slammer UDP
packets received during each second, which is ![]() as we use one second for the discrete time interval. The
monitored /16 network has two Internet connections. At 150 seconds, one connection went down and caused the
monitored Slammer scans dropped suddenly. At 217 seconds, one internal computer was infected and its scanning
traffic caused local congestion, and hence, the monitored Slammer scans dropped suddenly for the second time.
as we use one second for the discrete time interval. The
monitored /16 network has two Internet connections. At 150 seconds, one connection went down and caused the
monitored Slammer scans dropped suddenly. At 217 seconds, one internal computer was infected and its scanning
traffic caused local congestion, and hence, the monitored Slammer scans dropped suddenly for the second time.
The bottom graph of Fig. 8 shows how the defense system responds to the attack changes
by adjusting ![]() (in this experiment,
(in this experiment,
![]() ).
). ![]() is the most aggressive defense that the
system can operate: any host will be blocked (on the suspicious port only) as soon as one illegal scan from
it is observed.
is the most aggressive defense that the
system can operate: any host will be blocked (on the suspicious port only) as soon as one illegal scan from
it is observed.
Fig. 9 shows the number of worm scans entering the /16 network -- the other worm
scans are blocked by the defense system (the peak level of original worm scans is 1000 per second). For
comparison, we also show in this figure the case of a fixed-parameter system where ![]() . Note that since the
number of vulnerable computers in a local network is usually much smaller than the number of
addresses allocated to the network, only a very small percentage of passed worm scans could possibly cause
infection. Of course, if we are very concerned with the worm infection, we can increase the ratio of
. Note that since the
number of vulnerable computers in a local network is usually much smaller than the number of
addresses allocated to the network, only a very small percentage of passed worm scans could possibly cause
infection. Of course, if we are very concerned with the worm infection, we can increase the ratio of
![]() to make the defense system quickly updates its threshold
to make the defense system quickly updates its threshold ![]() to 1 when
to 1 when ![]() increases (at the
cost of increasing the number of falsely blocked normal hosts).
increases (at the
cost of increasing the number of falsely blocked normal hosts).
For the evaluation of false positives,[4] and [15] have used real network traces to show that the ``Threshold Random Walk" algorithm has very limited false positives (most of those falsely detected hosts are web crawlers or proxies). Since our adaptive worm defense system uses the similar underlying detection algorithm, we do not repeat such an evaluation here.
There are still many work to do on the adaptive defense design. First, we want to further study how to choose
the cost factors ![]() and
and ![]() quantitatively according to the defense requirements. Second, in order to
understand accurately the impact of false positives/negatives, we plan to evaluate the adaptive defense
system based on real monitored traces that include both attack and normal traffic. Third, when defense
settings are adaptive, attackers might be able to influence the detection in such a way as to deny service to
legitimate traffic. We plan to further study this system robustness issue.
quantitatively according to the defense requirements. Second, in order to
understand accurately the impact of false positives/negatives, we plan to evaluate the adaptive defense
system based on real monitored traces that include both attack and normal traffic. Third, when defense
settings are adaptive, attackers might be able to influence the detection in such a way as to deny service to
legitimate traffic. We plan to further study this system robustness issue.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons feedbackDefense.tex
The translation was initiated by root on 2005-05-22