Single Sequential Stream

For simplicity, assume that there is only one request to each track. Multiple consecutive requests do not change the final algorithm in any way.

Every track in cache has a time stamp that is updated with the current time whenever the track is placed at the MRU position of either list. Let $T$ denote the temporal length, that is, the time difference between the MRU and LRU time stamps of SEQ.

Let $s_1$ and $s_1^a$ denote the rates of sequential misses of one stream when synchronous and synchronous+asynchronous prefetching, respectively, are employed.

Figure 3: Via simulation for a single sequential stream, we depict behavior of $s_1$ (rate of sequential misses for synchronous prefetching), $s_1^a$ (rate of sequential misses for synchronous+asynchronous prefetching), and $s_1'$ (an approximation to $s_1^a$). The hyperbolic curve $s_1$ flattens out at point $(T_1, s_1^s)$.

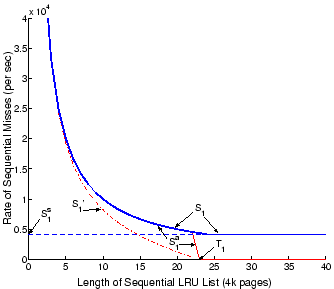Figure 3 displays the behavior of $s_1$ and $s_1^a$ as the temporal length varies. As discussed in Section II-B, under synchronous prefetching, sequential misses or its rate is inversely proportional to the degree of read-ahead. If, however, the read-ahead are discarded before they are accessed, the effective degree of read-ahead decreases. Whenever he effective degree of read-ahead is less than the actual degree, it is proportional to the temporal length of the list. Hence, we have that

$$s_1 = \begin{cases}\text{(constant)}/T & 0 \leq T \leq T_1 s_1^s & T_1 < T, \end{cases}$$ (1)

where $s_1^s > 0$ is the smallest attainable rate of sequential misses (which is inversely proportional to the actual degree of read-ahead) and $T_1$ is the smallest temporal length that attains $s_1^s$. As previously discussed in Section II-B and depicted in Figure 3, $s_1^a$ drops to zero when $s_1$ flattens out:

$$s_1^a = \begin{cases}s_1 & 0 \leq T \leq T_1 0 & T_1 < T. \end{cases}$$ (2)

For later use, we define the curve $s_1'$ as:

$$s_1' = \begin{cases}s_1 - T(s_1^s)/(T_1) & 0 \leq T \leq T_1 0 & T_1 < T. \end{cases}$$ (3)

Observe that the curve $s_1'$ distributes the discontinuity of $s_1^a$ throughout the interval $[0, T_1]$.