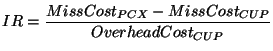
We evaluate CUP by comparing it with PCX with coalescing. We perform our simulation experiments using models derived from measurements of real peer-to-peer workloads [10,11,8,12].
For our experiments, we simulate a content-addressable network (CAN) [4] using the Stanford Narses simulator [13]. Again, we stress that CUP is independent of the specific search mechanism used by the peer-to-peer network and can be used as a cache maintenance protocol in any peer-to-peer network.
As in previous studies (e.g., [4,5,14,1,15,6,7]), we measure CUP performance in terms of the number of hops traversed in the overlay network. Miss cost is the total number of hops incurred by all misses, i.e. freshness and first-time misses. CUP overhead is the total number of hops traveled by all updates sent downstream plus the total number of hops traveled by all clear-bit messages upstream. (We assume clear-bit messages are not piggybacked onto updates. This somewhat inflates the overhead measure.) Total cost is the sum of the miss cost and all overhead hops incurred. Note that in PCX, the total cost is equal to the miss cost. Average query latency is the average number of hops a query must travel to reach a fresh answer plus the number of hops the answer must travel downstream to reach the node where the query was posted. For coalesced queries, we count the number of hops each coalesced query waits until the answer arrives. Thus, the average latency is over all queries, including hits, coalesced misses and non-coalesced misses.
We compute investment return (IR) as the overall ratio of saved miss cost to overhead incurred by CUP:
Thus, as long as IR is greater than or equal to 1, CUP fully recovers its cost.
The simulation takes as input the number of nodes in the overlay
peer-to-peer network, the number of keys owned per node, the
distribution of queries for keys, the distribution of query
inter-arrival times, the number of replicas per key, the lifetime of
index entries in the system, and the fraction of an entry's lifetime
remaining at which refreshes for the entry are pushed out from the
authority node. We present experiments for n = 
nodes where k
ranges from 7 to 14. After a warm-up period for allowing the
peer-to-peer network to connect, the measured simulation time is 3000
seconds. Since both Poisson and Pareto query inter-arrival
distributions have been observed in peer-to-peer
environments [8,10], we present experiments for both
distributions. Nodes are randomly selected to post queries. We also
performed experiments where queries are posted at particular ``hot
spots'' in the network and found similar results. These, as well as
other results which we omit in the interest of space, can be found
elsewhere [16].
We present results for experiments where index entry lifetimes are five minutes and refreshes occur one minute before expiration. We choose these values to reflect the dynamic and unpredictable nature of peer-to-peer networks. It has been found that the median user session duration of a peer is approximately sixty minutes [11]. However, content may become available on a peer or be deleted from the peer at any point during the user session. This results in actual content availability that is on the order of a few minutes [17]. We therefore take the safe approach of validating that the content is still available every few minutes. This is also in line with designers of structured peer-to-peer networks who advocate periodic refreshes (keep-alive messages) between the peers storing replicas of a particular content and the authority node for that content [4,6]. If there were some way to ensure that lifetimes of entries could be set for longer, then we find that CUP continues to provide benefits, albeit reduced, since PCX would incur fewer misses. Unfortunately, making such guarantees would require placing a global availability policy across autonomous peer nodes.
We present six sets of experiments. First, we compare the effect on CUP performance of different incentive-based cut-off policies and compare the performance of these policies to that of PCX. Second, using the best cut-off policy of the first experiment, we study how CUP performs as we scale the network. Third, we study the effect on CUP performance of varying the topology of the network by increasing the average node degree, thus decreasing the diameter of the network. Fourth, we study the effect on CUP performance of limiting the outgoing update capacities of nodes. Fifth, we study how CUP performs when queries arrive in bursts, as observed with Pareto inter-arrivals. These five experiments show the per-key benefits of CUP when keys are queried for according to a uniform distribution. In the last experiment, we show the overall benefits of CUP when keys are queried for according to a Zipf-like distribution.
| Network Size | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | |
|---|---|---|---|---|---|---|---|---|---|
| CUP/PCX MissCost | 0.10 | 0.10 | 0.15 | 0.17 | 0.19 | 0.22 | 0.20 | 0.21 | |
PCX AvgLat ( ) |
1.51 (2.77) | 2.67 (3.96) | 4.49 (5.92) | 6.74 (8.25) | 11.01 (12.11) | 17.47 (17.49) | 29.29 (27.79) | 45.56 (40.31) | |
|
CUP AvgLat () |
0.21 (1.10) | 0.46 (1.60) | 1.25 (3.19) | 2.17 (4.37) | 4.18 (7.13) | 7.70 (11.28) | 11.48 (15.08) | 19.17 (23.75) | |
| IR/CUPOvhd Hop | 4.15 | 4.88 | 6.29 | 7.83 | 11.43 | 16.14 | 24.85 | 35.98 |
