|
USENIX 2001 Paper
[USENIX '01 Tech Program Index]
| Pp. 245–260 of the Proceedings |  |
Virtual-Time Round-Robin:
An O(1) Proportional Share Scheduler
Jason Nieh Chris Vaill Hua Zhong
Department of Computer Science
Columbia University
{nieh, cvaill, huaz}@cs.columbia.edu
Abstract
Proportional share resource management provides a flexible and useful
abstraction for multiplexing time-shared resources. However, previous
proportional share mechanisms have either weak proportional sharing
accuracy or high scheduling overhead. We present Virtual-Time
Round-Robin (VTRR), a proportional share scheduler that can provide
good proportional sharing accuracy with O(1) scheduling overhead.
VTRR achieves this by combining the benefits of fair queueing
algorithms with a round-robin scheduling mechanism. Unlike many other
schedulers, VTRR is simple to implement. We have implemented a VTRR
CPU scheduler in Linux in less than 100 lines of code. Our performance
results demonstrate that VTRR provides accurate proportional share
allocation with constant, sub-microsecond scheduling overhead. The
scheduling overhead using VTRR is two orders of magnitude less than
the standard Linux scheduler for large numbers of clients.
1 Introduction
Proportional share resource management provides a flexible and useful
abstraction for multiplexing scarce resources among users and
applications. The basic idea is that each client has an associated
weight, and resources are allocated to the clients in proportion to
their respective weights. Because of its usefulness, many proportional
share scheduling mechanisms have been developed [3, 8, 10, 14, 16, 18, 25, 28, 30, 33, 34]. In addition, higher-level abstractions have been
developed on top of these proportional share mechanisms to support
flexible, modular resource management policies [30, 33].
Proportional share scheduling mechanisms were first developed decades
ago with the introduction of weighted round-robin
scheduling [29]. Later, fair-share algorithms based
on controlling priority values were developed and incorporated into
some UNIX operating systems [10, 16, 18]. These earlier mechanisms were typically fast,
requiring only constant time to select a client for
execution. However, they were limited in the accuracy with which they
could achieve proportional sharing. As a result starting in the late
1980s, fair queueing algorithms were developed [3, 8, 14, 25, 28, 30, 33, 34], first for network packet
scheduling and later for CPU scheduling. These algorithms provided
better proportional sharing accuracy. However, the time to select a
client for execution using these algorithms grows with the number of
clients. Most implementations require linear time to select a client
for execution. For server systems which may service large numbers of
clients, the scheduling overhead of linear time algorithms can waste
more than 20 percent of system resources [5] for
large numbers of clients. Hierarchical data structures can be used to
reduce the selection time complexity, but they are not generally used
as they are often less efficient in practice. This is because they add
implementation complexity and their performance depends on being able
to balance the data structures efficiently.
In this paper, we introduce VTRR, a Virtual-Time Round-Robin scheduler
for proportional share resource management. VTRR combines the benefits
of low overhead round-robin execution with high accuracy virtual-time
allocations. It provides accurate control over client computation
rates, and it can schedule clients for execution in O(1) time. The
constant scheduling overhead makes VTRR particularly suitable for
server systems that must manage large numbers of clients. VTRR is
simple to implement and can be easily incorporated into existing
scheduling frameworks in commercial operating systems. We have
implemented a prototype VTRR CPU scheduler in Linux in less than 100
lines of code. We have compared our VTRR Linux prototype against
schedulers commonly used in practice and research, including the
standard Linux scheduler [2] and fair queueing. Our
performance results on micro-benchmarks and real applications
demonstrate that VTRR delivers excellent proportional share control
with lower scheduling overhead than other approaches.
This paper is organized as follows: Section 2
discusses background and related work. Section 3
presents the VTRR scheduling algorithm.
Section 4 describes our prototype Linux
implementation. Section 5 presents performance
results from both simulation studies and real kernel measurements
that compare VTRR against weighted round-robin, fair queueing, and
standard Linux scheduling. Finally, we present some concluding remarks
and directions for future work.
2 Background
Previous proportional sharing mechanisms can be classified into four
categories: those that are fast but have weaker proportional fairness
guarantees, those that map well to existing scheduler frameworks in
current commercial operating systems but have no well-defined
proportional fairness guarantees, those that have strong proportional
fairness guarantees and higher scheduling overhead, and those that
have weaker proportional fairness guarantees but have higher
scheduling overhead. The four categories correspond to round-robin,
fair-share, fair queueing, and lottery mechanisms.
To discuss these different approaches, we first present in
Section 2.1 a simple proportional share model for
scheduling a time-multiplexed resource and more precisely define the
notion of proportional fairness. In Sections 2.2
to 2.4, we use this background to explain the
round-robin, fair-share, fair queueing, and lottery sharing mechanisms
in further detail. We briefly mention other related work in
Section 2.6.
2.1 Proportional Fairness
Proportional share scheduling has a clear colloquial meaning: given a
set of clients with associated weights, a proportional share scheduler
should allocate resources to each client in proportion to its
respective weight. In this paper, we use the term share and weight
interchangeably. Without loss of generality, we can model the process
of scheduling a time-multiplexed resource among a set of clients in
two steps: 1) the scheduler orders the clients in a queue, 2) the
scheduler runs the first client in the queue for its time quantum,
which is the maximum time interval the client is allowed to run before
another scheduling decision is made.
Note that the time quantum is typically expressed in time units of
constant size determined by the hardware. As a result, we refer to
the units of time quanta as time units (tu) in this paper rather than
an absolute time measure such as seconds.
Based on the above scheduler model, a scheduler can achieve
proportional sharing in one of two ways. One way is to adjust the
frequency that a client is selected to run by adjusting the position
of the client in the queue so that it ends up at the front of the
queue more or less often. The other way is to adjust the size of the
time quantum of a client so that it runs longer for a given
allocation. The manner in which a scheduler determines how often a
client runs and how long a client runs directly affects the accuracy
and scheduling overhead of the scheduler.
A proportional share scheduler is more accurate if it allocates
resources in a manner that is more proportionally fair. We can
formalize this notion of proportional fairness in more technical
terms. The definition we use is a simple one that suffices for our
discussion; more extended definitions are presented
in [12, 15, 26, 32]. Our definition draws heavily from the ideal
sharing mechanism GPS [19]. To simplify the discussion, we
assume that clients do not sleep or block and can consume whatever
resources they are allocated.
We first define perfect fairness, an ideal state in which each
client has received service exactly proportional to its share. We
denote the proportional share of client A as SA, and the amount
of service received by client A during the time interval (t1,
t2) as WA(t1, t2). Formally, a proportional sharing algorithm
achieves perfect fairness for time interval (t1, t2) if, for any
client A,
|
WA(t1, t2) = (t2 - t1) |
|
(1) |
If we had an ideal system in which all clients could consume their
resource allocations simultaneously, then an ideal proportional share
scheduler could maintain the above relationship for all time
intervals. However, in scheduling a time-multiplexed resource in time
units of finite size, it is not possible for a scheduler to be
perfectly proportionally fair as defined by
Equation 1 for all intervals.
Although no real-world scheduling algorithm can maintain perfect
fairness, some algorithms stay closer to perfect fairness than others.
To evaluate the fairness performance of a proportional sharing
mechanism, we must quantify how close an algorithm gets to perfect
fairness. We can use a variation of
Equation 1 to define the service time
error EA(t1, t2) for client A over interval (t1, t2). The
error is the difference between the amount time allocated to the
client during interval (t1, t2) under the given algorithm, and the
amount of time that would have been allocated under an ideal scheme
that maintains perfect fairness for all clients over all intervals.
Service time error is computed as:
|
EA(t1, t2) = WA(t1, t2) - (t2 - t1) |
|
(2) |
A positive service time error indicates that a client has received
more than its ideal share over an interval; a negative error indicates
that a client has received less. To be precise, the error EA
measures how much time client A has received beyond its ideal
allocation.
The goal of a proportional share scheduler should be to minimize the
allocation error between clients. In this context, we now consider how
effectively different classes of proportional share algorithms are in
minimizing this allocation error.
2.2 Round-Robin
One of the oldest, simplest and most widely used proportional share
scheduling algorithms is round-robin. Clients are placed in a queue
and allowed to execute in turn.
When all client shares are equal, each client is assigned the same
size time quantum. In the weighted round-robin case, each client is
assigned a time quantum equal to its share. A client with a larger
share, then, effectively gets a larger quantum than a client with a
small share. Weighted round-robin (WRR) provides proportional sharing
by running all clients with the same frequency but adjusting the size
of their time quanta.
A more recent variant called deficit
round-robin [28] has been developed for network
packet scheduling with similar behavior to a weighted round-robin CPU
scheduler.
WRR is simple to implement and schedules clients in O(1)
time. However, it has a relatively weak proportional fairness
guarantee as its service ratio error can be quite large. Consider an
example in which 3 clients A, B, and C, have shares 3, 2, and 1,
respectively. WRR will execute these clients in the following order of
time units: A, A, A, B, B, C. The error in this example gets as low
as -1 tu and as high as +1.5 tu. The real trouble comes with large
share values: if the shares in the previous example are changed to
3000, 2000, and 1000, the error ranges instead from -1000 to +1500
tu. A large error range like this illustrates the major drawback of
round-robin scheduling: each client gets all service due to it all at
once, while other clients get no service. After a client has received
all its service, it is well ahead of its ideal allocation (it has a
high positive error), and all other clients are behind their
allocations (they have low negative errors).
2.3 Fair-Share
Fair-share schedulers [10, 16, 18] arose as a result of a need to provide proportional
sharing among users in a way compatible with a UNIX-style time-sharing
framework. In UNIX time-sharing, scheduling is done based on
multi-level feedback with a set of priority queues. Each client has a
priority which is adjusted as it executes. The scheduler executes the
client with the highest priority. The idea of fair-share was to
provide proportional sharing among users by adjusting the priorities
of a user's clients in a suitable way.
Fair-share provides proportional sharing by effectively running
clients at different frequencies, as opposed to WRR which only adjusts
the size of the clients' time quanta.
Fair-share schedulers were compatible with UNIX scheduling frameworks
and relatively easy to deploy in existing UNIX environments. Unlike
round-robin scheduling, the focus was on providing proportional
sharing to groups of users as opposed to individual clients. However,
the approaches were often ad-hoc and it is difficult to formalize the
proportional fairness guarantees they provided. Empirical measurements
of show that these approaches only provide reasonable proportional
fairness over relatively large time intervals [10]. It is
almost certainly the case that the allocation errors in these
approaches can be very large.
The priority adjustments done by fair-share schedulers can generally
be computed quickly in O(1) time. In some cases, the schedulers need
to do an expensive periodic re-adjustment of all client priorities,
which required O(N) time, where N is the number of clients.
2.4 Fair Queueing
Fair queueing was first proposed by Demers et. al. for network
packet scheduling as Weighted Fair Queueing (WFQ) [8],
with a more extensive analysis provided by Parekh and
Gallager [25], and later applied by Waldspurger and Weihl
to CPU scheduling as stride scheduling [33]. WFQ
introduced the idea of a virtual finishing time (VFT) to do
proportional sharing scheduling. To explain what a VFT is, we first
explain the notion of virtual time. The virtual time of a
client is a measure of the degree to which a client has received its
proportional allocation relative to other clients. When a client
executes, its virtual time advances at a rate inversely proportional
to the client's share. In other words, the virtual time of a client
A at time t is the ratio of WA(t) to SA:
Given a client's virtual time, the client's virtual finishing
time (VFT) is defined as the virtual time the client would have after
executing for one time quantum. WFQ then schedules clients by
selecting the client with the smallest VFT. This is implemented by
keeping an ordered queue of clients sorted from smallest to largest
VFT, and then selecting the first client in the queue. After a client
executes, its VFT is updated and the client is inserted back into the
queue. Its position in the queue is determined by its updated VFT.
Fair queueing provides proportional sharing by running clients at
different frequencies by adjusting the position in at which each
client is inserted back into the queue; the same size time quantum is
used for all clients.
To illustrate how this works, consider again the example in which 3
clients A, B, and C, have shares 3, 2, and 1, respectively. Their
initial VFTs are then 1/3, 1/2, and 1, respectively. WFQ would then
execute the clients in the following order of time units: A, B, A, B,
C, A. In contrast to WRR, WFQ's service time error ranges from
-5/6 to +1 tu in this example, which is less than the allocation
error of -1 to +1.5 tu for WRR. The difference between WFQ
and WRR is greatly exaggerated if larger share values are chosen: if
we make the shares 3000, 2000, and 1000 instead of 3, 2, and 1, WFQ
has the same service time error range while WRR's error range balloons
to -1000 to +1500 tu.
It has been shown that WFQ guarantees that the service time error for
any client never falls below -1, which means that a client can never
fall behind its ideal allocation by more than a single time
quantum [25]. More recent fair queueing
algorithms [3, 30] provide more accurate
proportional sharing (by also guaranteeing an upper bound on error) at
the expense of additional scheduling overhead. Fair queueing provides
stronger proportional fairness guarantees than round-robin or
fair-share scheduling. Unfortunately, fair queueing is more difficult
to implement, and the time it takes to select a client to execute is
O(N) time for most implementations, where N is the number of
clients. With more complex data structures, is possible to implement
fair queueing such that selection of a client requires O(log N)
time. However, the added difficulty of managing complex data
structures in kernel space causes most implementers of fair queueing
to choose the more straightforward O(N) implementation.
2.5 Lottery
Lottery scheduling was proposed by Waldspurger and
Weihl [33] after WFQ was first developed.
In lottery scheduling, each client is given a number of tickets
proportional to its share. A ticket is then randomly selected by the
scheduler and the client that owns the selected ticket is scheduled to
run for a time quantum. Like fair queueing, lottery scheduling
provides proportional sharing by running clients at different
frequencies by adjusting the position in at which each client is
inserted back into the queue; the same size time quantum is typically
used for all clients.
Lottery scheduling is somewhat simpler to implement than fair
queueing, but has the same high scheduling overhead as fair queueing,
O(N) for most implementations or O(log N) for more complex data
structures. However, because lottery scheduling relies on the law of
large numbers for providing proportional fairness, its accuracy is
much worse than WFQ [33], and is also worse than
WRR for smaller share values.
2.6 Other Related Work
Higher-level resource management abstractions have also been
developed [1, 33], and a number
of these abstractions can be used with proportional share scheduling
mechanisms. This work is complementary to our focus here on the
underlying scheduling mechanisms. Other scheduling work has also been
done in supporting clients with real-time
requirements [4, 6, 13, 17, 20, 21, 22, 23, 24] and improving
the response time of interactive clients [9, 11, 24]. Considering these issues in depth is
beyond the scope of this paper.
3 VTRR Scheduling
VTRR is an accurate, low-overhead proportional share scheduler for
multiplexing time-shared resources among a set of clients. VTRR
combines the benefit of low overhead round-robin scheduling with the
high accuracy mechanisms of virtual time and virtual finishing time
used in fair queueing algorithms. At a high-level, the VTRR
scheduling algorithm can be briefly described in three steps:
-
Order the clients in the run queue from largest to smallest share.
Unlike fair queueing, a client's position on the run queue only
changes when its share changes, an infrequent event, not on each
scheduling decision.
- Starting from the beginning of the run queue, run each client for
one time quantum in a round-robin manner. VTRR uses the fixed
ordering property of round-robin in order to choose in constant
time which client to run. Unlike round-robin, the time quantum is
the same size for all clients.
- In step 2, if a client has received more than its proportional
allocation, skip the remaining clients in the run queue and start
running clients from the beginning of the run queue again. Since
the clients with larger share values are placed first in the queue,
this allows them to get more service than the lower-share clients
at the end of the queue.
To provide a more in depth description of VTRR, we first define the
state VTRR associates with each client, then describe precisely how
VTRR uses that state to schedule clients.
In VTRR, a client has five values associated with its execution state:
share, virtual finishing time, time counter, id number, and run
state. A client's share defines its resource rights. Each
client receives a resource allocation that is directly proportional to
its share. A client's virtual finishing time (VFT) is defined
in the same way as in Section 2.4. Since a client
has a VFT, it also has an implicit virtual time. A client's VFT
advances at a rate proportional to its resource consumption divided by
its share. The VFT is used to decide when VTRR should reset to the
first client in the queue. This is described in greater detail in
Section 3.1, below. A client's time counter
ensures that the pattern of allocations is periodic, and that perfect
fairness is achieved at the end of each period. Specifically, the
time counter tracks the number of quanta the client must receive
before the period is over and perfect fairness is reached.
A client's id number is a unique client identifier that is
assigned when the client is created. A client's run state is
an indication of whether or not the client can be executed. A client
is runnable if it can be executed, and not runnable if it
cannot. For example for a CPU scheduler, a client would not be
runnable if it is blocked waiting for I/O and cannot execute.
3.1 Basic VTRR Algorithm
We will initially only consider runnable clients in our discussion of
the basic VTRR scheduling algorithm. We will discuss dynamic changes
in a client's run state in Section 3.2. VTRR maintains
the following scheduler state: time quantum, run queue, total shares,
and queue virtual time. As discussed in
Section 2.1, the time quantum is the
duration of a standard time slice assigned to a client to execute. The
run queue is a sorted queue of all runnable clients ordered
from largest to smallest share client. Ties can be broken either
arbitrarily or using the client id numbers, which are unique. The
total shares is the sum of the shares of all runnable
clients. The queue virtual time (QVT) is a measure of what a
client's VFT should be if it has received exactly its proportional
share allocation.
Previous work in the domain of packet scheduling provides the
theoretical basis for the QVT [8, 25]. The QVT
advances whenever a client executes at a rate inversely proportional
to the total shares. If we denote the system time quantum as Q and
the share of client i as Si, then the QVT is updated as follows:
|
QVT(t + Q) = QVT(t) + |
|
(4) |
The difference between the QVT and a client's virtual time is a
measure of whether the respective client has consumed its proportional
allocation of resources. If a client's virtual time is equal to the
queue virtual time, it is considered to have received its proportional
allocation of resources. An earlier virtual time indicates that the
client has used less than its proportional share. Similarly, a later
virtual time indicates that it has used more than its proportional
share. Since the QVT advances at the same rate for all clients on the
run queue, the relative magnitudes of the virtual times provide a
relative measure of the degree to which each client has received its
proportional share of resources.
First, we explain the role of the time counters in VTRR. In relation
to this, we define a scheduling cycle as a sequence of
allocations whose length is equal to the sum of all client shares.
For example, for a queue of three clients with shares 3, 2, and 1, a
scheduling cycle is a sequence of 6 allocations. The time counter for
each client is reset at the beginning of each scheduling cycle to the
client's share value, and is decremented every time a client receives
a time quantum. VTRR uses the time counters to ensure that perfect
fairness is attained at the end of every scheduling cycle. At the end
of the cycle, every counter is zero, meaning that for each client A,
the number of quanta received during the cycle is exactly SA, the
client's share value. Clearly, then, each client has received service
proportional to its share. In order to guarantee that all counters
are zero at the end of the cycle, we enforce an invariant on the
queue, called the time counter invariant: we require that, for
any two consecutive clients in the queue A and B, the counter
value for B must always be no greater than the counter value for
A.
The VTRR scheduling algorithm starts at the beginning of the run queue
and executes the first client for one time quantum. We refer to the
client selected for execution as the current client. Once the
current client has completed its time quantum, its time counter is
decremented by one and its VFT is incremented by the time quantum
divided by its share. If we denote the system time quantum as Q, the
current client's share as SC, and the current client's VFT as
VFTC(t), VFTC(t) is updated as follows:
|
VFTC(t + Q) = VFTC(t) + |
|
(5) |
The scheduler then moves on to the next client in the run queue.
First, the scheduler checks for violation of the time counter
invariant: if the counter value of the next client is greater than the
counter of the current client, the scheduler makes the next client the
current client and executes it for a quantum, without question. This
causes its counter to be decremented, preserving the invariant.
If the next client's counter is not greater than the current client's
counter, the time counter invariant cannot be violated whether the
next client is run or not, so
the scheduler makes a decision using virtual time: the scheduler
compares the VFT of the next client with the QVT the system would have
after the next time quantum a client executes. We call this comparison
the VFT inequality. If we denote the system time quantum as
Q, the current client's VFT as VFTC(t), and its share as
SC, the VFT inequality is true if:
|
VFTC(t) - QVT(t + Q) < |
|
(6) |
If the VFT inequality is true, the scheduler selects and executes the
next client in the run queue for one time quantum and the process
repeats with the subsequent clients in the run queue. If the scheduler
reaches a point in the run queue when the VFT inequality is not true,
the scheduler returns to the beginning of the run queue and selects
the first client to execute. At the end of the scheduling cycle, when
the time counters of all clients reach zero, the time counters are all
reset to their initial values corresponding to the respective client's
share, and the scheduler starts from the beginning of the run queue
again to select a client to execute. Note that throughout this
scheduling process, the ordering of clients on the run queue does not
change.
To illustrate how this works, consider again the example in which 3
clients A, B, and C, have shares 3, 2, and 1, respectively. Their
initial VFTs are then 1/3, 1/2, and 1, respectively. VTRR would then
execute the clients in the following repeating order of time units: A,
B, C, A, B, A. In contrast to WRR and WFQ, VTRR has a maximum
allocation error between A and B of 1/3 tu in this example. This
allocation error is much better than WRR and comparable to WFQ.
Since VTRR simply selects each client in turn to execute, selecting a
client for execution can be done in O(1) time. We defer a more
detailed discussion of the complexity of VTRR to Section
3.3.
3.2 VTRR Dynamic Considerations
In the previous section, we presented the basic VTRR scheduling
algorithm, but we did not discuss how VTRR deals with dynamic
considerations that are a necessary part of any on-line scheduling
algorithm. We now discuss how VTRR allows clients to be dynamically
created, terminated, change run state, and change their share
assignments.
We distinguish between clients that are runnable and not runnable. As
mentioned earlier, clients that are runnable can be selected for
execution by the scheduler, while clients that are not runnable
cannot. Only runnable clients are placed in the run queue. With no
loss of generality, we assume that a client is created before it can
become runnable, and a client becomes not runnable before it is
terminated. As a result, client creation and termination have no
affect on the VTRR run queue.
When a client becomes runnable, it is inserted into the run queue so
that the run queue remains sorted from largest to smallest share
client. Ties can be broken either arbitrarily or using the unique
client id numbers. One issue remains, which is how to determine the
new client's initial VFT. When a client is created and becomes
runnable, it has not yet consumed any resources, so it is neither
below or above its proportional share in terms of resource
consumption. As a result, we set the client's implicit virtual time to
be the same as the QVT. We can then calculate the VFT of a new
client A with share SA as:
After a client is executed, it may become not runnable. If the client
is the current client and becomes not runnable, it is preempted and
another client is selected by the scheduler using the basic algorithm
described in Section 3.1. The client that is not
runnable is removed from the run queue. If the client becomes not
runnable and is not the current client, the client is simply removed
from the run queue. While the client is not runnable, its VFT is not
updated. When the client is removed from the run queue, it records
the client that was before it on the run queue, and the client that
was after it on the run queue. We refer to these clients as the
last-previous client and last-next client, respectively.
When a client that is not runnable becomes runnable again, VTRR
inserts the now runnable client back into the run queue. If the
client's references to its last-previous and last-next client are
still valid, it can use those references to determine its position in
the run queue. If either the last-previous or the last-next reference
is not valid, VTRR then simply traverses the run queue to find the
insertion point for the now runnable client.
Determining whether the last-previous and last-next references are
valid can be done efficiently as follows. The last-previous and
last-next client references are valid if both clients have not exited
and are runnable, if there are no clients between them on the run
queue, and if the share of the newly-runnable client is no more than
the last-previous client and no less than the last-next client. Care
must be taken, however, to ensure that the last-previous and last-next
references are still valid before dereferencing them: if either client
has exited and been deallocated, last-previous and last-next may no
longer refer to valid memory regions. To deal with this, a hash table
can be kept that stores identifiers of valid clients. Hash function
collisions can be resolved by simple replacement, so the table can be
implemented as an array of identifiers. A client's identifier is put
into the table when it is created, and deleted when the client exits.
The last-previous and last-next pointers are not dereferenced, then,
unless the identifier of the last-previous and last-next clients exist
in the hash table. As described in Section 4,
the use of a hash table was not necessary in our Linux VTRR
implementation.
Once the now runnable client has been inserted in the run queue, the
client's VFT must be updated. The update is analogous to the VFT
initialization used when a new client becomes runnable. The
difference is that we also account for the client's original VFT in
updating the VFT. If we denote the original VFT of a client A as
VFTA(t'), then the client's VFT is updated as follows:
|
VFTA(t) = MAX{QVTA(t) + |
|
,
VFTA(t')}
(8) |
This treats a client that has been not runnable for a while like a new
client that has not yet executed. At the same time, the system keeps
track of the client's VFT so that if it that has recently used more
than its proportional allocation, it cannot somehow game the system by
making itself not runnable and becoming runnable again.
We use an analogous policy to set the initial value of a client's time
counter. A client's time counter tracks the number of quanta due to
the client before the end of the current scheduling cycle, and is
reset at the beginning of each new cycle. We set the time counter of
a newly-inserted client to a value which will give it the correct
proportion of remaining quanta in this cycle. The counter CA for
the new client A is computed:
Note that this is computed before client A is inserted, so
SA is not included in the åi Si summation.
This value is modified by a rule similar to the rule enacted for the
VFT: we require that a client cannot come back in the same cycle and
receive a larger time count than it had previously. Therefore, if the
client is being inserted during the same cycle in which it was
removed, the counter is set to the minimum of CA and the previous
counter value. Finally, to preserve the time counter invariant (as
described in Section 3.1), the counter value must be
restricted to be between the time counter values of the clients before
and after the inserted client.
If a client's share changes, there are two cases to consider based on
the run state of the client. If the client is not runnable, no run
queue modifications are needed. If the client is runnable and its
share changes, the client's position in the run queue may need to be
changed. This operation can be simplified by removing the client from
the run queue, changing the share, and then reinserting it. Removal
and insertion can then be performed just as described above.
3.3 Complexity
The primary function of a scheduler is to select a client to execute
when the resource is available. A key benefit of VTRR is that it can
select a client to execute in O(1) time. To do this, VTRR simply has
to maintain a sorted run queue of clients and keep track of its
current position in the run queue. Updating the current run queue
position and updating a client's VFT are both O(1) time
operations. While the run queue needs to be sorted by client shares,
the ordering of clients on the run queue does not change in the normal
process of selecting clients to execute. This is an important
advantage over fair queueing algorithms, in which a client needs to be
reinserted into a sorted run queue after each time it executes. As a
result, fair queueing has much higher complexity than VTRR, requiring
O(N) time to select a client to execute, or O(log N) time if more
complex data structures are used (but this is rarely implemented in
practice).
When all clients on the run queue have zero counter values, VTRR
resets the counter values of all clients on the run queue. The
complete counter reset takes O(N) time, where N is the number of
clients. However, this reset is done at most once every N times the
scheduler selects a client to execute (and much less frequently in
practice). As a result, the reset of the time counters is amortized
over many client selections so that the effective running time of VTRR
is still O(1) time. In addition, the counter resets can be done
incrementally on the first pass through the run queue with the new
counter values.
In addition to selecting a client to execute, a scheduler must also
allow clients to be dynamically created and terminated, change run
state, and change scheduling parameters such as a client's
share. These scheduling operations typically occur much less
frequently than client selection. In VTRR, operations such as client
creation and termination can be done in O(1) time since they do not
directly affect the run queue. Changing a client's run state from
runnable to not runnable can also be done in O(1) time for any
reasonable run queue implementation since all it involves is removing
the respective client from the run queue. The scheduling operations
with the highest complexity are those that involve changing a client's
share assignment and changing a client's run state to runnable. In
particular, a client typically becomes runnable after it is created or
after an I/O operation that it was waiting for completes. If a
client's share changes, the client's position in the run queue may
have change as well. If a client becomes runnable, the client will
have to be inserted into the run queue in the proper position based on
its share. Using a doubly linked list run queue implementation,
insertion into the sorted queue can require O(N) time, where N is
the number of runnable clients. A priority queue implementation could
be used for the run queue to reduce the insertion cost to O(log N),
but probably does not have better overall performance than a simple
sorted list in practice.
Because queue insertion is required much less frequently than client
selection in practice, the queue insertion cost is not likely to
dominate the scheduling cost. In particular, if only a constant number
of queue insertions are required for every N times a client
selection is done, then the effective cost of the queue insertions is
still only O(1) time. Furthermore, the most common scheduling
operation that would require queue insertion is when a client becomes
runnable again after it was blocked waiting on a resource. In this
case, the insertion overhead can be O(1) time if the last-previous
client and last-next client references remain valid at queue insertion
time. If the references are valid, then the position of the client is
already known on the run queue so the scheduler does not have to find
the insertion point.
An alternative implementation can be done that allows all queue
insertions to be done in O(1) time, if the range of share values is
fixed in advance. The idea is similar to priority schedulers which
have a fixed range of priority values and have separate run queue for
each priority. Instead of using priorities, we can have a separate run
queue for each share value and keep track of the run queues using an
array. We can then find the queue corresponding to a client's share
and insert the client at the end of the corresponding queue in O(1)
time. Such an implementation maps well to scheduling frameworks in a
number of commercial operating systems, including
Solaris [31] and Windows NT [7].
4 Implementation
We have implemented a prototype VTRR CPU scheduler in the Linux
operating system. For this work, we used the Red Hat Linux version 6.1
distribution and the Linux version 2.2.12-20 kernel. We had to add or
modify less than 100 lines of kernel code to complete the VTRR
scheduler implementation. We describe our Linux VTRR implementation in
further detail to illustrate how easy VTRR is to implement.
These scheduling frameworks are commonly found in commercial operating
systems. While VTRR can be used in a multiprocessor scheduling
context, we only discuss the single CPU implementation here.
The Linux scheduling framework for a single CPU is based on a run
queue implemented as a single doubly linked list. We first describe
how the standard Linux scheduler works, and then discusses the changes
we made to implement VTRR in Linux.
The standard Linux scheduler multiplexes a set of clients that can be
assigned different priorities. The priorities are used to compute a
per client measure called goodness to schedule the set of
clients. Each time the scheduler is called, the goodness value for
each client in the run queue is calculated. The client with the
highest goodness value is then selected as the next client to
execute. In the case of ties, the first client with the highest
goodness value is selected. Because the goodness of each client is
calculated each time the scheduler is called, the scheduling overhead
of the Linux scheduler is O(N), where N is the number of runnable
clients.
The standard way Linux calculates the goodness for all clients is
based on a client's priority and counter. The counter is not the same
as the time counter value used by VTRR, but is instead a measure of
the remaining time left in a client's time quantum. The standard time
unit used in Linux for the counter and time quantum is called a jiffy,
which is 10 ms by default. The basic idea is that the goodness of a
client is its priority plus its counter value. The client's counter is
initially set equal to the client's priority, which has a value of 20
by default. Each time a client is executed for a jiffy, the client's
counter is decremented. A client's counter is decremented until it
drops below zero, at which point the client cannot be selected to
execute. As a result, the default time quantum for each client is 21
jiffies, or 210 ms.
When the counters of all runnable clients drop below zero, the
scheduler resets all the counters to their initial value. There is
some additional logic to support static priority real-time clients and
clients that become not runnable, but an overview of the basic way in
which the Linux scheduler works is sufficient for our discussion
here. Further details are available elsewhere [2].
To implement VTRR in Linux, we reused much of the existing scheduling
infrastructure. We used the same doubly linked list run queue
structure as the standard Linux scheduler. The primary change to the
run queue was sorting the clients from largest to smallest
share. Rather than scanning all the clients when a scheduling decision
needs to be made, our VTRR Linux implementation simply picks the next
client in the run queue based on the VTRR scheduling algorithm.
One idiosyncrasy of the Linux scheduler that is relevant to this work
is that the smallest counter value that may be assigned to a client is
1. This means that the smallest time quantum a client can have is 2
jiffies. To provide a comparable implementation of VTRR, the default
time quantum used in our VTRR implementation is also 2 jiffies, or 20
ms.
In addition to the VTRR client state, two fields that were added to
the standard client data structure in Linux were last-previous and
last-next pointers which were used to optimize run queue insertion
efficiency. In the Linux 2.2 kernel, memory for the client data
structures is statically allocated, and never reclaimed for anything
other than new client data structures. Therefore, in our
implementation, we were free to reference the last-next and
last-previous pointers to check their validity, as they always refer
to some client's data; the hash table method described in
Section 3.2 was unnecessary.
5 Measurements and Results
To demonstrate the effectiveness of VTRR, we have quantitatively
measured and compared its performance against other leading approaches
from both industrial practice and research. We have conducted both
extensive simulation studies and detailed measurements of real kernel
scheduler performance on real applications.
We conducted simulation studies to compare the proportional sharing
accuracy of VTRR against both WRR and WFQ. We used a simulator for
these studies for two reasons. First, our simulator enabled us to
isolate impact of the scheduling algorithms themselves and
purposefully do not include the effects of other activity present in
an actual kernel implementation. Second, our simulator enabled us to
examine the scheduling behavior of these different algorithms across
hundreds of thousands of different combinations of clients with
different share values. It would have been much more difficult to
obtain this volume of data in a repeatable fashion from just
measurements of a kernel scheduler implementation. Our simulation
results are presented in Section 5.1.
We also conducted detailed measurements of real kernel scheduler
performance by comparing our prototype VTRR Linux implementation
against both the standard Linux scheduler and a WFQ scheduler. In
particular, comparing against the standard Linux scheduler and
measuring its performance is important because of its growing
popularity as a platform for server as well as desktop systems. The
experiments we have done quantify the scheduling overhead and
proportional share allocation accuracy of these schedulers in a real
operating system environment under a number of different workloads.
Our measurements of kernel scheduler performance are presented in
Sections 5.2 to 5.4.
All of our kernel scheduler measurements were performed on a Gateway
2000 E1400 system with a 433 MHz Intel Celeron CPU, 128 MB RAM, and 10
GB hard drive. The system was installed with the Red Hat Linux 6.1
distribution running the Linux version 2.2.12-20 kernel. The
measurements were done by using a minimally intrusive tracing facility
that logs events at significant points in the application and the
operating system code. This is done via a light-weight mechanism that
writes timestamped event identifiers into a memory log. The mechanism
takes advantage of the high-resolution clock cycle counter available
with the Intel CPU to provide measurement resolution at the
granularity of a few nanoseconds. Getting a timestamp simply involved
reading the hardware cycle counter register, which could be read from
user-level or kernel-level code. We measured the cost of the mechanism
on the system to be roughly 70 ns per event.
The kernel scheduler measurements were performed on a fully functional
system to represent a realistic system environment. By fully
functional, we mean that all experiments were performed with all
system functions running and the system connected to the network. At
the same time, an effort was made to eliminate variations in the test
environment to make the experiments repeatable.
5.1 Simulation Studies
We built a scheduling simulator that we used to evaluate the
proportional fairness of VTRR in comparison to two other schedulers,
WRR and WFQ. The simulator is a user-space program that measures the
service time error, described in Section 2.1, of a
scheduler on a set of clients. The simulator takes four inputs, the
scheduling algorithm, the number of clients N, the total number of
shares S, and the number of client-share combinations. The
simulator randomly assigns shares to clients and scales the share
values to ensure that they sum to S. It then schedules the clients
using the specified algorithm as a real scheduler would, and tracks
the resulting service time error. The simulator runs the scheduler
until the resulting schedule repeats, then computes the maximum (most
positive) and minimum (most negative) service time error across the
nonrepeating portion of the schedule for the given set of clients and
share assignments. The simulator assumes that all clients are
runnable at all times. This process of random share allocation and
scheduler simulation is repeated for the specified number of
client-share combinations. We then compute an average highest service
time error and average lowest service time error for the specified
number of client-share combinations to obtain an ``average-case''
error range.
To measure proportional fairness accuracy, we ran simulations for each
scheduling algorithm considered on 40 different combinations of N and
S. For each set of (N, S), we ran 10,000 client-share
combinations and determined the resulting average error ranges.
The average service time error ranges for VTRR, WRR, and WFQ are shown
in Figures 1 and 2.
Figure 1 shows a comparison of the error ranges for
VTRR versus WRR, one graph showing the error ranges for VTRR and the
other showing the error ranges for WRR.
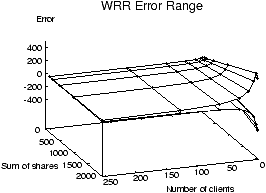
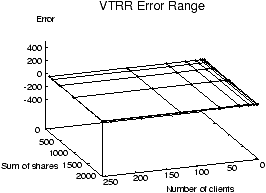
Figure 1: VTRR vs. WRR service time error
Each graph shows two surfaces plotted on axes of the same scale,
representing the maximum and minimum service time error as a function
of N and S. Within the range of values of N and S shown,
WRR's error range reaches as low as -398 tu and as high as 479 tu.
With the time units expressed in 10 ms jiffies as in Linux, a client
under WRR can on average get ahead of its correct CPU time allocation
by 4.79 seconds, or behind by 3.98 seconds, which is a substantial
amount of service time error. In contrast, Figure 1
shows that VTRR has a much smaller error range than WRR and is much
more accurate. Because the error axis is scaled to display the wide
range of WRR's error values, it is difficult to even distinguish the
two surfaces for VTRR in Figure 1. VTRR's service
time error only ranges from -3.8 to 10.6 tu; this can be seen more
clearly in Figure 2.
Figure 2 shows a comparison of the error ranges for
VTRR versus WFQ, one graph showing the error ranges for VTRR and the
other showing the error ranges for WFQ.
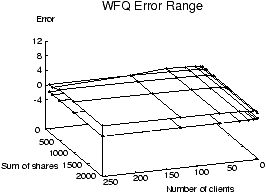
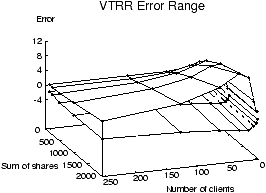
Figure 2: VTRR vs. WFQ service time error
As in the case in Figure 2, each graph shows two
surfaces plotted on axes of the same scale, representing the maximum
and minimum service time error as a function of N and S.
The VTRR graph in Figure 2 includes the same
data as the VTRR graph in Figure 1, but the error
axis is scaled more naturally. Within the range of values of N and
S shown, WFQ's average error range reaches as low as -1 tu and as
high as 2 tu, as opposed to VTRR's error range from -3.8 to 10.6
tu. The error ranges for WFQ are smaller than VTRR, but the difference
between WFQ and VTRR is much smaller than the difference between VTRR
and WRR.
With the time units expressed in 10 ms jiffies as in Linux, a client
under WFQ can on average get ahead of its correct CPU time allocation
by 10 ms, or behind by 20 ms, while a client under VTRR can get ahead by
38 ms or behind by 106 ms. In both cases, the service time errors are
small. In fact, the service time errors are even below the threshold
of delay noticeable by most human beings for response time on
interactive applications [27].
Note that another fair queueing algorithm WF2Q was not
simulated, but its error is mathematically bounded [3]
between -1 and +1 tu, and so would be very similar to WFQ in
practice.
The data produced by our simulations confirm that VTRR has fairness
properties that are much better than WRR, and nearly as good as WFQ.
For the domain of values simulated, the service time error for VTRR
falls into an average range almost two orders of magnitude smaller
than WRR's error range. While VTRR's error range is not quite as good
as WFQ, even the largest error measured, 10.6 tu, would likely be
unnoticeable in most applications, given the size of time unit used by
most schedulers. Furthermore, we show in Section 5.2
that VTRR provides this degree of accuracy at much lower overhead than
WFQ.
5.2 Scheduling Overhead
To evaluate the scheduling overhead of VTRR, we implemented VTRR in
the Linux operating system and compared the overhead of our prototype
VTRR implementation against the overhead of both the Linux scheduler
and a WFQ scheduler. We conducted a series of experiments to
quantify how the scheduling overhead for each scheduler varies as the
number of clients increases. For this experiment, each client executed
a simple micro-benchmark which performed a few operations in a while
loop. A control program was used to fork a specified number of
clients. Once all clients were runnable, we measured the execution
time of each scheduling operation that occurred during a fixed time
duration of 30 seconds. This was done by inserting a counter and
timestamped event identifiers in the Linux scheduling framework. The
measurements required two timestamps for each scheduling decision, so
variations of 140 ns are possible due to measurement overhead. We
performed these experiments on the standard Linux scheduler, WFQ, and
VTRR for 1 client up to 200 clients.
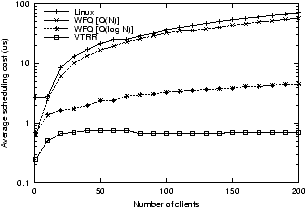
Figure 3: Average scheduling overhead
Figure 3 shows the average execution time required
by each scheduler to select a client to execute. For this experiment,
the particular implementation details of the WFQ scheduler affect
the overhead, so we include results from two different implementations
of WFQ. In the first, labeled ``WFQ [O(N)]'' the run queue is
implemented as a simple linked list which must be searched on every
scheduling decision. The second, labeled ``WFQ [O(log N)]''
uses a heap-based priority queue with O(log N) insertion time.
Most fair queueing-based schedulers are implemented in the first
fashion, due to the difficulty of maintaining complex data structures
in the kernel. In our implementation, for example, a separate,
fixed-length array was necessary to maintain the heap-based priority
queue. If the number of clients ever exceeds the length of the array,
a costly array reallocation must be performed. We chose an initial
array size large enough to contain more than 200 clients, so this
additional cost is not reflected in our measurements.
As shown in Figure 3, the increase in scheduling
overhead as the number of clients increases varies a great deal
between different schedulers. VTRR has the smallest scheduling
overhead. It requires less than 800 ns to select a client to execute
and the scheduling overhead is essentially constant for all numbers of
clients. In contrast, the overhead for Linux and for O(N) WFQ
scheduling grows linearly with the number of clients. The Linux
scheduler imposes 100 times more overhead than VTRR when scheduling a
mix of 200 clients. In fact, the Linux scheduler still spends almost
10 times as long scheduling a single micro-benchmark client as VTRR
does scheduling 200 clients. VTRR outperforms Linux and WFQ even for
small numbers of clients because the VTRR scheduling code is simpler
and hence runs significantly faster. VTRR performs even better
compared to Linux and WFQ for large numbers of clients because it
has constant time overhead as opposed to the linear time overhead of
the other schedulers.
While O(log N) WFQ has much smaller overhead than Linux or
O(N) WFQ, it still imposes significantly more overhead than VTRR,
particularly with large numbers of clients. With 200 clients, O(log
N) WFQ has an overhead more than 6 times that of VTRR. WFQ's more
complex data structures require more time to maintain, and the time
required to make a scheduling decision is still dependent on the
number of clients, so the overhead would only continue to grow worse
as more clients are added. VTRR's scheduling decisions always take
the same amount of time, regardless of the number of clients.
5.3 Microscopic View of Scheduling
Using our prototype VTRR implementation, we conducted a number of
experiments to measure the scheduling behavior of the standard Linux
scheduler, WFQ, and VTRR at fine time resolutions. We discuss the
results of one of the studies in which we ran a 30 second workload of
five micro-benchmarks with different proportional sharing
parameters. Using VTRR and WFQ, we ran the five micro-benchmarks
with shares 1, 2, 3, 4, and 5, respectively. To provide similar
proportional sharing behavior using the Linux scheduler, we ran the
five micro-benchmarks with user priorities 19, 17, 15, 13, and 11,
respectively. This translates to internal priorities used by the
scheduler of 1, 3, 5, 7, and 9, respectively. This then translates
into the clients running for 20 ms, 40 ms, 60 ms, 80 ms, and 100 ms
time quanta, respectively. The smallest time quantum used is the same
for all three schedulers. At the very least, the mapping between
proportional sharing and user input priorities is non-intuitive in
Linux. The scheduling behavior for this workload appears similar
across all of the schedulers when viewed at a coarse granularity. The
relative resource consumption rates of the micro-benchmarks are
virtually identical to their respective shares at a coarse
granularity.
We can see more interesting behavior when we view the measurements
over a shorter time scale of one second. We show the actual scheduling
sequences on each scheduler over this time interval in
Figures 4, 5, and
6. These measurements were made by sampling a
client's execution from within the client by recording multiple high
resolution timestamps each time that a client was executed. We can see
that the Linux scheduler does the poorest job of scheduling the
clients evenly and predictably. Both WFQ and VTRR do a much better
job of scheduling the clients proportionally at a fine granularity. In
both cases, there is a clear repeating scheduling pattern every 300
ms.
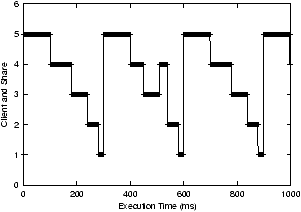
Figure 4: Linux scheduling behavior
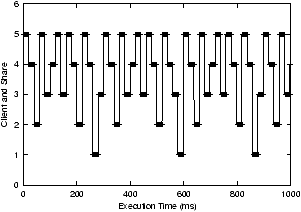
Figure 5: WFQ scheduling behavior
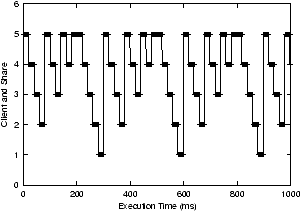
Figure 6: VTRR scheduling behavior
Linux does not have a perfect repeating pattern because the order in
which it schedules clients changes depending on exactly when the
scheduler function is called. This is because once Linux selects a
client to execute, it does not preempt the client even if its goodness
drops below that of other clients. Instead, it runs the client until
its counter drops below zero or an interrupt or other scheduling event
occurs. If a scheduling event occurs, then Linux will again consider
the goodness of all clients, otherwise it does not. Since interrupts
can cause a scheduling event and can occur at arbitrary times, the
resulting order in which clients are scheduled does not have a
repeating pattern. As a result, applications being scheduled using
WFQ and VTRR will receive a more even level of CPU service than if
they are scheduled using the Linux scheduler.
5.4 Application Workloads
To demonstrate VTRR's efficient proportional sharing of resources on
real applications, we briefly describe two of our experiments, one
running multimedia applications and the other running virtual
machines. We contrast the performance of VTRR versus the standard
Linux scheduler and WFQ.
One experiment we performed was to run multiple MPEG audio encoders
with different shares on each of the three schedulers. The encoder
test was implemented by running five copies of an MPEG audio
encoder. The encoder clients were allotted shares of 1, 2, 3, 4, and
5, and were instrumented with time stamp event recorders in a manner
similar to how we recorded time in our micro-benchmark programs. Each
encoder took its input from the same file, but wrote output to its own
file. MPEG audio is encoded in chunks called frames, so our
instrumented encoder records a timestamp after each frame is encoded,
allowing us to easily observe the effect of resource share on
single-frame encoding time.
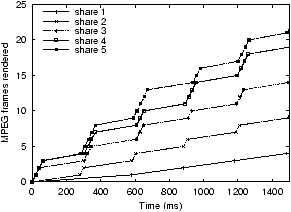
Figure 7: MPEG encoding with Linux
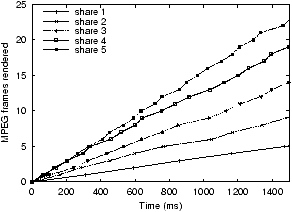
Figure 8: MPEG encoding with WFQ
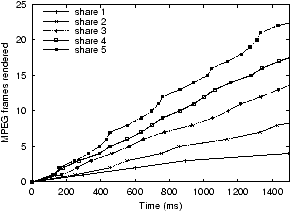
Figure 9: MPEG encoding with VTRR
Figures 7, 8, and
9 show the number of frames encoded over time for
the Linux default scheduler, WFQ, and VTRR. The Linux scheduler
clearly does not provide sharing as fairly as WFQ or VTRR when viewed
over a short time interval. The ``staircase'' effect indicates
that CPU resources are provided in bursts, which, for a time-critical
task like audio streaming, can mean extra jitter, resulting in delays
and dropouts. It can be inferred from the smoother curves of the
WFQ and VTRR graphs that WFQ and VTRR scheduling provide fair resource
allocation at a much smaller granularity. When analyzed at a fine
resolution, we can detect some differences in the proportional sharing
behavior of the applications when running under WFQ versus VTRR, but
the difference is far smaller than the difference compared with Linux,
which is clearly visible. VTRR trades some precision in instantaneous
proportional fairness for much lower scheduling overhead.
Schedulers that explicitly support time constraints can do a more
effective job than just proportional share schedulers of ensuring that
real-time applications can meet their
deadlines [24]. However, these real-time schedulers
typically require modifying an application in order for the
application to make use of scheduler-supported time constraints. For
applications that have soft timing constraints but can adapt to the
availability of resources, accurate proportional sharing may provide
sufficient benefit in some cases without the cost of having to modify
the applications.
Another experiment we performed was to run several VMware virtual
machines on top a Linux operating system, and then compare the
performance of applications within the virtual machines when the
virtual machines were scheduled using different schedulers. For this
experiment, we ran three virtual machines simultaneously with
respective shares of 1, 2, and 3. We then executed a simple timing
benchmark within each virtual machine to measure the relative
performance of the virtual machine. We were careful to make use of the
hardware clock cycle counters in doing these measurements as the
standard operating system timing mechanisms within a virtual machine
are a poor measure of elapsed time. We conducted the experiment using
the standard Linux scheduler, WFQ, and VTRR. The results were
similar to the previous experiments, with Linux doing the worst job in
terms of evenly distributing CPU cycles, and VTRR and WFQ scheduling
providing more comparable scheduling accuracy in proportionally
allocating resources.
6 Conclusions and Future Work
We have designed, implemented, and evaluated Virtual-Time Round-Robin
scheduling in the Linux operating system. Our experiences with VTRR
show that it is simple to implement and easy to integrate into
existing commercial operating systems. We have measured the
performance of our Linux implementation and demonstrated that VTRR
combines the benefits of accurate proportional share resource
management with very low overhead. Our results show that VTRR
scheduling overhead is constant, even for large numbers of
clients. Despite the popularity of the Linux operating system, our
results also show that the standard Linux scheduler suffers from
O(N) scheduling overhead and performs much worse than VTRR,
especially for larger workloads.
VTRR's ability to provide low overhead proportional share resource
allocation make it a particularly promising solution for managing
resources in large-scale server systems. Since these systems are
typically multiprocessor machines, we are continuing our evaluation of
VTRR in a multiprocessor context to demonstrate its effectiveness in
supporting large numbers of users and applications in these systems.
7 Acknowledgments
We thank the anonymous referees for their helpful comments on earlier
drafts of this paper. This work was supported in part by NSF grant
EIA-0071954 and an NSF CAREER Award.
References
- [1]
-
G. Banga, P. Druschel, and J. Mogul, ``Resource Containers: A New Facility
for Resource Management in Server Systems,'' in Proceedings of the 3rd
Symposium on Operating Systans Design and Implementation, USENIX, Berkeley,
CA, Feb. 22--25 1999, pp. 45--58.
- [2]
-
M. Beck, H. Bohme, M. Dziadzka, and U. Kunitz, Linux Kernel Internals.
Reading, MA: Addison-Wesley, 2nd ed., 1998.
- [3]
-
J. Bennett and H. Zhang, ``WF2Q: Worst-case Fair Weighted Fair
Queueing,'' in Proceedings of INFOCOM '96, San Francisco, CA, Mar.
1996.
- [4]
-
G. Bollella and K. Jeffay, ``Support for Real-Time Computing Within General
Purpose Operating Systems: Supporting Co-resident Operating Systems,'' in
Proceedings of the Real-Time Technology and Applications Symposium,
IEEE Computer Society Press, 1109 Spring Street, Suite 300, Silver Spring, MD
20910, USA, 1995, pp. 4--14.
- [5]
-
R. Bryant and B. Hartner, ``Java Technology, Threads, and Scheduling in
Linux,'' IBM developerWorks Library Paper, IBM Linux Technology Center,
Jan. 2000.
- [6]
-
G. Coulson, A. Campbell, P. Robin, G. Blair, M. Papathomas, and D. Hutchinson,
``Design of a QoS Controlled ATM Based Communication System in Chorus,''
in IEEE Journal of Selected Areas in Communications (JSAC), 13(4), May
1995, pp. 686--699.
- [7]
-
H. Custer, Inside Windows NT.
Redmond, WA, USA: Microsoft Press, 1993.
- [8]
-
A. Demers, S. Keshav, and S. Shenker, ``Analysis and Simulation of a Fair
Queueing Algorithm,'' in Proceedings of ACM SIGCOMM '89, Austin, TX,
Sept. 1989, pp. 1--12.
- [9]
-
K. Duda and D. Cheriton, ``Borrowed-Virtual-Time (BVT) Scheduling: Supporting
Latency-Sensitive Threads in a General-Purpose Scheduler,'' in Proceedings of the 17th Symposium on Operating Systems Principles, ACM
Press, New York, Dec. 1999, pp. 261--276.
- [10]
-
R. Essick, ``An Event-Based Fair Share Scheduler,'' in Proceedings of the
Winter 1990 USENIX Conference, USENIX, Berkeley, CA, USA, Jan. 1990,
pp. 147--162.
- [11]
-
S. Evans, K. Clarke, D. Singleton, and B. Smaalders, ``Optimizing Unix
Resource Scheduling for User Interaction,'' in 1993 Summer Usenix,
USENIX, June 1993, pp. 205--218.
- [12]
-
E. Gafni and D. Bertsekas, ``Dynamic Control of Session Input Rates in
Communication Networks,'' in IEEE Transactions on Automatic Control,
29(10), 1984, pp. 1009--1016.
- [13]
-
D. Golub, ``Operating System Support for Coexistence of Real-Time and
Conventional Scheduling,'' Tech. Rep. CMU-CS-94-212, School of Computer
Science, Carnegie Mellon University, Nov. 1994.
- [14]
-
P. Goyal, X. Guo, and H. Vin, ``A Hierarchical CPU Scheduler for Multimedia
Operating System,'' in Proceedings of the Second Symposium on Operating
Systems Design and Implementation, USENIX, Berkeley, CA, Oct. 1996,
pp. 107--121.
- [15]
-
E. Hahne and R. Gallager, ``Round Robin Scheduling for Fair Flow Control in
Data Communication Networks,'' Tech. Rep. LIDS-TH-1631, Laboratory for
Information and Decision Systems, Massachusetts Institute of Technology, Dec.
1986.
- [16]
-
G. Henry, ``The Fair Share Scheduler,'' AT&T Bell Laboratories
Technical Journal, 63(8), Oct. 1984, pp. 1845--1857.
- [17]
-
M. Jones, D. Rosu, and M. Rosu, ``CPU Reservations and Time
Constraints: Efficient, Predictable Scheduling of Independent Activities,''
in Proceedings of the 16th Symposium on Operating Systems Principles,
ACM Press, New York, Oct. 1997, pp. 198--211.
- [18]
-
J. Kay and P. Lauder, ``A Fair Share Scheduler,'' Communications of the
ACM, 31(1), Jan. 1988, pp. 44--55.
- [19]
-
L. Kleinrock, Queueing Systems, Volume II: Computer Applications.
New York: John Wiley & Sons, 1976.
- [20]
-
I. Lehoczky, L. Sha, and Y. Ding, ``The Rate Monotonic Scheduling Algorithm:
Exact Characterization and Average Case Behavior,'' in Proceedings of
the Real-Time Systems Symposium - 1989, IEEE Computer Society Press, Santa
Monica, California, USA, Dec. 1989, pp. 166--171.
- [21]
-
C. Liu and J. Layland, ``Scheduling Algorithms for Multiprogramming in a
Hard-Real-Time Environment,'' Journal of the ACM, 20(1), Jan. 1973,
pp. 46--61.
- [22]
-
C. Locke, Best-Effort Decision Making for Real-Time Scheduling.
PhD thesis, Department of Computer Science, Carnegie-Mellon
University, May 1986.
- [23]
-
C. Mercer, S. Savage, and H. Tokuda, ``Processor Capacity Reserves: Operating
System Support for Multimedia Applications,'' in Proceedings of the
International Conference on Multimedia Computing and Systems, IEEE Computer
Society Press, 1109 Spring Street, Suite 300, Silver Spring, MD 20910, USA,
1994, pp. 90--99.
- [24]
-
J. Nieh and M. Lam, ``The Design, Implementation and Evaluation of SMART: A
Scheduler for Multimedia Applications,'' in Proceedings of the 16th
Symposium on Operating Systems Principles, 31(5), ACM Press, New York,
Oct. 5--8 1997, pp. 184--197.
- [25]
-
A. Parekh and R. Gallager, ``A Generalized Processor Sharing Approach to Flow
Control in Integrated Services Networks: The Single-Node Case,'' IEEE/ACM Transactions on Networking, 1(3), June 1993, pp. 344--357.
- [26]
-
K. Ramakrishnan, D. Chiu, and R. Jain, ``Congestion Avoidance in Computer
Networks with a Connectionless Network Layer, Part IV: A Selective Binary
Feedback Scheme for General Topologies,'' Tech. Rep. DEC-TR-510, DEC, Nov.
1987.
- [27]
-
B. Shneiderman, Designing the User Interface: Strategies for Effective
Human-Computer Interaction.
Reading, MA: Addison-Wesley, 2nd ed., 1992.
- [28]
-
M. Shreedhar and G. Varghese, ``Efficient Fair Queueing Using Deficit
Round-Robin,'' in Proceedings of ACM SIGCOMM '95, 4(3), Sept. 1995,
pp. 231--242.
- [29]
-
A. Silberschatz and P. Galvin, Operating System Concepts.
Reading, MA, USA: Addison-Wesley, 5th ed., 1998.
- [30]
-
I. Stoica, H. Abdel-Wahab, and K. Jeffay, ``On the Duality between Resource
Reservation and Proportional Share Resource Allocation,'' in Multimedia
Computing and Networking Proceedings, SPIE Proceedings Series, 3020, Feb.
1997, pp. 207--214.
- [31]
-
``UNIX System V Release 4 Internals Student Guide, Vol. I, Unit 2.4.2.''
AT&T, 1990.
- [32]
-
R. Tijdeman, ``The Chairman Assignment Problem,'' Discrete Mathematics,
32, 1980, pp. 323--330.
- [33]
-
C. Waldspurger, Lottery and Stride Scheduling: Flexible Proportional-Share
Resource Management.
PhD thesis, Department of Electrical Engineering and Computer
Science, Massachusetts Institute of Technology, Sept. 1995.
- [34]
-
L. Zhang, ``Virtual Clock: A New Traffic Control Algorithm for Packet Switched
Networks,'' in ACM Transactions on Computer Systems, 9(2), May 1991,
pp. 101--125.
This document was translated from LATEX by
HEVEA.
|
