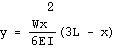The following paper was originally published in the
Proceedings of the
USENIX
Fourth Annual
Tcl/Tk Workshop
Monterey, California, July 1996.
For more information about
USENIX Association
contact:
[Next]
TclSolver: An Algebraic Constraint Manager for Tcl
Kevin B. Kenny
GE Corporate R&D Center
Schenectady, N. Y., USA
kennykb@crd.ge.com[1]
Abstract.
TclSolver is a simple algebraic constraint manager for use in Tcl applications. It enforces two-way declarative relationships among variables. If, for example, it is provided with a formula like A / B = C / D, it can determine the value of any of the four variables A, B, C, and D when the user supplies values for the other three. It is not a general-purpose equation solver; it is limited to solving for variables that appear only once in their formulae. This paper presents the design and implementation of TclSolver, and an example application that uses TclSolver to perform simple engineering calculations on the World-Wide Web.
1. Introduction.
Constraint propagation is a technique that allows programmers to specify the relationships among the variables in a program declaratively, and update selected variables automatically in response to changes in other variables. This style of programming has been used for many years, beginning with Sutherland's seminal Sketchpad system [9]. It has been introduced into Tcl by the TclProp system of Iyengar and Konstan [3].
Constraint propagation is a convenient means for performing geometry management, for tracking state in a user interface, and for evaluating algebraic formulas. This paper concentrates on this last application, presenting TclSolver, an algebraic constraint manager that is used in a powerful spreadsheet-like calculator for engineering applications. TclSolver adds a new command, solver, to the Tcl language. The solver command allows the programmer to define a network of constraints (via the load and compile subcommands), to set and interrogate the values of variables (via the set subcommand), and to perform various housekeeping tasks. The solver command is implemented in C++, and is, in fact, a Tcl-based interface to a C++ constraint system that can be used alone, without a Tcl interpreter.
The rest of this paper is organized as follows. Section 2 presents part of the history of declarative constraint management and introduces an engineering calculator application to show how constraint management can provide a powerful yet simple framework for calculations. Section 3 discusses the solver command, its use and its internal implementation. Section 4 presents experience with the solver command, including performance results, and Section 5 presents plans for future work in the area.
2. Background and Motivation.
The author first began working with constraint management in Tcl when work began on the ARPA CAMNET (Computer-Aided Manufacturing NETwork) initiative [7]. Among the tasks undertaken was deploying four manufacturing applications on the World-Wide Web (WWW), one of which was an interactive calculator supporting the design of injection-molded plastic parts. An early prototype of the interactive calculator was built in Tcl and Fortran, using a locally-developed library of Tcl tools for WWW applications [2]. The prototype calculator was unidirectional; it took as input the dimensions of a part (a snap-fit finger) and computed several key attributes of part performance.
Users' initial reviews of this prototype were not altogether favorable. While the users were intrigued by the user interface, and particularly by WWW as the delivery vehicle, they had serious misgivings about the functionality. The commonest concern they raised was that the calculator had to be bidirectional. Sometimes, said the users, they wanted to compute the performance of the part from its dimensions. At other times, however, they wanted to specify the part's performance and compute dimensions that would yield that performance. Each of the fields in the worksheet describing the part ought to be both an input and an output. The system should calculate values that the user left blank based on the values that the user supplied.
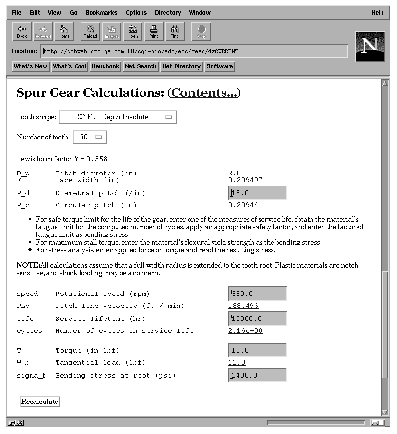
FIGURE 1. Worksheet from the engineering design calculator.
The value of PLV was obtained by computing
PLV = pi * D_p / 12 * speed
The rule that computed it was titled:
Definition of pitch line velocity
FIGURE 2. Explanation of a calculation
Figure 1 shows a worksheet from the system as it was redesigned in light of these comments. This particular worksheet performs stress and strain calculations on gears [6]. The users also requested the ability to get explanations of how the system arrived at the values of the outputs -- that is, what formulae were used to calculate them (Figure 2).
Now that the design was revised, there remained the question of how to implement it. Clearly, some sort of declarative programming was needed; coding all the combinations of inputs and outputs in a system of sixty or so equations would be a nightmare. It was also desirable to continue to integrate the system in a Tcl framework, because the CAMNET team already had a substantial body of software tools and expertise in integrating Tcl and the World-Wide Web. Fortunately, the author had seen the TclProp system (Figure 3) and realized that constraint programming in Tcl was viable.
TclProp itself, however, was rapidly rejected because it propagated values only in one direction. If it were used, each constraint equation would have to be entered many times. A typical equation like 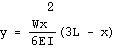
would have to be solved by hand and entered five times, once for each variable appearing in the equation. This process would be tedious and prone to error. A more sophisticated system was needed.
The next route explored was to integrate a general-purpose equation solver like Mathematica, Macsyma, or Reduce. All of the commercial ones, however, had no way to divorce the solver itself from the user interface, making it infeasible to integrate them into the Web. The Bertrand augmented term rewriting system [5] looked promising at first, but its solution rules were too rudimentary to be useful, addressing only systems of linear equations. It appeared possible to implement a suitable constraint manager in less time than it would take to make Bertrand's rule base powerful enough to address the issues in question. Work therefore commenced on implementing TclSolver. To mitigate the risk of this approach, a parallel implementation of the calculator using a commercial numeric (as opposed to symbolic) constraint solver [10] was also pursued.
3. Implementation.
TclSolver comprises a single command, solver, that is implemented in C++, lex, and yacc. A use of TclSolver consists of three phases. First, a system of equations is created. Second, input values are supplied to the system, and the output values are calculated. Finally, the output values are queried, and, optionally, the equations that computed them are constructed.
3.1 Building a system of equations.
A system of equations is constructed by the solver command:
% solver mySystem
mySystem
It is then populated by either loading it from a file:
% mySystem load myFile
or compiling it from a Tcl string:
% mySystem compile {
E : "Voltage";
I : "Current";
P : "Power";
R : "Resistance";
E = I * R "Ohm's Law";
P = I * E "Power law";
}
In either case, the system comprises variable declarations, which are variable names followed by colons and titles of the variables, and equations (annotated with quoted titles). The equations are in a C-like notation. They support the operators =, +, -, *, /, and ** (for exponentiation), and the functions exp, log, sin, asin, cos, acos, tan, atan, sqrt, and square. The load and compile subcommands may be invoked multiple times to add additional variables and equations.
Internally, a system of equations is represented as a network derived from its parse tree. The system of equations above, for instance, would be represented by the network in Figure 3.
3.2 Assigning and propagating values.
Once a system of constraints is built, the set subcommand is used to assign values to some set of its variables:
% MySystem set E 10.0
10.0
% MySystem set R 50.0
50.0
TclSolver operates by propagating values in the forward direction, as was pioneered in the "Constraints" system of Sussman and Steele [8]. In other words, it takes a set of known values and a network representing a system of equations. It examines each equation to find out whether the known values uniquely determine the value of another variable, and if so, defines that variable's value as being known as well. To clarify this process, consider the constraint network for the system of equations in Section 3.1, which is shown in Figure 3. It comprises two multipliers, shown as triangles, and four cells to hold numeric values, shown as squares. Each multiplier allows passage of data in either direction; when values are known at any two of its ports, it asserts the value at the third.
When the value of E is set to 10, nothing further can happen (R, I and P are still unknown). Now the value of 50 is assigned to R. The multiplier at upper right has known values at two of its ports (E and R), so it can compute the value of the third (I) by dividing E by R. It does so, giving a value of 0.2. Now the multiplier at lower left has known values at two of its ports (E and I), and can multiply them to give the value of 2 for P. Similar data flows result from assignments to most other pairs of variables: E and R, I and R, P and I, or P and E.
All operators, not just multipliers, pass data in either direction. The number of required types of operators is therefore less than half of what one would expect at first. There is no need for a "divider" operator -- a division is represented by connecting a multiplier backwards. The three equations:
A = B * C ,
B = A / C , and
C = A / B ,
result in identical constraint networks. Similarly, subtraction is addition run backwards, and a single type of operator handles powers, logarithms and roots. Three operator types represent the three circular functions (and, of course, their inverses).
3.3 Getting outputs and explanations.
Of course, once the values of variables have been assigned and the constraints have been propagated, the program needs to be able to deal with the results. Computed values are extracted with the same set command:
% MySystem set I
0.2
The equations that derived a value can also be extracted, using the source command:
MySystem source I
{E / R} {Ohm's Law}
The source command returns a two-element list. The first element is the expression that was evaluated to extract the value, and the second is the title of the constraint that was used.
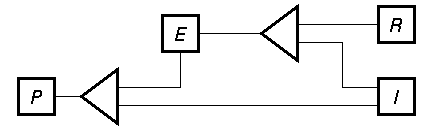
FIGURE 3. Sample constraint network.
3.4 Dealing with cycles in the constraint network.
TclSolver is not a general-purpose computer algebra system, even though its ability to propagate values through the constraint network in two directions gives something of the same flavor to it. In particular, there are common systems of equations that TclSolver is unable to solve. All of these involve cycles in the constraint network.
Consider, for example, presenting the network shown in Figure 3 with values for P and R. The constraint manager will be unable to determine E and I. The reason is that each depends on the other. Each of the multipliers will be unable to determine a value for E without knowing I, and vice versa.
This situation also arises in single equations. Any time that a single variable appears more than once in an equation, (for example, y=(x-1)/(x+1)), the resulting network will be unable to solve for that variable because it depends on itself.
It is possible to program around the difficulty by adding additional, redundant constraints. In Figure 3, for instance, adding the equation P=I**2*R will allow TclSolver to solve for any two of the variables given the other two. The single equation y=(x-1)/(x+1) can be solved by adding the redundant constraint x=(1+y)/(1-y). The effort of programming these redundant constraints is less in TclSolver than it would be in a unidirectional system like TclProp [3] since only a few equations need to be inverted by hand.
3.5 Miscellaneous commands.
TclSolver has a few additional commands that query and maintain the state of the system. The variables command gets a list of the variables that have been defined. The state command determines the state (input, output, or unknown) of a variable. The describe command retrieves the title of a variable. These commands allow ugly first attempts at the user interface to be generated automatically and then modified by hand for improved ease of use.
3.6 Extending TclSolver.
Some calculations, obviously, cannot be expressed as simple systems of equations. TclSolver has been used successfully to combine complex calculations such as numerical integration with simple relations. The complex calculations are integrated by augmenting TclSolver's C++ class library with new functions that perform the desired calculations. The calculations need not be invertible; the class library allows for operators that propagate data in only one direction. Typically, it takes anywhere from two to a few dozen lines of C++ code to add a new operator, depending on the complexity of its interface.
4. Experience with TclSolver.
TclSolver has been used to implement a plastics injection-molding calculator as an interactive World-Wide Web application. It has proven easy both to program and to use. Programmers report that the effort required is intermediate between setting up the same calculation in a spreadsheet and writing a program in a language such as Basic or C. Users report that the system is reasonably friendly, once they learn the paradigm. (Many reported confusion when first trying to adapt to the concept of a field that is both an input and an output.) A typical worksheet having sixteen variables, two dozen constraints, and graphs showing variation of two variables over time required 150 lines of Tcl code and 63 lines of source code for TclSolver, including whitespace and comments, and was implemented in an afternoon.
Performance results have been gratifying. Propagating the values through the constraint system takes a comparable amount of time to evaluating the same set of equations with the Tcl expr command. Attempting to manage forward evaluation only with Tcl trace operations roughly doubles the amount of time. TclProp [3] takes an order of magnitude more time when run in the forward direction only, and this time is increased by another order of magnitude if redundant constraints are added to allow values to propagate in both directions. Table 1 summarizes these results for the system of Figure 3. It reports the time to assign values to P and R, and extract the resulting values of E and I.
The chief drawback of TclSolver has been the limited capability of simple forward propagation as a solution technique. Programmers can easily miss cycles in the constraint networks, resulting in a worksheet's failure to solve for variables whose values are determined. Moreover, programmers and users have expressed the desire to solve in the backward direction, even when using unidirectional calculation techniques such as numerical integration. A few users have also asked for the ability to bound the calculations, generating error messages when values fall outside certain preset ranges.
TABLE 1. Performance of TclSolver relative to
other techniques
| | Time (ms) | |
| Method | Forward | Bidirectional |
Tcl expr command | 0.9 | -- |
Tcl expr command inside trace action | 1.8 | -- |
| TclProp | 11.0 | 78.5 |
| TclSolver | -- | 1.0 |
5. Plans for future work.
TclSolver has proven to be a useful tool in implementing spreadsheet-style calculations on the World-Wide Web. An initial release is available from the archive at https://camnet.ge.com/software/.
At present, TclSolver must be linked statically with a Tcl interpreter. It does not function as a dynamic load module, because the C++ code includes static objects that must be constructed, and the dynamic loader has no provision for invoking static constructor calls when a module is loaded. The team intends to address this problem in the future by replacing static objects with static pointers to objects that are constructed at run time.
The chief enhancements that are planned to TclSolver itself are inequality constraints and better handling of cycles in the constraint graph. Inequality constraints, initially, will simply report errors when the inputs fail to satisfy them, and will be used to bound calculations,
Special techniques will be required to handle cycles in the constraint graph. Given that certain of the functions will not be amenable to algebraic solution (several of the functions mentioned in Section 3.6 have no closed-form solution), it is anticipated that breaking cycles through algebraic manipulation will be infeasible. Rather, numeric techniques will be used, giving the TclSolver system something of the flavor of ThingLab [1] or Tk!Solver [4]. For variables that cannot be evaluated directly, the user will be prompted to supply guesses at the values, and a modified Newton-Raphson technique will be used to refine these guesses to consistent values. Optimization (minimization or maximization of a selected variable, subject to the constraints) will likely be added to the system at the same time.
6. References.
- Borning, Alan. "The programming language aspects of ThingLab, a constraint-oriented simulation laboratory." ACM Trans. on Programming Languages and Systems 3: 4 (October, 1981) pp. 353-387.
- Erkes, Joseph W., et al., "Implementing shared manufacturing services on the World-Wide Web." Commun. ACM 39:2(February, 1996) pp. 34-45.
- Iyengar, Sunanda, and Joseph A. Konstan. "TclProp: A data-propagation formula manager for Tcl and Tk." Proc. 1995 Tcl/Tk Workshop, July 1995, Toronto, Ontario, Canada, pp. 25-30.
- Konopasek, Milos, and Sundaresan Jayaraman. "Constraint and declarative languages for engineering applications: The Tk!Solver contribution." Proc. IEEE 73:12 (December, 1985) pp. 1791-1806.
- Leler, Wm. Constraint programming languages: Their specification and generation. Reading, Mass.: Addison-Wesley, 1988.
- Roark, Raymond J., and Warren C. Young. Formulae for stress and strain. New York: McGraw-Hill, 1975.
- Sobolewski, Michael W. and Joseph W. Erkes. "CAMNET: Architecture and applications." Proc. Concurrent Engineering 1995 Conf., McLean, Virginia, August 1995, pp. 627-634.
- Sussman, Gerald J., and Guy L. Steele. "Constraints: A language for expressing almost-hierarchical descriptions." Artificial Intelligence 14:1 (January, 1980) pp. 1-39.
- Sutherland, Ivan. "Sketchpad: A man-machine graphical communication system." Lincoln Laboratory Technical Report 296. Cambridge, Mass.: MIT, January, 1963. An abridged version appears in Proc. 1963 AFIPS Summer Joint Computer Conf.
- Vanderplaats, G. N. "ADS: A Fortran program for automated design synthesis." Santa Barbara, Calif.: Engineering Design Optimization, 1987.
[1] This research was supported in part by the Advanced Research Projects Agency (ARPA) Manufacturing Automation and Design Environment (MADE) Initiative through ARPA Contract F33615-94-C-4400.
- Abstract.
-
- 1. - Introduction.
-
- 2. - Background and Motivation.
-
- 3. - Implementation.
-
- 3.1 - Building a system of equations.
-
- 3.2 - Assigning and propagating values.
-
- 3.3 - Getting outputs and explanations.
-
- 3.4 - Dealing with cycles in the constraint network.
-
- 3.5 - Miscellaneous commands.
-
- 3.6 - Extending TclSolver.
-
- 4. - Experience with TclSolver.
-
- 5. - Plans for future work.
-
- 6. - References.
-
TclSolver: An algebraic constraint manager for Tcl - 24 MAY 1996
[Next]
Generated with Harlequin WebMaker