
The cqual tool needs to know not only how integer types with qualifiers relate but also how qualifiers affect pointer types, pointer-to-pointer types, function types, and so on. Fortunately, standard results on subtyping tell us how to extend the subtyping on integers to other data types [1,28].
We supply cqual with a configuration file placing the qualifiers
(in this case, tainted and untainted) in a lattice [14].
A lattice is a partial order where for each pair of elements ![]() and
and
![]() , the least upper bound and greatest lower bound of
, the least upper bound and greatest lower bound of ![]() and
and ![]() both always exist. Using a lattice makes the implementation slightly easier.
For finding format string bugs, we specify in the lattice configuration file
that
both always exist. Using a lattice makes the implementation slightly easier.
For finding format string bugs, we specify in the lattice configuration file
that
![]() .
.
Given this configuration file, cqual extends the supplied lattice on qualifiers to a subtyping relation on qualified C types. We have already seen one of the subtyping rules:
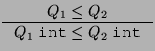
For pointer types, we need to be a little careful. Naively, we might expect to use the following rule for pointers:
![$\displaystyle \inference[(Wrong)]{Q_1 \leq Q_2 & T_1 \leq T_2}
{Q_1\;\textit{ptr}(T_1) \leq Q_2\;\textit{ptr}(T_2)}
$](img32.png)
typedef T1 *ptr_to_t1; typedef Q1 ptr_to_t1 q1_ptr_to_t1;The rule (Wrong) says that if
Unfortunately, this turns out to be unsound, as illustrated by the following code fragment:
tainted char *t;
untainted char *u;
t = u; /* Allowed by (Wrong) */
*t = <tainted data>;
/* Oops! This writes tainted data
into untainted buffer *u */
According to (Wrong), the first assignment t = u typechecks,
because
This is a well-known problem, and the standard solution, which is followed by cqual, is to use the following rule:
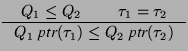
 |