 . This address is guaranteed by the kernel to be valid
and aligned on an 8-byte boundary.
. This address is guaranteed by the kernel to be valid
and aligned on an 8-byte boundary.

The abstract machine as given above describes safety in terms of the abstract notions of readable and writable memory locations. For this to be useful, the code consumer must specify an interface to binaries that identifies the readable and writable memory locations. We do this by specifying a precondition, which is a predicate in first-order logic that the code consumer guarantees to be valid when the binary is invoked.
Consider the following simple example. Suppose an operating-system kernel
maintains an internal table with data pertaining to various user processes.
Each table entry consists of two consecutive memory words--a tag and a data
word. The tag describes whether the data word is user writable or not. The
kernel also provides a resource access service through which user
processes are given permission to access their table entry by installing native
code in the kernel. To make this possible the kernel invokes the user-installed
code with the address of the table entry corresponding to the parent process in
machine register  . This address is guaranteed by the kernel to be valid
and aligned on an 8-byte boundary.
. This address is guaranteed by the kernel to be valid
and aligned on an 8-byte boundary.
Although this example is somewhat contrived, we can imagine that entries in the table represent capabilities (perhaps file descriptors), and so we would like to provide user-installed code with full access to the correct table entries, while maintaining the integrity of the rest of the table and other parts of the kernel state.
Informally, the safety policy for the resource access service requires that:
(1) the user code cannot access other table entries besides the one pointed to
by 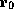 , (2) the tag is read only, (3) the data word is also read only
unless the tag value is non zero, and, (4) the code does not modify reserved
and callee-saves registers. The last condition ensures that the kernel can
safely invoke the user code using a normal C function call.
, (2) the tag is read only, (3) the data word is also read only
unless the tag value is non zero, and, (4) the code does not modify reserved
and callee-saves registers. The last condition ensures that the kernel can
safely invoke the user code using a normal C function call.
More formally, the kernel specifies a precondition 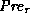 , which states
that it is safe to read the tag pointed to by
, which states
that it is safe to read the tag pointed to by 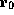 , and that it is
also safe to write the data at offset 8 from
, and that it is
also safe to write the data at offset 8 from 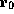 if the contents of
the tag is not 0. In formal notation, this is written as
follows:
if the contents of
the tag is not 0. In formal notation, this is written as
follows:
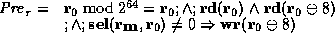
What remains now is to prove for a particular client of the resource access
service that all  and
and 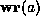 checks will always succeed, given
this precondition and abstract machine. In general, we can also specify a
postcondition as part of the safety policy, which would require particular
invariants to be valid when the user code terminates. Conceptually, in our
example the postcondition is the predicate
checks will always succeed, given
this precondition and abstract machine. In general, we can also specify a
postcondition as part of the safety policy, which would require particular
invariants to be valid when the user code terminates. Conceptually, in our
example the postcondition is the predicate  , meaning that no additional
conditions are imposed on the final machine state.
, meaning that no additional
conditions are imposed on the final machine state.
Before moving on to a discussion of the proof generation process, we note that the safety policy we have described here can be thought of as enforcing fine-grained memory protection. In general, one could imagine having much more involved safety requirements. For example, we could change the tag word in the table entry to be a semaphore that the user code must acquire (e.g., atomically test-and-set to zero) before trying to write the data word; furthermore, we could also require (via a simple postcondition) that the code releases the semaphore before returning. Again, for purposes of the current presentation, we stick to the simpler memory-safety requirements.