|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
4th USENIX OSDI Symposium
[Technical Program]
Abstract: We explore the abstraction of failure transparency in which the operating system provides the illusion of failure-free operation. To provide failure transparency, an operating system must recover applications after hardware, operating system, and application failures, and must do so without help from the programmer or unduly slowing failure-free performance. We describe two invariants that must be upheld to provide failure transparency: one that ensures sufficient application state is saved to guarantee the user cannot discern failures, and another that ensures sufficient application state is lost to allow recovery from failures affecting application state. We find that several real applications get failure transparency in the presence of simple stop failures with overhead of 0-12%. Less encouragingly, we find that applications violate one invariant in the course of upholding the other for more than 90% of application faults and 3-15% of operating system faults, rendering transparent recovery impossible for these cases. 1. IntroductionOne of the most important jobs
of the operating system is to conceal the complexities and inadequacies
of the underlying machine. Towards this end, modern operating systems provide
a variety of abstractions. To conceal machines' limited memory, for example,
operating systems provide the abstraction of practically boundless virtual
memory. Similarly, operating systems give the abstraction of multithreading
for those applications that might benefit from more processors than are
present in hardware. Failures by computer system
components, be they hardware, software, or the application, are a shortcoming
of modern systems that has not been abstracted away. Instead, computer
programmers and users routinely have to deal with the effects of failures,
even on machines running state-of-the-art operating systems. With this paper we explore
the abstraction of failure transparency in which the operating system generates
the illusion of failure-free operation. To provide this illusion, the operating
system must handle all hardware, software, and application failures to
keep them from affecting what the user sees. Furthermore, the operating
system must do so without help from the programmer and without unduly slowing
down failure-free operation. Fault-tolerance research has
established many of the components of failure transparency, such as programmer-transparent
recovery [4, 11, 25, 28], and recovery for general applications [4, 14].
Some researchers have even discussed handling application failures [13,
17, 31]. However, significant questions
surrounding failure transparency remain. The focus of this paper is on
delving into several of these unanswered questions. First, we will explore
the question "how does one guarantee failure transparency in general?"
The answer to this question comes in the form of two invariants. The first
invariant is a reformulation of existing recovery theory, governing when
an application must save its work to ensure that the user does not discern
failures. In contrast, the second invariant governs how much work an application
must lose to avoid forcing the same failure during recovery. The Save-work invariant can
require applications to commit their state frequently to stable storage.
The question therefore arises "how expensive is it for general applications
to uphold the Save-work invariant?" In answering this question we find,
to our surprise, that even complex, general applications are able to efficiently
uphold Save-work. Given that the Save-work invariant
forces applications to preserve work and the Lose-work invariant forces
applications to throw work away, we conclude by investigating the question,
"how often do these invariants conflict, making failure transparency impossible?"
The unfortunate answer is that the invariants conflict all too often. 2. Guaranteeing Failure TransparencyWe first delve into the question:
how does one guarantee failure transparency in general? Our exploration
begins with a synthesis of existing recovery theory that culminates in
the Save-work invariant. In Section 2.4.,
we then extend recovery theory to point out a parameterization of the space
of recovery protocols, as well as the relationship between protocols at
different points in the space. Finally, we develop a new theory and second
invariant for ensuring the possibility of recovery from failures that affect
application state.
2.1. Primitives for general recoveryIn attempting to provide failure
transparency, the goal is to recover applications using only general techniques
that require no help from the application. There are several recovery primitives
available to us in this domain: commit events, rollback of a process, and
reexecution from a prior state. A process can execute commit
events to aid recovery after a failure. By executing a commit event, a
process preserves its state at the time of the commit so that it can later
restore that state and continue execution. Although how commit events are
implemented is not important to our discussion, executing a commit event
might involve writing out a full-process checkpoint to stable storage,
ending a transaction, or sending a state-update message to a backup process. When a failure occurs, the
application undergoes rollback of its failed processes; each failed process
is returned to its last committed state. From that state, the recovering
process begins reexecution, possibly recomputing work lost in the failure. Providing generic recovery
requires that applications tolerate forced rollback and reexecution. As
a result, all application operations must be either undoable or redoable. Most application operations
that simply modify process state are easily undone. However, some events,
such as message sends, are hard to undo. Undoing a send can involve the
added challenge of rolling back the recipient's state. Other events can
be impossible to undo. For example, we cannot undo the effects on the user
resulting from visible output. However, systems providing failure transparency
ensure that these user-visible events will never be undone. Similarly, since simple state
changes by the application are idempotent, most application events can
be safely redone. However, events like message sends and receives are more
difficult to redo. For message send events to be redoable, the application
must either tolerate or filter duplicate messages. For receive events to
be redoable, messages must be saved at either the sender or receiver so
they can be re-delivered after a failure. Luckily, these reexecution requirements
are very similar to the demands made of systems that transmit messages
on unreliable channels (e.g. UDP). Such systems must already work correctly
even with lost or duplicated messages. For many recovery systems, an application
or protocol layer's natural filtering and retransmission mechanisms will
be enough to support the needs of reexecution recovery. For others, messages
may have to be held in a recovery buffer of some kind so they can be re-delivered
should a receive event be redone.
2.2. Computation and failure modelWe will informally present
a recovery theory that will let us relate the challenge of guaranteeing
failure transparency to the precise events executed by an application.
For a more formal version of the theory, please see [22]. We begin by constructing a
model of computing. One or more processes working together on a task is
called a computation. We model each process as a finite state machine.
That is, each process has state and computes by transitioning from state
to state according to the inputs it receives. Each state transition executed
by a process is an event. An event 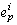 is the
i'th event executed by process p. Events can correspond in real programs
to simple changes of application state, sending and receiving messages,
and so on. We call events that have an effect on the user visible events
(these events have traditionally been called "output events" [11]). Under
our model, computation proceeds asynchronously, that is, without known
bounds on message delivery time or the relative speeds of processes. is the
i'th event executed by process p. Events can correspond in real programs
to simple changes of application state, sending and receiving messages,
and so on. We call events that have an effect on the user visible events
(these events have traditionally been called "output events" [11]). Under
our model, computation proceeds asynchronously, that is, without known
bounds on message delivery time or the relative speeds of processes.As needed, we will order events
in our asynchronous computations with Lamport's happens-before relation
[19]. We may also need to discuss the causal relationship between events.
For example, we may need to ask, "did event e in some way cause event 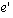 ?" We will use happens-before as an approximation of causality. We will
however distinguish between happens-before's use as an ordering constraint
and its use as an approximation of causality by using the expression causally
precedes in this latter role. That is, we say event e causally precedes
event
?" We will use happens-before as an approximation of causality. We will
however distinguish between happens-before's use as an ordering constraint
and its use as an approximation of causality by using the expression causally
precedes in this latter role. That is, we say event e causally precedes
event 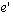 if and only if e happens-before if and only if e happens-before 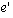 and we intend to convey that e causes event
and we intend to convey that e causes event 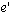 .
.We will consider failures of
two forms. A stop failure is one in which execution of one or more processes
in the computation simply ceases. Stop failures do occur in real systems--the
loss of power, the frying of a processor, or the abrupt halting of the
operating system all appear to the recovery system as stop failures. Since
stop failures instantaneously stop the execution of the application and
do not corrupt application state, recovering from them is relatively easy. Harder to handle are propagation
failures. We define a propagation failure to be one in which a bug somewhere
in the system causes the application to enter a state it would not enter
in a failure-free execution. A propagation failure can begin with a bug
in hardware, the operating system, or the application. Bugs in the application
are always propagation failures, but bugs in hardware and the operating
system are propagation failures only once they affect application state. Recovering from propagation
failures is hard because a process can execute for some time after the
failure is triggered. During that time the process can propagate buggy
data into larger portions of its state, to other processes, or onto stable
storage. We can imagine bugs that do
not cause crashes, but that simply cause incorrect visible output by the
application. However, our focus with this work is on recovering from failures.
Therefore, we will assume that applications will detect faults and fail
before generating incorrect output. 2.3. Failure transparency for stop failuresWe start by examining how to
ensure failure transparency in the presence of stop failures. We must first
fix a precise notion of "correct" recovery from failures. We could establish
almost any standard: recovering the exact pre-failure state, losing less
than 10 seconds of work, and so on. However, given that our end goal is
to mask failures from the user, we will define correct recovery in terms
of the application output seen by the user. Definition: Consistent RecoveryRecovery is consistent if and only if there exists a complete, failure-free execution of the computation that would result in a sequence of visible events equivalent to the sequence of visible events actually output in the failed and recovered run. Thus for an application's recovery
to be consistent, the sum total of the application's visible output before
and after a failure must be equivalent to the output from some failure-free
execution of the application. It is possible that many different
modes of consistent recovery could be allowed depending on how one defines
"equivalent". For our purposes, we will call a sequence of visible events
V output by a recovered computation equivalent to sequence 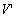 output by a failure-free run if the only events in V that differ from
output by a failure-free run if the only events in V that differ from 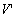 are repeats of earlier events from V.
are repeats of earlier events from V.We use equivalence in which
duplicate visible events are allowed because guaranteeing no duplication
is very hard (exactly once delivery problem). Furthermore, allowing duplicates
provides some flexibility in how one attains consistent recovery. More
importantly, users can probably overlook duplicated visible events. See
[22] for a more detailed discussion of equivalence. Our definition of consistent
recovery places two constraints on recovering applications. First, computations
must always execute visible events that extend a legal, failure-free sequence
of visible events, even in the presence of failures. We will call this
the visible constraint. Second, computations must always be able to execute
to completion. This latter constraint follows from the fact that consistent
recovery is defined in terms of complete sequences of visible events. If
a failure prevents an application from running to completion, its sequence
can never be complete. For reasons that will become clear later, we will
call this second constraint on recovery the no-orphan constraint. Although consistent recovery
and failure transparency are closely related, they are not the same thing.
Providing failure transparency amounts to guaranteeing consistent recovery
without any help from the application, and without slowing the application's
execution appreciably. Our next task is to examine
how to guarantee applications get consistent recovery. One particular class
of events poses the greatest challenge: non-deterministic events. In a
state-machine, a non-deterministic event is a transition from a state that
has multiple possible next states. For example, in Figure
1, events 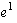 and and 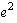 are both non-deterministic. In real systems, non-deterministic events correspond
to actions that can have different results before and after a failure,
like checking the time-of-day clock, taking a signal, reading user input,
or receiving a message.
are both non-deterministic. In real systems, non-deterministic events correspond
to actions that can have different results before and after a failure,
like checking the time-of-day clock, taking a signal, reading user input,
or receiving a message.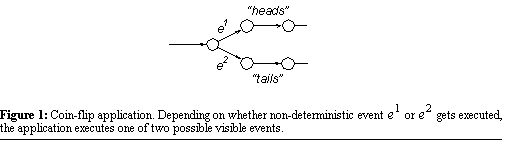 Non-deterministic events are intimately related to consistent recovery.
To see how, again consider the application shown in Figure
1. Imagine that the application executes non-deterministic event As discussed in Section 2.1.,
applications can execute commit events to aid later rollback. We would
like to use commit events to guarantee consistent recovery, avoiding the
inconsistency non-deterministic events can cause. The following theorem
provides the necessary and sufficient condition for doing exactly that
under stop failures. Save-work TheoremA computation is guaranteed consistent recovery from stop failures if and only if for each executed non-deterministic event This theorem dictates when
processes must commit in order to ensure consistent recovery. At the heart
of this theorem is the Save-work invariant, which informally states "each
process has to commit all its non-deterministic events that causally precede
visible or commit events". We can further divide this invariant into separate
rules, one that enforces the visible constraint of consistent recovery,
and one that enforces the no-orphan constraint. If we follow the rule "commit
every non-deterministic event that causally precedes a visible event",
we are assured that the application's visible output will always extend
a legal sequence of visible events. We'll call this the Save-work-visible
invariant. If we follow the rule "commit every non-deterministic event
that causally precedes a commit event", we are assured that a finite number
of stop failures cannot prevent the application from executing to completion.
We'll call this the Save-work-orphan invariant. To better understand this
latter rule, consider the computation depicted in Figure
2. A process is called an orphan
if it has committed a dependence on another process's non-deterministic
event that has been lost and may not be reexecuted. For example, Process
A in Figure 2 is an orphan
because it has committed its dependence on Process B's lost non-deterministic
event.
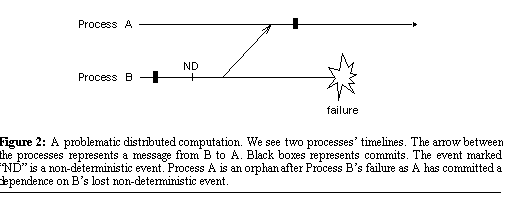
An orphan can prevent an application from executing to completion when it is upholding Save-work-visible. Consider an orphan that has committed a dependence on a lost non-deterministic event 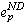 . If the orphan attempts to execute a visible event e, Save-work-visible
requires that process p commit
. If the orphan attempts to execute a visible event e, Save-work-visible
requires that process p commit 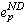 . However,
since process p has already failed and aborted . However,
since process p has already failed and aborted 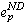 , it cannot commit it. Furthermore, since the orphan cannot abort its dependence
on
, it cannot commit it. Furthermore, since the orphan cannot abort its dependence
on 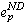 , it can never execute e and the computation
will not be able to complete. , it can never execute e and the computation
will not be able to complete.The remedy for this scenario
is to uphold Save-work-orphan, which ensures that any non-deterministic
event that causally precedes a commit is committed. We must make two assumptions
for the Save-work Theorem to be necessary. We ensure the necessity of Save-work-visible
by assuming that all non-deterministic events can cause inconsistency.
We ensure the necessity of Save-work-orphan by assuming that all processes
in the computation affect the computation's visible output. For the details
of these assumptions as well as the proof of the Save-work Theorem, please
see [22]. 2.4. Upholding Save-workThere are many ways an application
can uphold the Save-work invariant to ensure consistent recovery for stop
failures. For example, an application can execute a commit event for every
event executed by the application. Although such a protocol will cause
a very large number of commits, it has the advantage of being trivial to
implement: the protocol does not need to figure out which events are non-deterministic,
or which events are visible. Even without knowing event types, it correctly
upholds the Save-work invariant. Consider a protocol in which
each process executes a commit event immediately after each non-deterministic
event. In committing all non-deterministic events, this protocol will certainly
commit those non-deterministic events that causally precede visible or
commit events. Therefore it upholds Save-work and will guarantee consistent
recovery. We call this protocol Commit After Non-Deterministic, or CAND. We can also uphold Save-work
without knowing about the non-determinism in the computation. Under the
Commit Prior to Visible or Send protocol (CPVS), each process commits just
before doing a visible event or a send to another process. When a process
commits before each of its visible events, it is assured that all its non-determinism
that causally precedes the visible event is committed. If each process
also commits before every send event, then it cannot pass a dependence
on an uncommitted non-deterministic event to another process. Thus, CPVS
also upholds Save-work. The Commit Between Non-Deterministic
and Visible or Send (CBNDVS) protocol takes advantage of knowledge of both
non-determinism and visible and send events in order to uphold Save-work.
Under this protocol, each process commits immediately before a visible
or send event if the process has executed a non-deterministic event since
its last commit. Since commit events can involve
writing lots of data to stable storage, they can be slow. Therefore, minimizing
the number of commits executed can be important to failure-free performance.
There exist several general techniques for minimizing commits. Logging is a general technique
for reducing an application's non-determinism [12]. If an application writes
the result of a non-deterministic event to a persistent log, and then uses
that log record during recovery to ensure the event executes with the same
result, the event is effectively rendered deterministic. Logging some of
an application's non-determinism can significantly reduce commit frequency.
Logging all an application's non-determinism lets the application uphold
Save-work without committing at all. Tracking whether one process's
non-determinism causally precedes events on another process can be complex.
In fact, we can think of the CPVS protocol as pessimistically committing
before send events rather than track causality between processes. However,
applications can avoid committing before sends without tracking causality
by employing a distributed commit, such as two-phase commit (2PC)--all
processes would commit whenever any process does a visible event. Using
two-phase commit can reduce commit frequency if visible events are less
frequent than sends. Applications can further reduce commits by tracking
causality between processes, involving in the coordinated commit only those
processes with relevant non-deterministic events. Not only can each of these
protocols be viewed as a different technique for upholding Save-work, but
so can all existing protocols from the recovery literature. For example, pure message logging
protocols make all message receive events deterministic, allowing applications
whose only non-deterministic events are receives to uphold Save-work without
committing. The different message logging protocols differ in how the logging
is carried out. For example, Sender-based Logging (SBL) protocols keep
the log record for the receive event in the volatile memory of the sender
[15], while Family-based Logging (FBL) keeps log entries in the memory
of downstream processes [2]. In the Manetho system, each
process maintains log records for all the non-deterministic events it depends
on in an antecedence graph. When a process wants to execute a visible event,
it upholds Save-work by writing the antecedence graph to stable storage
[11]. In the Optimistic Logging protocol, processes write log records to
stable storage asynchronously [28]. When a process wants to do a visible
event, it upholds Save-work by first waiting for all relevant log records
to make it to disk. The Targon/32 system attempts
to handle more non-determinism than these other logging protocols [4].
All sources of non-determinism except signals are converted into messages
that are logged in the memory of a backup process on another processor.
Whenever a signal is delivered (an event that remains non-deterministic),
Targon/32 forces a commit to uphold Save-work. The Hypervisor system logs
all sources of non-determinism using a virtual machine under the operating
system [5]. Under a Coordinated Checkpointing
protocol, a process executing a visible event essentially assumes that
all processes in the computation with which it has recently communicated
have executed non-deterministic events that causally precede the visible
event [18]. To uphold the Save-work invariant, the process executing the
visible event initiates an agreement protocol to force all these other
processes to commit. Each of these recovery protocols
represents a different technique for upholding Save-work. Each to varying
degrees trades off programmer effort and system complexity for reduced
commit frequency (and hopefully overhead). Some protocols focus their
effort to reduce commit frequency on the challenge of identifying and reducing
non-determinism. Others endeavor to use knowledge of an application's visible
events. Still others do some of each. Each protocol can be seen as representing
a point in a two-dimensional space of protocols. One axis in the space
represents effort made to identify and possibly convert application non-determinism.
The other axis represents effort made to identify visible events and to
commit as few non-visible events as possible. Such a protocol space is useful
because it helps us understand the relationships between historically disparate
protocols and to identify new ones. Figure
3 shows how the protocols we have described in this section might
appear in such a protocol space. A protocol falling at the
origin of the space would uphold Save-work by committing every event executed
by each process, exerting no effort to determine which events are non-deterministic
or visible. As protocols fall further out the horizontal axis, they make
sufficient effort to recognize that some events are deterministic and therefore
do not require commits. At the point occupied by CAND, the protocol makes
sufficient effort to distinguish all of the application's deterministic
and non-deterministic events, executing a commit only after non-deterministic
ones. Beyond that point, the protocols begin to employ logging, exerting
effort to convert more and more of the application's non-deterministic
events into deterministic ones. A protocol in that portion of the space
forces a commit only when the application executes some unlogged non-determinism.
At the point occupied by Hypervisor, the protocol makes sufficient effort
to log all non-determinism, never forcing a commit. 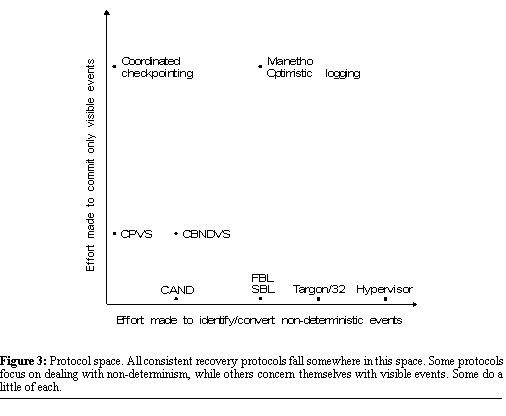 For the vertical axis, we
can think of the protocol at the origin as committing all events rather
than exert the effort needed to determine which events are visible. Protocols
falling further up the axis exert more effort to avoid committing events
that are not visible. At the point occupied by CPVS, protocols commit only
the true visible events and send events--committing before sends takes
less effort than tracking whether that send leads to a visible event on
another process. Protocols falling yet further up in the space (such as
Coordinated Checkpointing) are able to ask remote processes to commit if
needed. Under those protocols, applications are forced to commit before
visible events only. Some protocols fall in the
middle of the space, applying techniques both for identifying and converting
non-determinism, as well as for tracking the causal relationship between
non-deterministic events and the visible events they cause. Although all protocols in the
space are equivalent in terms of upholding Save-work, they do differ in
terms of other design variables. As shown in Figure
4, we can map trends in several important design variables onto the
protocol space.
The farther a protocol falls from the origin, the lower its commit frequency is likely to be, and therefore, the better its performance. However, this improved performance comes at the expense of simplicity and reliability. Protocols close to the origin are very simple to implement, and therefore are more likely to be implemented correctly. For protocols that fall on
the vertical axis, the recovery system needs only rollback failed processes
and let them continue normally. Protocols further to the right in the protocol
space have longer recovery times because after rollback, the recovery system
must for some time constrain reexecution to follow the path taken before
the failure. The further a protocol falls
from the horizontal axis, the more non-determinism it safely leaves in
the application. As we will discuss in Section 2.6.,
the more non-determinism in an application, the better the chance it will
survive propagation failures. 2.5. Failure transparency for stop and propagation failuresAs mentioned in Section 2.2.,
failures can take two forms: stop failures and propagation failures. Upholding
the Save-work invariant is enough to guarantee consistent recovery only
in the presence of stop failures. To illustrate this observation, consider
a protocol that commits all events a process executes. This protocol clearly
upholds Save-work. However, if the process experiences a propagation failure
(which by definition involves executing buggy events), this protocol is
guaranteed to commit buggy state. As a result, the process will fail again
during recovery, and the application will never be able to complete after
the failure. Thus, in order to guarantee
consistent recovery in the presence of propagation failures, an application
must not only commit to uphold Save-work, but when it commits it must avoid
preserving the conditions of its failure. In this section we examine what
exactly an application must do to guarantee consistent recovery in the
presence of propagation failures. As was the case in our discussion
of consistent recovery, non-deterministic events are central to the issue
of recovering from propagation failures. Imagine an application that, as
a result of non-deterministic event e, overruns a buffer it is clearing
and zeroes out a pointer down the stack (see Figure 5). Later, it attempts to dereference the pointer and crashes. Obviously
if the application commits after zeroing the pointer, recovery is doomed.
However, if the application commits any time before zeroing the pointer
and after e, recovery will still be doomed if there are no other non-deterministic
events after e. In this case, the pointer is not corrupted in the last
committed state, but it is guaranteed to be re-corrupted during recovery.
Note that had the application committed just before e and not after, all could be well. During recovery, the application would redo the non-deterministic event which could execute with a different result and avoid this failure altogether. Thus non-determinism helps
our prospects for recovering from propagation failures by limiting the
scope of what is preserved by a commit. But, not all non-determinism
is created equal in this regard. In building up the Save-work invariant,
we conservatively treated as non-deterministic any event that could conceivably
have a different result during recovery. However, some non-deterministic
events are likely to have the same result before and after a failure, and
the recovery system cannot depend on these events to change after recovery.
We will called these events fixed non-deterministic events. A common example of a fixed
non-deterministic event is user input. We cannot depend on the user to
aid recovery by entering different input values after a failure. Other
examples of fixed non-deterministic events include non-deterministic events
whose results are based on the fullness of the disk (such as the write
system call), or that depend on the number of slots left in the operating
system's open file table (such as the open system call). Non-deterministic events that
are not fixed we will call transient non-deterministic events. Scheduler
decisions, signals, message ordering, the timing of user input, and system
calls like gettimeofday are all transient non-deterministic events. We need to incorporate into
our computational model a way to represent the eventual crash of a process
during a propagation failure. We will model a process's crash as the execution
of a crash event. When a process executes a crash event, it transitions
into a state from which it cannot continue execution. In the example in
Figure 5, the crash event is the dereferencing of the null pointer. As mentioned above, an untimely
commit during a propagation failure can ensure that recovery fails. Let
us examine in more detail when a process should not commit. Clearly a process should not
commit while executing a string of deterministic events that end in a crash
event. Doing so is guaranteed to either commit the buggy state that leads
to the crash, or to ensure that the faulty state is regenerated during
recovery. This case is shown in Figure 6A. 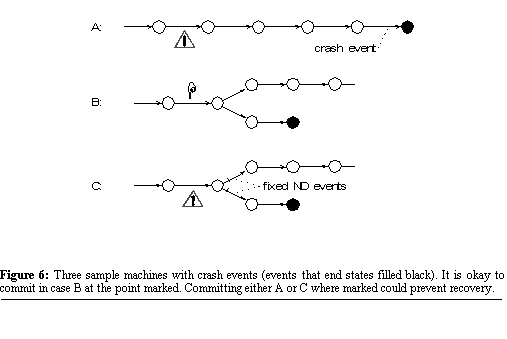 However, a process can safely commit before a transient non-deterministic event as long as at least one of the possible results of that event does not lead to the execution of a crash event (see Figure 6B). How about committing before
a fixed non-deterministic event where one of the event's possible results
leads to a crash? This case is shown in Figure 6C. If the application commits before the fixed non-deterministic
event, recovery is possible only if the event executes with a result that
leads down the path not including the crash event. If the application is
unlucky and the fixed non-deterministic event sends the application down
the path towards the crash, the commit will ensure recovery always fails.
Since we cannot rely on fixed non-deterministic events having results conducive
to recovery, we cannot commit before any fixed non-deterministic events
that might lead to a crash. We can infer that some paths
through a portion of a state machine are problematic for handling propagation
failures--committing anywhere along the paths could prevent recovery. We
next present an algorithm for finding these paths. For this discussion,
we assume perfect knowledge of each process's crash events. We recognize
that this is not practical--if we knew all the crash events, we could likely
fix all the bugs! However, making this assumption will help us to analyze
when recovery is possible with the best possible knowledge. Single-Process Dangerous Paths Algorithm
We call all the paths in the
state machine colored by this algorithm dangerous paths. A portion of a
state machine with its dangerous paths highlighted is shown in Figure
7. 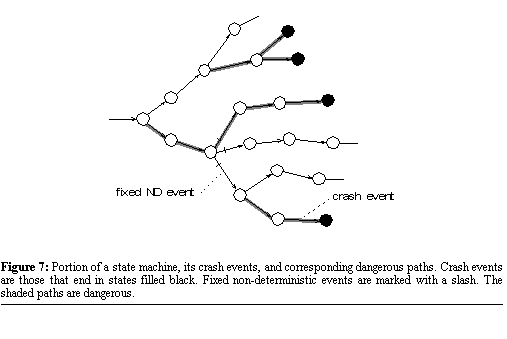 We now present without proof a theorem which governs when recovery is possible in the presence of propagation failures. Lose-work TheoremApplication-generic recovery from propagation failures is guaranteed to be possible if and only if the application executes no commit event on a dangerous path. This theorem provides an invariant for ensuring the possibility of recovery from propagation failures: processes must not commit on dangerous paths. It is interesting to note that the location of the initial bug that caused the crash is surprisingly irrelevant. In the end, all that matters is the eventual crash event (or events) that result from that bug and its location relative to the application's transient non-deterministic events. How about for multi-process
applications? The challenge for distributed applications is in computing
their dangerous paths. Unlike the dangerous paths algorithm presented above,
computing dangerous paths for a distributed application cannot be done
statically: whether one process's path is dangerous can depend on the paths
taken by the other processes in the computation and where they have committed. Given a process P that wants
to determine its dangerous paths (presumably so it can commit without violating
Lose-work): Multi-Process Dangerous Paths Algorithm
2.6. Upholding Lose-workThe simplest way to uphold
Lose-work is to ensure that no process ever commits. Although this solution
has the advantage of requiring no application-specific knowledge to implement,
it also prohibits guaranteeing consistent recovery. Clearly, without perfect knowledge
of the application's non-determinism and crash events it is impossible
to guarantee a committing application upholds Lose-work. Despite the impossibility
of directly upholding the invariant, we can use the Lose-work Theorem to
draw some conclusions about recovering from propagation failures. First, we observe that it is
impossible to uphold both Save-work and Lose-work for some applications.
Consider an application with a visible event on a dangerous path. The dangerous
path will extend back at least to the last non-deterministic event. Upholding
Save-work forces the application to commit between the last non-deterministic
event and the visible event, which will violate Lose-work. Second, some protocols designed
to uphold Save-work for stop failures guarantee that applications will
not recover from propagation failures. These protocols either commit or
convert all non-determinism, ensuring a commit after the non-deterministic
event that steers a process onto a dangerous path, thus violating Lose-work.
CAND, Sender-based logging, Targon/32, and Hypervisor are all examples
of protocols that prevent applications from surviving propagation failures.
Indeed, any protocol that falls on the horizontal axis of the Save-work
protocol space (see Figure 3)
will prevent upholding Lose-work. The farther a protocol falls from the
horizontal axis, the more it focuses its attention on handling visible
events and the more non-determinism it leaves safely uncommitted, thus
decreasing the chances of violating Lose-work (see Figure 4). Although directly upholding
Lose-work is impossible, some applications with mostly "non-repeatable"
bugs (so called "Heisenbugs" [13]) may be able to commit with a low probability
of violating the invariant. There are also a number of ways applications
can deliberately endeavor to minimize the chance that one of their commits
causes them to violate Lose-work. First, applications should
try to crash as soon as possible after their bugs get triggered. Doing
so shortens dangerous paths and thus lowers the probability of the application
committing while executing on one. In order to move crashes sooner, processes
can try to catch erroneous state by performing consistency checks. For
example, a process could traverse its data structures looking for corruption,
it could compute a checksum over some data, or it could inspect guard bands
at the ends of its buffers and malloc'ed data. Voting amongst independent
replicas is a general but expensive way to detect erroneous execution [27].
When a process fails one of these checks, it simply terminates execution,
effectively crashing. Although it is a good idea
for processes to perform these consistency checks frequently, performing
them right before committing is particularly important. Applications may also be able
to reduce the likelihood they will violate Lose-work by not committing
all their state. Applications may have knowledge of which data absolutely
must be preserved, and which data can be recomputed from an earlier (hopefully
bug-free) state. Should a bug corrupt state that is not written to stable
storage during commit, recomputing that state after a failure leaves open
the possibility of not retriggering the bug. Applications can also try to
commit as infrequently as possible. When upholding Save-work, applications
should do so with a protocol that commits less often and that leaves as
much non-determinism as possible. Some applications may be able to add
non-determinism to their execution, or they may be able to choose a non-deterministic
algorithm over a deterministic one. The application or the operating
system may also able to make some fixed non-deterministic events into transient
ones by increasing disk space or other application resource limits after
a failure. In Section 4.
we will measure how often several applications violate Lose-work in the
process of upholding Save-work. 3. Cost of Upholding Save-workIn Section 2.3.,
we presented the Save-work invariant, which applications can uphold to
guarantee consistent recovery in the presence of stop failures. However,
we have not talked about the performance penalty applications incur to
uphold it. As mentioned above, executing commits can be expensive. It may
be the case for real applications that adhering to Save-work may be prohibitively
expensive. In this section we measure the performance penalty incurred
for several real applications upholding Save-work. For this experiment we have
selected four real applications: nvi, magic, xpilot and TreadMarks. nvi
is a public domain version of the well known Unix text editor vi. magic
is a VLSI CAD tool. xpilot is a distributed, multi-user game. Finally,
TreadMarks is a distributed shared memory system. Within TreadMarks's shared
memory environment we run an N-body simulation called Barnes-Hut. Of these applications, all
but TreadMarks are interactive. We chose mainly interactive applications
for several reasons. First, interactive applications are important recipients
of failure transparency (when these applications fail there is always an
annoyed user nearby). Second, interactive applications have been little
studied in recovery literature. Finally, interactive applications can be
hard to recover: they have copious system state, non-determinism, and visible
output, all of which requiring an able recovery system. To recover these applications
we run them on top of Discount Checking, a system designed to provide failure
transparency efficiently using lightweight, full-process checkpoints [24].
Discount Checking is built on top of reliable memory provided by the Rio
File Cache [9], and lightweight transactions provided by the Vista transaction
library [23]. In order to preserve the full
user-level state of a process, Discount Checking maps the process's entire
address space into a segment of reliable memory managed by Vista. Vista
traps updates to the process's address space using copy-on-write, and logs
the before-images of updated regions to its persistent undo log. To capture
the application state in the register file (which cannot be mapped into
persistent memory), Discount Checking copies the register file into a persistent
buffer at commit time. Thus, taking a checkpoint amounts to copying the
register file, atomically discarding the undo log, and resetting page protections. Although the steps outlined
so far will allow Discount Checking to checkpoint and recover user-level
state, Discount Checking must also preserve and recover the application's
kernel state. To capture system state, the library implements a form of
copy-on-write for kernel data: it traps system calls, copies their parameter
values into persistent buffers, and then uses those parameter values to
directly reconstruct relevant kernel state during recovery. For more on
the inner workings of Discount Checking, please see [24]. As mentioned in Section 2.4.,
there exist a large variety of protocols for upholding Save-work. In order
to get a sense of which work best for our suite of applications, we implemented
seven different protocols within Discount Checking. Our core protocols
are CAND, CPVS, and CBNDVS, which we described in Section 2.4..
Recall that CAND upholds Save-work by committing immediately after every
non-deterministic event. CPVS commits just before all visible and send
events. CBNDVS commits before a visible or send event if the process has
executed a non-deterministic event since its last commit. We also added
to Discount Checking the ability to log non-deterministic user input and
message receive events to render them deterministic, as well as the ability
to use two-phase commit so one process can safely pass a dependency on
an uncommitted non-deterministic event to another process. Adding these
techniques to our core protocols yielded an additional four protocols:
CAND-LOG, CBNDVS-LOG, CPV-2PC, and CBNDV-2PC. For example, CAND-LOG executes
a commit immediately after any non-deterministic event that has not been
logged. CPV-2PC commits all processes whenever any process executes a visible,
but does not need to commit before a process does a send.
In order to implement these protocols, Discount Checking needs to get notification of an application's non-deterministic, visible, and send events. To learn of an application's non-deterministic events, Discount Checking intercepts a process's signals and non-deterministic system calls such as gettimeofday , bind , select , read , recvmsg , recv , and recvfrom . To learn of a process's visible and send events, Discount Checking intercepts calls to write , send , sendto , and sendmsg . In addition to measuring the
performance of our applications on Discount Checking on Rio, we wanted
to get a sense of how our applications performed using a disk-based recovery
system. We created a modified version of Discount Checking called DC-disk
that wrote out a redo log synchronously to disk at checkpoint time. Although
we did not add the code needed to let DC-disk truncate its redo log, or
even properly recover applications, its overhead should be representative
of what a lightweight disk-based recovery system can do. We ran our experiments on
400 MHz Pentium II computers each with 128 MB of memory (100 MHz SDRAM).
Each machine runs FreeBSD 2.2.7 with Rio and is connected to a 100 Mb/s
switched Ethernet. Rio was turned off when using DC-disk. Each computer
has a single IBM Ultrastar DCAS-34330W ultra-wide SCSI disk. All points
represent the average of five runs. The standard deviation for each data
point was less than 1% of the mean for Discount Checking, and less than
4% of the mean for DC-disk. The distributed workloads (TreadMarks and xpilot)
were both run on four computers. We simulate fast interactive rates by
delaying 100 ms between each keystroke in nvi and by delaying 1
second between each mouse-generated command in magic . We present the result of our
runs in Figure 8. For each
application we show the protocol space developed in Section 2.4..
In each application's protocol space we plot the protocol used for each
data point, and the number of checkpoints taken during the complete run
of the application when running on that protocol. For each protocol's data
point we also show the percent expansion in execution time that protocol
caused compared to an unrecoverable version of the application, first for
Discount Checking, then for DC-disk. Because xpilot is a real-time,
continuous program we report its performance as the frame rate it can sustain
rather than runtime overhead. Higher frame rates indicate better interactivity,
with full speed being 15 frames-per-second. xpilot's number of checkpoints
is given as the largest checkpointing frequency (in checkpoints per second)
amongst its processes. We can make a number of interesting
observations based on these results. As expected, commit frequency generally
decreases, and performance increases, with radial distance from the origin.
The sole exception to this rule is xpilot, where having all processes commit
whenever any one of them wants to execute a visible event (as is done in
protocols using two-phase commit) results in a net increase in commit frequency. Despite the fact that several
of these applications generate many commits, there is at least one protocol
for each application with very low overhead for Discount Checking. We conclude
that the cost of upholding Save-work using Discount Checking on these applications
is low. For all the interactive applications,
the overhead of using DC-disk is not prohibitive. We see overhead of 12%
and 27% for nvi and magic respectively. xpilot is able to sustain a usable
9 frames per second. On the other hand, no protocol for DC-disk was able
to keep up with TreadMarks. From our experiments, we conclude that Save-work
can be upheld with a disk-based recovery system for many interactive applications
with reasonably low overhead. We observe that the protocols
that perform best for each application are the ones that exploit the infrequent
class of events for that application in deciding when to commit. For example,
TreadMarks has very few visible events, despite having copious non-deterministic
and send events. For it, the 2PC protocols which let it commit only for
the rare visible events are the big win. While overhead is low for
many applications, we can conceive of applications for which Save-work
incurs a large performance overhead. These applications would have copious
visible and non-deterministic events--that is, no rare class of events--and
they would be compute bound rather than user bound. Applications that might
fall into this category include interactive scientific or engineering simulation,
online transaction processing, and medical visualization. 4. Measuring Conflict between the Save-work and Lose-work InvariantsGuaranteeing consistent recovery
in the presence of stop and propagation failures requires upholding both
the Save-work and Lose-work invariants. Unfortunately, some failure scenarios
make it impossible to uphold both invariants simultaneously. For example, consider the
failure timeline shown in Figure 9. In this timeline, the application executes a transient non-deterministic
event that causes it to execute down a code path containing a bug. The
application eventually executes the buggy code (shown as "fault activation"),
then correctly executes a visible event. After this visible event, the
program crashes. Section 2.5.'s
coloring algorithm shows that the entire execution path from the transient
non-deterministic event to the crash forms a dangerous path, along which
the Lose-work invariant prohibits a commit. Unfortunately, the Save-work
invariant specifically requires a commit between the transient non-deterministic
event and the visible event. For this application, both invariants cannot
be upheld simultaneously. Some applications may have
bugs that prevent upholding Lose-work even without committing to uphold
Save-work. For example, many applications contain repeatable bugs (so called,
"Bohrbugs"[13]). With these faults it is possible to execute from the initial
state of the program to the bug without ever executing a transient non-deterministic
event. In other words, the dangerous path resulting from the bug extends
all the way back to the initial state of the program. And since the initial
state of any application is always committed, applications with Bohrbugs
inherently violate Lose-work. In this section, we endeavor
to examine how often in practice faults cause a fundamental conflict between
the Save-work and Lose-work invariants. Our focus is on software faults
(both in the application and operating system), which field studies and
everyday experience teach is the dominant cause of failures today [13]. 4.1. Application faults
We would like to measure how often upholding Save-work forces an application to commit on a dangerous path, like the application depicted in Figure 9. We divide this problem into three subproblems. First, how often does an application bug create a dangerous path beginning at the start state of the application? As described above, this scenario arises from Bohrbugs in the application. Second, given an application fault that does depend on a transient non-deterministic event (a Heisenbug), how often is the application forced to commit between the transient non-deterministic event at the beginning of the dangerous path and the fault activation? Third, how often is the application forced to commit between the fault activation and the crash? We examine this third question first using a fault-injection study. Our strategy is to force crashes
of real applications, recover the applications, and measure after the fact
whether any of their commits to uphold Save-work occurred between fault
activation and the crash. We induce faults in the application by running
a version of the application with changes in the source code to simulate
a variety of programming errors. These errors include actions like overwriting
random data in the stack or heap, changing the destination variable, neglecting
to initialize a variable, deleting a branch, deleting a random line of
source code, and off-by-one errors in conditions like >= and <. See
[6] for more information on our fault model. We only consider runs where
the program crashes. Checkpointing and recovery
for the applications is provided by Discount Checking using the CPVS protocol.
CPVS is the best protocol possible for not violating Lose-work for non-distributed
applications. For our experiments, we use two applications: the Unix text
editor nvi , and postgres , a large, publicly available relational
database. These two applications differ greatly in their code size and
amount of data they touch while executing. We detect a run in which the
application commits between fault activation and the crash by instrumenting
Discount Checking to log each fault activation and commit event. If the
program commits after activating the fault, it has violated the Lose-work
invariant. We also conduct an end-to-end check of this criteria by suppressing
the fault activation during recovery, recovering the process, and trying
to complete the run. As expected, we found that runs recovered from crashes
if and only if they did not commit after fault activation. We collected data from approximately
50 crashes for each fault type. Table 1 shows the fraction of crashes that violated the Lose-work invariant
by committing after fault activation. For both nvi and postgres
, approximately 35% of faults caused the process to commit along this portion
of the dangerous path. While not included in the table, 7-9% of the runs
did not crash but resulted in incorrect program output.
We next turn our attention
to question one, namely, for what fraction of bugs does the dangerous path
extend back to the initial state of the program? That is, of the bugs users
encounter, what portion are deterministic (Bohrbugs), and what portion
depend on a transient non-deterministic event (Heisenbugs)? Although it
is difficult to measure this fraction directly, several prior studies have
attempted to shed light on this issue. Chandra and Chen showed that
for Apache, GNOME, and MySQL, three large, publicly available software
packages, only 5-15% of the bugs in the developer's bug log were Heisenbugs
(for shipping versions of the applications) [7]. The remaining bugs were
Bohrbugs. Most of these deterministic bugs resulted from untested boundary
conditions (e.g. an older version of Apache crashed when the URL was too
long). Several other researchers have found a similarly low occurrence
(5-29%) of application bugs that depend on transient non-deterministic
events like timing [20, 29, 30]. Note that these results conflict with
the conventional wisdom that mature code is populated mainly by Heisenbugs--it
has been held that the easier-to-find Bohrbugs will be captured more often
during development [13, 17]. It appears that for non-mission-critical applications,
the current software culture tolerates a surprising number of deterministic
bugs. We have yet to tackle the
second question, which asks how often an application is forced to commit
on the dangerous path between the transient non-deterministic event and
fault activation (see Figure 9).
Unfortunately, we are unable to measure this frequency using our fault-injection
technique because no realistic model exists for placing injected bugs relative
to an application's transient non-deterministic events. However, as we
will see, the case for generic recovery from application failures is already
sufficiently discouraging, even optimistically assuming no commits on this
portion of the dangerous path. We would like to compose these
separate experimental results in order to illuminate the overarching question
of this section. Our fault-injection study shows that nvi and postgres
violate Lose-work in at least 35% of crashes from non-deterministic faults.
If we assume the same distribution of deterministic and non-deterministic
bugs in nvi and postgres as found in Apache, GNOME, and MySQL by Chandra
and Chen, these non-deterministic faults make up only 5-15% of crashes.
Therefore, Lose-work is upheld in at most 65% of 15%, or 10% of application
crashes. Lose-work and Save-work appear to conflict in the remaining 90%
of failures by these applications. While extrapolating other applications'
fault distributions to nvi and postgres is somewhat questionable, as is
generalizing to all applications from the measurement of two, these preliminary
results raise serious questions about the feasibility of generic recovery
from propagation failures. 4.2. Operating systems faultsAlthough failures due to application
faults appear to frequently violate Lose-work, we can hope for better news
for faults in the operating system. In contrast to application faults,
not all operating system faults cause propagation failures: some crash
the system before they affect application state. Commits at any time by
the application are okay in the presence of these stop failures. Thus if
failures by the operating system usually manifest as stop failures, we
would rarely observe system failures causing Lose-work violations. We wanted to measure the fraction
of operating system failures for which applications are able to successfully
recover. This fraction will include cases where the operating system experienced
a stop failure, as well as cases in which the system failure was a propagation
failure and the application did not violate Lose-work. In order to perform this measurement,
we again use a fault-injection study. This time we inject faults into the
running kernel rather than into the application [9]. We again ran nvi and postgres
with Discount Checking upholding Save-work using CPVS. For each run, we
started the application and injected a particular type of fault into the
kernel. We discarded runs in which neither the system nor the application
crashed. If either the operating system or the application crashed, we
rebooted the system and attempted to recover the application. We repeated
this process until each fault type had induced approximately 50 crashes.
The results of this experiment are shown in Table 2.
Of the 350 operating system
crashes we induced for each application, we found that nvi failed to properly
recover in 15% of crashes. postgres did better, only failing to recover
3% of the time. These numbers are encouraging: application-generic recovery
is likely to work for operating systems failures, despite the challenge
of upholding Lose-work. If we assume that all propagation
failures will violate Lose-work with the probabilities in Table Table
1: (regardless of whether the propagation failure began in the operating
system or application), we can infer how often system failures manifest
as propagation failures in our experiments. Combining our application crash
results with our operating system crash results implies that for nvi, 41%
of system failures were propagation failures. For postgres, 10% of system
failures manifest as propagation failures. We hypothesize that the proportion
of propagation failures differs for the two applications because of the
different rate at which they communicate with the operating system: the
non-interactive version of nvi used in our crash tests executes almost
10 times as many system calls per second as postgres executes. 5. Related WorkMany fault-tolerant systems
are constructed using transactions to aid recovery. Transactions simplify
recovery by grouping separate operations into atomic units, reducing the
number of states from which an application must recover after a crash.
However, the programmer must still bear the responsibility for building
recoverability into his or her applications, a task that is difficult even
with transactions. We have focused on higher-level application-generic
techniques that absolve programmers from adding recovery abilities to their
software. However, we use transactions to implement our abstraction. A number of researchers have
endeavored to build systems that provide some flavor of failure transparency
for stop failures [3, 4, 5, 11, 14, 21, 25, 26]. Our work extends their
work by analyzing propagation failures as well. The theory of distributed
recovery has been studied at length [10]. Prior work has established that
committed states in distributed systems must form a consistent cut to prevent
orphan processes [8], that recoverable systems must preserve a consistent
cut before visible events [28], and that non-determinism bounds the states
preserved by commits [11, 16]. Our Save-work invariant is equivalent to
the confluence of these prior results. The Save-work invariant contributes
to recovery theory by expressing the established rules for recovery in
a single, elemental invariant. Viewing consistent recovery through the
lens of Save-work, we exposed the protocol space and the relationships
between the disparate protocols on it, as well as several new protocols. To the best of our knowledge,
no prior work has proposed an invariant for surviving propagation failures
that relates all relevant events in a process, nor has any prior work attempted
to evaluate the fraction of propagation failures for which consistent recovery
is not possible. CAND, CPVS, and CBNDVS all
bear a resemblance to simple communication-induced checkpointing protocols
(CIC) [1]. However there are some important differences. First, all CIC
protocols assume no knowledge of application non-determinism. As a result,
they are forced to roll back any process that has received a message from
an aborted sender. Commits under these protocols serve primarily to limit
rollback distance, and to prevent the domino effect. In contrast, our protocols
all to varying degrees make use of knowledge of application non-determinism.
Rather than abort the receivers of lost messages, they allow senders to
deterministically regenerate the messages. Under our protocols, only failed
processes are forced to roll back. Recovery systems often depend
on the assumption that applications will not commit faulty state--a so
called "fail-stop assumption" [27]. Our examination of propagation failures
amounts to a fine parsing of the traditional fail-stop assumption in which
we consider a single commit's ability to preserve not just past execution,
but all future execution up to the next non-deterministic event. Making
a fail-stop assumption in the presence of propagation failures is the same
as assuming that applications can safely commit at any time without violating
the Lose-work invariant. 6. ConclusionThe lure of operating systems
that conceal failures is quite powerful. After all, what user or programmer
wants to be burdened with the complexities of dealing with failures? Ideally,
we could handle all those complexities once and for all in the operating
system. Our goal with this paper has
been to explore the subject of failure transparency, looking at what it
takes to provide it and exposing the circumstances where providing it is
not possible. We find that providing failure transparency in general involves
upholding two invariants, a Save-work invariant which constrains when an
application must preserve its work before a failure, and a Lose-work invariant
which constrains how much work the application has to throw away after
a failure. For stop failures, which do
not require upholding Lose-work, the picture is quite rosy. We show that
Save-work can be efficiently upheld for a variety of real applications.
Using a transparent recovery system based on reliable memory, we find overheads
of only 0-12% for our suite of real applications. We also find that disk-based
recovery makes a credible go of it, with interactive applications experiencing
only moderate overhead. Unfortunately, the picture
is somewhat bleaker for surviving propagation failures. Guaranteeing that
an application can recover from a propagation failure requires upholding
our Lose-work invariant, and Save-work and Lose-work can directly conflict
for some fault scenarios. In our measurements of application faults in
nvi and postgres, upholding Save-work causes them to violate Lose-work
for at least 35% of crashes. Even worse, studies have suggested that 85-95%
of application bugs today cause crashes that violate the Lose-work invariant
by extending the dangerous path to the initial state. We conclude that providing
failure transparency for stop failures alone is feasible, but that recovering
from propagation failures requires help from the application. Applications
can help by performing better error detection, masking errors through N-version
programming, reducing commit frequency by allowing the loss of some visible
events, or reducing the comprehensiveness of the state saved by the recovery
system. Our results point to interesting future work. Since pure application-generic
recovery is not always possible, what is the proper balance between generic
recovery services provided by the operating system and application-specific
aids to recovery provided by the programmer? 7. AcknowledgementsMany people have thoughtfully
contributed to this work. Thank you to the anonymous reviewers for their
helpful feedback. Special thanks to Miguel Castro and Paul Resnick for
their contributions to the theory. Thanks to George Dunlap for adding support
for our user-level TCP to the XFree86 server. Finally, thanks to Christine
Subietas, WRL's administrator. This research was supported
in part by NSF grant MIP-9521386, AT&T Labs, IBM University Partnership
Program, and Intel Corporation. Peter Chen was also supported by an NSF
CAREER Award (MIP-9624869). 8. Software AvailabilityThe Rio version of the FreeBSD
2.2.7 kernel, as well as Vista and Discount Checking are all available
for download at https://www.eecs.umich.edu/Rio. 9. References[1] Lorenzo Alvisi, Elmootazbellah
Elnozahy, Sriram Rao, Syed Amir Husain, and Asanka Del Mel. An Analysis
of Communication-Induced Checkpointing. In Proceedings of the 1999 International
Symposium on Fault-Tolerant Computing (FTCS), June 1999. [2] Lorenzo Alvisi, Bruce
Hoppe, and Keith Marzullo. Nonblocking and Orphan-Free Message Logging
Protocols. In Proceedings of the 1993 International Symposium on Fault-Tolerant
Computing (FTCS), pages 145-154, 1994. [3] Joel F. Bartlett.
A NonStop Kernel. In Proceedings of the 1981 Symposium on Operating System
Principles, pages 22-29, December 1981. [4] Anita Borg, Wolfgang
Blau, Wolfgang Graetsch, Ferdinand Herrman, and Wolfgang Oberle. Fault
Tolerance Under UNIX. ACM Transactions on Computer Systems, 7(1):1-24,
February 1989. [5] Thomas C. Bressoud
and Fred B. Schneider. Hypervisor-based Fault-tolerance. In Proceedings
of the 1995 Symposium on Operating Systems Principles, pages 1-11, December
1995. [6] Subhachandra Chandra.
Evaluating the Recovery-Related Properties of Software Faults. PhD thesis,
University of Michigan, 2000. [7] Subhachandra Chandra
and Peter M. Chen. Whither Generic Recovery from Application Faults? A
Fault Study using Open-Source Software. In Proceedings of the 2000 International
Conference on Dependable Systems and Networks (formerly FTCS), June 2000. [8] K. Mani Chandy and
Leslie Lamport. Distributed Snapshots: Determining Global States in Distributed
Systems. ACM Transactions on Computer Systems, 3(1):63-75, February 1985. [9] Peter M. Chen, Wee
Teck Ng, Subhachandra Chandra, Christopher M. Aycock, Gurushankar Rajamani,
and David Lowell. The Rio File Cache: Surviving Operating System Crashes.
In Proceedings of the 1996 International Conference on Architectural Support
for Programming Languages and Operating Systems (ASPLOS), October 1996. [10] Elmootazbellah N.
Elnozahy, Lorenzo Alvisi, Yi-Min Wang, and David B. Johnson. A Survey of
Rollback-Recovery Protocols in Message-Passing Systems. Technical Report
CMU-CS-99-148, Carnegie Mellon University, June 1999. [11] Elmootazbellah N.
Elnozahy and Willy Zwaenepoel. Manetho: Transparent Rollback-Recovery with
Low Overhead, Limited Rollback, and Fast Output Commit. IEEE Transactions
on Computers, C-41(5):526-531, May 1992. [12] Jim Gray. Operating
Systems: An Advanced Course. Springer-Verlag, 1978. Notes on Database Operating
Systems. [13] Jim Gray. Why do
computers stop and what can be done about it? In Proceedings of the 1986
Symposium on Reliability in Distributed Software and Database Systems,
pages 3-12, January 1986. [14] Y. Huang, P. Y.
Chung, C. M. R. Kintala, D. Liang, and C. Wang. NT-SwiFT: Software-implemented
Fault Tolerance for Windows-NT. In Proceedings of the 1998 USENIX WindowsNT
Symposium, August 1998. [15] David B. Johnson
and Willy Zwaenepoel. Sender-Based Message Logging. In Proceedings of the
1987 International Symposium on Fault-Tolerant Computing, pages 14-19,
July 1987. [16] David B. Johnson
and Willy Zwaenepoel. Recovery in Distributed Systems Using Optimistic
Message Logging and Checkpointing. In Proceedings of the 1988 Symposium
on Principles of Distributed Computing (PODC), pages 171-181, August 1988. [17] Zbigniew T. Kalbarczyk,
Saurabh Bagchi, Keith Whisnant, and Ravishankar K. Iyer. Chameleon: A Software
Infrastructure for Adaptive Fault Tolerance. IEEE Transactions on Parallel
and Distributed Systems, 10(6):560-579, June 1999. [18] Richard Koo and
Sam Toueg. Checkpointing and Rollback-Recovery for Distributed Systems.
IEEE Transactions on Software Engineering, SE-13(1):23-31, January 1987. [19] Leslie Lamport.
Time, Clocks, and the Ordering of Events in a Distributed System. Communications
of the ACM, 21(7):558-565, July 1978. [20] Inhwan Lee and Ravishankar
K. Iyer. Faults, Symptoms, and Software Fault Tolerance in the Tandem GUARDIAN
Operating System. In Proceedings of the 1993 International Symposium on
Fault-Tolerant Computing (FTCS), pages 20-29, 1993. [21] David Lomet and
Gerhard Weikum. Efficient Transparent Application Recovery in Client-Server
Information Systems. In Proceedings of the 1998 ACM SIGMOD International
Conference on Management of Data, pages 460-471, June 1998. [22] David E. Lowell. Theory and Practice of Failure Transparency. PhD thesis, University of Michigan, 1999. [23] David E. Lowell and Peter M. Chen. Free Transactions with Rio Vista. In Proceedings of the 1997 Symposium on Operating Systems Principles, October 1997. [24] David E. Lowell and Peter M. Chen. Discount Checking: Transparent, Low-Overhead Recovery for General Applications. Technical Report CSE-TR-410-99, University of Michigan, December 1998. [25] James S. Plank, Micah Beck, and Gerry Kingsley. Libckpt: Transparent Checkpointing under Unix. In Proceedings of the Winter 1995 USENIX Conference, January 1995. [26] Michael L. Powell and David L. Presotto. PUBLISHING: A Reliable Broadcast Communication Mechanism. In Proceedings of the 1983 Symposium on Operating Systems Principles, October 1983. [27] Fred B. Schneider. Byzantine Generals in Action: Implementing Fail-Stop Processors. ACM Transactions on Computer Systems, 2(2):145-154, May 1984. [28] Robert E. Strom and Shaula Yemini. Optimistic Recovery in Distributed Systems. ACM Transactions on Computer Systems, 3(3):204-226, August 1985. [29] Mark Sullivan and R. Chillarege. Software Defects and Their Impact on System Availability-A Study of Field Failures in Operating Systems. In Proceedings of the 1991 International Symposium on Fault-Tolerant Computing, June 1991. [30] Mark Sullivan and Ram Chillarege. A Comparison of Software Defects in Database Management Systems and Operating Systems. In Proceedings of the 1992 International Symposium on Fault-Tolerant Computing, pages 475-484, July 1992. [31] Yi-Min Wang. Maximum and minimum consistent global checkpoints and their applications. In Proceedings of the 1995 Symposium on Reliable Distributed Systems, pages 86-95, September 1995. |
|
This paper was originally published in the
Proceedings of the 4th USENIX OSDI Symposium,
October 23-25, 2000, San Diego, California, USA.
Last changed: 16 Jan. 2002 ml |
|