 , Cherniavsky [4],
they do provide a basis for some validation of complexity metrics short
of using experimental data. As shown by Weyuker,
with such properties it is possible to filter out measurements with
undesirable properties.
, Cherniavsky [4],
they do provide a basis for some validation of complexity metrics short
of using experimental data. As shown by Weyuker,
with such properties it is possible to filter out measurements with
undesirable properties.




Weyuker[25] listed a set of properties (necessary
but not sufficient) that are
desired of a complexity measure for procedural programs. Although
these properties have been criticized , Cherniavsky [4],
they do provide a basis for some validation of complexity metrics short
of using experimental data. As shown by Weyuker,
with such properties it is possible to filter out measurements with
undesirable properties.
, Cherniavsky [4],
they do provide a basis for some validation of complexity metrics short
of using experimental data. As shown by Weyuker,
with such properties it is possible to filter out measurements with
undesirable properties.
We have not used all of the properties defined by Weyuker. These properties were defined for metrics intended to measure procedural programs and, as such, define some constraints that are not applicable to object-oriented software. In particular, assuming a single entry, single exit module does not address the object-oriented aggregation of methods into a class. Where there is an obvious mismatch between our goals and the properties we have omitted the property.
In the list of properties below, E, F and G represent classes
and the complexity of E computed by an ideal measure
is represented by 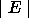 .
Classes can be concatenated either by inheritance
or composition (collaboration).
When a class F inherits from another class E, we depict
the resulting subclass as
.
Classes can be concatenated either by inheritance
or composition (collaboration).
When a class F inherits from another class E, we depict
the resulting subclass as 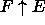 Also, when a class E
collaborates with another class F, the collaborating class is shown by
Also, when a class E
collaborates with another class F, the collaborating class is shown by
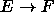 . Two classes are said to be equivalent
if they have the same behaviour for the classes.
. Two classes are said to be equivalent
if they have the same behaviour for the classes.
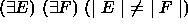 .
.
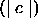 . Each series in the
combination represents a particular set of attribute Visibilities. Since
there is a finite number of distinct series, the number of classes with the
Visibility Component, c is finite.
. Each series in the
combination represents a particular set of attribute Visibilities. Since
there is a finite number of distinct series, the number of classes with the
Visibility Component, c is finite.
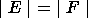 .
.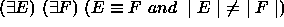 .
.
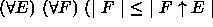 ).
).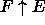 is greater than or equal to the
original complexity of F.
Due to the inheritance, class F has access to all the public and
protected data attributes of E.
This increase in the implicit parameters of class F making the
measure sensitive to inheritance.
is greater than or equal to the
original complexity of F.
Due to the inheritance, class F has access to all the public and
protected data attributes of E.
This increase in the implicit parameters of class F making the
measure sensitive to inheritance.
Since our measure happens to satisfy all the above properties it can be considered to have passed a significant part of the theoretically validation process. The measure has been tested againt those axioms proposed by Weyuker that are applicable to both procedural and object-oriented software systems.


