COOTS '01 Paper
[COOTS '01 Tech Program Index]
| Pp. 61–76 of the Proceedings |  |
Distributed Garbage Collection for
Wide Area Replicated Memory
Alfonso Sánchez Luís Veiga Paulo Ferreira
INESC/IST,
Rua Alves Redol No 9,
Lisboa 1000-029, Portugal
{alfonso.sanchez, luis.veiga, paulo.ferreira}@inesc.pt
Abstract
It is well known that distributed systems pose serious difficulties
concerning memory management: when done manually, it leads to memory
leaks and dangling references causing applications to fail.
We address this problem by presenting a distributed garbage collection
(DGC) algorithm for distributed systems supporting replicated data
over wide area networks.
Current DGC algorithms are not well suited for such systems because
either (i) they do not consider the existence of replication, or (ii)
they impose severe constraints on scalability by requiring causal
delivery to be provided by the underlying communication layer.
Our algorithm solves these problems by (i) adapting classical
reference-counting DGC algorithms that were conceived for
non-replicated systems (e.g. indirect reference-counting, SSP chains,
etc.), and (ii) improving our previous algorithm for replicated
systems (i.e. Larchant).
The result is a DGC algorithm that, besides being correct in presence
of replicated data and independent of the protocol that maintains
such replicas coherent among processes, it does not require causal
delivery to be ensured by the underlying communications support.
In addition, it has minimal performance impact on applications.
1 Introduction
Modern distributed applications sharing long-term data over many places,
geographically separated, appear each day.
Typical examples are found in the fields of concurrent engineering,
cooperative applications, etc.
Manual memory management is extremely difficult when developing the
aforementioned distributed applications.
The reason is that graphs of reachability are large, widely distributed
and frequently modified through assignment operations executed by
applications.
In addition, data replicated in many processes is not necessarily
coherent making manual memory management much harder.
For these reasons it is impossible to do manual memory management
without generating dangling references and/or memory leaks.
Automatic memory management, also known as Garbage Collection (GC), is
the single realistic option which is able to maintain referential
integrity (i.e. no dangling references or memory leaks) in Wide Area
Replicated Memory (WARM) systems.
As a result, program reliability and programmer productivity are
clearly improved.
1.1 Shortcomings of Current Solutions
Current DGC algorithms [1,15] are
not well suited for WARM systems based on data-shipping because of the
following drawbacks: either (i) they do not consider the existence of
replication, or (ii) they impose severe constraints on scalability by
requiring causal delivery to be supported by the underlying
communication layer.
The first drawback, i.e. not considering replicated data, concerns all
the classical DGC algorithms that were designed for function-shipping
based systems, such as Indirect Reference Counting
(IRC) [14] or SSP Chains [16].
As a matter of fact, these algorithms are not safe in presence of
replicated data, as explained now.
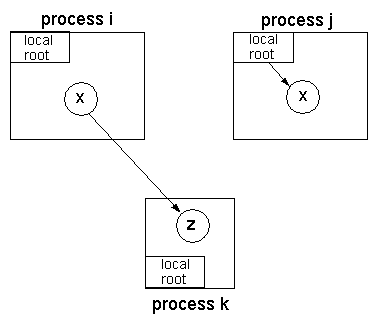
Figure 1: Safety problem of current DGC algorithms which do not handle replicated data: z is erroneously considered unreachable.
Consider Figure 1 in which an object x is
replicated in processes i and j; each replica of x is noted
xi and xj, respectively.
Now, suppose that xi contains a reference to an object z in
another process k, xj points to no other object, xi
is locally unreachable and xj is locally
reachable1.
Then, the question is: should z be considered garbage?
Classical DGC algorithms consider that z is effectively garbage.
However, this is wrong because, in a WARM system, it is possible for
an application in j to ``acquire'' a replica of x from some other
process, in particular, xi2.
Thus, the fact that xi is locally unreachable in process
i does not mean that x is globally unreachable; as a
matter of fact, xi contents can be accessed by an application
in process j by means of an ``acquire''.
Therefore, in a WARM system, a target object z is considered
unreachable only if the union of all the replicas of the source
object, x in this example, do not refer to it.
We call this the Union Rule (more details in
Section 4.2.2).
The second drawback, i.e. imposing severe constraints on scalability,
affects current DGC algorithms conceived for WARM systems, such as
Larchant [5,10].
As a matter of fact, such algorithms are not scalable because they
require the underlying communication layer to support causal delivery.
So, in conclusion, classical DGC algorithms, such as IRC and SSP
Chains, are not safe for WARM systems but promise to be scalable, in
particular, do not require causal delivery; on the other hand, WARM
specific DGC algorithms, such as Larchant, deals safely with
replication but lacks scalability.
Thus, the main contribution of this work is the following: showing how
classical DGC algorithms (conceived for function-shipping based
systems) can be extended to handle replication while keeping their
scalability.
We do not address the issue of fault-tolerance, i.e. it is out of the
scope of the paper how the algorithm behaves in presence of
communication failures and processes crashes.
However, solutions similar to those found in classical DGC algorithms
can also be applied (for example, leasings as in RMI [18].
This paper is organized as follows.
In Section 2 we present the model of a WARM for which the DGC was
defined.
The DGC algorithm is described in Sections 3 and 4.
Section 5 highlights some of the most important
implementation aspects.
Section 6 presents some performance results from a real
application.
The paper ends with some related work and conclusions in
Section 7 and 8, respectively.
2 WARM Model
This section presents the model for Wide Area Replicated Memory (WARM).
A WARM is a replicated distributed memory spanning several processes.
These processes are connected in a network and communicate only by
asynchronous message passing.
We indicate that a message M has been sent from process i to
process j as < send.M > i ® j; the delivery of that
message is noted < deliver.M > i ® j.
In a WARM, the only way to share information is by replication of
data, which can be done with a DSM based
mechanism[12].
Thus, processes do not use Remote Procedure Call (RPC) to access
remote data.
It's worthy to note that application code inside a process never
sends messages explicitly.
Instead, application code access data always locally; transparently to
the application code, the WARM runtime system is responsible to
replicate data locally when needed.
Each participating process in the WARM encloses, at least, the
following entities: memory, mutator3, and a coherence engine.
In our WARM model, for each one of these entities, we consider only
the operations that are relevant for GC purposes.
We believe that our model is sufficiently general to describe most
distributed systems supporting wide area applications using data
shipping.
This model clearly defines the environment for which the DGC algorithm
is conceived.
2.1 Memory Organization
An object is defined to be a consecutive sequence of bytes in
memory.
Applications can have different views of objects and can see
them as language-level class instances, memory pages, data base
records, web pages, etc.
Objects can contain references pointing to other objects.
An outgoing inter-process reference is a reference to a target
object in a different process.
An incoming inter-process reference is a reference to an object
that is pointed from a different process.
Our model does not restrict how references are actually implemented.
They can be virtual memory pointers, URLs, etc.
An object is said to be reachable if it is attainable directly
or indirectly from a GC root (defined in Section 3.1).
An object is said to be unreachable if there is no reference
path (direct or indirect) from a GC root leading to that object.
The unit for coherence is the object.
Any object can be replicated (i.e. cached) in any process.
A replica of object x in process i is noted xi.
Each process can cache a replica of any object for reading or writing
according to the coherence protocol being used.
2.2 Mutator model
The single operation executed by mutators, which is relevant for GC
purposes, is reference assignment; this is the only way for
applications to modify the graph of objects.
The reference assignment operation executed by a mutator in some
process i is noted < x : = y > i.
This means that a reference contained in object x is assigned to
the value of a reference contained in object y.4
This assignment operation results in the creation of a new
inter-process reference from x to z, as illustrated in
Figure 2.
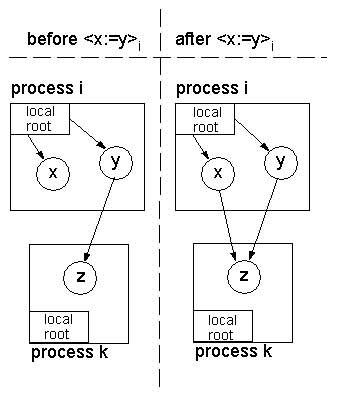
Figure 2: Creation of a new inter-process reference to object z
through an assignment operation.
Obviously, other assignments can delete references transforming objects
in garbage.
For example, in Figure 2, if the mutators in processes
i and j perform < x : = 0 > i and < y : = 0 > i, object
z becomes unreachable, i.e. garbage, given that there are no
references pointing to it.
In conclusion, assignment operations (done by mutators) modify the
object graph either creating or deleting references.
An object becomes unreachable when the last reference to it
disappears; when this occurs, such an object can be safely reclaimed
by the garbage collector because there is no possibility for any
process to access it.
2.3 Coherence Model
The coherence engine is the entity of the WARM that is responsible to
manage the coherence of replicas.
The coherence protocol effectively used varies from system to system
and depends on several factors such as the number of replicas, distances
between processes, and others.
However, the only coherence operation, which is relevant for GC
purposes, is the propagation of an object, i.e. the replication of
an object from one process to another.
The propagation of an object y from process i to process j is
noted propagate(y)i ® j.
We assume that any process can propagate a replica into itself as long
as the mutator causing the propagation holds a reference to the object
being propagated.
Thus, if an object x is locally unreachable in process i, the
mutator in that process can not force the propagation of x to some
other process; however, if some other process j holds a reference
to x, it can request x to be propagated from i to j (as
occurs in Figure 1).

Figure 3: inPropList and outPropList internal data.
We assume that, in each process, the coherence engine holds two data
structures, called inPropList and outPropList; these
indicate the process from which each object has been propagated,
and the processes to which each object has been propagated,
respectively 5. Thus, each entry
of the inPropList/outPropList contains the following
information (see Figure 3):
- propObj - the reference of the object that has been
propagated into/to a process;
- propProc - the process from/to which the object
propObj has been propagated;
- sentUmess/recUmess - bit indicating if a unreachable
message (more details in Section 3.2) has been
sent/received.
When an object is propagated to a process we say that its enclosed
references are exported from the sending process to the
receiving process; on the receiving process, i.e. the one receiving
the propagated object, we say that the object references are
imported.
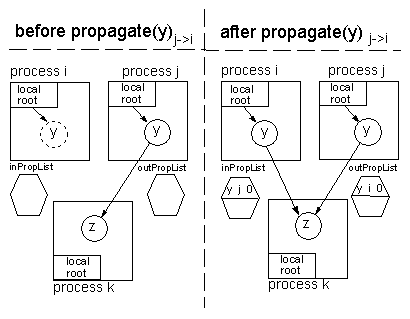
Figure 4: Coherence engine propagates object y from process j
to process i. The dashed line of yi means that initially, in
process i, y is not yet replicated in i.
Figure 4 illustrates the effect of a propagation.
Object z has no replicas.
Initially, only process j caches a replica of y; thus, both
outPropList and inPropList of processes j and i are
empty.
In addition, yj points to z.
After y has been replicated from process j to process i, a
new inter-process reference from yi to z is created; this
is due to the fact that the reference to z was exported
from process j to (be imported by) process i.
The inPropList and outPropList reflect this situation.
In order to understand how the DGC algorithm works it is important to
emphasize the following aspects concerning the creation of
inter-process references.
The only way a process can create an inter-process reference is
through the execution of only two operations: (i) reference
assignment, which is performed explicitly by the mutator, and (ii)
object propagation, which is performed by the coherence engine in
order to allow the mutator to access some object6.
3 Distributed Garbage Collection Algorithm
In this section we describe the DGC algorithm and its data structures.
Then, in Section 4 we go into more detail by describing a
prototypical example which addresses all the aspects of the DGC algorithm.
The DGC algorithm is an hybrid of tracing and reference-counting.
Thus, each process has two GC components: a local tracing
collector, and a distributed collector.
Each process does its local tracing independently from any other
process.
The local tracing can be done by any mark-and-sweep based collector.
The distributed collectors, based on reference-counting, work together
by changing asynchronous messages, as described in the following
sections.
In the rest of the paper we focus on distributed collection.
3.1 Data Structures
A stub describes an outgoing inter-process reference, from a
source process to a target process.
A scion describes an incoming inter-process reference,
from a source process to a target process.
It is important to note that stubs and scions do not impose any
indirection on the native reference mechanism.
In other words, they do not interfere either with the structure of
references or the invocation mechanism.
They are simply GC specific auxiliary data structures.
A stub stores in its internal data structures the following
information:
- OutRef - the reference of the target object;
- SourceObj - the reference of the local object
containing the outgoing inter-process reference;
- Scion - the identification of the corresponding scion;
and
- Chain - the identification of a stub or a scion in the
same process.
A scion stores in its internal data structures the following
information:
- InRef - the reference of the target object;
- Stub - the identification of the corresponding stub;
and
- Chain - the identification of a stub or a scion in the
same process.
Finally, a process's GC root includes: (i) the local root,
i.e. stacks and static variables, (ii) the set of scions of that
process, and (iii) the lists inPropList and outPropList.
3.2 Algorithm
The local and distributed collectors depend on each other to perform
their job in the following way.
A local collector running inside a process traces the object graph
locally cached; the starting point of the trace is the process's GC
root.
A local tracing generates a new set of stubs; it is based on this new
set that the distributed collector, in that process, may decide to
update remote scions in other processes.
3.2.1 Local Collector
The local collector starts the graph tracing from the process's local
root and set of scions.
For each outgoing inter-process reference it creates a stub in the new
set of stubs.
Once this tracing is completed, every object locally reachable by the
mutator has been found (e.g. marked, if a mark-and-sweep algorithm is
used); objects not yet found are locally unreachable; however, they
can still be reachable from some other process holding a replica of,
at least, one of such objects (as is the case of xi in
Figure 1).
To prevent the erroneous deletion of such objects, the collector
traces the objects graph from the lists inPropList and
outPropList, and performs as follows.
- When a locally reachable object (previously discovered by the
local collector) is found, the tracing along that reference path ends.
- When an outgoing inter-process reference is found the
corresponding stub is created in the new set of stubs.
- For an object which is reachable only from the inPropList,
a message unreachable is sent to the site from where that object
has been propagated; this sending event is registered by changing a
sentUmess bit in the corresponding inPropList entry from 0
to 1.7
When a unreachable message reaches a process, this delivery
event is registered by changing a recUmess bit in the
corresponding outPropList entry from 0 to 1.
- For an object which is reachable only from the
outPropList, and the enclosing process has already received a
unreachable message from all the processes to which that object has
been previously propagated, a reclaim message is sent to all
those processes and the corresponding entries in the outPropList
are deleted; otherwise, nothing is done.
When a process receives a reclaim message it deletes the
corresponding entry in the inPropList.
| message | sent/received by | sent when |
| unreachable | LGC/DGC | object replica is reachable only from the inPropList |
| reclaim | LGC/DGC | all object replicas are reachable only from the inPropLists |
| newSetStubs | DGC/DGC | a new set of stubs is available |
Table 1:
GC related messages.
3.2.2 Distributed Collector
The main ideas behind the DGC algorithm can be summarized as follows.
- As already mentioned, an object can be reclaimed only when all
its replicas are no longer reachable. This is ensured by tracing the
objects graph from the lists inPropList and outPropList;
objects that are reachable only from these lists are not locally
reachable (i.e. by the local mutator); however, they can not be
reclaimed without ensuring their global unreachability, i.e. that none
of their replicas are accessible. This will be explained in detail in
the following section.
- The DGC algorithm is independent of the particular coherence
protocol implemented by the coherence engine.
In other words, the DGC algorithm does not require waiting for replicas
to be coherent.
- Whatever the coherence protocol, there is only one interaction with
the DGC algorithm.
This interaction is twofold: (i) immediately before a propagate
message is sent, the references being
exported (contained in the propagated object) must be found in order
to create the corresponding scions, and
(ii) immediately before a propagate message is delivered, the outgoing
inter-process references being imported must be found in order
to create the corresponding local stubs, if they do not exist
yet.8
- From time to time, possibly after a local collection, the
distributed collector sends a message called newSetStubs; this
message contains the new set of stubs that resulted from the local
collection; this message is sent to the processes holding the scions
corresponding to the stubs in the previous stub set.
In each of the receiving processes, the distributed collector matches
the just received set of stubs with its set of scions; those scions
that no longer have the corresponding stub, are deleted.
- As previously described, when a local collection takes place two
kinds of messages may be sent: unreachable and reclaim.
On the receiving process, these messages are handled by the
distributed collector that performs the following operations: sets
the recUmess bit in the corresponding outPropList entry,
and deletes the corresponding entry in the inPropList,
respectively.
- The DGC algorithm does not require the underlying
communication layer to support causal delivery.
| event | occurs when | action taken |
| reference exported | propagate an object | create scion |
| from a process | |
| reference imported | propagate an object | create stub |
| into a process | |
| object replica | LGC runs | send unreachable message to |
| reachable only | | the process with the corresponding |
| from the inPropList | | outPropList entry; set the |
| | sentUmess bit accordingly |
| unreachable message | unreachable message sent | set the recUmess bit accordingly; |
| received | | if all recUmess bits for a |
| | particular object are set, then send |
| | the corresponding reclaim messages |
| | and delete the outPropList entry |
| reclaim message | reclaim message sent | delete corresponding inPropList |
| received | | entry |
| new set of stubs | LGC runs | newSetStubs message sent to the |
| available | | processes holding the scions corres- |
| | ponding to the previous set of stubs |
| newSetStubs message | newSetStubs message sent | compare stubs set with set of scions; |
| received | | delete scions with no |
| | corresponding stubs |
Table 2:
GC related events.
Table 1 presents all the GC related messages of the model,
the components responsible for sending and receiving them, and when
they occur.
In Table 2 we present all the events with impact on the GC
and the corresponding actions taken.
These two tables summarize the way GC is performed.
In the next section we describe the DGC algorithm in more detail using
a prototypical example.
4 Prototypical Example
We use a prototypical example, illustrated in Figures 5
and 6.
This example evolves along a sequence of steps covering all the
situations, relevant for GC, that occur in a WARM: (i) creation of a
new outgoing inter-process reference by means of a propagate
operation, (ii) creation of a new outgoing inter-process reference by
means of an assignment operation, and (iii) deletion of outgoing
inter-process references by means of assignment and propagate
operations.
We show how all these occurrences affect the GC specific data
structures and messages.
In the initial situation both x and y are cached in processes
i and j.
However, only the replica yj points to object z in process
k.
There is a single stub-scion pair (s2-s1) describing the
only outgoing inter-process reference from yj to z.
For the sake of simplicity of our description, we assume that this
stub-scion pair is created when the system boots.9
Then, the sequence of steps of the prototypical example considers the
following operations (see Figures 5 and 6;
the effects of the operations are shown in bold).
- Step 1 - Propagate y from process j to process i; this
results in the creation of a new outgoing inter-process reference from
object y in i to object z in k.
- Step 2 - The operation < x: = y > i is performed by the
mutator in i; this creates a new outgoing inter-process reference
from object x in i to object z in k.
- Step 3 - Propagate x from process i to process j; this
results in the creation of a new outgoing inter-process reference
from object x in j to object z in k.
- Step 4 - The operation < y: = 0 > j is performed by the
mutator in j; this results in the deletion of an outgoing
inter-process reference from object y in j to object z in
k.
- Step 5 - Propagate y from process j to process i; this
results in the deletion of an outgoing inter-process reference from
object y in i to object z in k.
- Step 6 - The operation < x: = 0 > i is performed by the
mutator in i; this results in the deletion of an outgoing
inter-process reference from object x in i to object z in
k.
- Step 7 - the mutator in j deletes the reference from the
local root to object x.
- Step 8 - the mutator makes xi unreachable by deleting the
reference from the local root; thus, every replica of x becomes
garbage.
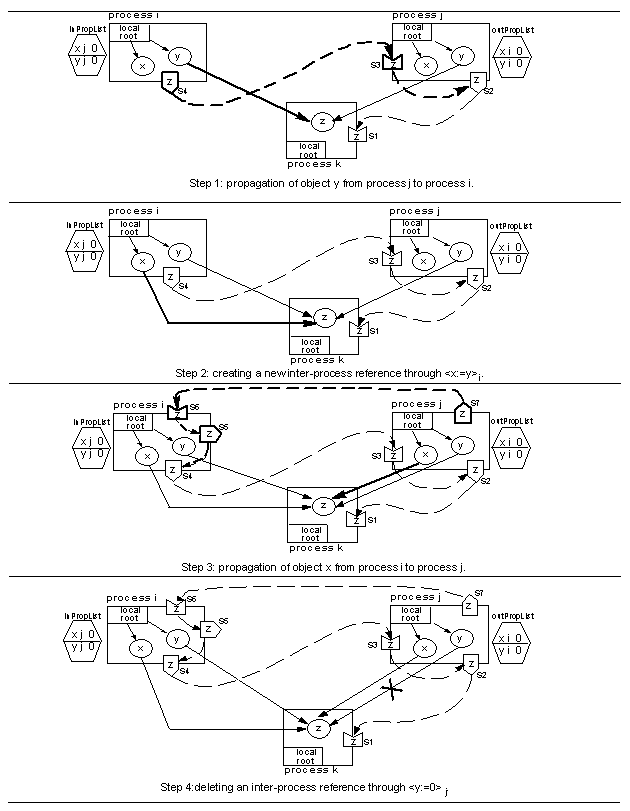
Figure 5: Prototypical example (part 1).
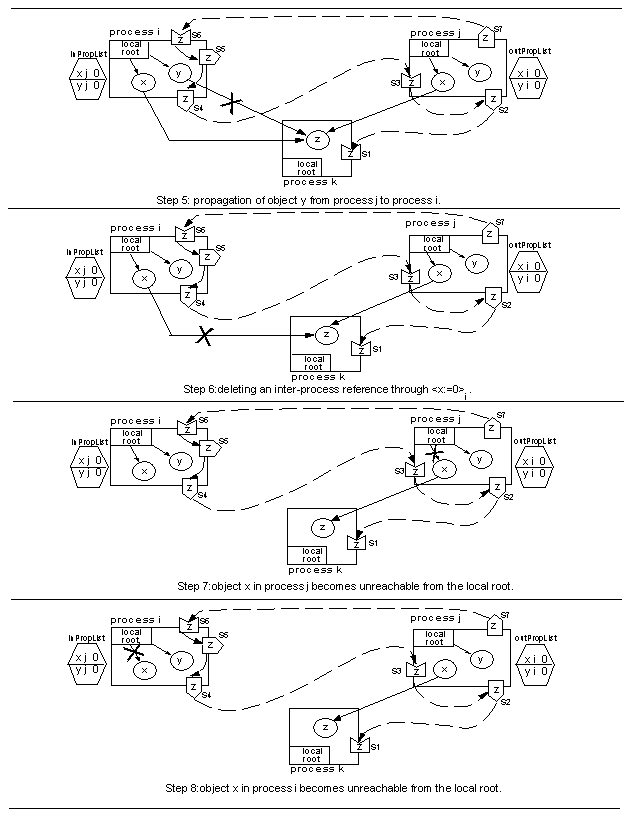
Figure 6: Prototypical example (part 2).
The prototypical example presented above has two parts: the first
three steps results in the creation of new outgoing inter-process
references; the last five steps result in z becoming unreachable.
In the next sections we describe how the DGC works in order to deal
with this prototypical example.
4.1 Creation of Outgoing Inter-process References
In the prototypical example, the creation of outgoing inter-process
references occurs first by propagation (step 1), then by reference
assignment (step 2), and finally by propagation again (step 3).
We address these cases now.
4.1.1 Propagation
The first operation in the prototypical example is
propagate(y)j ® i (Figure 5, step 1).
Immediately before this message is sent from process j, object y
must be scanned for references being exported.
For each one of these references, the corresponding scion must be
created.
In this case, y contains only one reference (pointing to z); the
corresponding scion s3 is shown in bold.
Note that the scion just created, through its Chain field,
refers to the already existing stub s2 (describing the outgoing
inter-process reference from object y to object z).
Immediately before propagate(y)j ® i is delivered
in process i, object y has to be scanned for imported outgoing
inter-process references in order to create the corresponding stubs in
process i, if they do not exist yet.
In the prototypical example, y contains a single reference and there
is no stub describing it in process i.
Thus, the corresponding stub s4 is created (shown in bold); this stub,
through its internal data structures, refers to the scion previously
created in process j.
Then, the mutator may freely access object y in process i.
Thus, the information stored in the stub-scion pair just created,
s4-s3, is the following:
- stub s4: OutRef refers to object z in process
k, sourceObj refers to object y in process i,
Scion identifies the corresponding scion s3 previously created
in process j, and Chain is null;
- scion s3: InRef refers to object z in process
k, Stub identifies the corresponding stub s4 in process
i, and Chain refers to the stub describing the outgoing
inter-process reference from object y to object z.
It is worthy to note that the mutator does not have to be blocked
while the GC specific operations mentioned above are executed
(scanning the object being propagated and creating the corresponding
scion and stub); such operations can be executed in the background.
To summarize, there are the following rules:
Safety Rule I: Clean Before Send Propagate.
Before sending a propagate message for an object y from a process
j, y must be cleaned (i.e. it must be scanned for
references) and the corresponding scions created in j.
Safety Rule II: Clean Before Deliver Propagate.
Before delivering a propagate message for an object y in a process
i, y must be cleaned (i.e. it must be scanned for outgoing
inter-process references) and the corresponding stubs created in i,
if they do not exist yet.
4.1.2 Assignment
The second step of the prototypical example is the execution of the
operation < x: = y > i .
This results in the creation of a new outgoing inter-process
reference: from object x in process i to z in process
k.
There is absolutely no operation to be done on behalf of the DGC
algorithm.
This might seem strange because, according to traditional reference
counting algorithms [20], each time a reference is
created, a counter (at least) must be incremented.
In a WARM, where mutators may create inter-process references very
easily and frequently, through a simple reference assignment
operation, such increment would be extremely inefficient.
As a matter of fact, this would require instrumenting every reference
assignment and increment a counter accordingly, possibly on some
remote process.
In the following sections it will become clear that such increment (or
equivalent operation) does not need to be performed immediately.
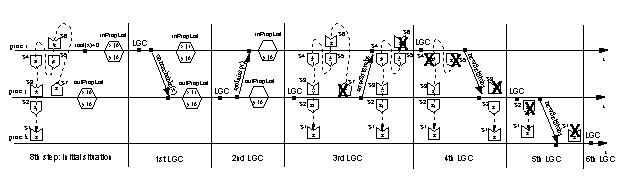
Figure 7: Timeline describing the GC operations after the 8th step
of the prototypical example.
4.1.3 Propagation
The third step of the prototypical example is the propagation of
object x from process i to process j.
This results in the creation of a new outgoing inter-process
reference: from object x in process j to object z in
process k(shown in bold in Figure 5, step 3).
According to Safety Rule Clean Before Send Propagate, before the
propagate message is sent, the following has to be done in process
i: scan object x, find its enclosed references and create the
corresponding scions.
In this case, object x has only one reference; thus, as a result of
the scan, scion s6 is created in process i (shown in bold,
Figure 5, step 3).
In addition, it is created stub s5 describing the outgoing
inter-process reference from object x in process i to object
z in process k.10
According to Safety Rule Clean Before Deliver Propagate, before
the propagate message is delivered in process j, object x must be
cleaned and the corresponding stub s7 created (shown in bold,
Figure 5, step 3).
4.2 Deletion of Outgoing Inter-process References
In the prototypical example, the deletion of outgoing inter-process
references occurs first by reference assignment, then by propagation,
then by reference assignment again, and finally by propagation again.
After all these operations, object z is unreachable.
We address these steps now.
4.2.1 Assignments and Propagations
The fourth step of the prototypical example is the execution of the
operation < y: = 0 > j .
This results in the deletion of the outgoing inter-process reference,
from object y to object z (Figure 5, step 4).
At this moment, there is absolutely no operation to be done for
GC purposes.
The fifth step of the prototypical example is
propagate(y)j ® i.
Given that the replica that is being propagated to i no longer
points to any object, after the propagate is delivered, the outgoing
inter-process reference from object y in process i to z,
is (implicitly) deleted (Figure 6, step 5).
At this moment, there is absolutely no operation to be done for GC
purposes.
Note that, given that the object being propagated contains no
references, both safety rules do not imply the execution of any
particular operation.
The sixth step of the prototypical example is the execution of the
operation < x: = 0 > i .
This results in the deletion of the outgoing inter-process reference,
from object x in process i to object z in process k
(Figure 6, step 6).
At this moment, there is absolutely no operation to be done for GC
purposes.
The seventh step of the prototypical example makes object x in
process j unreachable from the local root.
The last step makes object x in process i unreachable from the
local root.
In both cases there is absolutely no operation to be done for GC
purposes.
So far, the DGC has performed no operation.
In particular, no scion has been deleted.
Consequently, object z, which is no longer reachable, has not
been reclaimed yet.
This will happen only after its protecting scion s1 in process
k is deleted and the local collector is executed.
Now we address the modification and deletion of stubs and scions.
4.2.2 Collecting Garbage
In step 8 of the prototypical example we see that object z will be
reclaimed by the local collector in process k only after its
protecting scion s1 has been deleted.
This scion will be deleted only after the corresponding stub s2
in process j has disappeared; this will occur only after all the
chain of stub-scion pairs s7-...-s3 gets deleted.
According to Section 3.2, the stubs and scions
will disappear as a result of the local and distributed collectors in
processes i and j, as explained now (see
Figure 7).
- 1st LGC - The local collector in process i detects that object
x is reachable only from the inPropList; thus, a message
unreachable is sent to process j and the corresponding
sentUmess bit is set.
When this message is delivered in process j, the recUmess bit
in the corresponding entry of outPropList is set.
- 2nd LGC - The local collector in process j detects that object
x is reachable only from the outPropList and the
corresponding entry has its recUmess bit set to one; thus a message
reclaim is sent to process i and the entry in the
outPropList is deleted.
When this message is delivered in process i, the corresponding
entry in inPropList is deleted.
- 3rd LGC - As a result of a local collection in process j, x
is reclaimed and, consequently, stub s7 describing its
outgoing inter-process reference to object z is not in the new set
of stubs. This new set of stubs is sent as a newSetStubs
message from process j to process i; then, the distributed
collector in i deletes the corresponding scion s6.
Note that stub s2, in spite of the fact that y in j holds
no outgoing inter-process reference anymore, is still in the new set
of stubs because is reachable from scion s3 through its
Chain data structure.
- 4th LGC - As a result of a local collection in process i,
object x is reclaimed and the new set of stubs does not contain any
stub (s5 and s4, in particular) because there are no
outgoing inter-process references.
This new set of stubs is sent as a newSetStubs message from
process i to process j; then, the distributed collector in j
deletes the corresponding scion s3.
- 5th LGC - As a result of a local collection in process j a new
set of stubs is generated in which there is no stub (i.e. s2)
because there are no outgoing inter-process references.
This new set of stubs is sent as a newSetStubs message from
process j to process k; then, the distributed collector in k
deletes the corresponding scion s1.
- 6th LGC - Finally, a local collection occurs in process k and
object z is reclaimed.
In conclusion, we have the following rule for replicated objects:
Safety Rule III: Union Rule.
A target object z is considered unreachable only if the union of
all the replicas of the source objects do not refer to it.
In the prototypical example the objects pointing to z were the
replicas of x and y.
From Figure 7 it is clear that the union rule is
respected.
In addition, it is clear that there is no need for causal delivery to
be ensured by the communication layer.
5 Implementation
We implemented our WARM distributed and local garbage collectors
within a system called News Gathering (NG).
In this section we briefly describe the NG application; then, we focus
on the most important implementation aspects of the DGC: how the
safety rules are implemented, and the stub/scion data structures.
5.1 NG Application
NG is a web-based client-server application that we developed, to
support the sharing of files over the web by means of replication
[19].
From the user point of view the client side of NG is a normal web
browser with an extra menu button called ``make-replica''.
This function allows the user to propagate a file into his machine, i.e.,
to create a local replica of the file he is looking at.
Once replicated, the file can be freely accessed with any other
application (possibly making the replicas to diverge).
Later, this replica can be propagated back to the site from where it
came from by means of a make-replica operation performed by other user
running on that site. (Figure 8 illustrates the general
architecture of this application.)
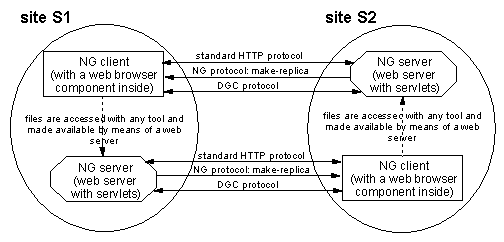
Figure 8: General architecture of the NG application. Obviously,
any number of sites is supported and not all are forced to have both a
client and a server, i.e. some can be just clients or servers.
With NG, a typical user in site S1 browses the web (web servers
supporting the NG application) and makes-replicas of some of the pages
from, for example, the S2 site.
These pages are then edited by the user and, once ready, are made
available from the user's local NG server.
These replicas may hold references to other (not locally replicated)
S2 pages.
Thus, it is desirable that such pages in the S2 web site remain
available as long as there are references pointing to them.
Figure 9 illustrates this scenario.
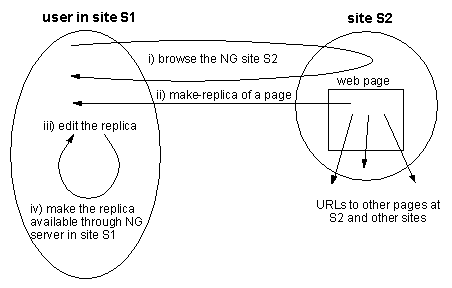
Figure 9: Example of NG usage: i) browse the S2 web site, ii)
make-replicas of a page, iii) edit the replica, and iv) make the
replica available for others.
The NG application, due to the WARM distributed garbage collector,
ensures that such pages at the S2 site remain there as long as they
are pointed from some other NG site.
In addition, files at the S2 site, which are no longer referenced
from any other NG site are automatically deleted by the garbage
collector.
This means that neither dangling references nor memory leaks occur.
The NG application is implemented in Java; this includes the client
code (that uses the Microsoft Internet Explorer component) and the
servlets running within an Apache web server.
5.2 Distributed Garbage Collector
All the code of the local and distributed collectors is written in
Java.
The local collector is implemented as a stand-alone application.
The distributed collector is implemented by the servlets and by
the client.
Basically, the code in the servlets implements the safety rule Clean
Before Send Propagate (applied when a make-replica is requested); the
client code implements the safety rule Clean Before Deliver Propagate
(applied when the reply to a make-replica request is received).
The implementation of these rules consists on scanning the web pages
being propagated and creating the corresponding scions (at the server)
and stubs (at the client).
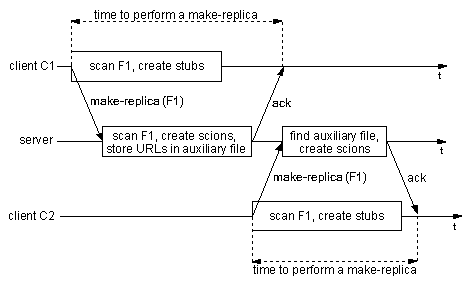
Figure 10: Propagation of file F1.
The first time a file is propagated, at the server site its contents
are scanned, the corresponding scions created, and the enclosed set of
URLs is kept in an auxiliary file.
Later, if this same page is propagated again, at the server site it
only has to be scanned again if it has been modified after the last
scan.
The timeline presented in Figure 10 shows how the scanning
needed to enforce safety rules I and II relates to the make-replica
request of file F1 11.
Another important aspect concerning the implementation of the garbage
collectors (both local and distributed) is the data structures
supporting the stubs and scions.
These were conceived taking into account their use, in particular, to
optimize the kind of information exchanged between sites that occurs
when a newSetStubs message is sent.
This message implies that the new set of stubs, resulting from a local
collection, is sent to the processes holding the scions corresponding
to the stubs in the previous stub set.
Then, in each of the receiving processes, the distributed collector
matches the just received set of stubs with its set of scions; those
scions that no longer have the corresponding stub, are deleted.
Thus, stubs are grouped by site, i.e. there is one hash table for each
site holding scions corresponding to the stubs in that table.
Sending a new set of stubs to a particular site is just a matter of
sending the new hash table.
The same reasoning applies to scions: they are stored in hash tables,
each table grouping the scions whose corresponding stubs are in the
same site.
6 Performance
In this section we present the most relevant performance results
concerning the DGC.
The critical performance results are those related to the
implementation of safety rules I and II.
Thus, we downloaded a well-known web site (cnn.com) and ran on each
file the code implementing the safety rules.
All results were obtained in a local 100 Mbits network, connecting PCs
with Windows NT, with 64 Mb of memory and a Pentium II at 233 MHz.
We downloaded all the 155 HTML files of the cnn.com web
site12
and obtained for each one the time it takes to: scan it, create the
corresponding stubs, and serialize the hash table (including writing to
disk).
In this section, for clarity, we simply refer to the time it takes to
create stubs and their size because the same values apply to scions.
| file | number | scan | stub | hash | time |
| size | of | time | creation | table | to se- |
| URLs | | time | size | rialize |
| 43563 | 326 | 38 | 3 | 19252 | 67 |
Table 3:
Mean values obtained with all the files
automatically downloaded from the cnn.com site (Sizes in bytes and
times in milliseconds.).
In Table 3 we present, for each one of the 155 files: the
mean file size, the mean number of URLs enclosed in each file,
the mean time to scan a file,
the mean time it takes to create a stub in the corresponding hash table,
the mean size of the hash table containing all the stubs corresponding to
all the URLs enclosed in a file (that depends on the size of the
corresponding URL),
and the mean time it takes to serialize a hash table with all the
stubs corresponding to a single file.
| file | file | number | scan | stub | hash | URLs | time to |
| name | size | of URLs | time | creation | table | size | serialize |
| | | | time | size | | |
| europe.htm | 49055 | 493 | 36 | 10 | 25485 | 22367 | 60 |
| health.htm | 102933 | 491 | 45 | 10 | 26268 | 23465 | 60 |
| law.htm | 79460 | 523 | 117 | 10 | 31373 | 30194 | 70 |
| main.htm | 67081 | 588 | 40 | 10 | 38548 | 34108 | 71 |
| politics.htm | 59079 | 470 | 90 | 10 | 25963 | 22939 | 60 |
| showbiz.htm | 71579 | 498 | 40 | 10 | 26481 | 24944 | 111 |
| space.htm | 58488 | 478 | 78 | 50 | 24835 | 23614 | 50 |
| sports.htm | 41778 | 366 | 27 | 10 | 23308 | 18908 | 60 |
| tech.htm | 49645 | 462 | 34 | 10 | 21820 | 20491 | 50 |
| world.htm | 54863 | 554 | 40 | 10 | 24489 | 23870 | 50 |
Table 4:
Values for the top-set group of
files. (Sizes in bytes, times in milliseconds.)
| file | file | number | scan | stub | hash | URLs | time to |
| name | size | of URLs | time | creation | table | size | serialize |
| | | | time | size | | |
| index.htm | 46960 | 360 | 27 | 10 | 22692 | 21400 | 60 |
| default.htm | 48419 | 380 | 33 | 10 | 24504 | 23870 | 50 |
| 01/index.htm | 45504 | 369 | 95 | 10 | 22817 | 22444 | 60 |
| 02/index.htm | 26753 | 200 | 16 | 20 | 14084 | 10789 | 40 |
| 03/index.htm | 31834 | 279 | 22 | 10 | 18493 | 17033 | 50 |
| 04/index.htm | 45247 | 360 | 26 | 10 | 21855 | 21656 | 50 |
| 05/index.htm | 53778 | 411 | 30 | 10 | 25817 | 24490 | 60 |
| 06/index.htm | 42476 | 362 | 25 | 10 | 22706 | 22081 | 70 |
| 01/default.htm | 16843 | 150 | 20 | 10 | 8032 | 7934 | 10 |
| 02/default.htm | 33473 | 173 | 24 | 10 | 8675 | 8090 | 30 |
Table 5:
Values for the branch-set group of
files in the branch world/europe. (Sizes in bytes, times in milliseconds.)
However, in a normal browsing session, the user does not makes-replica
of all the files.
We expect the user to browse a few top-level pages and then pick one
or more branches of the hierarchy.
Some of these files will be replicated into the users local computer.
So, in order to obtain more realistic numbers, we performed the
following.
We picked 10 files from the top of the cnn.com hierarchy.
These files are mostly entry points to the others with more specific
contents. We call this set of files, the top-set.
We also picked other 10 files representing a branch of the cnn.com
hierarchy. We call this set of files, the branch-set.
In Tables 4 and 5, for each file in the
top-set and in the branch-set, respectively, we present the times
mentioned above along with the size of each file and the number of
URLs enclosed.
These performance results are worst-case because they assume all the
URLs enclosed in a file refer to a file in another site, which is not
the usual case.
However, they give us a good notion of the performance limits of the
current implementation.
In particular, we see that the most relevant performance costs are due
to the scanning of a file and the serialization of the hash table.
However, we believe that these values are acceptable taking into
account the functionality of the system, i.e. it ensures that no
dangling references and no memory leaks occur.
In addition, when a user runs the NG browser and accesses any web page
without making a local replica of any file, there is absolutely no
performance overhead due to DGC.
We can also conclude that the size on disk of the hash table
containing all the stubs for a file is about half the size of the HTML
file.
This rather large size is mostly due to the size of the URLs which are
responsible for about 90% of that size.
The size of the file containing the stubs can certainly be reduced
using regular compression techniques.
7 Related work
Much previous work in distributed garbage collection, such as SSP
Chains [16] or Network Objects [4,18],
considers processes communicating by messages (without shared memory),
using a hybrid of tracing and counting. Each process traces its
internal pointers; references across process boundaries are counted as
they are sent in messages.
Some object-oriented databases use a similar approach
[2,6,21], i.e. a partition can
be collected independently from the rest of the database.
In particular, Thor is a research OODB [13] that stores
data in a small number of servers.
This data is cached at workstations for processing.
A Thor server counts references contained in objects cached at a client.
Thor defers counting references originating from some object x cached
at a client, until x is modified at the server.
The work most directly related to this one is Skubiszewski and Porteix's
GC-consistent cuts [17].
They consider asynchronous tracing of an object-oriented database, with no
distribution or replication.
The collector is allowed to trace an arbitrary database page at any time,
subject to the following ordering rule.
For every transaction accessing a page traced by the collector, if the
transaction copies a pointer from one page to another, the collector either
traces the source page before the write, or traces both the source and the
destination page after the write.
The authors prove that this is a sufficient condition for safety and liveness.
Most previous work on garbage collection in shared memory deals either with
multiprocessors [3,8] or with a small-scale DSM
[9,11].
These authors make strong coherence assumptions, and they ignore the
fundamental issue of scalability.
Yu and Cox [22] describe a conservative collector for the TreadMarks DSM
system.
It uses partitioned GC on a process basis; it is strongly integrated
with TreadMarks and all messages are scanned for possible contained
pointers.
Previous work in DGC as IRC [14], SSP
chains [16] and Larchant [10] served as the
starting point of the DGC algorithm presented in this paper.
Our new algorithm builds on these previous two algorithms in such a
way that combines their advantages: no need for causal delivery support
to be provided by the underlying communicating layer (from the first
two), and capability to deal with replicated objects (from Larchant).
8 Conclusions and Future Work
In this paper we presented a new DGC algorithm for a WARM.
The algorithm is general enough to be widely applicable given the
minimal assumptions of the underlying model.
The fundamental aspects of the DGC algorithm are the following.
- It does not interfere with the protocol that maintains the
replicas coherent among the participating processes. This means that
the DGC does not require replicas to be coherent.
- It does not require causal delivery to be supported by the
underlying communication layer.
Given that supporting causal delivery in wide area networks is
difficult and inefficient, this is a fundamental aspect to ensure the
DGC algorithm scalability.
- It is safe in presence of replicated objects, i.e. it respects
the union rule.
We presented our DGC algorithm as an evolution of two previous ones: a
classical one designed for distributed systems based on
function-shipping with no replication support, SSP chains, and
Larchant which is targeted to distributed systems with replicated
objects.
However, it's important to note that any classical distributed garbage
collection algorithm based on reference-counting can be used instead
of SSP Chains (e.g. IRC).
The only requirement would be its integration with the WARM in such a
way that the safety rules are respected.
Concerning future research directions, we intend to address the
fault-tolerance of the DGC algorithm.
In other words, we are starting to study how the DGC algorithm should
be designed so that it can remain safe, live and complete in spite of
process crashes and permanent communication failures.
We are also investigating how the DGC algorithm is affected if the
WARM is accessed using transactions.
References
- [1]
-
Saleh E. Abdullahi, and Graem A. Ringwood.
Garbage collecting the internet: A survey of distributed garbage
collection.
ACM Computing Surveys, 30(3):330-373, September 1998.
- [2]
-
L. Amsaleg, M. Franklin, and O. Gruber.
Efficient Incremental Garbage Collection for Client-Server Object
Database Systems.
In Proc. of the 21th VLDB Int. Conf., Zürich, Switzerland,
September 1995.
- [3]
-
Andrew W. Appel.
Simple Generational Garbage Collection and Fast
Allocation.
Software Practice and Experience, 19(2):171-183, February
1989.
- [4]
-
Andrew Birrell, Greg Nelson, Susan Owicki, and Edward Wobber.
Network objects.
Software Practice and Experience, S4(25):87-130, December
1995.
- [5]
-
Xavier Blondel, Paulo Ferreira, and Marc Shapiro.
Implementing garbage collection in the PerDiS system.
In Proc. of the Eigth International Workshop on Persistent
Object Systems: Design, Implementation and Use (POS-8), 1998.
- [6]
-
Jonathan E. Cook, Alexander L. Wolf, and Benjamin G. Zorn.
Partition selection policies in object database garbage collection.
In Proc. Int. Conf. on Management of Data (SIGMOD), pages
371-382, Minneapolis MN (USA), May 1994. ACM SIGMOD.
- [7]
-
Edsger W. Dijkstra, Leslie Lamport, A. J. Martin, C. S. Scholten, and E. F. M.
Steffens.
On-The-Fly Garbage Collection: An Exercise in Cooperation.
Communications of the ACM, pages 966-975, Vol. 21, N. 11,
November 1978.
- [8]
-
Damien Doligez and Xavier Leroy.
A concurrent, generational garbage collector for a multithreaded
implementation of ML.
In Proc. of the 20th Annual ACM SIGPLAN-SIGACT Symp. on
Principles of Programming Lang., pages 113-123, Charleston SC (USA),
January 1993.
- [9]
-
Paulo Ferreira and Marc Shapiro.
Garbage collection and DSM consistency.
In Proc. of the First Symposium on Operating Systems Design and
Implementation (OSDI), pages 229-241, Monterey CA (USA), November 1994.
ACM.
- [10]
-
Paulo Ferreira and Marc Shapiro.
Modelling a distributed cached store for garbage collection: the
algorithm and its correctness proof.
In ECOOP'98, Proc. of the Eight European Conf. on
Object-Oriented Programming, Brussels (Belgium), July 1998.
- [11]
-
T. Le Sergent and B. Berthomieu.
Incremental multi-threaded garbage collection on virtually shared
memory architectures.
In Proc. Int. Workshop on Memory Management, number 637 in
Lecture Notes in Computer Science, pages 179-199, Saint-Malo (France),
September 1992. Springer-Verlag.
- [12]
-
Kai Li and Paul Hudak.
Memory coherence in shared virtual memory systems.
ACM Transactions on Computer Systems, 7(4):321-359, November
1989.
- [13]
-
U. Maheshwari and B. Liskov.
Fault-tolerant distributed garbage collection in a client-server,
object database.
In Proceedings of the Parallel and Distributed Information
Systems, pages 239-248, Austin, Texas (USA), September 1994.
- [14]
-
José M. Piquer.
Indirect reference-counting, a distributed garbage collection
algorithm.
In PARLE'91-Parallel Architectures and Languages Europe,
volume 505 of Lecture Notes in Computer Science, pages 150-165,
Eindhoven (the Netherlands), June 1991. Springer-Verlag.
- [15]
-
David Plainfossé and Marc Shapiro.
A survey of distributed garbage collection techniques.
In Proc. Int. Workshop on Memory Management, Kinross Scotland
(UK), September 1995.
- [16]
-
Marc Shapiro, Peter Dickman, and David Plainfossé.
SSP chains: Robust, distributed references supporting acyclic
garbage collection.
Rapport de Recherche 1799, Institut National de Recherche en
Informatique et Automatique, Rocquencourt (France), November 1992.
- [17]
-
Marcin Skubiszewski and Patrick Valduriez.
Concurrent Garbage Collection in O2.
In Proceedings of the 23rd VLDB Conference, Athens Greece, 1997.
- [18]
-
Sun Microsystems Inc.
JavaTM Remote Method Invocation Specification, Revision 1.50, JDK 1.2.
Documentation supplied with JDK 1.2 FCS, Oct. 1998.
- [19]
-
Luis Veiga and Paulo Ferreira.
World wide news gathering automatic management.
In 2nd International Conference Enterprise Information Systems,
Stafford, UK, July 2000.
- [20]
-
Paul R. Wilson.
Uniprocessor garbage collection techniques.
In Proc. Int. Workshop on Memory Management, number 637 in
Lecture Notes in Computer Science, Saint-Malo (France), September 1992.
Springer-Verlag.
- [21]
-
V. Yong, J. Naughton, and J. Yu.
Storage reclamation and reorganization in client-server persistent
object stores.
In Proc. Data Engineering Int. Conf., pages 120-133, Houston
TX (USA), February 1994.
- [22]
-
Weimin Yu and Alan Cox.
Conservative garbage collection on distributed shared memory systems.
In 16th Int. Conf. on Distributed Computing Syst., pages
402-410, Hong Kong, May 1996. IEEE Computer Society.
Footnotes:
1 Locally (un)reachability is related to (un)accessibility
from the enclosing process's local root.
2 In distributed systems with
replicated data, an ``acquire'' operation allows a process to update
its local replica of a particular object with the contents of another
replica, of that same object, residing in some other process with a
data-shipping mechanism.
3 The term mutator [7]
designates the application code which, from the point of view of the
garbage collector, mutates (or modifies) the reachability graph
of objects.
4 This
notation is not fully accurate but it simplifies the explanation of
the DGC algorithm. As a matter of fact, to be more precise we should
write x.ref = y.ref (C++ style notation). However, this
improved precision is not important for the DGC algorithm description
and would complicate it un-necessarily.
5 Usually, this information does exist in the
coherence engine in order to manage the replicas.
6 For example,
in some DSM-based systems, when the mutator tries to access an object
that is not yet cached locally, a page fault is generated; then, this
fault is automatically recovered by the coherence engine that obtains
a replica of the faulted object from some other process.
7 Note that from now on, the replica is not reachable by
the local mutator; if another propagate operation occurs bringing a
new replica of that same object into the process, the old
replica remains locally unreachable, and a new entry is created in the
inPropList with the corresponding sentUmess set to 0.
8 Note that this may result in the creation of chains of
stub-scion pairs, as it happens in the SSP Chains
algorithm [16].
9 For
example, the reference to z could be obtained from a name service.
10 Note that if a local collection has
previously taken place in process i, stub s5 would have been
already created.
11 Note that the client can scan the page
immediately after sending a make-replica request because its contents
are already available locally (for browsing).
12 Using an automatic tool called WebReaper available from
http://www.otway.com/webreaper configured with a depth level of 5.
File translated from TEX by TTH, version 2.00.
On 04 Dec 2000, 16:19.
|






