USITS '01 Paper
[USITS '01 Tech Program Index]
| Pp. 85–96 of the Proceedings |  |
On Line Markets for Distributed Object Services:
the MAJIC system
Lior Levy, Liad Blumrosen and Noam Nisan1
Institute of Computer Science,
The Hebrew University of Jerusalem,
Jerusalem, Israel.
Abstract
We describe a general-purpose architecture for applying economic mechanisms
for resource allocation in distributed systems. Such economic mechanisms
are required in settings such as the Internet, where resources belong to
different owners. Our architecture is built above standard distributed-object
frameworks, and provides a ``market'' for arbitrary distributed object
resources. We first describe the abstract elements and properties of an
architecture that can be applied over essentially any distributed object-based
platform. We then describe the MAJIC2
system that we have implemented over Suns' Jini platform. A key novel aspect
of our system is that it handles multiple parameters in the allocation
and in the specification of utilities and costs for each distributed service.
We provide both theoretical and experimental results showing the following
three key properties of this system: (1) Efficient resource allocation.
(2) Motivation for resource owners to share them with others. (3) Load
balancing.
1 Introduction
1.1 Motivation
The following concept may be viewed as the holy grail of ``Internet Computing'':
Every user connected to the Internet should have complete access to all
resources available anywhere on the Internet. The user should be presented
with an illusion of a single centrally organized ``global computer''. The
main challenge of computer engineering, in this context, is to design the
protocols, algorithms, paradigms, and systems that achieve this illusion
by using the aggregation of the physical computers, communication links,
and other resources that are available on the Internet.
Ideally, such systems would optimally allocate all available
resources across the Internet. There are indeed a wide variety of such
resources: computational resources (such as CPU time, or file servers),
information resources (Databases, video), communication resources (links,
QoS), services (help-desk, access to specialized algorithms), hardware
(printers, cameras), and more. A dream suite of protocols and algorithms
for the Internet would allow all these resources, as well as others, to
be optimally and transparently allocated across the Internet.
There are clearly many aspects that need to be addressed on
the way to this ``holy grail'', and many of these aspects have received
much attention in the literature. In this paper we concentrate on the interplay
and synergy between two key paradigms that address different aspects of
this challenge: the distributed objects paradigm for basic technological
interoperability and the economic paradigm for motivating resource sharing
by different users or organizations.
1.2 Distributed Objects Paradigm
In recent years the paradigm of distributed object services is becoming
the basic backbone of communication and cooperation between components
of a distributed system. In a distributed object framework, computers on
a network encapsulate their shareable resources (services) in well defined
procedural interfaces. Other computers then use these resources by performing
remote procedure calls (RPC), or in an OOP terminology, remote method invocations
(RMI) on them. In its pure object-oriented variant this paradigm is the
basis of most modern commercial distributed platforms: CORBA [5],
Microsoft's DCOM [6],
Java's RMI [33].
Taking a wider perspective, web servers follow this paradigm on the level
of web pages (static or dynamic), and with standards such as XML [46]
and protocols such as SOAP [38],
a true web-like infrastructure for distributed processing that follows
this paradigm emerges. Indeed many authors have proposed variants and implementations
of this vision under names such as ``Web of Objects'', ``Distributed Objects
Everywhere'', etc [3,44,9,45,39].
1.3 Economic Paradigms for Resources Sharing
A major difficulty in achieving efficient sharing of resources across the
Internet is the obvious fact that the different computers and resources
belong to different organizations. An Internet-wide resource sharing system
must provide motivation for the owners of resources to share them with
others. Any such motivation leads to some kind of economic system, and
in its simplest form involves payments for services. Such economic systems
for distributed allocation of computing resources have been applied to
CPU time [10,43,42,41,27,32],
communication [19,36,37,],
and other resources [21,7,34,41],
and have received much theoretical interest lately [19,24,11,31,16,35,25,26].
Such systems pursue two complementary goals: that participants are indeed
motivated to share these resources with others and that the resources are
indeed allocated well.
1.4 This Paper
We first propose a general architecture for augmenting a distributed-object
system with payments, and a market-based mechanism for allocating resources.
We then describe a system of this sort, the MAJIC system, that we have
implemented over Sun's Jini infrastructure. More details are available
in the MAJIC web site []. This architecture allows, for the first time,
applying the ideas of economic-based cooperation to the full spectrum of
resources available on the Internet: CPU time, file servers, Databases,
online entertainment, communication bandwidth, algorithms, printers and
other hardware, etc. Moreover, this is done in a way that is easily inter-operable
with the current leading technologies. We provide both general arguments
(and mathematical proofs) showing that such an augmented system would indeed
function well, and specific experimental results from MAJIC, supporting
these findings.
This architecture provides, for the first time, an economy based general-purpose
infrastructure for all kind of resources, compared with earlier similar
systems, which were dedicated to one kind of resource. A key novel aspect
of our architecture is that it allows multiple parameters in specifying
utilities and costs for each service request and handles these parameters
in an efficient and non-trivial way.
It is clear that any system that achieves serious resource sharing over
the Internet must address both the issue of technical inter-component communication
and the issue of motivating selfish entities to share their resources.
We believe that systems built along the principles laid here answer both
issues in an integrated, inter-operable, and efficient way and could provide
a general-purpose architecture that allows true efficient resource sharing
on the Internet!
2 A blueprint for a
market of distributed object services
2.1 Basic idea
The starting point of our architecture is simple: each object that provides
a service may attach a ``price-tag'' to it. When another object wishes
to use a particular type of service, it calls a central ``service market
place'' that functions as the object request broker. The market performs
a ``reverse auction'' for this service, where all available objects (service
providers) that provide a service of this type can participate. The provider
that charges the lowest price wins, and gets to service the request for
the agreed-upon price.
A simple example that we will use throughout the paper is a printing
service. Our starting point assumes that printers provide the service of
printing a page by providing the simple remote method: printer.print(page).
Each printer has a price for this service: printer.getPrice(). A
computer that wants to print a page on a printer that does not belong to
him gets the reference to the cheapest printer from the ``printing market''
and can then print on this printer: market.getPrinter().print(page).
Several basic issues need to be addressed before this can be made into
a workable system, and we describe the major ones.
2.2 Parameterized Services
Looking at the previous printing example, one is immediately concerned
with the differences between different printers and printing jobs. In reality
many parameters distinguish one print job from another: number of pages,
page size, printer's location, printing speed, print quality, etc. Clearly
any serious system that handles printing services must be aware of these
differences. More generally, distributed object services receive input
parameters - it is quite clear that the price requested for a service must
be tightly related to these parameters. Additionally, inter-changeable
distributed service providers are still not totally equivalent in many
of their parameters (such as their quality, virtual location or their speed).
This is not a simple issue to tackle when one attempts to produce a
``market'' for these services. Ignoring the parameters in the market will
simply make any type of efficiency in resource allocation impossible. Taking
all the parameters into account in the definition of the ``market'' will
lead to a logically separate market for each request and for each service
provider, eliminating competition and thus any flexibility in allocations.
The solution is clearly to work within a single market, but take parameters
into account during resource assignment.
In our system each service type specifies the set of parameters
of the service, defining the parameter space of the service. Each
service provider can supply the service in some specified subset of the
parameter space. Back to our example, a certain printer may only be able
to print on ``A4'' or ``letter'' page sizes, but not on ``A3'' size, while
another may also offer ``A3'' size. Similarly, a printer will usually only
supply the printing service at a certain physical location or with a certain
time delay (depending on its current load). Each service request may be
in a single point of the parameter space (``I need A4 pages''), or may
be satisfied with a whole subset of the parameter space (``A4 or letter
is fine''), possibly with preferences among the different possibilities.
In economic terms, each point in the parameter space of a service type
is a separate product type. The products that correspond to different points
in the parameter space of a single service type are partial substitutes
to each other - both for service providers and for service requesters.
The challenge we face (and solve below) is to organize a single market
for all these products, while handling the partial substitution in an economically
efficient way.
2.3 Sellers' Quote and Buyers' Utility
Our economic system is based on a common currency in which all participants
can express their economic preferences. Thus we assume that each service
provider - seller - has a certain internal cost for supplying the
service at each point of the parameter space that can be provided by him.
Similarly, each service requester - buyer - has a certain economic
benefit from receiving the service, a benefit that may depend on the parameters.
Denote by P the parameter space of a certain service type, our economic
model of participants is given by the following two functions: (1) Sellers'
cost function: cS:P® R+
. For a point p Î P , cS(p)
specifies seller S 's internal cost for supplying the service with parameters
p . I.e., he would like to provide this service with these parameters if
he is paid more than cS(p) , and would not agree to provide
the service for a lower price. We take the convention that if S cannot
provide the service with parameters p at all then cS(p)=¥.
(2) Buyers' utility function: uB:P®
R+ . For a point p Î P , uB(p)
specifies buyer B 's benefit from receiving the service with parameters
p . I.e., he would like to receive this service with these parameters if
he pays less than uB(p) , and would not agree to buy the service
for a higher price. We take the convention that if the service with parameters
p is not acceptable at all to him, then uB(p)=0 .
In our system, each seller sends to the market a function corresponding
to his cost function - called the quote function qS:P®
R+ . For a point p Î P , qS(p)
specifies his ``quote'' for the service with parameters p - i.e. the amount
of money he demands for providing the service with these parameters. The
quote function qS is essentially a catalog specifying a price
for each choice of parameters that can be supplied by S . Informally speaking,
the quote function qS of a seller should correspond tightly
to his cost function cS . This however cannot be guaranteed
at this point as a seller will likely send to the market a quote function
aimed for maximizing his profits - not aimed at any particular correspondence
with his cost function. We will return to this point below. The system
allow sellers to modify their quote functions occasionally, taking into
account changes in status.
When a buyer requests a service he sends to the market a representation
of his
utility function. The market matches this buyer with the
seller that fits him best. The abstract process that takes place is that
the market creates an agent for the buyer based on his utility function.
This agent is presented with the catalogs (quote functions) of all
sellers, and chooses the best seller and parameters. The details of this
process are explained in section 2.4.
The representation of the quote and utility functions
as objects may be given by specifying the formulas that define them as
a function of the different parameter values or may be given by opaque
distributed objects that encapsulate these functions. The choice of representation
will usually depend on the service type and has consequences in how the
system can function.
2.4 The Market Mechanism
As mentioned, the market holds the current quotes from all sellers {qS}
, and when it receives a request from a buyer - specified by the buyer's
utility function uB - it attempts matching this request to the
best seller and choosing the best parameter values. The optimization criteria
is the surplus: surplusB,S(p)=uB(p)-qS(p)
. For a given supplier S , the parameters p are chosen as to maximize this
surplus: pB,S*=argmaxp{surplusB,S(p)}
. In case this search over the parameter space is computationally feasible
(this depends on the representations of the parameter space and the quote
and utility functions), the buyers' agent can directly find these optimal
parameters. Otherwise, the system allows each buyer to supply a ``parameter
search engine'' that attempts finding these parameters, given a quote function
(encapsulated by an object) as input. We expect this mechanism to be computationally
efficient in many cases, either because of the simplicity of the parameter
space, or because of the small number of parameters. However, when searching
in complex parameter space, we expect the buyer's search engine to find
a close approximation in reasonable time.
The optimal supplier is chosen as to optimize the surplus under the
optimal parameters: S*=argmaxS{surplusB,S(pB,S*)}
. At this point the buyers' agent must check that this surplus is indeed
positive: surplusB,S*(pB,S**)
> 0 . Otherwise, the buyer is not willing to pay as much as the optimal
seller is asking, and the service request should be canceled. As analyzed
theoretically in section 4, and demonstrated
experimentally in section 5, this agent-based
allocation produces efficient allocations in terms of reported utilities
and quotes.
Once the optimal S* and p* are found, the market
may in principle fix any payment d in the range qS*(p*)
£ d £
uB(p*) . Any price in this range will be acceptable
both to the buyer and to the seller. The simplest choice would be to use
the quote function as the price: the buyer must pay the seller the amount
of qS*(p*) . This is certainly the usual
choice in commerce as it corresponds to the catalog price of the chosen
product. In terms of auction theory, this corresponds to a first price
auction [,].
We suggest also a different choice of payment, generalizing Vickrey's
second price auction [40].
The motivation for this payment rule is to motivate sellers to send the
market a quote that is equal to their cost function qS=cS
- a property known as incentive compatibility. This is extremely
important due to the fact that otherwise the assignment does not
optimize the allocation according to the true costs but rather according
to the quotes. Indeed the previously mentioned payment rule motivates sellers
to announce a quote that is higher than their costs - thus potentially
leading to a wrong choice of seller. For general background on this topic
see [15,4,22],
and for specific discussion in the context of computation resources see
[25,,,].
The payment rule we suggest is as follows. Let S2 be the
second best choice for supplier: S2=SB2=argmaxS
¹ SB*{surplusB,S(pB,S*)}
. The surplus with supplier S2 is less or equal to the surplus
with supplier S* . This payment method mandates that the buyer
only gets the surplus of S2 , while the optimal seller gets
the difference between the two surpluses. Thus the payment to supplier
S* is given by: d = uB(p*B,S*)
- surplusB,S2(p*B,S2)
. The main theoretical result we show, using the standard game-theoretic
models of rational behavior, is that this payment method results in incentive
compatibility, and thus all rational sellers indeed quote their true costs
leading to efficiency of allocations in the system.
2.5 Load Balancing as a By Product
As described above, this type of system ensures optimal allocation of each
request to the service provider that is best for it. In cases that requests
do not conflict with each other, this implies that the system obtains optimal
global performance. This is clearly not the usual case! The whole point
of allocation in distributed systems is handling the conflicts - different
requests should normally be split between the available servers. Going
back to our printing example, not everyone can gain access to the best
and cheapest printer - this would likely cause a bottleneck there. Indeed,
perhaps the most basic requirement from a distributed system is that of
load balance: the load should be reasonably split between available servers.
A key observation is that economic-based systems can provide this load
balancing - if designed correctly. Specifically, when one considers the
underlying reason why load balancing is usually desired, it seems that
the reason is simply that users want their requests to be served quickly.
Putting this into economic terms, users' utilities depend on the time until
their request is serviced. This is rarely formalized, but may be easily
formalized if service-time is a parameter in the parameter space of the
service type - as it is in our system. E.g., a request may specify a firm
deadline by setting the utility to be zero if the service-time is greater
than the required deadline. Similarly, gentler penalties for tardiness
may be applied by tailoring the utility function's dependence on time.
Suppliers, on the other hand, must make sure that their quotes do indeed
reflect their current capabilities in terms of service-time and must modify
them when their load changes.
Load balancing emerges automatically once the quotes of the different
suppliers do indeed reflect their actual service-time capabilities. As
a certain service supplier gets more requests assigned to it, it must raise
the service-time promised in his quotes. This will automatically cause
time-sensitive requests to be allocated to other service suppliers - those
with lower loads. Requests that are less sensitive to service-time and
more sensitive to other parameters that are optimized by a loaded supplier
may still be assigned to it. This form of load balancing strikes a balance
between optimized matching of service parameters and reducing the service-time
in a way that is locally perfect: exactly according to the specification
of the service request.
This local optimization does not necessarily imply global optimal balance
of load: an assignment of a certain supplier to one request may result
in a heavy penalty for the next request. Indeed, any formalization of optimal
global allocation is computationally intractable (NP-complete) [], and
moreover, cannot be done in an online mode - servicing requests as they
come []. Yet, we supply theoretical evidence as well as experimental results,
suggesting that load balance emerges.
3 The MAJIC system: Multiparameter Auctions
for JIni Components
The MAJIC system is built on top of Sun's Jini platform, while implementing
the basic architecture described above. We chose the Jini platform since
it is a simple yet powerful distributed object system with open source.
Moreover, Jini's object-broker mechanism - the lookup service -
turned out to be easily adapted to our purposes. In addition, Jini uses
Java's code mobility capabilities, which in our case allows transfer of
utility functions and quote functions encapsulated in objects.
3.1 Jini overview
The JiniTM system is a distributed systems technology released
by Sun Microsystems in 1999. The Jini technology enables all types of digital
devices to work together in a community, without extensive planning or
installation. It is built on top of the Java environment [] and the RMI
mechanism [33].
Detailed specifications and explanations regarding the Jini system can
be found in [1,8];
on-line documentation can be found in [23].
We now describe only the bare essentials that are directly required for
our purposes.
The Jini technology infrastructure provides mechanisms for devices,
services, and users to join and detach spontaneously from a network, and
be visible and available to those who wants to use it. Each Jini system
is built around one or more lookup services. A lookup service
is a service that maintains a list of known services and provides the ability
to search and find services via the lookup protocol. When a service
is booted on to the network, it uses the discovery protocol to find
the local lookup service. The service then registers its proxy object (a
Java object) with the lookup service using the join protocol. When
a client program queries the lookup service for a particular service (using
the lookup protocol), the lookup service returns the appropriate
service proxy (or a set of service proxies) to the client. Then, the client
can invoke methods of the chosen service using the proxy. The invocation
can be done either locally or remotely (using Java RMI protocol).
Figure 1 illustrates the system normal flow.
|
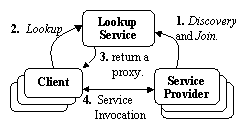 Figure Figure |
|
|
Figure 1 - Jini protocols flow
We use two other Jini concepts inside MAJIC; the first is the leasing
mechanism ([8]
ch. 10), which provides Jini its self-healing nature. This mechanism is
a timed-based resource reservation: if a service fails or stops (either
intentionally or unintentionally) without ``cleaning up'' after itself,
its leases will eventually expire and the service will be deleted. The
second concept is the service attribute set ([8]
ch. 7), a flexible way for services to annotate their proxy objects with
information describing the service; thus helping clients to find their
required services.
3.2 MAJIC Architecture overview
The MAJIC architecture is based on the general blueprint described above
applied to Jini platform. The main considerations were to preserve interoperability
and the programming paradigms of the original Jini platform, while providing
maximal flexibility. In addition, the market mechanisms should have minimal
effect on the performance of the system.
3.2.1 Service Types
Each service type in our architecture is implemented as a Jini service
that additionally implements the Economy Service Interface (ESI).
Each service type has a well known set of parameters that defines the parameter
space. The parameters are partitioned into seller parameters,
those that are totally fixed by each seller, and buyer parameters
which can be chosen by each buyer. Each service type defines a Service
Contract class (a subclass of the abstract SC class described below)
for sellers and a Buyer Valuation class (a subclass of the abstract
BV class described below) for buyers.
3.2.2 The market
The market is implemented as an extension (subclass) of Jini's lookup
service that uses economic mechanisms to perform efficient allocation.
When service providers (sellers) join the market, they submit their
quote wrapped in a Seller Contract (SC) object, passed as
one of the service attributes. Whenever a buyer performs a lookup
using the market, the buyer submits his utility function and its
parameter search engine, both wrapped in a Buyer Valuation
(BV) object. This is used by the market to create a buyer agent that performs
the economic search for the optimal seller and parameters. Finally, the
market returns a proxy to the optimal seller as the result of the lookup
request. Additionally, a Final Contract object encapsulating the
closed deal is created and sent to the buyer and to the seller. We have
implemented two distinct markets, corresponding to the two payment methods
described in the blueprint (first or second price).
3.2.3 The seller
The seller is a Jini service provider (thus additionally implementing the
ESI interface). When joining a market, the seller should submit its quote
function encapsulated in the SC object. Note that the quote function may
be implemented as an arbitrary Java method; the method's code is actually
transferred to the market. In addition to the quote function, the SC object
also includes the fixed values of all seller parameters as well some timing-control
information to be described below. Using the ESI interface, the
seller receives online notifications of all Final Contracts (described
below) and must be able to update and resubmit its SC object to the market.
When the seller is actually invoked by a buyer using a previously obtained
proxy, it must verify the validity of the corresponding FC.
3.2.4 The buyer
The buyer is a simple Jini client that in a lookup request sends the market
its BV object. The BV object encapsulates both the utility function
and the parameter search engine that finds the best values for the
buyer parameters (accessed through a getBuyerParameters()
method). Both of these may be implemented as arbitrary Java methods
whose code is transferred to the market and used as the buyers' agent.
The parameter search engine may use well-known structure information regarding
the parameter space of a particular service type, or may perform an exhaustive
search of the parameter space.
3.2.5 Final contract
The Final Contract (FC) is a sealed contract that represents
a closed deal between a buyer and a seller; it is constructed by the market
and contains the following: a unique identifier, the SC, the chosen Buyer
Parameters (BP), and the payment details. The FC should, in principle,
be digitally signed by the market (this is not currently implemented) and
is to be used as the basis for the actual electronic fund transfers.
3.2.6 Time-control mechanisms
Two mechanisms are supplied for ensuring that sellers' time-dependent quotes
are used only if they are up to date. Every SC that is submitted to the
market allows specifying a maximum number of contracts that may be created
according to this SC. Whenever the maximum is reached, the market removes
this seller from its list of service providers. Sellers with time-dependent
quotes can specify a low maximum and then must periodically update their
SC prior to this maximum being reached. In addition, each FC contains a
lease control object (LCO) that ensures sellers that their services will
be invoked by buyers within a predefined time interval. When the lease
expires, the service proxy can no longer be used and an exception is raised.
3.3 Participants obligations
There are some implicit contracts (commitments and obligations) between
all entities (players). The most significant assumption is that the market
is trustable and accepted by all sides.
The market can assign buyers to a seller, as long as its SC is valid.
The SC is valid as long as the service is registered at the lookup
service and the seller hasn't supplied the maximum number of contracts
mentioned in his SC. The seller must provide the service according to the
parameters published in the FC, as long as the FC is valid (i.e.
the FC lease hasn't expired). The seller is required to change all necessary
parameters inside its SC whenever relevant (time dependent parameters).
The buyer can execute the service during the lease duration, defined in
the FC. Both seller and buyer accept the payment details described inside
the FC.
4 Theoretical
Analysis
We describe a theoretical model that analyze our multiparameter market
system.
4.1 The Model
The Model is based on two types of players: a buyer and a seller, and a
market place. Denote by P the parameter space of a certain service type.
Each Seller S , has:
-
A private cost function: cS:P®
R+ . If S cannot provide the service with parameters p , then
cS(p)=¥.
-
A public quote function qS:P®
R+ . This function is sent to the market.
Each Buyer B , has two functions that are coupled together:
-
A utility function: uB:P®
R+ . If the service with parameters p is not acceptable at all
to him, then uB(p)=0 .
-
A function gB:Q® P , where Q
is the space of all possible quote functions. This function acts
as the parameter search engine that finds appropriate parameters,
given a quote function.
See section 2.3 for explanations.
Definition 1. gB is called optimal if "qS,
gB(qS) Î argmaxp
Î P{uB(p)-qS(p)}
. I.e., gB finds the parameters that maximize the buyer surplus.
4.1.1 The assignment mechanism
The market holds the current quotes from all sellers {qS}
, and when it receives a request from a buyer B , (uB,gB)
, it attempts matching this request to the best seller and choosing the
best parameter values. The optimization criteria is the surplus.
For a given supplier S , the parameters p are chosen by the buyer's parameter
search engine: pB,S*=gB(qS)
. The optimal seller is chosen as to optimize the surplus under these parameters:
S*=argmaxS{surplusB,S(pB,S*)}
. If surplusB,S* £
0 then the request is denied. Otherwise, the market fixes a payment dB,S*
according to one of the following payment methods:
-
first price: dB,S*=qS*(p*B,S*)
-
second price:
let S2=argmaxS ¹ S*{surplusB,S}
.
dB,S*=uB(p*B,S*)-surplusB,S2(p*B,S2)
If surplusB,S2 £
0 or S2 does not exist then dB,S*=uB(p*B,S*)
.
Finally, the market outputs the assignment B«
S* and the payment dB,S* .
We assume the following: (1) Several sellers have registered at the
market and can alter their quote functions at any moment. (2) Buyers
arrive to the market online and immediately receive a seller assignment.
4.2 Model Properties
We show that this model has the following properties: incentive compatibility,
allocation efficiency and load balancing. Our analysis uses game theoretic
notions that are standard in the field of mechanism design (see [22,29]).
Proofs for all theorems can be found in the full version of the paper [].
Definition 2. (seller gain) For a fixed buyer (uB,gB)
the gain of seller S is
where q-S is a vector of the quotes
of all other sellers.
Definition 3. (Dominant strategy) A strategy (quote)
qS of seller S is called dominant if for every other
declared quote [^(qS)] and for every declarations of all other
players q-S , gainS(qS,q-S)
³ gainS([^(qS)],q-S)
.
Definition 4. (Incentive Compatibility) A market mechanism will
be called incentive compatible if declaring the true cost function
( qS=cS ) is a dominant strategy for all sellers.
Note: We do not discuss in this paper incentive compatibility
for buyers as it is known that this can not be achieved concurrently with
incentive compatibility of sellers as known from the analysis of bilateral
trade [22].
Theorem 1 Assume that (1) the assignment of services does
not cause changes in any cS and (2) gB is optimal
for all buyers, then the second price MAJIC mechanism is incentive compatible.
According to [26],
when gB is not optimal, the VCG mechanism is not incentive compatible.
Nevertheless, there are methods that achieve feasible approximation to
incentive compatibility; such methods are described in [26].
Lemma 2 Under assumptions of theorem 4.1, "uB"[^(qS)]"q-S
gainS(cS,q-S)
³ gainS([^(qS)],q-S)
.
Definition 5. The total welfare achieved by the market is åB
gets S with p.(uB(p)-cS(p))
.
Theorem 2 Assume that (1) for all sellers qS=cS ; (2) for
each buyer gB is optimal; (3) the assignment of services does not cause
changes in any cS . Then, for every sequence of service requests the total
welfare is optimized by the market's allocation.
We can show that the load balancing achieved by this economic-based
model is good in many situations. Specifically, if all service suppliers
are identical, then we would expect for almost uniform allocation of work
among the suppliers.
Theorem 3 Assume that (1) All the service providers are identical;
(2) All buyers place a positive utility on faster service-time; (3) All
quotes are correctly updated to reflect to the service suppliers true load.
Then, the allocation obtained by the market achieves a makespan (last completion
time of a service) that is within a factor of 2 w.r.t. the optimal allocation.
It is shown in [2]
that no algorithm can achieve a better competitive ratio. As usual, and
as demonstrated by our experiments, typical behavior is much better and
applies in a wider class of situations.
5 Experimental results
We have performed several kinds of tests on the MAJIC system: the system
performance overhead, the load balancing effect, and the resource allocation
efficiency. We have created two types of services and corresponding clients:
a trivial service, called Simple, and a complex one, called Printer.
The simple service has a single parameter (price) and the corresponding
client has a fixed utility function. The printer service has several parameters:
price per page, service-time (the time that the client request can be served),
quality and speed. The service-time parameter varies with time to achieve
simulation of time dependent services.
5.1 Testing environment description
We have built a network based testing environment that enables us to execute
services and clients on several machines simultaneously. The entities (lookup
service, services and clients) and their parameters can be externally configured.
We
have used a single machine (PIII-600 processor, 128KB RAM, WinNT 4.0 OS)
for invoking the lookup service and the service providers, and another
machine (PIII-600 processor, 2GB RAM, Linux OS) for invoking the clients.
The machines were connected by LAN (Ethernet 10Mb/s).
The flow of events of each test was as follows: (1) Activating a specific
type of lookup service. (2) Activating the required service providers.
(3) Activating the clients with configurable time interval between their
invocations. (4) The clients initiate the lookup protocol and eventually
invoke the given service.
5.2 Results
5.2.1 System performance
The performance of the system has been measured by the lookup protocol
response time, since it is the most significant difference between the
Jini and the MAJIC systems. This is measured at the buyer side and contains
the lookup search time and the network latency. Fig 2 shows the performance
results in high load scenario (no time interval between clients). In low
load scenarios the results are similar, but the relative overhead is larger
(see the full version of the paper []). The tests have been performed using
1000 clients and variable number of ``simple'' services. The main purpose
of this test is to examine the MAJIC system overhead due to the market
mechanism (including the parameter search engine) and the additional message
(FC) that is being sent to the chosen seller after every assignment. We
should emphasis that the additional overhead is only for the lookup
service itself, which is normally insignificant compared to invocations
of services. From these results, we see indeed that the MAJIC overhead
is not prohibitive: in the low load case, we observed a 50% MAJIC overhead,
while in the high load case we observed only 15% overhead. The difference
between the two cases can be explained by the fact that in the high load
scenario most of the lookup time is spent on waiting for entering
the lookup service and therefore the MAJIC overhead is less significant.
|
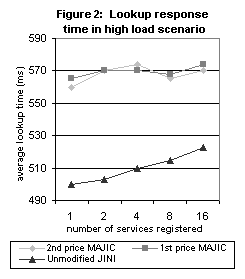 Figure Figure |
|
|
5.2.2 Load balancing
The load balancing tests have been performed on 8 printer services with
500 clients (500ms time interval between clients invocations). The services
were identical in all parameters. Each seller's service-time was constantly
updated to reflect its current load. Each buyer had a 60 ms job duration
and a utility function: uB=120-0.05·service-time
. Fig 3 shows the assignments of clients to services by the MAJIC system
(for example, service number 1 was assigned to 64 clients). The average
number of clients assigned to a service is 62.5, moreover, the maximal
deviation from the average is 10%. Pure online algorithms geared to load
balancing, which are 2-competitive, show similar results [14].
|
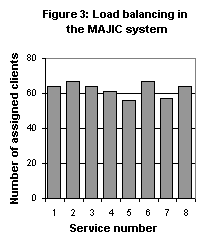 Figure Figure |
|
|
5.2.3 Resource allocation efficiency
In order to demonstrate resource allocation efficiency, we chose to perform
tests on the quality attribute of a printer service. We have designed
a system that contains printer services with different printing qualities.
In this system, each buyer had a particular preference for a printing quality.
We expected from the MAJIC system to assign buyers with preference for
higher quality to high quality printers and vice versa. We have used 3
printer services with the following qualities: High (quality=150, price=15),
Medium (quality=100, price=10) and Low (quality=50, price=5). Note that
as quality decreases the printing price decreases as well. Each buyer has
a parameter, fq , which is a continuous quality factor that
is chosen uniformly in the range of [0,1]. This factor represents the buyer's
preference for printing quality. We activated 100 clients using the following
utility function: uB=40+fq·quality . As fq
increases, the buyer utility grows faster with quality. Thus, we expect
that as the quality factor gets higher, the client will tend to be assigned
to higher quality printer, although it charges higher price. In Fig 4,
we show buyers assignments on the described services with respect to their
quality . As we can see, buyer with higher quality factor is assigned to
higher quality service. For example, the buyer with fq=0.8 is
assigned to the High quality service.
|
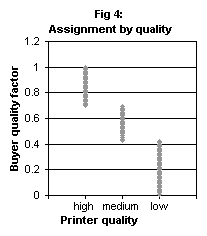 Figure Figure |
|
|
|
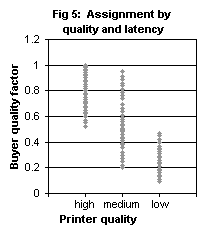 Figure Figure |
|
|
In addition, we have tested the same scenario when the printer service-time
had also been taken into consideration: uB=100+fq·quality-0.25·service_time
. As we can see in Fig 5, the service-time parameter caused a load balancing
effect; when one of the services was loaded, the clients that were supposed
to be assigned to this service have been assigned to an adjacent service
instead. We observe that even when the system manifests load balancing,
the clients' quality preferences still effect the assignments.
6 Conclusions
We have introduced a blueprint for an infrastructure that performs on line
auctions for computer services over distributed object systems. We implemented
such a system on top of Sun's Jini system. We have presented both theoretical
and initial empirical studies showing the efficiency of such systems. Two
major aspects of our architecture distinguishes our work from previous
related systems: (1) we provide a general-purpose architecture as opposed
to previous economically-based systems that were dedicated to a single
resources. (2) Our infrastructure handles a multiparameter space in a non
trivial way.
The main future test that should be applied to our system is using it
on a large scale for some specific service types. This way, we can examine
some parameters of the MAJIC system: the system efficiency, possible implementations
of parameters search engines, integration with existing security
environments, etc.
We thank Ron Lavi, Ahuva Mu'alem and Zinovi Rabinovich for their helpful
comments. We thank Yoav Etsion and Motti Beaton for technical assistance.
References
-
[1]
-
K. Arnold, B. O'Sullivan, R.W. Scheifler, J. Waldo, and A. Wollrath. The
Jini Specification. Addison-Wesley Publishing, Reading MA, 1999.
-
[2]
-
Y. Azar and L. Epstein. On-line load balancing of temporary tasks on identical
machines. 5th Israeli Symposum on Theory of Computing and Systems,
pages 119 - 130, 1993.
-
[3]
-
O. Rees N. Edwards M. Madsen M. Beasley and A. McClenaghan. A web of distributed
objects. World Wide Web Journal, 1(1):75 - 88, 1995.
-
[4]
-
E. H. Clarke. Multipart pricing of public goods. Public Choice,
pages 17-33, 1971.
-
[5]
-
The omg's corba website. Web Page: https://www.corbe.org/.
-
[6]
-
Microsoft dcom technology - distributed component object model. Web Page:
https://www.microsoft.com/com/tech/DCOM.asp.
-
[7]
-
Bernardo Huberman (ed.). The Ecology of Computation. Elsevier Science
Publishers/North-Holland, 1988.
-
[8]
-
W. Kieth Edwards. Core Jini. Prentice Hall PTR, Upper Saddle River
NJ, 1999.
-
[9]
-
Amin Vahdat et al. Webos: Operating system services for wide area applications.
The Seventh IEEE Symposium on High Performance Distributed Computing,
1998.
-
[10]
-
Carl A. Waldspurger et al. Spawn: A distributed computational economy.
IEEE Trans. on Software Engineering, 18(2), 1992.
-
[11]
-
Christos Ferguson, Donald F. Nikolaou and Yechiam Yemini. Economic models
for allocating resources in computer systems. In Scott Clearwater, editor,
Market-Based Control: A Paradigm for Distributed Resource Allocation.
World Scientific, 1995.
-
[12]
-
A. Fiat and G. J. Woeginer. Online Algorithms The state of the Art,
Lecture Notes in Computer Science, 1442. Springer, Verlag Berlin Heidelberg,
1998.
-
[13]
-
R. L. Graham. Bounds for certain multiprocessing anomalies. Bell System
Techincal Journal, 45:1563 - 1581, 1966.
-
[14]
-
R. L. Graham. Bounds on multiprocessing timing anomalies. SIAM J. Appl.
Math, 17:263 - 269, 1969.
-
[15]
-
T. Groves. Incentives in teams. Econometrica, pages 617-631, 1973.
-
[16]
-
Brnardo A. Huberman and Tad Hogg. Distributed computation as an economic
system. Journal of Economic Perspectives, pages 141-152, 1995.
-
[17]
-
Jini organization. Web Page: https://www.jini.org.
-
[18]
-
Y. A. Korilis and A. A. Lazar. On the existence of equilibria in non-cooperative
optimal flow control. Journal of the ACM, 42(3), 1995.
-
[19]
-
A.A. Lazar and N. Semret. The progressive second price auction mechanism
for network resource sharing. In 8th International Symposium on Dynamic
Games, Maastricht, The Netherlands, July 1998.
-
[20]
-
Nathan Lineal. Game theoretic aspects of computing. In Handbook of Game
Theory, volume 2, pages 1339-1395. Elsevier Science Publishers B.V,
1994.
-
[21]
-
J. K. Mackie-Mason and H. R. Varian. Pricing the internet. In B. Kahn and
J. Keller, editors, Public Access to the Internet. Prentice Hall,
1994.
-
[22]
-
A. Mas-Collel, W. Whinston, and J. Green. Microeconomic Theory.
Oxford university press, 1995.
-
[23]
-
The jini homepage. Web Page: https://www.sun.com/jini.
-
[24]
-
Dov Monderer and Moshe Tennenholtz. Distributed games. To appear in Games
and Economic Behaviour.
-
[25]
-
Noam Nisan and Amir Ronen. Algorithmic mechanism design. In STOC,
1999. Avilable at https://www.cs.huji.ac.il/~ amiry.
-
[26]
-
Noam Nisan and Amir Ronen. Computationally feasible vcg-based mechanisms.
In EC, 2000.
-
[27]
-
Ori Regev Noam Nisan, Shmulik London and Noam Camiel. Globally distributed
computation over the internet - the popcorn project. In ICDCS, 1998.
-
[28]
-
Orb/os task force. Web Page: https://www.omg.org/homepages/orbos/.
-
[29]
-
M. J. Osborne and A. Rubistein. A Course in Game Theory. MIT press,
1994.
-
[30]
-
T. R Palfrey. Handbook of Game Theory, chapter Implementation Theory.
Elsevier Science B.V., 1995.
-
[31]
-
Christos H. Papadimitriou. Computational aspects of organization theory.
In Proceedings of the 1996 European Symposium on Algorithms. Springer
LNCS, 1996.
-
[32]
-
Ori Regev and Noam Nisan. The popcorn market - an online market for computational
resources. In ICE, 1998.
-
[33]
-
Java remote method invocation. Web Page: https://java.sun.com/products/jdk/1.2/docs/guide/rmi/spec/rmiTOC.doc.html.
-
[34]
-
Tuomas Sandholm. An algorithm for optimal winner determination in combinatorial
auctions. In IJCAI-99, 1999.
-
[35]
-
Tuomas W. Sandholm. Limitations of the vickrey auction in computational
multiagent systems. In Proceedings of the Second International Conference
on Multiagent Systems (ICMAS-96), pages 299-306, Keihanna Plaza, Kyoto,
Japan, December 1996.
-
[36]
-
S. Clark D. E. Shenkar and Hertzog S. Pricing in computer networks: Reshaping
the research agenda. ACM Computational Comm. Review, pages 19-43,
1996.
-
[37]
-
S. Shenker. Making greed work in networks: A game-theoretic analysis of
switch service disciplines. In Proc. of the ACM SIGCOMM, 1994.
-
[38]
-
The simple object access protocol. Web Page: https://www.microsoft.com/mind/0100/soap/soap.asp.
-
[39]
-
A. Bakker E. Amade G. Ballintijn I. Kuz P. Verkaik I. van der Wijk M. van
Steen and A.S. Tanenbaum. The globe distribution network. Proc. 2000
USENIX Annual Conf., 1:141 - 152, 2000.
-
[40]
-
W. Vickrey. Counterspeculation, auctions and competitive sealed tenders.
Journal of Finance, pages 8-37, 1961.
-
[41]
-
C. A. Waldspurger, T. Hogg, B. A. Huberman, J. O. Kephart, and W. S. Stornetta.
Spawn: A distributed computational ecology. Ieee Transactions on Software
Engineering, 18(2), 1992.
-
[42]
-
W.E. Walsh and M.P. Wellman. A market protocol for decentralized task allocation:
Extended version. In The Proceedings of the Third International Conference
on Multi-Agent Systems (ICMAS-98), 1998.
-
[43]
-
W.E. Walsh, M.P. Wellman, P.R. Wurman, and J.K. MacKie-Mason. Auction protocols
for decentralized scheduling. In Proceedings of The Eighteenth International
Conference on Distributed Computing Systems (ICDCS-98), Amsterdam,
The Netherlands, 1998.
-
[44]
-
Webbroker: Distributed object communication on the web. Web Page: https://www.w3.org/TR/1998/NOTE-webbroker/.
-
[45]
-
Andrew S. Grimshaw Wm. A. Wulf and the Legion team. The legion vision of
a worldwide virtual computer. Communications of the ACM, 40(1),
1997.
-
[46]
-
Xml home page. Web Page: https://www.xml.com/pub.
-
[47]
-
Extensible markup language (xml) 1.0. Web Page: https://www.w3.org/TR/REC-xml.
Footnotes:
1 Email:
{liorl,liad,noam}@cs.huji.ac.il. Supported by grants from the Israeli Ministry
of Science and the Israeli Academy of Sciences.
2Multiparameter
Auctions for JIni Components
File translated from TEX by TTH,
version 2.86.
On 17 Jan 2001, 17:42.
|
