A Compacting Real-Time Memory Management System

We propose a real real-time memory management system called Compact-fit that offers both time and space predictability. Compact-fit is a compacting memory management system for allocating, deallocating, and accessing memory in real time. The system provides predictable memory fragmentation and response times that are constant or linear in the size of the request, independently of the global memory state. We present two Compact-fit implementations and compare them to established memory management systems, which all fail to provide predictable memory fragmentation. The experiments confirm our theoretical complexity bounds and demonstrate competitive performance. In addition, we can control the performance versus fragmentation trade-off via our concept of partial compaction. The system can be parameterized with the needed level of compaction, improving the performance while keeping memory fragmentation predictable.

1 Introduction

We present a compacting real-time memory management system called Compact-fit (CF) together with a moving and a non-moving implementation. Compact-fit is an explicit memory management system for allocating, deallocating, and accessing memory objects. Memory fragmentation in CF is bounded by a compile-time parameter. In CF compaction may only happen upon freeing a memory object and involves moving a single memory object of the same size.

Memory in CF is partitioned into 16KB pages. Each page is an instance of a so-called size-class, which partitions a page further into same-sized page-blocks. We adapt the concept of pages and size-classes from [2]. A memory object is always allocated in a page of the smallest-size size-class whose page-blocks still fit the object. Memory objects larger than 16KB are currently not supported. However, in a future version, arraylets [3] may be used to handle objects of larger size with CF's complexity bounds.

The key idea in CF is to keep the memory size-class-compact at all times. In other words, at most one page of each size-class may be not-full at any time while all other pages of the size-class are always kept full. Whenever a memory object is freed, a memory object in the not-full page is moved to take its place and thus maintain the invariant. If the not-full page becomes empty, it can be reused in any size-class. Using several list and bitmap data structures, free space can be found in constant time, upon an allocation request.

The moving CF implementation maps page-blocks directly to physically contiguous pieces of memory, and therefore requires moving memory objects for compaction. Allocation takes constant time in the moving implementation, whereas deallocation takes linear time if compaction occurs. Dereferencing requires an additional pointer indirection and takes constant time.

The non-moving CF implementation uses a block table (effectively creating a virtual memory) to map page-blocks into physical block-frames that can be located anywhere in memory. In this case, compaction merely requires re-programming the block table rather than moving memory objects. However, although compaction may be faster, deallocation still takes linear time in the size of the object due to the block table administration. For the same reason allocation also takes linear time in the non-moving implementation. Our experiments show that deallocation is faster in the non-moving implementation for configurations in which block-frames are at least 80B. Dereferencing requires two additional pointer indirection and takes constant time.

A pointer in CF is an address and an offset. The CF system therefore supports offset-based rather than address-based pointer arithmetics, which we elaborate on later in the paper. Note that, in principle, the moving implementation may also support address-based pointer arithmetics since each memory object is allocated in a single physically contiguous piece, that may however move during compaction.

In both implementations we can relax the always-compact-requirement allowing for more than one not-full page per size-class. As a result deallocation takes less time: it reduces up to constant time. This way we formalize, control, and implement the trade-off between temporal performance and memory fragmentation.

We present the results of benchmarking both implementations, as well as implementations of non-compacting real-time memory management systems (Half-fit [11] and TLSF [10]) and traditional (non-real-time) memory management systems (First-fit [7], Best-fit [7], and Doug Lea's allocator [8]) using synthetic workloads.

The contributions of this paper are: the CF system, the moving and non-moving implementations, and the experimental results on bare metal and Linux.

The rest of the paper is organized as follows: Section 2 discusses the principles behind the design of the compacting real-time memory management system. The implementation details and the complexity issues are presented in Section 3. We discuss related work in Section 4, and present the experiments, results and comparisons in Section 5. Section 6 wraps up with discussion and conclusion.

2 Principles of Compact-Fit

We start by introducing the goals of memory management in general and the requirements for real-time performance in particular. Having the basis set, we present our proposal for a compacting memory management system that meets the real-time requirements. We focus on the conceptual issues in this section and on the technical details in the following section.

2.1 Basics of Memory Management

By memory management we mean dynamic memory management. Applications use the dynamic memory management system to allocate and free (deallocate) memory blocks of arbitrary size in arbitrary order. In addition, applications can use the memory management system for accessing already allocated memory, dereferencing. Memory deallocation can lead to memory holes, which can not be reused for future allocation requests, if they are too small: this is the fragmentation problem. The complexity of allocation and deallocation depends on the fragmentation. A way to fight fragmentation is by performing compaction or defragmentation: a process of rearranging the used memory space so that larger contiguous pieces of memory become available.

2.2 Real-Time Requirements

Traditional dynamic memory management strategies are typically non-deterministic and have thus been avoided in the real-time domain. The memory used by real-time programs is usually allocated statically, which used to be a sufficient solution in many real-time applications. Nowadays increasing complexity demands greater flexibility of memory allocation, so there is a need of designing dynamic real-time memory management systems. Even in soft real-time systems and general purpose operating systems there exist time-critical components such as device drivers that operate on limited amount of memory because of resource and/or security constraints and may require predictable memory management.

In an ideal dynamic real-time memory management system each unit operation (memory allocation, deallocation, and dereferencing) takes constant time. We refer to this time as the response time of the operation of the memory management. If constant response times can not be achieved, then bounded response times are also acceptable. However, the response times have to be predictable, i.e., bounded by the size of the actual request and not by the global state of the memory.

More precisely, real-time systems should exhibit predictability of response times and of available resources.

The fragmentation problem affects the predictability of the response times. For example, if moving objects in order to create enough contiguous space is done upon an allocation request, then the response time of allocation may depend on the global state of the memory.

Predictability of available memory means that the number of the actual allocations together with their sizes determines how many more allocations of a given size will succeed before running out of memory, independently of the allocation and deallocation history. In a predictable system also the amount of fragmentation is predictable and depends only on the actual allocated objects. In addition to predictability, fragmentation should be minimized for better utilization of the available memory.

Most of the established explicit dynamic memory management systems [8,7] are optimized to offer excellent best-case and average-case response times, but in the worst-case they are unbounded, i.e., they depend on the global state of the memory. Hence these systems do not meet the above mentioned requirement on predictability of response times.

Moreover, to the best of our knowledge, none of the established explicit dynamic memory management systems meets the memory predictability requirement since fragmentation depends on the allocation and deallocation history.

The memory management system that we propose offers bounded response times (constant or linear in the size of the request) and predictable memory fragmentation, which is achieved via compaction.

Performing compaction operations could be done in either event- or time-triggered manner. As the names suggest, event-triggered compaction is initiated upon the occurrence of a significant event, whereas time-triggered compaction happens at predetermined points in time. Our compaction algorithm is event-triggered, compaction may be invoked upon deallocation.

2.3 Abstract and Concrete Address Space

We now describe the compacting real-time memory management system. At first, we focus on the management of memory addresses. Conceptually, there are two memory layers: the abstract address space and the concrete address space. Allocated objects are placed in contiguous portions of the concrete address space. For each allocated object, there is exactly one abstract address in the abstract address space. No direct references from applications to the concrete address space are possible: an application references the abstract address of an object, which furthermore uniquely determines the object in the concrete space. Therefore the applications and the memory objects (in the concrete space) are decoupled. All memory operations operate on abstract addresses. We start by defining the needed notions and notations.

The abstract address space is a finite set of integers denoted by $\mathbb{A}$ . An abstract address

is an element of the abstract address space, $a \in \mathbb{A}$ .

The concrete address space is a finite interval of integers denoted by $\mathbb{C}$ . Note that, since it is an interval, $\mathbb{C}$ is contiguous. Moreover, both the concrete and the abstract address spaces are linearly ordered by the standard ordering of the integers. A concrete address

is an element of the concrete address space, $c \in \mathbb{C}$ .

A memory object

is a subinterval of the concrete address space, $m \in \mathcal{I}(\mathbb{C})$ . For each memory object, two concrete addresses $c_1, c_2 \in \mathbb{C}$ , such that $c_1 \leq c_2$ , define its range, i.e., we have $m = [c_1,c_2] = \{x\mid c_1 \leq x \leq c_2\}$ .

As mentioned above, a used abstract address refers to a unique range of concrete addresses, which represents a memory object. Vice versa, the concrete addresses of an allocated memory object are assigned to a unique abstract address. To express this formally, we define a partial map that assigns to an abstract address the interval of concrete addresses that it refers to. The abstract address partial map

$\displaystyle \address:\mathbb{A} \hookrightarrow \mathcal{I}(\mathbb{C})$

maps abstract addresses to memory objects. We say that an abstract address

is in use if $\address(a)$ is defined. The abstract address map is injective, i.e., different abstract addresses are mapped to different subintervals, and moreover for all abstract addresses $a_1,a_2 \in \mathbb{A}$ that are in use, if $a_1 \neq a_2$ , then $\address(a_1)\cap\address(a_2) = \emptyset$ .

Accessing a specific element in the concrete address space $\mathbb{C}$ requires two pieces of information: the abstract address

and an offset

, pointing out which element in the memory object $m = \address(a)$ is desired. Therefore the next definition: An abstract pointer denoted by

is a pair $a_{p} = (a, o)$ , where

is an abstract address in use (!) and

is an offset, $o \in \{0, \ldots, \vert\address(a)\vert - 1\}$ . By $\vert.\vert$ we denote the cardinality of a set. The abstract pointer space is the set of all abstract pointers

, and it is denoted by $\mathbb{A}_p$ . There is a one-to-one correspondence between $\mathbb{A}_p$ and the allocated subset of $\mathbb{C}$ . Each abstract pointer $a_{p}$ refers to a unique concrete address

via the abstract pointer mapping

$\displaystyle {\mathrm{pointer}}: \mathbb{A}_{p} \to \mathbb{C}.$

It maps an abstract pointer

to the concrete address of the memory object $m = \address(a)$ that is at position

with respect to the order on $\address(a)$ .

Let $\mathbb{A}=\{1,2,3\}$ and $\mathbb{C}=\{1,2,\ldots,10\}$ . Assume that three memory objects of different size are allocated: $\address(1)=[2,3]$ , $\address(2)=[6,7]$ and $\address(3)=[8,10]$ . The abstract addresses together with their offsets create abstract pointers, which are mapped to $\mathbb{C}$ . For example, ${\mathrm{pointer}}(1,1) = 3$ and ${\mathrm{pointer}}(3,1) = 9$ . Figure 1 depicts this situation.

We now elaborate the benefits of using an abstract memory space. All references are redirected via the abstract memory space. An application points to a concrete memory location via an abstract pointer, cf. Figure 2(a).

Large data-structures often consist of a number of allocated memory objects connected via references (e.g. linked lists or trees) that depict the dependencies between the objects. These dependencies are handled via abstract pointers as well. This situation is also shown in Figure 2(a).

Indirect referencing facilitates predictability of reference updates during compaction. If fragmentation occurs, the concrete address space $\mathbb{C}$ gets compacted and the references from the abstract address space $\mathbb{A}$ to the concrete address space $\mathbb{C}$ are updated, as shown in Figure 2. Hence, objects are moved in $\mathbb{C}$ and references are updated in $\mathbb{A}$ . The number of reference updates is bounded: movement of one memory object in $\mathbb{C}$ leads to exactly one reference update in $\mathbb{A}$ . In contrast, direct referencing (related to object dependencies) would imply unpredictable number of reference updates. This is why we chose for an abstract address space design. However, note that the abstract address space is only required for predictable reference updating during compaction but otherwise completely orthogonal to the compaction algorithm and its moving and non-moving implementations described below.

**Figure 2:** Compaction
(a) Before: fragmented concrete space
(b) After: compact concrete space

The CF system provides three explicit memory operations (whose implementation we discuss in Section 3):

Note that the abstract address of an allocated memory object never changes until the object gets freed. The abstract address can therefore be used for sharing objects. The concrete address(es) of an allocated memory object may change due to compaction. To this end, we point out another difference between the abstract and the concrete address space. Over time, they may both get fragmented. The fragmentation of the concrete space presents a problem since upon an allocation request the memory management system must provide a sufficiently large contiguous memory range. In the case of the abstract address space, a single address is used per memory object, independently of its size. Hence, upon an allocation request, the memory management system needs to find only a single unused abstract address. We can achieve this within a constant-time bound, without keeping the abstract address space compact.

2.4 Size-Classes

For administration of the concrete address space, we adopt the approach set for Metronome [2,3,1].

The following ingredients describe the organization of the concrete address space.

Every allocation request is handled by a single page-block. When an allocation request malloc(

) arrives, CF determines the best fitting page-block size

and inserts the object into a page-block in a page that belongs to size-class

. The best fitting page-block size is the unique page-block size

that satisfies $S_{i-1} < size \le S_i$ .

If a used page becomes free upon deallocation, then the page is removed from its size-class and can be reused in any possible size-class.

Figure 3 shows an exemplary view of the organization of the concrete address space: There are three size-classes: in one of them there are two pages, in the other two there is a single page per class.

2.5 Fragmentation

The size-classes approach is exposed to several types of fragmentation: page-block-internal fragmentation, page-internal fragmentation, and size-external fragmentation [2]. We will briefly discuss each of them and the impact they have on our design decisions. Figure 3 shows the different types of fragmentation as well.

2.5.1 Page-Block-Internal Fragmentation

Page-block-internal fragmentation is the unused space at the end of a page-block. Given a page

in size class

(the page-blocks in

have size

), let

for $j =1, \dots, B_p$ be the page-blocks appearing in the page

, where $B_p = P {\mathrm{div}}S_i$ . For a page-block

we define ${\mathrm{used}}(b_j) = 1$ if

is in use, and ${\mathrm{used}}(b_j) = 0$ otherwise. We also write ${\mathrm{data}}(b_j)$ for the amount of memory of

that is allocated. The page-block-internal fragmentation for the page

is calculated as

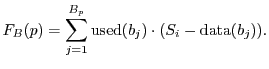
$\displaystyle F_{B}(p) = \sum_{j = 1}^{B_p}{\mathrm{used}}(b_j)\cdot(S_i - {\mathrm{data}}(b_j)).$

One can also calculate the total page-block-internal fragmentation in the memory by summing up the page-block-internal fragmentation for each page.

The total page-block-internal fragmentation can be bounded by a factor

if the page-block sizes are chosen carefully. Namely, Berger et al. [4] suggest the following ratio between adjacent page-block sizes:

for

. The size of the smallest page-blocks

and the parameter

can be chosen program-specifically. Bacon et al. [2] propose a value for the parameter

, which leads to minor size differences for smaller size-classes and major size differences for larger size-classes.

2.5.2 Page-Internal Fragmentation

Page-internal fragmentation is the unused space at the end of a page. If all possible page-block sizes $S_1, \dots, S_n$ are divisors of the page size

, then there is no page-internal fragmentation in the system. However, if one uses Equation (1) for the choice of page-block sizes, then one also has to acknowledge the page-internal fragmentation. For a page

in size-class

, it is defined as

2.5.3 Size-External Fragmentation

Size-external fragmentation measures the unused space in a used page. This space is considered fragmented or ``wasted'' because it can only be used for allocation requests in the given size-class. For example, let

be a page in size-class

with

32B. If only one page-block of

is allocated, then there is

32B unused memory in this page. If no more allocation requests arrive for this size-class, then this unused memory can never be used again. In such a situation an object of size 32B consumes the whole page. The size-external fragmentation of a page

in size-class

is bounded by

The total size-external fragmentation in the system is bounded by the sum of

, over all pages.

The more size-classes there are in the system, the less page-block-internal fragmentation occurs, but therefore the size-external fragmentation may grow. Hence, there is a trade-off between page-block-internal and size-external fragmentation, which must be considered when defining the size-classes.

2.6 The Compaction Algorithm

The compaction algorithm of CF behaves as follows. Compaction is performed after deallocation in the size-class affected by the deallocation request. It implies movement of only one memory object in the affected size-class. Before presenting the algorithm, we state two invariants and two rules that are related to our compaction strategy. Recall that each size-class is a doubly-circularly-linked list.

Invariant 1 In each size-class there exists at most one page which is not full.

Invariant 2 In each size-class, if there is a not-full page, then this is the last page in the size-class list.

Rule 1 If a memory object of a full page in a size-class gets freed, and there exists no not-full page, then becomes the not-full page of its size-class and it is placed at the end of the size-class list.

Rule 2 If a memory object of a full page in a size-class gets freed, and there exists a not-full page in the size-class, then one memory object of moves to . If becomes empty, then it is removed from the size-class.

Not every deallocation request requires moving of a memory object. The cases when no moving is necessary are:

Note that when a memory object moves from one page to another, then we need to perform a reference update in the abstract address space, in order that the abstract address of a memory object points to its new location.

$\begin{figure}\renewedcommand{baselinestretch}{1} \begin{lstlisting}[frame=tb,ca... ...e); abstract_address_space_update(object); } } } \end{lstlisting}\end{figure}$

3 Details and Complexity

In this section we elaborate on the implementation details of CF. We start by discussing the details of the concrete address space management, i.e., administration of the page-blocks, pages, and size-classes. Next we describe the implementation and the complexity results for both the moving and the non-moving version of CF. At the end of this section we also explain the concept of partial compaction.

3.1 Managing Size-Classes

As mentioned above, we use pages of size 16KB. If needed, the page size can be modified for specific applications. The minimal page-block size

in our benchmarks is

B, but it can also be reduced to a smaller size. Successive page-block sizes are determined by Equation (1) taking

In addition to the 16KB storage space, each page has a header with additional information used for the memory management. The layout of a page with all administrative information is illustrated in Figure 4.

The fields Next Page and Previous Page contain references to the next and the previous page within the size-class, respectively. These two references build the size-class list. The field Size-Class refers to the size-class instance of the page, which further refers to the head of the size-class list. Hence, we can directly access the head and therefore also the tail of the size-class list from any page, which is important for compaction.

A page consists of page-blocks, some of which are in use and some are free. For memory object allocation, we must find a free page-block in a page in constant time and for compaction, we must find a used page-block in a page in constant time. Therefore, the state of the page (the status of all page-blocks) is recorded in a two-dimensional bitmap, as shown in Figure 4. A bitmap of size $16\times 32$ is enough to record the status of the page-blocks since we have at most 512 page-blocks per page. In addition, we need 16 more bits to record if at least one bit is set for each row of the bitmap. This additional bitstring is essential for constant-time access to a used page-block within the page and it is used to determine whether a page is full or not in constant time (one comparison). There are CPU instructions that find a set bit in a bitstring in constant time. These instructions are limited to bitstrings of length 32 (on a 32-bit CPU), which is the reason why we use such a two-dimensional bitmap. In order to get a used (respectively free) page-block we first find a set bit in the additional bitstring, and then get a set bit in the corresponding row of the bitmap.

The free pages are organized in a special LIFO list. Since all pages are arranged contiguously in memory, no list initialization is necessary. If the LIFO list is empty and a free element is required, the next unused element of the contiguous space is returned (if such an element exists). We refer to this list construction as free-list.

Note that the administrative information of a page, as shown in Figure 4, takes 78B out of the 16KB page memory. Hence, the memory overhead is less than 0.47%.

3.2 Moving Implementation

The abstract address space is implemented in a contiguous piece of memory. The free entries of the abstract address space are organized in a free-list.

The concrete address space is organized as described in Section 3.1. Each page is implemented as a contiguous piece of memory as well. Moreover, each page-block contains an explicit reference to its abstract address in the abstract address space. This reference is located at the end of the page-block. In the worst case, it occupies 12.5% of the page-block size. These backward references allow us to find in constant time the abstract address of a memory object of which we only know its concrete address. Therefore they are essential for constant-time update of the abstract address space during compaction.

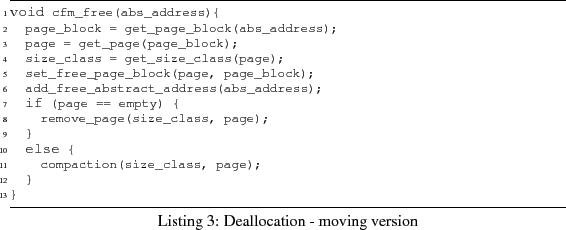
We next present the allocation, deallocation, and dereferencing algorithms and discuss their complexity. The algorithm for allocation cfm_malloc is presented in Listing 2. The function get_page_of_size_class returns a page of the corresponding size-class in constant time: if all pages in the size-class are full, then with help of the free-list of free pages, we get a new page; otherwise the not-full page of the size-class is returned. Hence this function needs constant time. The function get_free_page_block takes constant time, using the inverse of the two-dimensional bitmap of a page. Declaring a page-block used is just a bit-set operation. As mentioned above, the free abstract addresses are organized in a free-list, so the function create_abstract_address takes constant time. As a result, cfm_malloc takes constant time, i.e., $\Theta($ cfm_malloc(

) $) = \Theta(1)$ .

$\begin{figure}\renewedcommand{baselinestretch}{1} \begin{lstlisting}[frame=tb,ca... ...ge); return create_abstract_address(page_block); } \end{lstlisting}\end{figure}$

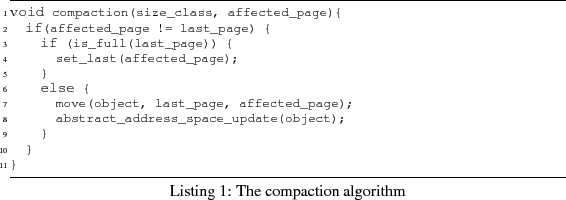
The deallocation algorithm cfm_free is shown in Listing 3. The function get_page_block takes constant time, since it only accesses the memory location to which the abstract address refers. The function get_page takes several arithmetic operations, i.e., constant time. Namely, pages are linearly aligned in memory so for a given page-block we can calculate the starting address of its page. The function get_size_class is executed in constant time, since every page contains a field Size-Class. The function set_free_page_block changes the value of a single bit in the bitmap, so it also requires constant time and add_free_abstract_address amounts to adding a new element to the corresponding free-list, which is done in constant time too. Removing a page from a size-class remove_page requires also constant time: first a page is removed from the size-class list; then it is added to the free-list of empty pages. Therefore, the complexity of cfm_free equals the complexity of the compaction algorithm.

The complexity of the compaction algorithm, compaction, is linear in the size of the page-blocks in the corresponding size-class since it involves moving a memory object. Note that the complexity of the abstract address space update is constant, due to the direct reference from page-blocks to abstract addresses.

Hence, the worst-case complexity of cfm_free is linear in the size of the page-block: $\mathcal O($ cfm_free(abs_address) $) = \mathcal O(s)$ for

being the size of page-blocks in the size-class where abs_address refers to. Thus, for a fixed size-class, we have constant complexity.

$\begin{figure}\renewedcommand{baselinestretch}{1} \begin{lstlisting}[frame=tb,ca... ...ge); } else { compaction(size_class, page); } } \end{lstlisting}\end{figure}$

In this moving implementation, the physical location of a memory object is accessed by dereferencing an abstract pointer. The dereferencing contains a single line of code *(*abs_address + offset); given an abstract pointer (abs_address, offset).

To conclude, the only source of non-constant (linear) complexity in the moving implementation is the moving of objects during compaction. In an attempt to lower this bound by a constant factor, we implement the non-moving version.

3.3 Non-Moving Implementation

We call this implementation non-moving, since memory objects do not change their location in physical memory throughout their lifetime, even if compaction is performed.

In the non-moving implementation, the abstract address space is still a contiguous piece of memory. However, we no longer use the free-list for administrating free abstract addresses, since now there is an implicit mapping from the memory objects to the abstract addresses. We will elaborate on this in the next paragraph. The implicit references (from memory objects to abstract addresses) are used for constant-time updates of the abstract address space.

First, let us explain the difference in the implementation of the concrete address space. The concrete address space is managed by a virtual memory. The virtual memory consists of blocks of equal size. The physical memory is contiguous and correspondingly divided into block-frames of equal size. For further reference we denote this size by

. These blocks and block-frames must not be confused with the page-blocks: they are global, for the whole memory, above the page concept. Therefore, each block-frame is directly accessible by its ordinal number. The free block-frames are also organized in a free-list. The abstract address space is pre-allocated, and contains as many potential abstract addresses as there are block-frames. A unique abstract address corresponds to a memory object

: the abstract address at position

in the abstract address space, where

is the ordinal number of the first block-frame of

in the physical memory. This way, we do not need an explicit reference stored in each page-block, thus we avoid the space overhead characteristic to the moving implementation. Moreover, getting a free abstract address is immediate, as long as we can allocate a block-frame in physical memory.

A block table records the mapping from virtual memory blocks to memory block-frames. In our implementation, the block table is distributed over the pages, which simplifies the page-specific operations. The organization of the memory in this implementation is shown in Figure 5.

Objects are allocated in contiguous virtual memory ranges, but actually stored in arbitrarily distributed physical memory block-frames. We still use the concepts of pages, size-classes and page-blocks, with some differences. A page is now a virtual page: It does not contain any data; in its Data segment it contains the part of the block table that points to the actual data in the physical memory. Moreover, for administration purposes all page-block sizes are multiples of the unique block size. Hence, each page-block consists of an integer number of blocks. This implies that we can not directly use Equation (1), we need to round-up the page-block sizes to the next multiple of the block size.

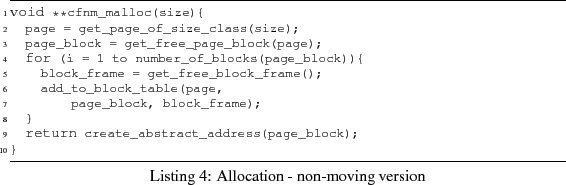
The allocation algorithm is shown in Listing 4. In comparison to the moving implementation, we have now a loop that handles the allocation block-frame-wise. Note that number_of_blocks(page_block) is constant for a given size-class. Getting a free block-frame, and creating a corresponding block-table entry, takes constant time. Therefore, the complexity of the allocation algorithm is linear in the number of block-frames in a page-block, i.e., $\Theta($ cfnm_malloc(size)) $= \Theta(n)$ where

for

the page-block size of the size-class. Again, this means constant complexity in the size-class.

The function create_abstract_address in the non-moving implementation uses the implicit references from memory objects to abstract addresses.

$\begin{figure}\renewedcommand{baselinestretch}{1} \begin{lstlisting}[frame=tb,ca... ...; } return create_abstract_address(page_block); } \end{lstlisting}\end{figure}$

$\begin{figure}\renewedcommand{baselinestretch}{1} \begin{lstlisting}[frame=tb,ca... ...ge); } else { compaction(size_class, page); } } \end{lstlisting}\end{figure}$

In comparison to the moving implementation, we have to free each block-frame in the memory occupied by the freed memory object. This requires a loop with as many iterations as there are block-frames for the memory object. As above, there are

block-frames, where

is the size of the size-class and

the size of the block-frame. Moreover, the compaction algorithm is implemented differently: memory objects are only virtually moved, by updating the block table. This is still linear in the size of the size-class, but we achieve a constant speed-up: it actually takes

updates of the block table. As a result, the complexity of the deallocation algorithm in the non-moving implementation is $\Theta($ cfnm_free) $= \Theta(n)$ , which is again constant for a given size-class.

Finally, we consider the dereference algorithm. It provides direct access to a memory location corresponding to a given abstract pointer (abs_address, offset). Dereferencing takes constant time, with several more calculations than in the moving implementation. The algorithm is shown in Listing 6. In the code, s_b stands for the size of a block,

$\begin{figure}\renewedcommand{baselinestretch}{1} \begin{lstlisting}[frame=tb,ca... ...address + (offset div s_b)) + (offset mod s_b)); } \end{lstlisting}\end{figure}$

We conclude that the non-moving implementation achieves a constant speed-up of the compaction algorithm, while the complexity of the allocation algorithm grows from constant to linear. The complexity of deallocation and dereference is the same in both implementations.

3.4 Partial Compaction

Up to now we always considered the very strong aim of ``always compact size-classes", i.e., our invariant was that at any moment in time in each size-class at most one page is not full. We now relax this invariant by allowing for a given number of not-full pages per size-class. Varying the number of allowed not-full pages per size-class, max_nr_nf_pages, results in various levels of compaction. For example, max_nr_nf_pages

means always compact memory (as described above), but therefore larger compaction overhead, whereas high values of max_nr_nf_pages lead to faster memory management, for the price of higher fragmentation. This way we formalize, control, and implement the trade-off between temporal performance and memory fragmentation.

We implement this new approach as follows. A size-class instance now consists of three fields: head_full_pages, head_not_full_pages, and nr_not_full_pages. Therefore it consists of two doubly-circularly-linked lists: one containing the full pages and another one containing the not-full pages. The initial value of nr_not_full_pages is zero and it never exceeds a pre-given number, max_nr_nf_pages. If all pages are full, then allocation produces a new not-full page, so nr_not_full_pages is incremented. In case a not-full page gets full after allocation, it is moved to the list of full pages, and nr_not_full_pages is decremented. If deallocation happens on a page-block that is in a not-full page, no compaction is done. If it happens on a page-block which is in a full page, then compaction is called if nr_not_full_pages

max_nr_nf_pages. Otherwise, no compaction is done, the affected page is moved from the list of full pages to the list of not-full pages, and nr_not_full_pages is incremented.

For better average-case temporal and spatial performance, we keep pages that are more than half-full at the end of the not-full list, and pages that are at most half-full at the head of the list. Allocation is served by the last page of the not-full list, which may increase the chances that this page gets full. Used page-blocks that need to be moved because of compaction are taken from the first page of the not-full list, which might increase the chances that this page gets empty. Note that, for the best possible spatial performance, it would be better to keep the not-full list sorted according to the number of free page-blocks in each non-full page. However, inserting a page in a sorted list is too time-consuming for our purposes and can not be done in constant time.

It should be clear that each deallocation when nr_not_full_pages

max_nr_nf_pages takes constant time, i.e., involves no compaction. However, this guarantee is not very useful in practice: given a mutator we can not find out (at compile time) the maximal number of not-full pages it produces. Therefore we describe another guarantee.

Given a size-class, let

count deallocations for which no subsequent allocation was done. Initially,

. Whenever deallocation happens,

is incremented. Whenever allocation happens,

is decremented, unless it is already zero. We can now state the following guarantee.

Proposition 1 Each deallocation that happens when max_nr_nf_pages takes constant time in the CF moving implementation, i.e., it involves no compaction.

Namely, a simple analysis shows that ${\tt \small\verb+nr_not_full_pages+}\le n_f + 1$ is an invariant for a given size-class. It holds initially since then ${\tt \small\verb+nr_not_full_pages+} = n_f = 0$ . Each allocation and deallocation keeps the property valid. Therefore, if a deallocation happens when ${n_f \tt\small\verb+ < max_nr_nf_pages+} - 1$ , then ${\tt \small\verb+nr_not_full_pages < max_nr_nf_pages+}$ and hence compaction is not called.

Program analysis can be used to determine the maximum value of

for a given mutator at compile time. More advanced program analysis (e.g. analysis of sequences of allocations and deallocations) might provide us with a stronger guarantee than the one above. Employing program analysis is one of our future-work aims. The effect of partial compaction can be seen in the experiments in Section 5.

3.5 Pointer Arithmetic

Since we make the distinction between abstract and concrete address space, our malloc function returns a reference to an abstract address, instead of a reference to a memory location. Therefore, pointer arithmetic needs adjustment, so that it fits our model. In order to enable standard pointer arithmetic, we need the structure of an abstract pointer. It contains a field abs_address and a field offset. Consider the example of C code in Listing 7. The same is achieved in CF by the code presented in Listing 8.

$\begin{figure}\renewedcommand{baselinestretch}{1} \begin{lstlisting}[frame=tb,ca... ...*value; value = malloc(40); value++; print(*value); \end{lstlisting}\end{figure}$

$\begin{figure}\renewedcommand{baselinestretch}{1} \begin{lstlisting}[frame=tb,ca... ...int(dereference(value.abs_address, value.offset)); \end{lstlisting}\end{figure}$

A virtual machine (e.g. a Java VM) can encapsulate the abstract pointer concept. C programs which use CF instead of a conventional memory management system have to be translated into code that uses the abstract pointer concept. An automatic translation tool is left for future work.

On an Intel architecture running Linux, GCC translates a standard pointer dereference (including offset addition) to 6 assembler instructions, whereas a CFM abstract pointer dereference results in 7 assembler instructions (one additional pointer dereference instruction is needed). A CFNM abstract pointer dereference results in 11 assembler instructions. The additional 5 assembler instructions consist of one dereference operation and 4 instructions that calculate the memory target address and move the pointer to that address.

4 Related Work

In this section we briefly discuss existing memory management systems (mostly for real time). We distinguish explicit and implicit memory management systems and consider both non-compacting real-time, and non-real-time memory management systems. Jones [6] maintains an extensive online bibliography of memory management publications.

4.1 Explicit Memory Management

There are several established explicit memory management systems: First-fit [7], Best-fit [7], Doug Lea's allocator (DL) [8], Half-fit [11], and Two-level-segregated-fit (TLSF) [10]. A detailed overview of the explicit memory management systems can be found in [9,13].

First-fit and Best-fit are sequential fit allocators, not suitable for real-time applications. In the worst case, they scan almost the whole memory in order to satisfy an allocation request. DL is a non-real-time allocator used in many systems, e.g. in some versions of Linux.

Half-fit and TLSF offer constant response-time bounds for allocation and deallocation. However, both approaches may suffer from unbounded memory fragmentation.

None of the above mentioned algorithms perform compaction. Instead, they attempt to fight fragmentation by clever allocation, and therefore can not give explicit fragmentation guarantees.

In Section 5 we present a comparison of the CF implementations with First-fit, Best-fit, DL, Half-fit, and TLSF.

4.2 Implicit Memory Management

We elaborate on two established implicit real-time memory management systems: Jamaica [14] and Metronome [2].

Jamaica splits memory objects into fixed-size blocks that can be arbitrarily located in memory and connected in a linked list (or tree) structure. Allocation and deallocation achieve the same bounds like our non-moving implementation. Dereferencing in Jamaica involves going through the list of memory object blocks, therefore it takes linear (or logarithmic) time in the size of the object. Compaction is not needed for Jamaica, since memory objects do not occupy contiguous pieces of memory.

Metronome is a time-triggered garbage collector. As mentioned above, we adapt some concepts like pages and size-classes from Metronome. Compaction in Metronome is part of the garbage collection cycles. The time used for compaction is estimated to at most 6% of the collection time [2].

5 Experiments and Results

In this section, we benchmark the moving (CFM) and non-moving (CFNM) implementations as well as the partial compaction strategy of CF in a number of experiments. Moreover, we compare both CF implementations with the dynamic memory management algorithms First-fit, Best-fit, DL, Half-fit, and TLSF. The implementations of First-fit, Best-fit, Half-fit, and TLSF we borrow from Masmano et al. [9]. We took the original implementation of DL from Doug Lea's web page [8].

5.1 Testing Environment

We have performed processor-instruction measurements of our algorithms on a standard Linux system, and bare-metal execution-time measurements on a Gumstix connex400 board [5] running a minimal hardware abstraction layer (HAL).

Processor-instruction measurements eliminate interferences like cache effects. For measurement purposes, our mutators are instrumented using the ptrace [12] system call. The processor-instruction and execution-time measurements are almost the same except that the former are cleaner, free of side effects. For this reason, we present the processor-instruction results only.

Our mutators provide synthetic workloads designed to create worst-case and average-case scenarios. We have not obtained standardized macrobenchmark results for lack of an automatic code translator or virtual machine implementation that incorporate the abstract pointer concept.

5.2 Results: Incremental Tests

In this benchmark, we run a mutator with incremental behavior: it allocates memory objects of increasing size starting from 8B increasing by 4B until the memory gets full at 7MB. Then, it deallocates each second object. We measure this process in the deallocation experiments. Finally, the mutator allocates the deallocated objects once more. We measure this process in the allocation experiments. In Figure 6, the

-axes show the number of invoked memory operations, whereas the

-axes represent the corresponding measured number of executed instructions.

**Figure 6:** Incremental microbenchmark
(a) Allocation
(b) Deallocation with compaction
(c) Deallocation, partial compaction

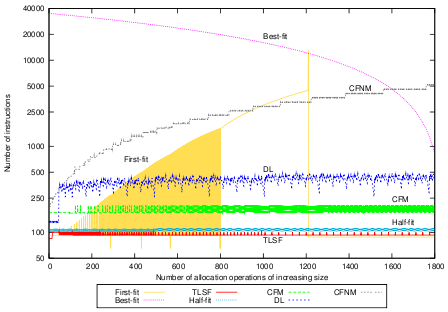
Figure 6(a) shows the number of processor instructions for allocation. The behavior of First-fit and Best-fit is highly unpredictable. DL appears more bounded. Half-fit and TLSF perform allocation operations fast and in constant time. The behavior of the CF implementations is according to our theoretical results: constant for CFM and linear for CFNM. Note that the

-axes of the graphs have logarithmic scale. Both CF implementations are bounded but slower than Half-fit and TLSF due to the additional administrative work for (potential) compaction. CFM is as fast as DL, and faster than First-fit and Best-fit. The average number of instructions for allocation with CFM is 169.61, the standard deviation is 8.63.

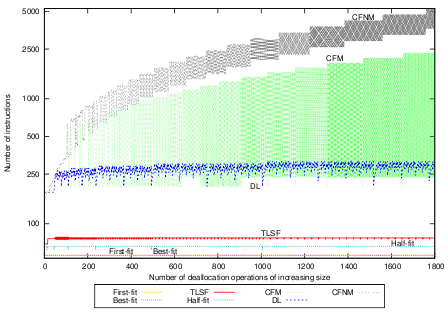
The deallocation benchmark, with full compaction, is presented in Figure 6(b). All algorithms except CF perform deallocation in constant time by adding the deallocated memory range to a data structure that keeps track of the free memory slots. CF performs compaction upon deallocation, and therefore takes linear time (in the size of the memory object) for deallocation. The overhead of performing compaction leads to longer execution time, but both CF implementations are bounded and create predictable memory. For the given block-frame size of 32B, CFNM does not perform better than CFM since returning blocks to the free-list of free block-frames takes approximately the same time as moving a whole memory object. Experiments showed that the minimum block-frame size for which deallocation in CFNM is faster than in CFM is 80B.

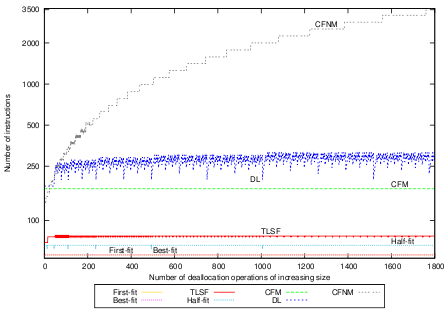
Using the partial compaction strategy results in constant deallocation times for CFM, as shown in Figure 6(c). Note that this graph shows the same picture as Figure 6(b) except for CFM and CFNM where partial compaction is applied. The compaction bounds for partial compaction are set sufficiently wide to avoid compaction. CFNM shows a step function with tight bounds per size-class. The average number of instructions for deallocation with CFM and partial compaction is 185.91, the standard deviation is 16.58.

5.3 Results: Rate-Monotonic Tests

In the rate-monotonic scheduling benchmarks, we use a set of five periodic tasks resembling a typical scenario found in many real-time applications. Each task allocates memory objects of a given size, and deallocates them when the task's holding time expires. Three of the tasks allocate larger objects and have long holding times, the other two allocate small objects and have short holding times. The tasks have various periods and deadlines. They are scheduled using a rate-monotonic scheduling policy. Since the different tasks create a highly fragmented memory, this benchmark represents a memory fragmentation stress test.

For better readability, the

-axes of the graphs show the cumulative number of instructions, i.e., the sum of the number of executed instructions for all operations starting from the first invoked operation up to the currently invoked one. The

-axes show the number of invoked operations, as before. Note that a linear function represents memory operations that take constant time.

**Figure 7:** Rate-monotonic microbenchmark
(a) Allocation
(b) Deallocation with compaction
(c) Deallocation, partial compaction

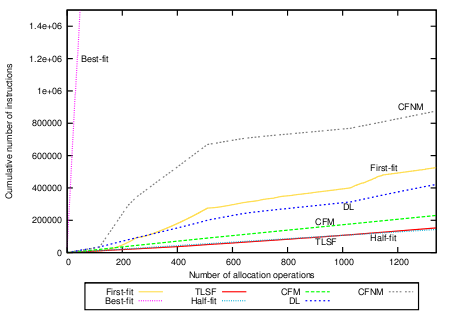
The allocation measurements are presented in Figure 7(a). Best-fit is highly unpredictable. Half-fit and TLSF are constant and fast. CFM is also constant, faster than DL, but slightly slower than Half-fit and TLSF. On average, a CFM allocation request takes 169.61 instructions with a standard deviation of 8.63.

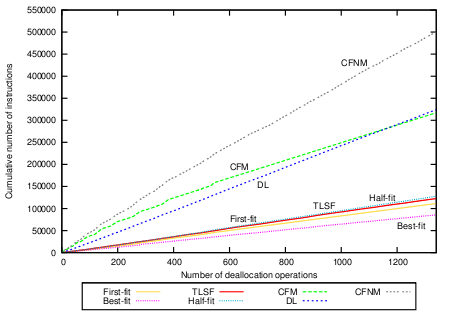
Figure 7(b) shows the deallocation measurements. The differences in growth of the CFM curve correspond to compaction. During the first 550 deallocation operations CFM has to perform a lot of compaction operations but afterwards no compaction is necessary. The total runtime is shorter than the time needed for DL. CFNM takes linear time in the size of the memory object even if there is no compaction performed. The curve reflects this property.

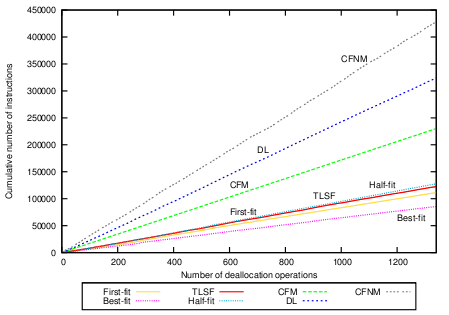
Applying partial compaction leads to constant-time deallocation with CFM and makes it fast and more predictable, as shown in Figure 7(c). This graph shows the same picture as Figure 7(b) except for CFM and CFNM where partial compaction is applied. In order to apply partial compaction we have used the following compaction bounds on the 46 size-classes in the system: In the size-classes 15-18 and 28-29, two not-full pages are allowed. In the size-classes 19-27, we allow for three not-full pages. All other size-classes can have at most one not-full page. The mean number of instructions for CFM deallocation with partial compaction is 171.61, the standard deviation is 5.09.

5.4 Results: Fragmentation Tests

Our final experiments measure fragmentation. We compare CFM (with partial compaction) with TLSF, since the latter is considered the best existing real-time memory management system in terms of fragmentation [9]. The results are shown in Figure 8. The numbers next to CFM, e.g. CFM 3, denote the maximal number of not-full pages allowed in each size-class.

**Figure 8:** Fragmentation

For the experiments we have used a mutator that allocates the whole memory using memory objects of size 20B-100B. Before we run the fragmentation test around 20% of the number of allocated objects is freed. The memory holes are randomly distributed throughout the memory. The fragmentation tests count how many objects (

-axis) of size 20B-16000B (

-axis) are still allocatable by each memory management system. CFM obviously deals with fragmentation better than TLSF, even if we allow up to nine not-full pages in each size-class. Moreover, the fragmentation in CFM is fully controlled and predictable.

6 Discussion and Conclusion

Compact-fit is an explicit real-time memory management system that handles fragmentation through compaction like some implicit real-time memory management systems do. Its main new contribution is predictable response times in combination with predictable memory fragmentation.

We have designed and implemented two versions of Compact-fit. Allocating an object takes constant time in the moving implementation and linear time (in the object's size) in the non-moving implementation. Deallocating an object takes linear time (in its size) in both implementations. If no compaction occurs, deallocating takes constant time in the moving implementation. Dereferencing takes constant time in both implementations.

Hence, we provide tight bounds on the response times of memory operations. Moreover, we keep each size-class (partially) compact, i.e., we have predictable memory. Hence, unlike the other existing real-time memory management systems that do not fully control fragmentation, our compacting real-time memory management system is truly suitable for real-time and even safety-critical applications.

Finally, another real-time characteristic of our memory management system is the constant initialization time. This is achieved using the free-list concept for all resources (abstract addresses, pages, block-frames, etc.) that need initialization.

The experiments validate our asymptotic complexity results. Due to more administrative work related to compaction, our system is slightly slower than the existing systems with real-time response bounds.

There are several possible improvements to our design and implementation that we leave for future work. In our present work, the abstract address space is statically pre-allocated to fit the worst case. For less memory overhead, we could implement a dynamic abstract address space allocation by using the pages from the concrete address space also for storing abstract addresses. Moreover, the present implementation allows for memory objects of size at most 16KB, the size of a page. Arraylets [3] can be used in order to handle objects of larger size. Other topics for future work are concurrency support, program analysis for determining optimal partial compaction bounds and needed amount of abstract addresses, and allocatability analysis.

Silviu S. Craciunas	Christoph M. Kirsch	Hannes Payer
Ana Sokolova	Horst Stadler	Robert Staudinger
	Department of Computer Sciences University of Salzburg, Austria firstname.lastname@cs.uni-salzburg.at