
2007 USENIX Annual Technical Conference
Pp. 143–156 of the Proceedings
POTSHARDS: Secure Long-Term Storage Without Encryption
Mark W. Storer Kevin M. Greenan Ethan L. Miller
University of California, Santa Cruz
Kaladhar Voruganti
Network Appliance*
|
Abstract: Users are storing ever-increasing amounts of information digitally,
driven by many factors including government regulations and the
public's desire to digitally record their personal histories.
Unfortunately, many of the security mechanisms that modern systems
rely upon, such as encryption, are poorly suited for storing data
for indefinitely long periods of time—it is very difficult to
manage keys and update cryptosystems to provide secrecy through
encryption over periods of decades. Worse, an adversary who can
compromise an archive need only wait for cryptanalysis techniques to
catch up to the encryption algorithm used at the time of the
compromise in order to obtain “secure” data. To address these concerns, we have developed POTSHARDS, an archival
storage system that provides long-term security for data with very
long lifetimes without using encryption. Secrecy is achieved by
using provably secure secret splitting and spreading the resulting
shares across separately-managed archives. Providing availability
and data recovery in such a system can be difficult; thus, we use a
new technique, approximate pointers, in conjunction with secure
distributed RAID techniques to provide availability and reliability
across independent archives. To validate our design, we developed a
prototype POTSHARDS implementation, which has demonstrated
“normal” storage and retrieval of user data using indexes, the
recovery of user data using only the pieces a user has stored across
the archives and the reconstruction of an entire failed archive.
1 Introduction
Many factors motivate the need for secure long-term
archives, ranging from the relatively short-term (for archival
purposes) requirements on preservation, retrieval and security
properties demanded by recent
legislation [20, 1] to the
indefinite lifetimes of cultural and family heritage data. As users
increasingly create and store images, video, family documents, medical
records and legal records digitally, the need to securely preserve
this data for future generations grows correspondingly. This
information often needs to be stored securely; data such as medical
records and legal documents that could be important to future
generations must be kept indefinitely but must not be publicly
accessible. The goal of a secure, long-term archive is to provide security for
relatively static data with an indefinite lifetime. There are three
primary security properties that such archives aim to provide. First,
the data stored must only be viewable by authorized readers. Second,
the data must be available and accessible to authorized users within a
reasonable amount of time, even to those who might lack a specific
key. Third, there must be a way to confirm the integrity of the
data so that a reader can be reasonably assured that the data that is
read is the same as the data that was written. The usage model of secure, long-term archival storage is write-once,
read-maybe, and thus stresses throughput over low-latency performance.
This is quite different from the top storage tier of a hierarchical
storage solution that stresses low-latency access or even bottom-tier
backup storage. The usage model of long-term archives also has the
unique property that the reader may have little knowledge of the
system's contents and no contact with the original writer; while file
lifetimes may be indefinite, user lifetimes certainly are not. For
digital “time capsules” that must last for decades or even
centuries, the writer is assumed to be gone soon after the data has
been written. There are many novel storage
problems [3, 32] that result from
the potentially indefinite data lifetimes found in long-term storage.
This is partially due to mechanisms such as cryptography that work
well in the short-term but are less effective in the long-term. In
long-term applications, encryption introduces the problems of lost
keys, compromised keys and even compromised cryptosystems.
Additionally, the management of keys becomes difficult because data will
experience many key rotations and cryptosystem migrations over the
course of several decades; this must all be done without user
intervention because the user who stored the data may be unavailable.
Thus, security for archival storage must be designed explicitly for
the unique demands of long-term storage. To address the many security requirements for long-term archival
storage, we designed and implemented
POTSHARDS (Protection
Over Time, Securely Harboring And Reliably Distributing Stuff),
which uses three primary techniques to provide security for long-term
storage. The first technique is secret
splitting [28], which is used to provide secrecy for
the system's contents. Secret splitting breaks a block into n
pieces, m of which must be obtained to reconstitute the block; it
can be proven that any set of fewer than m pieces contains no
information about the original block. As a result, secret splitting
does not require the same updating as encryption, which is only
computationally secure. By providing data secrecy without the use of
encryption, POTSHARDS is able to move security from encryption to the
more flexible and secure authentication realm; unlike encryption,
authentication need not be done by computer, and authentication
schemes can be easily changed in response to new vulnerabilities. Our
second technique, approximate pointers, makes it possible to
reconstitute the data in a reasonable time even if all indices over a
user's data have been lost. This is achieved without sacrificing the
secrecy property provided by the secret splitting. The third
technique is the use of secure, distributed RAID techniques across
multiple independent archives. In the event that an archive fails,
the data it stored can be recovered without the need for other
archives to reveal their own data. We implemented a prototype of POTSHARDS and conducted
several experiments to test its performance and resistance to failure.
The current, CPU-bound implementation of POTSHARDS can read and write
data at 2.5–5 MB/s on commodity hardware but is highly
parallelizable. It also survives the failure of an entire archive
with no data loss and little effect seen by users. In addition, we
demonstrated the ability to rebuild a user's data from all of the
user's stored shares without the use of a user index. These
experiments demonstrate the system's suitability to the unique usage
model of long-term archival storage.
2 Background
Since POTSHARDS was designed specifically for secure, long-term
storage, we identified three basic design tenets to help focus our
efforts. First, we assumed that encrypted data could be read by
anyone given sufficient CPU cycles and advances in cryptanalysis.
This means that, if all of an archives encrypted contents are
obtained, an attacker can recover the original information. Second,
data must be recoverable without any information from outside the set
of archives. Thus, fulfilling requests in a reasonable time cannot
require anything stored outside the archives, including external
indexes or encryption keys. If this assumption is violated, there is
a high risk that data will be unrecoverable after sufficient time has
passed because the needed external information has been lost. Third,
we assume that individuals are more likely to be malicious than an
aggregate. In other words, our system can trust a group of archives
even though it may not trust an individual archive. The chances of
every archive in the system colluding maliciously is small; thus, we
designed the system to allow rebuilding of stored data if all
archives cooperate.
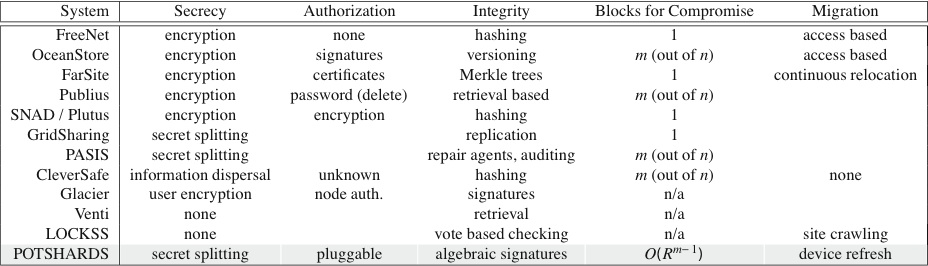
| Table 1: Capability overview of the storage systems described in
Section 2. “Blocks to compromise” lists
the number of data blocks needed to brute-force recover data
given advanced cryptanalysis; for POTSHARDS, we assume that an
approximate pointer points to R shard identifiers.
“Migration” is the mechanism for automatic replication or
movement of data between nodes in the system. |
In designing POTSHARDS to meet these goals, we used concepts from
various research projects and developed additional techniques. There
are many existing storage systems that satisfy some of the design
tenets discussed above, ranging from general-purpose distributed
storage systems to distributed content delivery systems, to archival
systems designed for short-term storage and archival systems designed
for very specific uses such as public content delivery. A
representative sample of these systems is summarized in
Table 1. The remainder of this section
discusses each of these primary tenets within the context of the
related systems. Since these existing systems were not designed with
secure, archival storage in mind, none has the combination of
long-term data security and proof against obsolescence that POTSHARDS provides.
2.1 Archival Storage Models
Storage systems such as Venti [23] and
Elephant [26] are concerned with archival storage, but
tend to focus on the near-term time scale. Both systems are based on
the philosophy that inexpensive storage makes it feasible to store
many versions of data. Other systems, such as
Glacier [13], are designed to take advantage of the
underutilized client storage of a local network. These systems, and
others that employ “checkpoint-style” backups, address neither the
security concerns of the data content nor the needs of long-term
archival storage. Venti and commercial systems such as the EMC
Centera [12] use content-based storage techniques to
achieve their goals, naming blocks based on a secure hash of their
data. This approach increases reliability by providing an easy way to
verify the content of a block against its name. As with the
short-term storage systems described above, security is ensured by
encrypting data using standard encryption algorithms. Some systems, such as LOCKSS [18] and
Intermemory [10], are aimed at long-term storage of
open content, preserving digital data for libraries and archives where
file consistency and accessibility are paramount. These systems are
developed around the core idea of very long-term access for public
information; thus file secrecy is explicitly not part of the design.
Rather, the systems exchange information about their own copies of each
document to obtain consensus between archives, ensuring that a rogue
archive does not “alter history” by changing the content of a document
that it holds.
2.2 Storage Security
Many storage systems seek to enforce a policy of secrecy for their contents.
Two common mechanisms for enforcing data secrecy are encryption and secret
splitting.
2.2.1 Secrecy via EncryptionMany systems such as OceanStore [25],
FARSITE [2],
SNAD [19], Plutus [16], and
e-Vault [15] address file secrecy but rely on the
explicit use of keyed encryption. While this may work reasonably well
for short-term secrecy needs, it is less than ideal for the very
long-term security problem that POTSHARDS is addressing. Encryption
is only computationally secure and the struggle between cryptography
and cryptanalysis can be viewed as an arms race. For example, a DES
encrypted message was considered secure in 1976; just 23 years later,
in 1999, the same DES message could be cracked in under a
day [29]; future advances in quantum computing
have the potential to make many modern cryptographic algorithms
obsolete. The use of long-lived encryption implies that re-encryption must occur
to keep pace with advances in cryptanalysis in order to ensure
secrecy. To prevent a single archive from obtaining the unencrypted
data, re-encryption must occur over the old encryption, resulting in a
long key history for each file. Since these keys are all external
data, a problem with any of the keys in the key history can render the
data inaccessible when it is requested. Keyed cryptography is only computationally secure, so compromise of an
archive of encrypted data is a potential problem regardless of the
encryption algorithm that is used. An adversary who compromises an
encrypted archive need only wait for cryptanalysis techniques to catch
up to the encryption used at the time of the compromise. If an
insider at a given archive gains access to all of its data, he can
decrypt any desired information even if the data is subsequently
re-encrypted by the archive, since the insider will have access to the
new key by virtue of his internal access. This is unacceptable, since
the data's existence on a secure, long-term archive suggests that data
will still be valuable even if the malicious user must wait several
years to read it. Some content publishing systems utilize encryption, but its use
is not motivated solely by secrecy. Publius [34]
utilizes encryption for write-level access control.
Freenet [6] is designed for anonymous publication and
encryption is used for plausible deniability over the contents of a
users local store. As with secrecy, the use of encryption to enforce
long-lived policy is problematic due to the mechanism's computationally
secure nature.
2.2.2 Secrecy via SplittingTo address the issues resulting from the use of encryption, several
recent systems including PASIS [36, 11]
and GridSharing [33] have used or suggested the
use [31] of secret splitting
schemes [28, 24, 22, 5]; a
related approach used by Mnemosyne [14] and
CleverSafe [7] uses encryption followed
by information dispersal (IDA) to attempt to gain the same security.
In secret splitting, a secret is distributed by splitting it into a set
number n of shares such that no group of k shares (k < m ≤ n)
reveals any information about the secret; this approach is called an
(m,n) threshold scheme. In such a scheme, any m of the n shares
can be combined to reconstitute the secret; combining fewer than m
shares reveals no information. A simple example of an (n,n)
secret splitting scheme for a block B is to randomly generate
X0,…,Xn−2, where |Xi| = |B|, and choose Xn−1 so
that X0 ⊕ ⋯ ⊕ Xn−2 ⊕ Xn−1 = B. Secret
splitting satisfies the second of our three tenets—data can be
rebuilt without external information—but it can have the undesirable
side-effect of combining the secrecy and redundancy aspects of the
systems. Although related, these two elements of security are, in
many respects, orthogonal to one another. Combining these elements
also risks introducing compromises into the system by restricting the
choices of secret splitting schemes. To ensure that our third design tenet is satisfied, a secure long-term
storage system must ensure that an attempt to breach security will be
noticed by somebody, ensuring that the trust placed in the
collection of archives can be upheld. Existing systems do not meet
this goal because the secret splitting and data layout schemes they
use are minimally effective against an inside attacker that knows the
location of each of the secret shares. None of PASIS, CleverSafe, or
GridSharing are designed to prevent attacks by insiders at one or more
sites who can determine which pieces they need from other sites and
steal those specific blocks of data, enabling a breach of secrecy with
relatively minor effort. This problem is particularly difficult given
the long time that data must remain secret, since such breaches could
occur over years, making detection of small-scale intrusions nearly
impossible. PASIS addressed the issue of refactoring secret
shares [35]; however, this approach could
compromise data in the system because the refactoring process may
reveal information during the reconstruction process that a malicious
archive could use to recover user data. By keeping this on
separate nodes, the PASIS designers hoped to avoid information
leakage. Mnemosyne used a local steganographic file system to hide
chunks of data, but this approach is still vulnerable to rapid
information leakage if the encryption algorithm is compromised
because the IDA provides no additional protection to the distributed
pieces.
2.3 Disaster RecoveryWith long data lifetimes, hardware failure is a given; thus, dealing
with a failed archive is inevitable. In addition, a long-term
archival storage solution that relies upon multiple archives must be
able to survive the loss of an archive for other reasons, such as
business failure. Recovering from such large-scale disasters has long
been a concern for storage systems [17]. To address
this issue, systems
such as distributed RAID [30],
Myriad [4] and OceanStore [25] use
RAID-style algorithms or more general redundancy techniques including
(m,n) error correcting codes along with geographic distribution to
guard against individual site failure.
Secure, long-term storage adds the
requirement that the secrecy of the distributed data must be ensured
at all times, including during disaster recovery scenarios.
3 System Overview
POTSHARDS is structured as a client communicating with a number of
independent archives. Though the archives are independent, they
assist each other through distributed RAID techniques to protect
the system from archive loss. POTSHARDS stores user data by
first splitting it into secure shards. These shards are then
distributed to a number of archives, where each archive exists within
its own security domain. The read procedure is similar but reversed;
a client requests shards from archives and reconstitutes the data.
| Figure 1: An overview of POTSHARDS showing the data transformation
component producing shards from objects and distributing them to
independent archives. The archives utilize distributed RAID
algorithms to securely recover shards in the event of a
failure. |
Data is prepared for storage during ingestion by a
data transformation component that transforms
objects into a set of secure shards which are distributed to the
archives, as shown in Figure 1; similarly,
this component is also responsible for reconstituting objects from
shards during extraction. The data transformation component runs
on a system separate from the archives on which
the shards reside, and can fulfill requests from either a single
client or many clients, depending on the implementation. This
approach provides two benefits: the data never reaches an archive in
an unsecured form; and multiple CPU-bound data transformation processes can
generate shards in parallel for a single set of physical archives. The archives operate in a manner similar to financial banks in that
they are relatively stable and they have a incentive (financial or
otherwise) to monitor and maintain the security of their contents.
Additionally, the barrier to entry for a new archive should be relatively
high (although POTSHARDS does takes precautions against a malicious
insider); security is strengthened by distributing shards amongst the
archives, so it is important that each archive can demonstrate an
ability to protect its data. Other benefits of archive independence
include reducing the effectiveness of insider attacks and making it
easier to exploit the benefits of geographic diversity in physical
archive locations. For these reasons, a single entity, such as a
multinational company, should still maintain multiple independent
archives to gain these security and reliability benefits.
3.1 Data Entities and NamingThere are three main data objects in POTSHARDS: objects,
fragments and shards. As Figure 1
shows, objects contain the data that users submit to the system at the
top level. Fragments are used within the data transformation
component during the production of shards, which are the pieces
actually stored on the archives. The details of these data entities
can be seen in Figure 2.
| Figure 2: Data entities in POTSHARDS, with size (in bits) indicated
above each field. Note that entities are not shown to scale
relative to one another. S is the number of shards that the
fragment produces. split1 is an XOR secret split
and split2 is a Shamir secret split in POTSHARDS. |
All data entities in the current implementation of POTSHARDS are
given unique 128-bit identifiers. The first 40 bits of the name uniquely
identify the client in the same manner as a bank account is identified by
an account number. The remaining 88 bits are used to identify the data
entity. The length of the identifier could be extended relatively easily
in future implementations. The names for entities that do not directly
contribute to security within POTSHARDS, such as those for objects, can be
generated in any way desired. However, the security and recovery time for
a set of shards is directly related to the shards' names; thus, shards' IDs
must be chosen with great care to ensure a proper density of names, providing
sufficient security. In addition to uniquely identifying data entities within the system,
IDs play an important role in the secret splitting algorithms used in
POTSHARDS. For secret splitting techniques that rely on linear
interpolation [28], the reconstitution algorithm must
know the original order of the secret shares. Knowing the order of
the shards in a shard tuple can greatly reduce the time taken to
reconstitute the data by avoiding the need to try each permutation of
share ordering. Currently, this ordering is done by ensuring that the
numerical ordering of the shard IDs reflects the input order to the
reconstitution algorithm.
3.2 Secrecy and Reliability TechniquesPOTSHARDS utilizes three primary techniques in the creation and
long-term storage of shards. First, secret splitting algorithms
provide file secrecy without the need to periodically update the
algorithm. This is due to the fact that perfect secret splitting is
information-theoretically secure as opposed to only computationally secure.
Second, approximate pointers between shards allow objects to be
recovered from only the shards themselves. Thus, even if all indices
over a user's shards are lost, their data can be recovered in a
reasonable amount of time. Third, secure, distributed RAID techniques
across multiple independent archives allow data to be recovered in the
event of an archive failure without exposing the original data during
archive reconstruction. POTSHARDS provides data secrecy through the use of secret splitting
algorithms; thus, there is no need to maintain key history because POTSHARDS does not use traditional encryption keys.Additionally, POTSHARDS utilizes secret
splitting in a way that does not combine the secrecy and redundancy
parameters. Storage of the secret shares is also handled in a manner
that dramatically reduces the effectiveness of insider attacks. By
using secret splitting techniques, the secrecy in POTSHARDS has a
degree of future-proofing built into it—it can be proven that an
adversary with infinite computational power cannot gain any of the
original data, even if an entire archive is compromised. While not
strictly necessary, the introduction of a small amount of redundancy
at the secret splitting layer allows POTSHARDS to handle transient
archive unavailability by not requiring that a reader obtain
all of the shards for an object; however, redundancy at this
level is used primarily for short-term failures.
| Figure 3: Approximate pointers point to R “candidate” shards
(R=4 in this example) that might be next in a valid shard tuple.
Shards0X make up a valid shard tuple. If an intruder
mistakenly picks shard21, he will not discover his error until
he has retrieved sufficient shards and validation fails on the
reassembled
data. |
POTSHARDS provides approximate pointers to enable the reasonably
quick reconstitution of user data without any information that exists
outside of the shards themselves. POTSHARDS users normally keep
indexes allowing them to quickly locate the shards that they need to
reconstitute a particular object, as described in
Section 4.3, so normal shard retrieval consists of
asking archives for the specific shards that make up an object, and is
relatively fast. Approximate pointers are used when these user
indexes are lost or otherwise unavailable. Since POTSHARDS can be
used as a time capsule to secure data, it is foreseeable that a future
user may be able to access the shards that they have a legal right to
but have no idea how to combine them. The shards that can be combined
together to reconstitute data form a shard tuple; an approximate
pointer indicates the region in the user's private namespace where the
next shard in the shard tuple exists, as shown in
Figure 3. An approximate pointer has the
benefit of making emergency data regeneration tractable while still
making it difficult for an adversary to launch a targeted attack. If
exact pointers were used, an adversary would know exactly which shards
to target to rebuild an object. On the other hand, keeping no pointer
at all makes it intractable to combine the correct shards without
outside knowledge of which shards to combine. With approximate
pointers, an attacker with one shard would only know the region
where the next shard exists. Thus, a brute force attack requesting
every shard in the region would be quite noticeable because the
POTSHARDS namespace is intentionally kept sparse and an attack would
result in requests for shards that do not exist. Unlike an index
relating shards to objects that users would keep (and not store in the
clear on an archive), an approximate pointer is part of the shard and
is stored on the archive. The archive layer in which the shards are stored consists of
independent archives utilizing secure, distributed RAID techniques to
provide reliability. As Figure 1 shows,
archive-level redundancy is computed across sets of unrelated
shards, so redundancy groups provide no insight into shard reassembly.
POTSHARDS includes two novel modifications beyond the distributed
redundancy explored earlier [30, 4].
The first is a secure reconstruction procedure, described in
Section 4.2.1, that allows a failed
archive's data to be regenerated in a manner that prevents archives
from obtaining additional shards during the reconstruction; shards
from the failed archive are rebuilt only at the new archive that is
replacing it. Second, POTSHARDS uses algebraic
signatures [27] to ensure intra-archive integrity as
well as inter-archive integrity. Algebraic signatures have the
desirable property that the parity of a signature is the same as the
signature of the parity, which can be used to prove the existence of
data on other archives without revealing the data.
4 Implementation DetailsThis section details the components of POTSHARDS and how each
contributes to providing long-term, secure storage. We first describe
the transformation that POTSHARDS performs to ensure data secrecy.
Next, we detail the inter-archive techniques POTSHARDS uses to
provide long-term reliability. We then describe index construction;
the use of indices makes “normal” data retrieval much simpler.
Finally, we describe how we use approximate pointers to recover data
with no additional information beyond the shards themselves, thus
ensuring that POTSHARDS archives will be readable by future
generations.
4.1 Data Transformation: Secrecy
[Four data transformation layers in POTSHARDS.] [Inputs and outputs for each transformation layer.] | Figure 4: The transformation component consists of four levels.
Approximate pointers are utilized at the second secret split.
Note that locating one shard tuple provides no information about
locating the shards from other tuples. |
Before being stored at the archive layer, user data travels through
the data transformation component of POTSHARDS. This component is
made up of four layers as shown in Figure 4. -
- The pre-processing layer divides files into
fixed-sized, b-byte objects. Additionally, objects include a hash
that is used to confirm correct reconstitution.
- A secret splitting layer tuned for secrecy takes an object
and produces a set of fragments.
- A secret splitting layer tuned for availability takes a
fragment and produces a tuple of shards. It is also at this layer
that the approximate pointers between the shards are created.
- The placement layer determines how to distribute the
shards to the archives.
4.1.1 Secret Splitting LayersFragments are generated at the first level of secret splitting, which
is tuned for secrecy. Currently we use an XOR-based algorithm that
produces n fragments from an object. To ensure security, the random
data required for XOR splitting can be obtained through a physical
process such as radio-active decay or thermal noise. As
Figure 2 illustrates, fragments also contain
metadata including a hash of the fragment's data which can be used to
confirm a successful reconstitution. A tuple of shards is produced from a fragment using another layer of
secret splitting. This second split is tuned for availability which
allows reconstitution in the event that an archive is down or
unavailable when a request is made. In this version of POTSHARDS,
shards are generated from a fragment using an (m, n) secret
splitting algorithm [28, 24]. As the
Figure 2 shows, shards contain no information
about the fragments that they make up. The two levels of secret splitting provide three important security
advantages. First, as Figure 4 illustrates, the
two-levels of splitting can be viewed as a tree with an increased fan
out compared to one level of splitting. Thus, even if an attacker is
able to locate all of the members of a shard tuple they can only rebuild
a fragment and they have no information to help them find shards
for the other fragments. Second, it separates the secrecy and
availability aspects of the system. With two levels of secret splitting
we do not need to compromise one aspect for the other. Third, it allows
useful metadata to be stored with the fragments as this data will be kept
secret by the second level of splitting. The details of shards and
fragments are shown in Figure 2. One cost of two-level secret splitting is that the overall storage
requirements for the system are increased. A two-way XOR split
followed by a (2,3) secret split increases storage requirements by a
factor of six; distributed RAID further increases the overhead.
If a user desires to offset this cost, data can be submitted in a
compressed archival form [37]; compressed data is handled
just like any other type of data.
4.1.2 Placement LayerThe placement layer determines which archive will store each shard.
The decision takes into account which shards belong in the same tuple
and ensures that no single archive is given enough shards to recover
data. This layer contributes to security in POTSHARDS in four ways. First,
since it is part of the data transformation component, no knowledge of
which shards belong to an object need exist outside of the component.
Second, the effectiveness of a insider attack at the archives is
reduced because no single archive contains enough shards to
reconstitute any data. Third, the effectiveness of an external attack
is decreased because shards are distributed to multiple archives, each
of which can exist in their own security domain. Fourth, the
placement layer can take into account the geographic location of
archives in order to maximize the availability of data.
4.2 Archive Design: Reliability
Storage in POTSHARDS is handled by a set of independent archives that
store shards, actively monitor their own security and actively
question the security of the other archives. The archives do not know
which shards form a tuple, nor do they have any information about
fragments or object reconstitution. A compromised archive does not
provide an adversary with enough shards to rebuild user data. Nor
does it provide an adversary with enough information to know where
to find the appropriate shards needed to rebuild user data. Absent
such precautions, the archive model would likely weaken the strong
security properties provided by the other system components. Since POTSHARDS is designed for long-term storage, it is inevitable
that disasters will occur and archive membership will change over
time. To deal with the threat of data loss from these events,
POTSHARDS utilizes distributed RAID techniques. This is accomplished
by dividing each archive into fixed-sized blocks and requiring all
archives to agree on distributed, RAID-based methods over these
blocks. Each block on the archive holds either shards or redundancy
data. When shards arrive at an archive for storage, ingestion occurs in
three steps. First, a random block is chosen as the storage location
of the shard. Next, the shard is placed in the last available slot in
the the block. Finally, the corresponding parity updates are sent to
the proper archives. Each parity update contains the data stored in
the block and the appropriate parity block location. The failure of
any parity update will result in a roll-back of the parity updates and
re-placement of the shard into another block. Although it is assumed
that all of the archives are trusted, we are currently analyzing the
security effects of passing shard data between the archives during
parity updates and exploring techniques for preventing archives from
maliciously accumulating shards. The distributed RAID techniques used in POTSHARDS are based on those
from existing systems [30, 4]. In such
systems, cost-effective, fault-tolerant, distributed storage is
achieved by computing parity across unrelated data in wide area
redundancy groups. Given an (n,k) erasure code, a redundancy group
is an ordered set of k data blocks and n−k parity blocks where
each block resides on one of n distinct archives. The redundancy
group can survive the loss of up to n−k archives with no data loss.
The current implementation of POTSHARDS has the ability to use
Reed-Solomon codes or single parity to provide flexible and
space-efficient redundancy across the archives. POTSHARDS enhances the security of existing distributed RAID
techniques through two important additions. First, the risk of
information leakage during archive recovery is greatly mitigated
through secure reconstruction techniques. Second, POTSHARDS utilizes
algebraic signatures [27] to implement a secure
protocol for both storage verification and data integrity checking.
4.2.1 Secure Archive Reconstruction
Reconstruction of data can pose a significant security risk because
it can involve many archives and considerable amounts of data
passing between archives. The secure recovery algorithm implemented
within POTSHARDS exploits the independence of the archives
participating in a redundancy group and the commutativity of
evaluating the parity. Our reconstruction algorithm permits each
archive to independently reconstruct a block of failed data
without revealing any information about its data. The commutativity
of the reconstruction procedure results in a reconstruction protocol
that can occur in permutations, which greatly decreases the likelihood
of successful collusion during archive recovery.
| Figure 5: A single round of archive recovery in a RAID 5 redundancy group.
Each round consists of multiple steps. Archive N contains data
n and generates random blocks rn. |
The recovery protocol begins with the confirmation of a partial or whole
archive failure and, since each archive is a member of one or more
redundancy groups, proceeds one redundancy group at a time. If a failure
is confirmed, the archives in the system must agree on the destination of
recovered data. A fail-over archive is chosen based on two criteria: the
fail-over archive must not be a member of the redundancy group being
recovered and it must have the capacity to store the recovered data. Due to
these constraints multiple fail-over archives may be needed to perform
reconstruction and redistribution. Future work will include ensuring
that the choice of fail-over archives prevent any archive from
acquiring enough shards to reconstruct user data. Once the fail-over archive is selected, recovery occurs in multiple
rounds. A single round of our secure recovery protocol over a single
redundancy group is illustrated in Figure 5. In
this example, the available members of a redundancy group collaborate
to reconstruct the data from a failed archive onto a chosen archive X.
An archive (which cannot be the fail-over and cannot be one of the
collaborating archives) is appointed to manage the protocol by rebuilding
one block at a time through multiple rounds of chained requests. A
request contains an ordered list of archives, corresponding block
identifiers and a data buffer and proceeds as follows at each archive in
the chain: -
- Request α involving local block n arrives at archive N.
- The archive creates a random block rn and computes
n ⊕ rn = n'.
- The archive computes β = α ⊕ n' and
removes its entry from the request
- The archive sends rn directly to archive X.
- β is sent to the next archive in the list.
This continues at each archive until the chain ends at archive X and the
block is reconstructed. The commutativity of the rebuild process allows
us to decrease the likelihood of data exposure by permuting the order
of the chain in each round. This procedure is easily parallelized and
continues until all of the failed blocks for the redundancy group are
reconstructed. Additionally, this approach can be generalized to any
linear erasure code; as long as the generator matrix for the code is
known, the protocol remains unchanged.
4.2.2 Secure Integrity CheckingPreserving data integrity is a critical task in all long-term
archives. POTSHARDS actively verifies the integrity of data
using two different forms of integrity checking. The first technique
requires each of the archives to periodically check its data for integrity
violations using a hash stored in the header of each block on disk. The
second technique is a form of inter-archive integrity checking that utilizes
algebraic signatures [27] across the redundancy groups.
Algebraic signatures have the property that the signatures of the parity equals
the parity of the signatures. This property is used to verify that the
archives in a given redundancy group are properly storing data and are
performing the required internal checks [27]. Secure, inter-archive integrity checking is achieved through algebraic
signature requests over a specific interval of data. A check begins when
an archive asks the members of a redundancy group for an algebraic signature
over a specified interval of data. The algebraic signature forms a codeword
in the erasure code used by the redundancy group and integrity over the
interval of data is checked by comparing the parity of the data signatures
to the signature of the parity. If the comparison check fails, then the
archive(s) in violation may be found as long as the number of incorrect
signatures is within the error-correction capability of the code. In general,
a small signature (typically 4 bytes) is computed from a few megabytes of
data. This results in very little information leakage. If necessary,
restrictions may be placed on algebraic signature requests to ensure that no
data is exposed during the integrity check process.
4.3 User Indexes
When shards are created, the exact names of the shards are
returned to the user along with their archive placement locations;
however, these exact pointers are not stored in the shards
themselves, so they are not available to someone attacking the
archives. Typically, a user maintains this information and the
relationship between shards, fragments, objects, and files in an index
to allow for fast retrieval. In the general case, the user consults
her index and requests specific shards from the system. This index
can, in turn, be stored within POTSHARDS, resulting in an index
that can be rebuilt from a users shards with no outside information. The index for each user can be stored in POTSHARDS as a linked list
of index pages with new pages inserted at the head of the list, as
shown in Figure 6. Since the index pages are
designed to be stored within POTSHARDS, each page is immutable. When
a user submits a file to the system, a list of mappings from the file
to its shards is returned. This data is recorded in a new index page,
along with a list of shards corresponding to the previous head of the
index list. This new page is then submitted to the system and the
shard list returned is maintained as the new head of the index list.
These index root-shards can be maintained by the client application or
even on a physical token, such as a flash drive or smart card.
| Figure 6: User index made up of two pages. One page was created at
time t0 and the other at time t1. |
This approach of each user maintaining their own private index has
three advantages. First, since each user maintains his own index, the
compromise of a user index does not affect the security of other
users' data. Second, the index for one user can be recovered with no
effect on other users. Third, the system does not know about the
relationship between a user's shards and their data. In some ways, the index over a user's shards can be compared to an
encryption key because it contains the information needed to rebuild a
user's data. However, the user's index is different from an
encryption key in two important ways. First, the user's index is not
a single point of failure like an encryption key. If the index is
lost or damaged, it can be recovered from the data without any input
from the owner of the index. Second, full archive collusion can
rebuild the index. If a user can prove a legal right to data, such as
by a court subpoena, than the archives can provide all of the user's
shards and allow the reconstitution of the data. If the data was
encrypted, the files without the encryption key might not be
accessible in a reasonable period of time.
4.4 Approximate Pointers and Recovery
Approximate pointers are used to relate shards in the same shard tuple
to one another in a manner that allows recovery while still reducing
an adversary's ability to launch a targeted attack. Each shard has an
approximate pointer to the next shard in the fragment, with the last
shard pointing back to the first and completing the cycle, as shown in
Figure 3. This allows a user to recover
data from their shards even if all other outside information, such as
the index, is lost. There are two ways that approximate pointers can be implemented:
randomly picking a value within R/2 above or below the next shard's
identifier, or masking off the low-order r bits (R = 2r) of the
next shard's identifier, hiding the true value. Currently, POTSHARDS uses the latter approach; we are investigating the tradeoffs between
the two approaches. One benefit to using the R/2 approach is that
it allows a finer-grained level of adjustment compared to the relatively
coarse-grained bitmask approach. The use of approximate pointers provides a great deal of security by
preventing an intruder who compromises an archive or an inside
attacker from knowing exactly which shards to steal from other
archives. An intruder would have to steal all of the shards an
approximate pointer could refer to, and would have to steal all of the
shards they refer to, and so on. All of this would have to bypass the
authentication mechanisms of each archive, and archives would be able
to identify the access pattern of a thief, who would be attempting to
obtains shards that may not exist. Since partially reconstituted
fragments cannot be verified, the intruder might have to steal
all of the potential shards to ensure that he was able to
reconstitute the fragment. For example, if an approximate pointer
points to R shards and a fragment is split using (m, n) secret
splitting, an intruder would have to steal, on average, Rm−1/2
shards to decode the fragment. In contrast to a malicious user, a legitimate user with access to all
of his shards can easily rebuild the fragments and, from them, the
objects and files they comprise. Suppose this user created shards
from fragments using an (m,n) secret splitting algorithm. A user
would start by obtaining all of her shards which, in the case of
recoveries, might require additional authentication steps. Once she
obtains all of her shards from the archives, there are two approaches
to regenerating those fragments. First, she could try every possible
chain of length m, rebuilding the fragment and attempting to verify
it. Second, she could narrow the list of possible chains by only
attempting to verify chains of length n that represented cycles, an
approach we call the ring heuristic. As
Figure 2 illustrates, fragments include a hash
that is used to confirm successful reconstitution. Fragments also
include the identifier for the object from which they are derived,
making the combination of fragments into objects a straightforward
process. Because the Shamir secret splitting algorithm is computationally
expensive, even when combining shards that do not generate valid
fragments, we use the ring heuristic to reduce the number of failed
reconstitution attempts in two ways. First, the number of cycles of
length n is lower than the number of paths of length m since many
paths of length n do not make cycles. Second, reconstitution using
the Shamir secret splitting algorithm requires that the shares be
properly ordered and positioned within the share list. Though the
shard ID provides a natural ordering for shards, it does not assist
with positioning. For example, suppose the shards were produced with
a 3 of 5 split. A chain of three shards, (s1,
s2, s3), would potentially need to be
submitted to the secret splitting algorithm three times to test each possible
order: (s1, s2, s3,
φ, φ), (φ, s1, s2,
s3, φ), and (φ, φ, s1, s2, s3).
5 Experimental EvaluationOur experiments using the current implementation of POTSHARDS were
designed to measure several things. First, we wanted to evaluate the
performance of the system and identify any bottlenecks. Next, we
compared the behavior of the system in an environment with heavy
contention for processing and network resources against that in a
dedicated, lightly loaded environment. Finally, we evaluated
POTSHARDS' ability to recover from the loss of an archive as well as
the loss of a user index. During our experiments, the data transformation component was run from
the client's system using object sizes of 750 KB. The first layer of
secret splitting used an XOR based algorithm and produced two
fragments per object, and the second layer utilized a (2,3) Shamir
threshold scheme. The workloads contained a mixture of PDF,
Postscript files, and images. These files are representative of the
content that a long-term archive might contain, although it is
important to note that POTSHARDS sees all objects as the same
regardless the objects' origin or content. File sizes ranged from
about half a megabyte to several megabytes in size; thus, most
were ingested and extracted as multiple objects. For the local experiments, all systems were located on the same
1 Gbps network with little outside contention for computing or
network resources. The client computers were equipped with two
2.74 GHz Pentium 4 processors, 2 GB of RAM and Linux version
2.6.9-22.01.1. Each of the sixteen archives were equipped with two
2.74 GHz Pentium 4 processors, 3 GB of RAM, 7.3 GB of available
local hard drive space and Linux version 2.6.9-34. In contrast to the
local experiments, the global-scale experiments were conducted using
PlanetLab [21], resulting in considerable
contention for shared resources. For these experiments, both the
clients and archives were run in a slice that contained twelve
PlanetLab nodes (eight archives and four clients) distributed across
the globe. The POTSHARDS prototype system itself consists of roughly 15,000
lines of Java 5.0 code. Communications between layers used Java
sockets over standard TCP/IP, and the archives used Sleepycat
Software's BerkeleyDB version 3.0 for persistent storage of shards.
5.1 Read and Write PerformanceOur first set of experiments evaluated the performance of ingestion
and extraction on a dedicated set of systems and on PlanetLab.
Table 2 profiles the ingestion and extraction of one
block of data. comparing the time taken on an unloaded local
cluster of machines and the heavily loaded, global scale PlanetLab.
In addition to the time, the table details the number of messages
exchanged during the request.
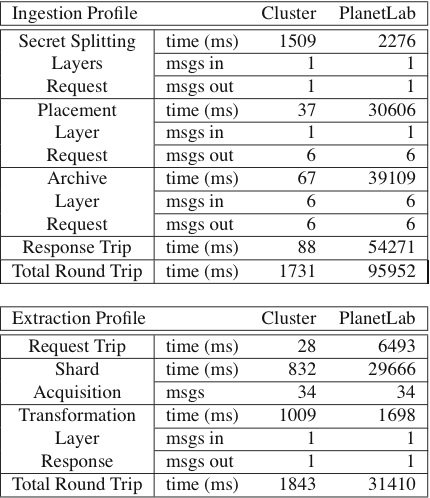
| Table 2: Profile of the ingestion and extraction of one object,
comparing trials run on a lightly-loaded local cluster with the
global-scale PlanetLab. Results are the average of 3 runs of
36 blocks per run using a (2,2) XOR split to generate
fragments and a (2,3) Shamir split to generate shards. |
As Table 2 shows, most of the time on the local
cluster is spent in the transformation layer. This is to be expected
as Shamir secret-splitting algorithm is compute-intensive. While
slower than many encryption algorithms, such secret-splitting
algorithms do not suffer from the problems discussed earlier with
long-term encryption and are fast enough for archival storage. The
compute-intensive nature of secret-splitting is further highlighted in
the local experiments due to the local cluster's dedicated network
with almost no outside cross-traffic. The transformation time for
ingestion is greater than for extraction for two reasons. First,
during ingestion, the transformation must generate many random values.
Second, during extraction, the transformation layer performs linear
interpolation using only those shards that are necessary. That is,
given an (m,n) secret split, all n are retrieved but calculation
is only done on the first m shards; the minimum required to rebuild
the data. During extraction, the speed improvements in
the transformation layer are balanced by the time required to collect
the requested shards from the archive layer. In a congested, heavily loaded system, the time to move data through
the system begins to dominate the transformation time as the
PlanetLab performance figures in Table 2 show. This
is evident in the comparable times spent in the transformation layers
in the two environments contrasted with the very divergent times spent
on requests and responses in the two environments. For example, the
extraction request trip took only 28 ms on the local cluster but
required about 6.5 seconds on the PlanetLab trials. Since request
messages are quite small, the difference is even more dramatic in the
shard acquisition times for extraction. Here, moving the shards from
the archives to the transformation layer took only 832 ms on the local
cluster but over 29.5 seconds on PlanetLab. The measurements per object represent two distinct scenarios. The
cluster numbers are from a lightly-loaded, well-equipped and
homogeneous network with unsaturated communication channels. In
contrast, the PlanetLab numbers feature far more congestion and
resource demands as POTSHARDS contended with other processes for both
host and network facilities. However, in archival storage, latency is
not as important as throughput. Thus, while these times are not
adequate for low-latency applications, they are acceptable for
archival storage.
| Figure 7: System throughput with sixteen archives and a workload of
100 MB per client using the same system parameters as in
Table 2. |
The results from local tests show a per client throughput of
0.50 MB/s extraction and 0.43 MB/s ingestion—per-client
performance is largely limited by the current design of the data
transformation layer. In the current version, both XOR splitting
and linear interpolation splitting is performed in a Java-based
implementation; future versions will use GF(216) arithmetic
in an optimized C based library. Additionally, clients
currently submit objects to the data transformation component and
synchronously await a response from the system before submitting
the next object. In contrast, the remainder of the system is highly
asynchronous. The high level of parallelism in the lower
layer is demonstrated in the throughput as the number of clients
increases. As Figure 7 shows, the read and
write throughput scales as the number of clients increases. With a low
number of clients, much of the system's time is spent waiting for a
request from the secret splitting layers. As the number of clients
increases, however, the system is able to take advantage of the increased
aggregate requests of the clients to achieve system throughput of
4.66 MB/s for extraction and 2.86 MB/s for ingestion. Write
performance is further improved through the use of asynchronous parity
updates. While an ingestion response waits for the archive to write
the data before being sent, it does not need to wait for the parity
updates. An additional factor to consider in measuring throughput is the
storage blow-up introduced by the two levels of secret splitting.
Using parameters of (2,2) XOR splitting and (2,3) shard splitting
requires six bytes to be stored for every byte of user data. In our
experiments, system throughput is measured from the client perspective
even though demands inside the system are six times those seen by the
client. Nonetheless, one goal for future work is to improve system
throughput by implementing asynchronous communication in the client.
5.2 User Data Recovery
In the event that the index over a user's shards is lost or damaged,
user data, including the index, if it was stored in POTSHARDS, can be
recovered from the shards themselves. To begin the procedure, the
user authenticates herself to each of the individual archives and
obtains all of her shards. The user then applies the algorithm
described in Section 4.4 to rebuild the fragments and
the objects that make up her data.
| Figure 8: Brute force recovery time for an increasing number
of shards generated using different secret splitting parameters. |
We ran experiments to measure the speed of the recovery process for
both algorithm options. While the recovery process is not fast enough
to use as the sole extraction method, it is fast enough for use as a
recovery tool. Figure 8 shows the
recovery times for two different secret splitting parameters. Using
the ring heuristic provides a near-linear recovery time as the number
of shards increases, and is much faster than the naïve approach.
In contrast, recovery without using the ring heuristic results in an
exponential growth. This is very apparent in Figure 8(b),
which must potentially try each path three times. The ring heuristic
provides an additional layer of security because a user that can
properly authenticate to all of the archives and acquire all of their
shards can recover their data very quickly. In contrast, an intruder
that cannot acquire all of the needed shards must search in
exponential time.
| Table 3: Recovery time in a name space with 5447 allocated names for
two different name space sizes. For larger systems, this time increases
approximately linearly with system size; name density and secret
splitting parameters determine the slope of the line. |
The density of the name space has a large effect on the time required
to recover the shards. As shown in
Table 3, a sparse name space results in
fewer false shard rings (none in this experiment) and is almost 30 times
faster than a densely packed name space. An area of future research
is to design name allocation policies that balance the recovery times
with the security of the shards. One simple option would be to
utilize a sliding window into the name space from which names are
drawn. As the current window becomes saturated it moves within the
name space. This would ensure adequate density for both new names and
existing names.
5.3 Archive ReconstructionThe archive recovery mechanisms were run on our local system using
eight 1.5 GB archives. Each redundancy group in the experiment
contained eight archives encoded using RAID 5. A 25 MB client
workload was ingested into the system using (2,2) XOR splitting and
(2,3) Shamir splitting, resulting in 150 MB of client shards,
excluding the appropriate parity. After the workload was ingested, an
archive was failed. We then used a static recovery manager that sent
reconstruction requests to all of the available archives and waited
for successful responses from a fail-over archive. Once the procedure
completed, the contents of the failed archive and the reconstructed
archive were compared. This procedure was run three times, recovering
at 14.5 MB/s, with the verification proving successful on each trial.
The procedure was also run with faults injected into the recovery
process to ensure that the verification process was correct.
6 DiscussionWhile we have designed and implemented an infrastructure that supports
secure long-term archival storage without the use of encryption, there
are still some outstanding issues. POTSHARDS assumes that individual
archives are relatively reliable; however, automated maintenance of
large-scale archival storage remains challenging [3].
We plan to explore the construction of archives from autonomous
power-managed disk arrays as an alternative to tape [8].
The goal would be devices that can distribute and replicate storage amongst
themselves, reducing the level of human intervention to replacing disks when sufficiently many have failed. A secure, archival system must deal with the often conflicting requirements
of maintaining the secrecy of data while also providing a degree of
redundancy. To this end, further work will explore the contention between
these two demands in such areas as parity building. In future versions,
we hope to improve the security of parity updates in which sensitive
data must be passed between archives. Currently, POTSHARDS depends on strong authentication and intrusion
detection to keep data safe, but it is not clear how to defend against
intrusions that may occur over many years, even if such attacks are
detected. We are exploring approaches that can refactor the
data [35] so that partial progress in an intrusion
can be erased by making new shards “incompatible” with old shards.
Unlike the failure of an encryption algorithm, which would necessitate
wholesale re-encryption, refactoring for security could be done over
time to limit the window over which a slow attack could succeed.
Refactoring could also be applicable to secure migration of data to
new storage devices. We have introduced the approximate pointer mechanism as a means of
making data recovery more tractable while maintaining security. While
we believe they are useful in this capacity, we admit that there is
more work to be done in understanding their nature. Specifically,
we plan on exploring the relationship between the ID namespace and
approximate pointer parameters. We would also like to reduce the storage overhead in POTSHARDS, and
are considering several approaches to do so. Some information dispersal
algorithms may have lower overheads than Shamir secret splitting; we plan
to explore their use, assuming that they maintain the information-theoretic
security provided by our current algorithm. The research in POTSHARDS is only concerned with preserving the bits
that make up files; understanding the bits is an orthogonal problem
that must also be solved. Others have begun to address this
problem [9], but maintaining the semantic meanings
of bits over decades-long periods may prove to be an even more
difficult problem than securely maintaining the bits themselves.
7 ConclusionsThis paper introduced POTSHARDS, a system designed to provide secure
long-term archival storage to address the new challenges and new
security threats posed by archives that must securely preserve data
for decades or longer. In developing POTSHARDS, we made several key contributions to secure
long-term data archival. First, we use multiple layers of secret
splitting, approximate pointers, and archives located in independent
authorization domains to ensure secrecy, shifting security of
long-lived data away from a reliance on encryption. The combination
of secret splitting and approximate pointers forces an attacker to
steal an exponential number of shares in order to reconstitute a single
fragment of user data; because he does not know which particular
shares are needed, he must obtain all of the possibly-required
shares. Second, we demonstrated that a user's data can be rebuilt in
a relatively short time from the stored shares only if
sufficiently many pieces can be acquired. Even a sizable (but
incomplete) fraction of the stored pieces from a subset of the
archives will not leak information, ensuring that data stored in
POTSHARDS will remain secret. Third, we made intrusion detection
easier by dramatically increasing the amount of information that an
attacker would have to steal and requiring a relatively unusual access
pattern to mount the attack. Fourth, we ensure long-term data
integrity through the use of RAID algorithms across multiple archives,
allowing POTSHARDS to utilize heterogeneous storage systems with the
ability to recover from failed or defunct archives and a facility to
migrate data to newer storage devices. Our experiments show that the current prototype implementation can
store user data at nearly 3 MB/s and retrieve user data at 5 MB/s.
Since POTSHARDS is an archival storage system, throughput is more of
a concern than latency, and these throughputs exceed typical long-term
data creation rates for most environments. Since the storage process
is parallelizable, additional clients increase throughput until the
archives' maximum throughput is reached; similarly, additional
archives linearly increase maximum system throughput. By addressing the long-term threats to archival data while providing
reasonable performance, POTSHARDS provides reliable data protection
specifically designed for the unique challenges of secure archival
storage. Storing data in POTSHARDS ensures not only that it will
remain available for decades to come, but also that it will remain
secure and can be recovered by authorized users even if all indexing
is lost.
AcknowledgmentsWe would like to thank our colleagues in the Storage Systems
Research Center (SSRC) who provided valuable feedback on the ideas
in this paper. This research was supported by the Petascale Data
Storage Institute, UCSC/LANL Institute for Scalable Scientific Data
Management and by SSRC sponsors including Los Alamos National Lab,
Livermore National Lab, Sandia National Lab, Digisense,
Hewlett-Packard Laboratories, IBM Research, Intel, LSI Logic,
Microsoft Research, Network Appliance, Seagate, Symantec, and Yahoo.
References
[1]
Health Information Portability and Accountability act, Oct. 1996.[2]
Adya, A., Bolosky, W. J., Castro, M., Chaiken, R., Cermak, G., Douceur,
J. R., Howell, J., Lorch, J. R., Theimer, M., and Wattenhofer, R.
FARSITE: Federated, available, and reliable storage for an
incompletely trusted environment.
In Proceedings of the 5th Symposium on Operating Systems Design
and Implementation (OSDI) (Boston, MA, Dec. 2002), USENIX.[3]
Baker, M., Shah, M., Rosenthal, D. S. H., Roussopoulos, M., Maniatis, P.,
Giuli, T., and Bungale, P.
A fresh look at the reliability of long-term digital storage.
In Proceedings of EuroSys 2006 (Apr. 2006), pp. 221–234.[4]
Chang, F., Ji, M., Leung, S.-T. A., MacCormick, J., Perl, S. E., and
Zhang, L.
Myriad: Cost-effective disaster tolerance.
In Proceedings of the 2002 Conference on File and Storage
Technologies (FAST) (San Francisco, CA, Jan. 2002).[5]
Choi, S. J., Youn, H. Y., and Lee, B. K.
An efficient dispersal and encryption scheme for secure distributed
information storage.
Lecture Notes in Computer Science 2660 (Jan. 2003), 958–967.[6]
Clarke, I., Sandberg, O., Wiley, B., and Hong, T. W.
Freenet: A distributed anonymous information storage and retrieval
system.
Lecture Notes in Computer Science 2009 (2001), 46+.[7]
CleverSafe.
Highly secure, highly reliable, open source storage solution.
Available from https://www.cleversafe.org/, June 2006.[8]
Colarelli, D., and Grunwald, D.
Massive arrays of idle disks for storage archives.
In Proceedings of the 2002 ACM/IEEE Conference on Supercomputing
(SC '02) (Nov. 2002).[9]
Gladney, H. M., and Lorie, R. A.
Trustworthy 100-year digital objects: Durable encoding for when it's
too late to ask.
ACM Transactions on Information Systems 23, 3 (July 2005),
299–324.[10]
Goldberg, A. V., and Yianilos, P. N.
Towards an archival intermemory.
In Advances in Digital Libraries ADL'98 (April 1998),
pp. 1–9.[11]
Goodson, G. R., Wylie, J. J., Ganger, G. R., and Reiter, M. K.
Efficient Byzantine-tolerant erasure-coded storage.
In Proceedings of the 2004 Int'l Conference on Dependable
Systems and Networking (DSN 2004) (June 2004).[12]
Gunawi, H. S., Agrawal, N., Arpaci-Dusseau, A. C., Arpaci-Dusseau, R. H.,
and Schindler, J.
Deconstructing commodity storage clusters.
In Proceedings of the 32nd Int'l Symposium on Computer
Architecture (June 2005), pp. 60–71.[13]
Haeberlen, A., Mislove, A., and Druschel, P.
Glacier: Highly durable, decentralized storage despite massive
correlated failures.
In Proceedings of the 2nd Symposium on Networked Systems Design
and Implementation (NSDI) (May 2005).[14]
Hand, S., and Roscoe, T.
Mnemosyne: Peer-to-peer steganographic storage.
Lecture Notes in Computer Science 2429 (2002), 130–140.[15]
Iyengar, A., Cahn, R., Garay, J. A., and Jutla, C.
Design and implementation of a secure distributed data repository.
In Proceedings of the 14th IFIP International Information
Security Conference (SEC '98) (Sept. 1998), pp. 123–135.[16]
Kallahalla, M., Riedel, E., Swaminathan, R., Wang, Q., and Fu, K.
Plutus: scalable secure file sharing on untrusted storage.
In Proceedings of the Second USENIX Conference on File and
Storage Technologies (FAST) (San Francisco, CA, Mar. 2003), USENIX,
pp. 29–42.[17]
Keeton, K., Santos, C., Beyer, D., Chase, J., and Wilkes, J.
Designing for disasters.
In Proceedings of the Third USENIX Conference on File and
Storage Technologies (FAST) (San Francisco, CA, Apr. 2004).[18]
Maniatis, P., Roussopoulos, M., Giuli, T. J., Rosenthal, D. S. H., and
Baker, M.
The LOCKSS peer-to-peer digital preservation system.
ACM Transactions on Computer Systems 23, 1 (2005), 2–50.[19]
Miller, E. L., Long, D. D. E., Freeman, W. E., and Reed, B. C.
Strong security for network-attached storage.
In Proceedings of the 2002 Conference on File and Storage
Technologies (FAST) (Monterey, CA, Jan. 2002), pp. 1–13.[20]
Oxley, M. G.
(H.R.3763) Sarbanes-Oxley Act of 2002, Feb. 2002.[21]
Peterson, L., Muir, S., Roscoe, T., and Klingaman, A.
PlanetLab Architecture: An Overview.
Tech. Rep. PDN–06–031, PlanetLab Consortium, May 2006.[22]
Plank, J. S.
A tutorial on Reed-Solomon coding for fault-tolerance in
RAID-like systems.
Software—Practice and Experience (SPE) 27, 9 (Sept. 1997),
995–1012.
Correction in James S. Plank and Ying Ding, Technical Report
UT-CS-03-504, U Tennessee, 2003.[23]
Quinlan, S., and Dorward, S.
Venti: A new approach to archival storage.
In Proceedings of the 2002 Conference on File and Storage
Technologies (FAST) (Monterey, California, USA, 2002), USENIX,
pp. 89–101.[24]
Rabin, M. O.
Efficient dispersal of information for security, load balancing, and
fault tolerance.
Journal of the ACM 36 (1989), 335–348.[25]
Rhea, S., Eaton, P., Geels, D., Weatherspoon, H., Zhao, B., and
Kubiatowicz, J.
Pond: the OceanStore prototype.
In Proceedings of the Second USENIX Conference on File and
Storage Technologies (FAST) (Mar. 2003), pp. 1–14.[26]
Santry, D. S., Feeley, M. J., Hutchinson, N. C., Veitch, A. C., Carton,
R. W., and Ofir, J.
Deciding when to forget in the Elephant file system.
In Proceedings of the 17th ACM Symposium on Operating Systems
Principles (SOSP '99) (Dec. 1999), pp. 110–123.[27]
Schwarz, S. J., T., and Miller, E. L.
Store, forget, and check: Using algebraic signatures to check
remotely administered storage.
In Proceedings of the 26th International Conference on
Distributed Computing Systems (ICDCS '06) (Lisboa, Portugal, July 2006),
IEEE.[28]
Shamir, A.
How to share a secret.
Communications of the ACM 22, 11 (Nov. 1979), 612–613.[29]
Stinson, D. R.
Cryptography Theory and Practice, 2nd ed.
Chapman & Hall/CRC, Boca Raton, FL, 2002.[30]
Stonebraker, M., and Schloss, G. A.
Distributed RAID—a new multiple copy algorithm.
In Proceedings of the 6th International Conference on Data
Engineering (ICDE '90) (Feb. 1990), pp. 430–437.[31]
Storer, M., Greenan, K., Miller, E. L., and Maltzahn, C.
POTSHARDS: Storing data for the long-term without encryption.
In Proceedings of the 3rd International IEEE Security in Storage
Workshop (Dec. 2005).[32]
Storer, M. W., Greenan, K. M., and Miller, E. L.
Long-term threats to secure archives.
In Proceedings of the 2006 ACM Workshop on Storage Security and
Survivability (Oct. 2006).[33]
Subbiah, A., and Blough, D. M.
An approach for fault tolerant and secure data storage in
collaborative work environements.
In Proceedings of the 2005 ACM Workshop on Storage Security and
Survivability (Fairfax, VA, Nov. 2005), pp. 84–93.[34]
Waldman, M., Rubin, A. D., and Cranor, L. F.
Publius: A robust, tamper-evident, censorship-resistant web
publishing system.
In Proceedings of the 9th USENIX Security Symposium (Aug.
2000).[35]
Wong, T. M., Wang, C., and Wing, J. M.
Verifiable secret redistribution for threshold sharing schemes.
Tech. Rep. CMU-CS-02-114-R, Carnegie Mellon University, Oct. 2002.[36]
Wylie, J. J., Bigrigg, M. W., Strunk, J. D., Ganger, G. R.,
Kiliççöte, H., and Khosla, P. K.
Survivable storage systems.
IEEE Computer (Aug. 2000), 61–68.[37]
You, L. L., Pollack, K. T., and Long, D. D. E.
Deep Store: An archival storage system architecture.
In Proceedings of the 21st International Conference on Data
Engineering (ICDE '05) (Tokyo, Japan, Apr. 2005), IEEE.
This document was translated from LATEX by
HEVEA.
|
