
16th USENIX Security Symposium
Pp. 213–228 of the Proceedings
  
Towards Automatic Discovery of Deviations in Binary
Implementations with Applications to Error Detection and Fingerprint
Generation
David "../../artley, Juan Caballero, Zhenkai Liang,
James Newsome, Dawn Song
Carnegie Mellon University
{d"../../artley,jcaballero,zliang,jnewsome,dawnsong}@cmu.edu
Abstract:
Different implementations of the same protocol specification usually
contain deviations, i.e., differences in how they check and
process some of their inputs. Deviations are commonly introduced as
implementation errors or as different interpretations of the same
specification. Automatic discovery of these deviations is important
for several applications. In this paper, we focus on automatic
discovery of deviations for two particular applications: error
detection and
fingerprint generation.
We propose a novel approach for automatically detecting
deviations in the way different implementations of the same
specification check and process their input. Our approach has several
advantages: (1) by automatically building symbolic formulas from the
implementation, our
approach is precisely faithful to the implementation; (2) by solving
formulas created from
two different implementations of the same specification, our approach
significantly reduces the number of inputs needed to find
deviations; (3) our approach works on binaries
directly, without access to the source code.
We have built a prototype implementation of our approach and have
evaluated it using multiple implementations of two different protocols:
HTTP and NTP.
Our results show that our approach successfully finds deviations
between different implementations, including errors in input checking,
and differences in the interpretation of the specification, which can
be used as fingerprints.
1 Introduction
Many different implementations usually exist for the same protocol.
Due to the abundance of coding errors and protocol specification
ambiguities, these implementations usually contain deviations,
i.e., differences in how they check and process some of their inputs.
As a result, same inputs can cause different implementations to reach
semantically different protocol states. For example, an
implementation may not perform sufficient input checking to verify if
an input is well-formed as specified in the protocol specification.
Thus, for some inputs, it might exhibit a deviation from another
implementation, which follows the protocol specification and performs
the correct input checking.
Finding these deviations in implementations is
important for several applications. In particular, in this paper we
show 1) how we can automatically discover these deviations, and 2) how
we can apply the discovered deviations to two particular applications:
error detection and fingerprint generation .
First, finding a deviation between two different implementations of
the same specification may
indicate that at least one of the two implementations has an error,
which we call error detection. Finding such errors is
important to guarantee that the protocol is correctly implemented,
to ensure proper interoperability with other implementations, and to
enhance system security since errors often represent vulnerabilities
that can be exploited. Enabling error detection by automatically
finding deviations between two different implementations is
particularly attractive because it does not require a manually written
model of the protocol specification. These models are usually complex,
tedious, and error-prone to generate. Note that such deviations do not
necessarily flag an error in one of
the two implementations, since deviations can also be caused by
ambiguity in the specification or when some parts are not fully
specified. However, automatic discovery of such deviations is a good
way to provide candidate implementation errors.
Second, such deviations naturally give rise to fingerprints,
which are inputs that, when given to two different implementations,
will result in semantically different output states. Fingerprints can
be used to distinguish between the different implementations and we
call the discovery of such inputs fingerprint generation .
Fingerprinting has been in use for more than a
decade [25] and is an important
tool in network security for
remotely identifying which implementation of an application or
operating system a remote host is running. Fingerprinting tools [8,11,15] need fingerprints to operate and
constantly require new fingerprints as new implementations, or new
versions of existing implementations, become available. Thus, the
process of automatically finding these fingerprints, i.e., the
fingerprint generation, is crucial for these tools.
Automatic deviation discovery is a challenging task--
deviations usually happen in corner cases, and discovering deviations
is often like finding needles in a haystack. Previous work in related
areas is largely insufficient. For example, the most commonly used
technique is random or semi-random generation of inputs [20,43]
(also called fuzz testing). In this line of approach, random inputs are
generated and sent to different implementations to observe if they
trigger a difference in outputs. The obvious drawback of this approach
is that it may take many such random inputs before finding a deviation.
In this paper, we propose a novel approach to automatically discover
deviations in input checking and processing between different
implementations of the same protocol specification. We are given two
programs 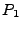 and and 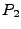 implementing the
same protocol. At a high
level, we build two formulas, implementing the
same protocol. At a high
level, we build two formulas, 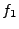 and and 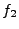 , which capture how each
program processes a single input. Then, we check whether the formula , which capture how each
program processes a single input. Then, we check whether the formula
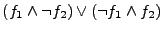 is satisfiable,
using
a solver such as a decision procedure. If the formula is satisfiable,
it means that we can find an input, which will satisfy is satisfiable,
using
a solver such as a decision procedure. If the formula is satisfiable,
it means that we can find an input, which will satisfy 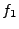 but not but not
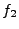 or vice versa, in which case it may lead the two program
executions to semantically different output states. Such inputs are
good candidates to trigger
a deviation. We then send such candidate inputs to the two programs
and monitor their output states. If the two programs end up in two
semantically different output states, then we have successfully found a
deviation between the
two implementations, and the corresponding input that triggers the
deviation. or vice versa, in which case it may lead the two program
executions to semantically different output states. Such inputs are
good candidates to trigger
a deviation. We then send such candidate inputs to the two programs
and monitor their output states. If the two programs end up in two
semantically different output states, then we have successfully found a
deviation between the
two implementations, and the corresponding input that triggers the
deviation.
We have built a prototype implementation of our approach. It handles
both Windows and Linux binaries running on an x86 platform. We have
evaluated our approach using multiple
implementations of two different protocols: HTTP and NTP. Our
approach has successfully identified deviations between servers and
automatically generated inputs that triggered different server
behaviors. These deviations include errors and differences in the
interpretation of the protocol specification. The evaluation shows that
our approach is accurate: in one case, the relevant part of the
generated input is
only three bits. Our approach is also efficient: we found deviations
using a single request in about one minute.
In summary, in this paper, we make the following contributions:
- Automatic discovery of deviations: We propose a novel
approach to automatically discover deviations in the way different
implementations of the same protocol specification check and process
their input. Our approach has several advantages: (1) by
automatically building symbolic formulas from an implementation, our
approach is precisely faithful to the implementation; (2) by solving
formulas created from two different implementations of the same
specification, our approach significantly reduces the number of inputs
needed to find deviations; (3) our approach works on
binaries directly, without access to the source code. This is important
for
wide applicability, since implementations may be proprietary and thus
not have the source code available. In addition, the binary is what
gets executed, and thus it represents the true behavior of the
program.
- Error detection using deviation discovery: We show how
to apply our approach for automatically discovering deviations to the
problem of error detection--the discovered
deviations provide candidate implementation errors. One fundamental
advantage of our approach is that it does not require a user to
manually generate a model of the
protocol specification, which is often complex, tedious, and
error-prone to generate.
- Fingerprint generation using deviation discovery:
We show how to apply our approach for automatically discovering
deviations to the problem of fingerprint generation--the discovered
deviations naturally give rise to fingerprints.
Compared to previous approaches, our solution significantly reduces the
number of candidate inputs that need to be tested to discover a
fingerprint [20].
- Implementing the approach:
We have built a prototype that implements our approach. Our evaluation
shows that our approach is accurate and efficient. It can identify
deviations with few example inputs at
bit-level accuracy.
The remainder of the paper is organized as follows. Section 2 introduces the problem and presents an
overview of our approach.
In Section 3 we present the different
phases and elements that comprise our approach and in Section 4 we describe the details of our
implementation.
Then, in Section 5 we present the
evaluation results of our approach over different protocols. We discuss
future enhancements to our approach in Section 6.
Finally, we present the related work in Section 7 and conclude in Section 8.
2 Problem Statement and Approach Overview
In this section, we first describe the problem statement, then we
present the intuition behind our approach, and finally we give an
overview of our approach.
In this paper we focus on the problem of automatically detecting
deviations in protocol implementations. In particular, we aim to find
inputs that cause two different implementations of the same protocol
specification to reach semantically different output states. When we
find such an input, we
say we have found a candidate deviation.
The output states need to be externally observable. We use two
methods to observe such states: (a) monitoring the network output of
the program, and (b) supervising its environment, which allows us to
detect unexpected states such as program halt, reboot, crash, or
resource
starvation. However, we cannot simply compare the complete
output from both implementations, since the output
may be different but semantically equivalent. For example,
many protocols contain sequence numbers, and we would expect the output
from two different implementations to contain two different sequence
numbers. However, the output messages may still be semantically
equivalent.
Therefore, we may use some domain knowledge about the specific
protocol being analyzed to determine when two output states are
semantically different. For example, many protocols such as HTTP,
include a status code in the response to provide feedback about the
status of the request. We use this
information to determine if two output states are semantically
equivalent or
not. In other cases, we observe the effect of a particular query
in the program, such as program crash or reboot. Clearly these cases
are
semantically different from a response being emitted by the program.
We are given two implementations 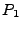 and and 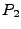 of the same protocol
specification. Each implementation at a high level can be viewed as a
mapping function
from the protocol input space of the same protocol
specification. Each implementation at a high level can be viewed as a
mapping function
from the protocol input space 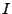 to the protocol
output state space to the protocol
output state space
 . Let . Let 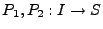 represent the mapping function of
the two implementations.
Each implementation accepts inputs represent the mapping function of
the two implementations.
Each implementation accepts inputs 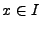 (e.g.,
an HTTP request), and then processes the input resulting in a
particular protocol output state
(e.g.,
an HTTP request), and then processes the input resulting in a
particular protocol output state  (e.g., an HTTP
reply). At a
high level, we wish to find inputs such that the same input, when sent
to the two implementations, will cause
each implementation to result in a different protocol output state. (e.g., an HTTP
reply). At a
high level, we wish to find inputs such that the same input, when sent
to the two implementations, will cause
each implementation to result in a different protocol output state.
Our goal is to find an input 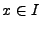 such that such that
 .
Finding such an input through random testing is usually hard. .
Finding such an input through random testing is usually hard.
However, in general it is easy to find an input 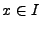 such that
such that
 , i.e., most inputs will result in the same
protocol
output state , i.e., most inputs will result in the same
protocol
output state 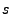 for different implementations of the same
specification. Let for different implementations of the same
specification. Let 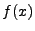 be the formula representing the set
of inputs be the formula representing the set
of inputs 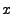 such that such that
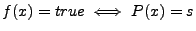 . When . When 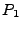 and and 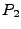 implement the same
protocol differently, there may be some input where implement the same
protocol differently, there may be some input where 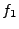 will
not be the same as will
not be the same as 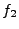 : :
The intuition behind the above expression is that when
 , then , then
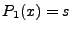 (because (because
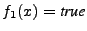 ) while ) while  (because
(because  ), thus the two implementations reach different
output states for the same input ), thus the two implementations reach different
output states for the same input 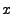 . Similarly, . Similarly,
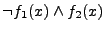 indicates when indicates when
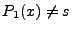 , but , but 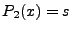 . We take the
disjunction since we only care whether the implementations differ from
each other. . We take the
disjunction since we only care whether the implementations differ from
each other.
Given the above intuition, the central idea is to create the formula
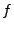 using the technique of weakest
precondition [19,26]. Let using the technique of weakest
precondition [19,26]. Let 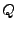 be a
predicate over the state space of a program. The weakest precondition be a
predicate over the state space of a program. The weakest precondition
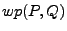 for a program for a program 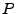 and post-condition and post-condition 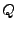 is a boolean
formula is a boolean
formula 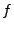 over the input space of the program. In our
setting, if over the input space of the program. In our
setting, if
 , then , then 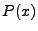 will terminate in a state
satisfying will terminate in a state
satisfying 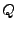 , and if , and if
 , then , then 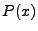 will
not
terminate in a state satisfying will
not
terminate in a state satisfying 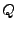 (it either ``goes
wrong'' or does
not terminate). For example, if the post-condition (it either ``goes
wrong'' or does
not terminate). For example, if the post-condition 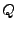 is that is that 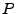 outputs a successful HTTP reply, then outputs a successful HTTP reply, then
 characterizes all inputs which lead characterizes all inputs which lead 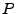 to output a
successful HTTP reply. The boolean formula output by the
weakest precondition is our formula to output a
successful HTTP reply. The boolean formula output by the
weakest precondition is our formula 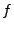 . .
Furthermore, we observe that the above method can still be used even
if we do not consider the entire program and only consider a single
execution path (we discuss multiple execution paths in
Section 6). In that case, the formula 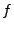 represents the subset of protocol inputs that follow one of the
execution paths considered and still reach the protocol output state
represents the subset of protocol inputs that follow one of the
execution paths considered and still reach the protocol output state
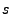 . Thus, . Thus, 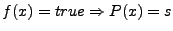 , since if an input
satisfies , since if an input
satisfies 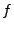 then for sure it will make program then for sure it will make program 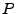 go to state go to state 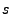 ,
but the converse is not necessarily true--an input which makes ,
but the converse is not necessarily true--an input which makes 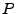 go
to state go
to state 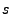 may not satisfy may not satisfy 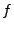 . In our
problem, this means that the
difference between . In our
problem, this means that the
difference between 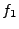 and and 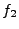 may not
necessarily result in a
true deviation, as shown in Figure 2.
Instead, the difference between may not
necessarily result in a
true deviation, as shown in Figure 2.
Instead, the difference between 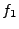 and and 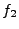 is a
good candidate, which we can then test to validate whether it is a
true deviation. is a
good candidate, which we can then test to validate whether it is a
true deviation.
Figure 1:
Overview of our approach.
|
|
Our approach is an iterative process, and each iteration consists of
three phases, as shown in Figure 1. First,
in the
formula extraction phase, we are given two binaries 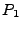 and and 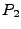 implementing the same protocol
specification, such as HTTP, and an input implementing the same protocol
specification, such as HTTP, and an input 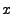 , such as
an HTTP GET request.
For each implementation, we log an execution trace of the binary
as it processes the input, and record what output state it reaches,
such as halting or sending a reply. We assume that the execution from
both binaries reaches semantically equivalent output states; otherwise
we have already found a deviation! For each
implementation , such as
an HTTP GET request.
For each implementation, we log an execution trace of the binary
as it processes the input, and record what output state it reaches,
such as halting or sending a reply. We assume that the execution from
both binaries reaches semantically equivalent output states; otherwise
we have already found a deviation! For each
implementation 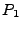 and and 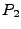 , we
then use this information to produce a
boolean formula over the input, , we
then use this information to produce a
boolean formula over the input, 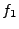 and and 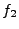 respectively, each
of which is satisfied for inputs that cause the binary to reach the
same output state as the original input did. respectively, each
of which is satisfied for inputs that cause the binary to reach the
same output state as the original input did.
Next, in the deviation detection phase, we use a solver
(such as a
decision procedure) to find differences in the two formulas 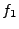 and and
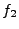 . In particular, we ask the solver if . In particular, we ask the solver if
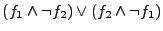 is satisfiable.
When satisfiable the
solver will return an example satisfying input. We call these inputs
the candidate deviation inputs. is satisfiable.
When satisfiable the
solver will return an example satisfying input. We call these inputs
the candidate deviation inputs.
Finally, in the validation phase we evaluate the
candidate deviation inputs obtained in the formula extraction phase on
both implementations and check
whether the implementations do in fact reach semantically different
output states. This phase is necessary because the symbolic formula
might not include all possible execution paths, then an input that
satisfies 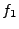 is guaranteed to make is guaranteed to make 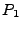 reach the same semantically equivalent output state as the original
input
reach the same semantically equivalent output state as the original
input 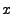 but an input that
does not satisfy but an input that
does not satisfy 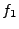 may also make may also make 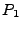 reach a
semantically equivalent output state. Hence, the
generated candidate deviation inputs may actually still cause both
implementations to reach semantically equivalent output states. reach a
semantically equivalent output state. Hence, the
generated candidate deviation inputs may actually still cause both
implementations to reach semantically equivalent output states.
If the implementations do reach semantically different
output states, then we have found
a deviation triggered by that input. This deviation is useful for two
things: (1) it may represent an implementation error in at least
one of the implementations, which can then be checked against
the protocol specification to verify whether it is truly an error; (2)
it can be used as a fingerprint to distinguish
between the two implementations.
We can iterate this entire process to examine other input
types.
Continuing with the HTTP example, we can
compare how the two implementations process other types of HTTP
requests, such as HEAD and POST, by repeating the process on those
types of requests.
3 Design
In this section, we describe the details of the three phases in our
approach, the formula extraction phase, the deviation detection phase,
and the validation phase.
The goal of the formula extraction phase is that given an input 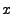 such that such that
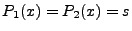 , where , where 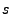 is the output state when executing
input is the output state when executing
input
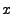 with the two given programs, we would like to compute two
formulas, with the two given programs, we would like to compute two
formulas, 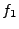 and and 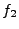 , such that, , such that,
and
This matches well
with the technique of weakest precondition (WP) [19,26]. The weakest precondition,
denoted 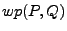 , is a
boolean formula , is a
boolean formula 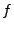 over the input space over the input space 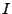 of of 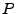 such that if such that if
 , then , then 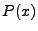 will
terminate in a
state satisfying will
terminate in a
state satisfying 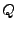 .
In our setting, the post-condition is the protocol output state, and
the weakest precondition is a formula characterizing protocol inputs,
which will cause the implementation to reach the specified protocol
output
state. .
In our setting, the post-condition is the protocol output state, and
the weakest precondition is a formula characterizing protocol inputs,
which will cause the implementation to reach the specified protocol
output
state.
Unfortunately, calculating the weakest precondition over an entire
real-world binary program can easily result in a formula that is too
big to solve. First, there may be many program paths which can lead to
a particular output state. We show that we can generate
interesting deviations even when considering a single program path.
Second, we observe that in many cases only a small subset of
instructions operate on data derived from the original input. There is
no need to model the instructions that do not operate on data derived
from the original input, since the result they compute will be the
same as in the original execution. Therefore we eliminate these
instructions from the WP calculation, and replace them with only a
series of assignments of concrete values to the relevant program state
just before an instruction operates on data derived from the input.
Hence, in our design, we build the symbolic formula
in two distinct steps. We first execute the program on the original
input, while recording a trace of the execution. We then use this
execution trace to build the symbolic formula.
In order to generate the symbolic formula, we perform the following
steps:
- Record the execution trace of the executed program path.
- Process the execution trace. This step translates the execution
trace into a program
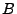 written in our simplified
intermediate representation (IR). written in our simplified
intermediate representation (IR).
- Generate the appropriate post-condition
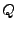 . .
- Calculate the weakest precondition on
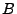 by: by:
- Translating
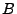 into a single assignment form. into a single assignment form.
- Translating the (single assignment) IR program into the
guarded
command language (GCL). The GCL program, denoted
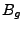 , is
semantically equivalent to the input IR statements, but appropriate
for the weakest precondition calculation. , is
semantically equivalent to the input IR statements, but appropriate
for the weakest precondition calculation.
- Computing the weakest precondition
 in a syntax-directed
fashion on the GCL. in a syntax-directed
fashion on the GCL.
The output of this phase is the symbolic formula 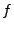 . Below we
describe these steps in more detail. . Below we
describe these steps in more detail.
We generate formulas based upon the program path for a single
execution. We have implemented a path recorder which records the
execution trace of the program. The execution trace is the sequence of
machine instructions executed, and for each executed instruction, the
value of each operand, whether each operand is derived from the input,
and if it is derived from the input, an identifier for the original
input stream it comes from.
The trace also has information about the first use of each input byte,
identified by its offset in the input stream. For example, for data
derived from network inputs, the identifier
specifies which session the input came from, and the offset
specifies the original position in the session data.
We process the execution trace to include only relevant
instructions. An instruction is relevant if it operates on data
derived from the input 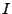 . For each relevant instruction, we: . For each relevant instruction, we:
- Translate the x86 instruction to an easier-to-analyze
intermediate representation (IR). The generated IR is semantically
equivalent to the original instruction.
The advantage of our IR is that it allows us to perform
subsequent steps over
the simpler IR statements, instead of the hundreds of x86
instructions. The translation from an x86 instruction to our IR is
designed to correctly model the semantics of the original x86
instruction, including making otherwise implicit side effects explicit.
For example, we insert code to correctly model instructions that set
the eflags register, single instruction loops (e.g., rep
instructions), and instructions that behave differently depending
on the operands (e.g., shifts).
Table 1:
Our RISC-like assembly IR. We convert x86 assembly instructions into
this IR.
 |
Our IR is shown in Table 1. We
translate
x86
instruction into this IR. Our IR has assignments (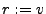 ),
binary
and unary operations ( ),
binary
and unary operations ( 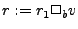 and and 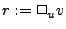 where where 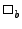 and and 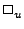 are binary and unary
operators), loading a value
from memory into a register ( are binary and unary
operators), loading a value
from memory into a register ( 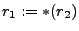 ), storing a value ( ), storing a value (
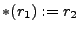 ), direct jumps (jmp ), direct jumps (jmp 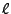 ) to a known target label (label ) to a known target label (label 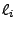 ),
indirect jumps to a computed value stored in
a register
(ijmp ),
indirect jumps to a computed value stored in
a register
(ijmp 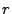 ), and conditional jumps (if ), and conditional jumps (if 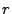 then jmp then jmp 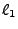 else jmp else jmp 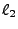 ). ).
- Translate the information logged about the operands into a
sequence of initialization statements. For each operand:
- If it is not derived from input, the operand is assigned the
concrete value logged in the execution trace. These assignments
effectively model the sequences of instructions that we do not
explicitly include.
- For operands derived from input, the first time we
encounter a byte derived from a particular input identifier and offset,
we initialize the corresponding byte of the operand with a symbolic
value that uniquely identifies that input identifier and offset. On
subsequent instructions that operate on data derived from that
particular input identifier and offset, we do not initialize
the corresponding operand, since we want to accurately model the
sequence of computations on the input.
The output of this step is an IR program 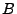 consisting of a sequence
of IR statements.
consisting of a sequence
of IR statements.
Once we have generated the IR program from the execution trace, the
next step is to select a post-condition, and compute the weakest
precondition of this post-condition over the program, yielding our
symbolic formula.
The post-condition specifies the desired protocol output state, such
as what kind of response to a request message is desired. In our
current setting, an ideal post-condition would specify that ``The input
results in an execution that results in an output state that is
semantically equivalent to the output state reached when processing
the original input.'' That is, we want our formula to be true for
exactly the inputs that are considered ``semantically equivalent'' to
the original input by the modeled program binary.
In our approach, the post-condition specified the output state
should
be the same as in the trace. In order to make the overall formula size
reasonable, we add additional constraints to the post-condition which
constraint the formula to the same program path taken as in the trace.
We do this by iterating over all conditional jumps and indirect jumps
in the IR, and for each jump, add a clause to the post-condition that
ensures that the final formula only considers inputs that also result
in the same destination for the given jump. For example, if in the
trace if  then then 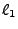 else else 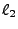 was evaluated and the
next instruction executed was was evaluated and the
next instruction executed was 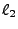 , then , then  must have evaluated
to false, and we add a clause restricting must have evaluated
to false, and we add a clause restricting
 to the post-condition. to the post-condition.
In some programs, there may be multiple paths that reach the same
output state. Our techniques can be generalized to handle this case,
as discussed in Section 6. In practice, we
have found
this post-condition to be sufficient for finding interesting
deviations. Typically, inputs that cause the same execution path to
be followed are treated equivalently by the program, and result in
equivalent output states. Conversely, inputs that follow a different
execution path often result in a semantically different output state
of the program. Although more complicated and general post-conditions
are possible, one interesting result from our experiments is that the
simple approach was all that was needed to generate interesting
deviations.
The weakest precondition (WP) calculation step takes as input the IR
program 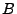 from Step 2, and the desired post-condition from Step 2, and the desired post-condition 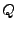 from Step 3. The weakest precondition, denoted
from Step 3. The weakest precondition, denoted 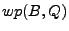 , is
a
boolean formula , is
a
boolean formula 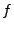 over the input space such that if over the input space such that if
 , then , then 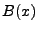 will
terminate in a
state satisfying will
terminate in a
state satisfying 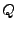 .
For example, if the program is .
For example, if the program is 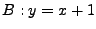 and and 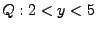 , then , then
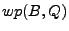 is is  . .
We describe the steps for computing the weakest precondition below.
Step 4a: Translating into single assignment form.
We translate the IR program  from the previous
step into
a form in which every variable is assigned at most once. (The
transformed program is semantically equivalent to the input IR.) We
perform
this step to enable additional optimizations described
in [29,36,19], which
further reduce the formula
size. For example, this transformation will rewrite the
program x := x+1; x := x+1; as x1 := x0+1; x2 := x1+1;.
We
carry out this transformation by maintaining a mapping from the
variable name to its current incarnation, e.g., the original variable
x may have incarnations x0, x1, and x2.
We iterate
through the program and replace each variable use with its current
incarnation. This step is similar to computing the SSA form of a
program [39], and is a
widely used technique. from the previous
step into
a form in which every variable is assigned at most once. (The
transformed program is semantically equivalent to the input IR.) We
perform
this step to enable additional optimizations described
in [29,36,19], which
further reduce the formula
size. For example, this transformation will rewrite the
program x := x+1; x := x+1; as x1 := x0+1; x2 := x1+1;.
We
carry out this transformation by maintaining a mapping from the
variable name to its current incarnation, e.g., the original variable
x may have incarnations x0, x1, and x2.
We iterate
through the program and replace each variable use with its current
incarnation. This step is similar to computing the SSA form of a
program [39], and is a
widely used technique.
Step 4b: Translating to GCL.
The translation to GCL takes as input the single assignment form from
step 4a, and outputs a semantically equivalent GCL program 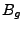 .
We perform this step since the weakest precondition is calculated over
the GCL language [26]. The
resulting program .
We perform this step since the weakest precondition is calculated over
the GCL language [26]. The
resulting program 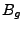 is semantically equivalent to
the input single-assignment IR statements. The weakest precondition is
calculated in a syntax-directed manner over is semantically equivalent to
the input single-assignment IR statements. The weakest precondition is
calculated in a syntax-directed manner over 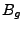 . .
Table 2:
The guarded command language (left), along with the corresponding
weakest precondition predicate transformer (right).
 |
The GCL language constructs we use are shown in Table 2.
Although GCL may look unimpressive, it is sufficiently expressive for
reasoning about complex
programs [26,29,28,24] 1. Statements  in our
GCL programs will mirror statements in assembly,
e.g., store, load, assign, etc. GCL has assignments of the form in our
GCL programs will mirror statements in assembly,
e.g., store, load, assign, etc. GCL has assignments of the form 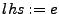 where where 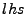 is a register or memory location,
and is a register or memory location,
and  is a
(side-effect) free expression. assume is a
(side-effect) free expression. assume  assumes a
particular
(side-effect free) expression is true. An assume statement is
used to reason about conditional jump predicates, i.e., we add ``assume assumes a
particular
(side-effect free) expression is true. An assume statement is
used to reason about conditional jump predicates, i.e., we add ``assume
 '' for the true branch of a conditional jump, and ``assume '' for the true branch of a conditional jump, and ``assume
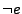 '' for the false branch of the conditional
jump. assert '' for the false branch of the conditional
jump. assert  asserts that asserts that  must be
true for execution to continue,
else the program fails. In other words, must be
true for execution to continue,
else the program fails. In other words, 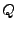 cannot be satisfied
if
assert cannot be satisfied
if
assert  is false. skip is a semantic no-op. is false. skip is a semantic no-op. 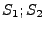 denotes a sequence where first statement denotes a sequence where first statement 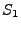 is executed and then statement is executed and then statement  is
executed. is
executed.  is called a choice statement, and indicates that either
is called a choice statement, and indicates that either 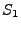 or or  may be executed. Choice statements
are used for if-then-else constructs. may be executed. Choice statements
are used for if-then-else constructs.
For example, the IR:
![\begin{lstlisting}[mathescape=true]
if ($x_0 < 0$){
$x_1 := x_0-1$;
} else {
$x_1 := x_0+1$;
}
\end{lstlisting}](img85.png)
will be translated as:
The above allows calculating the WP over multiple paths (we discuss
multiple paths in Section 6). In our
setting, we only
consider a single path. For each branch condition  evaluated
in the
trace, we could add the GCL statement assert evaluated
in the
trace, we could add the GCL statement assert  if if  evaluated to true (else assert
evaluated to true (else assert 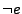 if if  evaluated
to false). In our implementation, using assert in this
manner is equivalent to adding a clause for each branch predicate to
the post-condition (e.g., making the post-condition evaluated
to false). In our implementation, using assert in this
manner is equivalent to adding a clause for each branch predicate to
the post-condition (e.g., making the post-condition  when when
 evaluated to true in the trace). evaluated to true in the trace).
Step 4c: Computing the weakest precondition. We compute the
weakest
precondition for 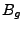 from the previous step in a
syntax-directed
manner. The rules for computing the weakest precondition are shown
in Table 2. Most rules are straightforward,
e.g., to
calculate the weakest precondition from the previous step in a
syntax-directed
manner. The rules for computing the weakest precondition are shown
in Table 2. Most rules are straightforward,
e.g., to
calculate the weakest precondition 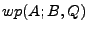 , we calculate , we calculate 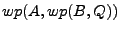 . Similarly . Similarly
 . For assignments . For assignments 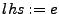 , we generate a let expression which
binds the variable name , we generate a let expression which
binds the variable name 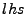 to the expression to the expression  . We also take
advantage of a technical transformation, which can further reduce the
size of the formula by using the single assignment form
from Step 4a [29,36,19]. . We also take
advantage of a technical transformation, which can further reduce the
size of the formula by using the single assignment form
from Step 4a [29,36,19].
3.1.3 Memory Reads and Writes to Symbolic Addresses
If the instruction accesses memory using an address that is derived
from the input, then in the formula the address will be symbolic, and
we must choose what set of possible addresses to consider. In order to
remain sound, we add a clause to our post-condition to only consider
executions that would calculate an address within the selected set.
Considering more possible addresses increases the generality of our
approach, at the cost of more analysis.
When reading from a memory location selected by an address derived from
the input, we must process the memory locations in the set of addresses
being considered as operands, generating any appropriate initialization
statements, as above.
We achieve good results considering only the address that was
actually used in the logged execution trace and adding the
corresponding constraints to the post-condition to preserve soundness.
In practice, if useful deviations are not found from the corresponding
formula, we could consider a larger range of addresses, achieving a
more descriptive formula at the cost of performance. We have
implemented an analysis that bounds the range of symbolic memory
addresses [2], but have found we
get good results without preforming this additional step.
We need not transform writes to memory locations selected by an address
derived from the input. Instead we record the selected set of addresses
to consider, and add the corresponding clause to the post-condition to
preserve soundness. These conditions force the solver to reason about
any potential alias relationships. As part of the weakest precondition
calculation, subsequent memory reads that could use one of the
addresses being considered are transformed to a conditional statement
handling these potential aliasing relationships.
As with memory reads, we achieve good results only considering the
address that was actually used in the logged execution trace. Again, we
could generalize the formula to consider more values, by selecting a
range of addresses to consider.
In this phase, we use a solver to find candidate inputs
which may cause deviations. This phase takes as input the formulas
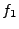 and and 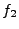 generated for the programs generated for the programs 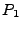 and and 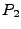 in the formula extraction phase. We
rewrite the variables in each formula so that they
refer to the same input, but each to their own internal states. in the formula extraction phase. We
rewrite the variables in each formula so that they
refer to the same input, but each to their own internal states.
We then query the solver whether the combined formula
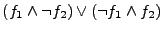 is satisfiable, and
if so, to provide an example that satisfies the combined formula. If
the solver returns an example, then we have found an input that
satisfies one program's
formula, but not the other. If we had perfectly and fully modeled each
program, and perfectly specified the post-condition to be that ``the
input results in a semantically equivalent output state'', then this
input would be guaranteed to produce a semantically equivalent output
state in one program, but not the other. Since we only consider one
program path and do not perfectly specify the post-condition in this
way, this input is only a candidate deviation input. is satisfiable, and
if so, to provide an example that satisfies the combined formula. If
the solver returns an example, then we have found an input that
satisfies one program's
formula, but not the other. If we had perfectly and fully modeled each
program, and perfectly specified the post-condition to be that ``the
input results in a semantically equivalent output state'', then this
input would be guaranteed to produce a semantically equivalent output
state in one program, but not the other. Since we only consider one
program path and do not perfectly specify the post-condition in this
way, this input is only a candidate deviation input.
Figure 2:
Different execution paths could end up in the same output states. The
validation phase checks whether the new execution path explored by the
candidate deviation input obtained in the deviation detection phase
truly ends up in a different state.
|
|
|
Finally, we validate the generated candidate deviation inputs to
determine whether they actually result in semantically different
output states in the two implementations. As
illustrated in Figure 2, it is
possible
that while an input does not satisfy the symbolic formula generated
for a server, it actually does result in an identical or semantically
equivalent output state.
We send each candidate deviation input to the implementations being
examined, and compare their outputs to determine whether they result in
semantically equivalent or semantically different output states.
In theory, this testing requires some domain knowledge about the
protocol implemented by the binaries, to determine
whether their outputs are semantically equivalent. In practice, we have
found
deviations that are quite obvious. Typically, the server whose
symbolic formula is satisfied by the input
produces a response similar to its response to the original input, and
the server whose symbolic formula is not satisfied by the input
produces an error message, drops the connection, etc.
4 Implementation
Our implementation consists of several components: a path recorder,
the symbolic formula generator, the solver, and a validator. We
describe each below.
The symbolic formula generator component is based on QEMU, a complete
system emulator [10]. We use a
modified version of QEMU, that has
been enhanced with the ability to track how specified external inputs,
such as keyboard or received network data are procesed. The formula
generator monitors the execution of a binary and
records the execution trace, containing all instructions executed by
the program and the information of their operands, such as their value
and whether they are derived from specified external inputs. We start
monitoring the execution before sending requests to the server and
stop the trace when we observe a response from the server. We use a
no-response timer to stop the trace if no answer is observed from the
server after a configurable amount of time.
We implemented our symbolic
formula generator as part of our BitBlaze binary analysis
platform [1].
The BitBlaze platform can parse executables and instruction traces,
disassemble each instruction, and translate the instructions into the
IR shown in Table 1. The entire platform
consists of
about 16,000 lines of C/C++ code and 28,000 lines of OCaml, with about
1,600 lines of OCaml specifically written for our approach.
We use STP [30,31] as our solver. It is a
decision
procedure specialized in modeling bit-vectors. After taking our
symbolic formula as input, it either outputs an input that can satisfy
the formula, or decides that the formula is not satisfiable.
Once a candidate deviation input has been returned by the solver, we
need to validate it against both server implementations and monitor
the output states. For this we have built small HTTP and NTP
clients that read the inputs, send them over the network to the
servers, and capture the responses, if any.
After sending candidate inputs to both implementations, we determine
the output state by looking at the response sent from the server. For
those protocols that contain some type of status code in the response,
such as HTTP in the Status-Line, each different value of the status
code represents a different output state for the server. For those
protocols that do not contain a status code in the response, such as
NTP, we define a generic valid state and consider the server
to
have reached that state, as a consequence of an input, if it sends any
well-formed response to the input, independently of the values of the
fields in the response.
In addition, we define three special output states: a fatal
state
that includes any behavior that is likely to cause the server to stop
processing future queries such as a crash, reboot, halt or resource
starvation, a no-response state that indicates that the
server
is not in the fatal state but still did not respond before a
configurable timer expired, and a malformed state that
includes
any response from the server that is missing mandatory fields. This
last state is needed because servers might send messages back to the
client that do not follow the guidelines in the corresponding
specification. For example several HTTP servers, such as Apache or
Savant, might respond to an incorrect request with a raw message
written into the socket, such as the string ``IOError'' without
including the expected HTTP Status-Line such as ``HTTP/1.1 400 Bad
Request''.
5 Evaluation
We have evaluated our approach on two different protocols: HTTP and
NTP.
We selected these two protocols as representatives of two large
families of protocols: text protocols (e.g. HTTP) and binary protocols
(e.g. NTP). Text and binary protocols present significant differences
in encoding, field ordering, and methods used to separate fields. Thus,
it is valuable to study both families.
In particular, we use three HTTP server implementations and two NTP
server implementations, as shown in Table 3.
All the implementations are Windows binaries and the evaluation is
performed on a Linux host running Fedora Core 5.
Table 3:
Different server implementations used in our evaluation.
| Server |
Version |
Type |
Binary Size |
| Apache |
2.2.4 |
HTTP server |
4,344kB |
| Miniweb |
0.8.1 |
HTTP server |
528kB |
| Savant |
3.1 |
HTTP server |
280kB |
| NetTime |
2.0 beta 7 |
NTP server |
3,702kB |
| Ntpd |
4.1.72 |
NTP server |
192kB |
|
The original inputs, which we need to send to the servers during the
formula extraction phase to generate the execution traces, were
obtained by capturing a network trace from one of our workstations and
selecting all the HTTP and
NTP requests that it contained.
For each HTTP request in the trace, we send it to each of the HTTP
servers and monitor its execution, generating an execution trace as
output. We proceed similarly for each NTP request, obtaining an
execution trace for each request/server pair. In Section 5.1, we show the
deviations we discovered in the web servers, and in Section 5.2, the deviations we discovered in the
NTP servers.
Figure 3:
One of the original HTTP requests we used to generate execution traces
from all HTTP servers, during the formula extraction phase.
|
|
Table 4:
Summary of deviations found for the HTTP servers, including the number
of candidate input queries requested to the solver and the number of
deviations found. Each cell represents the results from one query to
the solver and each query to the solver handles half of the combined
formula for each server pair. For example Case 3 shows the results when
querying the solver for 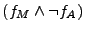 and the combined formula for the
Apache-Miniweb pair is the disjunction of Cases 1 and 3. and the combined formula for the
Apache-Miniweb pair is the disjunction of Cases 1 and 3.
| |
 |
 |
 |
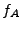 |
N/A |
Case 1: unsatisfiable |
Case 2: 5/0 |
 |
Case 3: 5/5 |
N/A |
Case 4: 5/5 |
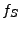 |
Case 5: unsatisfiable |
Case 6: unsatisfiable |
N/A |
|
5.1 Deviations in Web Servers
This section shows the deviations we found among three web server
implementations: Apache, Miniweb, and Savant. For brevity and clarity,
we only show results for a specific HTTP query, which we find to be
specially important because it discovered deviations between different
server pairs. Figure 3 shows this
query, which is an HTTP GET request for the file /index.html.
For each server we first calculate a symbolic formula that represents
how the server handled the original HTTP request shown in Figure 3.
We call these formulas: 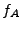 , , 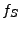 , ,  for Apache, Savant and Miniweb
respectively.
Then, for each of the three possible server pairs: Apache-Miniweb,
Apache-Savant and Savant-Miniweb, we calculate the combined formula as
explained in Section 3. For example, for
the Apache-Miniweb pair, the combined formula is for Apache, Savant and Miniweb
respectively.
Then, for each of the three possible server pairs: Apache-Miniweb,
Apache-Savant and Savant-Miniweb, we calculate the combined formula as
explained in Section 3. For example, for
the Apache-Miniweb pair, the combined formula is
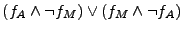 .
To obtain more detailed information, we break the combined formula into
two separates queries to the solver, one representing each side of the
disjunction. For example, for the Apache-Miniweb pair, we query the
solver twice: one for .
To obtain more detailed information, we break the combined formula into
two separates queries to the solver, one representing each side of the
disjunction. For example, for the Apache-Miniweb pair, we query the
solver twice: one for 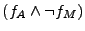 and another time for and another time for
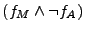 . The combined formula is the
disjunction of
the two responses from the solver. . The combined formula is the
disjunction of
the two responses from the solver.
Table 4 summarizes our results
when sending the HTTP GET request in Figure 3 to the three servers. Each cell of the
table represents a different query to the solver, that is, half of the
combined formula for each server pair. Thus, the table has six possible
cells.
For example, the combined formula for the Apache-Miniweb pair, is shown
as the disjunction of Cases 1 and 3.
Out of the six possible cases, the solver returned unsatisfiable for
three of them (Cases 1, 5, and 6). For the remaining cases, where the
solver was able to generate at least one candidate deviation input, we
show two numbers in the format X/Y. The X value represents the number
of different candidate deviation inputs we obtained from the solver,
and the Y value represents the number
of these candidate deviation inputs that actually generated
semantically different output states when sent to the servers in the
validation phase. Thus, the Y value represents the number of inputs
that triggered a deviation.
In Case 2, none of the five candidate deviation inputs
returned by the solver were able to generate semantically different
output states when sent to the servers, that is, no deviations were
found.
For Cases 3 and 4, all candidate deviation inputs triggered a deviation
when sent to the servers during the validation phase.
In both cases, the Miniweb server accepted some input that
was rejected by the other server. We analyze these cases in more detail
next.
Figure 4 shows one of the
deviations found for the Apache-Miniweb pair.
It presents one of the candidate deviation inputs obtained from the
solver in Case 3, and the responses received from both Apache and
Miniweb when that candidate input was sent to them during the
validation phase.
The key difference is on the fifth byte of the candidate deviation
input, whose original ASCII value represented a slash, indicating an
absolute path. In the generated candidate deviation input, the byte has
value 0xE8. We have confirmed that Miniweb does indeed accept any value
on this byte. So, this deviation reflects an error by Miniweb: it
ignores the first
character of the requested URI and assumes it to be a slash, which is a
deviation from the URI specification [16].
Figure 4:
Example deviation found for Case 3, where Miniweb's formula is
satisfied while Apache's isn't. The figure includes the candidate
deviation input being sent and the responses obtained from the servers,
which show two different output states.
|
|
Figure 5:
Example deviation found for Case 4, where Miniweb's formula is
satisfied while Savant's isn't. The output states show that Miniweb
accepts the input but Savant rejects it with a malformed response.
|
|
Figure 6:
Another example deviation for Case 4, between Miniweb and Savant. The
main different is on byte 21, which is part of the Version string. In
this case Miniweb accepts the request but Savant rejects it.
|
|
Figure 5 shows one of the
deviations found for the Savant-Miniweb pair.
It presents one of the candidate deviation inputs obtained from the
solver in Case 4, including the responses received from both Savant and
Miniweb when the
candidate deviation input was sent to them during the validation phase.
Again, the candidate deviation input has a different value on the fifth
byte, but in this case the response from Savant is only a raw ``File
not found'' string. Note that this string does not include the HTTP
Status-Line, the first line in the response that includes the response
code, as required by the HTTP
specification and can be considered malformed [27]. Thus, this deviation identifies an
error though in this case both servers (i.e. Miniweb and Savant) are
deviating from the HTTP specification.
Figure 6 shows another
deviation found in Case 4 for the Savant-Miniweb pair. The HTTP
specification mandates that the
first line of an HTTP request must include a protocol version string.
There are 3 possible valid values for this version string:
``HTTP/1.1'', ``HTTP/1.0'', and ``HTTP/0.9'', corresponding to
different versions of the HTTP protocol.
However, we see that the candidate deviation input produced by the
solver uses instead a different version string, "HTTP/
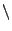 b.1". Since Miniweb accepts this answer, it
indicates that Miniweb is not properly verifying the values received on
this field. On the other hand, Savant is sending an error to the client
indicating an invalid HTTP version, which indicates that it is properly
checking the value it received in the version field.
This deviation shows another error in Miniweb's implementation. b.1". Since Miniweb accepts this answer, it
indicates that Miniweb is not properly verifying the values received on
this field. On the other hand, Savant is sending an error to the client
indicating an invalid HTTP version, which indicates that it is properly
checking the value it received in the version field.
This deviation shows another error in Miniweb's implementation.
To summarize, in this section we have shown that our approach is
able to discover multiple inputs that trigger deviations between real
protocol implementations. We have presented detailed analysis of three
of them, and confirmed the deviations they trigger as errors. Out of
the three inputs analyzed in detail, two of them can be attributed to
be Miniweb's implementation errors, while the other one was an
implementation error by both Miniweb and Savant.
The discovered inputs that trigger deviations can potentially be used
as fingerprints to differentiate among these implementations.
5.2 Deviations in Time Servers
In this section we show our results for the NTP protocol using two
different servers: NetTime [7]
and Ntpd [13]. Again, for
simplicity, we focus on a single request that we show in Figure 7. This request represents a simple query for
time synchronization from a client. The request uses the Simple Network
Time Protocol (SNTP) Version 4 protocol,
which is a subset of NTP [38].
First, we generate the symbolic formulas for both servers:  and and 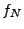 for NetTime and Ntpd respectively
using the original request shown in Figure 7.
Since we have one server pair, we need to query the solver twice. In
Case 7, we query the solver for for NetTime and Ntpd respectively
using the original request shown in Figure 7.
Since we have one server pair, we need to query the solver twice. In
Case 7, we query the solver for  and in Case 8 we
query it for and in Case 8 we
query it for  .
The solver returns unsatisfiable for Case 7.
For Case 8, the solver returns several candidate deviation inputs.
Figure 7 presents one of the deviations
found for Case 8. It presents the candidate deviation input returned by
the solver, and the response obtained from both NTP servers when that
candidate deviation input was sent to them during the validation phase. .
The solver returns unsatisfiable for Case 7.
For Case 8, the solver returns several candidate deviation inputs.
Figure 7 presents one of the deviations
found for Case 8. It presents the candidate deviation input returned by
the solver, and the response obtained from both NTP servers when that
candidate deviation input was sent to them during the validation phase.
Figure 7:
Example deviation obtained for the NTP servers. It includes the
original request sent in the formula extraction phase, the candidate
deviation input output by the solver, and the responses received from
the servers, when replaying the candidate deviation input. Note that
the output states are different since NetTime does send a response,
while Ntpd does not.
|
|
The results in Figure 7 show that the
candidate deviation input returned by the solver in Case 8 has
different values at bytes 0, 2 and 3. First, bytes 2 and 3 have been
zeroed out in the candidate deviation input. This is not relevant since
these bytes represent the ``Poll'' and ``Precision'' fields and are
only
significant in messages sent by servers, not in the queries sent by
the clients, and thus can be ignored.
The important difference is on byte 0, which is presented in detail
on the right hand side of Figure 7.
Byte 0 contains three fields: ``Leap Indicator'' (LI),
``Version'' (VN) and ``Mode'' (MD) fields. The difference with the
original request is in the Version field.
The candidate deviation input has a decimal value of 0 for this field
(note that the field length is 3 bits), instead of the original decimal
value of 4. When this candidate deviation input was sent to both
servers, Ntpd ignored it, choosing not to respond, while NetTime
responded with a version number with value 0. Thus, this candidate
deviation input leads the two servers into semantically different
output states.
We check the specification for this case to find out that a zero
value for the Version field is reserved, and according to
the latest specification should no longer be supported by current and
future NTP/SNTP servers [38].
However, the previous specification states that the server should copy
the version number received from the client in the request, into the
response, without dictating any special handling for the zero value.
Since both implementations seem to be following different versions of
the specification, we cannot definitely assign this error to one of the
specifications. Instead, this example shows that we can identify
inconsistencies or ambiguity in protocol specifications.
In addition, we can use this query as a fingerprint to differentiate
between the two implementations.
Table 5:
Execution time and formula size obtained during the formula extraction
phase.
| Program |
Trace-to-IR time |
% of Symbolic Instructions |
IR-to-formula time |
Formula Size |
| Apache |
7.6s |
3.9% |
31.87s |
49786 |
| Miniweb |
5.6s |
1.0% |
14.9s |
25628 |
| Savant |
6.3s |
2.2% |
15.2s |
24789 |
| Ntpd |
0.073s |
0.1% |
5.3s |
1695 |
| NetTime |
0.75s |
0.1% |
4.3s |
5059 |
|
Table 6:
Execution time needed to calculate a candidate deviation input for each
server pair.
| |
Input Calculation Time |
| Apache - Miniweb |
21.3s |
| Apache - Savant |
11.8s |
| Savant - Miniweb |
9.0s |
| NetTime - Ntpd |
0.56s |
|
5.3 Performance
In this section, we measure the execution time and the output size at
different steps in our approach. The results from the formula
extraction phase and the deviation detection phase are
shown in Table 5 and Table 6,
respectively. In Table 5, the
column ``Trace-to-IR time''
shows the time spent in converting an execution trace into our IR
program. The values show that the time spent to convert the execution
trace is significantly larger for the web servers, when compared to the
time spent on the NTP servers. This is likely due to a larger
complexity of the HTTP protocol, specifically a larger number of
conditions affecting the input. This is shown in the second column as
the percentage of all instructions that operate on symbolic data, i.e.,
on data derived from the input.
The ``IR-to-formula time'' column shows the time spent in generating a
symbolic formula from the IR program. Finally, the ``Formula Size''
column shows the size of the generated symbolic formulas, measured by
the number of nodes that they contain. The formula size shows again the
larger complexity in the HTTP implementations, when compared to the NTP
implementations.
In Table 6, we show the time
used by the solver in the deviation detection phase to produce a
candidate deviation input from the combined symbolic formula. The
results show that our approach is very efficient in discovering
deviations. In many cases, we can discover deviation inputs between two
implementations in approximately one minute.
Fuzz testing approaches are likely to take much longer, since they
usually need to test many more examples.
6 Discussion and Future Work
Our current implementation is only a first step. In this section we
discuss some natural extensions that we plan to pursue in the future.
Currently, we have evaluated our approach over protocols that use
request/response interactions (e.g. HTTP, NTP), where we examine the
request being received by a server program. Note that our approach
could be used in other scenarios as well. For example, with clients
programs, we could analyze the response being received by the client.
In protocol interactions involving multiple steps, we could consider
the protocol output state to be the state of the program after the last
step is finished.
Some errors are hidden in rarely used program paths and finding them
can take multiple iterations in our approach. For each iteration, we
need a protocol input that drives both implementations to semantically
equivalent output states. These protocol inputs are usually obtained
from a network trace. Thus, the more different inputs contained in the
trace the more paths we can potentially cover.
In addition, we can query the solver for multiple candidate deviation
inputs, each time requiring the new candidate input to be different
than the previous ones. The obtained candidate inputs often result in
different paths. We have done work on symbolic execution techniques to
explore multiple program paths and plan to apply those techniques
here [2,17].
In this paper, we apply the weakest precondition on IR programs that
contain a single program path, i.e., the processing of the original
input by one implementation. However, our weakest precondition
algorithm is capable of handling IR programs containing multiple
paths [19]. In the
future, we plan to explore how to create formulas that include multiple
paths.
Our current implementation for generating the symbolic formula works
offline. We first record an execution trace for each implementation
while it processes an input. Then, we process the execution trace by
converting it into the IR representation, and computing the symbolic
formula.
Another alternative would be to generate the symbolic formulas in an
on-line manner as the program performs operations on the received
input, as in BitScope [2,17].
7 Related Work
Symbolic execution was first proposed by
King [34], and has been used
for a wide variety of
problems including generating vulnerability
signatures [18],
automatic test case
generation [32], proving
the viability of evasion techniques [35], and finding bugs in
programs [21,47]. Weakest precondition was
originally proposed for developing correct programs from the ground
up [24,26]. It has been used for
different applications including finding bugs in programs [28] and for sound replay of
application
dialog [42].
Chen et al. [23] manually identify
rules representing ordered
sequences of security-relevant operations, and use model checking
techniques to detect violations of those rules in software. Udrea et
al. [45] use static source code
analysis to check if a C
implementation of a protocol matches a manually specified rule-based
specification of its behavior.
Although these techniques are useful, our approach is quite
different.
Instead of comparing an implementation to a manually defined model, we
compare
implementations against each other. Another significant difference is
that our approach works directly on binaries, and does not require
access to the source code.
There has been considerable research on testing network protocol
implementations, with heavy emphasis on
automatically detecting errors in network protocols using fuzz
testing [3,4,5,6,9,12,14,33,37,43,46].
Fuzz testing is a technique in which random
or semi-random inputs are generated and fed to the program under
study, while monitoring for unexpected program output, usually an
unexpected final state such as program crash or reboot.
Compared to fuzz testing, our approach is more efficient
for discovering deviations since it requires testing far fewer inputs.
It can detect deviations by comparing how two implementations process
the same input, even if this input leads both implementation to
semantically equivalent states. In contrast, fuzz testing techniques
need observable differences between implementations to detect a
deviation.
There is a line of research using model checking to find errors in
protocol implementations. Musuvathi et.al. [41,40] use a
model checker that operates directly on C and C++ code and use it to
check for errors in TCP/IP and AODV implementations. Chaki et al. [22] build models from implementations and
checks it against a specification
model. Compared to our approach, these approaches need reference models
to detect errors.
There has also been previous research on protocol
fingerprinting [25,44] but available
fingerprinting tools [8,11,15] use
manually extracted
fingerprints. More recently, automatic fingerprint generation
techniques, working only on network input and output, have been
proposed [20]. Our approach is
different in that we
use binary analysis to generate the candidate inputs.
8 Conclusion
In this paper, we have presented a novel approach to automatically
detect
deviations in the way different implementations of the same
specification check and process their input. Our approach has several
advantages: (1) by automatically building the
symbolic formulas from the implementation, our approach is
precisely truthful to the implementation; (2) automatically
identifying the deviation by solving formulas generated from
the two implementations enables us to find the needle in the haystack
without having to try each straw (input) individually, thus a
tremendous performance gain; (3) our approach works on binaries
directly, i.e., without access to source code. We then show how to
apply our automatic deviation techniques for automatic error detection
and automatic fingerprint generation.
We have presented our prototype system to evaluate our techniques,
and
have used it to automatically discover deviations in multiple
implementations of two different protocols: HTTP and NTP. Our
results show that our approach successfully finds deviations between
different implementations, including errors in input checking, and
differences in the interpretation of the specification, which can be
used as fingerprints.
We would like to thank Heng Yin for his support on QEMU and Ivan Jager
for his help in developing BitBlaze, our binary analysis platform. We
would also like to thank Vijay Ganesh and David Dill for their support
with STP, and the anonymous reviewers for their insightful comments.
This material is based upon work partially supported by the National
Science Foundation under Grants No. 0311808, No. 0433540, No. 0448452,
No. 0627511, and CCF-0424422. Partial support was also provided by the
International Technology Alliance, and by the U.S. Army Research Office
under the
Cyber-TA Research Grant No. W911NF-06-1-0316, and under grant
DAAD19-02-1-0389 through CyLab at Carnegie Mellon.
The views and conclusions contained here are those of the authors
and
should not be interpreted as necessarily representing the official
policies or endorsements, either expressed or implied, of ARO, NSF, or
the U.S. Government or any of its
agencies.
-
- 1
- The BitBlaze binary analysis platform.
https://www.cs.cmu.edu/~d"../../artley/bitblaze.
- 2
- Bitscope.
https://www.cs.cmu.edu/~chartwig/bitscope.
- 3
- IrcFuzz.
https://www.digitaldwarf.be/products
/ircfuzz.c.
- 4
- ISIC: IP stack integrity checker.
https://www.packetfactory.net/Projects/ISIC.
- 5
- JBroFuzz.
https://www.owasp.org/index.php/Category:OWASP_JBroFuzz.
- 6
- MangleMe.
https://lcamtuf.coredump.cx.
- 7
- NetTime.
https://nettime.sourceforge.net.
- 8
- Nmap.
https://www.insecure.org.
- 9
- Peach.
https://peachfuzz.sourceforge.net.
- 10
- QEMU: an open source processor emulator.
https://www.qemu.org.
- 11
- Queso.
https://ftp.cerias.purdue.edu/pub/tools/unix/scanners/queso.
- 12
- Spike.
https://www.immunitysec.com/resources-freesoftware.shtml.
- 13
- Windows NTP server.
https://www.ee.udel.edu/~mills/ntp/html/build/hints/winnt.html.
- 14
- Wireshark: fuzz testing tools.
https://wiki.wireshark.org/FuzzTesting.
- 15
- Xprobe.
https://www.sys-security.com.
- 16
- BERNERS-LEE, T., FIELDING, R.,
AND MASINTER, L.
Uniform Resource Identifier (URI): Generic Syntax.
RFC 3986 (Standard), 2005.
- 17
- BRUMLEY, D., HARTWIG, C., LIANG,
Z., NEWSOME, J., SONG, D., AND
YIN, H.
Towards automatically identifying trigger-based behavior in malware
using symbolic execution and binary analysis.
Tech. Rep. CMU-CS-07-105, Carnegie Mellon University School of Computer
Science, 2007.
- 18
- BRUMLEY, D., NEWSOME, J., SONG,
D., W., H., AND JHA, S.
Towards automatic generation of vulnerability-based signatures.
In Proceedings of the 2006 IEEE Symposium on Security and Privacy
(2006).
- 19
- BRUMLEY, D., WANG, H., JHA,
S., AND SONG, D.
Creating vulnerability signatures using weakest pre-conditions.
In Proceedings of the 2007 Symposium on Computer Security
Foundations Symposium (2007).
- 20
- CABALLERO, J., VENKATARAMAN, S., POOSANKAM,
P., KANG, M. G., SONG, D.,
AND BLUM, A.
Fig: Automatic fingerprint generation.
In 14th Annual Network and Distributed System Security Conference
(NDSS) (2007).
- 21
- CADAR, C., GANESH, V., PAWLOWSKI,
P., DILL, D., AND ENGLER,
D.
EXE: A system for automatically generating inputs of death using
symbolic execution.
In Proceedings of the 13th ACM Conference on Computer and
Communications Security (CCS) (2006).
- 22
- CHAKI, S., CLARKE, E., GROCE,
A., JHA, S., AND VEITH,
H.
Modular verification of software components in C.
In Proceedings of the 25th International Conference on Software
Engineering (ICSE) (2003).
- 23
- CHEN, H., AND WAGNER, D.
MOPS: an infrastructure for examining security properties of software.
In Proceedings of the 9th ACM conference on Computer and
Communications Security (CCS) (2002).
- 24
- COHEN, E.
Programming in the 1990's.
Springer-Verlag, 1990.
- 25
- COMER, D., AND LIN, J. C.
Probing TCP implementations.
In USENIX Summer 1994 (1994).
- 26
- DIJKSTRA, E.
A Discipline of Programming.
Prentice Hall, Englewood Cliffs, NJ, 1976.
- 27
- FIELDING, R., GETTYS, J., MOGUL,
J., FRYSTYK, H., MASINTER, L.,
LEACH, P., AND BERNERS-LEE,
T.
Hypertext Transfer Protocol - HTTP/1.1.
RFC 2616 (Draft Standard), June 1999.
Updated by RFC 2817.
- 28
- FLANAGAN, C., LEINO, K.
R. M., LILLIBRIDGE, M., NELSON, G.,
SAXE, J. B., AND STATA, R.
Estended static checking for Java.
In ACM Conference on the Programming Language Design and
Implementation (PLDI) (2002).
- 29
- FLANAGAN, C., AND SAXE, J.
Avoiding exponential explosion: Generating compact verification
conditions.
In Proceedings of the 28th ACM Symposium on the Principles of
Programming Languages (POPL) (2001).
- 30
- GANESH, V., AND DILL, D.
STP: A decision procedure for bitvectors and arrays.
https://theory.stanford.edu/~vganesh/stp.html.
- 31
- GANESH, V., AND DILL, D.
A decision procedure for bit-vectors and arrays.
In Proceedings of the Computer Aided Verification Conference
(2007).
- 32
- GODEFROID, P., KLARLUND, N., AND
SEN, K.
DART: Directed automated random testing.
In Proceedings of the 2005 Programming Language Design and
Implementation Conference (PLDI) (2005).
- 33
- KAKSONEN, R.
A Functional Method for Assessing Protocol Implementation
Security.
PhD thesis, Technical Research Centre of Finland, 2001.
- 34
- KING, J.
Symbolic execution and program testing.
Communications of the ACM 19 (1976), 386-394.
- 35
- KRUEGEL, C., KIRDA, E., MUTZ,
D., ROBERTSON, W., AND VIGNA,
G.
Automating mimicry attacks using static binary analysis.
In Proceedings of the 14th USENIX Security Symposium (2005).
- 36
- LEINO, K. R. M.
Efficient weakest preconditions.
Information Processing Letters 93, 6 (2005), 281-288.
- 37
- MARQUIS, S., DEAN, T. R., AND
KNIGHT, S.
SCL: a language for security testing of network applications.
In Proceedings of the 2005 conference of the Centre for Advanced
Studies on Collaborative research (2005).
- 38
- MILLS, D.
Simple Network Time Protocol (SNTP) Version 4 for IPv4, IPv6 and OSI.
RFC 4330 (Informational), 2006.
- 39
- MUCHNICK, S.
Advanced Compiler Design and Implementation.
Academic Press, 1997.
- 40
- MUSUVATHI, M., AND ENGLER,
D. R.
Model checking large network protocol implementations.
In Proceedings of the First Symposium on Networked Systems Design
and Implementation (NSDI) (2004).
- 41
- MUSUVATHI, M., PARK, D. Y., CHOU,
A., ENGLER, D. R., , AND DILL,
D. L.
CMC: A pragmatic approach to model checking real code.
In Proceedings of the 5th Symposium on Operating Systems Design
and Implementation (OSDI) (2002).
- 42
- NEWSOME, J., BRUMLEY, D., FRANKLIN,
J., AND SONG, D.
Replayer: Automatic protocol replay by binary analysis.
In Proceedings of the  ACM Conference on
Computer and and Communications Security (CCS) (2006). ACM Conference on
Computer and and Communications Security (CCS) (2006).
- 43
- OEHLERT, P.
Violating assumptions with fuzzing.
IEEE Security and Privacy Magazine 3, 2 (2005), 58 - 62.
- 44
- PAXSON, V.
Automated packet trace analysis of TCP implementations.
In ACM SIGCOMM 1997 (1997).
- 45
- UDREA, O., LUMEZANU, C., AND
FOSTER, J. S.
Rule-based static analysis of network protocol implementations.
In Proceedings of the 15th USENIX Security Symposium (2006).
- 46
- XIAO, S., DENG, L., LI, S.,
AND WANG, X.
Integrated tcp/ip protocol software testing for vulnerability
detection.
In Proceedgins of International Conference on Computer Networks
and Mobile Computing (2003).
- 47
- YANG, J., SAR, C., TWOHEY,
P., CADAR, C., AND ENGLER,
D.
Automatically generating malicious disks using symbolic execution.
In Proceedings of the 2006 IEEE Symposium on Security and Privacy
(2006).
Footnotes
- 1
- The GCL defines a few additional commands such as a do-while
loop, which we do not need.
  
2007-05-17
|
