
15th USENIX Security Symposium
Pp. 241–256 of the Proceedings
Polymorphic Blending Attacks
Prahlad Fogla Monirul Sharif Roberto Perdisci Oleg Kolesnikov Wenke Lee
College of Computing, Georgia Institute of Technology
801 Atlantic Drive, Atlanta, Georgia 30332
{prahlad,msharif,rperdisc,ok,wenke}@cc.gatech.edu
Abstract:
A very effective means to evade signature-based intrusion detection
systems (IDS) is to employ polymorphic techniques to generate attack
instances that do not share a fixed signature. Anomaly-based intrusion
detection systems provide good defense because existing
polymorphic techniques can make the attack instances look different
from each other, but cannot make them look like normal. In this paper
we introduce a new class of polymorphic attacks, called polymorphic blending attacks, that can effectively evade
byte frequency-based network anomaly IDS by carefully matching the statistics of the mutated
attack instances to the normal profiles. The proposed polymorphic blending attacks can be viewed as
a subclass of the mimicry attacks.
We take a systematic approach to the problem and formally
describe the algorithms and steps required to carry out such attacks.
We not only show that such attacks
are feasible but also analyze the hardness of evasion under different
circumstances.
We present detailed techniques using PAYL, a byte frequency-based anomaly
IDS, as a case study and demonstrate that these attacks are indeed feasible.
We also provide some insight into possible countermeasures that can be
used as defense.
1 Introduction
In the continuing arms race in computer and network security, a common trend
is that attackers are employing polymorphic techniques. Toolkits such as
ADMmutate [17], PHATBOT [10], and CLET [5] are
available for novices to generate polymorphic
attacks. The purpose of using polymorphism is to evade
detection by an intrusion detection system (IDS). Every instance of a
polymorphic attack looks
different and yet carries out the same malicious activities. For
example, the payload of each instance of a polymorphic worm can have
different byte contents. It follows that signature-based (misuse)
IDS may not reliably
detect a polymorphic attack because it may not have a fixed or
predictable signature,
or because the invariant parts of the attack may not
be sufficient to construct a signature that produces very few false positives.
On the other hand, each instance of a polymorphic attack needs to
contain exploit code that
is typically not used in normal activities. Thus, each instance looks
different from normal. Existing polymorphic techniques [28] focus on
making the attack instances look different from each other, and not
much on making them look like normal. This means that network payload anomaly
detection systems can provide a good defense against the current
generation of polymorphic attacks. However, if a polymorphic attack
can blend in with (or look like) normal traffic, it can successfully evade
an anomaly-based IDS that relies solely on payload statistics.
In this paper, we show that it is possible to evade network anomaly IDS
based on payload statistics
using a class of polymorphism that we call polymorphic
blending. A polymorphic blending attack is a polymorphic attack that
also has the ability to evade
a payload statistics-based anomaly IDS.
In addition to making
all the mutated attack instances different, an attacker (or the attack
code) attempts to make them appear normal by transforming each
instance in such a way that its payload characteristics
(e.g., the byte frequency distribution)
fit the normal profile used by the anomaly IDS.
Since polymorphic blending attacks try to evade the IDS by making the attacks look
like normal, they can be viewed as a subclass of the mimicry attacks [29,33].
This paper makes several contributions. We study the class of
polymorphic blending attacks
against byte frequency-based network anomaly IDS,
which was introduced by Kolesnikov et al. in [12].
We present the general techniques and design considerations for such attacks.
We provide rationales of why these
attacks are practical
and show that network anomaly IDS based on payload statistics do not guarantee
adequate protection against sophisticated attacks.
Using 1-gram and 2-gram PAYL [35,36] as a case study,
we take a systematic approach to the problem
and describe the necessary steps required to carry out an effective attack.
Our work provides insight into not only how such an attack can be performed, but
also how hard it is to launch these attacks under different circumstances. We analyze
the amount of learning required for the attacker and the time and space
complexity required for blending.
We use a real attack vector [8] to implement a polymorphic blending attack and
provide experimental evidence that our attack can effectively evade detection. We also
discuss possible countermeasures that a defender (e.g., IDS designer or
operator) can take to decrease the likelihood that a
polymorphic blending attack will succeed.
The rest of the paper is organized as follows. We discuss related work
in polymorphic attacks and detection in Section 2. In
Section 3, we introduce polymorphic blending
attacks and discuss the general techniques and
design issues of polymorphic blending attacks. We present our case study
in Section 4 and conclude the paper in Section 5.
2 Related Work
Transforming attack packets to avoid detection is a common practice
among attackers. Attackers can exploit the ambiguities present in the
traffic stream to transform an attack instance to another so that an
IDS is not able to recognize the attack pattern. IP and TCP
transformations ([11,22]) techniques are used to evade NIDS
that analyzes TCP/IP headers. Vigna et al. [31] discussed
multiple network, application and exploit layer (shellcode
polymorphism) mutation mechanisms. A formal model to combine multiple
transformations was presented by Rubin et al. [24]. Multiple
tools such as Fragroute [26], Whisker [23], and AGENT [24]
are available that can perform attack mutation.
Code polymorphism has been used extensively by virus writers to write
polymorphic viruses. Mistfall, tPE, EXPO, and DINA [28,37]
are some of the polymorphic engines used by virus writers. Worm
writers have also started using polymorphic
engines. ADMmutate [17], PHATBOT [10], and
JempiScodes [25] are some of the polymorphic shellcode
generators commonly used to write polymorphic worms. Garbage and NOP
insertions, register shuffling, equivalent code substitution, and
encryption/decryption are some of the common techniques used to write
polymorphic shellcodes.
Quite a few approaches have been proposed to detect polymorphic
attacks. In [30], Toth et al. proposed a technique to locate the presence of executable
shellcode inside the payload. They used abstract execution of network flows
to find the MEL (Maximum Executable Length) of the payload. The flow is marked
suspicious if its MEL is above certain length. Chinchani et al. [2] performed
fast static analysis to check if a network flow contains exploit
code.
STRIDE [1] focuses on detecting polymorphic sleds used by
buffer overflow attacks.
In [14], Kruegel et al. used structural analysis of binary code to find
similarities between different worm instances. Using a graph coloring
technique on a worm's control flow graph, this approach is able to
accurately model the structure of the worm. Given a set of suspicious
flows, Polygraph [20] generates a set of disjoint
invariant substrings that are present in multiple suspicious
flows. These substrings can then be used as a signature to detect
worm instances.
In a recent work, Perdisci et al. [21] proposed an attack on
Polygraph [20] where noise is injected into the dataset of suspicious
flows so that Polygraph is not able to generate a reliable signature for
the worm.
Shield [34] uses transport layer
filters to block the traffic that exploits a known
vulnerability. Filters are exploit-independent, and vulnerabilities are
described as a partial state machines of the vulnerable application.
In [3], Christodorescu et al. proposed an instruction semantics
based worm detection technique. The proposed approach can detect code polymorphism that
uses instruction reordering, register shuffling, and garbage
insertions.
It is worth noting that unless the attacker combines the polymorphic blending attack proposed in this paper
with other evasion techniques, the approaches cited above
[1,2,3,14,20,30,34] may be able to detect the attack.
We further discuss possible countermeasures against the polymorphic blending attack in Section 4.7.
A number of attacks aimed at evading Host-based anomaly IDS have been
developed. Wagner et al. [33] and Tan et al. [29]
presented mimicry attacks against the stide model [9] developed
by Forrest et al. The main idea behind these mimicry attacks was to
inject dummy system calls into an attack sequence to make the final
system call sequence look similar to the normal system call
sequence.
As a defense against mimicry attacks as well as other
impossible path attacks [7,32], more advanced
detection approaches (e.g., [6,7]) were proposed,
which use call stack information along with the system call
sequences. Recently, a more sophisticated mimicry attack was proposed
by Kruegel et al. [13], which can evade most system call
based anomaly IDS.
Several application payload-based anomaly IDS [15,18,19]
have been proposed which monitor the payload of a packet for anomalies.
In [16], Kruegel et al. proposed four different models, namely, length,
character distribution, probabilistic grammar, and token finder, for
the detection of HTTP attacks.
PAYL, proposed by Wang and Stolfo [35], records the average
frequency of occurrences of each byte in the payload of a normal
packet. A separate profile is created for each port and packet
length. In their recent work [36], the authors suggested
an improved version of PAYL that computes several profiles for each
port. At the end of the training, clustering is performed to reduce
the number of profiles. They proposed that instead of byte frequency,
one can also use an n-gram model in a similar fashion. One main
drawback of the system is that they do not consider an advanced
attacker, who may know the IDS running at the target
and actively try to evade it. In this paper we provide strong evidence
that such byte frequency based anomaly IDS are open to attacks and may be
easily evaded.
CLET [5], an advanced polymorphic engine,
comes closest to our polymorphic blending attack.
It performs spectrum analysis to evade IDS that use data
mining methods for worm detection.
Given an attack payload,
CLET adds padding bytes in a separate cramming bytes zone (of a given length) to try and make
the byte frequency distribution of the attack close to the normal traffic.
However, the encoded shellcode (using XOR) in CLET may still deviate significantly
from the normal distribution and the obtained polymorphic attack may be detected by the IDS.
A preliminary work by Kolesnikov et al. [12]
introduced and cursorily explored polymorphic blending attacks.
In this paper we present a systematic approach
for evading byte frequency-based network anomaly IDS, and provide detailed analysis of the design,
complexity and possible countermeasures for the polymorphic blending attacks.
We also show that our polymorphic blending technique is much more effective than CLET
in evading byte frequency-based anomaly IDS.
3 Blending Attacks
A polymorphic attack is an attack that is able to change its
appearance with every instance.
Thus, there may be no fixed or predictable signature for the attack.
As a result, it may evade detection
because most current intrusion detection systems and anti-virus
systems are signature-based. Exploit mutation and shellcode
polymorphism are two common ways to generate polymorphic attacks. In
general, there are three components in a polymorphic attack:
- Attack Vector: an attack vector is used for exploiting the
vulnerability of the target host. Certain parts of the attack vector
can be modified to create mutated but still valid exploits.
There might still be certain parts, called the invariant, of the
attack vector that have to be present in every mutant for the attack to
work. If the attack invariant is very small and exists in the normal
traffic, then an IDS may not be able to use it as a signature because
it will result in a high number of false positives.
- Attack Body: the code that performs the intended malicious actions
after the vulnerability is exploited. Common techniques to achieve
attack body (shellcode) polymorphism include register shuffling,
equivalent instruction substitution, instruction reordering, garbage
insertions, and encryption. Different keys can be used in encryption
for different instances of the attack to ensure that the byte sequence is
different every time.
- Polymorphic Decryptor: this section contains the part of the
code that decrypts the shellcode. It decrypts the encrypted attack
body and transfers control to it.
Polymorphism of the decryptor can be achieved using various code obfuscation
techniques.
All attack instances contain exploit code and/or input data that
are typically not used in normal activities. For example,
an attack instance, especially its decryptor and encrypted shellcode,
may contain characters that have very low probability of appearing in
a normal packet. Thus, an anomaly-based IDS can detect the polymorphic
attack instances by recognizing their deviation from the normal
profile. For example, Wang et al. [35,36] showed that the
byte frequency distribution of an (polymorphic) attack is quite
different from that of normal traffic, and can thus be used by the
anomaly-based IDS PAYL to detect simple polymorphic attacks.
However, detection of a sophisticated polymorphic attack is much more challenging.
Clearly, if a polymorphic attack can ``blend in'' with (or ``look''
like) normal, it can evade detection by an anomaly-based IDS. Normal
traffic contains a lot of syntactic and semantic information, but only a
very small amount of such information can be used by a
high speed network-based anomaly IDS. This is
due to fundamental difficulties in modeling complex systems and
performance overhead concerns in real-time monitoring.
The network traffic profile used by
high speed
anomaly IDS, e.g., PAYL,
typically includes simple statistics such as maximum or average size
and rate of packets, frequency distribution of bytes in packets, and
range of tokens at different offsets.
Given the incompleteness and the imprecision of the normal profiles
based on simple traffic statistics,
it is quite feasible to launch what we call polymorphic blending
attacks. The main idea is that, when generating a polymorphic
attack instance, care can be taken so that its payload characteristics, as
measured by the anomaly IDS, will match the normal profile. For
example, in order to evade detection by PAYL [35,36],
the polymorphic attack instance can carefully choose the characters
used in encryption and pad the attack payload with a
chosen set of characters, so that the resulting byte frequency of the
attack instance closely matches the normal profiles and thus will be
considered normal by PAYL.
Before presenting the general strategies and techniques used in
polymorphic blending attacks, we present an attack scenario and argue that such attacks
are realistic. Figure 1 shows the attack scenario that
is the basis of our case study. There are a few assumptions behind
this scenario:
- The adversary has already compromised a host X inside a
network A which communicates with the target host Y inside
network B. Network A and host X may lack sufficient security so that
the attack can penetrate without getting detected, or
the adversary may collude with an insider.
- The adversary has knowledge of the IDS (IDSB) that monitors the victim host network. This might be
possible using a variety of approaches, e.g.,
social engineering (e.g., company sales or purchase data),
fingerprinting, or trial-and-error. We argue that one
cannot assume that the
IDS deployment is a secret, and security by obscurity is a very weak position.
We assume IDSB is a payload statistics based system
(e.g., PAYL).
Since the adversary knows the learning algorithm being used by IDSB, given some packet data from X to Y, the adversary will
be able to generate its own version of the statistical normal
profile used by IDSB.
- A typical anomaly IDS has a threshold setting that can be
adjusted to obtain a desired false positive rate. We assume that the
adversary does not know the exact value of the threshold used
by IDSB, but has an estimation of the generally
acceptable false positive and false negative rates. With this
knowledge, the adversary can estimate the error threshold when
crafting a new attack instance to match the IDS profile.
Figure 1:
Attack Scenario of Polymorphic Blending Attack
|
We now explain the attack scenario. Once the adversary has control of
host X, it observes the normal traffic going from X to Y. The
adversary estimates a normal profile for this traffic using
the same modeling technique that IDSB uses. We call this an artificial profile. With it, the adversary creates a mutated
instance of itself in such a way that the statistics of the mutated
instance match the artificial profile. When IDSB analyzes these
mutated attack packets, it is unable to discern them from normal
traffic because the artificial profile can be very close to the actual
profile in use by IDSB. Thus, the attack successfully infiltrates the
network B and compromises host Y.
3.2.2 Desirable Properties of Polymorphic Blending Attacks
Clearly, the key for a polymorphic blending attack to succeed in
evading an IDS is to be able to learn an artificial profile that is
very close to the actual normal profile used by the IDS, and create
polymorphic instances that match the artificial profile. There are
other desirable properties. First, the blending process (e.g., with
encoding and padding) should not result in an abnormally large
attack size. Otherwise, a simple detection heuristic will be to
monitor the network flow size. Second, although we do not put any constraint
on the resources available to the adversary, the polymorphic
blending process should be economical in terms of time and
space. Otherwise, it will not only slow down the attack, but also
increase the chance of detection by the local
IDS (e.g., IDSA or host-based IDS.) More formally, given a description of the
algorithm that the IDS uses to learn and match the normal profile and an
attack instance, the time (and space) complexity of the algorithm used
to apply polymorphic blending to the attack instance should be a small
degree polynomial with respect to the initial attack size.
Algorithms that require exponential time and space may not be practical.
Since the learning time should be small,
the blending algorithm should not require to collect a lot of normal
packets to learn the normal statistics.
3.3 Steps of Polymorphic Blending Attacks
The polymorphic blending attack has
three basic steps: (1) learn the IDS normal profile; (2)
encrypt the attack body; (3) and generate a polymorphic decryptor.
3.3.1 Learning The IDS Normal Profile
The task at hand for the adversary is to observe the normal
traffic going from a host, say X, to another host in the target
network, say Y, and generate a normal profile close to the one used
by the IDS at the target network, say IDSB, using the same
algorithm used by the IDS.
A simple method to get the normal data is by sniffing the network traffic going from
network A to host Y. This can be easily accomplished in a bus
network. In a switched environment, it may be harder to obtain
such data. Since the adversary knows the type of service running at the
target host, he can simply generate normal request packets
and learn the artificial profile using these packets.
In theory, even if the adversary learns a profile from just a
single normal packet, and then mutates an attack instance so that it matches
the statistics of the normal packet perfectly, the resulting
polymorphic blended attack packet should not be flagged as an anomaly
by IDSB, provided the normal packet does not result in a false positive in
the first place. On the other hand, it is beneficial to generate an
artificial profile that is as close to the normal profile used
by IDSB as possible, so that if a polymorphic blended attack packet
matches the artificial profile closely it has a high chance of
evading IDSB. In general, if more normal packets are captured and
used by the adversary, she will be able to learn an artificial
normal profile that is closer to the normal profile used by
IDSB.
3.3.2 Attack Body Encryption
After learning the normal profile, the adversary creates a new attack
instance and encrypts (and blends) it to match the normal profile.
A straightforward byte substitution scheme followed by padding
can be used for encryption. The main idea here is that every character
in the attack body can be substituted by a character(s) observed from
the normal traffic using a substitution table. The encrypted attack
body can then be padded with some more garbage normal data so that
the polymorphic blended attack packet can match the normal profile
even better. To keep the padding (and hence the packet size) minimal,
the substituted attack body should already match the normal profile
closely. We can use this design criterion to produce a suitable
substitution table.
To ensure that the substitution algorithm is reversible (for decrypting
and running the attack code), a one-to-one or one-to-many mapping can be used.
A single-byte substitution is preferred over multi-byte substitution because
multi-byte substitution will inflate the size of the attack body after substitution.
An obvious requirement of such encryption scheme is that the encrypted attack
body should contain characters from only the normal traffic. Although
this may be hard for a general encryption technique (because the
output typically looks random), it is an easy requirement for a simple
byte substitution scheme. However, finding an optimal substitution table
that requires minimal padding is a complex problem. In
Section 4, we show that for certain cases this
is a very hard problem. We can instead use a greedy method to find an
acceptable substitution table. The main idea is to first sort the
statistical features in the descending order of the frequency for both
the attack body and normal traffic. Then, for each unassigned entry with the
highest frequency in the attack body, we simply map it to an available (not yet
mapped) normal entry with the highest frequency.
This procedure is repeated until all
entries in the attack body are mapped. The feature mapping can be
translated to a character mapping and a substitution table can
be created for encryption and decryption purposes.
3.3.3 Polymorphic Decryptor
A decryptor first removes all the extra padding from the encrypted
attack body and then uses a reverse substitution table (or decoding table)
to decrypt the attack body to produce the original attack code
(shellcode).
The decryptor is not encrypted but can be mutated using multiple
iterations of shellcode polymorphism processing (e.g., mapping an
instruction to an equivalent one randomly chosen from a set of
candidates). To reverse the substitution done during blending, the
decryptor needs to look up a decoding table that contains the required
reverse mappings.
The decoding table for one-to-one mapping can be stored in an array where
the i-th entry of the array represents the normal character used to
substitute attack character i. Such an decoding table contains only
normal characters. Unused entries in the table can be used for padding.
On the other hand,
storage of decoding tables for one-to-many mapping or variable-length
mapping is complicated and typically requires larger space.
3.4 Attack Design Issues
3.4.1 Incorporating Attack Vector and Polymorphic Decryptor in
Blending
We discussed in Section 3.3.2 that the encryption of
the attack body is guided by the need to make the attack packet match
the normal statistical profile (or more precisely, the learned
artificial profile).
The attack vector, decryptor, and substitution table are not encrypted.
Their addition to the attack packet payload alters the packet statistics.
The new statistics may deviate significantly from the normal profile.
In such a case, we must find a new substitution table in order to match the
whole attack packet to the normal profile. First,
we take the normal profile and subtract the frequencies of characters
in the attack vector, decryptor, and existing substitution table.
Next, we find a new substitution table using the adjusted normal
profile. If the statistics of the new substitution table
is not significantly different from the old substitution table, we
use the new substitution table for encryption. Otherwise we
repeat the above steps.
3.4.2 Packet Length based IDS Profile
If IDSB has different profiles for packets of different lengths, as
in the case of PAYL, the substitution phase and padding phase
need to use the normal profile corresponding to the final attack
packet size. A target length greater than the length of the original
attack packet (before polymorphic blending) is chosen at first.
The encryption step is then applied and the packet
is padded to the target length. If the statistics of the resulting
attack packet is not very close to the normal profile, a different
target length is chosen and the above process is repeated. Another
strategy is to divide the attack body into multiple small packets and
perform the polymorphic blending process for all of them separately.
4 Evaluation and Results
To demonstrate that polymorphic blending attacks are feasible and
practical, we show how an attack can use polymorphic blending to
evade the anomaly IDS PAYL.
In this section, we first describe the polymorphic blending techniques
to evade PAYL. Then we report the results of the experiments we ran to evaluate the
evasion capabilities of the polymorphic blending attacks.
In our evaluation, we first established a baseline performance by
sending polymorphic instances (generated using the CLET polymorphic
engine)
of the attack to PAYL and
verified that all of the instances were detected by the IDS as
anomalies. Then, without changing the configuration of PAYL, we
used our polymorphic blending techniques to generate attack instances to
see how well they can evade the IDS.
PAYL
has been shown to be effective in detecting polymorphic attacks
and worms [35,36]. For this reason we used PAYL in our case
study. We used the 2-gram version in addition to the 1-gram version to evaluate how
polymorphic blending attack is affected when an
IDS uses a more comprehensive model.
PAYL uses n-gram analysis by recording the frequency
distribution of n-grams in the payload of a packet.
A sliding window of width n is used to record the number of occurrences
of all the n-grams present in the payload.
A separate model
is generated for each packet length. These models are clustered
together at the end of the training to reduce the number of
models. Furthermore, the length of a packet is also monitored for
anomalies. Thus a packet with an unseen or very low frequency
length is flagged as an anomaly. {
 } represents the
PAYL model of normal traffic, where xi is the ith gram,
which is a character in 1-gram PAYL,
and a tuple in 2-gram PAYL. f(xi) is the average
relative frequency of xi in the normal traffic, and } represents the
PAYL model of normal traffic, where xi is the ith gram,
which is a character in 1-gram PAYL,
and a tuple in 2-gram PAYL. f(xi) is the average
relative frequency of xi in the normal traffic, and  is the standard deviation of
xi in the normal traffic. The anomaly score as calculated by PAYL
is shown in Equation 1. is the standard deviation of
xi in the normal traffic. The anomaly score as calculated by PAYL
is shown in Equation 1.
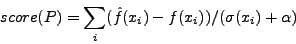 |
(1) |
Here, P is the monitored packet,  is the relative frequency of the
ith gram xi in P, and is the relative frequency of the
ith gram xi in P, and  is a smoothing factor used to
prevent division by zero. For convenience we will use the term frequency to denote
relative frequency. is a smoothing factor used to
prevent division by zero. For convenience we will use the term frequency to denote
relative frequency.
We evaluated our polymorphic blending attack with the first version of
PAYL as described in [35]. Wang et al. [36]
proposed some improvements on PAYL in their recent version. We
believe that our attack still works for this new version of PAYL. The
main improvement of the new version is to use multiple centroids for a
given packet length, so that a low false positive rate can be achieved
using a relatively low anomaly threshold. In this case, our
polymorphic blending attack has to use the same learning algorithm as the new
version of PAYL. Furthermore, more normal traffic needs to be
used to learn an artificial profile that is close to the actual normal
profile. Thus, the effect is that our attack may take a little more
time. The new version also matches ingress suspicious traffic with
egress suspicious traffic to find worms. This feature does not
have any effect on our attack because the attack instances blend in
with normal.
To evade 1-gram PAYL, the frequency of each character in the
attack packet should be close to the average frequency recorded during
the learning phase. We substitute the characters in the attack packet with
the characters seen in the normal traffic, and apply sufficient amount
of padding so that the 1-gram frequencies of the resulting packet
match the normal profile very closely. We first present analytical
results on the amount of padding required to match the substituted
attack body with the normal profile perfectly. Then we present a
substitution algorithm that uses the padding criteria to minimize the
amount of required padding.
In the following sections, we assume that the normal frequency f(x) has already been
adjusted for the attack vector, the decryptor, and the decoding table (as
discussed in Section 3.4.1, these parts need to be
accounted for when computing the frequencies of characters to find
a suitable substitution).
4.2.1 Padding
Let 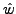 and and  be the substituted attack body before
and after padding, respectively. Let n be the number of distinct characters in the
normal traffic. be the substituted attack body before
and after padding, respectively. Let n be the number of distinct characters in the
normal traffic. 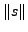 denotes the length of a
string s, and denotes the length of a
string s, and 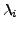 denotes the number of occurrences of the normal
character xi in the padding section of the blending packet. Then, denotes the number of occurrences of the normal
character xi in the padding section of the blending packet. Then,
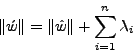 |
(2) |
Suppose the relative frequency of character xi in the normal traffic and the
substituted attack body is f(xi) and  ,
respectively. Since the final desired frequency of xi is f(xi),
the number of occurrences of xi in the blending packet should be ,
respectively. Since the final desired frequency of xi is f(xi),
the number of occurrences of xi in the blending packet should be
 . Thus, . Thus, 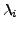 can be defined using the following
equation: can be defined using the following
equation:
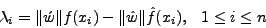 |
(3) |
Equation 3 can be re-written as,
 |
(4) |
Since f(x) and 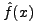 are relative frequency distributions, are relative frequency distributions,
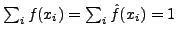 . Unless they are identical,
there exists some character xi for which . Unless they are identical,
there exists some character xi for which
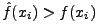 . The character xi is perhaps ``overused'' in
the substituted attack body. It is trivial to see that we need to pad
all the characters except the one that is most overused. Let xk be
the character that has highest overuse and . The character xi is perhaps ``overused'' in
the substituted attack body. It is trivial to see that we need to pad
all the characters except the one that is most overused. Let xk be
the character that has highest overuse and 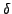 be the degree of
overuse. That is, be the degree of
overuse. That is,
 |
(5) |
Since no padding is required for character xk,
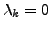 . Putting this value in Equation (4) we get: . Putting this value in Equation (4) we get:
 |
(6) |
The amount of padding required for each character xi can be calculated
by substituting the value of 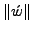 in Equation
(3): in Equation
(3):
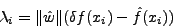 |
(7) |
Thus, using the padding defined by the above equation, we can match the
final attack packet perfectly to the normal frequency
f(x). Furthermore, the amount of padding required by the above
equation is the minimum amount that is needed to match the normal profile exactly. Please refer
to Appendix 6.1 for the proof.
4.2.2 Substitution
The analysis in Section 4.2.1 shows that the amount
of padding can be minimized by minimizing 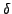 , which is , which is
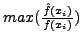 . This in turn means that the
objective of the substitution process is to minimize the resulting . This in turn means that the
objective of the substitution process is to minimize the resulting
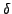 . There are two possible cases for substitution. The first is when
the number of distinct characters present in the attack body (m) is
less than or equal to the number of distinct characters present in the
normal traffic (n), i.e. . There are two possible cases for substitution. The first is when
the number of distinct characters present in the attack body (m) is
less than or equal to the number of distinct characters present in the
normal traffic (n), i.e. 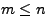 . In this case we can perform single-byte
encoding, either one-to-one or one-to-many. If m>n, we
need to use multi-byte encoding. . In this case we can perform single-byte
encoding, either one-to-one or one-to-many. If m>n, we
need to use multi-byte encoding.
We suggest a greedy algorithm to
generate a one-to-many mapping from the attack characters to the normal
characters that provides an acceptable solution and is computationally
efficient. Our algorithm tries to minimize the ratio 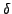 locally for each substitution assignment.
locally for each substitution assignment.
Let xi represents a normal character and yj represent an attack
character. Let f(xi) be the frequency of character xi in normal
traffic and g(yj) be the frequency of character yj in the attack
body. Let S(yj) be the set of normal characters to which yj is
mapped. Let
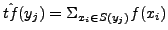 . The
probability that yj is substituted by . The
probability that yj is substituted by
 , during
substitution is , during
substitution is
 . Thus, the number of
occurrences of xi in the substituted attack body is . Thus, the number of
occurrences of xi in the substituted attack body is
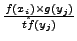 . We then have . We then have
 . Our greedy algorithm tries to minimize
this ratio . Our greedy algorithm tries to minimize
this ratio  locally. The substitution algorithm is as
follows. locally. The substitution algorithm is as
follows.
Sort the normal character frequency f(x) and the attack character
frequency g(y) in descending order. For the first m characters,
map yi to xi and set
S(yi) = {xi} and
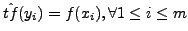 . For the (m+1)th normal
character, xm+1, find an attack character (yj) with maximum
ratio of . For the (m+1)th normal
character, xm+1, find an attack character (yj) with maximum
ratio of
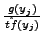 . Assign xm+1 to
yj and set . Assign xm+1 to
yj and set
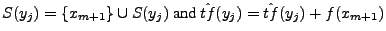 . This is performed for
each of the remaining characters until we reach the end of the frequency
list f(x). While substituting alphabet yj in the attack body, we
choose a character xi from the set S(yj) with probability . This is performed for
each of the remaining characters until we reach the end of the frequency
list f(x). While substituting alphabet yj in the attack body, we
choose a character xi from the set S(yj) with probability
 . .
Consider an example where
f(a,b,c) = {0.3, 0.4, 0.3}, attack body
w = qpqppqpq, and
g(p,q) = {0.5, 0.5}. According to the above
algorithm, initially, b and a are assigned to p and q
respectively. At this point, ratio
 and
and
 . So we assign c to
q. Thus, p will be substituted by b and q will be substituted
by a with probability 0.5 and by c with probability
0.5. Thus, the attack after substitution can be . So we assign c to
q. Thus, p will be substituted by b and q will be substituted
by a with probability 0.5 and by c with probability
0.5. Thus, the attack after substitution can be
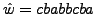 . .
In our experiments, we used a simple one-to-one mapping where
characters with the highest frequencies in the attack packet are mapped to
characters with the highest frequencies in normal traffic. This simple
mapping is shown to be sufficient for the blending purpose.
4.2.2.2 Case: m > n
We suggest a heuristic based on Huffman encoding scheme to obtain a small attack size
after encoding. Given the frequency distribution of the characters in the
attack body being encoded, Huffman encoding provides a minimum length packet after
encoding. The weights of the nodes in Huffman tree is the sum of the relative
frequencies of all its descendant leaf nodes. The weight of a leaf node is the
frequency of a given character in the attack body. Every edge in the tree is
assigned to a character from the normal profile. In the original Huffman coding the
edges of the Huffman tree are labeled randomly. Random labeling of the edges
may give us a very large value of 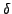 . We developed a heuristic to assign
labels to edges of Huffman tree to find a mapping that gives us a very small . We developed a heuristic to assign
labels to edges of Huffman tree to find a mapping that gives us a very small 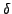 .
Before stating the heuristic, we present the problem of optimally
assigning the labels to the edges in Huffman tree: .
Before stating the heuristic, we present the problem of optimally
assigning the labels to the edges in Huffman tree:
Given a Huffman tree, assign labels 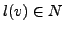 to the vertices v in the tree, such
that after substitution, to the vertices v in the tree, such
that after substitution,
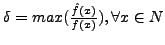 , is minimum. The
constraint on the label l(v) is that if
parent(v1) = parent(v2), then , is minimum. The
constraint on the label l(v) is that if
parent(v1) = parent(v2), then
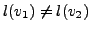 . .
We propose a greedy algorithm to find an approximate solution for the above problem.
First sort the vertices in descending order of their weight and initialize the
capacity of each character
 . Then
starting from the leftmost unlabeled vertex vj, find a character xi
with the maximum cap(xi) and that is not assigned to any of the direct
siblings of vj. Assign xi to vj and reduce the capacity of xi by
the weight of the vertex. Repeat until all the vertices are assigned.
The labels generated by the above algorithm are used for the substitution process.
An example is explained in Figure 2. . Then
starting from the leftmost unlabeled vertex vj, find a character xi
with the maximum cap(xi) and that is not assigned to any of the direct
siblings of vj. Assign xi to vj and reduce the capacity of xi by
the weight of the vertex. Repeat until all the vertices are assigned.
The labels generated by the above algorithm are used for the substitution process.
An example is explained in Figure 2.
Figure:
1-gram multibyte encoding.
The frequency of the normal character is
f(a,b) = {0.5, 0.5}.
Sorted weights of the nodes are
{0.6, 0.4, 0.35, 0.25, 0.25, 0.15}.
Using the proposed algorithm we get
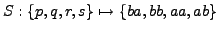
|
Figure:
2-gram multibyte encoding.
e0=da, e1=bc. w=01101010.
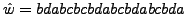
|
The 1-gram PAYL model assumes that the bytes occurring in the
stream are independent. It does not try to capture any information of
byte sequencing of the normal traffic. The 2-gram model on the other
hand can capture some byte sequencing information. It records the
frequencies of all the 2-grams present in the normal traffic. It is
easy to see that by matching 2-grams we are inherently performing
1-gram matching as well.
For 2-gram, the polymorphic blending process needs to match the
frequencies of not only all the characters but also all the
tuples. Similar to 1-gram substitution, one can either use single-byte
encoding or multi-byte encoding for substitution. For single-byte
encoding, the goal is to find a one-to-one or one-to-many mapping that
ensures that all the tuples in the substituted attack body are also
present in normal profile. In Appendix 6.2, we
show that this is NP-complete for
the general case by reducing the well known sub-graph isomorphism
problem [4] to the mapping problem.
Unlike single-byte encoding, it is possible for an attacker to find a multi-byte
encoding scheme that produces only valid 2-grams. Here, we present a viable
multi-byte encoding scheme.
4.3.1 Multi-byte Encoding
A 2-gram normal profile can be viewed as a Moore machine (FSM) which has a state
for each character in N. Every state is a start state and end state. A
transition from state v1 to state v2 exists if and only if 2-gram
v1v2 exists in normal profile. This FSM represents the language accepted by
the IDS with given 2-gram profile. Strings generated by the FSM contain only
normal 2-grams. Characters in an attack body can be mapped to paths in this
FSM. For example, suppose the state machine has two cycles reachable from each
other. e1 and e2 be two edges such that e1 is present only in the first
cycle and e2 is present only in the second cycle. Given a bit representation of the
attack body, we can encode 0 using e0 and 1 using e1. We can
generate any bit string represented using these two tuples interleaved by other
non-informative characters present in the cycles and in the paths between two
cycles. Figure 3 shows an example of such an encoding scheme.
Such an encoded attack string will have a very large size. We use it to show
the existence of an encoding scheme that is able to match the normal 2-grams. We can generate a
more efficient encoding scheme by using the entropy measure of transitions at each
state. The complete details of such an encoding scheme are not addressed in this paper.
The authors suggest readers to refer to coding theory for more on entropy based
encoding.
4.3.2 Approximate Single-Byte Encoding
As discussed above, the problem of finding a single-byte substitution
is hard for 2-gram. On the other hand, multi-byte encoding may
increase the size of the attack packets considerably. We can use a simple
approximation algorithm to find a good one-to-one substitution. The
algorithm performs single byte substitution in such a way that tuples
with high frequencies in the attack packet are greedily matched with
tuples with high frequencies in normal traffic.
The details of the algorithm are as follows. First, sort the normal tuple
frequencies f(xi,j) and the attack tuple frequencies g(yi,j) in
descending order. Initially, all tuples in the list f(xi,j) are
marked unused and the substitution table is cleared. The frequency
list g(y) is traversed from the top. For every tuple yi,j in the
sorted attack tuple list, the list f(x) is traversed from the beginning to
find an unmarked tuple xi',j' so that substituting yi with
xi' and yj with xj' does not violate any mappings that
were already made. The tuple xi',j' is marked and the
substitution table is updated. The above algorithm is fast and
provides consistent reversible matching. The algorithm does not
guarantee to provide the best substitution, i.e., the closest distance to
the target frequency distribution.
We introduce an efficient padding algorithm that does not provide
minimal padding but tries to match the target distribution in a greedy
manner. Let df(xi,j) be the difference between the
frequency of tuple xi,j in the normal profile and the substituted attack
body. Find a tuple xk,l from the list of normal tuples that starts
with the last padded character (xk) and that has
the highest
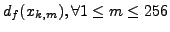 . The second
character of the tuple, xl, is padded
to the end of the packet and df(xk,l) is reduced. This step is
repeated until the blending attack size reaches a desired length. . The second
character of the tuple, xl, is padded
to the end of the packet and df(xk,l) is reduced. This step is
repeated until the blending attack size reaches a desired length.
We now summarize the methods provided above and analyze
the hardness of a polymorphic blending attack while keeping the
design goals (Section 3.2.2) in mind. For 1-gram blending, although finding
a substitution that minimizes the padding seems to be a hard-problem and may
take exponential time, we have proposed greedy algorithms that find a good
substitution that require small amount of padding to perfectly match the normal byte
frequency. For 2-gram blending, finding a single-byte substitution that
ensures only normal tuples after substitution is shown to be NP-hard
(see the proof in Appendix 6.2). An
approximation algorithm can be used to efficiently compute a substitution
that may introduce a few invalid tuples. A multibyte encoding scheme can
achieve a very good match with no invalid tuples at the expense of very
large attack sizes. An attacker has to therefore consider several
trade-offs between the degree of matching, attack size, and time complexity
to mount successful blending attacks.
We chose an attack that targets a vulnerability in Windows Media Services (MS03-022).
The attack vector we selected exploits a problem with the logging
ISAPI extension that handles incoming client requests. It is based on
the implementation by firew0rker [8]. The size of the
attack vector is 99 bytes and is required to be present at the start
of the HTTP request.
The attack needs to send approximately
10KB of data to cause the buffer overflow and compromise the
system. Our attack body opens a TCP client socket to an IP address and
sends system registry files. The size of the unencrypted attack body
is 558 bytes and contains 109 different characters. During the blending
process, we divided our attack into
several packets. If our final blending attack after padding does not
add up to 10KB, we just send some normal packets as a part of the attack to
cause the buffer overflow. The decryptor was
divided into multiple sections and distributed among different
packets. The attack body was divided among all the attack packets.
Figure 4:
Packet length distribution
|
Figure 5:
Observed Unique 1-grams and 2-grams
|
Table 1:
HTTP Traffic dataset
|
Data Type |
Feature |
Packet length |
|
|
|
|
418 |
730 |
1460 |
|
|
|
Num. of Pkts |
16,490 |
540 |
1,781 |
|
|
IDS Training |
One Grams |
106 |
90 |
128 |
|
|
|
Two Grams |
4,325 |
3,791 |
3,903 |
|
|
|
Num. of Pkts |
2,168 |
82 |
249 |
|
|
Attack Training |
One Grams |
89 |
86 |
86 |
|
|
|
Two Grams |
2,847 |
2,012 |
2,196 |
|
|
We collected around 15 days of HTTP traffic coming to our
department's network in November 2004.
We used several IDSs, including Snort, to verify that this data
contains no known attack.
We removed all the packets with no TCP
payload. We used the data of the first 14 days (4,356,565 packets, 1.9GB) for
IDS training to obtain the IDS normal profiles.
A separate profile was created for each TCP payload length
(or simply packet length). The full payload section of each
packet was used to compute the profiles. The last day of
the HTTP traffic was made available to the attacker to learn
the artificial profile. We also used cross-validation, i.e., randomly picking one of
the 15 days for attack training and the rest for IDS training, to
verify the results of our experiments.
The packet
length distributions in the IDS training dataset and the attack training
dataset are shown in Figure 4.
Among this packet lengths, we chose three different lengths to implement the blending attack, namely 418, 730 and 1460.
These packets lengths are large enough to accommodate the attack data into a small number of packets.
These lengths also occurred frequently in the training dataset.
A separate artificial profile was created for each packet length using the attack
training data of the same packet length. Thus, we generated three 1-gram models
and three 2-gram models for different packet lengths. Table 1 shows the
details of the datasets used for the evaluation.
The numbers of unique 1-grams and 2-grams in the data are also shown in the table.
4.6 Evaluation
Training time of 1-gram and 2-gram PAYL: We
performed experiments on the training time required to learn the
profiles used by PAYL. Figure 5 shows the
numbers of unique 1-grams and 2-grams observed in HTTP traffic
stream. Since the numbers of observed 1-gram and 2-gram continue to increase as new packets
arrive in the stream, the training of profiles for 1-gram and 2-gram
takes a long time to converge. We trained our IDS model using all of the
available IDS training data.
Traditional polymorphic attacks:
To the best of our knowledge, CLET [5] is the only publicly
available tool that implements evasion techniques against byte frequency-based anomaly IDS.
For this reason we used CLET as our baseline.
As mentioned in Section 2, given an attack CLET adds padding bytes in the
payload to make the byte frequency distribution of the attack close to the normal traffic.
However, CLET does not apply any byte substitution technique (see Section 4.2.2).
Further, CLET does not address the evasion of 2-gram PAYL explicitly.
We also generated polymorphic attacks using other well known tools (e.g., ADMutate [17]),
and verified that they are less effective than CLET in evading PAYL.
We generated multiple
polymorphic instances of our attack body using CLET and
tested them against PAYL. Each attack instance contained one or more
attack packets of given length. Different amount of bytes were crammed
(padded) to obtain the desired attack size. Attack training data was used to
generate spectral files used for cramming by the CLET engine.
A polymorphic attack instance will evade an IDS model if and only if all the
attack packets corresponding to the attack instance are able to evade the IDS.
Thus, the anomaly score of an attack instance was calculated as the highest
of all the anomaly scores (Equation 1) obtained by the
attack packets corresponding to the attack instance.
Table 2 shows the anomaly threshold setting of different PAYL models that result in the detection of all the attack instances. The anomaly
thresholds were calculated as the minimum anomaly score over all the attack
instances. Using the given thresholds, both 1-gram and 2-gram PAYL
were successful in detecting all the instances of the attack. Having
established this ``baseline'' performance, we would like to show that our
blending attacks can evade PAYL even if a lower threshold is used.
Table 2:
IDS anomaly threshold setting that detects all the polymorphic attacks sent by the CLET engine
|
Packet Length |
1-gram |
2-gram |
|
418 |
872 |
1,399 |
|
730 |
652 |
1,313 |
|
1460 |
355 |
977 |
|
Table 3:
Number of packets required for the convergence of attacker's training
|
Packet Length |
1-gram |
2-gram |
|
418 |
8 |
20 |
|
730 |
8 |
18 |
|
1460 |
14 |
40 |
|
Figure 6:
Anomaly score of Artificial Profile
|
We used a simple convergence technique, similar to PAYL, to stop the training
of the artificial profile. At every certain interval (convergence check
interval) we check if the Manhattan
1
distance between the artificial profiles at the
last interval and the current interval is smaller than a certain threshold (convergence
threshold). It stops training if the distance is smaller than the threshold. We
set the convergence threshold (=0.05) to be the same as the original implementation of PAYL.
The artificial profile does not have to become very stable or match the normal profile perfectly
because some deviation from the normal profile can be tolerated. To reduce
the training time we set the convergence check interval to 2 packets.
Thus, if we see two consecutive packets of a given length
that are close to the learned profile, we stop
training. Table 3 shows the number of
packets required to converge the artificial profile of different packet
lengths. As expected, the artificial profile converges very
fast. The 1-gram profile converges faster than the 2-gram profile
for the same packet length. We show that a small number of
packets are enough to create an effective polymorphic blending
attack. In practice, the attacker can use more learning data to create a
better profile.
Figure 6 shows the anomaly score
of the artificial normal profile, as calculated by the IDS normal profile, versus
the number of attack training packets used
to learn the artificial profile. As the number of attack training
packets increases, the anomaly score of artificial normal profile
decreases, which means that the artificial profile trained using more packets is a
better estimation of the PAYL normal profile. The score needs
to be less than the anomaly threshold of PAYL for the blending
attack packets to have a realistic chance of evading PAYL. For
all attack training sizes shown in Figure 6,
the score is well under the threshold (Table 2) used to configure PAYL
to detect all the traditional (without blending) polymorphic attack
instances.
For each packet length, we generated both the 1-gram and
2-gram PAYL normal profiles using the entire IDS training dataset (i.e.,
the first 14 days of HTTP traffic). For each packet length, the
1-gram and 2-gram artificial normal models were learned using a
fraction of the attack training dataset. The learning stops at the
point the models converge, as shown in Table 3.
We used the one-to-one single-byte substitution technique discussed in Section 4.2.2
for constructing the blending attack against 1-gram PAYL, and the single byte encoding scheme
discussed in Section 4.3.2 for the blending attack against 2-gram PAYL.
Two sets of blending experiments were performed. In the first set of experiments,
the substituted attack body was divided into multiple
packets and each packet was padded separately to match the normal profile.
A single decoding table is required to decode the whole attack flow.
In the second set of experiments, the attack body was first divided into a given number
of packets. Each of the attack body sections were substituted using one-to-one
single byte substitution and then padded to match the normal frequency.
Individually substituting the attack body for each packet allowed us to match the
statistical profile of the substituted attack body closer to the normal profile. But it
requires a separate decoding table for each packet, thus reducing the padding
space considerably. For convenience, we call
the first set of experiments global substitution, and the second local substitution.
If m>n for any of the above experiments, we simply substituted the low frequency
attack characters using non-existing characters in the normal. This increased the
error in blending attack but reduced the complexity of the blending attack algorithm.
Figure 7:
Comparison of frequency distribution of normal profile and attack packet
|
(a) Original attack packet
|
|
(b) 1-gram Blending Packet for packet length 1460
|
|
Figure 7 shows the comparison of the frequency
distribution of different characters present in the HTTP traffic.
The byte frequency distribution of the original attack instance is
very different from the
normal profile because the normal data has mainly printable ASCII
characters whereas the attack payload has many characters that are
unprintable. Thus, this was easily detected by both 1-gram
and 2-gram IDS models. The attack was substituted and padded to obtain a
single packet of length 1460. As shown in Figure 7(b),
the frequency distribution of attack
payload after substitution and padding
becomes almost identical to the PAYL normal profile. This demonstrates the
effectiveness of our polymorphic blending techniques.
Figure 8:
Anomaly score of the blending attack packets (with local substitution) for artificial profile and IDS profile
|
Figure 9:
Anomaly score of the blending attack packets (with global substitution) for artificial profile and IDS profile
|
We studied how dividing an attack instance into several packets and blending
them separately help match the attack packets with the artificial
profile and evade PAYL. The experiments were performed with the
number of attack packets ranging from 1 to 12.
We checked the anomaly score of each attack packet
as calculated by both the artificial profile and the IDS
profile.
Similar to the anomaly score of attack instances generated by CLET, the anomaly score
of a blending attack instance was calculated as the highest
of all the scores obtained by the attack packets corresponding to the blending attack
instance. Figure 8 and Figure 9 show
the anomaly scores of blending attacks with local substitution and global
substitution, respectively.
For each attack flow, we show the score of the packet with the
highest score. It is evident
that if the attack is divided into more packets, it
matches the profile more closely. The reason is that if the attack body is
divided into multiple fragments, for each packet there is more padding space available
to match the profile. Also, local
substitution works better than global substitution
scheme for all cases except for 2-gram blending for packet length 418. Since our substitution
table contains only normal 1-grams but may contain foreign 2-grams,
a large substitution table may produce a large error for the 2-gram model.
Considering that small packets have small padding space to reduce the error
caused by the substitution table, having an individual substitution table in each
packet can cause large error.
Although the score of the
blending attack as calculated by the IDS model is greater than the
score calculated by the artificial normal profile,
it is still much lower than the anomaly threshold set for the detection of
traditional polymorphic attacks.
Thus, our experiment clearly shows that unlike traditional
polymorphic attacks, our blending attack is very effective
in evading 1-gram and 2-gram PAYL for all the
packet lengths and number of attack packets.
Table 4:
Anomaly thresholds for different false positive rates in IDS models.
Bracketed entries are the the numbers of packets required to evade the
IDS using the local and global substitution scheme, respectively.
|
False Positive |
418 |
730 |
1460 |
|
|
1-gram |
2-gram |
1-gram |
2-gram |
1-gram |
2-gram |
|
0.1 |
61.07 (17,-) |
373.4 (-,12) |
63.70 (5,7) |
467.6 (5,5) |
74.50 (3,3) |
447.7 (2,2) |
|
0.01 |
78.61 (12,15) |
456.9 (22,8) |
143.6 (2,3) |
625.5 (3,3) |
81.98 (3,3) |
531.0 (2,2) |
|
0.001 |
125.5 (5,7) |
561.8 (7,6) |
164.6 (2,3) |
670.5 (3,3) |
239.2 (1,1) |
931.9 (1,1) |
|
0.0001 |
166.8 (5,5) |
582.6 (7,5) |
244.5 (2,2) |
805.0 (2,2) |
243.4 (1,1) |
935.0 (1,1) |
|
We also studied the effect of false positive rates on the detection of
blending attacks.
Anomaly threshold for a given false
positive rate (fp) is set such that only fp fraction of normal data
has anomaly score higher than the anomaly threshold.
The anomaly thresholds for different false positive rates are shown
in Table 4.
The number of attack packets required to evade the IDS
successfully for a given threshold is shown in
the parenthesis. As we increase the
false positive rate, we need to divide the attack into more
packets to keep the score below the anomaly threshold. Thus, keeping a high false positive
rate may increase the size of the blending attack. From the table we
can infer that even if the IDS keeps its false positive rate high to
detect more attacks, blending attack can still easily evade it using an
attack size as small as 3,650, i.e. five packets of length 730.
Since 2-gram PAYL records some sequence information along
with byte frequencies, it seems to be a good representation of
normal traffic. In our experiments we found that 2-gram PAYL
consistently produces higher anomaly score than 1-gram PAYL for all
attack packet lengths. But at the same time, the 2-gram IDS needs to set
very high anomaly thresholds to avoid high false positive
rates. Thus, in practice, the 2-gram PAYL is actually only marginally
more effective than the 1-gram version in detecting attacks.
Blending attacks can be successfully launched on both 1-gram and 2-gram models.
Larger packet lengths are more suitable for blending attacks. With few
exceptions, the local substitution scheme works better than the global substitution
scheme. The 2-gram model provides only marginal advantage over the 1-gram model in
detecting blending attacks but requires huge space to store the model. Thus,
the 2-gram model may not be a better choice over the 1-gram model.
4.7 Countermeasures
The experimental results reported above show that the statistical models used
by PAYL are not sufficiently accurate to detect deliberate evasion
attempts.
We believe this problem is common to other network anomaly IDS that use traffic statistics [15,18].
By following the ideas presented in this paper, it may be fairly easy to
devise different blending algorithms in order to evade other network anomaly IDSs that rely solely on some form of packet statistics.
The reason is that
traffic statistics used by such network-based anomaly IDS do not
provide a comprehensive representation of normal traffic.
Application syntax and semantics related information cannot be modeled accurately
using simple statistics of network packets. On the other hand, some of the IDS introduced
in Section 2, e.g., [1,2,30],
use syntax and semantics related information and could
be used to detect the polymorphic blending attack. Nevertheless, modeling application syntax and
semantic information is in general more expensive than measuring simple traffic statistics. Thus
the trade-off between detection accuracy, hardness of evasion and operational speed has to be considered.
A key direction to explore is to develop a more efficient semantic-based IDS that can be deployed
on high-speed networks.
Another defense approach is to use multiple IDS models that use independent features.
Such a collective set of models may be a better representation of the normal traffic.
In such a case, a polymorphic blending attack will need to evade all (or the majority) of the models.
One reason blending attacks work is that the attacker
has the complete knowledge of the IDS model being used. This gives the attacker an enormous
advantage. A possible countermeasure is to introduce randomness [27] in the IDS
model. Consider a model constructed by measuring the occurrence frequency of
pairs of non-consecutive bytes that are separated by
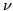 number of bytes. For example, given a payload containing the sequence of byte
values number of bytes. For example, given a payload containing the sequence of byte
values
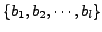 , the IDS could measure the occurrence frequency of
the pair of byte values , the IDS could measure the occurrence frequency of
the pair of byte values
 , where
l is the payload length. We call this a , where
l is the payload length. We call this a 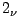 -gram model. For -gram model. For 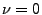 ,
the ,
the 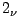 -gram model is the same as the 2-gram PAYL model. If the IDS
chooses -gram model is the same as the 2-gram PAYL model. If the IDS
chooses 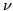 at random during the training phase, this makes the blending
attack more difficult given that the attacker needs to guess the value of at random during the training phase, this makes the blending
attack more difficult given that the attacker needs to guess the value of 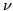 before applying the blending algorithm (note that
before applying the blending algorithm (note that 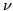 is chosen at random
before the model is created and is fixed for each packet. Therefore, the is chosen at random
before the model is created and is fixed for each packet. Therefore, the
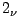 -gram model is as complex as the 2-gram model used by PAYL).
Furthermore, the IDS could construct m different models, each of them having a
different randomly chosen -gram model is as complex as the 2-gram model used by PAYL).
Furthermore, the IDS could construct m different models, each of them having a
different randomly chosen 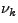 , with , with 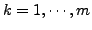 , and combine their output in
order to obtain a more accurate decision about the packets. In this case the
attacker needs to guess m values for the parameter , and combine their output in
order to obtain a more accurate decision about the packets. In this case the
attacker needs to guess m values for the parameter 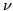 and needs to devise
a blending algorithm that ``satisfies'' all the m different models at the
same time. This means that even if the attacker knows exactly how the IDS
performs the training and test phases, it is much more difficult to evade it. and needs to devise
a blending algorithm that ``satisfies'' all the m different models at the
same time. This means that even if the attacker knows exactly how the IDS
performs the training and test phases, it is much more difficult to evade it.
Preliminary experimental results show that if 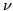 is small with respect to
the payload size, the is small with respect to
the payload size, the 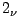 -gram model is able to capture a sufficient
amount of structural information that allows to construct an accurate IDS
model. Further, the combination of different -gram model is able to capture a sufficient
amount of structural information that allows to construct an accurate IDS
model. Further, the combination of different 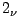 -gram models appears to
be a promising technique. However, the complexity of
the detection system grows linearly with m.
A thorough analysis of this modeling technique is beyond the scope of this
paper and will be the subject of our future work. -gram models appears to
be a promising technique. However, the complexity of
the detection system grows linearly with m.
A thorough analysis of this modeling technique is beyond the scope of this
paper and will be the subject of our future work.
While countermeasures may make evasion harder to
succeed, they typically require more resources and can be more complex
in design and implementation. It may also produce higher error rates
if the IDS uses too many features such that its models ``overfit'' the
data. In short, trade-offs between ``hardness of evasion'' and other
performance measures need to be carefully considered.
5 Conclusion
In this paper, we presented a new class of attacks called polymorphic
blending attacks. Existing polymorphic techniques can be used for
evading signature-based IDS because the attack instances do not share
a consistent signature.
But anomaly IDS can detect these attack instances
because the polymorphism techniques fail to mask their
statistical anomalies. Our proposed attack overcomes this very
shortcoming. The idea is to first learn the normal profiles used by
the IDS, and then, while creating a polymorphic instance of an attack,
make sure that its statistics match the normal profiles.
We described the basic steps and general techniques that can be used
to devise polymorphic blending attacks. We presented a case
study using the anomaly IDS PAYL to demonstrate that these
attacks are practical and feasible. Our experiments showed that
polymorphic blending attacks can evade PAYL while traditional
polymorphic attacks cannot.
We also showed that an attacker does not need a large number of
packets to learn the normal profile and blend in successfully. The
results with 2-gram PAYL suggested that simply using
more complex features or models do not always provide a good defense
against these polymorphic blending attacks.
We discussed some possible defenses against polymorphic blending
attacks.
This work is supported in part by NSF grant CCR-0133629 and Office of
Naval Research grant N000140410735. The contents of this work are
solely the responsibility of the authors and do not necessarily
represent the official views of NSF and the U.S. Navy. The authors
would like to thank the anonymous reviewers for helpful comments and
the shepherd of this paper Professor Fabian Monrose at The Johns
Hopkins University for very valuable suggestions.
- 1
-
P. Akritidis, E. P. Markatos, M. Polychronakis, and K. D. Anagnostakis.
Stride: Polymorphic sled detection through instruction sequence
analysis.
In Proceedings of the 20th IFIP International Information
Security Conference (IFIP/SEC 2005), 2005.
- 2
-
R. Chinchani and E.V.D. Berg.
A fast static analysis approach to detect exploit code inside network
flows.
In Recent Advances in Intrusion Detection, 2005.
- 3
-
M. Christodorescu, S. Jha, S. Seshia, D. Song, and R. Bryant.
Semantics-aware malware detection.
In Proceeding of the IEEE Security and Privacy Conference,
2005.
- 4
-
T. H. Cormen, C. E. Leiserson, and R. L. Rivest.
Introduction to algorithms.
The MIT Press, 1990.
- 5
-
T. Detristan, T. Ulenspiegel, Y. Malcom, and M. Underduk.
Polymorphic shellcode engine using spectrum analysis.
Phrack Issue 0x3d, 2003.
- 6
-
H. Feng, J. Giffin, Y. Huang, S. Jha, W. Lee, and B. Miller.
Formalizing sensitivity in static analysis for intrusion detection.
In Proceedings the IEEE Symposium on Security and Privacy,
2004.
- 7
-
H. Feng, O. Kolesnikov, P. Fogla, W. Lee, and W. Gong.
Anomaly detection using call stack information.
In Proceedings of the IEEE Security and Privacy Conference,
2003.
- 8
-
Firew0rker.
Windows media services remote command execution exploit.
https://www.k-otik.com/exploits/07.01.nsiilog-titbit.cpp.php,
2003.
- 9
-
S. Forrest, S.A. Hofmeyr, A. Somayaji, and T.A. Longstaff.
A sense of self for unix processes.
In Proceedings of the IEEE Symposium on Security and Privacy,
1996.
- 10
-
Threat Intelligence Group.
Phatbot trojan analysis.
https://www.lurhq.com/phatbot.html.
- 11
-
M. Handley and V. Paxson.
Network intrusion detection: Evasion, traffic normalization, and
end-to-end protocol semantics.
In 10th USENIX Security Symposium, 2001.
- 12
-
O. M. Kolesnikov, D. Dagon, and W. Lee.
Advanced polymorphic worms: Evading IDS by blending in with normal
traffic.
Technical Report GIT-CC-04-13, College of Computing, Georgia Tech,
2004.
- 13
-
C. Kruegel, E. Kirda, D. Mutz, W. Robertson, and G. Vigna.
Automating mimicry attacks using static binary analysis.
In 14th Usenix Security Symposium, 2005.
- 14
-
C. Kruegel, E. Kirda, D. Mutz, W. Robertson, and G. Vigna.
Polymorphic worm detection using structural information of
executables.
In Recent Advances in Intrusion Detection, 2005.
- 15
-
C. Kruegel, T. Toth, and E. Kirda.
Service specific anomaly detection for network intrusion detection.
In Proceedings of ACM SIGSAC, 2002.
- 16
-
C. Kruegel and G. Vigna.
Anomaly detection of web-based attacks.
In Proceedings of ACM CCS, pages 251-261, 2003.
- 17
-
Ktwo.
Admmutate: Shellcode mutation engine.
https://www.ktwo.ca/ADMmutate-0.8.4.tar.gz, 2001.
- 18
-
M. Mahoney.
Network traffic anomaly detection based on packet bytes.
In Proceedings of ACM SIGSAC, 2003.
- 19
-
M. Mahoney and P.K. Chan.
Learning nonstationary models of normal network traffic for detecting
novel attacks.
In Proceedings of SIGKDD, 2002.
- 20
-
J. Newsome, B. Karp, and D. Song.
Polygraph: Automatically generating signatures for polymorphic worms.
In Proceeding of the IEEE Security and Privacy Conference,
2005.
- 21
-
R. Perdisci, D. Dagon, W. Lee, P. Fogla, and M. Sharif.
Misleading worm signature generators using deliberate noise
injection.
In Proceedings of the IEEE Security and Privacy Conference,
2006.
- 22
-
T.H. Ptacek and T.N. Newsham.
Insertion, evasion, and denial of service: Eluding network intrusion
detection.
Technical Report T2R-0Y6, Secure Networks, Inc., 1998.
- 23
-
Rain Forest Puppy.
A look at whisker's anti- ids tactics just how bad can we ruin a good
thing?
www.wiretrip.net/rfp/txt/whiskerids.html, 1999.
- 24
-
S. Rubin, S. Jha, and B.P. Miller.
Automatic generation and analysis of nids attacks.
In Annual Computer Security Applications Conference (ACSAC),
2004.
- 25
-
M. Sedalo.
Jempiscodes: Polymorphic shellcode generator.
www.shellcode.com.ar/en/proyectos.html.
- 26
-
D. Song.
Fragroute: a tcp/ip fragmenter.
www.monkey.org/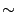 dugsong/fragroute, 2002. dugsong/fragroute, 2002.
- 27
-
Sal Stolfo.
Personal communication.
2005.
- 28
-
P. Szor.
Advanced code evolution techniques and computer virus generator kits.
The Art of Computer Virus Research and Defense, 2005.
- 29
-
K.M.C. Tan, K.S. Killourhy, and R.A. Maxion.
Undermining an anomaly-based intrusion detection system using common
exploits.
In Recent Advances in Intrusion Detection, 2002.
- 30
-
T. Toth and C. Kruegel.
Accurate buffer overflow detection via abstract payload execution.
In Recent Advances in Intrusion Detection, 2002.
- 31
-
G. Vigna, W. Robertson, and D. Balzarotti.
Testing network-based intrusion detection signatures using mutant
exploits.
In Proceedings of the ACM Conference on Computer and
Communication Security (ACM CCS), pages 21-30, 2004.
- 32
-
D. Wagner and D. Dean.
Intrusion detection via static analysis.
In Proceeding of IEEE Symposium on Security and Privacy, 2001.
- 33
-
D. Wagner and P. Soto.
Mimicry attacks on host-based intrusion detection systems.
In Proceedings of the ACM Conference on Computer and
Communication Security (ACM CCS), 2002.
- 34
-
H. J. Wang, C. Guo, D. R. Simon, and A. Zugenmaier.
Shield: Vulnerability-driven network filters for preventing known
vulnerability exploits.
In the Proceedings of ACM SIGCOMM, 2004.
- 35
-
K. Wang and S. Stolfo.
Anomalous payload-based network intrusion detection.
In Recent Advances in Intrusion Detection, 2004.
- 36
-
K. Wang and S. Stolfo.
Anomalous payload-based worm detection and signature generation.
In Recent Advances in Intrusion Detection, 2005.
- 37
-
T. Yetiser.
Polymorphic viruses: Implementation, detection, and protection.
Technical report, VDS Advanced Research Group, 1993.
6.1 Proof of Optimal Padding for 1-gram Blending Attack
We prove that the padding calculated using Equation (7) is minimum for matching the 1-gram profile exactly.
Proof 6.1
We prove the theorem by contradiction. Assume that for some j, 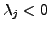 . Then from Equation (7), . Then from Equation (7),
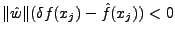 .
Thus, .
Thus,
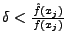 .
This contradicts Equation (5), therefore, all .
This contradicts Equation (5), therefore, all
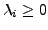 . .
The frequency of a character xi in the packet after padding is
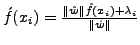 . Using Equation (7) and Equation (4), . Using Equation (7) and Equation (4),
 . Thus, the final attack packet after padding has the exact target distribution, f(xi). . Thus, the final attack packet after padding has the exact target distribution, f(xi).
Theorem 6.2
The padding calculated using Equation (7) is the minimum required padding to match frequencies exactly.
Proof 6.2
Suppose we perform padding using Equation (7). Suppose there exists another packet (say p,
 ) with smaller padding and matches the frequencies exactly. Since ) with smaller padding and matches the frequencies exactly. Since  , the number of occurrences of xk in p cannot decrease. Thus, frequency of xk in packet p is , the number of occurrences of xk in p cannot decrease. Thus, frequency of xk in packet p is
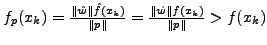 .
Thus, packet p does not match the normal frequencies exactly. Thus, we have reached a contradiction. .
Thus, packet p does not match the normal frequencies exactly. Thus, we have reached a contradiction.
6.2 Proof of Hardness of 2-gram Single-Byte Encoding
First, we look at the problem of evading a simple IDS that stores all the 2-grams present in the normal stream. While monitoring, it checks if all the 2-grams present in the traffic are also present in the normal 2-gram list. In the event that the IDS finds a 2-gram that was not present in normal traffic, IDS raises an alarm. Blending the attack packet with the normal traffic requires the attacker to transform the packet such that all the 2-grams in the packet after substitution are also present in the normal 2-gram list. Matching the frequencies of the tuples is at least as hard as the above simplified problem.
Suppose we have a normal traffic profile (N, TN) and an attack packet description (M, TM), where N and M is the set of normal and attack characters, respectively. TN and TM is the set of different 2-grams present in normal traffic and the attack, respectively. Also, the attacker is allowed to do only one-to-one substitution from M to N. Then, blending of the packet translates to finding a substitution S such that all the tuples in S(w) are also present the normal profile. That is if
 , then , then
 . .
Theorem 6.3
The problem of finding a one-to-one substitution S to match 2-grams is NP-complete.
Proof 6.3
To prove that the problem is in NP-complete, we need to show that the problem is polynomial time verifiable and NP-hard.
Given a solution substitution S for the 2-gram matching problem, we can calculate S(w) in  steps. For each 2-gram present in S(w), checking if it is present in TN can be done in steps. For each 2-gram present in S(w), checking if it is present in TN can be done in  steps. Thus, this problem is poly-verifiable and consequently in NP. steps. Thus, this problem is poly-verifiable and consequently in NP.
To show that the problem is NP-hard, we reduce the problem of sub-graph isomorphism to substitution problem. A sub-graph isomorphism problem is that given two graphs G(V, E) and G'(V', E'), decide whether G' is a sub-graph of G. Mathematically, we want to check if there is a mapping
 , s.t. , s.t.
 . .
Suppose, N = V. For each edge
 , add two 2-grams
(v1v2, v2v1) in the normal profile (TN). Suppose M = V'. For each edge , add two 2-grams
(v1v2, v2v1) in the normal profile (TN). Suppose M = V'. For each edge
 , we add two 2-grams
(v1v2, v2v1) in the attack profile (TM). , we add two 2-grams
(v1v2, v2v1) in the attack profile (TM).
If the above 2-gram matching problem has a solution, then we can find a mapping
 such that for all 2-grams such that for all 2-grams
 , ,
 . Since the 2-grams in TM correspond to edges in G' and the 2-grams in TN correspond to edges in G, the above statement suggests that . Since the 2-grams in TM correspond to edges in G' and the 2-grams in TN correspond to edges in G, the above statement suggests that
 . This means that graph G' is isomorphic to a sub-graph of G with mapping given by S. . This means that graph G' is isomorphic to a sub-graph of G with mapping given by S.
Also, if there does not exist a solution to the 2-gram matching problem, then there does not exists a substitution St such that G' is a sub-graph of G after substitution. Otherwise, St will result in a successful 2-gram mapping.
Thus, the 2-gram matching problem is at least as hard as the sub-graph isomorphism problem. It is known that the sub-graph isomorphism problem is NP-complete. Also, we have already proved that the 2-gram matching problem is in NP. Thus, the 2-gram matching problem is NP-complete.
Even if an IDS allows constant number of mismatches, it can be shown that the problem still remains NP-complete. This is followed by the result that sub-graph isomorphism with constant number of edge insertion, deletion, and substitution is also NP-complete. This means that an attacker cannot get the substitution that will match the normal profile with a small constant number of mismatched 2-grams. Also, the one-to-one substitution problem can be easily reduced to one-to-many substitution. Thus, solving one-to-many substitution is also hard.
Polymorphic Blending Attacks
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
-
1
Used by authors of PAYL to compare two models for convergence
|
