
15th USENIX Security Symposium
Pp. 29–41 of the Proceedings
Biometric Authentication Revisited: Understanding the Impact of Wolves in Sheep's Clothing
Biometric Authentication Revisited:
Understanding the Impact of Wolves in Sheep's Clothing
Lucas Ballard
Department of Computer Science
Johns Hopkins University
|
Fabian Monrose
Department of Computer Science
Johns Hopkins University
|
Daniel Lopresti
Department of Computer Science & Engineering
Lehigh University
|
Abstract
Biometric security is a topic of rapidly growing importance,
especially as it applies to user authentication and key generation.
In this paper, we describe our initial steps towards developing
evaluation methodologies for behavioral biometrics that take into
account threat models which have largely been ignored. We argue that the
pervasive assumption that forgers are minimally motivated (or, even
worse, naïve), or that attacks can only be mounted through manual
effort, is too optimistic and even dangerous. To illustrate our point,
we analyze a handwriting-based key-generation system and show
that the standard approach of evaluation significantly over-estimates
its security. Additionally, to overcome current
labor-intensive hurdles in performing more accurate assessments of
system security, we present a generative attack model based on
concatenative synthesis that can provide a rapid indication of the
security afforded by the system. We show that our generative attacks
match or exceed the effectiveness of forgeries rendered by the skilled
humans we have encountered.
1 Introduction
The security of many systems relies on obtaining human input that is
assumed to not be readily reproducible by an attacker. Passwords are
the most common example, though the assumption that these are not
reproducible is sensitive to the number of guesses that an attacker is
allowed. In online attacks, the adversary must submit each
request to a nonbypassable reference monitor (e.g., a login prompt)
that accepts or declines the password and permits a limited number of
incorrect attempts. In contrast, an offline attack permits the
attacker to make a number of guesses at the password that is limited
only by the resources available to the attacker, i.e., time and
memory. When passwords are used to derive cryptographic keys, they
are susceptible to offline attacks.
An alternative form of user input that is intended to be difficult for
attackers to reproduce are biometrics. Like passwords, biometrics
have typically been used as a technique for a user to authenticate
herself to a reference monitor that can become unresponsive after a certain number of failed attempts. However, biometrics also have been explored as
a means for generating user-specific cryptographic keys (see for
example, [30,21]). As with password-generated keys,
there is insufficient evidence that keys generated from biometric
features alone will typically survive offline attacks. As such, an
alternative that we and others have previously explored is
password hardening whereby a cryptographic key is generated from
both a password and dynamic biometric features of the user while
entering it [22,23].
While these directions may indeed allow for the use of biometrics in a
host of applications, we believe the manner in which biometric systems
have been tested in the literature (including our prior work) raises
some concerns. In particular, this work demonstrates the need for
adopting more realistic adversarial models when performing security
analyses. Indeed, as we show later, the impact of forgeries generated
under such conditions helps us to better understand the security of
certain biometric-based schemes.
Our motivation for performing this analysis is primarily to show that
there exists a disconnect between realistic threats and
typical "best" practices [17] for reporting biometric
performance-one that requires rethinking as both industry
and the research community gains momentum in the exploration of
biometric technologies. We believe that the type of analysis presented
herein is of primary importance
for the use of biometrics for authentication and cryptographic key
generation (e.g., [21,7,2,12]),
where weakest-link analysis is paramount.
Moreover, to raise awareness of this shortcoming we explore a particular methodology in which we assume that the adversary utilizes
indirect knowledge of the target user's biometric features. That is,
we presume that the attacker has observed measurements of the biometric in contexts outside its
use for security. For example, if the biometric is the user's
handwriting dynamics generated while providing input via a stylus, then we
presume the attacker has samples of the user's handwriting in another
context, captured hardcopies of the user's writing, or writings from users of a similar style. We argue that
doing so is more reflective of the real threats to biometric
security. In this paper, we explore how an attacker can use such data
to build generative models that predict how a user would, in
this case, write a text, and evaluate the significance of this to
biometric authentication.
2 Biometric Authentication
Despite the diversity of approaches examined by the biometrics community [1], from the standpoint of this
investigation several key points remain relatively constant. For
instance, the traditional procedure for applying a biometric as an
authentication paradigm involves sampling an input from a user,
extracting an appropriate set of features, and comparing these to
previously stored templates to confirm or deny the claimed identity.
While a wide range of features have been investigated, it is
universally true that system designers seek features that exhibit
large inter-class variability and small intra-class variability. In
other words, two different users should be unlikely to generate the
same input features, while a single user ought to be able to reproduce
her own features accurately and repeatably.
Likewise, the evaluation of most biometric systems usually follows a
standard model: enroll some number of users by collecting training
samples, e.g., of their handwriting or speech. At a later time, test
the rate at which users' attempts to recreate the biometric to within
a predetermined tolerance fail. This failure rate is denoted as the
False Reject Rate (FRR). Additionally, evaluation
usually involves assessing the rate at which one user's input (i.e.,
an impostor) is able to fool the system when presented as coming from
another user (i.e., the target). This evaluation yields the False
Accept Rate (FAR) for the system under consideration. A
tolerance setting to account for natural human variation is also vital
in assessing the limits within which a sample will be consider as
genuine, while at the same time, balancing the delicate trade-off of
resistance to forgeries. Typically, one uses the equal error rate
(EER)-that is, the point at which the FRR and the FAR are
equal-to describe the accuracy of a given biometric
system. Essentially, the lower the EER, the higher the accuracy.
Researchers also commonly distinguish between forgeries that
were never intended to defeat the system ("random" or naïve
forgeries), and those created by a user who was instructed to make
such an attempt given information about the targeted input (i.e.,
so-called "skilled" forgeries). However, the evaluation of
biometrics under such weak security assumptions can be misleading. Indeed, it may even be argued that because there is no strong means by which one can define a good forger and prove her
existence (or non-existence), such analysis is theoretically
impossible [29]. Nevertheless, the biometric community
continues to rely on relatively simple measures of adversarial
strength, and most studies to date only incorporate unskilled
adversaries, and very rarely, "skilled" impersonators [13,29,11,19,20,15].
This general practice is troubling as the evaluation of the
FAR is likely to be significantly underestimated [29,28].
Moreover, we believe that this relatively ad hoc approach to
evaluation misses a significant threat: the use of generative
models to create synthetic forgeries which can form the basis for
sophisticated automated attacks on biometric security. This
observation was recently reiterated in [32], where the authors
conjectured that although the complexity of successful impersonations
on various biometric modalities can be made formidable,
biometric-based systems might be defeated using various
strategies (see for example
[31,9,26,15]). As we show
later, even rather simplistic attacks launched by successive
replication of synthetic or actual samples from a representative
population can have adverse effects on the FAR-particularly
for the weakest users (i.e., the so-called "Lambs" in the biometric
jargon for a hypothetical menagerie of users [3]).
In what follows, we provide what we believe is the most in-depth study
to date that emphasizes the extent of this problem. Furthermore, as a
first step towards providing system evaluators with a stronger methodology for
quantifying performance under various threats, we describe our work on developing a prototype toolkit using handwriting dynamics as a case in point.
3 Handwriting Biometrics
Research on user authentication via handwriting has had a long, rich
history, with hundreds of papers written on the topic. The majority
of this work to date has focused on the problem of signature
verification [27]. Signatures have some well known
advantages: they are a natural and familiar way of confirming
identity, have already achieved acceptance for legal purposes, and
their capture is less invasive than most other biometric
schemes [6]. While each individual has only one true
signature-a notable limitation-handwriting in general contains
numerous idiosyncrasies that might allow a writer to be identified.
In considering the mathematical features that can be extracted from
the incoming signal to perform authentication, it is important to
distinguish between two different classes of inputs. Data captured by
sampling the position of a stylus tip over time on a digitizing tablet
or pen computer are referred to as online handwriting, whereas
inputs that are presented in the form of a 2-D bitmap (e.g., scanned off
of a piece of paper) are referred to as offline handwriting.
To avoid confusion with the traditional attack models in the security
community, later on in this paper we shall eschew that terminology and
refer to the former as covering both temporal and spatial information,
whereas the latter only covers spatial information.
Features extracted from offline handwriting samples include bounding
boxes and aspect ratios, stroke densities in a particular region,
curvature measurements, etc. In the online case, these features are
also available and, in addition, timing and stroke order information
that allows the computation of pen-tip velocities, accelerations, etc.
Studies on signature verification and the related topic of handwriting
recognition often make use of 50 or more features and, indeed, feature
selection is itself a topic for research. The features we use in our
own work are representative of those commonly reported in the
field [8,33,18,14].
Repeatability of features over time is, of course, a
key issue, and it has been found that dynamic and static features are
equally repeatable [8].
In the literature, performance figures (i.e., EER) typically range
from 2% to 10% (or higher), but are difficult to compare directly as
the sample sizes are often small and test conditions quite
dissimilar [5]. Unfortunately, forgers are rarely
employed in such studies and, when they are, there is usually no
indication of their proficiency. Attempts to model attackers with a
minimal degree of knowledge have involved showing a static image of
the target signature and asking the impostor to try to recreate the
dynamics [24]. The only serious attempt we are aware of, previous to our own,
to provide a tool for training forgers to explore the limits of their
abilities is the work by Zoebisch and Vielhauer [35]. In a
small preliminary study involving four users, they found that showing
an image of the target signature increased false accepts, and showing a dynamic replay doubled the susceptibility to
forgeries yet again. However, since the verification algorithm used
was simplistic and they do not report false reject rates, it
is difficult to draw more general conclusions.
To overcome the "one-signature-per-user" (and hence, one key) restriction, we employ more
general passphrases in our research. While signatures are likely to
be more user-specific than arbitrary handwriting, results from the
field of forensic analysis demonstrate that writer identification from
a relatively small sample set is feasible [10].
Indeed, since
this field focuses on handwriting extracted from scanned page images,
the problem we face is less challenging in some sense since we have
access to dynamic features in addition to static. Another concern,
user habituation [5], is addressed by giving each test
subject enough time to become comfortable with the experimental set-up
and requiring practice writing before the real samples are collected.
Still, this is an issue and the repeatability of non-signature
passphrases is a topic for future research.
4 Experimental Design
We collected data over a two month period to analyze six different forgery styles. We consider three standard evaluation metrics: naïve, static, and dynamic forgeries [13,29,11], as well as three metrics that will provide a more realistic definition of security: naïve*, trained, and generative. Naïve, or "accidental", forgeries are not really forgeries in the traditional sense; they are measured by authenticating one user's natural writing samples of a passphrase against another user's template for the same passphrase. Static (resp. dynamic) forgeries are created by humans after seeing static (resp. real-time) renderings of a target user's passphrase. Naïve* forgeries are similar to naïve forgeries except that only writings from users of a similar style are authenticated against a target user's template. Trained forgeries are generated by humans under certain conditions, which will be described in greater detail later. Lastly, generative forgeries exploit information about a target user to algorithmically generate forgeries. Such information may include samples of the user's writing from a different context or general population statistics.
4.1 Data Collection
Our results are based on 11,038
handwriting samples collected on digitized pen tablet computers from 50 users
during several rounds. We used NEC VersaLite Pad and HP Compaq TC1100
tablets as our writing platforms.
The specifics of each round will be addressed shortly. To
ensure that the participants were well motivated and provided writing
samples reflective of their natural writing (as well as forgery
attempts indicative of their innate abilities), several incentives
were awarded for the most consistent writers, the best/most dedicated forgers, etc.
Data collection was spread across three rounds. In round I, we collected two distinct data sets. The first set established a baseline of "typical" user writing. After habituation on the writing device [5], users were asked to write
five different phrases, consisting of two-word oxymorons, ten times
each. We chose these phrases as they were easy to remember (and therefore, can be written naturally) and could be considered of reasonable length. Signatures were not used due to
privacy concerns and strict restrictions on research involving
human-subjects. More importantly, in the context of key-generation, signatures are not a good choice for a hand-writing biometric as the compromise of keying material could prevent a user from using the system thereafter. This part of the data set was used for two purposes: to establish biometric templates to be used for authentication, and to provide samples for naive and naive* forgeries. To create a strong underlying representative system, users were given instructions to
write as naturally (and consistently) as possible.
The second data set from round I, our "generative corpus", was used to create our generative forgeries and consisted of a set of 65 oxymorons. This set was restricted so that it did not contain any of the five phrases from the first data set, yet provided coverage of the first set at the bi-gram level. As before, we chose oxymorons that were easy to recall, and users were asked to write one instance of each phrase as naturally as possible. The average elapsed
time for round I was approximately one hour.
Round II started approximately two weeks later. The same set of users wrote the five phrases from round
I ten times. Additionally, the users were asked to forge
representative samples (based on writing style, handedness of the
original writer, and gender) from round I to create two sets of 17
forgeries. First, users were required to forge samples after seeing
only a static representation. This data was used for our static forgeries. Next, users were asked to forge
the same phrases again, but this time, upon seeing a real-time
rendering of the phrase. At this stage, the users were instructed to
make use of the real-time
presentation to improve their rendering of the spatial features (for
example, to distinguish between one continuous stroke versus two
strokes that overlap) and to replicate the temporal features of the
writing. This data comprised our dynamic forgeries. On average, round II took approximately 90 minutes for each user.
Lastly, in round III we selected nine users from round II who,
when evaluated using the authentication system to be described in §4.2 and §4.3, exhibited a natural tendency to produce better forgeries than
the average user in our study (although we did not include all of the best forgers). This group consisted of three
"skilled" (but untrained) forgers for each writing style. (One of "cursive", "mixed", or "block", where the classification is based on the percent of the time that users connect adjacent characters.) Each skilled forger was asked to forge writing from the style which they exhibited an innate ability to replicate and was provided with a general overview
and examples of the types of temporal and spatial characteristics that handwriting systems typically capture.
As we were trying to examine (and develop) truly skilled adversaries, our forgers were asked to forge 15 writing samples from their
specified writing style, with 60% of the samples coming from the
weakest 10 targets, and the other 40% chosen at random. (In §5 we also provide the results of our trained forgeries against the entire population.) From this point on, these forgers (and their forgeries) will be referred to as "trained" forgers. We believe that the selection of the naturally skilled forgers, the additional training, and the selection of specific targets produced adversaries who realistically reflect a threat to biometric security.
The experimental setup for these educated forgers is as
follows. First, a real-time reproduction of the target sample is
displayed (at the top half of the tablet) and the forger is allowed to
attempt forgeries (at her own pace) with the option of saving the
attempts she liked. She can also select and replay her forgeries and
compare them to the target. In this way, she is able to fine-tune her
attempts by comparing the two writing samples. Next, she
selects the forgery she believes to be her best attempt, and proceeds
to the next target. The average elapsed time for this round was
approximately two hours.
4.2 Authentication System
In order to have a concrete platform to measure the FAR for each of our six forgery styles, we
loosely adapted the system presented in [34,33] for
generation of "biometric hashes".
We
note that our results are system-independent as we are only evaluating
biometric inputs, for which we evaluated features that are
reflective of the state of the art [14,18,8,33].
For completeness, we briefly describe relevant aspects of the system;
for a more detailed description see [33]. To input a sample to
the system, a human writes a passphrase on an electronic tablet. The
sample is represented as three signals parameterized by time. The
discrete signals x(t) and y(t) specify the location of the pen on
the writing surface at time t, and the binary signal p(t)
specifies whether the pen is up or down at time t. The tablet computes a set of n
statistical features (f1, ..., fn) over these signals.
These features comprise the actual input to the authentication or key-generation system.
During an enrollment phase, each legitimate user writes a passphrase a
pre-specified number (m) of times, and the feature values for each
sample are saved. Let fi,1, ..., fi,n denote the
feature values for sample i. Using the feature values from each user and passphrase, the system computes a global set of tolerance values (T = {e1, ..., en}) to be used to account for natural human variation [34].
Once the m readings have been captured, a biometric template is
generated for each user and passphrase as follows: Let l'j = min0 < i < m+1 fi,j,
h'j = max0 < i < m+1 fi,j, and
Dj = h'j - l'j + 1. Set lj = l'j - Djej,
and hj = h'j + Djej. The resulting template is an n×2 matrix of values { {l1, h1}, ..., {ln,hn}}.
Later, when a user provides a sample with feature values f1, ...,fn for authentication, the system checks whether
lj < fj < hj for each feature fj. Each fj < lj, or fj > hj is
deemed an error, and depending on the threshold of errors tolerated by
the system, the attempt is either accepted or denied. We note that as
defined here, templates are insecure because they leak information about
a user's feature values. We omit discussion of securely
representing biometric templates (see for example [22,4]) as this is not a primary concern of this research.
4.3 Feature Analysis
Clearly, the security of any biometric system is directly related to the
quality of the underlying features. A detailed analysis of proposed
features for handwriting verification is presented in [33],
although we argue that the security model of that work sufficiently differs
from our own and so we believe a new feature-evaluation metric was
required. In that work, the quality of a feature was measured by the
deviation of the feature and entropy of the feature across the
population. For our purposes, these evaluation metrics are not ideal:
we are not only concerned with the entropy of each feature, but rather how
difficult the feature is to forge - which we argue is a more
important criteria. When systems are evaluated using purely naïve
forgeries, then entropy could be an acceptable metric. However, as we
show later, evaluation under naïve forgeries is not appropriate .
As our main goal is to highlight limitations in current practices, we
needed to evaluate a robust yet usable system based on a strong
feature set. To this end, we implemented 144 state of the art
features [33,8,25,14] and
evaluated each based on a quality metric (Q) defined as follows. For
each feature f, we compute the proportion of times that f
was missed by legitimate users in our study, denoted rf, and the proportion of
times that f was missed by forgers from round II (with access
to dynamic information), denoted af. Then, Q(f) = (af - rf + 1)/2, and the range
of Q is [0,1]. Intuitively, features with a quality score of 0
are completely useless-i.e., they are never reliably
reproduced by original users and are always reproduced by
forgers. On the other hand, features with scores closer to 1 are
highly desirable when implementing biometric authentication systems.
For our evaluation, we divided our feature set into two groups
covering the temporal and spatial features, and ordered each according
to the quality score. We then chose the top 40 from each group,
and disregarded any with a FRR greater than 10%. Finally, we
discounted any features that could be inferred from others (e.g.,
given the width and height of a passphrase as rendered by a user, then
a feature representing the ratio between width and height is
redundant). This analysis resulted in what we deem the 36 best features-15 spatial and 21 temporal-described in Appendix A.
5 Human Evaluation
This section presents the results for the five evaluation metrics that use forgeries generated by humans. Before we computed the FRR and the FAR, we removed the outliers that are inherent to biometric systems. For each user, we removed all samples that had more than d = 3 features that fell outside k = 2 standard deviations from that user's mean feature value. The parameters d and k were empirically derived. We also did not include any samples from users (the so-called "Goats" [3]) who had more than 25% of their samples classified as outliers. Such users "Failed to Enroll" [17]; the FTE rate was ~ 8.7%. After combining this with outlier removal, we still had access to 79.2% of the original data set.
To compute the FRR and the FAR we use the system described in §4.2 using the features from §4.3. The FRR is computed as follows: we repeatedly randomly partition a user's samples into two groups and use the first group to build a template and authenticate the samples in the second group against the template. To compute the FAR we use all of the user's samples to generate a template and then authenticate the forgeries against this template.
5.1 Grooming Sheep into Wolves
Our experiments were designed to illustrate the discrepancy in perceived security when considering traditional forgery paradigms and a more stringent, but realistic, security model. In particular, we assume that at the very minimum, that a realistic adversary (1) attacks victims who have a writing style that the forger has a natural ability to replicate, (2) has knowledge of how biometric authentication systems operate, and (3) has a vested interest in accessing the system, and therefore is willing to devote significant effort towards these ends.
Figure 1 presents ROC curves for forgeries from
impersonators with varying levels of knowledge. The plot denoted
FAR-naïve depicts results for the traditional case of naïve forgeries widely used in the literature [13,29,11]. In these
cases, the impersonation attempts simply reflect taking one user's
natural rendering of phrase p as an impersonation attempt on the target
writing p. Therefore, in addition to ignoring the target writer's attributes as is naturally expected of forgers, this classification makes no differentiation
based on the forger's or the victim's style of writing, and so may include, for
example, block writers "forging" cursive writers. Arguably, such
forgeries may not do as well as the less standard (but more
reasonable) naïve* classification (FAR-naïve*) where one only
attempts to authenticate samples from writers of similar styles.
 Figure 1: Overall ROC curves for naïve, naïve*,
static, dynamic, and trained forgers.
Figure 1: Overall ROC curves for naïve, naïve*,
static, dynamic, and trained forgers.
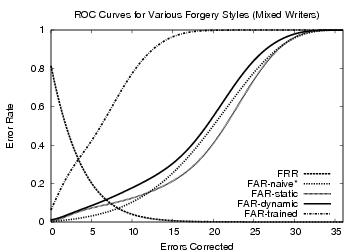 Figure 2: ROC curves against all mixed writers. This grouping
appeared the easiest to forge by the users in our
study.
The FAR-static plots represent the success rate of forgers who receive
access to only a static rendering of the passphrase. By contrast,
FAR-dynamic forgeries are produced after seeing (possibly many)
real-time renderings of the image. One can easily consider this a
realistic threat if we assume that a motivated adversary may capture
the writing on camera, or more likely, may have access to data written
electronically in another context. Lastly, FAR-trained presents the
resulting success rate of forgeries derived under our forgery model
which captures a more worthy opponent. Notice that
when classified by writing style, the trained forgers were very
successful against mixed writers (Figure 2).
Intuitively, one would expect that forgers with access to dynamic
and/or static representations of the target writing should be able to
produce better forgeries than those produced under the naïve*
classification. This is
not necessarily the case, as we see in
Figure 1 that at some points, the naïve*
forgeries do better than the forgeries generated by forgers who have access to static
and/or dynamic information. This is primarily due to the fact that the
naïve* classification reflects users' normal writing (as there is
really no forgery attempt here). The natural tendencies exhibited in
their writings appear to produce better "forgeries" than that of
static or dynamic forgers (beyond some point), who may suffer from
unnatural writing characteristics as a result of focusing on the
act of forging.
One of the most striking results depicted in the figures is the
significant discrepancy in the FAR between standard
evaluation methodologies and that of the
trained forgeries captured under our strengthened model. While it
is tempting to directly compare the results under the new model to
those under the more traditional metrics (i.e., by contrasting the
FAR-trained error rate at the EER under one of the older models),
such a comparison is not valid. This is because the forgers
under the new model were more knowledgeable with respect to the
intricacies of handwriting verification and had performed style-targeted forgeries.
However, the correct comparison considers the EERs under the two
models. For instance, the EER for this system under FAR-trained
forgeries is approximately 20.6% at four error corrections.
However, for the more traditional metrics, one would arrive at EERs of
7.9%, 6.0%, 5.5% under evaluations of dynamic, static and naïve
forgeries, respectively. These results are indeed
inline with the current state of the art [13,29,11]. Even worse, under
the most widely used form of adversary considered in the literature
(i.e., naïve) we see that the security of this system would be
over-estimated by nearly 375%!
Figure 2: ROC curves against all mixed writers. This grouping
appeared the easiest to forge by the users in our
study.
The FAR-static plots represent the success rate of forgers who receive
access to only a static rendering of the passphrase. By contrast,
FAR-dynamic forgeries are produced after seeing (possibly many)
real-time renderings of the image. One can easily consider this a
realistic threat if we assume that a motivated adversary may capture
the writing on camera, or more likely, may have access to data written
electronically in another context. Lastly, FAR-trained presents the
resulting success rate of forgeries derived under our forgery model
which captures a more worthy opponent. Notice that
when classified by writing style, the trained forgers were very
successful against mixed writers (Figure 2).
Intuitively, one would expect that forgers with access to dynamic
and/or static representations of the target writing should be able to
produce better forgeries than those produced under the naïve*
classification. This is
not necessarily the case, as we see in
Figure 1 that at some points, the naïve*
forgeries do better than the forgeries generated by forgers who have access to static
and/or dynamic information. This is primarily due to the fact that the
naïve* classification reflects users' normal writing (as there is
really no forgery attempt here). The natural tendencies exhibited in
their writings appear to produce better "forgeries" than that of
static or dynamic forgers (beyond some point), who may suffer from
unnatural writing characteristics as a result of focusing on the
act of forging.
One of the most striking results depicted in the figures is the
significant discrepancy in the FAR between standard
evaluation methodologies and that of the
trained forgeries captured under our strengthened model. While it
is tempting to directly compare the results under the new model to
those under the more traditional metrics (i.e., by contrasting the
FAR-trained error rate at the EER under one of the older models),
such a comparison is not valid. This is because the forgers
under the new model were more knowledgeable with respect to the
intricacies of handwriting verification and had performed style-targeted forgeries.
However, the correct comparison considers the EERs under the two
models. For instance, the EER for this system under FAR-trained
forgeries is approximately 20.6% at four error corrections.
However, for the more traditional metrics, one would arrive at EERs of
7.9%, 6.0%, 5.5% under evaluations of dynamic, static and naïve
forgeries, respectively. These results are indeed
inline with the current state of the art [13,29,11]. Even worse, under
the most widely used form of adversary considered in the literature
(i.e., naïve) we see that the security of this system would be
over-estimated by nearly 375%!
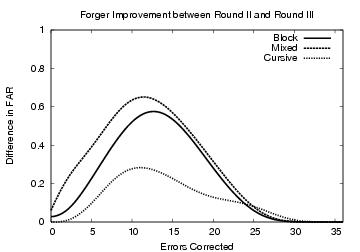 Figure 3: Forger improvement between rounds II and III.
Forger Improvement
Figure 3 should provide assurance that the
increase in forgery quality is not simply a function of selecting
naturally skilled individuals from round II to participate in round
III. The graph shows the improvement in FAR between
rounds II and III for the trained forgers. We
see that the improvement is significant, especially for the forgers who
focused on mixed and block writers. Notice that at the EER (at seven errors) induced
by forgers with access to dynamic information
(Figure 1), our trained mixed, block, and cursive forgers improved their FAR by 0.47, 0.34, and 0.18,
respectively. This improvement results from less than two hours of
training and effort, which is likely much less than what would be
exerted by a dedicated or truly skilled forger.
The observant reader will note that the trained
forgers faced a different distribution of "easy" targets in Round
III then they did in Round II. We did this to
analyze the system at its weakest link. However, after normalizing the results so that both rounds had the same makeup of
"easy" targets, the change in EER is statistically insignificant, shifting from 20.6% to 20.0% at four errors corrected.
Figure 3: Forger improvement between rounds II and III.
Forger Improvement
Figure 3 should provide assurance that the
increase in forgery quality is not simply a function of selecting
naturally skilled individuals from round II to participate in round
III. The graph shows the improvement in FAR between
rounds II and III for the trained forgers. We
see that the improvement is significant, especially for the forgers who
focused on mixed and block writers. Notice that at the EER (at seven errors) induced
by forgers with access to dynamic information
(Figure 1), our trained mixed, block, and cursive forgers improved their FAR by 0.47, 0.34, and 0.18,
respectively. This improvement results from less than two hours of
training and effort, which is likely much less than what would be
exerted by a dedicated or truly skilled forger.
The observant reader will note that the trained
forgers faced a different distribution of "easy" targets in Round
III then they did in Round II. We did this to
analyze the system at its weakest link. However, after normalizing the results so that both rounds had the same makeup of
"easy" targets, the change in EER is statistically insignificant, shifting from 20.6% to 20.0% at four errors corrected.
6 Generative Evaluation
Unfortunately, finding and training "skilled" forgers is a time
(and resource) consuming endeavor. To confront the obstacles posed by
wide-scale data collection and training of good impersonators, we
decided to explore the use of an automated approach using generative
models as a supplementary technique for evaluating behavioral
biometrics. We investigated whether an automated approach, using
limited writing samples from the target, could match the false accept
rates observed for our trained forgers in §5.1. We believe that such generative attacks themselves may be a far more
dangerous threat that, until now, have yet to be studied in sufficient
detail.
For the remaining discussion we explore a set of threats that stem
from generative attacks which assume knowledge that spans the
following spectrum:
- General population statistics: Gleaned, for example, via
the open sharing of test data sets by the research community, or by
recruiting colleagues to provide writing samples.
- Statistics specific to a demographic of the targeted user:
In the case of handwriting, we assume the
attacker can extract statistics from a corpus collected from other
users of a similar writing style (e.g., cursive).
- Data gathered from the targeted user: Excluding direct
capture of the secret itself, one can imagine the attacker capturing
copies of a user's handwriting, either through discarded documents
or by stealing a PDA.
To make this approach feasible, we also explore the impact of these
varying threats. A key issue that we consider is the amount of
recordings one needs to make these scenarios viable attack vectors. As
we show later, the amount of data required may be surprisingly small
for the case of authentication systems based on handwriting dynamics.
6.1 A generative toolkit for performance testing
The approach to synthesizing handwriting we explore here is to
assemble a collection of basic units (n-grams) that can be combined
in a concatenative fashion to mimic authentic handwriting. In this case, we do not make use of an underlying model of human physiology, rather, creation of the writing sample is accomplished by
choosing appropriate n-grams from an inventory that may cover
writing from the target user (scenario III above) as well as
representative writings by other members of the population at large
(scenarios I and II). The technique we apply here expands upon earlier
rudimentary work [16], and is similar in flavor to approaches
taken to generate synthesized speech [21] and for
text-to-handwriting conversion [9].
As noted earlier, each writing sample consists of three signals
parameterized by time: x(t), y(t) and p(t). The goal of our generative algorithm is to
generate t, x(t), y(t) and p(t) such that the sample is not
only accepted as authentic, but relies on acquiring a minimal amount of information from the target user (again, in a different
security context). In particular, when attacking user u, we assume the adversary has access
to a generative corpus Gu, in addition to samples from users of similar writing styles
GS; where S is one of "block", "mixed", or
"cursive". We assume that both Gu and GS are annotated so that there is a bijective map between the characters of each phrase and the portion of the signal that represents each character. As is the case with traditional computations of the
EER we also assume that passphrase p is known.
General Knowledge
Assume that the adversary wishes to forge user u with passphrase p
and writing style S. Ideally, she would like to do so using a
minimal amount of information directly collected from u.
Fortunately, the success of the naïve* forgeries from §5 suggests that a
user's writing style yields a fair amount of pertinent information
that can potentially be used to replicate that user's writing. Thus,
to aid in generating accurate forgeries, the adversary can make use of
several statistics computed from annotated writing samples in
GS \Gu. In what follows, we discuss what turn
out to be some very useful measures that can likely be easily
generalized for other behavioral biometrics.
Denote as Pc(i,j,c1,c2) the probability that writers of style S connect the ith stroke of c1 to c2, given that c1 is comprised of j strokes. Let Pc(i,j,c1,*) be the probability
that these writers connect the ith stroke of c1 (again rendered with j strokes) to any adjacent letter. For example, many cursive writers will connect the first stroke of the letter `i' to proceeding letters; for such writers Pc(1,2,i,*) ~ 1. Note that in this case, the dot of the `i' will be rendered after proceeding letters, we call this a "delayed" stroke.
Let dw(c1,c2) denote the median gap between the adjacent
characters c1 and c2 (i.e., the distance between the maximum value of x(t) for c1 and the minimum value of x(t) for c2), dw(c1,*) the median gap
between c1 and any proceeding character, and dw(*) the
median gap between any two adjacent characters. Intuitively,
dw(c1,c2) < 0 if users tend to overlap characters. Similarly,
let dt(c1,c2) denote the median time elapsed between the end
of c1 and the beginning of c2. Definitions of dt(c1,*)
and dt(*) are analogous to those for dw.
Finally, the generative algorithm clearly must also make use of a
user's pen-up velocity. This can be estimated from the population by
computing the pen-up velocity for each element in GS and
using the 75th percentile of these velocities. We denote
this value as vS.
Having acquired her generalized knowledge, the adversary can now select and
combine her choices of n-grams that will be used for
concatenative-synthesis in the following manner:
n-gram Selection
At a high level, the selection of n-grams that allow for a
concatenative-style rendering of p involves a search of
Gu for possible candidates. Let Gu,p be a set of u's
renderings of various n-grams in p. There may be more than one element in Gu,p for each
n-gram in p. The attacker selects k renderings g1, ..., gk
from Gu,p such that g1 || g2 || ... || gk = p. Our selection algorithm is randomized, but biased towards longer n-grams. However, the average length of each n-gram is small as shorter n-grams are required to "fill the gap" between larger n-grams. To explore the feasibility of our generative algorithm we
ensure that gi and gi+1 do not originate from the same writing
sample, but an actual adversary might benefit from using n-grams from the same writing sample.
n-gram Combination
Given the selection of n-grams (g1, ..., gk) the
attacker's task is to combine them to form a good representation of
p. Namely, she must adjust the signals that compose each gi
(tgi, x(tgi), y(tgi) and
p(tgi)) to create a final set of signals that
authenticates to the system. The algorithm is quite simple. At a
high level, it proceeds as follows: The adversary normalizes the
signals tgi, x(tgi) and y(tgi) by
subtracting the respective minimum values from each element in the
signal. The y(tgi) are shifted so that the baselines of the writing
match across gi. To finalize the spatial transforms, the adversary
horizontally shifts each x(tgi) by
|
dx,i = dx,i-1 + |
max
| (x(tgi-1)) + dw(ei-1,si) |
|
where ei (resp. si) is the last (resp. first)
character in gi and dx,1 = 0. Once the adversary has
fixed the (x,y) coordinates, she needs to fabricate t and p(t)
signals to complete the forgery. Modifying p(t) consists of
deciding whether or not to connect adjacent n-grams. To do this, the adversary uses knowledge
derived from the population. If ei-1 is rendered with j' strokes, and gi starts with si, the adversary connects the jth stroke of ei-1 to si with
probability Pc(j,j',ei-1,si). To generate a more realistic connection, the adversary smoothes the last points of ei-1 and the first points of si. Additionally, all strokes that occur after stroke j are "pushed" onto a stack, which is emptied on the next generated pen-up. This behavior simulates a true cursive writer returning to dot `i's and cross `t's at the end of a word, processing characters closest to the
end of the word first.
Adjusting the t signal is also straightforward. Let T be the time in tgi-1 that the last non-delayed stroke in ei-1 ends. If there are no delayed strokes in ei-1, T = max( tgi-1). Then, the adversary can simply shift tgi, i > 1 by
|
dt,i = dt,i-1 + T + dt(ei-1,si) |
|
and dt,1 = 0.
The only other time shift occurs when delayed strokes are
popped from the stack.
We can make use of global knowledge to estimate the time
delay by using vS and the distance between the end of the previous
stroke and the new stroke. Note that it is beneficial to take vS as the
75th percentile instead of the median velocity because,
for cursive writers in particular, the majority of pen-up velocities
is dominated by the time between words. However, these velocities are
intuitively slower as the writer is now thinking about creating a new
word as opposed to finishing a word that already exists.
If the adversary does not
have access to the statistical measure dw(ei-1,si), she
can first base her estimate of inter-character spacing on
dw(ei-1,*), and then on dw(*). She proceeds similarly
for the measures dt and Pc.
6.2 Results
To evaluate this concatenative approach we analyzed the quality of
the generated forgeries on user u writing passphrase p. However,
rather than using all 65 of the available samples from the generative
corpus, we instead choose 15 samples at random from
Gu,p - with the one restriction being that there must exist at
least one instance of each character in p among the 15
samples. Recall that this generative corpus contains writing
samples from u, but does not include p. The attacker's choice of n-grams g1,..., gk are selected from this restricted set.
Additionally, we limit GS to contain only 15 randomly selected
samples from each user with a similar writing style as u. Denote this set of writings as G'S. We purposefully chose to use small (and arguably, easily obtainable)
data sets to illustrate the power of this concatenative attack. Our
"general knowledge" statistics are computed from G'S. Example forgeries derived by this process are shown in
Figure 4.
Figure 4: Example generative forgeries against block, mixed and cursive
forgers. For each box, the second rendering is a trained human-generated
forgery of the first, and the third was created by our generative
algorithm.
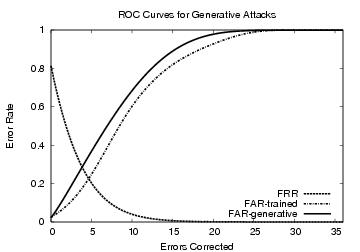 Figure 5: ROC curves for generative forgeries. Even with access to only limited information, the algorithm out-performs our
trained forgers, shifting the EER from 20.6% at four errors
to 27.4% at three errors.
We generated up to 25
forgery attempts for each user u and phrase p and used each as an
attempt to authenticate to the biometric template corresponding
to u under p. Figure 5
depicts the average FAR across all forgery attempts. As a baseline
for comparison, we replot the FRR and the FAR-trained plots from
§5. The FAR-generative plot shows the results of
the generative algorithm against the entire population. Observe that
under these forgeries there is an EER of 27.4% at
three error correction compared to an EER of 20.6% at four error
corrections when considering our trained forgers.
We note that on average each generative attempt only used information
from 6.67 of the target user's writing samples. Moreover, the
average length of an n-gram was 1.64 characters (and was never greater
than 4).
More importantly, as we make no attempt to filter the
output of the generative algorithm by rank-ordering the best
forgeries, the results could be much improved.
That said, we believe
that given the limited information assumed here, the results of this
generative attack on the security of the system warrant serious consideration.
Furthermore, we believe that this attack is feasible because annotation of the samples in Gu,p, while tedious, poses only a minor barrier to any determined adversary. For instance, in our case annotation
was accomplished with the aide of an annotation tool that we implemented
which is fairly automated, especially for block handwriting: taking
~ 30 sec. to annotate block phrases and ~ 1.5 min. for cursive phrases.
Figure 5: ROC curves for generative forgeries. Even with access to only limited information, the algorithm out-performs our
trained forgers, shifting the EER from 20.6% at four errors
to 27.4% at three errors.
We generated up to 25
forgery attempts for each user u and phrase p and used each as an
attempt to authenticate to the biometric template corresponding
to u under p. Figure 5
depicts the average FAR across all forgery attempts. As a baseline
for comparison, we replot the FRR and the FAR-trained plots from
§5. The FAR-generative plot shows the results of
the generative algorithm against the entire population. Observe that
under these forgeries there is an EER of 27.4% at
three error correction compared to an EER of 20.6% at four error
corrections when considering our trained forgers.
We note that on average each generative attempt only used information
from 6.67 of the target user's writing samples. Moreover, the
average length of an n-gram was 1.64 characters (and was never greater
than 4).
More importantly, as we make no attempt to filter the
output of the generative algorithm by rank-ordering the best
forgeries, the results could be much improved.
That said, we believe
that given the limited information assumed here, the results of this
generative attack on the security of the system warrant serious consideration.
Furthermore, we believe that this attack is feasible because annotation of the samples in Gu,p, while tedious, poses only a minor barrier to any determined adversary. For instance, in our case annotation
was accomplished with the aide of an annotation tool that we implemented
which is fairly automated, especially for block handwriting: taking
~ 30 sec. to annotate block phrases and ~ 1.5 min. for cursive phrases.
7 Other Related Work
There is, of course, a vast body of past work on the topic of
signature verification (see [27] for a comprehensive if
somewhat dated survey, [11] for a more up-to-date look at the
field). However, to the best of our knowledge, there is
relatively little work that encompass our goals and attack models
described herein.
Perhaps the work closest to ours, although it predominately involves
signatures, is that by Vielhauer and Steinmetz [33]. They use
50 features extracted from a handwriting sample to construct a
biometric hash. While they performed some preliminary testing on
PIN's and passphrases, the bulk of their study is on signatures, where
they evaluated features based on intrapersonal deviation,
interpersonal entropy with respect to their hash function, and the
correlation between these two values. That work however does not
report any results for meaningful attempts at forgery (i.e, other than
naïve attacks).
Also germane are a series of recent papers that have started to
examine the use of dynamic handwriting for the generation of
cryptographic keys. Kuan, et al. present a
method based on block-cipher principles to yield cryptographic keys
from signatures [12]. They test their algorithm on the
standard data set from the First International Signature
Verification Competition and report EERs between 6% and
14% if the forger has access to a stolen token. The production of
skilled forgeries in the SVC data set [37] resembles part
of the methodology used in round II of our studies and so does not account
for motivation, training, or talent.
In the realm of signature verification we also note work on an attack
based on hill-climbing, but that makes the assumption that the system
reveals how close of a match the input is [36]. We believe this
to be clearly unrealistic, and our attack models are chosen to be more
pragmatic than this.
Finally, there have been a handful of works on using generative models
to attack biometric authentication. However, we note there exists
significant disagreement in the literature concerning the potential
effectiveness of similar (but inherently simpler) attacks on speaker
verification systems (e.g., [26,21]). Lindberg and
Blomberg, for example, determined that synthesized passphrases were
not effective in their small-scale experiments [15], whereas
Masuko et al. found that their system was easily
defeated [20].
8 Conclusions
Several fundamental computer security mechanisms rest on the ability
of an intended user to generate an input that an attacker is unable to
reproduce. In the biometric community, the security of
biometric-based technologies hinges on this perceived inability of the
attacker to reproduce the target user's input. In particular, the
evaluation of biometric technologies is usually conducted under fairly
weak adversarial conditions. Unfortunately, this practice may
significantly underestimate the real risk of accepting forgeries as
authentic. To directly address this limitation we present an automated
technique for producing generative forgeries that assists in the
evaluation of biometric systems. We show that our generative approach
matches or exceeds the effectiveness of forgeries rendered by trained
humans in our study.
Our hope is that this work will serve as a solid foundation for the
work of other researchers and practitioners, particularly as it
pertains to evaluating biometric authentication or key-generation
systems. Admittedly, such evaluations are difficult to undertake due
to the reliance of recruiting large numbers of human subjects. In
that regard, the generative approach presented herein should reduce
the difficulty of this task and allow for more rigorous evaluations as
it pertains to biometric security.
Additionally, there is much future work related to the topics
presented here. For instance, although the forgeries generated by our
trained forgers were alarmingly successful, it remains unclear as
to the extent to which these forgeries would fool human judges,
including for example, forensic document examiners. Exploring this
question is one of our short term goals. Lastly, there are several
directions for incorporating more sophisticated generative algorithms
into our evaluation paradigm. We hope to explore these in the coming
months.
Acknowledgments
The authors would like to thank Dishant Patel and Carolyn Buckley for
their help in our data collection efforts. We especially thank the many people who devoted hours to providing
us with handwriting samples. We thank the anonymous reviewers, and in particular, our shepherd Tara Whalen, who provided helpful suggestions for improving this paper. We also thank Michael K. Reiter for insightful discussions during the course of this research. This work is supported by NSF grant
CNS-0430338.
References
- [1]
-
The biometrics consortium.
https://www.biometrics.org/.
- [2]
-
Y.-J. Chang, W. Zhung, and T. Chen.
Biometrics-based cryptographic key generation.
In Proceedings of the International Conference on Multimedia and
Expo, volume 3, pages 2203-2206, 2004.
- [3]
-
G. R. Doddington, W. Liggett, A. F. Martin, M. Przybocki, and D. A. Reynolds.
Sheep, goats, lambs and wolves: A statistical analysis of speaker
performance in the NIST 1998 speaker recognition evaluation.
In Proceedings of the Fifth International Conference on Spoken
Language Processing, November 1998.
- [4]
-
Y. Dodis, L. Reyzin, and A. Smith.
Fuzzy extractors: How to generate strong keys from biometrics and
other noisy data.
In Advances in Cryptology-EUROCRYPT 2004, pages 523-540,
2004.
- [5]
-
S. J. Elliott.
Development of a biometric testing protocol for dynamic signature
verification.
In Proceedings of the International Conference on Automation,
Robotics, and Computer Vision, pages 782-787, Singapore, 2002.
- [6]
-
M. C. Fairhurst.
Signature verification revisited: promoting practical exploitation of
biometric technology.
Electronics & Communication Engineering Journal, pages
273-280, December 1997.
- [7]
-
A. Goh and D. C. L. Ngo.
Computation of cryptographic keys from face biometrics.
In Proceedings of Communications and Multimedia Security, pages
1-13, 2003.
- [8]
-
R. M. Guest.
The repeatability of signatures.
In Proceedings of the Ninth International Workshop on Frontiers
in Handwriting Recognition, pages 492-497, October 2004.
- [9]
-
I. Guyon.
Handwriting synthesis from handwritten glyphs.
In Proceedings of the Fifth International Workshop on Frontiers
of Handwriting Recognition, pages 140-153, Colchester, England, 1996.
- [10]
-
C. Hertel and H. Bunke.
A set of novel features for writer identification.
In Proceedings of the International Conference on Audio- and
Video-based Biometric Person Authentication, pages 679-687. Guilford, UK,
2003.
- [11]
-
A. K. Jain, F. D. Griess, and S. D. Connell.
On-line signature verification.
Pattern Recognition, 35(12):2963-2972, 2002.
- [12]
-
Y. W. Kuan, A. Goh, D. Ngo, and A. Teoh.
Cryptographic keys from dynamic hand-signatures with biometric
security preservation and replaceability.
In Proceedings of the Fourth IEEE Workshop on Automatic
Identification Advanced Technologies, pages 27-32, Los Alamitos, CA, 2005.
IEEE Computer Society.
- [13]
-
F. Leclerc and R. Plamondon.
Automatic signature verification: the state of the art 1989-1993.
International Journal of Pattern Recognition and Artificial
Intelligence, 8(3):643-660, 1994.
- [14]
-
L. Lee, T. Berger, and E. Aviczer.
Reliable on-line human signature verification systems.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
18(6):643-647, June 1996.
- [15]
-
J. Lindberg and M. Blomberg.
Vulnerability in speaker verification - a study of technical
impostor techniques.
In Proceedings of the European Conference on Speech
Communication and Technology, volume 3, pages 1211-1214, Budapest, Hungary,
September 1999.
- [16]
-
D. P. Lopresti and J. D. Raim.
The effectiveness of generative attacks on an online handwriting
biometric.
In Proceedings of the International Conference on Audio- and
Video-based Biometric Person Authentication, pages 1090-1099. Hilton Rye
Town, NY, USA, 2005.
- [17]
-
A. J. Mansfield and J. L. Wayman.
Best practices in testing and reporting performance of biometric
devices.
Technical Report NPL Report CMSC 14/02, Centre for Mathematics and
Scientific Computing, National Physical Laboratory, August 2002.
- [18]
-
U.-V. Marti, R. Messerli, and H. Bunke.
Writer identification using text line based features.
In Proceedings of the Sixth International Conference on Document
Analysis and Recognition, pages 101-105, September 2001.
- [19]
-
T. Masuko, T. Hitotsumatsu, K. Tokuda, and T. Kobayashi.
On the security of hmm-based speaker verification systems against
imposture using synthetic speech.
In Proceedings of the European Conference on Speech
Communication and Technology, volume 3, pages 1223-1226, Budapest, Hungary,
September 1999.
- [20]
-
T. Masuko, K. Tokuda, and T. Kobayashi.
Imposture using synthetic speech against speaker verification based
on spectrum and pitch.
In Proceedings of the International Conference on Spoken
Language Processing, volume 3, pages 302-305, Beijing, China, October 2000.
- [21]
-
F. Monrose, M. Reiter, Q. Li, D. Lopresti, and C. Shih.
Towards speech-generated cryptographic keys on resource-constrained
devices.
In Proceedings of the Eleventh USENIX Security Symposium, pages
283-296, 2002.
- [22]
-
F. Monrose, M. K. Reiter, Q. Li, and S. Wetzel.
Cryptographic key generation from voice (extended abstract).
In Proceeedings of the 2001 IEEE Symposium on Security and
Privacy, pages 12-25, May 2001.
- [23]
-
F. Monrose, M. K. Reiter, and S. Wetzel.
Password hardening based on keystroke dynamics.
International Journal of Information Security, 1(2):69-83,
February 2002.
- [24]
-
I. Nakanishi, H. Sakamoto, Y. Itoh, and Y. Fukui.
Optimal user weighting fusion in DWT domain on-line signature
verification.
In Proceedings of the International Conference on Audio- and
Video-based Biometric Person Authentication, pages 758-766. Hilton Rye
Town, NY, USA, 2005.
- [25]
-
W. Nelson and E. Kishon.
Use of dynamic features for signature verification.
In Proceedings of the IEEE International Conference on Systems,
Man, and Cybernetics, pages 1504-1510, October 1991.
- [26]
-
B. L. Pellom and J. H. L. Hansen.
An experimental study of speaker verification sensitivity to computer
voice altered imposters.
In Proceedings of the 1999 International Conference on
Acoustics, Speech, and Signal Processing, March 1999.
- [27]
-
R. Plamondon, editor.
Progress in Automatic Signature Verification.
World Scientific, 1994.
- [28]
-
R. Plamondon and G. Lorette.
Automatic signature verification and writer identification - the
state of the art.
volume 22, pages 107-131, 1989.
- [29]
-
R. Plamondon and S. N. Srihari.
On-line and off-line handwriting recognition: a comprehensive survey.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
22(1):63-84, 2000.
- [30]
-
C. Soutar, D. Roberge, A. Stoianov, R. Gilroy, and B. V. Kumar.
Biometric encryption using image processing.
In Optical Security and Counterfeit Deterrence Techniques II,
volume 3314, pages 178-188. IS&T/SPIE, 1998.
- [31]
-
U. Uludag and A. K. Jain.
Fingerprint minutiae attack system.
In The Biometric Consortium Conference, September 2004.
- [32]
-
U. Uludag, S. Pankanti, S. Prabhakar, and A. K. Jain.
Biometric cryptosystems: Issues and challenges.
Proceedings of the IEEE: Special Issue on Multimedia Security of
Digital Rights Management, 92(6):948-960, 2004.
- [33]
-
C. Vielhauer and R. Steinmetz.
Handwriting: Feature correlation analysis for biometric hashes.
EURASIP Journal on Applied Signal Processing, 4:542-558, 2004.
- [34]
-
C. Vielhauer, R. Steinmetz, and A. Mayerhofer.
Biometric hash based on statistical features of online signatures.
In Proceedings of the Sixteenth International Conference on
Pattern Recognition, volume 1, pages 123-126, 2002.
- [35]
-
C. Vielhauer and F. Zöbisch.
A test tool to support brute-force online and offline signature
forgery tests on mobile devices.
In Proceedings of the International Conference on Multimedia and
Expo, volume 3, pages 225-228, 2003.
- [36]
-
Y. Yamazaki, A. Nakashima, K. Tasaka, and N. Komatsu.
A study on vulnerability in on-line writer verification system.
In Proceedings of the Eighth International Conference on
Document Analysis and Recognition, pages 640-644, Seoul, South Korea,
August-September 2005.
- [37]
-
D.-Y. Yeung, H. Chang, Y. Xiong, S. George, R. Kashi, T. Matsumoto, and
G. Rigoll.
SVC2004: First international signature verification competition.
In Proceedings of the International Conference on Biometric
Authentication (ICBA), Hong Kong, July 2004.
A Features
Using the quality metric, Q, as described in §4.3 we narrowed 144 state of the art features to the 36 most useful features (see Table 1). The 15 static features consisted of: the number of strokes used in rendering the phrase, the number of local horizontal and vertical extrema, and the integrated area to the left and below the writing [33]. Additional static features included the writing width and height, the total distance travelled by the pen on and off the tablet, the total area enclosed within writing loops, and the vertical centroid of these loops [8]. We also considered the distance between the upper (lower) baseline and the top (bottom) line [18], the median stroke-slant [18], and the distance between the last x (y) coordinate and the maximum x (y) coordinate [14]. Note that these final two features could be considered dynamic as one may not know which coordinate is the last one rendered without access to timing information.
The 21 dynamic features consisted of: The total time spent writing, the ratio of pen-up time to pen-down time, the median pen velocity, the number of times the pen ceases to move horizontally (vertically), and the total time spent moving to the left, right, up, and down [14]. Additional dynamic features included the time of occurrence of the following events: maximum pen velocity, maximum pen velocity in the horizontal (vertical) direction, minimum velocity in the horizontal (vertical) direction, and the maximum stroke slant [14]. Finally, we considered six invariant moments of the writing, which measure the number of samples, horizontal (vertical) mass, diagonality, and horizontal (vertical) divergence [8].
| Feature (f) | Description | Q(f) | |
| Spatial Features | |
| Pen-down distance | Total distance travelled by the pen-tip while touching the screen [8]. | 0.81 |
| Median q | Median stroke-slant, normalized to 0 < q < p [18]. | 0.71 |
| Vert. end dist. | Distance between the last y-coordinate and maximum y-coordinate [14]. | 0.67 |
| Y-Area | Integrated area beneath the writing [33]. | 0.65 |
| Writing width | Total width of the writing [33,8]. | 0.65 |
| Writing height | Total height of the writing [33,8]. | 0.65 |
| Pen-up distance | Euclidean distance between pen-up and pen-down events. | 0.64 |
| # of strokes | Number of strokes used to render the passphrase [33]. | 0.63 |
| # of extrema | Number of local extrema in the horizontal and vertical directions [33]. | 0.62 |
| Lower zone | Distance between baseline and bottomline of the writing [18]. | 0.62 |
| X-Area | Integrated area to the left of the writing [33]. | 0.62 |
| Loop y centroid | The average value of all y coordinates contained within writing loops [8]. | 0.62 |
| Loop area | Total area enclosed within loops generated by overlapping strokes [8]. | 0.61 |
| Upper zone | Distance between upper-baseline and topline of the writing [18]. | 0.61 |
| Horiz. end dist. | Distance between the last x-coordinate and maximum x-coordinate [14]. | 0.60 | |
| Temporal Features | |
| Time | Total time spent writing (measured in ms) [14]. | 0.87 |
| # of times vx = 0 | Number of times the pen ceases to move horizontally [14]. | 0.86 |
| # of times vy = 0 | Number of times the pen ceases to move vertically [14]. | 0.85 |
| Inv. Mom. 00 | åxåy f(x,y); f(x,y) = 1 if there is a point at (x,y) and 0 otherwise [8]. | 0.85 |
| Inv. Mom. 10 | åxåy f(x,y)·x. Measures the horizontal mass of the writing [8]. | 0.82 |
| Inv. Mom. 01 | åxåy f(x,y)·y. Measures the vertical mass of the writing [8]. | 0.79 |
| Inv. Mom. 11 | åxåy f(x,y)·xy. Measures diagonality of the writing sample [8]. | 0.78 |
| Time of max vx | Time of the maximum pen-velocity in the horizontal direction [14]. | 0.78 |
| Inv. Mom. 21 | åxåy f(x,y)·x2y. Measures vertical divergence [8]. | 0.76 |
| Inv. Mom. 12 | åxåy f(x,y)·xy2. Measures horizontal divergence [8]. | 0.75 |
| Median pen velocity | Median speed of the pen-tip [14]. | 0.74 |
| Duration vx > 0 | Total time the pen spends moving to the right [14]. | 0.73 |
| Duration vy > 0 | Total time the pen spends moving to the up [14]. | 0.73 |
| Time of max vel. | Time of the maximum pen-velocity [14]. | 0.72 |
| Pen up/down ratio | Ratio time spent with the pen off and on the tablet [14]. | 0.71 |
| Time of max q | Time of maximum stroke slant. | 0.70 |
| Duration vy < 0 | Total time the pen spends moving to the down [14]. | 0.70 |
| Duration vx < 0 | Total time the pen spends moving to the left [14]. | 0.69 |
| Time of min vx | Time of the minimum pen-velocity in the horizontal direction [14]. | 0.69 |
| Time of min vy | Time of the minimum pen-velocity in the vertical direction [14]. | 0.68 |
| Time of max vy | Time of the maximum pen-velocity in the vertical direction [14]. | 0.68 |
Table 1: The statistical features used to evaluate the biometric authentication system. Features were chosen based on the quality score Q defined in §4.3. q is the angle of a
given stroke, v, vx, vy are overall, horizontal, and vertical velocity, respectively.
|
