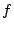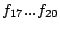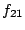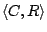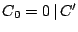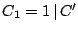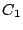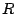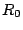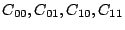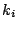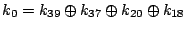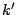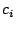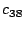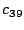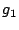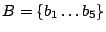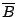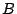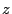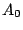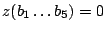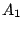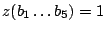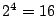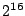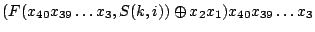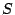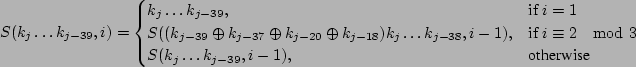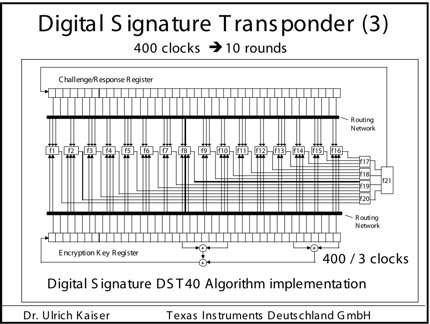
Security Analysis of a Cryptographically-Enabled

RFID Device

Stephen C. Bono - The Johns Hopkins University

Matthew Green - The Johns Hopkins University

Adam Stubblefield - The Johns Hopkins University

Ari Juels - RSA Laboratories

Aviel D. Rubin - The Johns Hopkins University

Michael Szydlo - RSA Laboratories

Abstract:

We describe our success in defeating the security of an RFID device known as a Digital Signature Transponder (DST). Manufactured by Texas Instruments, DST (and variant) devices help secure millions of SpeedPassTM payment transponders and automobile ignition keys.

Our analysis of the DST involved three phases:

    1     Reverse engineering: Starting from a rough published schematic, we determined the complete functional details of the cipher underpinning the challenge-response protocol in the DST. We accomplished this with only ``oracle'' or ``black-box'' access to an ordinary DST, that is, by experimental observation of responses output by the device.

    2     Key cracking: The key length for the DST is only 40 bits. With an array of of sixteen FPGAs operating in parallel, we can recover a DST key in under an hour using two responses to arbitrary challenges.

    3     Simulation: Given the key (and serial number) of a DST, we are able to simulate its RF output so as to spoof a reader. As validation of our results, we purchased gasoline at a service station and started an automobile using simulated DST devices.

We accomplished all of these steps using inexpensive off-the-shelf equipment, and with minimal RF expertise. This suggests that an attacker with modest resources can emulate a target DST after brief short-range scanning or long-range eavesdropping across several authentication sessions. We conclude that the cryptographic protection afforded by the DST device is relatively weak.

Key words: Digital Signature Transponder (DST), immobilizer, Hellman time-space tradeoff, RFID

Introduction

Radio-Frequency IDentification (RFID) is a general term for small, wireless devices that emit unique identifiers upon interrogation by RFID readers. Ambitious deployment plans by Wal-mart and other large organizations over the next couple of years have prompted intense commercial and scientific interest in RFID [23]. The form of RFID device likely to see the broadest use, particularly in commercial supply chains, is known as an EPC (Electronic Product Code) tag. This is the RFID device specified in the Class 1 Generation 2 standard recently ratified by a major industry consortium known as EPCglobal [9,19]. EPC tags are designed to be very inexpensive - and may soon be available for as little as five cents/unit in large quantities according to some projections [21,20]. They are sometimes viewed in effect as wireless barcodes: They aim to provide identification, but not digital authentication. Indeed, a basic EPC tag lacks sufficient circuitry to implement even symmetric-key cryptographic primitives [21].

The term RFID, however, denotes not just EPC tags, but a spectrum of wireless devices of varying capabilities. More sophisticated and expensive RFID devices can offer cryptographic functionality and therefore support authentication protocols. One of the most popular of such devices is known as a Digital Signature Transponder (DST). Manufactured by Texas Instruments, DSTs are deployed in several applications that are notable for wide-scale deployment and the high costs (financial and otherwise) of a large-scale security breach. These include:

    •     Vehicle Immobilizers: More than 150 million vehicle immobilizer keys shipped with many current automobiles, including e.g. 2005 model Fords [7], use Texas Instruments low-frequency RFID transponders. This number includes systems with fixed-code transponders that provide no cryptographic security, as well as newer models equipped with DSTs. Immobilizers deter vehicle theft by interrogating an RFID transponder embedded in the ignition key as a condition of enabling the fuel-injection system of the vehicle. The devices have been credited with significant reductions in auto theft rates, as much as 90% [1,8].

    •     Electronic Payment: DSTs are used in the ExxonMobil SpeedPassTM system, with more than seven million cryptographically-enabled keychain tags accepted at 10,000 locations worldwide [2].

A DST consists of a small microchip and antenna coil encapsulated in a plastic or glass capsule. It is a passive device, which is to say that it does not contain an on-board source of power, but rather receives its power via electromagnetic inductance from the interrogation signal transmitted by the reading device. This design choice allows for a compact design and long transponder life.

A DST contains a secret, 40-bit cryptographic key that is field-programmable via RF command. In its interaction with a reader, a DST emits a factory-set (24-bit) identifier, and then authenticates itself by engaging in a challenge-response protocol. The reader initiates the protocol by transmitting a 40-bit challenge. The DST encrypts this challenge under its key and, truncating the resulting ciphertext, returns a 24-bit response. It is thus the secrecy of the key that ultimately protects the DST against cloning and simulation.

In this paper, we describe our success in attacking the Texas Instruments DST system. We are able to recover the secret cryptographic key from a target DST device after harvesting just two challenge-response pairs. For arbitrary challenge-response pairs, we are able to recover a key in under an hour using an array of sixteen FPGAs. When the challenge-response pairs derive from pre-determined challenges, i.e., in a chosen-plaintext attack, a time-space trade-off is possible, reducing the cracking time to a matter of minutes. The full details of this chosen-response attack will appear in a future version of this work. Once we have recovered a key, we are able to use an inexpensive, commodity RF device to ``clone'' the target DST, that is, to simulate its radio output so as to convince a reader.

In consequence, we show how an attacker with modest resources -- just a few hundred dollars worth of commodity equipment and a PC -- can defeat the DST system. Such an attacker can succeed upon actively skimming a DST, that is, scanning it at short range for a fraction of a second. With additional use of an FPGA, an attacker can feasibly simulate a target DST after merely intercepting multiple authentication transcripts at longer range.

To validate our attack, we extracted the key from our own SpeedPassTM token and simulated it in an independent programmable RF device. We purchased gasoline successfully at an ExxonMobil station multiple times in the course of a single day using this digital simulator. Similarly, we recovered the cryptographic key from a DST in the ignition key of our 2005 model Ford Escape SUV. By simulating the DST, we spoofed the immobilizer authentication system and started the vehicle with a bare ignition key, that is, a copy of the metal portion of the key that possessed no DST. Viewed another way, we created the pre-conditions for hot-wiring the vehicle.

Our aim in demonstrating the vulnerability of the TI DST is twofold. First, we wish to reinforce the time-worn but oft neglected message that ``security through obscurity'' is generally ineffective in widely fielded cryptographic systems. Second, we wish to provide guidance to the data-security community in ascertaining the design requirements for secure RFID systems.

Our attack involved three phases:

    1     Reverse engineering: We obtained a rough published schematic of the block cipher underpinning the challenge-response protocol in the DST [14]. From this starting point, we determined the complete functional details of the cipher. We accomplished this with only ``oracle'' or ``black-box'' access to an ordinary DST, that is, by experimental observation of responses output by the device across selected programmed encryption keys and selected input challenges. This phase of the attack was the scientific heart of our endeavor, and involved the development of cryptanalytic techniques designed specially for the DST cipher.

    2     Key cracking: As mentioned above, the key length for the DST is only 40 bits. We assembled an array of sixteen FPGAs operating in parallel. With this system, we can recover a DST key in under an hour from two responses to arbitrary challenges. Additionally, we have constructed an FPGA for computing the well known time-space tradeoff of Hellman [12]. Although we pre-compute the underlying look-up tables using the FPGA (Field-Programmable Gate Array), we estimate that the resulting software will operate on an ordinary, unenhanced PC in under a minute. (With the aid of an FPGA at this stage, the cracking time can be reduced to seconds.) A full analysis of this system will appear in a future version of this work.

    3     Simulation: Given the key (and serial number) of a DST, we are able to simulate its RF output so as to spoof a reader. We perform the simulation in a software radio. Construction of this system required careful analysis of the RF output of the DST reader devices, which differed between SpeedPassTM readers and the automobile ignition system we examined.

Related work

The pre-eminent historical example of black-box reverse-engineering of a cipher was the reconstruction of the Japanese Foreign Office cipher Purple during the Second World War. Under the leadership of William F. Friedman, the United States Signals Intelligence Service performed the feat of duplicating the Purple enciphering machine without ever having physical access to one [13].

There are a number of well known contemporary examples of the reverse-engineering of proprietary cryptographic algorithms. For example, the RC4 cipher, formerly protected as a trade secret by RSA Data Security Inc., was publicly leaked in 1994 as the result of what was believed to be reverse-engineering of software implementations [4]. The A5/1 and A5/2 ciphers, employed for confidentiality in GSM phones, were likewise publicly disclosed as a result of reverse engineering. The exact method of reverse-engineering has not been disclosed, although the source was purportedly ``an actual GSM phone'' [6].

There are also numerous published fault-induction and side-channel attacks against hardware devices, e.g., [5]. These are related to our work, but involve rather different techniques, and generally aim to recover a key, rather than a cipher design.

In fact, we are unaware of any published black-box reverse-engineering of a contemporary cipher, whether the original source be a software or a hardware implementation. Having no literature to refer to, we developed techniques for our effort in an ad hoc manner. While our techniques are not easily generalizable, we hope that they will nonetheless aid future researchers at a conceptual level in similar endeavors.

In contrast, the key-recovery techniques we employed are well known. Our parallel FPGA key-recovery system operates on much the same principle, for example, as the well publicized Deep Crack machine that employed hardware-based key-space searching to recover DES keys [10,17].

As mentioned above, our system for key recovery in software using chosen-challenge pairs exploits the time-space tradeoff developed by Hellman. We also employ the ``distinguished point'' enhancement of Rivest. We have drawn on previous work by Quisquater et al. [18], who created a Hellman-based system for recovering keys from a variant of DES employing 40-bit keys.

We note that we have chosen in this document to reveal information about the DST cipher sufficient to elucidate our reverse-engineering and analysis techniques. We omit details about that would permit direct reconstruction of the cipher. Our goal is to offer our fullest possible contribution to the scientific community, but at the same time to avoid fomenting abuse of our results. Once the industry has had time to take adequate measures, we intend to divulge full cipher details in the interest of stimulating cryptanalytic research by the scientific community.

In general, the problem of achieving authentication in RFID devices - with and without full-blown cryptography - has seen a recent burgeoning in the data-security literature. An up-to-date bibliography may be found at [3].

Organization

 In section 2, we discuss the practical implications of our simulation attack against the DST. We then detail the three phases of our attack. In section 3, we discuss the techniques we employed in reverse-engineering the DST cipher. We describe our key-cracking system in section 4. In section 5, we recount the experimentation and analysis we performed to understand the DST protocol at the RF layer, as well as our simulation techniques. We conclude in section 6.

Practical Significance of Our Results

Our attack on the DST cipher by no means implies wholesale dismantling of the security of the SpeedPassTM network, nor easy theft of automobiles. The cryptographic challenge-response protocols of DST devices constitute only one of several layers of security in these systems. ExxonMobil informed us that the SpeedPassTM network has on-line fraud detection mechanisms loosely analogous to those employed for traditional credit-card transaction processing. Thus an attacker that simulates a target DST cannot do so with complete impunity; suspicious usage patterns may result in flagging and disabling of a SpeedPassTM device in the network. The most serious system-wide threat lies in the ability of an attacker to target and simulate multiple DSTs, as suggested in our example scenarios below.

In some sense, the threat to automobile immobilizers is more serious, as: (1) An automobile is effectively an off-line security system and (2) A single successful attack on an automobile immobilizer can result in full compromise of the vehicle. While compromise of a DST does not immediately permit theft of an automobile, it renders an automobile with an immobilizer as vulnerable to theft as an automobile without one. Such a rollback in automobile security has serious implications. As noted above, significant declines in automobile theft rates - up to 90% - have been attributed to immobilizers during their initial introduction. Even now, automobile theft is an enormous criminal industry, with 1,260,471 automobile thefts registered by the FBI in 2003 in the United States alone, for a total estimated loss of $8.6 billion [16].

Extracting the key from a DST device requires the harvesting of two challenge-response pairs. As a result, there are certain physical obstacles to successful attack. Nonetheless, bypassing the cryptographic protections in DST devices results in considerably elevated real-world threats. In this section we elaborate on the context and implications of our work.

Effective attack range

There are effectively two different methods by which an attacker may harvest signals from a target DST, and two different corresponding physical ranges.

The first mode of attack is active scanning: The attacker brings her own reader within scanning range of the target DST. DSTs of the type found in SpeedPassTM and automobile ignition keys are designed for short range scanning - on the order of a few centimeters. In practice, however, a longer range is achievable. In preliminary experiments, we have achieved an effective range of several inches for a DST on a keyring in the pocket of a simulated victim. A DST may respond to as many as eight queries per second. Thus, it is possible to perform the two scans requisite for our simulation attacks in as little as one-quarter of a second. At the limit of the range achievable by a given antenna, however, scanning becomes somewhat unreliable, and can require more time.

From the standpoint of an attacker, active scanning has the advantage of permitting a chosen-challenge attack. Hence this type of attack permits the use of pre-computed Hellman tables as touched on above. In principle, therefore, it would be possible for an attacker with appropriate engineering expertise to construct a completely self-contained cloning device about the size of an Apple iPod. When passed in close proximity to a target DST, this device would harvest two chosen-challenge transcripts, perform a lookup in an on-board set of pre-computed Hellman tables in the course of a minute or so, and then simulate the target DST. We estimate that the cost of constructing such a device would be on the order of several hundred dollars.

The second mode of attack is passive eavesdropping. Limitations on the effective range of active scanning stem from the requirement that a reader antenna furnish power to the target DST. An attacker might instead eavesdrop on the communication between a legitimate reader and a target DST during a valid authentication session. In this case, the attacker need not furnish power to the DST. The effective eavesdropping range then depends solely on the ability to intercept the signal emitted by the DST. We have not performed any experiments to determine the range at which this attack might be mounted. It is worth noting purported U.S. Department of Homeland Security reports, however, of successful eavesdropping of this kind on 13.56 Mhz tags at a distance of some tens of feet [24]. The DST, as we explain below, operates at 134 kHz. Signals at this considerably lower frequency penetrate obstacles more effectively, which may facilitate eavesdropping. On the other hand, larger antennas are required for effective signal interception.

Only careful experimentation will permit accurate assessment of the degree of these two threats. Our cursory experiments, however, suggest that the threats are well within the realm of practical execution.

Example attack scenarios

For further clarification of the implications of our work, we offer a few examples of possible DST exploits. We let Eve represent the malefactor in these scenarios.

Example 1 (Auto theft via eavesdropping) Eve runs an automobile theft ring. She owns a van with eavesdropping equipment. She parks this near a target automobile so as to eavesdrop on ignition-key-to-reader transmissions.4 After observing two turns of the ignition key, she is able to extract the cryptographic key of the DST at her leisure using an FPGA. She returns subsequently to steal the target automobile. To enter the vehicle, she picks or jimmies the door lock. She then hot-wires the ignition and deactivates the immobilizer by simulating the DST of the real key.

Example 2 (Auto theft via active attack) Eve runs an automobile theft ring. She suborns a valet at an expensive restaurant to scan the immobilizer keys of patrons while parking their cars, and to note their registration numbers. Based on these registration numbers, Eve looks up the addresses of her victims (such background checks being widely offered on the Internet). By simulating their DST devices, Eve is able to steal their automobiles from their homes.

Example 3 (SpeedPassTM theft via active attack) Eve carries a reader and short-range antenna with her onto a subway car. (Alternatively, Eve could carry a large ``package'' with a concealed antenna in some public place.) As she brushes up near other passengers, she harvests chosen challenge-response pairs (along with the serial numbers of target devices) from any SpeedPassTM tokens they may be carrying. Later, at her leisure, Eve recovers the associated cryptographic keys. She programs the keys into a software radio, which she uses to purchase gasoline. To allay suspicion, she takes care to simulate a compromised SpeedPassTM only once. Additionally, she hides the tag simulator itself under her clothing, interacting with the pump reader via an antenna passing through a sleeve up to an inactive SpeedPassTM casing.

Fixes

The most straightforward architectural fix to the problems we describe here is simple: The underlying cryptography should be based on a standard, publicly scrutinized algorithm with an adequate key length, e.g., the Advanced Encryption Standard (AES) in its 128-bit form, or more appropriately for this application, HMAC-SHA1 [15]. From a commercial standpoint, this approach may be problematic in two respects. First, the required circuitry would result in a substantially increased manufacturing cost, and might have other impacts on the overall system architecture due to increased power consumption. Second, there is the problem of backwards compatability. It would be expensive to replace all existing DST-based immobilizer keys. Indeed, given the long production cycles for automobiles, it might be difficult to introduce a new cipher into the immobilizers of a particular make of vehicle for a matter of years. On the other hand, it may be presumed from the Kaiser presentation [14] that Texas Instruments has plans to update their cipher designs in the DST. Additionally, TI has indicated to the authors that they have more secure RFID products available at present; in lieu of specifying these products, they have indicated the site www.ti-rfid.com for information.

In fact, RFID chips with somewhat longer key-lengths are already available in the marketplace and used in a range of automobile immobilizers. Philips offers two cryptographically enabled RFID chips for immobilizers [8]. The Philips HITAG 2, however, has a 48-bit secret key, and thus offers only marginally better resistance to a brute-force attack - certainly not a comfortable level for long-term security. The Philips SECT, in contrast, has a 128-bit key. The HITAG 2 algorithm is proprietary, while Philips data sheets do not appear to offer information about the cryptographic algorithm underpinning their SECT device. Thus, at present, we cannot say whether these algorithms are well designed.

Faraday shielding offers a short-term, partial remedy. In particular, users may encase their DSTs in aluminum foil or some suitable radio-reflective shielding when not using them. This would defend against active scanning attacks, but not against passive eavesdropping. Moreover, this approach is rather inconvenient, and would probably prove an unworkable imposition on most users. A different measure worth investigation is the placement of metal shielding in the form of a partial cylinder around the ignition-key slot in automobiles. This could have the effect of attenuating the effective eavesdropping range.

In the long-term, the best approach is, of course, the development of solid, well-modeled cryptographic protocols predicated on industry-standard algorithms, with key lengths suitable for long-term hardware deployment.

Reverse Engineering

We now present the details of our attack.

The 40-bit cipher underpinning the DST system is proprietary. We refer to this cipher, in accordance with the Texas Instruments documentation, as DST. The only substantive technical information we were able to locate on DST was a rough schematic available in a presentation by Dr. Ulrich Kaiser, which was published on the Internet [14], and in a published conference paper [11] co-authored by Dr. Kaiser with Texas Instruments employees. We show the schematic here in Figure 1. Although the general form and arrangement of functional components of the cipher are clear, critical details about the logic and interconnections of the components are lacking. Moreover, as we shall explain, certain features in the published schematic are inaccurate, in the sense that they do not correspond to the workings of the fielded versions of DST we have examined. To distinguish over the DST cipher employed in the implementations that we experimented with, we refer to the cipher adumbrated in Figure 1 as the Kaiser cipher.

Figure 1: Schematic of Kaiser Cipher.

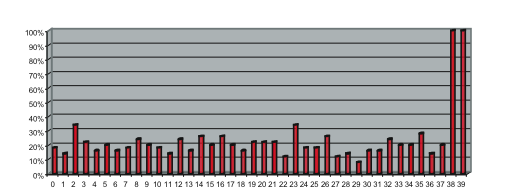
We considered several initial approaches to reverse-engineering DST. Software packages available from TI may include the DST cipher. These packages, however, include license agreements that prohibit reverse-engineering, so we did not make use of them. We might alternatively have attempted to probe a hardware implementation of DST-40. Lacking the resources for this approach and aiming, moreover, to explore the minimum resource requirements to attack the DST system successfully, we rejected this option. Instead, we chose to mount an ``oracle'' or ``black-box'' attack. This is to say that we chose to uncover the functional details of DST simply by examining the logical outputs of a DST device. As the keys of some DST devices are field-programmable, we were able to experiment with a set of chosen keys and inputs for DST. For our experiments, we purchased a TI Series 2000 - LF RFID Evaluation Kit; this kit contained a reader and antenna, as well as a variety of non-DST RFID devices. We were able to separately purchase small quantities of DST devices in two different form factors.

To explain our effort further, some nomenclature is in order. As the TI schematic of the Kaiser cipher suggests, DST is essentially a feedback shift register. In each round of operation, inputs from the challenge register and key register pass through a collection of logical units. These yield an output value that is fed back into the challenge register. We refer to the full collection of logical units operating in a single round, i.e., operating on a single set of inputs with no feedback, as . The function  comprises three logical layers.

The first layer, represented in the schematic by boxes , consists of a collection of sixteen functional units, each of which takes a small number of bits from the key register and a small number of bits from the challenge register and yields a one-bit output. We refer to these functional units as -boxes. Each -box takes either three key bits and two challenge bits or vice versa; two special -boxes take only two bits from each register as input.

The second layer, represented in the schematic by boxes , consists of four functional units, each of which takes as input the outputs of a set of four -boxes. We refer to each of these second-layer units as a -box.

Finally, the third layer consists of a single functional unit, labeled , into which feed the outputs of the -boxes. This last functional unit, which we refer to as the -box, yields the output of the full function .

There are two main technical lacunae in the TI schematic. Reverse-engineering DST required that we focus on these. In particular:

    1     The schematic does not describe the logical operations executed by the -boxes, the -boxes, and the -box.

    2     The mapping of key and challenge bits to the -boxes is governed by a routing array whose organization the TI schematic does not describe. In other words, there is no indication of which bits in the challenge and key registers are input to which -boxes.

In addition, as we shall explain, the TI schematic contains some inaccuracies, in the sense that the Kaiser cipher does not correspond exactly to DST as implemented in DST devices. Critically, the function  (and thus the -box) in DST actually outputs a pair of bits, and the clocking of the cipher is accordingly different. Moreover, two bits in the challenge register are XORed with the output of the -box.

Obtaining a single-round output

Because we did not know the contents of the -boxes, or other critical details such as the configuration of the routing networks in DST, we could not directly verify that production DSTs, such as those that we obtained for our experiments, implemented the Kaiser cipher of Figure 1. Instead we had to test and exploit structural features of the Kaiser cipher, using our evaluation DST as an oracle.

We first noted that the only round dependence of the Kaiser cipher is in the key scheduler. As seen in Figure 1, a key, i.e., string of `0' bits, will remain unchanged in the key register throughout the cipher execution. Using this key, it is possible to render each step of the algorithm independent of the round in which it takes place. We used the key for the experiments we now describe.

We next observed that each cycle, i.e., each execution of , results in only a small change to the state of the challenge register: The contents of the register are shifted right by one bit, and the output of the -box is inserted into the leftmost bit position. Consequently, for any given value submitted to the tag, the challenge register can assume only two possible values after one clock cycle, depending on whether the -box outputs a `0' or a `1' bit.

Using the DST as an oracle, we developed a test to recover the output of the -box for any value in the challenge/response register (which for brevity we henceforth refer to as the challenge register). Consider a given challenge/response pair . Upon input of  to the DST device, the challenge register initially contains the bits of . Let  denote the sequence of bits in  excluding the last bit, i.e., the first 39 bits in . Based on our observation above, after a single cycle, the challenge register in the DST contains one of two possible sequences, either  or , where  denotes concatenation. Therefore, recovering the output of the -box can be reduced to a determination of whether the challenge register assumes the value  or  after the first cycle.

Fortunately, access to the DST as a challenge/response oracle offers a simple way to make this determination. If  is truly the ``next-state'' value in the challenge register, then application of the full encryption process, i.e., the full 400 clock cycles on , will yield a result identical to the encryption of , but shifted one cycle ahead. The original response  will therefore appear in the challenge register exactly one clock cycle prior to the encryption finishing. Thus, the final result, which we call , will contain , but shifted right by one bit. Alternatively, if  is not the next-state value of the challenge register, the oracle will likely produce a response unrelated to the original response , as the single-bit difference will tend to be amplified by the cipher over hundreds of rounds. The analogous observation holds, of course, for .

Based on the assumption that the encryption circuitry in a production DST tag implements the algorithm of Figure 1, we performed this test using an evaluation DST purchased from Texas Instruments. First, we programmed the DST with the key, then submitted a challenge , along with the two possible ``next-state'' values and .

Unfortunately, this test failed to produce the results we expected, indicating that DST, the algorithm in the production DST, differs from the Kaiser cipher. After submitting a number of properly-formed challenges to the DST, we saw none of the expected correlations - i.e., neither  nor  produced responses correlated to the original response .

Through trial and error, we discovered that the method of testing next-state challenge-register values succeeded when we modeled the output of the -box as two bits. For a given challenge , this required that we instead compute four candidate next-state values, , i.e., one for each of the possible output bit-pairs of the -box. In our experiments, at least one of these four candidates always produced a response corresponding to the initial response , but shifted right by two bits.5 One possible explanation was that the circuit alters its operation every other clock cycle, causing our test to malfunction. It was far more likely, however, that the production cipher DST simply produces two bits per cycle. Such a divergence from the diagram of Figure 1 called into question other elements of the diagram, including the number of rounds in the encryption process, and the key update schedule.

With the ability to recover the output of  on a single cipher iteration, we were able to use our oracle to observe each round of a cipher execution from start to finish, by repeatedly guessing the next state of the challenge register. This approach established that the encryption process took place over 200 cycles, i.e., 200 executions of , and that the DST draws its response from the rightmost 24 bits of the challenge register on the conclusion of this process.

Recovering the key schedule

Our experiments, as described above, relied on the assumption that the  key remains constant through every cycle of the encryption process. Using only the  key, however, would restrict our ability to experiment with the algorithm internals. We required the ability to observe single-round outputs based on different values in the challenge and key registers.

Using a non-zero key again made the algorithm round-dependent, with the result that our previous tests would no longer produce useful results. In order for our ``next-state'' candidate challenges to be encrypted properly, we needed to provide the oracle with the equivalent next-state of the key register.

Our next step, therefore, was to reverse-engineer the key schedule. Following the diagram, we assumed that new key bits were computed every few cycles by the exclusive-or of several bits of the key. By querying our oracle, we determined that the key is updated every three cycles, beginning with the second cycle - not the first, as suggested by the Kaiser diagram. We also determined that while four bits are indeed exclusive-ored together, they are not the bits shown in the diagram. Let denote the bit in the key register, beginning with 0. The actual key update is defined by . Note that this design represents an LFSR with a primitive-characteristic polynomial, so all keys other than the key produce maximal length sequences of key register values. Using this model for the key schedule in place of the key, we were able to simulate steps of the algorithm for any key.

With the  key, we only had to guess each of the possibilities for the 2-bit output of a single round. To experiment with a non-zero key , we needed to guess six successive bits (three bit-pairs) of output for the -box simultaneously, because the key schedule only repeats every three cycles. (6 is the l.c.d. of 2 and 3.) This meant testing 64 possible candidate challenge-register states,  . To test one of these challenge-register states, we programmed into the DST device a key  corresponding to the key-register state after six cipher cycles applied to . A DST can process 6-8 challenges per second, so this test requires a minimum of 8 seconds or so. It is thus significantly more time-consuming than previous tests, although it returns the output of three execution cycles, rather than one.

Uncovering the Feistel structure of DST 

Figure 2 shows the probability that modifying an individual challenge bit results in a change to the output of . To measure this effect, we generated a random key and challenge, then determined the output of . Next, for each of the 40 challenge bits, we determined whether the output of changed upon flipping of the bit. We repeated this test for 150 initial key and challenge settings. (We performed a similar test involving the flipping of key bits, but the results were not significant.)

Figure 2: Frequency of change in single round output value on flipping of individual challenge bits.

Let  denote the  bit of the challenge register, starting with 0. The first notable feature of our graph is the effect of bits  and  of the challenge register. While the other key and challenge bits have limited influence on the output of a single round, these two bit always affect the output of the -box. Further experimentation revealed that the two bits affect the first and second bit of the two-bit round output respectively. 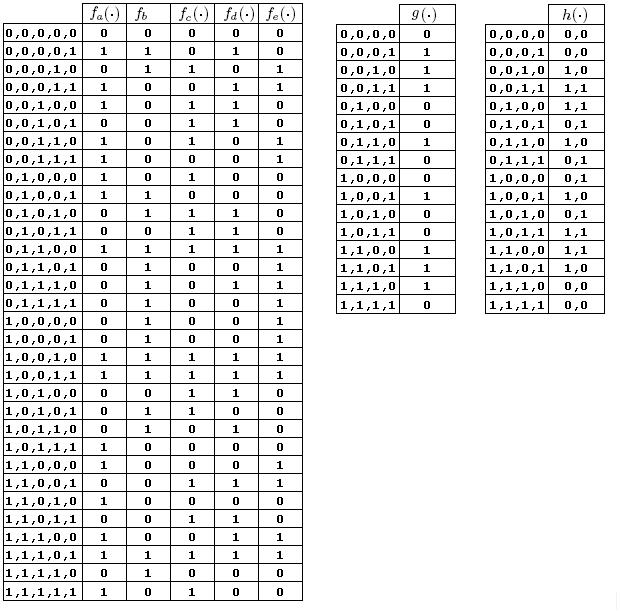This indicated that the cycle output derived from the exclusive-or of these bits with the output of the function.

The XOR effect of bits  and  shed new light on the algorithm's design. Not only is the algorithm an invertible permutation, but it is a form of Unbalanced Feistel Network [22].

For the DST, the choice of a Feistal cipher is not a necessary choice, although a useful one. We speculate that the round function was chosen to be a permutation, so that the effect of collisions would not multiply, and the responses would have a uniform distribution.

Recovering the bit routing networks

After identifying the general structure of the cipher, our next step was to uncover the internal routing network of bits, i.e., which bits act as inputs to each of the -boxes, as well as the boolean functions computed by each -box. We made the working assumption (eventually validated) that the -box () is the only box with a 2-bit output, and the rest each produce a single output bit.

The structure of the Kaiser cipher is such that  receives a single input bit from each of the -boxes, and produces one or four possible output values. This fact lays the groundwork for identifying which bits of the challenge and key are routed to each of the -boxes. It is clear that altering a single input bit of  can at most produce two distinct output values. In consequence, altering the output of only one -box can never cause to output more than two distinct values, whereas altering the output of more than one -box can produce up to four distinct output values.

Using this simple but powerful observation, we devised a test to determine which groups of input bits from the challenge and key are routed into each of the four -boxes. The test involves fixing a set of all but two challenge or key bits, and then iterating through all four combinations of these two bits. If at any time these four bit combinations produce more than two different outputs, then they cannot possibly be routed through the same -box. It should be noted that this test of -box membership produces false positives. In particular, it is very possible (and indeed common) that for two test bits that are not routed to the same -box, and for a given set of fixed bits, different value assignments to the test bits still produce two or fewer distinct outputs from the -box. Therefore this test requires many repetitions with different sets of fixed bits.

We employed this test first so as to exclude all bits that are not in the same -box as bit 0 of the challenge. After excluding 60 such bits, we discovered all of the bits that are routed to . We repeated the test for the remaining -boxes, ignoring bits previously associated with a box so as to decrease the search space. To our benefit, the routing network of bits that go through each -box is arranged in a rather regular pattern, and it was not necessary to perform an exhaustive search. After uncovering most of the bits related to , we were able to infer and then quickly verify the remainder of the -boxes.

A slightly more complicated task lay in determining the routing network for DST, namely which bits of the challenge and key registers serve as inputs to each -box. We already know that altering the output of any given -box will only affect a single -box, and therefore cause the output of  to assume only one of two distinct values. It is helpful, however, to note some other simple facts about the cipher. Let  be a set of challenge and key-register bits. Let  denote all other bits in the challenge and key registers. Our central observation is the output of the cipher will show a special invariant if  is the set of input bits to a single -box.

A given -box implements a fixed boolean function  on five bit inputs. (Two of the -boxes in DST have only four inputs, but the principle is the same.) Let us suppose that  is the set of inputs to this -box. We can then define  to be the set of value assignments to the bits in  such that , and define  analogously for . Observe that for a fixed setting of , the output of  will be invariant for the setting of  to any value in . Likewise, for a fixed value assignment to , the output of  will be invariant for any setting of  to a value in .

In contrast, suppose that  consists of register bits are are input to two or more -boxes. In this case, we are unlikely to see the invariant we have just described. For some, and perhaps many settings of , any given set of value assignments  (or ) may induce multiple output values in .

Using our invariant, we can perform a test to exclude combinations of bits that cannot be inputs to the same -box. We first select a set of five bits. We fix all other bits in the challenge and key registers. We iterate over all 32 value assignments to and record the pattern of outputs from . It may be the case that only a single output of results, in which case we repeat the experiment. In the case that there are two distinct outputs from , we record their correspondence to input values, i.e., we construct a hypothesis for and .6 We repeat this experiment over a new setting of . If we do not see the invariant described above for and , then cannot consist of inputs to a single -box. We successfully repeated this test until we excluded all possible -box input combinations except the correct ones.7

On first inspection, it would appear as though there is a large number of possible sets of input bits to any given -box. In fact, though, we can narrow the pool of candidate sets thanks to two observations: (1) The set of inputs to a single -box must also serve as inputs (at one remove) to the same -box; and (2) For any -box, three input bits come from the challenge register and two from the key register (or vice versa). By working with inputs corresponding to a single -box and by searching in particular for the -box that includes bit 0 of the challenge register, we started with a search space of size only . Moreover, once we identified the inputs to one -box, each subsequent -box corresponding to the same -box had far fewer combinations of input bits to test.

Furthermore, again to our benefit, the -box inputs in DST are ordered in a very regular manner. In particular, given the structure of inputs associated with one -box, we were readily able to infer those for the remaining -boxes.

Building logical tables for the , , and -boxes

Once we identified the bits corresponding to each -box, we constructed tables to represent the logical functions computed by the , , and -boxes. To construct the -box tables, we simply iterated through the  possible input values for the set  of bits that corresponds to the -box. Two different output values from  resulted (given a fortuitous setting of ). One of these values represented the case where the -box outputs a `0' bit, and the other when a `1' is output. We had no way of telling whether the actual output of the -box in question was a `0' or `1' bit; this is immaterial, however, as it may ultimately be treated as a naming convention. What learned from this experiment was, for each -box, a partition of the 32 input values into two sets corresponding to complementary output-box values.

Given this knowledge, we proceeded to construction of the -box tables. For a given -box, we simply selected the four corresponding -boxes and iterated over all  combinations of their output values, exploiting our knowledge from the previous experiment to do so. Construction of the -box table involved essentially the same technique. The only substantive difference is the fact that the -box yields two bits of output, rather than one.

Refer to Appendix A for the full DST algorithm description.

 Key Cracking

We were able to verify that our reverse engineering of the DST algorithm was successful by testing whether the responses computed by a software implementation of our hypothesized algorithm matched those returned by an evaluation DST when given the same challenge and key.

We also wished to test our implementation against actual fielded tags in SpeedPassTM tokens and automobile ignition keys. The cryptographic keys in these devices are immutable once locked at the factory. Without knowing the key on a fielded tag, we had no way to determine whether the algorithm used by such tags was as hypothesized. Therefore, recovering an actual key became necessary.

The DST Keycracker

We first coded our hypothesized DST40 in software. It quickly became clear that this implementation was not sufficiently fast for use in a keycracker: Even after hand-optimization, our software computed fewer than 200,000 encryptions per second on a 3.4 GHz Pentium workstation. At this rate it would take over two weeks for a cluster of ten computers to crack a single key. We instead chose to implement the keycracker in hardware.

Each node of our cracker consists of a single Xilinx XC3S1000 FPGA on a commercial evaluation board, available for under $200 in single quantities. In our VHDL implementation, each DST encryption core performs an encryption every 200 clock cycles, one clock cycle for each cycle of the cipher. Our cracker can therefore test a key in 200 clock cycles. The number of cores that fit on each FPGA depends on the other functions that the chip needs to perform; for our experiments we used 32 cores per FPGA. This utilized approximately 75% of the available resources, but simplified the dispatching (each core searched a prefix) and allowed us to easily add other I/O functionality.

In addition to the FPGA, each evaluation board contains switches, LEDs, support chips, and a variety of connectors. We chose to connect a PS/2 keyboard to the FPGAs to provide the inputs (the challenge/response pairs) while the outputs (the key) appeared on the LEDs. Because the DST outputs only 24 bits per 40 bit challenge, at least two challenge/response pairs are required to determine a key uniquely. The cracker tries each key on the first challenge, and when a response match is found, verifies that the key also works on the second challenge/response pair. At this point the cracking process stops and the display changes accordingly. The Xilinx software simulations indicated that our implementation could work at more than 150 MHz. We fixed the clock on our evaluation board to 100 MHz, however; this was the maximum speed achievable without an external clocking device, which we have not purchased. At this speed, each FPGA was able to crack nearly 16 million keys per second (the nearly being due to false positives and some very slight overhead), approximately a 100-fold increase over the software implementation on a very fast PC. Using an FPGA, the entire 40 bit key-space can be exhausted in under 21 hours.

A single board was sufficient to verify that our reverse engineering was correct with respect to fielded DST tags. In just under 11 hours the cracker recovered the key from a SpeedPassTM which we used to compute new responses that matched those from the tag. While 11 hours of computation is perfectly reasonable in many attack scenarios, we decided to engineer a cracker that a modestly funded adversary could use to recover keys in under an hour. By purchasing 16 evaluation boards at a cost of under $3500, and connecting the boards together with flat wire connectors, we were able to create a parallel version of our already parallel single-chip cracker.

The parallel cracker still allows a user to input the desired search points using a single keyboard; the information is then passed via a flat wire connector from board to board. The portion of the key-space that each board is responsible for is set using four switches and, when found, the key is displayed on the LEDs.

To assist us in validating our results, Texas Instruments provided us with five DST tags and challenged us to recover their keys. Using the parallel cracker, we were able to crack all five keys in under two hours. That this is shorter than the expected time for five keys can be explained by the lack of any hex digit above 9 in any of the five keys. While it appears that these keys were not chosen at random (and indeed were probably entered by hand), the actual keys in deployed DST devices do seem to be randomly distributed.

The Hellman time-space tradeoff

As explained above, we have constructed a software key cracker that uses Hellman tables based on the parameters set forth in the work by Quisquater et al. While table building is not yet complete, rough estimates suggest that a key-cracking program capable of a success rate of 99+% should require about 10 GB of storage, and should operate in under a minute on a fast PC. Construction of the tables requires considerable pre-computation. At the time of writing of this paper, we are in the process of table building and hope soon to report results of this work.

 RF Protocol Analysis and Simulation

Low-frequency RFID systems typically make use of powered readers and passive transponders. In the DST system, the reader transmits power to the transponder via a 15-to-50 ms electromagnetic pulse at 134.2 kHz. Once powered, a transponder can receive and respond to commands from the reader, including challenges and read and write operations. The transponder can also execute computations, including as cryptographic operations.

A reader transmits commands as a sequence of amplitude-modulated (AM) bits. Once a power burst has ended, the reader signal will drop significantly in amplitude for some period of time. It is the duration of this ``off-time'' that communicates a bit value to the transponder. A short off-time duration specifies a `0' bit, while a longer duration specifies a `1' bit. Between each bit transmission, the reader signals returns to full amplitude in order to delimit the off-time intervals and maintain the powered state of the transponder. In some cases, after sending a command to a transponder, a reader will transmit a short, supplementary power burst to energize the tag fully.

Once the transponder has fully received and processed a command, it discharges its stored power, while transmitting its response using frequency modulated frequency shift keying (FM-FSK). It communicates a bit via 16 RF cycles, specifying a `0' or `1' bit by transmitting at 134.2 kHz or 123.2 kHz respectively.8 A preamble of `0' bits followed by a start byte (7E hex) indicates the start of a transmission and allows the reader to synchronize.

Sniffing the protocol

Given an understanding of the communication medium between reader and transponder, eavesdropping on or creating protocol transmissions is a matter of having the right equipment and software applications. With this aim, we have equipped a small and easily portable PC with a Measurement Computing digital-to-analog conversion (DAC) board. This board is also capable of analog-to-digital conversion. The DAC board can perform 12-bit A/D conversions on an input signal at a rate of 1.25 MHz, and can perform D/A conversions and generate an output signal at a rate of 1 MHz. These rates are quite sufficient for our purposes. In our work with DSTs, we are manipulating signals with frequencies approximately 1/7th the maximum input and output rates of the DAC.

We connected the input and output channels on our DAC board to an antenna tuned to the 134 kHz range. The particular antenna we used in our experiments comes with TI's micro-reader evaluation kit, and is thus designed to receive and transmit analog signals within our desired frequency range.

We wrote modulation and demodulation software routines to decode and produce the analog AM signals transmitted by the TI reader, as well as FM-FSK analog signals transmitted by DST transponders. Using these routines, our equipment can eavesdrop on the communication protocol between a DST reader and transponder, or participate actively in a protocol by emulating either device.

Putting together the pieces: the full DST protocol

As explained above, the DST protocol hinges on a relatively straightforward challenge-response protocol. The reader first transmits a challenge request to a transponder, consisting of an 8-bit opcode followed by a 40-bit challenge. The opcode indicates the type of request being made (in this case an authentication request). As noted above, the transponder encrypts the challenge using the secret 40-bit key it shares with the reader; the resulting least significant 24 bits in the transponder challenge register constitutes a 24-bit signature. The transponder replies to the reader with its 24-bit serial number, the 24-bit signature and lastly a keyed 16-bit CRC of the data being transmitted. Using the shared encryption key (which it may look up based on the transponder serial number) and secret CRC start value, the reader can verify that the signature is correct.

The CRC appended to each transmission is intended to be an additional security measure as well as an error checking device. The DST protocol specification defines this as a 16-bit reverse CRC-CCITT that is initialized with a secret 16-bit start value. However, this feature provides no such security. A single interaction with a DST allows for the recovery of a transmission and accompanying keyed CRC. As this secret start value is shared among all DSTs, it is only a matter of trying the  possible start values and computing the CRC of the data returned to uncover the secret start value. The computational time required for this is less than a second.

Therefore, the security of authentication in this system depends on the supposition that the 40-bit secret key contained in a valid transponder is available only to the transponder and to valid readers, and that only knowledge of this shared secret allows the correct generation of a signature. The system architects specified as a design criterion that having access to a transponder or reader for short periods of time should not lead to recovery of the secret key [11]. Their stated aim was to make the DST system resistant to signature-guessing attacks, dictionary attacks using known challenge-response pairs, cryptanalytic attacks, and exhaustive key search - even for an attacker with full knowledge of the encryption algorithm.

Simulating a DST device

Given the secret 40-bit key for a DST, simulation is a simple matter: In the presence of a valid reader, we emulate the participation of the target DST in an authentication protocol using a software radio. In particular, our software performs the following steps: (1) It analyzes the A/D conversions received from the DAC board, (2) Decodes the AM signal containing the challenge sent from the reader, (3) Performs an encryption of this challenge using the recovered secret DST key, (4) Codes the FM-FSK signal representing the correct response, and (5) Outputs this FM-FSK signal to the DAC board. Of course, enhancing the software to implement any operation in the DST-protocol variants is a straightforward matter.

Conclusion

The weakness we have demonstrated in the TI system is ultimately due to the inadequate key-length of the underlying DST cipher. It is quite possible, however, that cryptanalysis will reveal weaknesses in the cipher itself. Indeed, we have preliminary experimental evidence that promises effective cryptanalytic attack. This would improve the efficacy of the attacks we have described.

The authors hope that future cryptographic RFID system designers will embrace a critical lesson preached by the scientific community: Cryptographic hardware systems are generally strongest when they employ industry standard cryptographic algorithms with key lengths sufficient to endure over the life of the devices and assets they protect.

Acknowledgments

Thanks to Dan Bailey, Cindy Cohn, Ed Felten, Kevin Fu, Ron Juels, Burt Kaliski, Kurt Opsahl, Ron Rivest, Marian Titerence, and David Wagner for their valuable suggestions and comments and their support of this work. We also thank Texas Instruments for their cooperation after we disclosed our results to them and for feedback on earlier drafts of this paper.

Notes

4 Note that although the metal panels of the automobile act as a Faraday cage, the low frequency of the DST signal may effectively penetrate the windows. This is a matter of speculation at present.

... bits.

5 Occasionally this experiment produces multiple candidates that generate a matching response. Some collisions are inevitable in an algorithm with a larger input than output size.

6 We cannot tell whether a particular output value for corresponds to a `0' output or a `1' output for a particular -box. This does not matter: The labeling of and is inconsequential in our experiment.

... ones.

7 We might instead have tested the hypothesis that -boxes are ``balanced,'' which is to say that and are of equal size. This is a natural design criterion, and one that we ultimately did observe. We chose instead to execute our invariant test, however, as it is more general.

8 The TI documentation indicates slightly different frequencies for different devices. The TI glass transponder transmits at 134.3 and 122.9 kHz, while the wedge-shaped transponder transmits at 134.5 and 123.7 kHz.

Bibliography

1

Automotive immobilizer anti-theft systems experience rapid growth in 1999, 1  June 1999.

Texas Instruments Press Release. Available at  https://www.ti.com/tiris/docs/news/news_releases/ 90s/rel06-01-99.shtml.

2

SpeedpassTM Press Kit Fact Sheet, June 2004.

Referenced at https://www.exxonmobil.com/corporate/files/  corporate/speedpass_fact_sheet.pdf.

3

Security and privacy in rfid systems, 2005.

Web-based bibliography. Referenced at  https://lasecwww.epfl.ch/gavoine/rfid/.

4

AN0NYM0US USER.

RC4?, September 1994.

Sci.crypt posting.

5

BIHAM, E., AND SHAMIR, A.

Differential fault analysis of secret key cryptosystems.

In CRYPTO '97 (1997), B. Kaliski, Ed., Springer-Verlag,  pp. 513-525.

6

BIRYUKOV, A., SHAMIR, A., AND WAGNER, D.

Real time cryptanalysis of A5/1 on a PC.

In Fast Software Encryption (FSE) (2000), pp. 1 - 18.

7

BOURQUE, D.

Technology update, chip status and development, October 2004.

Slide presentation. Referenced at  https://www.ris.averydennison.com/ris/ris2site.nsf/ (Image)/Texas_Instruments_(Eng.)/  $File/Texas%20Instruments%20(Eng.).pdf.

8

ELECTRONICS, R. P.

Identification applications - car immobilization, 2005.

Web page. Referenced at  https://www.semiconductors.philips.com/markets/ identification/products/automotive/transponders/ Contains links to data  sheets.

9

EPCglobal Web site. https://www.epcglobalinc.org, 2005.

10

GILMORE, J.

EFF builds DES cracker that proves that data encryption standard  is insecure.

EFF press release (July 1998).

11

GORDON, J., KAISER, U., AND SABETTI, T.

A low cost transponder for high security vehicle immobilizers.

In 29th ISATA Automotive Symposium (3-6 June 1996).

12

HELLMAN, M.

A cryptanalytic time-memory trade-off.

IEEE Transactions on Information Theory 26, 4 (July 1980),  410-416.

13

KAHN, D.

The Codebreakers: The Comprehensive History of Secret  Communication from Ancient Times to the Internet.

Macmillan, 1996.

14

KAISER, U.

Universal immobilizer crypto engine.

In Fourth Conference on the Advanced Encryption Standard  (AES) (2004).

Guest presentation. Slides referenced at  https://www.aes4.org/english/events/aes4/ program.html.

15

KRAWCZYK, H., BELLARE, M., AND CANETTI, R.

HMAC: Keyed-hashing for message authentication.

Internet Request For Comments (RFC) 2104 (February 1997).

16

OF INVESTIGATION (FBI), F. B.

Uniform crime report, 2003.

Referenced at https://www.fbi.gov/ucr/03cius.htm.

17

QUISQUATER, J., AND STANDAERT, F.

Exhaustive key search of the DES: Updates and refinements.

SHARCS 2005 (2005).

18

QUISQUATER, J.-J., STANDAERT, F.-X., ROUVROY, G., DAVID, J.-P., AND LEGAT,  J.-D.

A cryptanalytic time-memory tradeoff: First FPGA implementation,  2002.

19

ROBERTI, M.

EPCglobal ratifies Gen 2 standard.

RFID Journal (16 Dec. 2004).

Referenced at https://www.rfidjournal.com/article/articleview/  1293/1/1/.

20

SARMA, S.

Towards the five-cent tag.

Tech. Rep. MIT-AUTOID-WH-006, MIT Auto ID Center, 2001.

Referenced at https://www.epcglobalinc.org.

21

SARMA, S. E., WEIS, S. A., AND ENGELS, D.

Radio-frequency-identification security risks and challenges. rsa  laboratories.

CryptoBytes 6, 1 (2003).

22

SCHNEIER, B., AND KELSEY, J.

Unbalanced feistel networks and block cipher design.

In Fast Software Encryption (FSE) (1996), p. 121—144.

23

SULLIVAN, L.

Wal-Mart oulines RFID expansion plans.

InformationWeek (17 June 2004).

24

YOSHIDA, J.

Tests reveal e-passport security flaw.

EE Times (30 August 2004).

Referenced at https://www.eedesign.com/news/ showArticle.jhtml?articleID=45400010.

Appendix A - The Full DST Cipher

To facilitate further analysis of the DST algorithm, here we describe the full structure of the cipher. As described above, the cipher is composed of 200 individual rounds. For a key  and round input , the round output on round  is

where  is a key scheduling function and  is a boolean function that outputs two bits. On round one, the round input is the challenge, and on round 200 the response is the low 24 bits of the round output.

The key schedule, , updates the key every three rounds, beginning with the second round. It can be represented recursively as shown in Figure 3. The computation of the function is shown in Figure 4.

Figure 3: The key scheduler, , takes the cipher key, , and the round number, , and produces the round key.

Figure 4: The structure of the boolean function, . The truth tables for the , , and functions are included as Figure 5.

Figure 5: The , and functions for the DST cipher.

About this document ...

Security Analysis of a Cryptographically-Enabled

RFID Device

 This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.