4.1 Leaf Polymorphism

Type inference is a powerful tool for computing qualifiers given a few annotations. However, when inferring types of functions, we need to introduce some new machinery to avoid getting a large number of false positives.

To understand the problem, consider the following simple example code:

  char id(char x) { return x; }
  ...
  tainted char t;
  untainted char u;
  char a, b;

  a = id(t); /* 1 */
  b = id(u); /* 2 */

Because of call 1, we infer that x is a tainted char, and therefore we also infer that a is tainted. Then call 2 typechecks (because $\texttt{untainted char}\leq\texttt{tainted char}$), but we infer that b must also be tainted.

While this is a sound inference, it is clearly overly conservative. Even though this simple example looks unrealistic, we encounter this problem in practice, most notably with library functions such as strcpy. This leads to a large number of false positives.

The problem arises because we are summarizing multiple stack frames for distinct calls to id with a single function type--x has to either be untainted everywhere or tainted everywhere. The solution to this problem is to introduce polymorphism, which is a form of context-sensitivity.

A function is said to be polymorphic if it has more than one type. Notice that id behaves the same way no matter what qualifier is on its argument x: it always returns exactly x. Thus we can give id the signature $\alpha\;\texttt{char id(}\alpha\texttt{ char x)}$ for any qualifier $\alpha$.

Operationally, when we call a polymorphic function, we instantiate its type--we make a copy of its type, replacing all the generic qualifier variables $\alpha$ with fresh qualifier variables. Intuitively, this corresponds exactly to inlining the function, except that instead of making a fresh copy of the function's code, we make a fresh copy of the function's type.

We need a way to write down polymorphic type signatures--for example, we should be able to express that if the strcat() function is passed a tainted second argument, then its first argument should also be tainted, but not vice versa. We can do this by writing a polymorphic type with side constraints on the qualifiers:

$$\begin{array}{@{}l} \texttt{$\alpha$\ char *}\\ \texttt{strcat($... ...src);}\\ \quad \hspace{1.0in} \textrm{(where $\alpha \ge \beta$)} \end{array}$$

More generally, we want to be able to specify a polymorphic function

$$\texttt{$\alpha$\ f($\beta$\ arg0, $\delta$\ arg1, \ldots)};$$

with some arbitrary inequality constraints on the qualifier variables $\alpha$, $\beta$, $\delta$, etc. We define a concise notation for expressing these inequality constraints by using the following theorem.

Theorem 4.1   Let $(P,\leq)$ be any finite partial order. Let $(2^{\mathbb{N}}, \subseteq)$ be the lattice of subsets of $\mathbb{N}$ with the set inclusion ordering. Then $(P,\leq)$ can be embedded in $(2^{\mathbb{N}}, \subseteq)$, i.e., there exists a mapping $\phi : P \rightarrow 2^{\mathbb{N}}$, such that $a \leq b \iff \phi(a) \subseteq \phi(b)$ and $\phi(x)$ is a finite subset of $\mathbb{N}$ for all $x\in P$.

The theorem is formally proved in the appendix, and may be viewed as a concrete example of the Dedekind-MacNeille Completion [14].

This theorem enables us to define the partial order implicitly by the naming of the qualifier variables on the function arguments and return type. We represent a qualifier $a$ in the partial order $P$ by $\phi(a)$, which we denote as a '_' separated string of the integers in the set. If $\phi(a) = \{1,2\}$, then $a$ is represented as $\$\_1\_2$. Hence, the polymorphic declaration of strcat can now be written as

$$\begin{array}{l} \texttt{$\$\_1\_2$\ char *}\\ \texttt{strcat($\$\_1\_2$\ char *, $\$\_1$\ const char *)} \end{array}$$

which means that the qualifier on the return type is the same as the qualifier on the first argument, and that they are both supertypes of the second argument. In other words, since $\{1,2\} \supseteq \{1\}$, the names of the qualifiers encode the implicit inequality constraint $\$\_1\_2 \geq \$\_1$. Hence for any instantiation of strcat(), we have

$$\texttt{strcat\_ret\_p} = \texttt{strcat\_arg0\_p}$$

$$\geq \texttt{strcat\_arg1\_p}.$$

This avoids the need to write subtyping constraints on the side for each polymorphic function. Instead, the constraints are encoded implicitly in the annotations themselves, which provides a concise framework for expressing subtyping annotations.

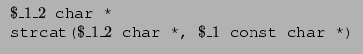
To keep our implementation simple, we only support polymorphism for library functions, i.e., functions with no code. To be more precise, any function may be declared polymorphically, but the polymorphic prototype will not be typechecked against its implementation. This restriction is not fundamental; there are well-known efficient algorithms for more general polymorphism [19,33]. Our standard prelude files contain appropriate polymorphic declarations for most of the standard library functions.