|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
4th USENIX OSDI Symposium
[Technical Program]
Surplus Fair Scheduling: A Proportional-Share CPU Scheduling
Algorithm for Symmetric Multiprocessors
|
| Department of Computer Science, | Ensim Corporation |
| University of Massachusetts Amherst | Sunnyvale, CA |
| {abhishek,micah,shenoy}@cs.umass.edu | goyal@ensim.com |
In this paper, we present surplus fair scheduling (SFS), a proportional-share CPU scheduler designed for symmetric multiprocessors. We first show that the infeasibility of certain weight assignments in multiprocessor environments results in unfairness or starvation in many existing proportional-share schedulers. We present a novel weight readjustment algorithm to translate infeasible weight assignments to a set of feasible weights. We show that weight readjustment enables existing proportional-share schedulers to significantly reduce, but not eliminate, the unfairness in their allocations. We then present surplus fair scheduling, a proportional-share scheduler that is designed explicitly for multiprocessor environments. We implement our scheduler in the Linux kernel and demonstrate its efficacy through an experimental evaluation. Our results show that SFS can achieve proportionate allocation, application isolation and good interactive performance, albeit at a slight increase in scheduling overhead. We conclude from our results that a proportional-share scheduler such as SFS is not only practical but also desirable for server operating systems.
The growing popularity of multimedia and web applications has spurred research in the design of large multiprocessor servers that can run a variety of demanding applications. To illustrate, many commercial web sites today employ multiprocessor servers to run a mix of HTTP applications (to service web requests), database applications (to store product and customer information), and streaming media applications (to deliver audio and video content). Moreover, Internet service providers that host third party web sites typically do so by mapping multiple web domains onto a single physical server, with each domain running a mix of these applications. These example scenarios illustrate the need for designing resource management mechanisms that multiplex server resources among diverse applications in a predictable manner.
Resource management mechanisms employed by a server operating system should have several desirable properties. First, these mechanisms should allow users to specify the fraction of the resource that should be allocated to each application. In the web hosting example, for instance, it should be possible to allocate a certain fraction of the processor and network bandwidth to each web domain [2]. The operating system should then allocate resources to applications based on these user-specified shares. It has been argued that such allocation should be both fine-grained and fair [3,9,15,17,20]. Another desirable property is application isolation--the resource management mechanisms employed by an operating system should effectively isolate applications from one another so that misbehaving or overloaded applications do not prevent other applications from receiving their specified shares. Finally, these mechanisms should be computationally efficient so as to minimize scheduling overheads. Thus, efficient, predictable and fair allocation of resources is key to designing server operating systems. The design of a CPU scheduling algorithm for symmetric multiprocessor servers that meets these objectives is the subject matter of this paper.
In the recent past, a number of resource management mechanisms have been developed for predictable allocation of processor bandwidth [2,7,11,12,14,16,18,24,28]. Many of these CPU scheduling mechanisms as well as their counterparts in the network packet scheduling domain [4,5,19,23] associate an intrinsic rate with each application and allocate resource bandwidth in proportion to this rate. For instance, many recently proposed algorithms such as start-time fair queuing (SFQ) [9], borrowed virtual time (BVT) [7], and SMART [16] are based on the concept of generalized processor sharing (GPS). GPS is an idealized algorithm that assigns a weight to each application and allocates bandwidth fairly to applications in proportion to their weights. GPS assumes that threads can be scheduled using infinitesimally small quanta to achieve weighted fairness. Practical instantiations, such as SFQ, emulate GPS using finite duration quanta. While GPS-based algorithms can provide strong fairness guarantees in uniprocessor environments, they can result in unbounded unfairness or starvation when employed in multiprocessor environments as illustrated by the following example.
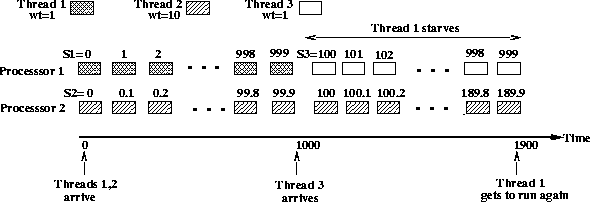
Example 1237 (1)
Consider a server that employs the start-time fair queueing (SFQ)
algorithm [9] to schedule threads. SFQ is a GPS-based fair
scheduling algorithm that assigns a weight wi to each thread and
allocates bandwidth in proportion to these weights. To do so, SFQ
maintains a counter Si for each application that is incremented by
![]() every time the thread is scheduled (q is the quantum
duration). At each scheduling instance, SFQ schedules the thread with
the minimum Si on a processor. Assume that the server has two
processors and runs two compute-bound threads that are assigned weights
w1 = 1 and w2 = 10, respectively. Let the quantum duration be q
= 1 ms. Since both threads are compute-bound and SFQ is
work-conserving,
every time the thread is scheduled (q is the quantum
duration). At each scheduling instance, SFQ schedules the thread with
the minimum Si on a processor. Assume that the server has two
processors and runs two compute-bound threads that are assigned weights
w1 = 1 and w2 = 10, respectively. Let the quantum duration be q
= 1 ms. Since both threads are compute-bound and SFQ is
work-conserving,![[*]](foot_motif.gif) each thread gets to continuously run on a
processor. After 1000 quantums, we have
each thread gets to continuously run on a
processor. After 1000 quantums, we have ![]() and
and ![]() . Assume that a third cpu-bound
thread arrives at this instant with a weight w3=1. The counter for
this thread is initialized to S3=100 (newly arriving threads are
assigned the minimum value of Si over all runnable threads). From
this point on, threads 2 and 3 get continuously scheduled until S2
and S3 ``catch up'' with S1. Thus, although thread 1 has the
same weight as thread 3, it starves for 900
quanta leading to unfairness in the scheduling algorithm. Figure
1 depicts this scenario.
. Assume that a third cpu-bound
thread arrives at this instant with a weight w3=1. The counter for
this thread is initialized to S3=100 (newly arriving threads are
assigned the minimum value of Si over all runnable threads). From
this point on, threads 2 and 3 get continuously scheduled until S2
and S3 ``catch up'' with S1. Thus, although thread 1 has the
same weight as thread 3, it starves for 900
quanta leading to unfairness in the scheduling algorithm. Figure
1 depicts this scenario.
 |
Many recently proposed GPS-based algorithms such as stride scheduling
[28], weighted fair queuing (WFQ) [18] and
borrowed virtual time (BVT) [7] also suffer from this
drawback when employed for multiprocessors (like SFQ, stride
scheduling and WFQ are instantiations of GPS, while BVT is a
derivative of SFQ with an additional latency parameter; BVT reduces to
SFQ when the latency parameter is set to zero). The primary reason
for this inadequacy is that while any arbitrary weight assignment
is feasible for uniprocessors, only certain weight assignments are
feasible for multiprocessors. In particular, those weight assignments
in which the bandwidth assigned to a single thread exceeds the
capacity of a processor are infeasible (since an individual thread
cannot consume more than the bandwidth of a single processor). In the
above example, the second thread was assigned ![]() of
the total bandwidth on a dual-processor server, whereas it can consume
no more than half the total bandwidth. Since GPS-based work-conserving
algorithms do not distinguish between feasible and infeasible weight
assignments, unfairness can result when a weight assignment is
infeasible.
In fact, even when the initial weights are carefully chosen to be
feasible, blocking events can cause the weights of the remaining
threads to become infeasible. For instance, a feasible weight
assignment of 1:1:2 on a dual-processor server becomes infeasible when
one of the threads with weight 1 blocks. Even when all weights are
feasible, an orthogonal problem occurs when frequent arrivals and
departures prevent a GPS-based scheduler such as SFQ from achieving
proportionate allocation. Consider the following example:
of
the total bandwidth on a dual-processor server, whereas it can consume
no more than half the total bandwidth. Since GPS-based work-conserving
algorithms do not distinguish between feasible and infeasible weight
assignments, unfairness can result when a weight assignment is
infeasible.
In fact, even when the initial weights are carefully chosen to be
feasible, blocking events can cause the weights of the remaining
threads to become infeasible. For instance, a feasible weight
assignment of 1:1:2 on a dual-processor server becomes infeasible when
one of the threads with weight 1 blocks. Even when all weights are
feasible, an orthogonal problem occurs when frequent arrivals and
departures prevent a GPS-based scheduler such as SFQ from achieving
proportionate allocation. Consider the following example:
Example 1242
Consider a dual-processor server that runs a thread with weight 10,000
and 10,000 threads with weight 1. Assume that short-lived threads with
weight 100 arrive every 100 quantums and run for 100 quantums
each. Note that the weight assignment is always feasible. If SFQ is
used to schedule these threads, then it will assign the current
minimum value of Si in the system to each newly arriving
thread. Hence, each short-lived thread is initialized with the lowest
value of Si and gets to run continuously on a processor until it
departs. The thread with weight 10,000 runs on the other processor;
all threads with weight 1 run infrequently. Thus, each short-lived
thread with weight 100 gets as much processor bandwidth as the thread
with weight 10,000 (instead of ![]() of the bandwidth).
Note that this problem does not occur in uniprocessor environments.
of the bandwidth).
Note that this problem does not occur in uniprocessor environments.
The inability to distinguish between feasible and infeasible weight assignments as well as to achieve proportionate allocation in the presence of frequent arrivals and departures are fundamental limitations of a proportional-share scheduler such as SFQ. Whereas randomized schedulers such as lottery scheduling [27] do not suffer from starvation problems due to infeasible weights, such weight assignments can, nevertheless, cause small inaccuracies in proportionate allocation for such schedulers. Several techniques can be employed to address the problem of infeasible bandwidth assignments. In the simplest case, processor bandwidth could be assigned to applications in absolute terms instead of using a relative mechanism such as weights (e.g., assign 20% of the bandwidth on a processor to a thread). A potential limitation of such absolute allocations is that bandwidth unused by an application is wasted, resulting in poor resource utilization. To overcome this drawback, most modern schedulers that employ this method reallocate unused processor bandwidth to needy applications in a fair-share manner [10,14]. In fact, it has been shown that relative allocations using weights and absolute allocations with fine-grained reassignment of unused bandwidth are duals of each other [22]. A more promising approach is to employ a GPS-based scheduler for each processor and partition the set of threads among processors such that each processor is load balanced. Such an approach has two advantages: (i) it can provide strong fairness guarantees on a per-processor basis, and (ii) binding a thread to a processor allows the scheduler to exploit processor cache locality. A limitation of the approach is that periodic repartitioning of threads may be necessary since blocked/terminated threads can cause imbalances across processors, which can be expensive. Nevertheless, such an approach has been successfully employed to isolate applications from one another [1,8,26].
In summary, GPS-based fair scheduling algorithms or simple modifications thereof are unsuitable for fair allocation of resources in multiprocessor environments. To overcome this limitation, we propose a CPU scheduling algorithm for multiprocessors that: (i) explicitly distinguishes between feasible and infeasible weight assignments and (ii) achieves proportionate allocation of processor bandwidth to applications.
In this paper, we present surplus fair scheduling (SFS), a predictable CPU scheduling algorithm for symmetric multiprocessors. The design of this algorithm has led to several key contributions.
First, we have developed a weight readjustment algorithm to explicitly deal with the problem of infeasible weight assignments; our algorithm translates a set of infeasible weights to the ``closest'' feasible weight assignment, thereby enabling all scheduling decisions to be based on feasible weights. Our weight readjustment algorithm is a novel approach for dealing with infeasible weights and one that can be combined with most existing GPS-based scheduling algorithms; doing so enables these algorithms to vastly reduce the unfairness in their allocations for multiprocessor environments. However, even with the readjustment algorithm, many GPS-based algorithms show unfairness in their allocations, especially in the presence of frequent arrival and departures of threads. To overcome this drawback, we develop the surplus fair scheduling algorithm for proportionate allocation of bandwidth in multiprocessor environments. A key feature of our algorithm is that it does not require the quantum length to be known a priori, and hence can handle quantums of variable length.
We have implemented the surplus fair scheduling algorithm in the Linux kernel and have made the source code available to the research community. We have experimentally demonstrated the benefits of our algorithm over a GPS-based scheduler such as SFQ using sample applications and benchmarks. Our experimental results show that surplus fair scheduling can achieve proportionate allocation, application isolation and good interactive performance for typical application mixes, albeit at the expense of a slight increase in the scheduling overhead. Together these results demonstrate that a proportional-share CPU scheduling algorithm such as surplus fair scheduling is not only practical but also desirable for server operating systems.
The rest of this paper is structured as follows. Section 2 presents the surplus fair scheduling algorithm. Section 3 discusses the implementation of our scheduling algorithm in Linux. Section 4 presents the results of our experimental evaluation. Section 5 presents some limitations of our approach and directions for future work. Finally, Section 6 presents some concluding remarks.
Consider a multiprocessor server with p processors that runs t
threads. Let us assume that a user can assign any arbitrary weight
to a thread. In such a scenario, a thread with weight wi should be
allocated ![]() fraction of the total processor
bandwidth. Since weights can be arbitrary, it is possible that a
thread may request more bandwidth than it can consume (this occurs
when the requested fraction
fraction of the total processor
bandwidth. Since weights can be arbitrary, it is possible that a
thread may request more bandwidth than it can consume (this occurs
when the requested fraction ![]() ). The CPU scheduler must somehow reconcile the presence
of such infeasible weights. To do so, we present an optimal weight
readjustment algorithm that can efficiently translate a set of
infeasible weights to the ``closest'' feasible weight assignment. By
running this algorithm every time the weight assignment becomes
infeasible, the CPU scheduler can ensure that all scheduling decisions
are always based on a set of feasible weights. Given such a weight
readjustment algorithm, we then present generalized
multiprocessor sharing (GMS)--an idealized algorithm for fair,
proportionate bandwidth allocation that is an analogue of GPS in the
multiprocessor domain. We use the insights provided by GMS to design
the surplus fair scheduling (SFS) algorithm. SFS is a practical
instantiation of GMS that has lower implementation overheads.
). The CPU scheduler must somehow reconcile the presence
of such infeasible weights. To do so, we present an optimal weight
readjustment algorithm that can efficiently translate a set of
infeasible weights to the ``closest'' feasible weight assignment. By
running this algorithm every time the weight assignment becomes
infeasible, the CPU scheduler can ensure that all scheduling decisions
are always based on a set of feasible weights. Given such a weight
readjustment algorithm, we then present generalized
multiprocessor sharing (GMS)--an idealized algorithm for fair,
proportionate bandwidth allocation that is an analogue of GPS in the
multiprocessor domain. We use the insights provided by GMS to design
the surplus fair scheduling (SFS) algorithm. SFS is a practical
instantiation of GMS that has lower implementation overheads.
In what follows, we first present our weight readjustment algorithm in Section 2.1. We present generalized multiprocessor sharing in Section 2.2 and then present the surplus fair scheduling algorithm in Section 2.3.
As illustrated in Section 1.2, weight assignments in which a thread requests a bandwidth share that exceeds the capacity of a processor are infeasible. Moreover, a feasible weight assignment may become infeasible or vice versa whenever a thread blocks or becomes runnable. To address these problems, we have developed a weight readjustment algorithm that is invoked every time a thread blocks or becomes runnable. The algorithm examines the set of runnable threads to determine if the weight assignment is feasible. A weight assigned to a thread is said to be feasible if
| |
(1) |
Conceptually, the weight readjustment algorithm proceeds by
examining each thread in descending order of weights to see if it
violates the feasibility constraint. Each thread that does so is
assigned the bandwidth of an entire processor, which is the maximum
bandwidth a thread can consume. The problem then reduces to checking the
feasibility of scheduling the remaining threads on the remaining
processors. In practice, the readjustment algorithm is implemented
using recursion--the algorithm recursively examines each thread to
see if it violates the constraint; the recursion terminates when a
thread that satisfies the constraint is found. The algorithm then
assigns a new weight to each thread that violates the constraint such
that its requested fraction equals 1/p. This is achieved by
computing the average weight of all feasible threads over the
remaining processors and assigning it to the current thread (i.e.,
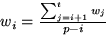 ).
Figure 2 illustrates the complete weight readjustment
algorithm.
).
Figure 2 illustrates the complete weight readjustment
algorithm.
Our weight readjustment algorithm has the following salient features:
The weight readjustment algorithm can also be employed in conjunction with a randomized proportional-share scheduler such as lottery scheduling [27]. Although such a scheduler does not suffer from starvation problems due to infeasible weights, a set of feasible weights can help such a randomized scheduler in making more accurate scheduling decisions.
 |
Given our weight readjustment algorithm, we now present an idealized algorithm for proportional-share scheduling in multiprocessor environments.
| |
(2) |
![[*]](foot_motif.gif)
Intuitively, GMS is similar to a weighted round-robin algorithm in which threads are scheduled in round-robin order (p at a time); each thread is assigned an infinitesimally small CPU quantum and the number of quanta assigned to a thread is proportional to its weight. In practice, however, threads must be scheduled using finite duration quanta so as to amortize context switch overheads. Consequently, in what follows, we present a CPU scheduling algorithm that employs finite duration quanta and is a practical approximation of GMS.
| |
(3) |
A scheduling algorithm that actually uses Equation 3 to
compute surplus values is impractical since it requires the scheduler
to compute AiGMS (which in turn requires a simulation of
GMS). Consequently, we derive an approximation of Equation
3 that enables efficient computation of the surplus
values for each thread. Let ![]() denote the
weighted CPU service received by each thread so far. If thread i
runs in a quantum, then Si is incremented as
denote the
weighted CPU service received by each thread so far. If thread i
runs in a quantum, then Si is incremented as ![]() , where q denotes the duration for which the thread ran
in that quantum. Since Si is the weighted CPU service received by
thread i,
, where q denotes the duration for which the thread ran
in that quantum. Since Si is the weighted CPU service received by
thread i, ![]() represents the total service received
by thread i so far.
Let v denote the minimum value
of Si over all runnable threads. Intuitively, v represents the
processor allocation of the thread that has received the minimum
service so far. Then the surplus service received by
thread i is defined to be
represents the total service received
by thread i so far.
Let v denote the minimum value
of Si over all runnable threads. Intuitively, v represents the
processor allocation of the thread that has received the minimum
service so far. Then the surplus service received by
thread i is defined to be
| (4) |
Having provided the intuition for our algorithm, the precise SFS algorithm is as follows:
| (5) |
 |
(6) |
![[*]](foot_motif.gif) The
entire implementation effort took less than three weeks and was around
1500 lines of code. In the rest of this section, we present the
details of our kernel implementation and explain some of our key
design decisions.
The
entire implementation effort took less than three weeks and was around
1500 lines of code. In the rest of this section, we present the
details of our kernel implementation and explain some of our key
design decisions.
The implementation of surplus fair scheduling was done in version 2.2.14 of the Linux kernel. Our implementation replaces the standard time sharing scheduler in Linux; the modified kernel schedules all threads/processes using SFS. Each thread in the system is assigned a default weight of 1; the weight assigned to a thread can be modified (or queried) using two new system calls--setweight and getweight. The parameters expected by these system calls are similar to the setpriority and getpriority system calls employed by the Linux time sharing scheduler. SFS allows the weight assigned to a thread to be modified at any time (just as the Linux time sharing scheduler allows the priority of a thread to be changed on-the-fly).
Our implementation of SFS maintains three queues. The first queue consists of all runnable threads in descending order of their weights. The other two queues consist of all runnable threads in increasing order of start tags and surplus values, respectively. The first queue is employed by the readjustment algorithm to determine the feasibility of the assigned weights (recall from Section 2.1 that maintaining a list of threads sorted by their weights enables the weight readjustment algorithm to be implemented efficiently). The second queue is employed by the scheduler to compute the virtual time; since the queue is sorted on start tags, the virtual time at any instant is simply the start tag of the thread at the head of the queue. The third queue is used to determine which thread to schedule next--maintaining threads sorted by their surplus values enables the scheduler to make scheduling decisions efficiently.
Given these data structures, the actual scheduling is performed as
follows. Whenever a quantum expires or one of the currently running
threads blocks, the Linux kernel invokes the SFS scheduler.
The SFS scheduler first updates the finish tag of the thread
relinquishing the processor and then computes its start tag (if the
thread is still runnable). The scheduler then computes the new virtual
time; if the virtual time changes from the previous scheduling
instance, then the scheduler must update the surplus values of all
runnable threads (since ![]() is a function of v) and re-sort
the queue. The scheduler then picks the thread with the minimum
surplus and schedules it for execution. Note that since a running
thread may not utilize its entire allocated quantum due to blocking
events, quantums on different processors are not synchronized; hence,
each processor independently invokes the SFS scheduler when its
currently running thread blocks or is preempted. Finally, the
readjustment algorithm is invoked every time the set of runnable threads
changes (i.e., after each arrival, departure, blocking event or wakeup
event), or if the user changes the weight of a thread.
is a function of v) and re-sort
the queue. The scheduler then picks the thread with the minimum
surplus and schedules it for execution. Note that since a running
thread may not utilize its entire allocated quantum due to blocking
events, quantums on different processors are not synchronized; hence,
each processor independently invokes the SFS scheduler when its
currently running thread blocks or is preempted. Finally, the
readjustment algorithm is invoked every time the set of runnable threads
changes (i.e., after each arrival, departure, blocking event or wakeup
event), or if the user changes the weight of a thread.
Since the scheduling overhead of SFS grows with the number of runnable
threads, we have developed a heuristic to limit the scheduling
overhead when the number of runnable threads becomes large. Our
heuristic is based on the observation that ![]() and hence, the thread with the minimum surplus
typically has either a small weight, a small start tag, or a small
surplus in the previous scheduling instance. Consequently, examining a
few threads with small start tags, small weights, or small prior
surplus values, computing their new surpluses and choosing the thread
with minimum surplus is a good heuristic in practice.
Since our implementation already maintains three queues sorted by
and hence, the thread with the minimum surplus
typically has either a small weight, a small start tag, or a small
surplus in the previous scheduling instance. Consequently, examining a
few threads with small start tags, small weights, or small prior
surplus values, computing their new surpluses and choosing the thread
with minimum surplus is a good heuristic in practice.
Since our implementation already maintains three queues sorted by
![]() , Si and
, Si and ![]() , this can be trivially done by
examining the first few threads in each queue, computing their new
surplus values and picking the thread with the least surplus.
This obviates the need to update the surpluses and to re-sort every
time the virtual time changes; the scheduler needs to do so only every
so often and can use the heuristic between updates (infrequent updates
and sorting are still required to maintain a high accuracy of the
heuristic). Hence, the scheduling overhead reduces to a constant and
becomes independent of the number of runnable threads in the system
(updates to
, this can be trivially done by
examining the first few threads in each queue, computing their new
surplus values and picking the thread with the least surplus.
This obviates the need to update the surpluses and to re-sort every
time the virtual time changes; the scheduler needs to do so only every
so often and can use the heuristic between updates (infrequent updates
and sorting are still required to maintain a high accuracy of the
heuristic). Hence, the scheduling overhead reduces to a constant and
becomes independent of the number of runnable threads in the system
(updates to ![]() and sorting continue to be
and sorting continue to be ![]() , but
this overhead is amortized over a large number of scheduling
instances). Moreover, since the heuristic examines multiple runnable
threads, it can be easily combined with the technique proposed in
Section 2.4 to account for processor affinities.
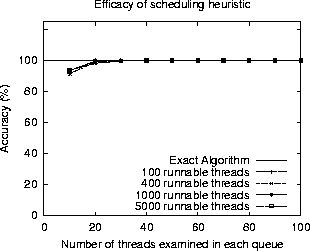
We conducted several simulation experiments to determine
the efficacy of this heuristic. Figure 3 plots the
percentage of the time our heuristic successfully picks the thread
with the minimum surplus (we omit detailed results due to space
constraints). The figure shows that, in a quad-processor system,
examining the first 20 threads in each queue provides sufficient
accuracy (
, but
this overhead is amortized over a large number of scheduling
instances). Moreover, since the heuristic examines multiple runnable
threads, it can be easily combined with the technique proposed in
Section 2.4 to account for processor affinities.
We conducted several simulation experiments to determine
the efficacy of this heuristic. Figure 3 plots the
percentage of the time our heuristic successfully picks the thread
with the minimum surplus (we omit detailed results due to space
constraints). The figure shows that, in a quad-processor system,
examining the first 20 threads in each queue provides sufficient
accuracy (![]() ) even when the number of runnable threads is as
large as 5000 (the actual number of threads in the system is typically
much larger).
) even when the number of runnable threads is as
large as 5000 (the actual number of threads in the system is typically
much larger).
 |
As a final caveat, the Linux kernel uses only integer variables for
efficiency reasons and avoids using floating point variables as a data
type. Since the computation of start tags, finish tags and surplus
values involves floating point operations, we simulate floating point
variables using integer variables. To do so we scale each floating
point operation in SFS by a constant factor. Employing a scaling
factor of 10n for each floating point operation enables us to
capture n places beyond the decimal point in an integer variable
(e.g., the finish tag is computed as ![]() ). The scaling factor is a compile time parameter and
can be chosen based on the desired accuracy--we found a scaling
factor of 104 to be adequate for most purposes. Observe that a
large scaling factor can hasten the warp-around in the start and
finish tags of long running threads; we deal with wraparound by
adjusting all start and finish tags with respect to the minimum start
tag in the system and resetting the virtual time.
). The scaling factor is a compile time parameter and
can be chosen based on the desired accuracy--we found a scaling
factor of 104 to be adequate for most purposes. Observe that a
large scaling factor can hasten the warp-around in the start and
finish tags of long running threads; we deal with wraparound by
adjusting all start and finish tags with respect to the minimum start
tag in the system and resetting the virtual time.
The workload for our experiments consisted of a combination of real-world applications, benchmarks, and sample applications that we wrote to demonstrate specific features. These applications include: (i) Inf, a compute-intensive application that performs computations in an infinite loop; (ii) Interact, an I/O bound interactive application; (iii) thttpd, a single-threaded event-based web server, (iv) mpeg_play, the Berkeley software MPEG-1 decoder, (v) gcc, the GNU C compiler, (vi) disksim, a publicly-available disk simulator, (vii) dhrystone, a compute-intensive benchmark for measuring integer performance, and (viii) lmbench, a benchmark that measures various aspects of operating system performance. Next, we describe the experimental results obtained using these applications and benchmarks.
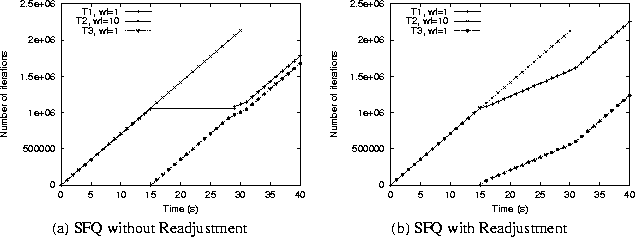 |
To show that the weight readjustment algorithm can be combined with existing GPS-based scheduling algorithms to reduce the unfairness in their allocations, we conducted the following experiment. At t=0, we started two Inf applications (T1 and T2) with weights 1:10. At t=15s, we started a third Inf application (T3) with a weight of 1. Task T2 was then stopped at t=30s.We measured the processor shares received by the three applications (in terms of number of loops executed) when scheduled using SFQ; we then repeated the experiment with SFQ coupled with the weight readjustment algorithm. Observe that this experimental scenario corresponds to the infeasible weights problem described in Example 1 of Section 1.2. As expected, SFQ is unable to distinguish between feasible and infeasible weight assignments, causing task T1 to starve upon the arrival of task T3 at t=15s (see Figure 4(a)). In contrast, when coupled with the readjustment algorithm, SFQ ensures that all tasks receive bandwidth in proportion to their instantaneous weights (1:1 from t=0 through t=15, and 1:2:1 from t=15 through t=30, and 1:1 from then on). See Figure 4(b). This demonstrates that the weight readjustment algorithm enables a GPS-based scheduler such as SFQ to reduce the unfairness in its allocations in multiprocessor environments.
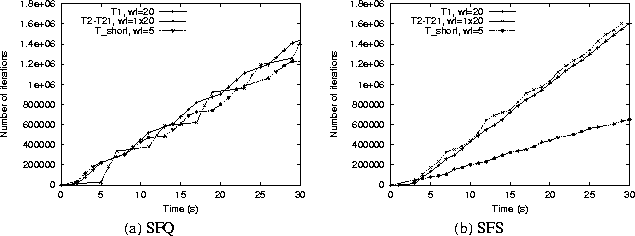 |
In this section, we demonstrate that even with the weight readjustment algorithm, SFQ can show unfairness in multiprocessor environments, especially in the presence of frequent arrivals and departures (as discussed in Example 2 of Section 1.2). We also show that SFS does not suffer from this limitation. To demonstrate this behavior, we started an Inf application (T1) with a weight of 20, and 20 Inf applications (collectively referred to as T2-21), each with weight of 1. To simulate frequent arrivals and departures, we then introduced a sequence of short Inf tasks (Tshort) into the system. Each of these short tasks was assigned a weight of 5 and ran for 300ms each; each short task was introduced only after the previous one finished. Observe that the weight assignment is feasible at all times, and the weight readjustment algorithm never modifies any weights. We measured the processor share received by each application (in terms of the cumulative number of loops executed). Since the weights of T1, T2-21 and Tshort are in the ratio 20:20:5, we expect T1 and T2-21 to receive an equal share of the total bandwidth and this share to be four times the bandwidth received by Tshort. However, as shown in Figure 5(a), SFQ is unable to allocate bandwidth in these proportions (in fact, each set of tasks receives approximately an equal share of the bandwidth). SFS, on the other hand, is able to allocate bandwidth approximately in the requested proportion of 4:4:1 (see Figure 5(b)).
The primary reason for this behavior is that SFQ schedules threads in ``spurts''--threads with larger weights (and hence, smaller start tags) run continuously for some number of quanta, then threads with smaller weights run for a few quanta and the cycle repeats. In the presence of frequent arrivals and departures, scheduling in such ``spurts'' allows tasks with higher weights (T1 and Tshort in our experiment) to run almost continuously on the two processors; T2-21 get to run infrequently. Thus, each Tshort task gets as much processor share as the higher weight task T1; since each Tshort task is short lived, SFQ is unable to account for the bandwidth allocated to the previous task when the next one arrives. SFS, on the other hand, schedules each application based on its surplus. Consequently, no task can run continuously and accumulate a large surplus without allowing other tasks to run first; this finer interleaving of tasks enables SFS to achieve proportionate allocation even with frequent arrivals and departures.
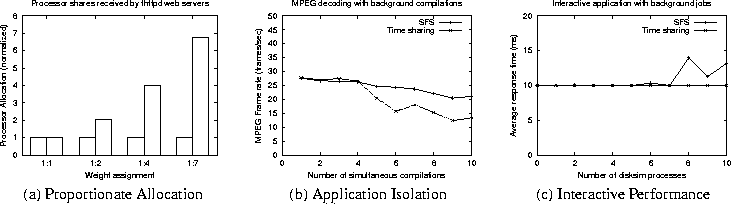 |
Next, we demonstrate proportionate allocation and application isolation of tasks in SFS. To demonstrate proportionate allocation, we ran 20 background dhrystone processes, each with a weight of 1. We then ran two thttpd web servers and assigned them different weights (1:1, 1:2, 1:4 and 1:7). A large number of requests were then sent to each web server. In each case, we measured the average processor bandwidth allocated to each web server (the background dhrystone processes were necessary to ensure that all weights were feasible at all times; without these processes, no weight assignment other than 1:1 would be feasible in a dual-processor system). As shown in Figure 6(a), the processor bandwidth allocated by SFS to each web server is in proportion to its weight.
To show that SFS can isolate applications from one another, we ran the mpeg_play software decoder in the presence of a background compilation workload. The decoder was given a large weight and used to decode a 5 minute long MPEG-1 clip that had an average bit rate of 1.49 Mb/s. Simultaneously, we ran a varying number of gcc compile jobs, each with a weight of 1. The scenario represents video playback in the presence of background compilations; running multiple compilations simultaneously corresponds to a parallel make job (i.e., make -j) that spawns multiple independent compilations in parallel. Observe that assigning a large weight to the decoder ensures that the readjustment algorithm will effectively assign it the bandwidth of one processor, and the compilations jobs share the bandwidth of the other processor.
We varied the compilation workload and measured the frame rate achieved by the software decoder. We then repeated the experiment with the Linux time sharing scheduler. As shown in Figure 6(b), SFS is able to isolate the video decoder from the compilation workload, whereas the Linux time sharing scheduler causes the processor share of the decoder to drop with increasing load. We hypothesize that the slight decrease in the frame rate in SFS is caused due to the increasing number of intermediate files created and written by the gcc compiler, which interferes with the reading of the MPEG-1 file by the decoder.
Our final experiment consisted of an I/O-bound interactive application Interact that ran in the presence of a background simulation workload (represented by some number of disksim processes). Each application was assigned a weight of 1, and we measured the response time of Interact for different background loads. As shown in Figure 6(c), even in the presence of a compute-intensive workload, SFS provides response times that are comparable to the time sharing scheduler (which is designed to give higher priority to I/O-bound applications).
We used lmbench, a publicly available operating system
benchmark, to measure the overheads imposed by the SFS scheduler. We
ran lmbench on a lightly loaded machine with SFS and repeated the
experiment with the Linux time sharing scheduler. In each case, we
averaged the statistics reported by Lmbench over several runs to
reduce experimental error. Note that the SFS code is untuned, while
the time sharing scheduler has benefited from careful tuning by the
Linux kernel developers. Table 1 summarizes our
results (we report only those lmbench statistics that are relevant to
the CPU scheduler). As shown in Table 1, the overhead
of creating processes (measured using the fork and exec
system calls) is comparable in both schedulers. The context switch
overhead, however, increases from 1 ![]() s to 4
s to 4 ![]() s for two 0KB
processes (the size associated with a process is the size of the array
manipulated by each process and has implications on processor cache
performance [13]). Although the overhead imposed by SFS is
higher, it is still considerably smaller than the 200 ms quantum
duration employed by Linux. The context switch overheads increase in
both schedulers with increasing number of processes and increasing
process sizes. SFS continues to have a slightly higher overhead, but
the percentage difference between the two schedulers decreases with
increasing process sizes (since the restoration of the cache state
becomes the dominating factor in context switches).
s for two 0KB
processes (the size associated with a process is the size of the array
manipulated by each process and has implications on processor cache
performance [13]). Although the overhead imposed by SFS is
higher, it is still considerably smaller than the 200 ms quantum
duration employed by Linux. The context switch overheads increase in
both schedulers with increasing number of processes and increasing
process sizes. SFS continues to have a slightly higher overhead, but
the percentage difference between the two schedulers decreases with
increasing process sizes (since the restoration of the cache state
becomes the dominating factor in context switches).
Figure 7 plots the context switch overhead imposed by the two schedulers for varying number of 0 KB processes (the array sizes manipulated by each process was set to zero to eliminate caching overheads from the context switch times). As shown in the figure, the context switch overhead increases sharply as the number of processes increases from 0 to 5, and then grows with the number of processes. The initial increase is due to the increased book-keeping overheads incurred with a larger number of runnable processes (scheduling decisions are trivial when there is only one runnable process and require minimal updates to kernel data structures). The increase in scheduling overhead thereafter is consistent with the complexity of SFS reported in Section 3.2 (the scheduling heuristic presented in that section was not used in this experiment). Interestingly, the Linux time sharing scheduler also imposes an overhead that grows with the number of processes.
In SFS, the QoS requirements of an application are distilled to a single dimension, namely its rate (which is specified using a weight). That is, SFS is a pure proportional-share CPU scheduler. Applications can have requirements along other dimensions. For instance, interactive applications tend to be more latency-sensitive than batched applications, or a certain application may need to have higher priority than other applications. Recent research has extended GPS-based proportional-share schedulers to account for these dimensions. For instance, SMART [16] enhances a GPS-based scheduler with priorities, while BVT [7] extends a GPS-based scheduler to handle latency requirements of threads. We plan to explore similar extensions for GMS-based schedulers such as SFS as part of our future work.
GPS-based schedulers such as SFQ can perform hierarchical
scheduling. This allows threads to be aggregated into classes and CPU
shares to be allocated on a per-class basis. Consequently,
hierarchical schedulers can handle resource principals (e.g.,
processes) consisting of multiple threads. Many hierarchical
schedulers also support class-specific schedulers, in which the bandwidth
allocated to a class is distributed among individual threads using a
class-specific scheduling policy. SFS is a single-level scheduler
and can only handle resource principals with a single thread. We are
currently enhancing SFS to overcome both limitations. To handle
resource principals with multiple threads, we are generalizing our
weight readjustment algorithm. Specifically, a resource principal with
![]() threads can be simultaneously scheduled on
threads can be simultaneously scheduled on ![]() processors. The feasibility constraint for such a resource
principal is specified as
processors. The feasibility constraint for such a resource
principal is specified as
| (7) |
SMP-based time-sharing schedulers employed by conventional operating systems take caching effects into account while scheduling threads [25]. As explained in Section 2.4, SFS can be modified to take such processor affinities into account while making scheduling decisions. However, the implications of doing so on fairness guarantees and cache performance need further investigation.
Regardless of whether resources are allocated in relative or absolute terms, a predictable scheduler will need to employ techniques to restrict the number of threads in the system in order to provide performance guarantees. While some schedulers integrate an admission control test with the scheduling algorithm, others implicitly assume that such an admission control test will be employed but do not specify a particular test. SFS falls into the latter category--the system will need to employ admission control if threads desire specific performance guarantees. Assuming such a test is employed, fair proportional-share schedulers have been shown to provide bounds on the throughput received and the latency incurred by threads [4,9]. We are currently analyzing SFS to determine the performance guarantees that can be provided to a thread. Note, however, that the scheduling heuristic and the processor affinity bias can weaken the guarantees provided by SFS.
Finally, proportional-share schedulers such as SFS need to be combined with tools that enable a user to determine an application's resource requirements. Such tools should, for instance, allow a user to determine the processing requirements of an application (for instance, by application profiling), translate these requirements to appropriate weights, and modify weights dynamically if these resource requirements change [6,21]. Translating application requirements such as rate to an appropriate set of weights is the subject of future research.
We would like to thank the anonymous reviewers and our shepherd Mike Jones for their comments.
|
This paper was originally published in the
Proceedings of the 4th USENIX OSDI Symposium,
October 23-25, 2000, San Diego, California, USA.
Last changed: 16 Jan. 2002 ml |
|