TCP Nice

The Nice extension adds three components to Vegas: first, a more sensitive congestion detector; second, multiplicative reduction in response to increasing round trip times; and third, the ability to reduce the congestion window below one. These additions are simple, but our analysis and experiments demonstrate that the omission of any of them would fundamentally increase the interference caused by background flows.

A Nice flow monitors round-trip delays, estimates the total queue size at the bottleneck router, and signals congestion when this total queue size exceeds a fraction of the estimated maximum queue capacity. Nice uses $minRTT$, the minimum observed round trip time, as the estimate of the round trip delay when queues are empty, and it uses $maxRTT$ as an estimate of the round trip time when the bottleneck queue is full. If more than $\textit{fraction}$ of the packets Nice sends during a RTT window encounter delays exceeding $minRTT + (maxRTT - minRTT) \cdot threshold$, our detector signals congestion. Round-trip delays of packets are indicative of the current bottleneck queue size and the threshold represents the fraction of the total queue capacity that starts to trigger congestion. The Nice congestion avoidance mechanism incorporating the interference trigger with threshold $t$ and fraction $f$ can be written as follows ($curRTT$ is the round-trip delay experienced by each packet):

per ack operation:

 if (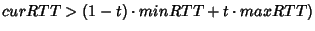$curRTT > (1-t)\cdot minRTT + t \cdot maxRTT)$ 

$numCong$++;


per round operation:

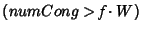
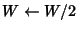
 if $(numCong > {\textit f}\cdot W)$ 

$W \leftarrow W/2$ 

else 		 { 

...  // Vegas congestion avoidance follows

}

If the congestion condition does not trigger, Nice falls back on Vegas' congestion avoidance rules. If a packet is lost, Nice falls back on Reno's rules. The final change to congestion control is to allow the window sizes to multiplicatively decrease below one, if so dictated by the congestion trigger and response. In order to affect window sizes less than one, we send a packet out after waiting for the appropriate number of smoothed round-trip delays.

Maintaining a window of less than one causes us to lose ack-clocking, but the flow continues to send at most as many packets into the network as it gets out. In this phase the packets act as network probes waiting for congestion to dissipate. By allowing the window to go below one, Nice retains the non-interference property even for a large number of flows. Both our analysis and our experiments confirm the importance of this feature: this optimization significantly reduces interference, particularly when testing against several background flows. A similar optimization has been suggested even for regular flows to handle cases when the number of flows starts to approach the bottleneck router buffer size [35].

When a Nice flow signals congestion, it halves its current congestion window. In contrast Vegas reduces its window by one packet each round that encounters long round trip times and only halves its window if packets are lost (falling back on Reno-like behavior.) The combination of more aggressive detection and more aggressive reaction may make it more difficult for Nice to maximize utilization of spare capacity, but our design goals lead us to minimize interference even at the potential cost of utilization. Our experimental results show that even with these aggressively timid policies, we achieve reasonable levels of utilization in practice.

As in TCP Vegas, maintaining running measures of $minRTT$ and $maxRTT$ have their limitations - for example, if the network is in a state of persistent congestion, a bad estimate of $minRTT$ is likely to be obtained. However, past studies  [1,44] have indicated that a good estimate of the minimum round-trip delay can typically be obtained in a short time; our experience supports this claim. The use of minimum and maximum values makes the prototype sensitive to outliers. Using the first and ninety-ninth percentile values could improve the robustness of this algorithm, but we have not tested this optimization. Route changes during a transfer can also contribute to inaccuracies in RTT estimates. However such changes are uncommon [40] and we speculate that they can be handled by maintaining exponentially decaying averages for $minRTT$ and $maxRTT$ estimates.