5th Symposium on Operating Systems Design and Implementation

Samuel Madden, Michael J. Franklin, Joseph M. Hellerstein and Wei Hong
{madden, franklin, jmh}@cs.berkeley.edu, whong@intel-research.net
UC Berkeley and Intel Research, Berkeley

Abstract:

We present the Tiny AGgregation (TAG) service for aggregation in low-power, distributed, wireless environments. TAG allows users to express simple, declarative queries and have them distributed and executed efficiently in networks of low-power, wireless sensors. We discuss various generic properties of aggregates, and show how those properties affect the performance of our in network approach. We include a performance study demonstrating the advantages of our approach over traditional centralized, out-of-network methods, and discuss a variety of optimizations for improving the performance and fault-tolerance of the basic solution.

1 Introduction

Recent advances in computing technology have led to the production of a new class of computing device: the wireless, battery powered, smart sensor (25). These new sensors are active, full fledged computers, capable not only of measuring real world phenomena but also filtering, sharing, and combining those measurements. One example of such small sensor devices are the motes under development at UC Berkeley. Current generation motes are roughly 2cm x 4cm x 1cm and are equipped with a radio, a processor, memory, a small battery pack, and a suite of sensors. The mote operating system, TinyOS, provides a set of primitives designed to facilitate the deployment of motes in ad-hoc networks. In such networks, devices can identify each other and route data without prior knowledge of or assumptions about the network topology, allowing the network topology to change as devices move, run out of power, or experience shifting waves of interference.

Due to the relative ease of deployment of mote-based sensor networks, practitioners in a variety of fields have begun considering them for a range of monitoring and data collection tasks. For example: civil engineers are using motes to monitor building integrity during earthquakes (31); biologists are planning mote deployments for habitat monitoring(5,21); administrators of large computer clusters are interested in using motes to monitor the temperature and power usage in their data centers.

All of these sensor applications depend on the ability to extract data from the network. Often, this data consists of summaries (or aggregations) rather than raw sensor readings. Other researchers have noted the importance of data aggregation in sensor networks (12,10,13). This previous work has tended to view aggregation as an application-specific mechanism that would be programmed into the devices on an as-needed basis, typically in error-prone, low-level languages like C. In contrast, our position is that because aggregation is so central to emerging sensor network applications, it must be provided as a core service by the system software. Instead of a set of extensible C APIs, we believe this service should consist of a generic, easily invoked high-level programming abstraction. This approach enables users of sensor networks, who often are not networking experts or even computer scientists, to focus on their applications free from the idiosyncrasies of the underlying embedded OS and hardware.

1.1 The TAG Approach

We have developed Tiny AGgregation (TAG), a generic aggregation service for ad hoc networks of TinyOS motes. There are two essential attributes of this service. First, it provides a simple, declarative interface for data collection and aggregation, inspired by selection and aggregation facilities in database query languages. Second, it intelligently distributes and executes aggregation queries in the sensor network in a time and power-efficient manner, and is sensitive to the resource constraints and lossy communication properties of wireless sensor networks. TAG processes aggregates in the network by computing over the data as it flows through the sensors, discarding irrelevant data and combining relevant readings into more compact records when possible.

TAG operates as follows: users pose aggregation queries from a powered, storage-rich basestation. Operators that implement the query are distributed into the network by piggybacking on the existing ad hoc networking protocol. Sensors route data back towards the user through a routing tree rooted at the basestation. As data flows up this tree, it is aggregated according to an aggregation function and value-based partitioning specified in the query. As an example, consider a query that counts the number of nodes in a network of indeterminate size. First, the request to count is injected into the network. Then, each leaf node in the tree reports a count of 1 to their parent; interior nodes sum the count of their children, add 1 to it, and report that value to their parent. Counts propagate up the tree in this manner, and flow out at the root.

1.2 Overview of the Paper

The remainder of the paper is structured as follows. In the next section, we briefly review the TinyOS hardware and software environment. Then, we discuss the syntax and semantics of queries in TAG and classify the types of aggregates supported by the system, focusing on the characteristics of aggregates that impact their performance and fault tolerance. We then present the core TAG algorithm and show how our solution satisfies the query requirements while providing performance and tolerance to network faults. We discuss several optimizations for improving the performance of the basic approach. Additionally, we include experimental results demonstrating the effectiveness and robustness of our algorithms in a simulation environment, as well as a brief study of a real-world deployment on TinyOS motes. Finally, we discuss related work and conclude.

2 Motes and Ad-Hoc Networks

2.1 Motes

The single-channel radio is half duplex, meaning motes cannot send and receive at the same time. Currently, the default TinyOS implementation uses a CSMA-like media access protocol with a random backoff scheme. Message delivery is unreliable by default, though applications can build up an acknowledgment layer. Often, a message acknowledgment can be obtained for free (see Section 2.2).

Power is supplied via an AA battery pack or a coin-cell attached through the expansion slot. The effective lifetime of the device is determined by this power supply. In turn, the power consumption of each sensor node tends to be dominated by the cost of transmitting and receiving messages. In terms of power consumption, transmitting a single bit of data is equivalent to 800 instructions. This energy tradeoff between communication and computation implies that many applications will benefit by processing the data inside the network rather than simply transmitting the sensor readings. An AA battery pack will allow a mote to send 5.52 million messages (if it does no other computation and only powers its radio up to transmit) which is equivalent to one message per second every day for about two months - not long if the goal is to deploy long lived, zero-maintenance ad-hoc sensor networks. Hence, power-conserving algorithms are particularly important. ¹ As we will discuss in Section 4.1 , our design is amenable to very low power modes in which the radio is kept powered down for long periods of time.

To understand how data is routed in our ad-hoc aggregation network, two properties of radio communication need to be emphasized. First, radio is a broadcast medium so that any mote within hearing distance hears a message, irrespective of whether or not that mote is the intended recipient. Second, we only make use of symmetric links (where if mote a can hear mote b, b can also hear a.) As is common in ad-hoc protocols, asymmetric links are detected and blacklisted using a technique similar to that proposed in AODV (24).

Messages in the current generation of TinyOS are a fixed size - by default, 30 bytes. Each device has a unique sensor ID that distinguishes it from others. All messages specify their recipient (or specify broadcast, meaning all available recipients), allowing motes to ignore messages not intended for them, although non-broadcast messages are received by all motes within range - unintended recipients simply drop messages not addressed to them.

2.2 Ad-Hoc Routing Algorithm

Given this overview of the mote environment, we now discuss how sensor devices route data. One common technique, which we sketch here, is to build a routing tree. We omit some details of this approach due to space constraints - a number routing protocols suitable for this purpose have been proposed; the reader is referred to (32,1,2,13,14) for more information. In general, TAG is agnostic to the choice of routing algorithm, requiring it to provide just two capabilities. First, it must be able to deliver query requests to all nodes in a network.² Second, it must be able to provide one or more routes from every node to the root of the network where aggregation data is being collected. These routes must guarantee that at most one copy of every message arrive (no duplicates are generated).

In the tree-based routing scheme, one mote is appointed to be the root, usually because it is the point where the user interfaces to the network. The root broadcasts a message asking motes to organize into a routing tree; in that message it specifies its own id and its level, or distance from the root (in this case, zero.) Any mote without an assigned level that hears this message assigns its own level to be the level in the message plus one. It also chooses the sender of the message as its parent, through which it will route messages to the root.

Each of these motes then rebroadcasts the routing message, inserting their own ids and levels. The routing message floods down the tree in this fashion, with each node rebroadcasting the message until all nodes have been assigned a level and a parent. These routing messages are periodically broadcast from the root, so that the process of topology discovery goes on continuously. This constant topology maintenance makes it relatively easy to adapt to network changes caused by mobility of certain nodes, or to the addition or deletion of motes. We describe a specific topology maintenance protocol used for our experiments on loss in Section 7.1 below. To maintain stability in the network, parents are retained unless a child does not hear from them for some long period of time, at which point it selects a new parent using this same process. We look in more detail at the robustness of this approach with respect to loss and its effect on aggregate values in Section 7.

When a mote wishes to send a message to the root, it broadcasts a message addressed to its parent, which in turn forwards the message on to its parent, and so on, eventually reaching the root. In Section 4, we show how, as data is routed towards the root, it can be combined with data from other motes to efficiently combine routing and aggregation. Now, however, we turn to the syntax and semantics of aggregate queries in TAG.

3 Query Model and Environment

Given our goal of allowing users to pose declarative queries over sensor networks, we needed a language for expressing such queries. Rather than inventing our own, we chose to adopt a SQL-style query syntax. We support SQL-style queries (without joins) over a single table called sensors, whose schema is known at the base station. As is the case in Cougar (23), this table can be thought of as an append-only relational table with one attribute per input of the motes (e.g., temperature, light.) In TAG, we focus on the problem of aggregate sensor readings, though facilities for collecting individual sensor readings also exist.

Before describing the semantics of queries in general, we begin with an example query. Consider a user who wishes to monitor the occupancy of the conference rooms on a particular floor of a building, which she chooses to do by using microphone sensors attached to motes, and looking for rooms where the average volume is over some threshold (assuming that rooms can have multiple sensors). Her query could be expressed as:

SELECT AVG(volume),room FROM sensors
WHERE floor = 6
GROUP BY room
HAVING AVG(volume) > threshold
EPOCH DURATION 30s

This query partitions motes on the 6th floor according to the room in which they are located (which may be a hard-coded constant in each device, or may be determined via some localization component available to the devices.) The query then reports all rooms where the average volume is over a specified threshold. Updates are delivered every 30 seconds, although the user may deregister her query at any time.

SELECT {agg(expr), attrs} FROM sensors
WHERE {selPreds}
GROUP BY {attrs}
HAVING {havingPreds}
EPOCH DURATION i

With the exception of the EPOCH DURATION clause, the semantics of this statement are similar to SQL aggregate queries. The SELECT clause specifies an arbitrary arithmetic expression over one or more aggregation attributes. We expect that the common case here is that expr will simply be the name of a single attribute. Attrs (optionally) selects the attributes by which the sensor readings are partitioned ; these can be any subset of attrs that appear in the GROUP BY clause. The syntax of the agg clause is discussed below; note that multiple aggreggates may be computed in a single query. The WHERE clause filters out individual sensor readings before they are aggregated. Such predicates can typically be executed locally at the mote before readings are communicated, as in (18,23). The GROUP BY clause specifies an attribute based partitioning of sensor readings. Logically, each reading belongs to exactly one group, and the evaluation of the query is a table of group identifiers and aggregate values. The HAVING clause filters that table by suppressing groups that do not satisfy the havingPreds predicates.

The primary semantic difference between TAG queries and SQL queries is that the output of a TAG query is a stream of values, rather than a single aggregate value (or batched result). In monitoring applications, such continuous results are often more useful than a single, isolated aggregate, as they allow users to understand how the network is behaving over time and observe transient effects (such as message losses) that make individual results, taken in isolation, hard to interpret. In these stream semantics, each record consists of one <group id,aggregate value> pair per group. Each group is time-stamped and the readings used to compute an aggregate record all belong to the same time interval, or epoch. The duration of each epoch is the argument of the EPOCH DURATION clause, which specifies the amount of time (in seconds) devices wait before acquiring and transmitting each successive sample. This value may be as large as the user desires; it must be at least as long as the time it takes for a mote to process and transmit a single radio message and do some local processing - about 30 ms (including average MAC backoff in a low-contention environment) for current generation motes (yielding a maximum sample rate of about 33 samples per second.) In section 4.1, we discuss situations that require longer lower bounds on epoch duration.

3.1 Structure of Aggregates

The problem of computing aggregate queries in large clusters of nodes has been addressed in the context of shared-nothing parallel query processing environments (26). Like sensor networks, those environments require the coordination of a large number of nodes to process aggregations. Thus, while the severe bandwidth limitations, lossy communications, and variable topology of sensor networks mean that the specific implementation techniques used in the two environments must differ, it is still useful to leverage the techniques for aggregate decomposition used in database systems (2,35).

The approach used in such systems (and followed in TAG) is to implement agg via three functions: a merging functionf, an initializer i, and an evaluator, e.

where <x> and <y> are multi-valued partial state records, computed over one or more sensor values, representing the intermediate state over those values that will be required to compute an aggregate. <z> is the partial-state record resulting from the application of function f to <x> and <y>. For example, if f is the merging function for AVERAGE, each partial state record will consist of a pair of values: SUM and COUNT, and f is specified as follows, given two state records <S₁, C₁> and <S₂, C₂>:

The initializer i is needed to specify how to instantiate a state record for a single sensor value; for an AVERAGE over a sensor value of x, the initializer i(x) returns the tuple <x, 1>. Finally, the evaluator e takes a partial state record and computes the actual value of the aggregate. For AVERAGE, the evaluator e(<S, C>) simply returns S / C.

These three functions can easily be derived for the basic SQL aggregates; in general, any operation that can be expressed as commutative applications of a binary function is expressible.

3.2 Taxonomy of Aggregates

Given our basic syntax and structure of aggregates, an obvious question remains: what aggregate functions can be expressed in TAG? The original SQL specification offers just five options: COUNT, MIN, MAX, SUM, and AVERAGE. Although these basic functions are suitable for a wide range of database applications, we did not wish to constrain TAG to only these choices. For this reason, we present a general classification of aggregate functions and show how the dimensions of that classification affect the performance of TAG throughout the paper. We will assume that when aggregation functions are registered with TAG, they are classified along the dimensions described below.³

	`MAX, MIN`	`COUNT, SUM`	`AVERAGE`	`MEDIAN`	`COUNT DISTINCT` ⁴	`HISTOGRAM` ⁵	Section
Duplicate Sensitive	No	Yes	Yes	Yes	No	Yes	Section 7.5
Exemplary (E), Summary (S)	E	S	S	E	S	S	Section 6.2
Monotonic	Yes	Yes	No	No	Yes	No	Section 4.2
Partial State	Distributive	Distributive	Algebraic	Holistic	Unique	Content-Sensitive	Section 5.1

We classify aggregates according to four properties that are particularly important to sensor networks. Table 1 shows how specific aggregation functions can be classified according to these properties, and indicates the sections of the paper where the various dimensions of the classification are emphasized.

The first dimension is duplicate sensitivity. Duplicate insensitive aggregates are unaffected by duplicate readings from a single device while duplicate sensitive aggregates will change when a duplicate reading is reported. Duplicate sensitivity implies restrictions on network properties and on certain optimizations, as described in Section 7.5.

Second, exemplary aggregates return one or more representative values from the set of all values; summary aggregates compute some property over all values. This distinction is important because exemplary aggregates behave unpredictably in the face of loss, and, for the same reason, are not amenable to sampling. Conversely, for summary aggregates, the aggregate applied to a subset can be treated as a robust approximation of the true aggregate value, assuming that either the subset is chosen randomly, or that the correlations in the subset can be accounted for in the approximation logic.

Third, monotonic aggregates have the property that when two partial state records, s₁ and s₂, are combined via f, the resulting state record s' will have the property that either $\forall s_1,s_2, e(s') \ge MAX(e(s_1),e(s_2))$ or $\forall s_1,s_2, e(s') \le MIN(e(s_1),e(s_2))$ . This is important when determining whether some predicates (such as HAVING) can be applied in network, before the final value of the aggregate is known. Early predicate evaluation saves messages by reducing the distance that partial state records must flow up the aggregation tree.

The fourth dimension relates to the amount of state required for each partial state record. For example, a partial AVERAGE record consists of a pair of values, while a partial COUNT record constitutes only a single value. Though TAG correctly computes any aggregate that conforms to the specification of f in Section 3 above, its performance is inversely related to the amount of intermediate state required per aggregate. The first three categories of this dimension (e.g. distributive, algebraic, holistic) were initially presented in work on data-cubes (9).

In summary, we have classified aggregates according to their state requirements, tolerance of loss, duplicate sensitivity, and monotonicity. We will refer back to this classification throughout the text, as these properties will determine the applicability of communication optimizations we present later. Understanding how aggregates fit into these categories is a cross-cutting issue that is critical (and useful) in many aspects of sensor data collection.

Note that our formulation of aggregate functions, combined with this taxonomy, is flexible enough to encompass a wide range of sophisticated operations. For example, we have implemented (in the simulator described in Section 5 below), an isobar finding aggregate. This is a duplicate-insensitive, summary, monotonic, content-sensitive aggregate that builds a topological map representing discrete bands of one attribute (light, for example) plotted against two other attributes (x and y position in some local coordinate space, for example.)

3.3 Attribute Catalog

Queries in TAG contain named attributes. Some mechanism is needed to allow users to determine the set of attributes they may query, and to allow motes to advertise the attributes they can provide. In TAG, we include on each mote a small catalog of attributes. This catalog can be searched for attributes of a specific name, or iterated through. To limit the burden of reporting catalog information from motes, we assume the central query processor caches or stores the attributes of all motes it may access.

When a TAG sensor receives a query, it converts named fields into local catalog identifiers. Nodes lacking attributes specified in the query simply tag missing attributes as NULL in their result records (alternatively, the query could specify that the lacking node should opt out of the query.) This technique increases the scalability of large sensor network deployments as it does not require all nodes to have global knowledge of all attributes.

As in relational databases, partial state records resulting from the evaluation of a query have the same layout across all nodes. Thus, tuples in TAG need not be self-describing; attribute names are not carried with results, leading to a significant reduction in the amount of data that must be propagated with each tuple. At the same time, it is not necessary for all nodes to have identical catalogs, which allows heterogeneous sensing capabilities and incremental deployment of motes.

Attributes in TAG may be direct representations of sensor values, such as light or temperature, or may be introspective, such as remaining energy or network neighborhood information. More generally, they can represent time-varying statistics over local sensor values, such as an exponentially decaying average of the last n light readings, or more complicated attributes such as a room number, GPS coordinate, or relative distance to some neighbor from a localization component. Individual software components in TinyOS choose which attributes they will make available, and provide an accessor function for acquiring the next attribute reading.

4 In Network Aggregates

Given the simple routing protocol from Section 2.2 and our query model, we now discuss the implementation of the core TAG algorithm for in network aggregation.

A naive implementation of sensor network aggregation would be to use a centralized, server-based approach where all sensor readings are sent to the base station, which then computes the aggregates. In TAG, however, we compute aggregates in network whenever possible, because, if properly implemented, this approach can be lower in number of message transmissions, latency, and power consumption than the server-based approach. We will measure the advantage of in network aggregation in Section 5 below; first, we present the basic algorithm in detail. We first consider the operation of the basic approach in the absence of grouping; we show how to extend it with grouping in Section 4.2.

4.1 Tiny Aggregation

TAG consists of two phases: a distribution phase, in which aggregate queries are pushed down into the network, and a collection phase, where the aggregate values are continually routed up from children to parents. Recall that our query semantics partition time into epochs of duration i, and that we must produce a single aggregate value (when not grouping) that combines the readings of all devices in the network during that epoch.

Given our goal of using as few messages as possible, the collection phase must ensure that parents in the routing tree wait until they have heard from their children before propagating an aggregate value for the current epoch. We will accomplish this by having parents subdivide the epoch such that children are required to deliver their partial state records during a parent-specified time interval. This interval is selected such that there is enough time for the parent to combine partial state records and propagate its own record to its parent.

When a mote p receives a request to aggregate, r, either from another mote or from the user, it awakens, synchronizes its clock according to timing information in the message, and prepares to participate in aggregation. In the tree based routing scheme, p chooses the sender of the message as its parent. In addition to the information in the query, r includes the interval when the sender is expecting to hear partial state records from p. p then forwards the query request r down the network, setting this delivery interval for children to be slightly before the time its parent expects to see p's partial state record. In the tree-based approach, this forwarding consists of a broadcast of r, to include any nodes that did not hear the previous round, and include them as children (if it has any.) These nodes continue to forward the request in this manner, until the query has been propagated throughout the network.

During the epoch after query propagation, each mote listens for messages from its children during the interval it specified when forwarding the query. It then computes a partial state record consisting of the combination of any child values it heard with its own local sensor readings. Finally, during the transmission interval requested by its parent, the mote transmits this partial state record up the network. Figure 1 illustrates the process. Notice that parents listen for longer than the transmission interval they specified, to overcome limitations in the quality of clock synchronization algorithms between parents and children. In this way, aggregates flow back up the tree interval-by-interval. Eventually, a complete aggregate arrives at the root. During each subsequent epoch, a new aggregate is produced. Notice that, for a significant portion of each epoch, motes are idle and can enter a low power state.

**Figure 1:** *Partial state records flowing up the tree during an epoch.*
$\begin{figure}\vspace{-.2in} \begin{displaymath}\psfig{figure=ick.eps,width = 2.4in}\end{displaymath}\vspace{-.4in} \vspace{-.1in} \end{figure}$

This scheme begs the question of how parents choose the duration of the interval in which they will receive values. It needs to be long enough such that all of a node's children can report, but not so long that the epoch ends before nodes deep in the tree can schedule their communication. Furthermore, longer intervals require radios to be powered up for more time, which consumes precious energy. In general, the proper choice of duration for these intervals is somewhat environment specific, as it depends on the density of radio cells and ``bushiness'' of the network topology. For the purposes of the simulations and experiments in this paper, we assume the network has a maximum depth d, and set the duration of each interval to be (EPOCH DURATION)/d, with nodes at level i transmitting during the ith interval. We rely on the TinyOS MAC layer (32) to avoid collisions between nodes transmitting during the same interval. Note that this provides a lower-bound on the EPOCH DURATION and constrains the maximum sample rate of the network, since the epoch must be long enough for partial state records from the bottom of the tree to propagate to the root.

To increase the sample rate, one could consider pipelining the communications schedule shown in Figure 1. With pipelining, the output of the network would be delayed by one or more epochs, as some nodes would wait until the next epoch to report the aggregates they collected during the current epoch. In exchange for such delays, the effective sample rate of the system is increased (for the same reason that pipelining a long processor stage increases the clock rate of a CPU.) We do not consider such schemes in detail here; we discussed a fully-pipelined approach to aggregation in a workshop submission (20).

In Section 5.1 we show how TAG can provide an order of magnitude decrease in communications costs over a centralized approach. However, before discussing performance, we extend the approach to support grouping.

4.2 Grouping

Grouping in TAG is functionally equivalent to the GROUP BY clause in SQL: each sensor reading is placed into exactly one group, and groups are partitioned according to an expression over one or more attributes. The basic grouping technique is to push the expression down with the query, ask nodes to choose the group they belong to, and then, as answers flow back, update aggregate values in the appropriate groups.

Partial state records are aggregated just as in the approach described above, except that those records are now tagged with a group id. When a node is a leaf, it applies the grouping expression to compute a group id. It then tags its partial state record with the group and forwards it on to its parent. When a node receives an aggregate from a child, it checks the group id. If the child is in the same group as the node, it combines the two values using the combining function f. If it is in a different group, it stores the value of the child's group along with its own value for forwarding in the next epoch. If another child message arrives with a value in either group, the node updates the appropriate aggregate. During the next epoch, the node sends the value of all the groups about which it collected information during the previous epoch, combining information about multiple groups into a single message as long as message size permits. Figure 2 shows an example of computing a query grouped by temperature that selects average light readings.

**Figure 2:** *A sensor network (left) with an in network, grouped aggregate applied to it (right).* Parenthesized numbers represent nodes that contribute to the average
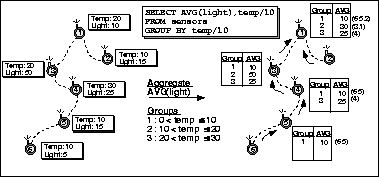$\begin{figure}\vspace{-.1in} \begin{displaymath}\psfig{figure=grouping.eps,width=3.3in}\end{displaymath}\vspace{-.4in} \end{figure}$

Recall that queries may contain a HAVING clause, which constrains the set of groups in the final query result. This predicate can sometimes be passed into the network along with the grouping expression. The predicate is only sent if it can potentially be used to reduce the number of messages that must be sent: for example, if the predicate is of the form MAX(attr) < x, then information about groups with MAX(attr) x need not be transmitted up the tree, and so the predicate is sent down into the network. When a node detects that a group does not satisfy a HAVING clause, it can notify other nodes in the network of this information to suppress transmission and storage of values from that group. Note that HAVING clauses can be pushed down only for monotonic aggregates; non-monotonic aggregates are not amenable to this technique. However, not all HAVING predicates on monotonic aggregates can be pushed down; for example, MAX(attr) > x cannot be applied in the network because a node cannot know that, just because its local value of attr is less than x, the MAX over the entire group is less than x.

Grouping introduces an additional problem: the number of groups can exceed available storage on any one (non-leaf) device. Our proposed solution is to evict one or more groups from local storage. Once an eviction victim is selected, it is forwarded to the node's parent, which may choose to hold on to the group or continue to forward it up the tree. Notice that a single node may evict several groups in a single epoch (or the same group multiple times, if a bad victim is selected). This is because, once group storage is full, if only one group is evicted at a time, a new eviction decision must be made every time a value representing an unknown or previously evicted group arrives. Because groups can be evicted, the base station at the top of the network may be called upon to combine partial groups to form an accurate aggregate value. Evicting partially computed groups is known as partial preaggregation, as described in (15).

Thus, we have shown how to partition sensor readings into a number of groups and properly compute aggregates over those groups, even when the amount of group information exceeds available storage in any one device. We will briefly mention experiments with grouping and group eviction policies in Section 5.2. First, we summarize some of the additional benefits of TAG.

4.3 Additional Advantages of TAG

The principal advantage of TAG is its ability to dramatically decrease the communication required to compute an aggregate versus a centralized aggregation approach. However, TAG has a number of additional benefits.

One of these is its ability to tolerate disconnections and loss. In sensor environments, it is very likely that some aggregation requests or partial state records will be garbled, or that devices will move or run out of power. These losses will invariably result in some nodes becoming lost, either without a parent or not incorporated into the aggregation network during the initial flooding phase. If we include information about queries in partial state records, lost nodes can reconnect by listening to other node's state records - not necessarily intended for them - as they flow up the tree. We revisit the issue of loss in Section 7.

A second advantage of the TAG approach is that, in most cases, each mote is required to transmit only a single message per epoch, regardless of its depth in the routing tree. In the centralized (non TAG) case, as data converges towards the root, nodes at the top of the tree are required to transmit significantly more data than nodes at the leaves; their batteries are drained faster and the lifetime of the network is limited. Furthermore, because the top of the routing tree must forward messages for every node in the network, the maximum sample rate of the system is inversely proportional to the total number of nodes. To see this, consider a radio channel with a capacity of n messages per second. If m motes are participating in a centralized aggregate, to obtain a sample rate of k samples per second, m x k messages must flow through the root during each epoch. m x k must be no larger than n, so the sample rate k can be at most n/m messages per mote per epoch, regardless of the network density. When using TAG, the maximum transmission rate is limited instead by the occupancy of the largest radio-cell; in general, we expect that each cell will contain far fewer than m motes.

Yet another advantage of TAG is that, by explicitly dividing time into epochs, a convenient mechanism for idling the processor is obtained. The long idle times in Figure 1 show how this is possible; during these intervals, the radio and processor can be put into deep sleep modes that use very little power. Of course, some bootstrapping phase is needed where motes can learn about queries currently in the system, acquire a parent, and synchronize clocks; a simple strategy involves requiring that every node wake up infrequently but periodically to advertise this information and that devices that have not received advertisements from their neighbors listen for several times this period between sleep intervals. Research on energy aware MAC protocols (34) presents a similar scheme in detail. That work also discusses issues such as time synchronization resolution and the maximum sleep duration to avoid the adverse effects of clock skew on individual devices.

Taken as a whole, these TAG features provide users with a stream of aggregate values that changes as sensor readings and the underlying network change. These readings are provided in an energy and bandwidth efficient manner.

5 Simulation-Based Evaluation

In this section, we present a simulation environment for TAG and evaluate its behavior using this simulator. We also have an initial, real-world deployment; we discuss its performance at the end of the paper, in Section 8.

To study the algorithms presented in this paper, we simulated TAG in Java. The simulator models mote behavior at a coarse level: time is divided into units of epochs, messages are encapsulated into Java objects that are passed directly into nodes without any model of the time to send or decode. Nodes are allowed to compute or transmit arbitrarily within a single epoch, and each node executes serially. Messages sent by all nodes during one epoch are delivered in random order during the next epoch to model a parallel execution. Note that this simulator cannot account for certain low-level properties of the network: for example, because there is no fine-grained model of time, it is not possible to model radio contention at a byte level.

Our simulation includes an interchangeable communication model that defines connectivity based on geographic distance. Figure 3 shows screenshots of a visualization component of our simulation; each square represents a single device, and shading (in these images) represents the number of radio hops the device is from the root (center); darker is closer. We measure the size of networks in terms of diameter, or width of the sensor grid (in nodes). Thus, a diameter 50 network contains 2500 devices.

We have run experiments with three communications models; 1) a simple model, where nodes have perfect (lossless) communication with their immediate neighbors, which are regularly placed (Figure 3(a)), 2) a random placement model (Figure 3(b)), and 3) a realistic model that attempts to capture the actual behavior of the radio and link layer on TinyOS motes (Figure 3(c).) In this last model, notice that the number of hops from a particular node to the root is no longer directly proportional to the geographic distance between the node and the root, although the two values are still related. This model uses results from real world experiments (7) to approximate the actual loss characteristics of the TinyOS radio. Loss rates are high in in the realistic model: a pair of adjacent nodes loses more than 20% of the traffic between them. Devices separated by larger distances lose still more traffic.

The simulator also models the costs of topology maintenance: if a node does not transmit a reading for several epochs (which will be the case in some of our optimizations below), that node must periodically send a heartbeat to advertise that it is still alive, so that its parents and children know to keep routing data through it. The interval between heartbeats can be chosen arbitrarily; choosing a longer interval means fewer messages must be sent, but requires nodes to wait longer before deciding that a parent or child has disconnected, making the network less adaptable to rapid change.

This simulation allows us to measure the the number of bytes, messages, and partial state records sent over the radio by each mote. Since we do not simulate the mote CPU, it does not give us an accurate measurement of the number of instructions executed in each mote. It does, however, allow us to obtain an approximate measure of the state required for various algorithms, based on the size of the data structures allocated by each mote.

Unless otherwise specified, our experiments are over the simple radio topology in which there is no loss. We also assume sensor values do not change over the course of a single simulation run.

Figure 3: The TAG Simulator, with Three Different Communications Models, Diameter = 20.

$\begin{displaymath}\psfig{figure=screenshot1.ps,width=1in}\end{displaymath}$

(a) Simple

$\begin{displaymath}\psfig{figure=screenshot3.ps,width=1in}\end{displaymath}$

(b) Random

$\begin{displaymath}\psfig{figure=screenshot2.ps,width=1in}\end{displaymath}$

5.1 Performance of TAG

In the first set of experiments, we compare the performance of the TAG in network approach to centralized approaches on queries for the different classes of aggregates discussed in Section 3.2. Centralized aggregates have the same communications cost irrespective of the aggregate function, since all data must be routed to the root. For this experiment, we compared this cost to the number of bytes required for distributive aggregates (MAX and COUNT), an algebraic aggregate (AVERAGE), a holistic aggregate (MEDIAN), a content-sensitive aggregate (HISTOGRAM), and a unique aggregate (COUNT DISTINCT); the results are shown in Figure 4.

Values in this experiment represent the steady-state cost to extract an additional aggregate from the network once the query has been propagated; the cost to flood a request down the tree in not considered.

In our 2500 node (d=50) network, MAX and COUNT have the same cost when processed in the network, about 5000 bytes per epoch (total over all nodes), since they both send just a single integer per partial state record; similarly AVERAGE requires just two integers, and thus always has double the cost of the distributive aggregates. MEDIAN costs the same as a centralized aggregate, about 90000 bytes per epoch, which is significantly more expensive than other aggregates, especially for larger networks, as parents have to forward all of their children's values to the root. COUNT DISTINCT is only slightly less expensive (73000 bytes), as there are few duplicate sensor values; a less uniform sensor-value distribution would reduce the cost of this aggregate. For the HISTOGRAM aggregate, we set the size of the fixed-width buckets to be 10; sensor values ranged over the interval [0..1000]. At about 9000 messages per epoch, HISTOGRAM provides an efficient means for extracting a density summary of readings from the network.

Note that the benefit of TAG will be more or less pronounced depending on the topology. In a flat, single-hop environment, where all motes are directly connected to the root, TAG is no better than the centralized approach. For a topology where n motes are arranged in a line, centralized aggregates will require n²/2 partial state records to be transmitted, whereas TAG will require only n records.

**Figure 4:** *In network Vs. Centralized Aggregates*
$\begin{figure}\vspace{-.2in} \begin{displaymath}\psfig{figure=innet_bar.eps,width=2.5in}\end{displaymath} \vspace{-.4in} \vspace{-.05in} \end{figure}$

Thus, we have shown that, for our simulation topology, in network aggregation can reduce communication costs by an order of magnitude over centralized approaches, and that, even in the worst case (such as with MEDIAN), it provides performance equal to the centralized approach.

5.2 Grouping Experiments

We also ran several experiments to measure the performance of grouping in TAG, focusing on the behavior of various eviction techniques. We tried a number of simple eviction policies, but found that the choice of policy made little difference for any of the sensor-value distributions we tested - in the most extreme case, the difference between the best and worst case eviction policy accounted for less than 10% of the total messages. Due to the relative insignificance of these results and space limitations, we omit a detailed discussion of the merits of various eviction policies.

6 Optimizations

In this section, we present several techniques to improve the performance and accuracy of the basic approach described above. Some of these techniques are function dependent; that is, they can only be used for certain classes of aggregates. Also note that, in general, these techniques can be applied in a user-transparent fashion, since they are not explicitly a part of the query syntax and do not affect the semantics of the results.

6.1 Taking Advantage of A Shared Channel

In Section 4.3, we saw an example of how a shared channel can be used to increase message efficiency when a node misses an initial request to begin aggregation: it can initiate aggregation even after missing the start request by snooping on the network traffic of nearby nodes. When it hears another device reporting an aggregate, it can assume it too should be aggregating. By allowing nodes to examine messages not directly addressed to them, motes are automatically integrated into the aggregation. Note that snooping does not require nodes to listen all the time; by listening at predefined intervals (which can be short once a mote has time-synchronized with its neighbors), duty cycles can be kept quite low.

Snooping can also be used to reduce the number of messages sent for some classes of aggregates. Consider computing a MAX over a group of motes: if a node hears a peer reporting a maximum value greater than its local maximum, it can elect to not send its own value and be sure it will not affecting the value of the final aggregate.

6.2 Hypothesis Testing

The snooping example above showed that we only need to hear from a particular node if that node's value will affect the end value of the aggregate. For some aggregates, this fact can be exploited to significantly reduce the number of nodes that need to report. This technique can be generalized to an approach we call hypothesis testing. For certain classes of aggregates, if a node is presented with a guess as to the proper value of an aggregate, it can decide locally whether contributing its reading and the readings of its children will affect the value of the aggregate.

For MAX, MIN and other monotonic, exemplary aggregates, this technique is directly applicable. There are a number of ways it can be applied - the snooping approach, where nodes suppress their local aggregates if they hear other aggregates that invalidate their own, is one. Alternatively, the root of the network (or any subtree of the network) seeking an exemplary sensor value, such as a MIN, might compute the minimum sensor value m over the highest levels of the subtree, and then abort the aggregate and issue a new request asking for values less than m over the whole tree. In this approach, leaf nodes need not send a message if their value is greater than the minimum observed over the top k levels; intermediate nodes, however, must still forward partial state records, so even if their value is suppressed, they may still have to transmit.

Assuming for a moment that sensor values are independent and uniformly distributed, then a particular leaf node must transmit with probability 1/b^k (where b is the branching factor, so 1/b^k is the number of nodes in the top k levels), which is quite low for even small values of k. For bushy routing trees, this technique offers a significant reduction in message transmissions - a completely balanced routing tree would cut the number of messages required to 1/k. Of course, the performance benefit may not be as substantial for other, non-uniform, sensor value distributions; for instance, a distribution in which all sensor readings are clustered around the minimum will not allow many messages to be saved by hypothesis testing. Similarly, less balanced topologies (e.g. a line of nodes) will not benefit from this approach.

For summary aggregates, such as AVERAGE or VARIANCE, hypothesis testing via a guess from the root can be applied, although the message savings are not as dramatic as with monotonic aggregates. Note that the snooping approach cannot be used: it only applies to monotonic, exemplary aggregates where values can be suppressed locally without any information from a central coordinator. To obtain any benefit with summary aggregates and hypothesis testing, the user must define a fixed-size error bound that he or she is willing to tolerate over the value of the aggregate; this error is sent into the network along with the hypothesis value.

Consider the case of an AVERAGE: any device whose sensor value is within the error bound of the hypothesis value need not answer - its parent will then assume its value is the same as the approximate answer and count it accordingly (to apply this technique with AVERAGE, parents must know how many children they have.) It can be shown that the total computed average will not be off from the actual average by more than the error bound, and leaf nodes with values close to the average will not be required to report. Obviously, the value of this scheme depends on the distribution of sensor values. In a uniform distribution, the fraction of leaves that need not report approximates the size of the error bound divided by the size of the sensor value distribution interval. If values are normally distributed, a much larger fraction of leaves do not report.

We conducted a simple experiment to measure the benefit of hypothesis testing and snooping for a MAX aggregate. The results are shown in Figure 5. In this experiment, sensor values were uniformly distributed over the range [0..100], and a hypothesis was made at the root. Notice that the performance savings are nearly two-fold for a hypothesis of 90. We compared the hypothesis testing approach with the snooping approach (which will be effective even in a non-uniform distribution); surprisingly, snooping beat the other approaches by offering a nearly three-fold performance increase over the no-hypothesis case. This is because in the densely packed simple node distribution, most devices have three or more neighbors to snoop on, suggesting that only about one in four devices will have to transmit. With topology maintenance and forwarding of child values by parents, the savings by snooping is reduced to a factor of three.

**Figure:** *Benefit of Hypothesis Testing for* `MAX`
$\begin{figure}\vspace{-.3in} \begin{displaymath}\psfig{figure=hyponew.ps,height=2.6in}\end{displaymath} \vspace{-.2in} \end{figure}$

7 Improving Tolerance to Loss

Up to this point in our experiments we used a reliable environment where no messages were dropped and no nodes disconnected or went offline. In this section, we address the problem of loss and its effect on the algorithms presented thus far. Unfortunately, unlike in traditional database systems, communication loss is a a fact of life in the sensor domain; the techniques described in the section seek to mitigate that loss.

7.1 Topology Maintenance and Recovery

TAG is designed to sit on top of a shifting network topology that adapts to the appearance and disappearance of nodes. Although a study of mechanisms for adapting topology is not central to this paper, for completeness we describe a basic topology maintenance and recovery algorithm which we use in both our simulation and implementation. This approach is similar to techniques used in practice in existing TinyOS sensor networks, and is derived from the general techniques proposed in the ad-hoc networking literature(22,28).

Networking faults are monitored and adapted to at two levels: First, each node maintains a small, fixed sized list of neighbors, and monitors the quality of the link to each of those neighbors by tracking the proportion of packets received from each neighbor. This is done via a locally unique sequence number associated with each message by its sender. When a node n observes that the link quality to its parent p is significantly worse than that of some other node p', it chooses p' as its new parent if p' is as close or closer to the root as p and p' does not believe n is its parent (the latter two conditions prevent routing cycles.)

Second, when a node observes that it has not heard from its parent for some fixed period of time (relative to the epoch duration of the query it is currently running), it assumes its parent has failed or moved away. It resets its local level (to $\infty$ ) and picks a new parent from the neighbor table according to the quality metric used for link-quality. Note that this can cause a parent to select a node in the routing subtree underneath it as its parent, so child nodes must reselect their parent (as though a failure had occurred) when they observe that their own parent's level has gone up.

Note that switching parents does not introduce the possibility of multiple records arriving from a single node, as each node transmits only once per epoch (even if it switches parents during that epoch.) Parent switching can cause temporary disconnections (and thus additional lost records) in the topology, however, due to children selecting a new parent when their parent's level goes up.

7.2 Effects of A Single Loss

Figure 6 shows the results of this experiment. Note that the maximum loss (Figure 6(a)) is highly variable and that some aggregates are considerably more sensitive to loss than others. COUNT, for instance, has a very large error in the worst case: if a node that connects the root to a large portion of the network is lost, the temporary error will be very high. The variability in maximum error is because a well connected subtree is not always selected as the victim. Indeed, assuming some uniformity of placement (e.g. the devices are not arranged in a line), as the network size increases, the chances of selecting such a node go down, since a larger proportion of the nodes are towards the leaves of the tree. In the average case(Figure 6(b)), the error associated with a COUNT is not as high: most losses do not result in a large number of disconnections. Note that MIN is insensitive to loss in this uniform distribution, since several nodes are at or near the true minimum. The error for MEDIAN and AVERAGE is less than COUNT and more than MIN: both are sensitive to the variations in the number of nodes, but not as dramatically as COUNT.

Figure 6: Effect of a Single Loss on Various Aggregate Functions. Computed over a total of 100 runs at each point. Error bars indicate standard error of the mean, 95% confidence intervals.

$\begin{displaymath}\psfig{figure=loss_tolerance_maxnew.ps,width=3in}\end{displaymath}$

(a) Maximum Error

$\begin{displaymath}\psfig{figure=loss_tolerance_avgnew.ps,width=3in}\end{displaymath}$

(b) Average Error

7.3 Effect of Realistic Communication

In the second experiment, we examine how well TAG performs in the realistic simulation environment (discussed in Section 5 above). In such an environment, without some technique to counteract loss, a large number of partial state records will invariably be dropped and not reach the root of the tree. We ran an experiment to measure the effect of this loss in the realistic environment. The simulation ran until the first aggregate arrived at the root, and then the average number of motes involved in the aggregate over the next several epochs was measured. The ``No Cache'' line of Figure 7 shows the performance of this approach; at diameter 10, about 40% of the partial state records are reflected in the aggregate at the root; by diameter 50, this percentage has fallen to less than 10%. Performance falls off as the number of hops between the average node and the root increases, since the probability of loss is compounded by each additional hop. Thus, the basic TAG approach presented so far, running on current prototype hardware (with its very high loss rates), is not highly tolerant to loss, especially for large networks. Note that any centralized approach would suffer from the same loss problems.

7.4 Child Cache

To improve the quality of aggregates, we propose a simple caching scheme: parents remember the partial state records their children reported for some number of rounds, and use those previous values when new values are unavailable due to lost child messages. As long as the duration of this memory is shorter than the interval at which children select new parents, this technique will increase the number of nodes included in the aggregate without over-counting any nodes. Of course, caching tends to temporally smear the aggregate values that are computed, reducing the temporal resolution of individual readings and possibly making caching undesirable for some workloads. Note that caching is a simple form of interpolation where the interpolated value is the same as the previous value. More sophisticated interpolation schemes, such as curve fitting or statistical observations based on past behavior, could be also be used.

We conducted some experiments to show the improvement caching offers over the basic approach; we allocate a fixed size buffer at each node and measure the average number of devices involved in the aggregation as in Section 7.3 above. The results are shown in the top three lines of Figure 7 - notice that even five epochs of cached state offer a significant increase in the number of nodes counted in any aggregate, and that 15 rounds increases the number of nodes involved in the diameter 50 network to 70% (versus less than 10% without a cache). Aside from the temporal smearing described above, there are two additional drawbacks to caching; First, it uses memory that could be used for group storage. Second, it sets a minimum bound on the time that devices must wait before determining their parent has gone offline; given the benefit it provides in terms of accuracy, however, we believe it to be useful despite these disadvantages. The substantial benefit of this technique suggests that allocating RAM to application level caching may be more beneficial than allocating it to lower-level schemes for reliable message delivery, as such schemes cannot take advantage of the semantics of the data being transmitted.

**Figure 7:** *Percentage of Network Participating in Aggregate For Varying Amounts of Child Cache*
$\begin{figure}\vspace{-.3in} \begin{displaymath}\psfig{figure=softstatenew.ps,height=2.4in}\end{displaymath} \vspace{-.2in} \end{figure}$

7.5 Using Available Redundancy

Because there may be situations where the RAM or latency costs of the child cache are not desirable, it is worthwhile to look at alternative approaches for improving loss tolerance. In this section, we show how the network topology can be leveraged to increase the quality of aggregates. Consider a mote with two possible choices of parent: instead of sending its aggregate value to just one parent, it can send it to both parents. A node can easily discover that it has multiple parents by building a list of nodes it has heard that are one step closer to the root. Of course, for duplicate-sensitive aggregates (see Section 3.2), sending results to multiple parents has the undesirable effect of causing the node to be counted multiple times. The solution to this is to send part of the aggregate to one parent and the rest to the other. Consider a COUNT; a mote with c-1 children and two parents can send a COUNT of c/2 to both parents instead of a count of c to a single parent. Generally, if the aggregate can be linearly decomposed in this fashion, it is possible to broadcast just a single message that is received and processed by both parents, so this scheme incurs no message overheads, as long as both parents are at the same level and request data delivery during the same sub-interval of the epoch.

A simple statistical analysis reveals the advantage of doing this: assume that a message is transmitted with probability p, and that losses are independent, so that if a message m from node s is lost in transition to parent P₁, it is no more likely to be lost in transit to P₂. ⁶ First, consider the case where s sends c to a single parent; the expected value of the transmitted count is p x c (0 with probability (1-p) and c with probability p), and the variance is c² x p x (1-p), since these are standard Bernoulli trials with a probability of success p multiplied by a constant c. For the case where s sends c/2 to both parents, linearity of expectation tells us the expected value is the sum of the expected value through each parent, or 2 x p x c/2 = p x c. Similarly, we can sum the variances through each parent:

Thus, the variance of the multiple parent COUNT is much less than with just a single parent, although its expected value is the same. This is because it is much less likely (assuming independence) for the message to both parents to be lost, and a single loss will less dramatically affect the computed value.

We ran an experiment to measure the benefit of this approach in the realistic topology for COUNT with a network diameter of 50. We measured the number of devices involved in the aggregation over a 50 epoch period. When sending to multiple parents, the mean COUNT was 974 ( $\sigma = 330$ ), while when sending to only one parent, the mean COUNT was 94 ( $\sigma = 41$ ). Surprisingly, sending to multiple parents substantially increases the mean aggregate value; most likely this is due to the fact that losses are not truly independent as we assumed above.

This technique applies equally well to any distributive or algebraic aggregate. For holistic aggregates, like MEDIAN, this technique cannot be applied, since partial state records cannot be easily decomposed.

8 Prototype Implementation

Based on the encouraging simulation results presented above, we have built an implementation of TAG for TinyOS Mica motes (19). The implementation does not currently include many of the optimizations discussed in this paper, but contains the core TAG aggregation algorithm and catalog support for querying arbitrary attributes with simple predicates. In this section, we briefly summarize results from experiments with this prototype, to demonstrate that the simulation numbers given above are consistent with actual behavior and to show that substantial message reductions over a centralized approach are possible in a real implementation.

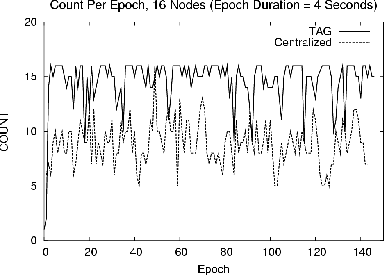
These experiments involved sixteen motes arranged in a depth four tree, computing a COUNT aggregate over 150 4-second epochs (a 10 minute run.) No child caching or snooping techniques were used. Figure 8 shows the COUNT observed at the root for a centralized approach, where all messages are forwarded to the root, versus the in network TAG approach. Notice that the quality of the aggregate is substantially better for TAG; this is due to reduced radio contention. To measure the extent of contention and compare the message costs of the two schemes, we instrumented motes to report the number of messages sent and received. The centralized approach required 4685 messages, whereas TAG required just 2330, representing a 50% communications reduction. This is less than the order-of-magnitude shown in Figure 4 for COUNT because our prototype network topology had a higher average fanout than the simulated environment, so messages in the centralized case had to be retransmitted fewer times to reach the root. Per hop loss rates were about 5% in the in network approach. In the centralized approach, increased network contention drove these loss rates to 15%. The poor performance of the centralized case is due to the multiplicative accumulation of loss, such that only 45% of the messages from nodes at the bottom of the routing tree arrived at to the root.

**Figure 8:** *Comparison of Centralized and TAG based Aggregation Approaches in Lossy, Prototype Environment Computing a COUNT over a 16 node network.*
$\begin{figure}\vspace{-.4in} \begin{displaymath}\psfig{figure=realworldnew.ps,height=2.5in}\end{displaymath} \vspace{-.3in} \vspace{-.04in} \end{figure}$

This completes our discussion of algorithms for TAG. We now turn to the extensive related work in the networking and database communities.

9 Related Work

The database community has proposed a number of distributed and push-down based approaches for aggregates in database systems (33,26), but these universally assume a well-connected, low-loss topology that is unavailable in sensor networks. None of these systems present techniques for loss tolerance or power sensitivity. Furthermore, their notion of aggregates is not tied to a taxonomy, and so techniques for transparently applying various aggregation and routing optimizations are lacking. The partial preaggregation techniques (15) used to enable group eviction were proposed as a technique to deal with very large numbers of groups to improve the efficiency of hash joins and other bucket-based database operators.

The first three components of the partial-state dimension of the taxonomy presented in Section 3.2 (e.g. algebraic, distributive, and holistic) were originally developed as a part of the research on data-cubes (9); the duplicate sensitivity, exemplary vs. summary, and monotonicity dimensions, as well as the unique and content-sensitive state components of partial-state are our own addition. (29) discusses online aggregation (11) in the context of nested-queries; it proposes optimizations to reduce tuple-flow between outer and inner queries that bear similarities to our technique of pushing HAVING clauses into the network.

With respect to query language, our epoch based approach is related to languages and models from the Temporal Database literature; see (27) for a survey of relevant work. The Cougar project at Cornell (23) discusses queries over sensor networks, as does our own work on Fjords (18), although the former only considers moving selections (not aggregates) into the network and neither presents specific algorithms for use in sensor networks.

Literature on active networks (30) identified the idea that the network could simultaneously route and transform data, rather than simply serving as an end-to-end data conduit. The recent SIGCOMM paper on ESP (4) provides a constrained framework for in network aggregation-like operations in a traditional network. Within the sensor network community, work on networks that perform data analysis is largely due to the USC/ISI and UCLA communities. Their work on directed diffusion (13) discusses techniques for moving specific pieces of information from one place in a network to another, and proposes aggregation-like operations that nodes may perform as data flows through them. Their work on low-level-naming(10) proposes a scheme for imposing names onto related groups of devices in a network, in much the way that our scheme partitions sensor networks into groups. Work on greedy aggregation (12) discusses networking protocols for routing data to improve the extent to which data can be combined as it flows up a sensor network - it provides low level techniques for building routing trees that could be useful in computing TAG style aggregates.

These papers recognize that aggregation dramatically reduces the amount of data routed through the network but present application-specific solutions that, unlike the declarative query approach approach of TAG, do not offer a particularly simple interface, flexible naming system, or any generic aggregation operators. Because aggregation is viewed as an application-specific operation in diffusion, it must always be coded in a low-level language. Although some TAG aggregates may also be application-specific, we ask that users provide certain functional guarantees, such as composability with other aggregates, and a classification of semantics (quantity of partial state, monotonicity, etc.) which enable transparent application of various optimizations and create the possibility of a library of common aggregates that TAG users can freely apply within their queries. Furthermore, directed diffusion puts aggregation APIs in the routing layer, so that expressing aggregates requires thinking about how data will be collected, rather than just what data will be collected. This is similar to old-fashioned query processing code that thought about navigating among records in the database - by contrast, our goal is to separate the expression of aggregation logic from the details of routing. This allows users to focus on application issues and enables the system to dynamically adjust routing decisions using general (taxonomic) information about each aggregation function.

Networking protocols for routing data in wireless networks are very popular within the literature (1,8,14), however, none of them address higher level issues of data processing, merely techniques for data routing. Our tree-based routing approach is clearly inferior to these approaches for peer to peer routing, but works well for the aggregation scenarios we are focusing on. Work on (N)ACKs (and suppression thereof) in scalable, reliable multicast trees (6,17) bears some similarity to the problem of propagating an aggregate up a routing tree in TAG. These systems, however, consider only fixed, limited types of aggregates (e.g. ACKs or NAKs for regions or recovery groups.) Finally, we presented an early version of this work in a workshop publication (20).

10 Conclusions

In summary, we have shown how declarative aggregate queries can be distributed and efficiently executed over sensor networks. Our in network approach can provide an order of magnitude reduction in bandwidth consumption over approaches where data is aggregated and processed centrally. The declarative query interface allows end-users to take advantage of this benefit for a wide range of aggregate operations without having to modify low-level code or confront the difficulties of topology construction, data routing, loss tolerance, or distributed computing. Furthermore, this interface is tightly integrated with the network, enabling transparent optimizations that further decrease message costs and improve tolerance to failure and loss.

We plan to extend this work as the data collection needs of the wireless sensor community evolve. We are moving towards an event-driven model where queries can be initiated and results collected in response to external events in the interior of the network, with the results of those internal sub-queries being aggregated across nodes and shipped to points on the network edge.

As sensor networks become more widely deployed, especially in remote, difficult to administer locations, bandwidth- and power-sensitive methods to extract data from those networks will become increasingly important. In such scenarios, the users are often scientists who lack fluency in embedded software development but are interested in using sensor networks to further their own research. For such users, high-level programming interfaces are a necessity; these interfaces must balance simplicity, expressiveness, and efficiency in order to meet data collection and battery lifetime requirements. Given this balance, we see TAG as a very promising service for data collection: the simplicity of declarative queries, combined with the ability of TAG to efficiently optimize and execute them makes it a good choice for a wide range of sensor network data processing situations.

Acknowledgments

Thanks to our shepherd, Deborah Estrin, and to our anonymous reviewers for their thoughtful reviews and advice. Robert Szewczyk, David Culler, Alec Woo, and Ramesh Govindan contributed to the design of the networking protocols discussed in this paper. Per Åke Larson suggested the use of partial preaggregation for group eviction. Kyle Stanek implemented isobar aggregates in our simulator.

TAG: a Tiny AGgregation Service for Ad-Hoc Sensor Networks