4th USENIX OSDI Symposium [Technical Program]

Pp. 45–58 of the Proceedings

Surplus Fair Scheduling: A Proportional-Share CPU Scheduling Algorithm for Symmetric Multiprocessors

Abhishek Chandra, Micah Adler, Pawan Goyal and Prashant Shenoy

Department of Computer Science, Ensim Corporation

University of Massachusetts Amherst Sunnyvale, CA

{abhishek,micah,shenoy}@cs.umass.edu goyal@ensim.com

Abstract:

In this paper, we present surplus fair scheduling (SFS), a proportional-share CPU scheduler designed for symmetric multiprocessors. We first show that the infeasibility of certain weight assignments in multiprocessor environments results in unfairness or starvation in many existing proportional-share schedulers. We present a novel weight readjustment algorithm to translate infeasible weight assignments to a set of feasible weights. We show that weight readjustment enables existing proportional-share schedulers to significantly reduce, but not eliminate, the unfairness in their allocations. We then present surplus fair scheduling, a proportional-share scheduler that is designed explicitly for multiprocessor environments. We implement our scheduler in the Linux kernel and demonstrate its efficacy through an experimental evaluation. Our results show that SFS can achieve proportionate allocation, application isolation and good interactive performance, albeit at a slight increase in scheduling overhead. We conclude from our results that a proportional-share scheduler such as SFS is not only practical but also desirable for server operating systems.

1 Introduction

1.1 Motivation

The growing popularity of multimedia and web applications has spurred research in the design of large multiprocessor servers that can run a variety of demanding applications. To illustrate, many commercial web sites today employ multiprocessor servers to run a mix of HTTP applications (to service web requests), database applications (to store product and customer information), and streaming media applications (to deliver audio and video content). Moreover, Internet service providers that host third party web sites typically do so by mapping multiple web domains onto a single physical server, with each domain running a mix of these applications. These example scenarios illustrate the need for designing resource management mechanisms that multiplex server resources among diverse applications in a predictable manner.

Resource management mechanisms employed by a server operating system should have several desirable properties. First, these mechanisms should allow users to specify the fraction of the resource that should be allocated to each application. In the web hosting example, for instance, it should be possible to allocate a certain fraction of the processor and network bandwidth to each web domain [2]. The operating system should then allocate resources to applications based on these user-specified shares. It has been argued that such allocation should be both fine-grained and fair [3,9,15,17,20]. Another desirable property is application isolation--the resource management mechanisms employed by an operating system should effectively isolate applications from one another so that misbehaving or overloaded applications do not prevent other applications from receiving their specified shares. Finally, these mechanisms should be computationally efficient so as to minimize scheduling overheads. Thus, efficient, predictable and fair allocation of resources is key to designing server operating systems. The design of a CPU scheduling algorithm for symmetric multiprocessor servers that meets these objectives is the subject matter of this paper.

1.2 Relation to Previous Work

In the recent past, a number of resource management mechanisms have been developed for predictable allocation of processor bandwidth [2,7,11,12,14,16,18,24,28]. Many of these CPU scheduling mechanisms as well as their counterparts in the network packet scheduling domain [4,5,19,23] associate an intrinsic rate with each application and allocate resource bandwidth in proportion to this rate. For instance, many recently proposed algorithms such as start-time fair queuing (SFQ) [9], borrowed virtual time (BVT) [7], and SMART [16] are based on the concept of generalized processor sharing (GPS). GPS is an idealized algorithm that assigns a weight to each application and allocates bandwidth fairly to applications in proportion to their weights. GPS assumes that threads can be scheduled using infinitesimally small quanta to achieve weighted fairness. Practical instantiations, such as SFQ, emulate GPS using finite duration quanta. While GPS-based algorithms can provide strong fairness guarantees in uniprocessor environments, they can result in unbounded unfairness or starvation when employed in multiprocessor environments as illustrated by the following example.

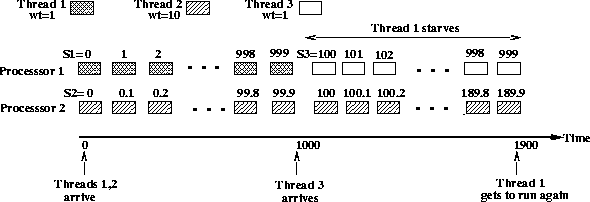
Example 1237 (1)

Consider a server that employs the start-time fair queueing (SFQ) algorithm [9] to schedule threads. SFQ is a GPS-based fair scheduling algorithm that assigns a weight w_i to each thread and allocates bandwidth in proportion to these weights. To do so, SFQ maintains a counter S_i for each application that is incremented by $\frac{q}{w_i}$ every time the thread is scheduled (q is the quantum duration). At each scheduling instance, SFQ schedules the thread with the minimum S_i on a processor. Assume that the server has two processors and runs two compute-bound threads that are assigned weights w₁ = 1 and w₂ = 10, respectively. Let the quantum duration be q = 1 ms. Since both threads are compute-bound and SFQ is work-conserving, each thread gets to continuously run on a processor. After 1000 quantums, we have $S_1= \frac{1000}{1} = 1000$ and $S_2 = \frac{1000}{10} = 100$ . Assume that a third cpu-bound thread arrives at this instant with a weight w₃=1. The counter for this thread is initialized to S₃=100 (newly arriving threads are assigned the minimum value of S_i over all runnable threads). From this point on, threads 2 and 3 get continuously scheduled until S₂ and S₃ ``catch up'' with S₁. Thus, although thread 1 has the same weight as thread 3, it starves for 900 quanta leading to unfairness in the scheduling algorithm. Figure 1 depicts this scenario.

**Figure 1:** The Infeasible Weights Problem: an infeasible weight assignment can lead to unfairness in allocated shares in multiprocessor environments.
$\begin{figure} \begin{center} \epsfig {figure=/usr/ast/users2/abhishek/conferences/osdi00/src/infeasible.ps,height=1.85in} \end{center}\end{figure}$

Many recently proposed GPS-based algorithms such as stride scheduling [28], weighted fair queuing (WFQ) [18] and borrowed virtual time (BVT) [7] also suffer from this drawback when employed for multiprocessors (like SFQ, stride scheduling and WFQ are instantiations of GPS, while BVT is a derivative of SFQ with an additional latency parameter; BVT reduces to SFQ when the latency parameter is set to zero). The primary reason for this inadequacy is that while any arbitrary weight assignment is feasible for uniprocessors, only certain weight assignments are feasible for multiprocessors. In particular, those weight assignments in which the bandwidth assigned to a single thread exceeds the capacity of a processor are infeasible (since an individual thread cannot consume more than the bandwidth of a single processor). In the above example, the second thread was assigned $\frac{10}{11}^{th}$ of the total bandwidth on a dual-processor server, whereas it can consume no more than half the total bandwidth. Since GPS-based work-conserving algorithms do not distinguish between feasible and infeasible weight assignments, unfairness can result when a weight assignment is infeasible. In fact, even when the initial weights are carefully chosen to be feasible, blocking events can cause the weights of the remaining threads to become infeasible. For instance, a feasible weight assignment of 1:1:2 on a dual-processor server becomes infeasible when one of the threads with weight 1 blocks. Even when all weights are feasible, an orthogonal problem occurs when frequent arrivals and departures prevent a GPS-based scheduler such as SFQ from achieving proportionate allocation. Consider the following example:

Example 1242

Consider a dual-processor server that runs a thread with weight 10,000 and 10,000 threads with weight 1. Assume that short-lived threads with weight 100 arrive every 100 quantums and run for 100 quantums each. Note that the weight assignment is always feasible. If SFQ is used to schedule these threads, then it will assign the current minimum value of S_i in the system to each newly arriving thread. Hence, each short-lived thread is initialized with the lowest value of S_i and gets to run continuously on a processor until it departs. The thread with weight 10,000 runs on the other processor; all threads with weight 1 run infrequently. Thus, each short-lived thread with weight 100 gets as much processor bandwidth as the thread with weight 10,000 (instead of $\frac{1}{100}$ of the bandwidth). Note that this problem does not occur in uniprocessor environments.

The inability to distinguish between feasible and infeasible weight assignments as well as to achieve proportionate allocation in the presence of frequent arrivals and departures are fundamental limitations of a proportional-share scheduler such as SFQ. Whereas randomized schedulers such as lottery scheduling [27] do not suffer from starvation problems due to infeasible weights, such weight assignments can, nevertheless, cause small inaccuracies in proportionate allocation for such schedulers. Several techniques can be employed to address the problem of infeasible bandwidth assignments. In the simplest case, processor bandwidth could be assigned to applications in absolute terms instead of using a relative mechanism such as weights (e.g., assign 20% of the bandwidth on a processor to a thread). A potential limitation of such absolute allocations is that bandwidth unused by an application is wasted, resulting in poor resource utilization. To overcome this drawback, most modern schedulers that employ this method reallocate unused processor bandwidth to needy applications in a fair-share manner [10,14]. In fact, it has been shown that relative allocations using weights and absolute allocations with fine-grained reassignment of unused bandwidth are duals of each other [22]. A more promising approach is to employ a GPS-based scheduler for each processor and partition the set of threads among processors such that each processor is load balanced. Such an approach has two advantages: (i) it can provide strong fairness guarantees on a per-processor basis, and (ii) binding a thread to a processor allows the scheduler to exploit processor cache locality. A limitation of the approach is that periodic repartitioning of threads may be necessary since blocked/terminated threads can cause imbalances across processors, which can be expensive. Nevertheless, such an approach has been successfully employed to isolate applications from one another [1,8,26].

In summary, GPS-based fair scheduling algorithms or simple modifications thereof are unsuitable for fair allocation of resources in multiprocessor environments. To overcome this limitation, we propose a CPU scheduling algorithm for multiprocessors that: (i) explicitly distinguishes between feasible and infeasible weight assignments and (ii) achieves proportionate allocation of processor bandwidth to applications.

1.3 Research Contributions of this Paper

In this paper, we present surplus fair scheduling (SFS), a predictable CPU scheduling algorithm for symmetric multiprocessors. The design of this algorithm has led to several key contributions.

First, we have developed a weight readjustment algorithm to explicitly deal with the problem of infeasible weight assignments; our algorithm translates a set of infeasible weights to the ``closest'' feasible weight assignment, thereby enabling all scheduling decisions to be based on feasible weights. Our weight readjustment algorithm is a novel approach for dealing with infeasible weights and one that can be combined with most existing GPS-based scheduling algorithms; doing so enables these algorithms to vastly reduce the unfairness in their allocations for multiprocessor environments. However, even with the readjustment algorithm, many GPS-based algorithms show unfairness in their allocations, especially in the presence of frequent arrival and departures of threads. To overcome this drawback, we develop the surplus fair scheduling algorithm for proportionate allocation of bandwidth in multiprocessor environments. A key feature of our algorithm is that it does not require the quantum length to be known a priori, and hence can handle quantums of variable length.

We have implemented the surplus fair scheduling algorithm in the Linux kernel and have made the source code available to the research community. We have experimentally demonstrated the benefits of our algorithm over a GPS-based scheduler such as SFQ using sample applications and benchmarks. Our experimental results show that surplus fair scheduling can achieve proportionate allocation, application isolation and good interactive performance for typical application mixes, albeit at the expense of a slight increase in the scheduling overhead. Together these results demonstrate that a proportional-share CPU scheduling algorithm such as surplus fair scheduling is not only practical but also desirable for server operating systems.

The rest of this paper is structured as follows. Section 2 presents the surplus fair scheduling algorithm. Section 3 discusses the implementation of our scheduling algorithm in Linux. Section 4 presents the results of our experimental evaluation. Section 5 presents some limitations of our approach and directions for future work. Finally, Section 6 presents some concluding remarks.

2 Proportional-Share CPU Scheduling for Multiprocessor Environments

Consider a multiprocessor server with p processors that runs t threads. Let us assume that a user can assign any arbitrary weight to a thread. In such a scenario, a thread with weight w_i should be allocated $(w_i/\sum_j w_j)$ fraction of the total processor bandwidth. Since weights can be arbitrary, it is possible that a thread may request more bandwidth than it can consume (this occurs when the requested fraction $\frac{w_i}{\sum_j w_j} \gt \frac{1}{p}$ ). The CPU scheduler must somehow reconcile the presence of such infeasible weights. To do so, we present an optimal weight readjustment algorithm that can efficiently translate a set of infeasible weights to the ``closest'' feasible weight assignment. By running this algorithm every time the weight assignment becomes infeasible, the CPU scheduler can ensure that all scheduling decisions are always based on a set of feasible weights. Given such a weight readjustment algorithm, we then present generalized multiprocessor sharing (GMS)--an idealized algorithm for fair, proportionate bandwidth allocation that is an analogue of GPS in the multiprocessor domain. We use the insights provided by GMS to design the surplus fair scheduling (SFS) algorithm. SFS is a practical instantiation of GMS that has lower implementation overheads.

In what follows, we first present our weight readjustment algorithm in Section 2.1. We present generalized multiprocessor sharing in Section 2.2 and then present the surplus fair scheduling algorithm in Section 2.3.

2.1 Efficient, Optimal Weight Readjustment

As illustrated in Section 1.2, weight assignments in which a thread requests a bandwidth share that exceeds the capacity of a processor are infeasible. Moreover, a feasible weight assignment may become infeasible or vice versa whenever a thread blocks or becomes runnable. To address these problems, we have developed a weight readjustment algorithm that is invoked every time a thread blocks or becomes runnable. The algorithm examines the set of runnable threads to determine if the weight assignment is feasible. A weight assigned to a thread is said to be feasible if

$\begin{displaymath} \frac{w_i}{\sum_j w_j} \leq \frac{1}{p}\end{displaymath}$ (1)

We refer to Equation 1 as the feasibility constraint. If a thread violates the feasibility constraint (i.e., requests a fraction that exceeds 1/p), then it is assigned a new weight so that its requested share reduces to 1/p (which is the maximum share an individual thread can consume). Doing so for each thread with infeasible weight ensures that the new weight assignment is feasible.

Conceptually, the weight readjustment algorithm proceeds by examining each thread in descending order of weights to see if it violates the feasibility constraint. Each thread that does so is assigned the bandwidth of an entire processor, which is the maximum bandwidth a thread can consume. The problem then reduces to checking the feasibility of scheduling the remaining threads on the remaining processors. In practice, the readjustment algorithm is implemented using recursion--the algorithm recursively examines each thread to see if it violates the constraint; the recursion terminates when a thread that satisfies the constraint is found. The algorithm then assigns a new weight to each thread that violates the constraint such that its requested fraction equals 1/p. This is achieved by computing the average weight of all feasible threads over the remaining processors and assigning it to the current thread (i.e., 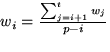$w_i = \frac{\sum_{j=i+1}^{t} w_j}{p-i}$ ). Figure 2 illustrates the complete weight readjustment algorithm.

Our weight readjustment algorithm has the following salient features:

The algorithm is optimal in the sense that it changes the weights of the minimum number of threads and the new weights are the ``closest'' weights that reflect the original assignment. This is because threads with infeasible weights are assigned the nearest feasible weight, and weights of threads that satisfy the feasibility constraint never change (and hence, they continue to receive bandwidth in their requested proportions).
The algorithm has an efficient implementation. To see why, observe that in a p-processor system, no more than (p-1) threads can have infeasible weights (since the sum of the requested fractions is 1, no more than (p-1) threads can request a fraction that exceeds $\frac{1}{p}$ ). Thus, the number of threads with infeasible weights depends solely on the number of processors and is independent of the total number of threads in the system. By maintaining a list of threads sorted in descending order of their weights, the algorithm needs to examine no more than the first (p-1) threads with the largest weights. In fact, the algorithm can stop scanning the sorted list at the first point where the feasibility constraint is satisfied (subsequent threads have even smaller weights and hence, request smaller and feasible fractions). Since the number of processors is typically much smaller than the number of threads (p << t), the overhead imposed by the readjustment algorithm is small.
Our weight readjustment algorithm can be employed with most existing GPS-based scheduling algorithms to deal with the problem of infeasible weights. We experimentally demonstrate in Section 4.2 that doing so enables these schedulers to significantly reduce (but not eliminate) the unfairness in their allocations for multiprocessor environments.
The weight readjustment algorithm can also be employed in conjunction with a randomized proportional-share scheduler such as lottery scheduling [27]. Although such a scheduler does not suffer from starvation problems due to infeasible weights, a set of feasible weights can help such a randomized scheduler in making more accurate scheduling decisions.

**Figure 2:** The weight readjustment algorithm: The algorithm is invoked with an array of weights sorted in decreasing order. Initially, i=1; p denotes the number of processors, and t denotes the number of runnable threads. If a thread violates the feasibility constraint, then the algorithm is recursively invoked for the remaining threads and the remaining processors. Each infeasible weight is then adjusted by setting its requested processor share to 1/p.
$\begin{figure} \begin{small} \begin{center} \begin{tabbing} xx \= xxx\=xxxxxxxxx... ...}{p-1}$\ \ gt end\ {\bf end.}\end{tabbing}\end{center}\end{small}\end{figure}$

Given our weight readjustment algorithm, we now present an idealized algorithm for proportional-share scheduling in multiprocessor environments.

2.2 Generalized Multiprocessor Sharing

Consider a server with p processors each with capacity ${\cal C}$ that runs t threads. Let the threads be assigned weights w₁, w₂, w₃, $\ldots$ , w_t. Let $\phi_i$ denote the instantaneous weight of a thread as computed by the readjustment algorithm. At any instant, depending on whether the thread satisfies or violates the feasibility constraint, $\phi_i$ is either the original weight w_i or the readjusted weight. From the definition of $\phi_i$ , it follows that $\frac{\phi_i}{\sum_j \phi_j} \leq \frac{1}{p}$ at all times (our weight readjustment algorithm ensures this property). Assume that threads can be scheduled for infinitesimally small quanta and let A_i(t₁,t₂) denote the CPU service received by thread i in the interval [t₁,t₂). Then the generalized multiprocessor sharing (GMS) algorithm has the following property: for any interval [t₁,t₂), the amount of CPU service received by thread i satisfies

$\begin{displaymath} \frac{A_i(t_1,t_2)}{A_j(t_1,t_2)} \geq \frac{\phi_i}{\phi_j}\end{displaymath}$

(2)

provided that (i) thread i is continuously runnable in the entire interval, and (ii) both $\phi_i$ and $\phi_j$ remain fixed in that interval. Note that the instantaneous weight $\phi$ remains fixed in an interval if the thread either satisfies the feasibility constraint in the entire interval, or continuously violates the constraint in the entire interval. It is easy to show that Equation 2 implies proportionate allocation of processor bandwidth.

Intuitively, GMS is similar to a weighted round-robin algorithm in which threads are scheduled in round-robin order (p at a time); each thread is assigned an infinitesimally small CPU quantum and the number of quanta assigned to a thread is proportional to its weight. In practice, however, threads must be scheduled using finite duration quanta so as to amortize context switch overheads. Consequently, in what follows, we present a CPU scheduling algorithm that employs finite duration quanta and is a practical approximation of GMS.

2.3 Surplus Fair Scheduling

Consider a GMS-based CPU scheduling algorithm that schedules threads in terms of finite duration quanta. To clearly understand how such an algorithm works, we first present the intuition behind the algorithm and then provide precise details. Let us assume that thread i is assigned a weight w_i and that the weight readjustment algorithm is employed to ensure that weights are feasible at all times. Let $\phi_i$ denote the instantaneous weight of thread i. Let A_i(t₁,t₂) denote the amount of CPU service received by thread i in the duration [t₁,t₂), and let A^GMS_i(t₁,t₂) denote the amount of service that the thread would have received if it were scheduled using GMS. Then, the quantity

$\begin{displaymath} \alpha_i = A_i(t_1,t_2) - A^{GMS}_i(t_1,t_2)\end{displaymath}$

(3)

represents the extra service (i.e., surplus) received by thread i when compared to GMS. To closely emulate GMS, a scheduling algorithm should schedule threads such that the surplus $\alpha_i$ for each thread is as close to zero as possible. Given a p-processor system, a simple approach for doing so is to actually compute $\alpha_i$ for each thread and schedule the p threads with the least surplus values. If the net surplus is negative, doing so allows a thread to catch up with its allocation in GMS. Even when the net surplus of a thread is positive, picking threads with the least positive surplus values enables the algorithm to ensure that the overall deviation from GMS is as small as possible (picking a thread with a larger $\alpha_i$ would cause a larger deviation from GMS).

A scheduling algorithm that actually uses Equation 3 to compute surplus values is impractical since it requires the scheduler to compute A_i^GMS (which in turn requires a simulation of GMS). Consequently, we derive an approximation of Equation 3 that enables efficient computation of the surplus values for each thread. Let $S_1, S_2, \ldots, S_t$ denote the weighted CPU service received by each thread so far. If thread i runs in a quantum, then S_i is incremented as $S_i= S_i + \frac{q}{\phi_i}$ , where q denotes the duration for which the thread ran in that quantum. Since S_i is the weighted CPU service received by thread i, $\phi_i \cdot S_i$ represents the total service received by thread i so far. Let v denote the minimum value of S_i over all runnable threads. Intuitively, v represents the processor allocation of the thread that has received the minimum service so far. Then the surplus service received by thread i is defined to be

$\begin{displaymath} \alpha_i = \phi_i \cdot (S_i - v)\end{displaymath}$ (4)

The first term $\phi_i \cdot S_i$ approximates A_i(0,t), which is the service received by thread i so far. The second term $\phi_i \cdot v$ approximates the quantity A_i^GMS in Equation 3. Thus, $\alpha_i$ measures the surplus service received by thread i when compared to the thread that has received the least service so far (i.e., v). It follows from this definition of $\alpha_i$ that $\alpha_i \geq 0$ for all runnable threads. Scheduling a thread with the smallest value of $\alpha_i$ ensures that the scheduler approximates GMS and each thread receives processor bandwidth in proportion to its weight. Since a thread is chosen based on its surplus value, we refer to the algorithm as surplus fair scheduling (SFS).

Having provided the intuition for our algorithm, the precise SFS algorithm is as follows:

Each thread in the system is associated with a weight w_i, a start tag S_i and a finish tag F_i. Let $\phi_i$ denote the instantaneous weight of a thread as computed by the readjustment algorithm. When a new thread arrives, its start tag is initialized as S_i=v, where v is the virtual time of the system (defined below). When a thread runs on a processor, its finish tag at the end of the quantum is updated as

$\begin{displaymath} F_i = S_i + \frac{q}{\phi_i}\end{displaymath}$ (5)

where q is the duration for which the thread ran in that quantum and $\phi_i$ is its instantaneous weight at the end of the quantum. Observe that q can vary depending on whether the thread utilizes its entire allocated quantum or relinquishes the processor before the quantum ends due to a blocking event. The start tag of a runnable thread is computed as

$\begin{displaymath} S_i = \left\{ \begin{array} {ll} \mbox{max}(F_i,v)& \mbox{i... ...ead is continuously}\ & \mbox{runnable}\ \end{array} \right.\end{displaymath}$ (6)
Initially, the virtual time of the system is zero. At any instant, the virtual time is defined to be the minimum of the start tags over all runnable threads. The virtual time remains unchanged if all processors are idle and is set to the finish tag of the thread that ran last.
At each scheduling instance, SFS computes the surplus values of all runnable threads as $\alpha_i = \phi_i \cdot (S_i - v)$ and schedules the thread with the least $\alpha_i$ ; ties are broken arbitrarily.

Our surplus fair scheduling algorithm has the following salient features. First, like most GPS-based algorithms, SFS is work-conserving in nature--the algorithm ensures that a processor will not idle so long as there are runnable threads in the system. Second, since the surplus $\alpha_i$ of a thread depends only on its start tag and not the finish tag, SFS does not require the quantum length to be known at the time of scheduling (the quantum duration q is required to compute the finish tag only after the quantum ends). This is a desirable feature since the duration of a quantum can vary if a thread blocks before it is preempted. Third, SFS ensures that blocked threads do not accumulate credit for the processor shares they do not utilize while sleeping--this is ensured by setting the start tag of a newly woken-up thread to at least the virtual time (this prevents a thread from accumulating credit by sleeping for a long duration and then starving other threads upon waking up). Finally, from the definition of $\alpha_i$ and the virtual time, it follows that at any instant there is always at least one thread with $\alpha_i = 0$ (this is the thread with the minimum start tag, i.e., S_i = v and also has the least surplus value). Since the thread with the minimum surplus value is also the one with the minimum start tag, surplus fair scheduling reduces to start-time fair queuing (SFQ) [9] in a uniprocessor system. Thus, SFS can be viewed as a generalization of SFQ for multiprocessor environments. We experimentally demonstrate in Section 4.3 that SFS addresses the problem of proportionate allocation in the presence of frequent arrivals and departures described in Example 2 of Section 1.2.

2.4 Fair Allocation versus Processor Affinities

SFS as defined in the previous section achieves pure fair-share allocation but does not take processor affinities [25] into account while making scheduling decisions. Scheduling a thread on the same processor enables it to benefit from data cached from previous scheduling instances and improves the effectiveness of a processor cache. SFS can be modified to account for processor affinities as follows. Instead of scheduling the thread with the least surplus value on a processor, SFS can instead examine the first ${\cal B}$ threads with the least surplus values and pick one which was previously scheduled on that processor. If no such thread exists, then the scheduler simply picks the thread with the least surplus value for execution. The quantity ${\cal B}$ is a tunable parameter and is referred to as the processor affinity bias. Using ${\cal B}=1$ reduces to pure fair-share scheduling; a large value of ${\cal B}$ increases the probability of finding a thread with an affinity for a particular processor. Observe that processor-affinity based scheduling and fair-share scheduling can be conflicting goals. Using a large processor affinity bias can cause SFS to deviate from GMS-based fair allocation but allows the scheduler to improve performance by exploiting cache locality. In contrast, a small value of the bias enables SFS to provide better fairness guarantees but can degrade cache performance.

3 Implementation Considerations

We have implemented surplus fair scheduling in the Linux kernel and have made the source code publicly available to the research community. The entire implementation effort took less than three weeks and was around 1500 lines of code. In the rest of this section, we present the details of our kernel implementation and explain some of our key design decisions.

3.1 SFS Data Structures and Implementation

The implementation of surplus fair scheduling was done in version 2.2.14 of the Linux kernel. Our implementation replaces the standard time sharing scheduler in Linux; the modified kernel schedules all threads/processes using SFS. Each thread in the system is assigned a default weight of 1; the weight assigned to a thread can be modified (or queried) using two new system calls--setweight and getweight. The parameters expected by these system calls are similar to the setpriority and getpriority system calls employed by the Linux time sharing scheduler. SFS allows the weight assigned to a thread to be modified at any time (just as the Linux time sharing scheduler allows the priority of a thread to be changed on-the-fly).

Our implementation of SFS maintains three queues. The first queue consists of all runnable threads in descending order of their weights. The other two queues consist of all runnable threads in increasing order of start tags and surplus values, respectively. The first queue is employed by the readjustment algorithm to determine the feasibility of the assigned weights (recall from Section 2.1 that maintaining a list of threads sorted by their weights enables the weight readjustment algorithm to be implemented efficiently). The second queue is employed by the scheduler to compute the virtual time; since the queue is sorted on start tags, the virtual time at any instant is simply the start tag of the thread at the head of the queue. The third queue is used to determine which thread to schedule next--maintaining threads sorted by their surplus values enables the scheduler to make scheduling decisions efficiently.

Given these data structures, the actual scheduling is performed as follows. Whenever a quantum expires or one of the currently running threads blocks, the Linux kernel invokes the SFS scheduler. The SFS scheduler first updates the finish tag of the thread relinquishing the processor and then computes its start tag (if the thread is still runnable). The scheduler then computes the new virtual time; if the virtual time changes from the previous scheduling instance, then the scheduler must update the surplus values of all runnable threads (since $\alpha_i$ is a function of v) and re-sort the queue. The scheduler then picks the thread with the minimum surplus and schedules it for execution. Note that since a running thread may not utilize its entire allocated quantum due to blocking events, quantums on different processors are not synchronized; hence, each processor independently invokes the SFS scheduler when its currently running thread blocks or is preempted. Finally, the readjustment algorithm is invoked every time the set of runnable threads changes (i.e., after each arrival, departure, blocking event or wakeup event), or if the user changes the weight of a thread.

3.2 Implementation Complexity and Optimizations

The implementation complexity of the SFS algorithm is as follows:

New arrival or a wakeup event: The newly arrived/woken up thread must be inserted at the appropriate position in the three run queues. Since the queues are in sorted order, using a linear search for insertions takes O(t), where t is the number of runnable threads. The complexity can be further reduced to $O(\log t)$ if binary search is used to determine the insert position. The readjustment algorithm is invoked after the insertion, which has a complexity of O(p). Hence, the total complexity is O(t+p).
Departure or a blocking event: The terminated/blocked thread must be deleted from the run queue, which is O(1) since our queues are doubly linked lists. The readjustment algorithm is then invoked for the new run queue, which takes O(p). Hence, the total complexity is O(p).
Scheduling decisions: The scheduler first updates finish and start tags of the thread relinquishing the processor and computes the new virtual time, all of which are constant time operations. If the virtual time is unchanged, the scheduler only needs to pick the thread with minimum surplus (which takes O(1) time). If the virtual time increases from the previous scheduling instance, then the scheduler must first update the surplus values of all runnable threads and re-sort the queue. Sorting is an $O(t \log t)$ operation, while updating surplus values takes O(t). Hence, the total complexity is $O(t \log t)$ . The run time performance, in the average case, can be improved by observing the following. Since the queue was in sorted order prior to the updates, in practice, the queue remains mostly in sorted order after the new surplus values are computed. Hence, we employ insertion sort to re-sort the queue, since it has good run time performance on mostly-sorted lists. Moreover, updates and sorting are required only when the virtual time changes. The virtual time is defined to be the minimum start tag in the system, and hence, in a p-processor system, typically only one of the p currently running threads have this start tag. Consequently, on average, the virtual time changes only once every p scheduling instances, which amortizes the scheduling overhead over a larger number of scheduling instances.
Synchronization issues: Synchronization overheads can become an issue in SMP servers if the scheduling algorithm imposes a large overhead. Despite its $O(t \log t)$ overhead, SFS can be implemented efficiently due to the following reasons. First, we have developed a scheduling heuristic (described next) that reduces the scheduling overhead to a constant. Second, although the readjustment algorithm needs to lock the run queue while examining the feasibility constraint for runnable threads, as explained earlier, these checks can be done efficiently in O(p) time (independent of the number of threads in the system). Finally, the granularity of locks required by SFS is identical to that in the Linux SMP scheduler. In fact, our implementation reuses that portion of the code.

Since the scheduling overhead of SFS grows with the number of runnable threads, we have developed a heuristic to limit the scheduling overhead when the number of runnable threads becomes large. Our heuristic is based on the observation that $\alpha_i = \phi_i \cdot (S_i - v)$ and hence, the thread with the minimum surplus typically has either a small weight, a small start tag, or a small surplus in the previous scheduling instance. Consequently, examining a few threads with small start tags, small weights, or small prior surplus values, computing their new surpluses and choosing the thread with minimum surplus is a good heuristic in practice. Since our implementation already maintains three queues sorted by $\phi_i$ , S_i and $\alpha_i$ , this can be trivially done by examining the first few threads in each queue, computing their new surplus values and picking the thread with the least surplus. This obviates the need to update the surpluses and to re-sort every time the virtual time changes; the scheduler needs to do so only every so often and can use the heuristic between updates (infrequent updates and sorting are still required to maintain a high accuracy of the heuristic). Hence, the scheduling overhead reduces to a constant and becomes independent of the number of runnable threads in the system (updates to $\alpha_i$ and sorting continue to be $O(t \log t)$ , but this overhead is amortized over a large number of scheduling instances). Moreover, since the heuristic examines multiple runnable threads, it can be easily combined with the technique proposed in Section 2.4 to account for processor affinities. We conducted several simulation experiments to determine the efficacy of this heuristic. Figure 3 plots the percentage of the time our heuristic successfully picks the thread with the minimum surplus (we omit detailed results due to space constraints). The figure shows that, in a quad-processor system, examining the first 20 threads in each queue provides sufficient accuracy ( $\gt 99\%$ ) even when the number of runnable threads is as large as 5000 (the actual number of threads in the system is typically much larger).

**Figure 3:** Efficacy of the scheduling heuristic: the figure plots the percentage of the time the heuristic successfully picks the thread with the least surplus for varying run queue lengths and varying number of threads examined.
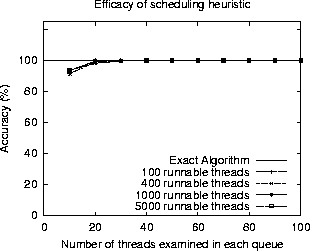
$\begin{figure} \begin{center} \epsfig {figure=/usr/ast/users2/abhishek/conferences/osdi00/src/depth.ps,width=2.85in} \end{center}\end{figure}$

As a final caveat, the Linux kernel uses only integer variables for efficiency reasons and avoids using floating point variables as a data type. Since the computation of start tags, finish tags and surplus values involves floating point operations, we simulate floating point variables using integer variables. To do so we scale each floating point operation in SFS by a constant factor. Employing a scaling factor of 10ⁿ for each floating point operation enables us to capture n places beyond the decimal point in an integer variable (e.g., the finish tag is computed as $F_i=S_i + \frac{q \cdot 10^n}{\phi_i}$ ). The scaling factor is a compile time parameter and can be chosen based on the desired accuracy--we found a scaling factor of 10⁴ to be adequate for most purposes. Observe that a large scaling factor can hasten the warp-around in the start and finish tags of long running threads; we deal with wraparound by adjusting all start and finish tags with respect to the minimum start tag in the system and resetting the virtual time.

4 Experimental Evaluation

In this section, we experimentally evaluate the surplus fair scheduling algorithm and demonstrate its efficacy. We conducted several experiments to (i) examine the benefits of the readjustment algorithm, (ii) demonstrate proportionate allocation of processor bandwidth in SFS, and (iii) measure the scheduling overheads imposed by SFS. We used SFQ and the Linux time sharing scheduler as the baseline for our comparisons. In what follows, we first describe the test-bed for our experiments and then present the results of our experimental evaluation.

4.1 Experimental Setup

The test-bed for our experiments consisted of a 500 MHz Pentium III-based dual-processor PC with 128 MB RAM, 13GB SCSI disk, and a 100 Mb/s 3-Com ethernet card (model 3c595). The PC ran the default installation of Red Hat Linux 6.0. We used version 2.2.14 of the Linux kernel for our experiments; depending on the experiment, the kernel employed either SFS, SFQ or the time sharing scheduler to schedule threads. In each case, we used a quantum duration of 200 ms, which is the default quantum duration employed by the Linux kernel. The Linux kernel (and hence, our SFS scheduler) can be configured to employ finer-grain quanta; however, we do not examine the implications of doing so in this paper. All experiments were run when the system was lightly loaded. Note that due to resource constraints, our experiments were run on a system with only two processors; we have verified the efficacy of SFS on a larger number of processors via simulations (we omit these results due to space constraints).

The workload for our experiments consisted of a combination of real-world applications, benchmarks, and sample applications that we wrote to demonstrate specific features. These applications include: (i) Inf, a compute-intensive application that performs computations in an infinite loop; (ii) Interact, an I/O bound interactive application; (iii) thttpd, a single-threaded event-based web server, (iv) mpeg_play, the Berkeley software MPEG-1 decoder, (v) gcc, the GNU C compiler, (vi) disksim, a publicly-available disk simulator, (vii) dhrystone, a compute-intensive benchmark for measuring integer performance, and (viii) lmbench, a benchmark that measures various aspects of operating system performance. Next, we describe the experimental results obtained using these applications and benchmarks.

4.2 Impact of the Weight Readjustment Algorithm

**Figure 4:** Impact of the weight readjustment algorithm: use of the readjustment algorithm enables SFQ to prevent starvation and reduces the unfairness in its allocations.
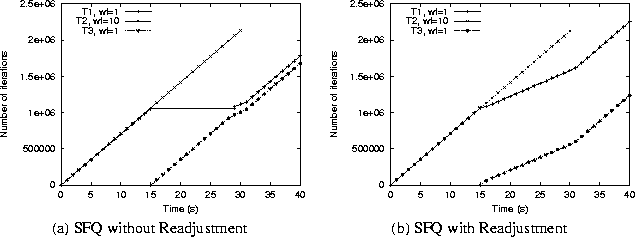$\begin{figure} \begin{center} \begin{tabular} {cc} \epsfig {figure=/usr/ast/us... ...t Readjustment & (b) SFQ with Readjustment\end{tabular}\end{center}\end{figure}$

To show that the weight readjustment algorithm can be combined with existing GPS-based scheduling algorithms to reduce the unfairness in their allocations, we conducted the following experiment. At t=0, we started two Inf applications (T₁ and T₂) with weights 1:10. At t=15s, we started a third Inf application (T₃) with a weight of 1. Task T₂ was then stopped at t=30s.We measured the processor shares received by the three applications (in terms of number of loops executed) when scheduled using SFQ; we then repeated the experiment with SFQ coupled with the weight readjustment algorithm. Observe that this experimental scenario corresponds to the infeasible weights problem described in Example 1 of Section 1.2. As expected, SFQ is unable to distinguish between feasible and infeasible weight assignments, causing task T₁ to starve upon the arrival of task T₃ at t=15s (see Figure 4(a)). In contrast, when coupled with the readjustment algorithm, SFQ ensures that all tasks receive bandwidth in proportion to their instantaneous weights (1:1 from t=0 through t=15, and 1:2:1 from t=15 through t=30, and 1:1 from then on). See Figure 4(b). This demonstrates that the weight readjustment algorithm enables a GPS-based scheduler such as SFQ to reduce the unfairness in its allocations in multiprocessor environments.

4.3 Comparing SFQ and SFS

**Figure 5:** The Short Jobs Problem. Frequent arrivals and departures in multiprocessor environments prevent SFQ from allocating bandwidth in the requested proportions. SFS does not have this drawback.
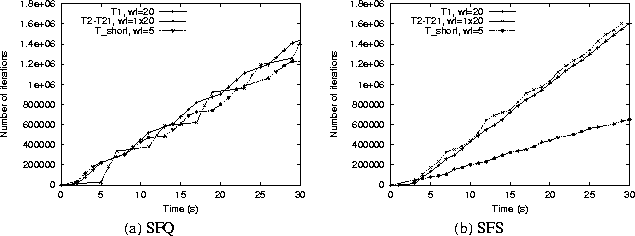$\begin{figure} \begin{center} \begin{tabular} {cc} \epsfig {figure=/usr/ast/us... ...c/sfs.ps,width=2.7in} \ (a) SFQ & (b) SFS\end{tabular}\end{center}\end{figure}$

In this section, we demonstrate that even with the weight readjustment algorithm, SFQ can show unfairness in multiprocessor environments, especially in the presence of frequent arrivals and departures (as discussed in Example 2 of Section 1.2). We also show that SFS does not suffer from this limitation. To demonstrate this behavior, we started an Inf application (T₁) with a weight of 20, and 20 Inf applications (collectively referred to as T_2-21), each with weight of 1. To simulate frequent arrivals and departures, we then introduced a sequence of short Inf tasks (T_short) into the system. Each of these short tasks was assigned a weight of 5 and ran for 300ms each; each short task was introduced only after the previous one finished. Observe that the weight assignment is feasible at all times, and the weight readjustment algorithm never modifies any weights. We measured the processor share received by each application (in terms of the cumulative number of loops executed). Since the weights of T₁, T_2-21 and T_short are in the ratio 20:20:5, we expect T₁ and T_2-21 to receive an equal share of the total bandwidth and this share to be four times the bandwidth received by T_short. However, as shown in Figure 5(a), SFQ is unable to allocate bandwidth in these proportions (in fact, each set of tasks receives approximately an equal share of the bandwidth). SFS, on the other hand, is able to allocate bandwidth approximately in the requested proportion of 4:4:1 (see Figure 5(b)).

The primary reason for this behavior is that SFQ schedules threads in ``spurts''--threads with larger weights (and hence, smaller start tags) run continuously for some number of quanta, then threads with smaller weights run for a few quanta and the cycle repeats. In the presence of frequent arrivals and departures, scheduling in such ``spurts'' allows tasks with higher weights (T₁ and T_short in our experiment) to run almost continuously on the two processors; T_2-21 get to run infrequently. Thus, each T_short task gets as much processor share as the higher weight task T₁; since each T_short task is short lived, SFQ is unable to account for the bandwidth allocated to the previous task when the next one arrives. SFS, on the other hand, schedules each application based on its surplus. Consequently, no task can run continuously and accumulate a large surplus without allowing other tasks to run first; this finer interleaving of tasks enables SFS to achieve proportionate allocation even with frequent arrivals and departures.

4.4 Proportionate Allocation and Application Isolation in SFS

**Figure 6:** Proportionate allocation and application isolation in SFS. Figure (a) shows that SFS allocates bandwidth in the requested proportions. Figure (b) shows that SFS can isolate a software video decoder from background compilations. Figure (c) shows that SFS provides interactive performance comparable to time sharing
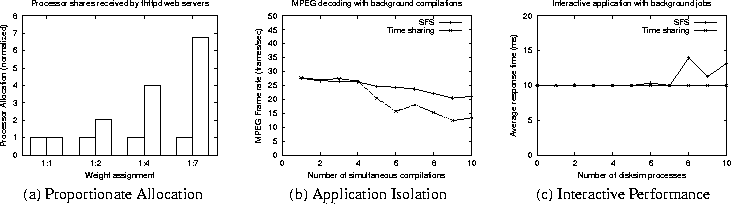$\begin{figure} \begin{center} \begin{tabular} {ccc} \epsfig {figure=/usr/ast/u... ...on Isolation & (c) Interactive Performance\end{tabular}\end{center}\end{figure}$

Next, we demonstrate proportionate allocation and application isolation of tasks in SFS. To demonstrate proportionate allocation, we ran 20 background dhrystone processes, each with a weight of 1. We then ran two thttpd web servers and assigned them different weights (1:1, 1:2, 1:4 and 1:7). A large number of requests were then sent to each web server. In each case, we measured the average processor bandwidth allocated to each web server (the background dhrystone processes were necessary to ensure that all weights were feasible at all times; without these processes, no weight assignment other than 1:1 would be feasible in a dual-processor system). As shown in Figure 6(a), the processor bandwidth allocated by SFS to each web server is in proportion to its weight.

To show that SFS can isolate applications from one another, we ran the mpeg_play software decoder in the presence of a background compilation workload. The decoder was given a large weight and used to decode a 5 minute long MPEG-1 clip that had an average bit rate of 1.49 Mb/s. Simultaneously, we ran a varying number of gcc compile jobs, each with a weight of 1. The scenario represents video playback in the presence of background compilations; running multiple compilations simultaneously corresponds to a parallel make job (i.e., make -j) that spawns multiple independent compilations in parallel. Observe that assigning a large weight to the decoder ensures that the readjustment algorithm will effectively assign it the bandwidth of one processor, and the compilations jobs share the bandwidth of the other processor.

We varied the compilation workload and measured the frame rate achieved by the software decoder. We then repeated the experiment with the Linux time sharing scheduler. As shown in Figure 6(b), SFS is able to isolate the video decoder from the compilation workload, whereas the Linux time sharing scheduler causes the processor share of the decoder to drop with increasing load. We hypothesize that the slight decrease in the frame rate in SFS is caused due to the increasing number of intermediate files created and written by the gcc compiler, which interferes with the reading of the MPEG-1 file by the decoder.

Our final experiment consisted of an I/O-bound interactive application Interact that ran in the presence of a background simulation workload (represented by some number of disksim processes). Each application was assigned a weight of 1, and we measured the response time of Interact for different background loads. As shown in Figure 6(c), even in the presence of a compute-intensive workload, SFS provides response times that are comparable to the time sharing scheduler (which is designed to give higher priority to I/O-bound applications).

4.5 Benchmarking SFS: Scheduling Overheads

**Table 1:** Scheduling Overheads reported by *lmbench*
Test	Time sharing	SFS
syscall overhead	0.7 $\mu$ s	0.7 $\mu$ s
`fork()`	400 $\mu$ s	400 $\mu$ s
`exec()`	2 ms	2 ms
Context switch (2 proc/ 0KB)	1 $\mu$ s	4 $\mu$ s
Context switch (8 proc/ 16KB)	15 $\mu$ s	19 $\mu$ s
Context switch (16 proc/ 64KB)	178 $\mu$ s	179 $\mu$ s

We used lmbench, a publicly available operating system benchmark, to measure the overheads imposed by the SFS scheduler. We ran lmbench on a lightly loaded machine with SFS and repeated the experiment with the Linux time sharing scheduler. In each case, we averaged the statistics reported by Lmbench over several runs to reduce experimental error. Note that the SFS code is untuned, while the time sharing scheduler has benefited from careful tuning by the Linux kernel developers. Table 1 summarizes our results (we report only those lmbench statistics that are relevant to the CPU scheduler). As shown in Table 1, the overhead of creating processes (measured using the fork and exec system calls) is comparable in both schedulers. The context switch overhead, however, increases from 1 $\mu$ s to 4 $\mu$ s for two 0KB processes (the size associated with a process is the size of the array manipulated by each process and has implications on processor cache performance [13]). Although the overhead imposed by SFS is higher, it is still considerably smaller than the 200 ms quantum duration employed by Linux. The context switch overheads increase in both schedulers with increasing number of processes and increasing process sizes. SFS continues to have a slightly higher overhead, but the percentage difference between the two schedulers decreases with increasing process sizes (since the restoration of the cache state becomes the dominating factor in context switches).

Figure 7 plots the context switch overhead imposed by the two schedulers for varying number of 0 KB processes (the array sizes manipulated by each process was set to zero to eliminate caching overheads from the context switch times). As shown in the figure, the context switch overhead increases sharply as the number of processes increases from 0 to 5, and then grows with the number of processes. The initial increase is due to the increased book-keeping overheads incurred with a larger number of runnable processes (scheduling decisions are trivial when there is only one runnable process and require minimal updates to kernel data structures). The increase in scheduling overhead thereafter is consistent with the complexity of SFS reported in Section 3.2 (the scheduling heuristic presented in that section was not used in this experiment). Interestingly, the Linux time sharing scheduler also imposes an overhead that grows with the number of processes.

**Figure 7:** Scheduling overheads reported by *lmbench* with varying number of processes.
$\begin{figure} \centerline{ \epsfig {figure=/usr/ast/users2/abhishek/conferences/osdi00/src/ctx.ps,width=2.7in} }\end{figure}$

5 Limitations and Directions for Future Work

Whereas surplus fair scheduling achieves proportionate allocation of bandwidth in multiprocessor environments, it has certain limitations. In what follows, we discuss some of the limitations of SFS and opportunities for future work.

In SFS, the QoS requirements of an application are distilled to a single dimension, namely its rate (which is specified using a weight). That is, SFS is a pure proportional-share CPU scheduler. Applications can have requirements along other dimensions. For instance, interactive applications tend to be more latency-sensitive than batched applications, or a certain application may need to have higher priority than other applications. Recent research has extended GPS-based proportional-share schedulers to account for these dimensions. For instance, SMART [16] enhances a GPS-based scheduler with priorities, while BVT [7] extends a GPS-based scheduler to handle latency requirements of threads. We plan to explore similar extensions for GMS-based schedulers such as SFS as part of our future work.

GPS-based schedulers such as SFQ can perform hierarchical scheduling. This allows threads to be aggregated into classes and CPU shares to be allocated on a per-class basis. Consequently, hierarchical schedulers can handle resource principals (e.g., processes) consisting of multiple threads. Many hierarchical schedulers also support class-specific schedulers, in which the bandwidth allocated to a class is distributed among individual threads using a class-specific scheduling policy. SFS is a single-level scheduler and can only handle resource principals with a single thread. We are currently enhancing SFS to overcome both limitations. To handle resource principals with multiple threads, we are generalizing our weight readjustment algorithm. Specifically, a resource principal with $\tau$ threads can be simultaneously scheduled on $\tau$ processors. The feasibility constraint for such a resource principal is specified as

$\begin{displaymath} \frac{w_i}{\sum_j w_j} \leq \mbox{min}(\frac{\tau}{p},1)\end{displaymath}$ (7)

We are modifying the weight readjustment algorithm to incorporate this constraint. To support hierarchical scheduling, we are modifying SFS to allow independent resource principals to be grouped into classes in a hierarchical manner. Assuming that these groups are specified in the form of a tree, our enhanced algorithm allows weights to be specified for each node (sub-class) in the tree. Our weight readjustment algorithm then ensures feasibility of the weights assigned to each node based on the number of runnable threads in that sub-tree.

SMP-based time-sharing schedulers employed by conventional operating systems take caching effects into account while scheduling threads [25]. As explained in Section 2.4, SFS can be modified to take such processor affinities into account while making scheduling decisions. However, the implications of doing so on fairness guarantees and cache performance need further investigation.

Regardless of whether resources are allocated in relative or absolute terms, a predictable scheduler will need to employ techniques to restrict the number of threads in the system in order to provide performance guarantees. While some schedulers integrate an admission control test with the scheduling algorithm, others implicitly assume that such an admission control test will be employed but do not specify a particular test. SFS falls into the latter category--the system will need to employ admission control if threads desire specific performance guarantees. Assuming such a test is employed, fair proportional-share schedulers have been shown to provide bounds on the throughput received and the latency incurred by threads [4,9]. We are currently analyzing SFS to determine the performance guarantees that can be provided to a thread. Note, however, that the scheduling heuristic and the processor affinity bias can weaken the guarantees provided by SFS.

Finally, proportional-share schedulers such as SFS need to be combined with tools that enable a user to determine an application's resource requirements. Such tools should, for instance, allow a user to determine the processing requirements of an application (for instance, by application profiling), translate these requirements to appropriate weights, and modify weights dynamically if these resource requirements change [6,21]. Translating application requirements such as rate to an appropriate set of weights is the subject of future research.

6 Concluding Remarks

In this paper, we argued that the infeasibility of certain weight assignments causes unfairness or starvation in many existing proportional-share schedulers when employed for multiprocessor servers. We presented a novel weight readjustment algorithm to translate infeasible weight assignments to a feasible set of weights. We showed that our algorithm enables existing proportional-share schedulers such as SFQ to significantly reduce, but not eliminate, the unfairness in their allocations. We then presented the idealized generalized multiprocessor sharing algorithm and derived surplus fair scheduling, which is a practical instantiation of GMS. We implemented SFS in the Linux kernel and demonstrated its efficacy through an experimental evaluation. Our experiments indicate that a proportional-share CPU scheduler such as SFS is not only practical but also desirable for general-purpose operating systems. As part of future work, we plan to extend SFS to do hierarchical scheduling as well as enhance proportional-share schedulers to account for priorities and delay.

Acknowledgements

We would like to thank the anonymous reviewers and our shepherd Mike Jones for their comments.

References

1

M. Aron, P. Druschel, and W. Zwaenepoel.
Cluster Reserves: A Mechanism for Resource Management in Cluster-based Network Servers.
In Proceedings of the ACM SIGMETRICS Conference, Santa Clara, CA, June 2000.

2

G. Banga, P. Druschel, and J. Mogul.
Resource Containers: A New Facility for Resource Management in Server Systems.
In Proceedings of the third Symposium on Operating System Design and Implementation (OSDI'99), New Orleans, pages 45-58, February 1999.

3

S. K. Baruah, N. K. Cohen, C. G. Plaxton, and D. A. Varvel.
Proportionate Progress: A Notion of Fairness in Resource Allocation.
Algorithmica, 15:600-625, 1996.

4

J.C.R. Bennett and H. Zhang.
Hierarchical Packet Fair Queuing Algorithms.
In Proceedings of SIGCOMM'96, pages 143-156, August 1996.

5

A. Demers, S. Keshav, and S. Shenker.
Analysis and Simulation of a Fair Queueing Algorithm.
In Proceedings of ACM SIGCOMM, pages 1-12, September 1989.

6

J R. Douceur and W J. Bolosky.
Progress-based Regulation of Low-importance Processes.
In Proceedings of the ACM Symposium on Operating Systems Principles (SOSP'99), Kiawah Island Resort, SC, pages 247-260, December 1999.

7

K. Duda and D. Cheriton.
Borrowed Virtual Time (BVT) Scheduling: Supporting Lantency-sensitive Threads in a General-Purpose Scheduler.
In Proceedings of the ACM Symposium on Operating Systems Principles (SOSP'99), Kiawah Island Resort, SC, pages 261-276, December 1999.

8

K. Govil, D. Teodosiu, Y. Huang, and M. Rosenblum.
Cellular Disco: Resource Management using Virtual Clusters on Shared-memory Multiprocessors.
In Proceedings of the ACM Symposium on Operating Systems Principles (SOSP'99), Kiawah Island Resort, SC, pages 154-169, December 1999.

9

P. Goyal, X. Guo, and H.M. Vin.
A Hierarchical CPU Scheduler for Multimedia Operating Systems.
In Proceedings of Operating System Design and Implementation (OSDI'96), Seattle, pages 107-122, October 1996.

10

M B. Jones and J. Regehr.
CPU Reservations and Time Constraints: Implementation Experience on Windows NT.
In Proceedings of the Third Windows NT Symposium, Seattle, WA, July 1999.

11

M B. Jones, D Rosu, and M Rosu.
CPU Reservations and Time Constraints: Efficient, Predictable Scheduling of Independent Activities.
In Proceedings of the sixteenth ACM symposium on Operating Systems Principles (SOSP'97), Saint-Malo, France, pages 198-211, December 1997.

12

Ian Leslie, Derek McAuley, Richard Black, Timothy Roscoe, Paul Barham, David Evers, Robin Fairbairns, and Eoin Hyden.
The Design and Implementation of an Operating System to Support Distributed Multimedia Applications.
IEEE Journal on Selected Areas in Communication, 14(7):1280-1297, September 1996.

13

L. McVoy and C. Staelin.
Lmbench: Portable Tools for Performance Analysis.
In Proceedings of USENIX'96 Technical Conference, Available from https://www.bitmover.com/lmbench, January 1996.

14

C. W. Mercer, S. Savage, and H. Tokuda.
Processor Capacity Reserves: Operating System Support for Multimedia Applications.
In Proceedings of the IEEE ICMCS'94, May 1994.

15

A. Mok and M. Dertouzos.
Multiprocessor Scheduling in a Hard Real-time Environment.
In Proceedings of the Seventh Texas Conf. on Computing Systems, November 1978.

16

J. Nieh and M S. Lam.
The Design, Implementation and Evaluation of SMART: A Scheduler for Multimedia Applications.
In Proceedings of the sixteenth ACM symposium on Operating systems principles (SOSP'97), Saint-Malo, France, pages 184-197, December 1997.

17

J. Nieh and M. S. Lam.
Multimedia on Multiprocessors: Where's the OS When You Really Need It?
In Proceedings of the Eighth International Workshop on Network and Operating System Support for Digital Audio and Video, Cambridge,U.K., July 1998.

18

A.K. Parekh.
A Generalized Processor Sharing Approach to Flow Control in Integrated Services Networks.
PhD thesis, Department of Electrical Engineering and Computer Science, MIT, 1992.

19

M. Shreedhar and G. Varghese.
Efficient Fair Queuing Using Deficit Round Robin.
In Proceedings of ACM SIGCOMM'95, pages 231-242, 1995.

20

J. Stankovic and K. Ramamritham.
The Spring Kernel: A New Paradigm for Real-time Systems.
IEEE Software, 8(3):62-73, 1991.

21

D C. Steere, A. Goel, J. Gruenberg, D. Mc Namee, C. Pu, and J. Walpole.
A Feedback-driven Proportion Allocator for Real-Rate Scheduling.
In Proceedings of the third ACM Symposium on Operating systems design and implementation (OSDI'99), New Orleans, LA, pages 145-158, February 1999.

22

I. Stoica, H. Abdel-Wahab, and K. Jeffay.
On the Duality between Resource Reservation and Proportional Share Resource Allocation.
In Proceedings of the ACM/SPIE Conference on Multimedia Computing and Networking (MMCN'97), San Jose, CA, pages 207-214, February 1997.

23

I. Stoica, H. Abdel-Wahab, K. Jeffay, S. Baruah, J. Gehrke, and G. Plaxton.
A Proportional Share Resource Allocation Algorithm for Real-Time, Time-Shared Systems.
In Proceedings of Real Time Systems Symposium, Washington, DC, pages 289-299, December 1996.

24

Solaris Resource Manager 1.0: Controlling System Resources Effectively.
Sun Microsystems, Inc., https://www.sun.com/software/white-papers/wp-srm/, 1998.

25

R. Vaswani and J. Zahorjan.
The Implications of Cache Affinity on Processor Scheduling for Multiprogrammed Shared Memory Multiprocessors.
In Proceedings of the 13th ACM Symposium on Operating Systems Principles, pages 26-40, October 1991.

26

B. Verghese, A. Gupta, and M. Rosenblum.
Performance Isolation: Sharing and Isolation in Shared-Memory Multiprocessors.
In Proceedings of ASPLOS-VIII, San Jose, CA, pages 181-192, October 1998.

27

C. Waldspurger and W. Weihl.
Lottery Scheduling: Flexible Proportional-Share Resource Management.
In Proceedings of the First Symposium on Operating Systems Design and Implementation, pages 1-12, November 1994.

28

C. Waldspurger and W. Weihl.
Stride Scheduling: Deterministic Proportional-share Resource Management.
Technical Report TM-528, MIT, Laboratory for Computer Science, June 1995.

Footnotes

...Multiprocessors: This research was supported in part by a NSF Career award CCR-9984030, NSF grants ANI 9977635, CDA-9502639, Intel, Sprint, and the University of Massachusetts.
...work-conserving,: A scheduling algorithm is said to be work-conserving if it never lets a processor idle so long as there are runnable threads in the system.
...bandwidth.: This can be observed by summing Equation 2 over all runnable threads j, which yields $A_i(t_1,t_2) \cdot \sum_j \phi_j \geq \phi_i \cdot \sum_j A_j(t_1,t_2)$ . Since $\sum_j A_j(t_1,t_2)$ is the total processor bandwidth allocated to all threads in the interval, we can substitute it by the quantity $p \cdot {\cal C} \cdot (t_2-t_1)$ Hence, we get $A_i(t_1,t_2) \geq \frac{\phi_i}{\sum_j \phi_j} \cdot p \cdot {\cal C} \cdot (t_2-t_1)$ . Thus each thread receives processor bandwidth in proportion to its instantaneous weight $\phi_i$ .
...community.: The source code for our implementation is available from https://www.cs.umass.edu/~lass/software/gms.

Abhishek Chandra
9/26/2000

This paper was originally published in the Proceedings of the 4th USENIX OSDI Symposium, October 23-25, 2000, San Diego, California, USA.
Last changed: 16 Jan. 2002 ml

Technical Program

4th USENIX OSDI Home

USENIX home