NSDI '06 Paper [NSDI '06 Technical Program]

Availability of Multi-Object Operations

Haifeng Yu
Intel Research Pittsburgh / CMU
yhf@cs.cmu.edu

Phillip B. Gibbons
Intel Research Pittsburgh
phillip.b.gibbons@intel.com

Suman Nath¹
Microsoft Research
sumann@microsoft.com

Abstract: Highly-available distributed storage systems are commonly designed to optimize the availability of individual data objects, despite the fact that user level tasks typically request multiple objects. In this paper, we show that the assignment of object replicas (or fragments, in the case of erasure coding) to machines plays a dramatic role in the availability of such multi-object operations, without affecting the availability of individual objects. For example, for the TPC-H benchmark under real-world failures, we observe differences of up to four nines between popular assignments used in existing systems. Experiments using our wide-area storage system prototype, MOAT, on the PlanetLab, as well as extensive simulations, show which assignments lead to the highest availability for a given setting.

1 Introduction

With the fast advance of systems research, performance is no longer the sole focus of systems design [19]. In particular, system availability is quickly gaining importance in both industry and the research community. Data redundancy (i.e., replication or erasure coding) is one of the key approaches for improving system availability. When designing highly-available systems, researchers typically optimize for the availability of individual data objects. For example CFS [9] aims to achieve a certain availability target for individual file blocks, while OceanStore [26] and Glacier [18] focus on the availability of individual (variable-size) objects. However, a user-level task or operation typically requests multiple data objects. For example, in order to compile a project, all of its files need to be available for the compilation to succeed. Similarly, a database query typically requests multiple database objects. This work is motivated by the following question: Is optimizing the availability of individual data objects an effective approach for ensuring the high availability of these multi-object operations? We observe that existing distributed storage systems can differ dramatically in how they assign replicas, relative to each other, to machines. For example, systems such as GFS [15], FARSITE [5], and RIO [33] assign replicas randomly to machines (we call this strategy RAND); others such as the original RAID [28] and Coda [25] manually partition the objects into sets and then mirror each set across multiple machines (we call this strategy PTN); others such as Chord [36] assign replicas to consecutive machines on the DHT ring. However, in spite of the existence of many different assignment strategies, previous studies have not provided general insight across strategies nor have they compared the availability among the strategies for multi-object operations. This leads to the central question of this paper: What is the impact of the replicas' relative assignment on the availability of multi-object operations? Answering the above two questions is crucial for designing highly-available distributed systems. A negative answer to the first question would suggest that system designers need to think about system availability in a different way—we should optimize availability for multi-object operations instead of simply for individual objects. An answer to the second question would provide valuable design guidelines toward such optimizations. This paper is the first to study and answer these two questions, using a combination of trace/model-driven simulation and real system deployment. Our results show that, surprisingly, different object assignment strategies result in dramatically different availability for multi-object operations, even though the strategies provide the same availability for individual objects and use the same degree of replication. For example, we observe differences of multiple nines arising between popular assignments used in existing systems such as CAN [29], CFS [9], Chord, Coda, FARSITE, GFS, GHT [30], Glacier [18], Pastry [31], R-CHash [22], RAID, and RIO. In particular, the difference under the TPC-H benchmark reaches four nines: some popular assignments provide less than 50% availability, even when individual objects have 5 nines availability, while others provide up to 99.97% availability for the same degree of replication. To answer the second question above, we examine the entire class of possible assignment strategies, including the aforementioned RAND and PTN, in the context of two types of multi-objects operations: strict operations that cannot tolerate any missing objects in the answer (i.e., that require complete answers) and more tolerant operations that are not strict. We design our simulation experiments based on an initial analytical study of assignment strategies under some specific parameter settings [44]. Our initial analysis [44] indicates that i) for strict operations, PTN provides the best availability while RAND provides the worst; ii) for certain operations that are more tolerant, RAND provides the best availability while PTN provides the worst; and iii) it is impossible to achieve the best of both PTN and RAND. Based on the above theoretical guidance, we design our simulation study to explore the large parameter space that is not covered by the analysis. Our simulation shows that although operations can have many different tolerance levels for missing objects, as a practical rule of thumb, only two levels matter when selecting an assignment: does the operation require all requested objects (strict) or not (loose)? The results show that the above analytical result for “certain operations that are more tolerant” generalizes to all loose operations. Namely, for all loose operations, RAND tends to provide the best availability while PTN tends to provide the worst. These results have the following implications for multi-object availability: PTN-based systems such as RAID and Coda are optimized for strict operations; RAND-based systems such as GFS, FARSITE, and RIO are optimized for loose operations; and other assignment strategies, such as the one used in Chord, lie between PTN and RAND. Next, we consider practical ways to implement PTN and RAND in distributed systems where objects and machines may be added or deleted over time. CAN approximates RAND in such a dynamic setting. On the other hand, PTN is more challenging to approximate due to its rigid structure. We propose a simple design that approximates PTN in dynamic settings. We have implemented our design for PTN, as well as other assignment strategies, in a prototype wide-area distributed storage system called MOAT (Multi-Object Assignment Toolkit). Although our prototype considers the challenges of wide-area distributed storage, our findings apply to local-area systems as well. Finally, we study multi-object availability in the presence of two important real-world factors: load imbalance resulting from the use of consistent hashing [22] and correlated machine failures experienced by most wide-area systems [42]. We study these effects using MOAT under a model for network failures, a real eight-month-long PlanetLab failure trace, a query trace obtained from the IrisLog network monitoring system [2], and the TPC-H benchmark. We use both live PlanetLab deployment and event-driven simulation as our testbed. Our results show three intriguing facts. First, both consistent hashing and machine failure correlation hurt the availability of more tolerant operations, but surprisingly, they slightly improve the availability of more strict operations (if the availability of individual objects is kept constant). Second, popular assignments such as Glacier that approximate PTN under perfect load balancing, fail to do so under consistent hashing. Third, our earlier conclusions (which assume perfect load balance and independent machine failures) hold even with consistent hashing and correlated failures: the relative ranking among the assignments remains unchanged. Although this paper focuses solely on availability, object assignment also affects performance—exploring the interaction between performance and availability goals is part of our future work. Note that in some cases, these goals can be achieved separately, by using a primary storage system for performance goals and a backup storage system (that uses replication or erasure coding) for availability goals [18]. In the next section we discuss motivating applications and examples. Section 3 defines our system model and gives a classification of popular assignments. Section 4 shows that PTN and RAND dominate other assignments. Section 5 presents our designs to approximate PTN in dynamic settings. Section 6 describes MOAT and evaluates assignments under real-world workloads and faultloads. Section 7 discusses related work and Section 8 presents conclusions.

2 Motivation

2.1 Motivating Applications

In most applications including traditional file systems and database systems, user operations tend to request multiple objects. These applications can easily motivate our work. In this section, however, we focus on two classes of applications that are extreme in terms of the number of objects requested by common operations. For each operation, we will focus on the number of objects requested and the tolerance for missing objects.
Image databases. In recent years, computer systems are increasingly being used to store and serve image data [6, 21, 35, 37]. These databases can be quite large. For example, with each 2D protein image object being 4MB, a distributed bio-molecular image database [35] can easily reach multiple terabytes of data. The SkyServer astronomy database [37], which stores the images of astronomical spheres, is rapidly growing, with the potential of generating one petabyte of new data per year [38]. Such large databases are typically distributed among multiple machines either residing in a LAN or distributed in the wide-area (e.g., similar to the Grid [1]). High availability has been an integral requirement of these systems. For example, the TerraServer system for aerial images explicitly aims for four nines availability [6]. Queries to these image databases can touch a non-trivial fraction of the entire database. For example, among the 35 typical queries used to benchmark SkyServer, at least one query touches over 9.7% of the entire database, while at least four other queries touch over 0.5% of the entire database [17]. Clearly, these queries touch a large number of objects. In other image databases [21], it is difficult to suitably index the data because queries are not known a priori and often require domain-specific knowledge. As a result, each query essentially searches every object in the database. The requirements from these queries can vary based on their semantics. For example, a SkyServer query “compute the average brightness of all galaxies” would likely be able to tolerate some missing objects. On the other hand, a query of “check whether any of the images in the database contain the face of a criminal” would likely require checking all objects in the database, and is thus a strict operation.
Data storage used in network monitoring. Our second class of applications is Internet-scale distributed storage systems such as IrisNet [2, 11, 16], SDIMS [41] and PIER [20] that are used for monitoring potentially hundreds of thousands of network endpoints. In order to avoid the unnecessary bandwidth consumption for data transfer, data are typically stored near their sources (e.g., at the hosts being monitored) [2, 11, 20, 41]. As a result, the database is distributed over a large number of wide-area hosts. Many queries from these applications request aggregated information over a large data set, e.g., the distribution of resource usage over the hosts, the correlation (join) of the worm-infected hosts and their operating systems, etc. Each such query touches a non-trivial fraction of the entire database. These aggregation queries are likely to be able to tolerate some missing objects. However, other queries, e.g., by a system administrator trying to pinpoint a network problem or find all virus-infected hosts, may not be able to tolerate any missing objects, and are thus strict operations.

2.2 Motivating Example

Figure 1: Four possible assignments of 8 objects, A through H, to 8 machines. Each box represents a machine. A dash (-) indicates an object that is not accessed by the given query.

With our motivating applications in mind, the following simple example illustrates the impact and the subtleties of object assignment.
A simple example with subtle answers. Consider an image database with 16 objects and a query that requests 8 of the 16 objects, namely A through H. An example is the query of “check whether any of the images in the database contain the face of a given male criminal”, where A through H are the images with male faces. Because of the nature of this operation, the query is successful only if all the 8 images A–H are available. Suppose each object has exactly two copies, there are 8 identical machines on which we can place these copies, and each machine may hold no more than four objects. Each machine may fail (crash), causing all its data to become unavailable. An object is unavailable if and only if both its copies are unavailable. For simplicity, assume that machines fail independently with the same probability p < 0.5. Figure 1 gives four (of the many) possible assignments of objects to machines, depicting only the 8 objects requested by the query. Which of these four assignments gives us a better chance that all 8 image objects are available so that the query for criminal faces succeeds? Intuitively, it may make sense that concentrating the objects on fewer machines, as in assignments I and II, gives us a better chance. However, that still leaves a choice between assignment I and assignment II. A careful calculation shows that in fact assignment I provides better availability than assignment II², and hence the best availability among all four assignments. Now consider a network monitoring database with 16 objects, and a query for the average load on U.S. hosts, where objects A– H contain the load information for the U.S. hosts. Suppose we are willing to tolerate some error in the average and the query succeeds as long as we can retrieve 5 or more objects. Intuitively, it may now make sense that spreading the objects across more machines, as in assignments III and IV, gives us a better chance that the query succeeds. However, that still leaves a choice between assignments III and IV and again it is not clear which is better. A careful calculation shows that the relative assignment of objects in assignment IV³ provides the best availability among all four assignments. What happens when the query requires 6 or 7 objects to succeed instead of 5 or 8? What about all the other possible assignments that place two objects per machine? Do any of them provide significantly better availability than assignment IV? For databases with millions of objects and hundreds of machines, answering these questions by brute-force calculation is not feasible, so effective guidelines are clearly needed.

Example remains valid under erasure coding. Our simple example uses replication for each object. The exact same problem also arises with erasure coding, where we assign fragments (instead of copies) to machines. If the number of fragments per object is the same as the total number of machines in the system (e.g., 8 in our example), then the assignment problem goes away. However, in large-scale systems, the total number of machines is typically much larger than the number of fragments per object. As a result, the same choice regarding fragment assignment arises. Also, in our simple example, it is possible to use erasure coding across all objects (i.e., treating them as a single piece of data). This would clearly minimize the failure probability if we need all the objects for the operation to be successful. However, due to the nature of erasure coding, it is not practical to use erasure coding across large amounts of data (e.g., using erasure coding across all the data in the database). Specifically, for queries that request only some of the objects (as in our example), erasure coding across all the objects means that much more data is fetched than is needed for the query. On the other hand, when objects are small, it is practical to use erasure coding across sets of objects. In such scenarios, we view each erasure-coded set of objects as a single logical object. In fact, we intentionally use a relatively large object size of 33MB in some of our later experiments to capture such scenarios.
Summary. The impact of object assignment on availability is complicated and subtle. Intuitive rules make sense, such as “concentrate objects on fewer machines for strict operations” and “spread objects across machines for more tolerant operations”. However, these intuitive rules are not useful for selecting among assignments with the same degree of concentration/spread (e.g, for choosing between assignments I and II in our example). This paper provides effective guidelines for selecting among all assignments, including among assignments with the same degree of concentration/spread. As our results show, such guidelines are crucial: popular assignments with the same degree of concentration/spread can still vary by multiple nines in the availability they provide for multi-object operations. For the example above, our results will show that for the query that cannot tolerate missing objects, assignment I is actually near optimal among all possible assignments. On the other hand, for more tolerant queries, a random assignment of the objects to the machines (with each machine holding two objects) will give us the highest availability.

3 Preliminaries

N number of objects in the system

k number of FORs per object

m number of FORs needed to reconstruct an object (out of the k FORs)

n number of objects requested by an operation

t number of objects needed for the operation to be successful (out of the n objects)

s number of machines in the system

l number of FORs on each machine (= Nk/s)

p failure probability of each machine

FP(α) failure probability of assignment α

Table 1: Notation used in this paper.

In this section, we set the context for our work by presenting our system model and then reviewing and classifying well-known assignments.

3.1 System Model

We begin by defining our system model for both replicated and erasure-coded objects. Table 1 summarizes the notation we use. There are N data objects in the system, where an object is, for example, a file block, a file, a database tuple, a group of database tuples, an image, etc. An operation requests (for reading and/or writing) n objects, 1 ≤ n ≤ N, to perform a certain user-level task. There are s machines in the system, each of which may experience crash (benign) failures with a certain probability p. Replication or erasure coding is used to provide fault tolerance. Each object has k replicas (for replication) or k fragments (for erasure coding). We use the same k for all objects to ensure a minimal level of fault tolerance for each object. Extending the model and our results to different k's is part of our future work. To unify terminology, we call each fragment or replica a FOR of the object. The k FORs of an object are numbered 1 through k. We assume that m out of k FORs are needed for a given object to be available for use. If an object has less then m FORs available, we say the object fails. A global assignment (or simply assignment) is a mapping from the kN FORs to the s machines in the system. An assignment is ideal (in terms of load balance) if each machine has exactly l = kN /s FORs. The value l is also called the load of a machine. For an operation requesting n objects, if not all n objects are available, the operation may or may not be considered successful, depending on its tolerance for missing objects. This paper studies threshold criteria: an operation is successful if and only if at least t out of the n objects are available. Here t is an operation-specific value from 1 to n based on the application semantics. We need to emphasize that the operation threshold t is not to be confused with the m in m-out-of-k erasure coding:

In erasure coding, a single object is encoded into k fragments, and we can reconstruct the object from any m fragments. Moreover, the reconstructed object is the same regardless of which m fragments are retrieved.
For an operation with a threshold t, it does not reconstruct the n objects. Rather, the user may be reasonably satisfied even if only t objects are retrieved because of the specific application semantics. Depending on which t objects are retrieved, the answer to the user query may be different. But the user is willing to accept any of these approximate answers.

Finally, we define the availability of an operation as the probability that it is successful. We use “number of nines” (i.e., log_0.1(1−availability)) to describe availability. The complement of availability is called unavailability or failure probability. For a given operation, we use FP(α) to denote the failure probability of a particular assignment α. When we say that one assignment α is x nines better than another assignment β, we mean log_0.1 FP(α) − log_0.1 FP(β) = x. Finally, our availability definition currently does not capture possible retries or the notion of “wait time” before a failed operation can succeed by retrying. We intend to investigate these aspects in our future work.

3.2 Classifying Well-Known Assignments

(a) Chord (b) Multi-hash (CAN) (c) Pastry (d) Glacier (e) Group

SW if PLB � RAND if PLB � SW if PLB � PTN if PLB � PTN if PLB

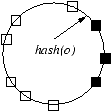
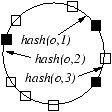
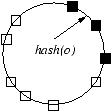
Figure 2: Placement of a single object o in different consistent hashing-based assignments used in various systems. The machines (shown as squares) have random IDs in the circular ID space. The object is replicated on three machines (shown as black solid squares). Each single object placement rule determines a different relative placement among objects, which in turn results in different availability. For each such assignment, we also note the corresponding ideal assignment if consistent hashing achieved perfect load balancing (PLB).

Non-ideal assignments (consistent-hashing-based) systems using similar non-ideal assignments

Chord [36] (Figure 2(a)): ith successor of hash(o)

Multi-hash (Figure 2(b)): 1st successor of hash(o, i) CAN [29], GFS [15], FARSITE [5], RIO [33]

Pastry [31] (Figure 2(c)): machine with the ith closest ID to hash(o)

Glacier [18] (Figure 2(d)): 1st successor of hash(o) + MaxID ⋅ (i−1)/k GHT [30], R-CHash [22, 40]

Group (Figure 2(e)): See Section 5.1 Original RAID [28], Coda [25, 34]⁴

Table 2: Salient object assignments. For the assignments in the first column, we note to which machine the ith FOR of object o is assigned.

Next, we review popular assignments from the literature, and then define three ideal assignments. We focus on well-known assignments based on consistent hashing [22]. In consistent hashing, each machine has a numerical ID (between 0 and MaxID) obtained by, for example, pseudo-randomly hashing its own IP address. All machines are organized into a single ring where the machine IDs are non-decreasing clockwise along the ring (except at the point where the ID space wraps around). Figure 2 visualizes and Table 2 describes the assignments used in Chord, CAN, Pastry and Glacier. Intuitively, in Chord, the object is hashed once and then assigned to the k successors of the hash value. In CAN (or Multi-hash), the object is hashed k times using k different hash functions, and assigned to the k immediate successors of the k hash results.⁵ Pastry also hashes the object, but it assigns the object to the machines with the k closest IDs to the hash value. Finally, Glacier hashes the object and then places the object at k equi-distant points on the ID ring. Because of the use of consistent hashing, machines in these assignments may not have exactly the same load; hence, by definition, the assignments are not ideal. Table 2 also lists other popular assignments that are similar to the ones discussed above. Next we define three ideal assignments. RAND is the assignment obtained by randomly permuting the Nk FORs and then assigning the permutation to the machines (l FORs per machine) sequentially. Note that strictly speaking, RAND is a distribution of assignments. If the machine IDs and the hashes of the objects in consistent hashing were exactly evenly distributed around the ring, then Multi-hash would be the same as RAND (Figure 2(b)). In PTN, we partition objects into sets and then mirror each set across multiple machines. Specifically, the FORs of l objects are assigned to machines 1 through k, the FORs of another l objects are assigned to machines k+1 through 2k, and so on. If consistent hashing provided perfect load balancing, then Glacier would be the same as PTN (Figure 2(d)). This is because all objects whose hashes fall into the three ID regions (delimited by black solid squares and their corresponding predecessors) will be placed on the three black solid squares, and those three machines will not host any other objects. Finally, in SW (sliding window), the FORs of l/k objects are assigned to machines 1 through k, the FORs of another l/k objects are assigned to machines 2 through k+1, and so on. If consistent hashing provided perfect load balancing, then Chord and Pastry would be the same as SW (Figures 2(a) and (c)), because all objects falling within the ID region between a machine and its predecessor will be assigned to the same k successors. Finally, we define the concept of a projected assignment for a given operation. For an assignment and a given operation requesting n objects, the projected assignment is the mapping from the nk FORs of the n objects to the machines. In other words, in the projected assignment, we ignore objects not requested by the operation. We extend the definitions of PTN and RAND to projected assignments. A projected assignment is called PTN if the global assignment is PTN and the nk FORs reside on exactly nk/l machines. Namely, the n objects should concentrate on as few machines as possible and obey the PTN rule within those machines (as in assignment I of Figure 1, where n=8 and k=2).⁶ Similarly, a projected assignment is called RAND if the global assignment is RAND and the nk FORs reside on exactly min(nk, s) machines. Here, RAND spreads the n objects on as many machines as possible. In Figure 1, assignments III and IV have the desired spread, but such well-structured assignments are highly unlikely to occur under the RAND rule. When the context is clear, we will not explicitly distinguish an assignment from its projected assignment.

4 Study of Ideal Assignments

In this section, we investigate the ideal assignments under independent machine failures. Later, Section 6 will study the more practical assignments under real failure traces.

4.1 Simulation of Ideal Assignments

We begin our study by using simulation to compare RAND, PTN and SW. We consider here the case where n=N and leave the cases for n < N to our later evaluation of practical assignments. There are six free parameters in our simulation: N, s, k, m, p and t. We have performed a thorough simulation over the entire parameter space and considered additional assignments beyond those in Section 3.2, but in this paper we are able to present only a small subset of our results (Figure 3). Each of the observations described below extends to all the other parameter settings and assignments with which we experimented. Note that Figure 3 and other figures in this paper use a relatively large failure probability p, in order to show the underlying trend with confidence, given the limited duration of our simulations. The observations and conclusions do not change with smaller p.

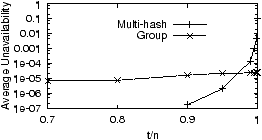
Figure 3: Unavailability of ideal assignments for an operation that requests all 24000 objects stored on 240 machines in the system. The number of machines is set to match our PlanetLab deployment. Each object has 3 replicas, and each machine fails with probability 0.1. The x-axis is the fraction (t/n) of the 24000 objects that needs to be available for the operation to succeed.

Figure 3 shows that when t=n, PTN has the lowest unavailability (roughly 0.08) among the three assignments in the figure. In contrast, when t=n RAND has the highest unavailability (nearly 1) among the three. Hence, PTN is the best and RAND is the worst when t=n. As t decreases, the unavailability of PTN does not change until we are able to tolerate 300 missing objects (i.e., t/n ≈ 98.7%). The reason is that in PTN, whenever one object is unavailable, then the other l−1 objects on the same set of machines become unavailable as well (l=300). For RAND, the unavailability decreases much faster as we are able to tolerate more and more missing objects. The curves for PTN and RAND cross when t/n ≈ 99.8%, below which point RAND becomes the best among all assignments while PTN roughly becomes the worst. This crossing point appears to be not far from the availability probability for individual objects, i.e., 1−p^k ≈ 99.9%. When t/n = 99.4%, the difference between PTN and RAND is already three nines. The intuition behind the above results is that each assignment has a certain amount of “inter-object correlation”. Because each machine may hold FORs of multiple objects, these objects become correlated even if machine failures are independent. Intuitively, PTN is the assignment that maximizes inter-object correlation, while RAND minimizes it. When t is very close to n, larger inter-object correlation is better because it does not help for a small number of objects to be available by themselves. On the other hand, if t is not close to n, smaller inter-object correlation is better because it decreases the chance that many objects fail together. It is important to note that the crossing between PTN and RAND occurs very close to 100%. As we mentioned earlier, in all our experiments, the crossing point occurs when t/n is near the availability of individual objects. As long as this availability is reasonably high, the crossing point will be close to 100%. This observation has significant practical importance. Namely, despite the fact that t can range from 1 to n, we can largely classify operations into “strict” operations and “loose” operations, as follows: An operation is strict if it cannot tolerate any missing objects, otherwise it is loose. With practical parameters, loose operations will most likely fall into the region where RAND is the best. On the other hand, PTN is best for strict operations.

4.2 Analytical Study of Ideal Assignments

The above simulation study shows that among the assignments we simulated, PTN and RAND are each the best in two different regions. But is this because we missed out on some other assignments? Do we need to consider additional assignments? Definitive answers to these questions are not readily obtained experimentally, because there are exponentially many possible assignments. We have separately obtained analytical results [44] on optimal assignments under some specific t values and assuming failure independence. Because these results are only for restricted parameter settings and are not the contribution of this paper, following we provide only a brief summary of the analytical results from [44]:⁷

For t = n (i.e., strict operations), PTN is the best (to within 0.25 nines) and RAND is the worst (to within 0.70 nines) among all possible ideal assignments.
For t = l+1 and n = N (or t = 1 and n < N), PTN is the worst and RAND is the best (to within 0.31 nines) among all possible ideal assignments.
It is impossible to achieve the best of both PTN and RAND.

The analysis in [44] also finds a rigorous mathematical definition for inter-object correlation, which confirms our earlier intuition.

5 Designs to Approximate Optimal Assignments

Our study in the previous section shows that PTN and RAND are (near) optimal for strict and loose operations, respectively. This motivates the exploration of practical designs that approximate these ideal assignments when objects and machines may be added or deleted on the fly. Our goal is to approximate not only PTN and RAND, but also their projected assignments for n < N. We have also explored optimizing solutions for systems where strict and loose operations may coexist. For lack of space, we defer the solutions to [43]. We refer the reader back to Table 2 for definitions of various non-ideal assignments. RAND is already approximated by Multi-hash. Moreover, for any operation requesting n objects, Multi-hash is likely to spread the nk FORs evenly on the ID ring. This means that the projected assignment will also approximate RAND. Thus, we do not need any further design in order to approximate RAND. For PTN, RAID [28] and Coda [34, 25] achieve PTN by considering only a static set of machines (or disks in the case of RAID). Adding or deleting machines requires human intervention. Glacier handles the dynamic case, and it would have achieved PTN if consistent hashing provided perfect load balancing. However, we will see later that in practice, it behaves similar to Chord (and hence far from PTN). Therefore, we propose a Group DHT (or Group in short) design that better approximates PTN. Regardless of whether we use Glacier, Chord, Pastry or Group, their projected assignments will not approximate PTN when n < N. Therefore, we further propose designs to ensure that the projected assignments approximate PTN for n < N. Our designs are compatible with the standard DHT routing mechanisms for locating objects. It is worth pointing out that when n is large, DHT routing will be inefficient. For those cases, multicast techniques such as in PIER [20] can be used to retrieve the objects. Our designs are compatible with those techniques as well. Finally, for cases where a centralized directory server is feasible (e.g., in a LAN cluster), neither DHT routing nor multicast techniques are required for our design.

5.1 Approximating `PTN` for n = N

This section describes how we approach PTN with Group DHT. The design itself is not the main contribution or focus of this paper – thus we will provide only a brief description, and leave the analysis of Group DHT's performance, as well as discussions of security issues, to [43].
Basic Group DHT design. In Group DHT (or Group), each DHT node is a group of exactly k machines (Figure 2(e) provides an example for k = 3).⁸ We assign the k FORs of an object to the k machines in the successor group of the object's hash value. Here we assume that all objects have the same number of FORs, and a more general design is part of our future work. There is a small number r (e.g., r = s/1000) of “rendezvous” machines in the system that help us form groups. For machine join, it is crucial to observe that a machine joins the system for two separate purposes: using the DHT (as a client) and providing service (as a server). A machine can always use the DHT by utilizing some other existing machine (that is already in the DHT) as a proxy, even before itself becomes part of the ring. It must be able to find such a proxy because it needs to know a bootstrap point to join the DHT. In order to provide service to other machines, a machine first registers with a random rendezvous. If there are less than k new machines registered with the rendezvous at this point, the new machine simply waits. Otherwise, the k new machines form a group, and join the DHT ring. During the delayed join, the new machine can still use the DHT as a client – it simply cannot contribute. The only factor we need to consider then is whether there will be a large fraction of machines that cannot contribute. With 1/1000 of the machines serving as rendezvous machines, each with at most k−1 waiting, the fraction of the machines that are waiting is at most (k−1)/1000. Given that k is a small number such as 5, this means that only 0.4% of the machines in the system are not being utilized, which is negligible. When a machine in a group fails or departs, the group has two options. The first option would be to dismiss itself entirely, and then have the k−1 remaining machines join the DHT again. This may result in thrashing because the leave/join rate is artificially inflated by a factor of k. The second option would be for the group to wait, and hope to recruit a new machine so that it can recover to k machines. However, doing so causes some objects to have fewer than k FORs for possibly an extended period of time. In our design, we use a mixture of both options. When a group loses a member, it registers with a random rendezvous. If the rendezvous has a new machine registered with it, the group will recruit the new machine as its member. If the group is not able to recruit a new machine before the total number of members drops from k−1 to k−2, it dismisses itself. The threshold of k−2 is tunable, and a smaller value will decrease the join/leave rate at the cost of having fewer replicas on average. However, our study shows that even a threshold of k−2 yields a near optimal join/leave rate, and hence we always use k−2 as the threshold. Finally, the group will also dismiss itself if it has waited longer than a certain threshold amount of time.
Rendezvous. It is important to remember that the rendezvous machines are contacted only upon machine join and leave, and not during object retrieval/lookup. In our system, we intend to maintain roughly r = s/1000 rendezvous in the group DHT. This r is well above the number of machines needed to sustain the load incurred by machine join/leave under practical settings, and yet small enough to keep the fraction of un-utilized machines negligible. We use the following design to dynamically increase/decrease r with s. Each group independently becomes a rendezvous with probability of 1/1000. These rendezvous then use the Redir [24] protocol to form a smaller rendezvous DHT. To contact a random rendezvous, a machine simply chooses a random key and searches for the successor of the key in the smaller rendezvous DHT. As with other groups in the system, rendezvous groups may fail or leave. Fortunately, the states maintained by rendezvous groups are soft states, and we simply use periodic refresh.

5.2 Approximating `PTN` for n < N

Group approximates a global PTN assignment. However, for an operation requesting n < N objects, the corresponding projected assignment will not be PTN. This is because the hash function spreads the n objects around the ring, whereas the projected PTN assignment requires the n objects to occupy as few machines as possible. Next we present designs for approximating projected PTN, using known designs for supporting range queries.
Defining a global ordering. To ensure that the projected assignments approximate PTN, we first define an ordering among all the objects. The ordering should be such that most operations roughly request a “range” of objects according to the ordering. Note that the operations need not be real range queries. In many applications, objects are semantically organized into a tree and operations tends to request entire subtrees. For example, in network monitoring systems, users tends to ask aggregation questions regarding some particular regions in the network. In the case of file systems, if a user requests one block in a file, she will likely request the entire file. Similarly, files in the same directories are likely to be requested together. For these hierarchical objects, we can easily use the full path from the root to the object as its name, and the order is directly defined alphabetically by object names.
Placing objects on the ID ring according to the order. After defining a global ordering among the objects, we use an order-preserving hash function [14] to generate the IDs of the objects. Compared to a standard hash function, for a given ordering “<” among the objects, an order-preserving hash function hash_order() has the extra guarantee that if o₁ < o₂, then hash_order(o₁) < hash_order(o₂). If we have some knowledge regarding the distribution of the object names (e.g., when the objects are names in a telephone directory), then it is possible [14] to make the hash function uniform as well. The “uniform” guarantee is important because it ensures the load balancing achieved by consistent hashing. Otherwise some ID regions may have more objects than others. For cases where a uniform order-preserving function is not possible to construct, we further adopt designs [7, 23] for supporting range queries in DHTs. In particular, MOAT uses the item-balancing DHT [23] design to achieve dynamic load balancing. Item-balancing DHT is the same as Chord except that each node periodically contacts a random other node in the system to adjust load (without disturbing the order). Finally, there are also cases where a single order cannot be defined over the objects. We are currently investigating how to address those cases using database clustering algorithms [46].

6 Study of Practical Assignments

In this section, we use our MOAT prototype, real failure traces, and real workloads to study consistent hashing-based assignments. In particular, we will answer the following two questions that were not answered in Section 4: Which assignment is the best under the effects of imperfect load balancing in consistent hashing, and also under the effects of machine failure correlation? How do the results change from our earlier study on ideal assignments? For lack of space, we will consider in this section only the scenario where each object has 3 replicas, unless otherwise noted. We have also performed extensive experiments for general erasure coding with different m and k values—the results we obtain are qualitatively similar and all our claims in this section still hold. In the following, we will first describe our MOAT prototype, the failure traces and the workload, and then thoroughly study consistent hashing-based assignments.

6.1 MOAT Implementation

We have incorporated the designs in the previous section into a read/write wide-area distributed storage system called MOAT. MOAT is similar to PAST [32], except that it supports all the consistent-hashing-based assignments discussed in this paper. Specifically, it supports Glacier, Chord, Group and Multi-hash.⁹ For Group, unless otherwise mentioned, we mean Group with the ordering technique from Section 5.2. Other assignments do not use the ordering technique. MOAT currently only supports optimistic (best effort) consistency. We have implemented MOAT by modifying FreePastry 1.3.2 [13]. MOAT is written in Java 1.4, and uses nonblocking I/O and Java serialization for communication. Despite the fact that we support DHT routing in MOAT, as we mentioned in Section 5, DHT routing will not be used if either a centralized server is feasible or when the number of objects requested by an operation is large. To isolate DHT routing failures (i.e., failures by the DHT to locate an object) from object failures and to better focus on the effects of assignments, in all our experiments we define availability as the probability that some live, accessible machine in the system has that object.

6.2 Faultloads and Workloads

A faultload is, intuitively, a failure workload, and describes when failures occur and on which machines. We consider two different faultloads intended to capture two different failure scenarios. The first faultload, NetModel, is a synthetic one and aims to capture short-term machine unavailability caused by local network failures that partition the local machine from the rest of the network, rendering it inaccessible. We use the network failure model from [10] with a MTTF of 11571 seconds, MTTR of 609 seconds, and a failure probability of p=0.05. The MTTR is directly from [10], while the MTTF is calculated from our choice of p. The second faultload, PLtrace, is a pair-wise ping trace [3] among over 200 PlanetLab machines from April 2004 to November 2004. Because of the relatively large (15 minutes) sampling interval, PLtrace mainly captures machine failures rather than network failures. This trace enables us to study the effects of failure correlation, FOR repair (i.e., generating new FORs to compensate for lost FORs due to machine failure), as well as heterogeneous machine failure probabilities. In our evaluation, we consider a machine to have failed if none of the other machines can ping it. Further details about how we process the trace can be found in [43]. We also use two real workloads for user operations, the TPC-H benchmark and a query log from IrisLog [2]. Our two workloads are intended to represent the two classes of applications in Section 2. Note that TPC-H is not actually a benchmark for image databases. However, it has a similar data-mining nature and most queries touch a large number of objects (e.g., several touch over 5% of the database). In our TPC-H workload, we use an 800GB database (i.e., a TPC-H scaling factor of 8000) and 240 MOAT machines. Because of our 3-fold replication overhead, the overall database size is 2.4TB.¹⁰ Each object is roughly 33MB and contains around 29,000 consecutive tuples in the relational tables. Note that we intentionally use a relatively large object size to take into account the potential effects of erasure coding across smaller objects (recall Section 2.2). Using smaller objects sizes will only further increase the differences among the assignments and magnify the importance of using the appropriate assignments. The ordering among the objects for TPC-H is defined to be the ordering determined by (table name, tuple name), where tuple name is the primary key of the first tuple in the object. Note that most queries in TPC-H are not actually range queries on the primary key. So this enables us to study the effect of a non-ideal ordering among objects. In our IrisLog workload, the query trace contains 6,467 queries processed by the system from 11/2003 to 8/2004. IrisLog maintains 3530 objects that correspond to the load, bandwidth, and other information about PlanetLab machines. The number of objects requested by each query ranges from 10 to 3530, with an average of 704. The objects in IrisLog form a logical tree based on domain names of the machines being monitored. The ordering among the objects is simply defined according to their full path from the root of the tree. In contrast to TPC-H, the operations in IrisLog request contiguous ranges of objects along the ordering.

6.3 Effects of Consistent Hashing

We perform this set of experiments by deploying the 240 MOAT machines on 80 PlanetLab machines and using the network failure faultload of NetModel. The machines span North America, Europe and Asia, and include both academic and non-academic sites. Each machine emulates locally whether it is experiencing a network failure according to NetModel, and logs the availability of its local objects. We then measure the availability of different operations by collecting and analyzing the logs. During the experiments, there were no failures caused by PlanetLab itself, and all failures experienced by the system were emulated failures. For Group, we use only a single rendezvous node. Figure 4 plots the unavailability of a single operation requesting all 24,000 objects in MOAT under Multi-hash, Glacier, Chord and Group. We focus on t values that are close to n, to highlight the crossing points between assignments. We also obtained three curves (via simulation as in Section 4.1) for their counterpart ideal assignments (i.e., PTN, SW, and RAND). For clarity, however, we omit the SW curve. The general trends indicate that our earlier claims about the optimality of PTN and RAND hold for Group and Multi-hash. Furthermore, the crossing point between PTN and RAND is rather close to n. The same conclusion holds for Figure 5, which plots the unavailability of a much smaller “range” operation (requesting only 600 objects). The large difference among different assignments shows that object assignments have dramatic availability impact even on operations that request a relatively small number of objects. The 600 objects requested only comprise of 2.5% of the 24,000 objects in the system. It is also easy to observe that for n<N, the order-preserving hash function (in Group with order) is necessary to ensure good availability. Next we look at two deeper aspects of these plots.

Figure 4: Unavailability of an operation requesting all 24,000 objects in the system, under the NetModel faultload. t/n is the fraction of objects that needs to be available for the operation to succeed.

Figure 5: Unavailability of a smaller operation that requests only 600 objects (among the 24,000 object in the system), under the NetModel faultload. Again, t/n is the fraction of the 600 objects that needs to be available for the operation to succeed.

Does consistent hashing increase or decrease availability?

In Figure 4, Group is close to PTN, which means it well-approximates the optimal assignment of PTN. Multi-hash has the same trend as RAND but it does depart from RAND significantly. The imperfect load balancing in consistent hashing decreases the slope of the Multi-hash curve (as compared to RAND), and makes it slightly closer to PTN. This means that the unavailability for loose operations is increased, while the unavailability for strict operations is decreased. We also observe similar effects of consistent hashing when comparing Chord against SW, and Group against PTN (except that the effects are much smaller). We pointed out in Section 4 that the key difference between PTN and RAND is that PTN maximizes the inter-object correlation while RAND minimizes the inter-object correlation. Imperfect load balancing (as in Group and Multi-hash) increases such inter-object correlation. As a result, consistent hashing makes all curves closer to PTN. We argue that this effect from imperfect load balancing in consistent hashing should be explicitly taken into account in systems design, because the difference between RAND and Multi-hash can easily reach multiple nines. For example, when t/n = 99.8% in Figure 4, the unavailability under Multi-hash is 1.12� 10⁻³, while the unavailability under RAND is only 1.67� 10⁻⁵ (not shown in the graph).

Does `Glacier` approximate `PTN` well?

As with Group, the counterpart ideal assignment for Glacier is PTN, the best assignment for strict operations. However, Figure 4 clearly shows that Glacier is much closer to Chord than to Group when t/n is close to 1.0. This can be explained by carefully investigating the inter-object correlation in these assignments and counting the number of machines intersecting with any given machine. Two machines intersect if they host FORs from the same objects. A smaller number of intersecting machines (as in PTN) roughly indicates larger inter-object correlation. In Chord, the total number of intersecting machines is roughly 2(k−1), where k is the number of replicas or fragments per object. In Group, this number is k. For Glacier, suppose that the given machine is responsible for ID region (v₁, v₂). The next set of FORs for the objects in this region will fall within (v₁ + MaxID/k, v₂ + MaxID/k). Unless this region exactly falls within a machine boundary, it will be split across two machines. Following this logic, the total number of intersecting machines is roughly 2(k−1). This explains why Glacier is closer to Chord than to Group when t/n is close to 1.0. When t = n in Figure 4, the unavailability of Chord (0.027) and Glacier (0.034) is about 4 times that of Group (0.0074). The advantage of Group becomes larger when k increases. We observe in our experiments that when using the NetModel faultload with p = 0.2 and 12-out-of-24 erasure coding (i.e., m = 12 and k = 24), the unavailability of Chord and Glacier is 0.0117 and 0.0147, respectively. On the other hand, Group has an unavailability of only 0.00067 – roughly a 20-fold advantage. In our other experiments we also consistently observe that the difference between Group and Glacier is about k times.

6.4 Effects of Failure Correlation

We next use our second faultload, PLtrace, to study the effects of correlated machine failures (together with consistent hashing). Given that we want to obtain a fair comparison across different assignments, we need the system to observe only failures injected according to the traces and not the (non-deterministic) failures on the PlanetLab. This is rather unlikely using our live PlanetLab deployment given our eight month long trace and the required duration of the experiments.
Simulation validation via real deployment. To solve this problem, we use a mixture of real deployment and event-driven simulation for PLtrace. Using trace compression, we are able to inject and replay a one-week portion of PLtrace into our MOAT deployment on the PlanetLab in around 12 hours. To observe a sufficient number of failures, we intentionally choose a week that has a relatively large number of failures. These 12-hour experiments are repeated many times (around 20 times) to obtain two runs (one for Group and one for Multi-hash) without non-deterministic failures. These two successful runs then serve as validation points for our event-driven simulator. We feed the same one-week trace into our event-driven simulator and then compare the results to validate its accuracy (Figure 6). It is easy to see that the two simulation curves almost exactly match the two curves from the PlanetLab deployment, which means our simulator has satisfactory accuracy. For space reasons, we omit other validation results. We next inject the entire PLtrace into our simulator.

Figure 6: Validation results: Unavailability of a single operation that requests all 24,000 objects in the system, as measured in WAN deployment and as observed in event-driven simulation. The number of machines and the machine failure probability are determined by PLtrace. We cannot observe any probability below 10⁻⁴ due to the duration of the experiment.

Figure 7: Effects of failure correlation: The availability of an operation that requests all 24,000 objects in the system. The legend “(c)” means that the curve is for PLtrace with correlated failures, while “(i)” means that the curve is obtained assuming independent failures.

(a) TPC-H (b) IrisLog query load

Figure 8: Overall availability under real workloads and the PLtrace faultload.

Does failure correlation increase or decrease availability?

Figure 7 plots the unavailability of a single operation under PLtrace for Glacier, Multi-hash, and Group. For clarity, we did not plot the curve for Chord, which is close to Glacier. The data (not included in Figure 7) show that for all three settings, the average unavailability of individual objects is around 10⁻⁵. We then perform a separate simulation assuming that each machine fails independently with a failure probability of 0.0215, a value chosen such that 0.0215^k ≈ 10⁻⁵ (recall k=3). We include the corresponding simulation curves (for the three assignments) under this independent failure model in Figure 7 as well. For clarity, we omit the curve for Glacier under independent failures. Comparing the two sets of curves reveals that machine failure correlation makes all the curves move toward Group and away from Multi-hash (i.e., decreasing the slope of the curves). The effect is the most prominent when we compare Multi-hash(c) and Multi-hash(i). In retrospect, this phenomenon is easy to explain. The reason is exactly the same as the effect of imperfect load balancing discussed in Section 6.3. Namely, machine failure correlation increases the inter-object correlation of all assignments. This also provides intuition regarding why our earlier conclusions (assuming failure independence) on the optimality of PTN and RAND hold even under correlated failures. Namely, even though all assignments become closer to PTN under correlated failures, their relative ranking will not change because the extra “amount” of correlation added is the same for all assignments.

6.5 Overall Availability for Real Workloads

Up to this point, we have presented results only for the availability of individual operations. This section investigates the overall availability of all operations in our two real workloads, via simulation driven by PLtrace. Because the queries in the workloads are of different sizes, here we assume that they have the same t/n values. These results provide a realistic view of how much availability improvement we can achieve by using appropriate assignments. The TPC-H benchmark consists of 22 different queries on a given database. To evaluate their availability in our simulator, we first instantiate the given database as a MySQL database and use it to process the queries. We then record the set of tuples touched by each query. Finally, we simulate a replicated and distributed TPC-H database and use the trace to determine the availability of each query. We plot only two assignments because our results so far have already shown that Group and Multi-hash are each near-optimal in different regions. In both Figure 8(a) and (b), we see that when t = n, Group outperforms Multi-hash by almost 4 nines. On the other hand, for t/n = 90%, Multi-hash achieves at least 2 more nines than Group; this difference becomes even larger when t/n < 90%. The absolute availability achieved under the two workloads are different largely due to the different sizes of the operations. In TPC-H, the operations request more objects than in the IrisLog trace. Finally, the crossing between Group and RAND again occurs when t is quite close to n. This indicates that from a practical perspective, we may consider only whether an operation is able to tolerate missing objects, rather than its specific t.

7 Related Work

To the best of our knowledge, this paper is the first to study the effects of object assignment on multi-object operation availability. On the surface, object assignment is related to replica placement. Replica placement has been extensively studied for both performance and availability. Replica placement research for availability [8, 12, 45] typically considers the availability of individual objects rather than multi-object operations. These previous results on replica placement cannot be easily extended to multi-object operations because the two problems are fundamentally different. For example, the replica placement problem goes away if all the machines are identical, but as our results show, assignment still affects availability even when all the machines are identical. Despite the fact that previous systems [5, 15, 22, 29, 31, 36, 39] use different assignments for objects, all systems except Chain Replication [39] study only the performance (rather than the availability) of object assignments (if the effects of assignment are explored at all). Chain replication [39] investigates the availability of individual objects in LAN environments. In their setting, the availability of individual objects is influenced by the different data repair times for different assignments. For example, after a machine failure, in order to restore (repair) the replication degree for the objects on that failed machine, it is faster to create new replicas of these objects on many different target machines in parallel. As a result, more randomized assignments such as Multi-hash are preferable to more structured assignments such as Group. Compared to Chain Replication, this paper studies the effects of assignments on multi-object operations. The findings from Chain Replication and this paper are orthogonal. For example, for strict operations, our study shows that Group yields much higher availability than Multi-hash. When restoring lost replicas, we can still use the pattern as suggested in Chain Replication, and temporarily restore the replicas of the objects on many different machines. The object replicas can then be lazily moved to the appropriate places as determined by the desired assignment (e.g., by Group). In this way, all assignments will enjoy the same minimum repair time. As in our Group design, the concept of grouping nodes is also used in Viceroy [27], but for a different purpose of bounding the in-degrees of nodes. Because of the different purpose, the size of each group in Viceroy can vary between c₁ logs to c₂ logs, where c₁ and c₂ are constants. Viceroy maintains the groups simply by splitting a group if it is too large, or merging a group with its adjacent group if it is too small. In our design, the group sizes have less variance, and we achieve this by the use of rendezvous. This paper studies the effects of object assignments experimentally. In [44], we have also obtained initial theoretical optimality results under some specific parameter settings (namely, when t = n and t = l+1). Using experimental methods, this paper answers the object assignment question for all t values. It also investigates the effects of two real-world factors—failure correlation and imperfect load balancing—that were not considered in [44].

8 Conclusion

This paper is the first to reveal the importance of object assignment to the availability of multi-object operations. Without affecting the availability of individual objects or resource usage, appropriate assignments can easily improve the availability of multi-object operations by multiple nines. We show that under realistic parameters, if an operation cannot tolerate missing objects, then PTN is the best assignment while RAND is the worst. Otherwise RAND is the best while PTN is the worst. Designs to approximate these assignments, Multi-hash and Group, respectively, have been implemented in MOAT and evaluated on the PlanetLab. Our results show differences of 2–4 nines between Group and Multi-hash for both an IrisLog query trace and the TPC-H benchmark.

References

[1]: Grid. http://www.grid.org.
[2]: IrisLog: A Distributed SysLog. http://www.intel-iris.net/irislog.
[3]: PlanetLab - All Pair Pings. http://www.pdos.lcs.mit.edu/~strib/pl_app/.
[4]: Top Ten TPC-H by Performance. http://www.tpc.org/tpch/results/tpch_perf_results.asp.
[5]: Adya, A., Bolosky, W. J., Castro, M., Cermak, G., Chaiken, R., Douceur, J. R., Howell, J., Lorch, J. R., Theimer, M., and Wattenhofer, R. P. FARSITE: Federated, Available, and Reliable Storage for an Incompletely Trusted Environment. In OSDI (2002).
[6]: Barclay, T., and Gray, J. Terraserver san-cluster architecture and operations experience. Tech. Rep. MSR-TR-2004-67, Microsoft Research, 2004.
[7]: Bharambe, A., Agrawal, M., and Seshan, S. Mercury: Supporting Scalable Multi-Attribute Range Queries. In SIGCOMM (2004).
[8]: Bolosky, W. J., Douceur, J. R., Ely, D., and Theimer, M. Feasibility of a Serverless Distributed File System Deployed on an Existing Set of Desktop PCs. In SIGMETRICS (2000).
[9]: Dabek, F., Kaashoek, M. F., Karger, D., Morris, R., and Stoica, I. Wide-area Cooperative Storage with CFS. In ACM SOSP (2001).
[10]: Dahlin, M., Chandra, B., Gao, L., and Nayate, A. End-to-end WAN Service Availability. ACM/IEEE Transactions on Networking 11, 2 (April 2003).
[11]: Deshpande, A., Nath, S., Gibbons, P. B., and Seshan, S. Cache-and-query for Wide Area Sensor Databases. In ACM SIGMOD (2003).
[12]: Douceur, J. R., and Wattenhofer, R. P. Competitive Hill-Climbing Strategies for Replica Placement in a Distributed File System. In DISC (2001).
[13]: FreePastry. http://www.cs.rice.edu/CS/Systems/Pastry/FreePastry.
[14]: Garg, A., and Gotlieb, C. Order-Preserving Key Transformations. ACM Transactions on Database Systems 11, 2 (June 1986), 213–234.
[15]: Ghemawat, S., Gobioff, H., and Leung, S.-T. The Google File System. In ACM SOSP (2003).
[16]: Gibbons, P. B., Karp, B., Ke, Y., Nath, S., and Seshan, S. IrisNet: An Architecture for a Worldwide Sensor Web. IEEE Pervasive Computing 2, 4 (2003).
[17]: Gray, J., Slutz, D., Szalay, A., Thakar, A., vandenBerg, J., Kunszt, P., and Stoughton, C. Data Mining the SDSS SkyServer Database. Tech. Rep. MSR-TR-2002-01, Microsoft Research, January 2002.
[18]: Haeberlen, A., Mislove, A., and Druschel, P. Glacier: Highly durable, decentralized storage despite massive correlated failures. In NSDI (2005).
[19]: Hennessy, J. The Future of Systems Research. IEEE Computer 32, 8 (August 1999), 27–33.
[20]: Huebsch, R., Hellerstein, J. M., Boon, N. L., Loo, T., Shenker, S., and Stoica, I. Querying the Internet with PIER. In VLDB (2003).
[21]: Huston, L., Sukthankar, R., Wickremesinghe, R., Satyanarayanan, M., Ganger, G., Riedel, E., and Ailamaki., A. Diamond: A storage architecture for early discard in interactive search. In USENIX (FAST) (2004).
[22]: Karger, D., Lehman, E., Leighton, T., Levine, M., Lewin, D., and Panigrahy, R. Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web. In ACM Symposium on Theory of Computing (May 1997).
[23]: Karger, D., and Ruhl, M. Simple Efficient Load Balancing Algorithms for Peer-to-Peer Systems. In ACM SPAA (2004).
[24]: Karp, B., Ratnasamy, S., Rhea, S., and Shenker, S. Spurring Adoption of DHTs with OpenHash, a Public DHT Service. In IPTPS (2004).
[25]: Kistler, J. J., and Satyanarayanan, M. Disconnected Operation in the Coda File System. ACM Transactions on Computer Systems 10, 1 (Feb. 1992), 3–25.
[26]: Kubiatowicz, J., Bindel, D., Chen, Y., Eaton, P., Geels, D., Gummadi, R., Rhea, S., Weatherspoon, H., Weimer, W., Wells, C., and Zhao, B. OceanStore: An Architecture for Global-scale Persistent Storage. In ACM ASPLOS (2000).
[27]: Malkhi, D., Naor, M., and Ratajczak, D. Viceroy: A Scalable and Dynamic Emulation of the Butterfly. In ACM PODC (2002).
[28]: Patterson, D. A., Gibson, G., and Katz, R. H. A Case for Redundant Arrays of Inexpensive Disks (RAID). In ACM SIGMOD (1988).
[29]: Ratnasamy, S., Francis, P., Handley, M., Karp, R., and Shenker, S. A Scalable Content-addressable Network. In ACM SIGCOMM (2001).
[30]: Ratnasamy, S., Karp, B., Shenker, S., Estrin, D., Govindan, R., Yin, L., and Yu, F. Data-Centric Storage in Sensornets with GHT, A Geographic Hash Table. Mobile Networks and Applications (MONET) 8, 4 (August 2003).
[31]: Rowstron, A., and Druschel, P. Pastry: Scalable, Distributed Object Location and Routing for Large-scale Peer-to-peer Systems. In ACM Middleware (2001).
[32]: Rowstron, A., and Druschel, P. Storage Management and Caching in PAST, A Large-scale, Persistent Peer-to-peer Storage Utility. In ACM SOSP (2001).
[33]: Santos, J., Muntz, R., and Ribeiro-Neto, B. Comparing Random Data Allocation and Data Striping in Multimedia Serviers. In ACM SIGMETRICS (2000).
[34]: Satyanarayanan, M. Private communication, 2005.
[35]: Singh, A. K., Manjunath, B. S., and Murphy, R. F. A Distributed Database for Bio-molecular Images. SIGMOD Rec. 33, 2 (2004), 65–71.
[36]: Stoica, I., Morris, R., Karger, D., Kaashoek, F., and Balakrishnan, H. Chord: A Scalable Peer-To-Peer Lookup Service for Internet Applications. In ACM SIGCOMM (2001).
[37]: Szalay, A., Kunszt, P., Thakar, A., Gray, J., and Slutz, D. Designing and Mining MultiTerabyte Astronomy Archives: The Sloan Digital Sky Survey. In ACM SIGMOD (June 1999).
[38]: Szalay, A. S., Gray, J., and vandenBerg, J. Petabyte Scale Data Mining: Dream or Reality? Tech. Rep. MSR-TR-2002-84, Microsoft Research, August 2002.
[39]: van Renesse, R., and Schneider, F. B. Chain Replication for Supporting High Throughput and Availability. In OSDI (2004).
[40]: Wang, L., Pai, V., and Peterson, L. The Effectiveness of Request Redirection on CDN Robustness. In OSDI (2002).
[41]: Yalagandula, P., and Dahlin, M. A scalable distributed information management system. In ACM SIGCOMM (2004).
[42]: Yalagandula, P., Nath, S., Yu, H., Gibbons, P. B., and Seshan, S. Beyond Availability: Towards a Deeper Understanding of Machine Failure Characteristics in Large Distributed Systems. In WORLDS (2004).
[43]: Yu, H., Gibbons, P. B., and Nath, S. K. Availability of Multi-Object Operations. Tech. rep., Intel Research Pittsburgh, 2005. Technical Report IRP-TR-05-53. Also available at http://www.cs.cmu.edu/~yhf/moattr.pdf.
[44]: Yu, H., Gibbons, P. B., and Nath, S. K. Optimal-Availability Inter-Object Correlation. Tech. rep., Intel Research Pittsburgh, 2006. Technical Report IRP-TR-06-03. Also available at http://www.cs.cmu.edu/~yhf/interobject.pdf.
[45]: Yu, H., and Vahdat, A. Minimal Replication Cost for Availability. In ACM PODC (2002).
[46]: Zhang, T., Ramakrishnan, R., and Livny, M. BIRCH: An Efficient Data Clustering Method for Very Large Databases. In ACM SIGMOD (1996).

1: Work done while this author was a graduate student at CMU and an intern at Intel Research Pittsburgh.
2: The failure probabilities are FP(I)= p⁴ + 4p³(1−p) + 2 p² (1−p)² and FP(II) = p⁴ + 4p³(1−p) + 4 p² (1−p)².
3: The failure probabilities are FP(III)= p⁸ + 8p⁷(1−p) + 28p⁶(1−p)² + 24 p⁵(1−p)³ + 6p⁴(1−p)⁴ and FP(IV) = p⁸ + 8p⁷(1−p) + 28p⁶(1−p)² + 8 p⁵(1−p)³.
4: Note that Coda [25] itself does not restrict the assignment from volumes to servers. However, in most Coda deployments [34], system administrators use an assignment similar to PTN.
5: Strictly speaking, CAN uses consistent hashing in multiple dimensions instead of a single dimension. Thus we use the term Multi-hash to describe this assignment.
6: Note that assignments II and III fail to have the PTN rule and the desired concentration, respectively.
7: Because it only wastes resources for one machine to host multiple FORs of the same object, we consider only assignments where each machine has ≤ 1 FOR of any given object. The only exception is RAND, where some assignments in the distribution may violate this property.
8: In this section, we use node to denote a logical node in the DHT and machine to denote one of the s physical machines.
9: In the remainder of the paper, we will not explicitly discuss Pastry as it is similar to Chord for the purposes of this paper.
10: For comparison, industrial vendors use a 10 TB database with TPC-H in clusters with 160 machines [4].

This document was translated from L^AT_EX by H^EV^EA.

This paper was originally published in the Proceedings of the 3rd Symposium on Networked Systems Design and Implementation (NSDI '06)
May 8–10, 2006, San Jose, CA

Last changed: 3 May 2006 jel