NSDI '06 Paper [NSDI '06 Technical Program]

Distributed Quota Enforcement for Spam Control

Michael Walfish, J.D. Zamfirescu, Hari Balakrishnan, David Karger		Scott Shenker
MIT Computer Science and AI Lab		UC Berkeley and ICSI

Abstract

Spam, by overwhelming inboxes, has made email a less reliable medium than it was just a few years ago. Spam filters are undeniably useful but unfortunately can flag non-spam as spam. To restore email's reliability, a recent spam control approach grants quotas of stamps to senders and has the receiver communicate with a well-known quota enforcer to verify that the stamp on the email is fresh and to cancel the stamp to prevent reuse. The literature has several proposals based on this general idea but no complete system design and implementation that: scales to today's email load (which requires the enforcer to be distributed over many hosts and to tolerate faults in them), imposes minimal trust assumptions, resists attack, and upholds today's email privacy. This paper describes the design, implementation, analysis, and experimental evaluation of DQE, a spam control system that meets these challenges. DQE's enforcer occupies a point in the design spectrum notable for simplicity: mutually untrusting nodes implement a storage abstraction but avoid neighbor maintenance, replica maintenance, and heavyweight cryptography.

1 Introduction

Email is a less reliable communication medium than it was just a few years ago. The culprit is spam (defined as unsolicited bulk email), which drowned inboxes, making it hard for users to see the email they cared about. Unfortunately, spam filters, which offer inboxes much-needed relief, have not restored reliability to email: false positives from filters are now a dominant mode of email failure. Anecdotal evidence suggests that the rate of false positives is 1% [46,11], with some estimating their economic damage at hundreds of millions of dollars annually [19,12]. While we have no way to verify these numbers, we can vouch for the personal inconvenience caused by false positives. And while our purpose here is not to cast aspersions on spam filters (indeed, we personally rely on them), we have nonetheless been vexed by what seems to be the inherent unreliability of content-based spam control.

Instead, we turn to an approach using quotas or bankable postage, where the goal is to limit the number of messages sent, not divine their intent. Several such schemes have been proposed before [1,36,5]. In general, these systems give every sender a quota of stamps. How this quota is determined varies among proposals; options include proof of CPU or memory cycles [1,47], annual payment [5], having an email account with an ISP [36], having a driver's license, etc. The sending host or its email server attaches a stamp to each email message, and the receiving host or its email server tests the incoming stamp by asking a quota enforcer whether the enforcer has seen the stamp before. If not, the receiving host infers that the stamp is "fresh" and then cancels it by asking the enforcer to store a record of the stamp. The receiving host delivers only messages with fresh stamps to the human user; messages with used stamps are assumed to be spam. The hope is that allocating reasonable quotas to everyone and then enforcing those quotas would cripple spammers, who need huge volumes to be profitable, while leaving legitimate users largely unaffected; see §8.2 for a basic economic analysis.¹

Of course, many defenses against spam have been proposed, each with advantages and disadvantages. The purpose of this paper is not to claim that ours is superior to all others or that its adoption will be easy. Rather, the purpose is to prove that many technical hurdles in quota-based systems, described below, can be overcome. To that end, this paper describes the design, implementation, analysis, and experimental evaluation of DQE (Distributed Quota Enforcement), a quota-based spam control system.

To be viable, DQE must meet two sets of design goals (see §2). The first set concerns the protocol between receivers and the enforcer. The protocol must never flag messages with fresh stamps as spam, must preserve the privacy of sender-receiver communication, and must not require that email servers and clients trust the enforcer. The second set applies to the enforcer: it must scale to current and future email volumes, requiring distribution over many machines, perhaps across several organizations; it must allow faults without letting much spam through; and it must resist attacks. Also, the enforcer should tolerate mutual mistrust among its constituent hosts (which is separate from the requirement, stated above, that the enforcer not be trusted by its clients). Finally, the enforcer should achieve high throughput to minimize management and hardware costs. Previous proposals do not meet these requirements (see §7.1).

Our main focus in this paper is the quota enforcer, which serves as a "clearing house" for canceled stamps. The enforcer stores billions of key-value pairs (canceled stamps) over a set of mutually untrusting nodes and tolerates Byzantine and crash faults. It relies on just one trust assumption, common in distributed systems: that the constituent hosts are determined by a trusted entity (§4). The enforcer uses a replication protocol in which churn generates no extra work but which gives tight guarantees on the average number of reuses per stamp (§4.1). Each node uses an optimized internal key-value map that balances storage and speed (§4.2), and nodes shed load with a technique that avoids "distributed livelock" (§4.3).

Apart from these techniques, what is most interesting to us about the enforcer is its simplicity. By tailoring our solution to the semantics of quota enforcement (specifically, that the effect of lost data is only that spammers' effective quotas increase), we can meet the various design challenges with an infrastructure in which the nodes need neither keep track of other nodes, nor perform replica maintenance, nor use heavyweight cryptography.

In part because of this simplicity, the enforcer is practical. We have a deployed (though lightly used) system, and our experimental results suggest that our implementation can handle the world's email volume-over 80 billion messages daily [30,50]-with a few thousand dedicated high-end PCs (§6).

This work is preceded by a workshop paper [5]. That paper argued, and this paper concurs, that quota allocation and enforcement should be separate. That paper proposed a receiver-enforcer protocol that DQE incorporates, but it sketched a very different (and more complex) enforcer design based on distributed hash tables (DHTs).

2 Requirements and Challenges

In this section we discuss general requirements for DQE and specific challenges for the enforcer. These requirements all concern quota enforcement; indeed, in this paper we address quota allocation only briefly (see §8). The reason for this focus is that these two are different concerns: the former is a purely technical matter while the latter involves social, economic, and policy factors.

2.1 Protocol Requirements

No false positives Our high-level goal is reliable email. We assume reused stamps indicate spam. Thus, a fresh stamp must never appear to have been used before.

Untrusted enforcer We do not know the likely economic model of the enforcer, whether monolithic (i.e., owned and operated by a single entity) or federated (i.e., many organizations with an interest in spam control donate resources to a distributed system). No matter what model is adopted, it would be wise to design the system so that clients place minimal trust in the infrastructure.

Privacy To reduce (already daunting) deployment hurdles, we seek to preserve the current "semantics" of email. In particular, queries of the quota enforcer should not identify email senders (otherwise, the enforcer knows which senders are communicating with which receivers, violating email's privacy model), and a receiver should not be able to use a stamp to prove to a third party that a sender communicated with it.

2.2 Challenges for the Enforcer

Scalability The enforcer must scale to current and future email volumes. Studies estimate that 80-90 billion emails will be sent daily this year [30,50]. (We admit that we have no way to verify these claims.) We set an initial target of 100 billion daily messages (an average of about 1.2 million stamp checks per second) and strive to keep pace with future growth. To cope with these rates, the enforcer must be composed of many hosts.

Fault-tolerance Given the required number of hosts, it is highly likely that some subset will experience crash faults (e.g., be down) or Byzantine faults (e.g., become subverted). The enforcer should be robust to these faults. In particular, it should guarantee no more than a small amount of stamp reuse, despite such failures.

High throughput To control management and hardware costs, we wish to minimize the required number of machines, which requires maximizing throughput.

Attack-resilience Spammers will have a strong incentive to cripple the enforcer; it should thus resist denial-of-service (DoS) and resource exhaustion attacks.

Mutually untrusting nodes In both federated and monolithic enforcer organizations, nodes could be compromised. In the federated case, even when the nodes are uncompromised, they may not trust each other. Thus, in either case, besides being untrusted (by clients), nodes should also be untrusting (of other nodes), even as they do storage operations for each other.

We now show how the above requirements are met, first discussing the general architecture in §3 and then, in §4, focusing on the detailed design of the enforcer.

3 DQE Architecture

The architecture is depicted in Figure 1. This section describes the format and allocation of stamps (§3.1), how stamps are checked and canceled (§3.2), and how that process satisfies the requirements in §2.1.² We also give an overview of the enforcer (§3.3) and describe attackers and vulnerabilities (§3.4). Although we will refer to "sender" and "receiver", we expect those will be, for ease of deployment, the sender's and receiver's respective email servers.

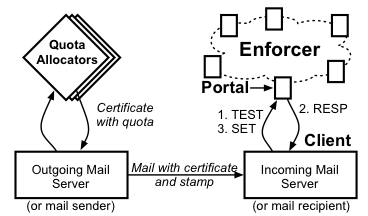Fig. 1: DQE architecture.

3.1 Stamp Allocation and Creation

The quota allocation policy is the purview of a few globally trusted quota allocators (QAs), each with distinct public/private key pair (QA_pub,QA_priv); the QA_pub are well known. A participant S constructs public/private key pair (S_pub,S_priv) and presents S_pub to a QA. The QA determines a quota for S and returns to S a signed certificate (the notation {A}_B means that string A is signed with key B):

C_S={ S_pub,expirationtime,quota}_{QA_priv}.

Anyone knowing QA_pub can verify, by inspecting C_S, that S has been allocated a quota. expiration time is when the certificate expires (in our implementation, certificates are valid for one year), and quota specifies the maximum number of stamps that S can use within a well-known epoch (in our implementation, each day is an epoch). Epochs free the enforcer from having to store canceled stamps for long time periods. Obtaining a certificate is the only interaction participants have with a QA, and it happens on, e.g., yearly time scales, so the QA can allocate quotas with great care.

Participants use the quota attribute of their certificates to create up to quota stamps in any epoch. A participant with a certificate may give its stamps to other email senders, which may be a practical way for an organization to acquire a large quota and then dole it out to individual users.

Each stamp has the form {C_S, {i, t}_{S_priv}}. Each i in [1,quota] is supposed to be used no more than once in the current epoch. t is a unique identifier of the current epoch. Because email can be delayed en route to a recipient, receivers accept stamps from the current epoch and the one just previous.

An alternative to senders creating their own stamps would be QAs distributing stamps to senders. We reject this approach because it would require a massive computational effort by the QAs.

3.2 Stamp Cancellation Protocol

Fig. 2: Stamp cancellation protocol followed by sender (S), receiver (R), and the enforcer (Enf.). The protocol upholds the design goals in §2.1: it gives no false positives, preserves privacy, and does not trust the enforcer.

This section describes the protocol followed by senders, receivers, and the enforcer. Figure 2 depicts the protocol.

For a given stamp attached to an email from sender S, the receiver R must check that the stamp is unused and must prevent reuse of the stamp in the current epoch. To this end, R checks that the value of i in the stamp is less than S's quota, that t identifies the current or just previous epoch, and that the signatures are valid. If the stamp passes these tests, R communicates with the enforcer using two UDP-based Remote Procedure Calls (RPCs): TEST and SET. R first calls TEST to check whether the enforcer has seen a fingerprint of the stamp; if the response is "not found", R then calls SET, presenting the fingerprint to be stored.³ The fingerprint of the stamp is HASH(STAMP), where HASH is a one-way hash function that is hard to invert. ⁴

Note that an adversary cannot cancel a victim's stamp before the victim has actually created it: the stamp contains a signature, so guessing HASH(STAMP) requires either finding a collision in HASH or forging a signature.

We now return to the design goals in §2.1. First, false positives are impossible: because HASH is one-way, a reply of the fingerprint- hash(STAMP)-in response to a TEST of the postmark- HASH(HASH(STAMP))-proves that the enforcer has seen the (postmark, fingerprint) pair. Thus, the enforcer cannot falsely cause an email with a novel stamp to be labeled spam. (The enforcer can, however, allow a reused stamp to be labeled novel; see §4.) Second, receivers do not trust the enforcer: they demand proof of reuse (i.e., the fingerprint). Third, the protocol upholds current email privacy semantics: the enforcer sees hashes of stamps and not stamps themselves, so it doesn't know who sent the message. More details about this protocol's privacy properties are in [5].

3.3 The Enforcer

The enforcer stores the fingerprints of stamps canceled (i.e., SET) in the current and previous epochs. It comprises thousands of untrusted storage nodes (which we often call just "nodes"), with the list of approved nodes published by a trusted authority. The nodes might come either from a single organization that operates the enforcer for profit (perhaps paid by organizations with an interest in spam control) or else from multiple contributing organizations.

Clients, typically incoming email servers, interact with the enforcer by calling its interface, TEST and SET. These two RPCs are implemented by every storage node. For a given TEST or SET, the node receiving the client's request is called the portal for that request. Clients discover a nearby portal either via hard-coding or via DNS.

3.4 Attackers and Remaining Vulnerabilities

Attackers will likely be spammers (we include in this term both authors and distributors of spam). Attackers may control armies of hundreds of thousands of bots that can send spam and mount attacks.

As discussed in §3.2, attackers cannot forge stamps, cancel stamps they have not seen, or induce false positives. DQE's remaining vulnerabilities are in two categories: unauthorized stamp use (i.e., theft) and stamp re-use. We discuss the first category below. Since the purpose of the enforcer is to prevent reuse, we address the second one when describing the enforcer's design in §4.

A spammer may be able to steal stamps from its "botted" hosts. However, such theft by a single spammer is unlikely to increase spam much: a botnet with 100,000 hosts and a daily quota of 100 stamps per machine leads to 10 million extra spams, a small fraction of the tens of billions of daily spams today. Moreover, out-of-band contact between the email provider and the customer could thwart such theft, in analogy with credit card companies contacting customers to verify anomalous activity.

A related attack is to compromise an email relay and appropriate the fresh stamps on legitimate email. The attacker could then send more spam (but not much more-one relay is unlikely to carry much of the world's email). More seriously, the emails that were robbed now look like spam and might not be read. But, though the attack has greater appeal under DQE, the vulnerability is not new: even without stamps, an attacker controlling a compromised email relay can drop email arriving at the relay. In any case, encrypting emails could prevent stamp theft.

4 Detailed Design of the Enforcer

The enforcer, depicted in Figure 3, is a high-throughput storage service that replicates immutable key-value pairs over a group of mutually untrusting, infrequently changing nodes. It tolerates Byzantine faults in these nodes. We assume a trusted bunker, an entity that communicates the system membership to the enforcer nodes. The bunker assigns random identifiers-whose purpose we describe below-to each node and infrequently (e.g., daily) distributes to each node an in-list, a digitally signed, authoritative list of the members' identifiers and IP addresses.

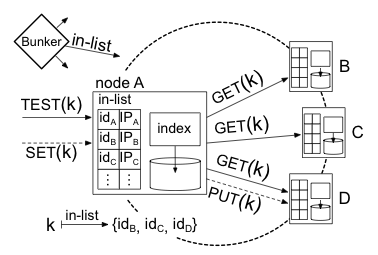Fig. 3: Enforcer design. A TEST causes multiple GETs; a SET causes one PUT. Here, A is the portal. The ids are in a circular identifier space with the identifiers determined by the bunker.

Given the required size of the system-thousands of nodes (§6.5)-we believe the bunker is a reasonable assumption. If a single organization operates the enforcer, the bunker can be simply the human who deploys the machines. If the enforcer is federated, a small number of neutral people can implement the bunker. Managing a list of several thousand relatively reliable machines that are donated by various organizations is a "human scale" job, and the vetting of machines can be light since the enforcer is robust to adversarial nodes. Of course, the bunker is a single point of vulnerability, but observe that humans, not computers, execute most of its functions. Nevertheless, to guard against a compromised bunker, nodes accept only limited daily changes to the in-list.

Clients' queries-e.g., TEST(HASH(HASH(stamp)))-are interpreted by the enforcer as queries on key-value pairs, i.e., as TEST(k) or SET(k,v), where k = HASH(v). (Throughout, we use k and v to mean keys and values.)

Portals implement TEST and SET by invoking at other nodes a UDP-based RPC interface, internal to the enforcer, of GET(k) and PUT(k,v). (Although the enforcer uses consistent hashing [33] to assign key-value pairs to nodes, which is reminiscent of DHTs, the enforcer and DHTs have different structures and different goals; see §7.2.) To ensure that GET and PUT are invoked only by other nodes, the in-list can include nodes' public keys, which nodes can use to establish pairwise shared secrets for lightweight packet authentication (e.g., HMAC [35]).

The rest of this section describes the detailed design of the enforcer. We first specify TEST and SET and show that even with crash failures (i.e., down or unreachable nodes), the enforcer guarantees little stamp reuse. We then show how nodes achieve high throughput with an efficient implementation of PUT and GET (§4.2) and a way to avoid degrading under load (§4.3). We then consider attacks on nodes (§4.4) and attacks by nodes, and we argue that a Byzantine failure reduces to a crash failure in our context (§4.5). Our design decisions are driven by the challenges in §2.2, but the map between them is not clean: multiple challenges are relevant to each design decision, and vice versa.

4.1 TEST, SET, and Fault-Tolerance

Each key k presented to a portal in TEST or SET has r assigned nodes that could store it; these nodes are a "random" subset (determined by k) of enforcer nodes. We say below how to determine r. To implement TEST(k), a portal invokes GET(k) at k's r assigned nodes in turn. The portal stops when either a node replies with a v such that k= HASH(v), in which case the portal returns v to its client, or else when it has tried all r nodes without such a reply, in which case the portal returns "not found". To implement SET(k,v), the portal chooses one of the r assigned nodes uniformly at random and invokes PUT(k,v) there. Pseudo-code for TEST and SET is shown in Figure 4. The purpose of 1 PUT and r GETs-as opposed to the usual r PUTs and 1 GET-is to conserve storage.

A key's assigned nodes are determined by consistent hashing [33] in a circular identifier space using r hash functions. The bunker-given identifier mentioned above is a random choice from this space. To achieve near-uniform per-node storage with high probability, each node actually has multiple identifiers [61] deterministically derived from its bunker-given one.

Fig. 4: Pseudo-code for TEST and SET in terms of GET and PUT.

Churn Churn generates no extra work for the system. To handle intra-day churn (i.e., nodes going down and coming up between daily distributions of the in-list), portals do not track which nodes are up; instead they apply to each PUT or GET request a timeout of several seconds with no retry, and interpret a timed-out GET as simply a "not found". (A few seconds of latency is not problematic for the portal's client-an incoming email server-because sender-receiver latency in email is often seconds and sometimes minutes.) Moreover, when a node fails, other nodes do not "take over" the failed node's data: the invariant "every (k,v) pair must always exist at r locations" is not needed for our application.

To handle inter-day churn (i.e., in-list changes), the assigned nodes for most (k,v) pairs must not change; otherwise, queries on previously SET stamps (e.g., "yesterday's" stamps) would fail. This requirement is satisfied because the bunker makes only minor in-list changes from day-to-day and because, from consistent hashing, these minor membership changes lead to proportionately minor changes in the assigned nodes [33].

Analysis

We now show how to set r to prevent significant stamp reuse. We will assume that nodes, even subverted ones, do not abuse their portal role; we revisit this assumption in §4.5.

Our analysis depends on a parameter p, the fraction of the n total machines that fail during a 2-day period (recall that an epoch is a day and that nodes store stamps' fingerprints for the current and previous epochs). We will consider only a stamp's expected reuse. A Chernoff bound (proof elided) can show that there is unlikely to be a set of pn nodes whose failure would result in much more than the expected stamp reuse.

We don't distinguish the causes of failures-some machines may be subverted, while others may simply crash. To keep the analysis simple, we also do not characterize machines as reliable for some fraction of the time-we simply count in p any machine that fails to operate perfectly over the 2-day period. Nodes that do operate perfectly (i.e., remain up and follow the protocol) during this period are called good. We believe that carefully chosen nodes can usually be good so that p = 0.1, for example, might be a reasonably conservative estimate. Nevertheless, observe that this model is very pessimistic: a node that is offline for a few minutes is no longer good, yet such an outage would scarcely increase total spam.

For a given stamp, portals can detect attempted reuses once the stamp's fingerprint is PUT on a good node. When most nodes are good, this event happens quickly. As shown in the appendix, the expected number of times a stamp is used before this event happens is less than [1/(1−2p)] + p^r n. The second term reflects the possibility (probability p^r) that none of the r assigned nodes is good. In this case, an adversary can reuse the stamp once for each of the n portals. (The "local PUT" in the first line of SET in Figure 4 prevents infinite reuse.) These "lucky" stamps do not worry us: our goal is to keep small the total number of reuses across all stamps. If we set r = 1+log_1/p n and take p=0.1, then a stamp's expected number of uses is less than [1/(1−2p)]+ p ≈ 1 + 3p = 1.3, close to the ideal of 1 use per stamp.

The above assumes that the network never loses RPCs. To handle packet loss, clients and portals can retry RPCs, thereby lowering the effective drop rate and making the false negatives from dropped packets a negligible contribution to total spam. Investigating whether such retries are necessary is future work.

4.2 Implementation of GET and PUT

In our early implementation, nodes stored their internal key-value maps in memory, which let them give fast "found" and "not found" answers to GETs. However, we realized that the total number of stamps that the enforcer must store makes RAM scarce. Thus, nodes need a way to store keys and values that conserves RAM yet, as much as possible, allows high PUT and GET throughput.

This section describes the nodes' key-value stores, the properties of which are: PUTs are fast; after a crash, nodes can recover most previously canceled stamps; each key-value pair costs 5.2 bytes rather than 40 bytes of RAM; "not found" answers to GETs are almost always fast; and "found" answers to GETs require a disk seek. We justify these properties below.

Fig. 5: Pseudo-code for GET and PUT. A node switches between batches of writes and reads; that asynchrony is not shown.

As in previous systems [54,39,49], nodes write incoming data-key-value pairs here-to a disk log sequentially and keep an index that maps keys to locations in the log. In our system, the index lives in memory and maps keys to log blocks, each of which contains multiple key-value pairs. Also, our index can return false locations: it occasionally "claims" that a given key is on the disk even though the node has never stored the key.

When a node looks up a key k, the index returns either "not stored" or a block b. In the latter case, the node reads b from the on-disk log and scans the keys in b to see if k is indeed stored. Pseudo-code describing how GETs and PUTs interact with the index is shown in Figure 5.

We now describe the structure of the index, depicted in Figure 6. The index has two components. First is a modified open addressing hash table, the entries of which are divided into an 8-bit checksum and a 24-bit pointer to a block (of size, e.g., 4 KBytes). A key k, like in standard open addressing as described by Knuth, "determines a `probe sequence,' namely a sequence of table positions that are to be inspected whenever k is inserted or looked up" [34], with insertion happening in the first empty position. When insertion happens, the node stores an 8-bit checksum of k as well as a pointer to the block that holds k. (The checksum and probe sequence should be unpredictable to an adversary.) A false location happens when a lookup on key k finds an entry for which the top 8 bits are k's checksum while the bottom bits point to a block that does not hold k. This case is handled by the index's second component, an overflow table storing those (k,v) pairs for which k wrongly appears to be in the hash table. INDEX.LOOKUP(), in Figure 5, checks this table.

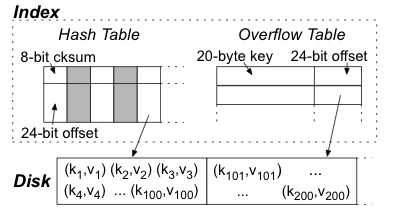Fig. 6: In-RAM index mapping from k to log block that holds (k,v).

We now return to the properties claimed above. PUTs are fast because the node, rather than interleaving reads and writes, does each in batches, yielding sequential disk writes. For crash recovery: on booting, a node scans its log to rebuild the index. For the RAM cost: the value of the hash table's load factor (i.e., ratio of non-empty entries to total entries) that is space-minimizing is ≈ 0.87 (see Claim 1 in [66]); the corresponding RAM cost is 1.3x entries (see Claim 2 in [66]), where x is the number of (k,v) pairs stored by the node. The 1.3x entries with 4 bytes per entry gives the 5.2 bytes claimed above. For negative GET(k) requests (i.e., k not found), nodes inspect an average of 8 entries in the probe sequence (see Claim 3 in [66]), and the rare false location incurs a disk seek. For affirmative GETs (i.e., reused stamps), the node visits an average of 8 entries to look up the block, b, that holds v; the node then does a disk seek to get b.

These seeks are one of the enforcer's principal bottlenecks, as shown in §6.3. To ease this bottleneck, nodes cache recently retrieved (k,v) pairs in RAM.

Nodes use the block device interface rather than the file system. With the file system, the kernel would, on retrieving a (k,v) pair from disk, put in its buffer cache the entire disk block holding (k,v). However, most of that cached block would be a waste of space: nodes' disk reads exhibit no reference locality.

4.3 Avoiding "Distributed Livelock"

The enforcer must not degrade under high load. Such load could be from heavy legitimate use or from attackers' spurious requests, as in §4.4. In fact, our implementation's capacity, measured by total correct TEST responses, did originally worsen under load. This section describes our change to avoid this behavior. See §6.6 for experimental evidence of the technique's effectiveness.

Observe that the packets causing nodes to do work are UDP RPC requests or responses and that these packets separate into three classes. The classes are: (1) TEST or SET requests from clients; (2) GET or PUT requests from other enforcer nodes; and (3) GET or PUT responses. To achieve the enforcer's throughput goal, which is to maximize the number of successful PUTs and GETs, we have the individual nodes prioritize these packet classes. The highest priority class is (3), the lowest (1).

When nodes did not prioritize and instead served these classes round-robin, overload-defined as the CPU being unable to do the work induced by all arriving packets-caused two problems. First, each packet class experienced drops, so many GETs and PUTs were unsuccessful since either the request or the response was dropped. Second, the system admitted too many TESTs and SETs, i.e., it overcommitted to clients. The combination was distributed livelock: nodes spent cycles on TESTs and SETs and meanwhile dropped GET and PUT requests and responses from other nodes.

Prioritizing the three classes, in contrast to round-robin, improves throughput and implements admission control: a node, in its role as portal, commits to handling a TEST or SET only if it has no other pending work in its role as node. We can view the work induced by a TEST or SET as a distributed pipeline; each stage is the arrival at any node of a packet related to the request. In this view, a GET or PUT response means the enforcer as a whole has done most of the work for the underlying request; dropping such a packet contradicts the throughput goal.

To implement the priorities, each of the three packet classes goes to its own UDP destination port and thus its own queue (socket) on the node. The node reads from the highest priority queue (socket) with data. If the node cannot keep up with a packet class, the associated socket buffer fills, and the kernel drops packets in that class.

A different way to avoid distributed livelock might be for a node to maintain a window of outstanding RPCs to every other node. This approach will not work well in general because it is hard to set the size of the window. We also note that avoiding distributed livelock and coping with network congestion are separate concerns; we briefly address the latter in §4.6.

The general approach described in this section-which does nothing more than apply the principle that, under load, one should drop from the beginning of a pipeline to maximize throughput-could be useful for other distributed systems. There is certainly much work addressing overload: see, e.g., SEDA [69,68], LRP [15], and Defensive Programming [48] and their bibliographies; these proposals use fine-grained resource allocation to protect servers from overload. Other work (see, e.g., Neptune [57] and its bibliography) focuses on clusters of equivalent servers, with the goal of proper allocation of requests to servers. All of this research concerns requests of single hosts and is orthogonal to the simple priority scheme described here, which concerns logical requests happening on several hosts.

4.4 Resource Exhaustion Attacks

Two years ago, a popular DNS-based block list (DNSBL) was forced offline [27], and a few months later another such service was attacked [63], suggesting that effective anti-spam services with open interfaces are targets for various denial-of-service (DoS) attacks. If successful, DQE would be a major threat to spammers, so we must ensure that the enforcer resists attack. We do not focus on packet floods, in which zombies [56,51] exhaust the enforcer's bandwidth with packets that are not well-formed requests. These attacks can be handled using various commercial (e.g., upstream firewalls) and academic (see [44] for a survey) solutions. We thus assume that enforcer nodes see only well-formed RPC requests.

A resource exhaustion attack is a flood of spurious RPCs (e.g., by zombies). Such floods would waste nodes' resources, specifically: disk seeks on affirmative GETs, entries in the RAM index (which is exhausted long before the disk fills) for PUTs, and CPU cycles to process RPCs. These attacks are difficult because one cannot differentiate "good" from "bad": requests are TEST(k) and SET(HASH(v),v) where k,v are any 20-byte values. Absent further mechanism, handling such an attack requires the enforcer to be provisioned for the legitimate load plus as many TESTs and SETs as the attacker can send.

Before we describe the defense, observe that attackers have some bandwidth limit. Let us make the assumption-which we revisit shortly-that attackers are sending as much spam as they can, and, specifically, that they are limited by bandwidth. This limit reflects either a constraint like the bots' access links or some threshold above which the attacker fears detection by the human owner of the compromised machine.

Observe, also, that the enforcer is indifferent between the attacker sending (1) a spurious TEST and (2) a single spam message, thereby inducing a legitimate TEST (and, rarely, a SET); the resources consumed by the enforcer are the same in (1) and (2). Now, under the assumption above, we can neutralize resource exhaustion attacks by arranging for a TEST or SET to require the same amount of bandwidth as sending a spam. For if attackers are "maxed out" and if sending a TEST and a spam cost the same bandwidth, then attackers cannot cause more TESTs and SETs than would be induced anyway by current email volumes-for which the enforcer is already provisioned. To realize this general approach (which is in the spirit of [65,58]), enforcer nodes have several options, such as asking for long requests or demanding many copies of each request. This approach does not address hotspots (i.e., individual, overloaded portals), but if any particular portal is attacked, clients can use another one.

Of course, despite our assumption above, today's attackers are unlikely to be "maxed out". However, they have some bandwidth limit. If this limit and current spam volumes are the same order of magnitude, then the approach described here reduces the enforcer's required over-provisioning to a small constant factor. Moreover, this over-provisioning is an upper bound: the most damaging spurious request is a TEST that causes a disk seek by asking a node for an existing stamp fingerprint (§6.3), yet nodes cache key-value pairs (§4.2). If, for example, half of spurious TESTs generate cache hits, the required provisioning halves.

4.5 Adversarial Nodes

We now argue that for the protocol described in §4.1, a Byzantine failure reduces to a crash failure. Nodes do not route requests for each other. A node cannot lie in response to GET(k) because for a false v, HASH(v) would not be k (so a node cannot make a fresh stamp look reused). A node's only attack is to cause a stamp to be reused by ignoring PUT and GET requests, but doing so is indistinguishable from a crash failure. Thus, the analysis in §4.1, which applies to crash failures, captures the effect of adversarial nodes. Of course, depending on the deployment (federated or monolithic), one might have to assume a higher or lower p.

However, the analysis does not cover a node that abuses its portal role and endlessly gives its clients false negative answers, letting much spam through. Note, though, that if adversarial portals are rare, then a random choice is unlikely to find an adversarial one. Furthermore, if a client receives much spam with apparently fresh stamps, it may become suspicious and switch portals, or it can query multiple portals.

Another attack for an adversarial node is to execute spurious PUTs and GETs at other nodes, exhausting their resources. In defense, nodes maintain "put quotas" and "get quotas" for each other, which relies on the fact that the assignment of (k,v) pairs to nodes is balanced. Deciding how to set these quotas is future work.

4.6 Limitations

The enforcer may be either clustered or wide-area. Because our present concern is throughput, our implementation and evaluation are geared only to the clustered case. We plan to address the wide-area case in future work and briefly consider it now. If the nodes are separated by low capacity links, distributed livelock avoidance (§4.3) is not needed, but congestion control is. Options include long-lived pairwise DCCP connections or a scheme like STP in Dhash++ [14].

5 Implementation

We describe our implementation of the enforcer nodes and DQE client software; the latter runs at email senders and receivers and has been handling the inbound and outbound email of several users for over six months.

5.1 Enforcer Node Software

The enforcer is a 5000-line event-driven C++ program that exposes its interfaces via XDR RPC over UDP. It uses libasync [42] and its asynchronous I/O daemon [39]. We modified libasync slightly to implement distributed livelock avoidance (§4.3). We have successfully tested the enforcer on Linux 2.6 and FreeBSD 5.3. We play the bunker role ourselves by configuring the enforcer nodes with an in-list that specifies random identifiers. We have not yet implemented per-portal quotas to defend against resource exhaustion by adversarial nodes (§4.5), a defense against resource exhaustion by clients (§4.4), or HMAC for inter-portal authentication (§4). The implementation is otherwise complete.

5.2 DQE Client Software

The DQE client software is two Python modules. The sender module is invoked by a sendmail hook; it creates a stamp (using a certificate signed by a virtual quota allocator) and inserts it in a new header in the departing message. The receiver module is invoked by procmail; it checks whether the email has a stamp and, if so, executes a TEST RPC over XDR to a portal. Depending on the results (no stamp, already canceled stamp, forged stamp, etc.), the module adds a header to the email for processing by filter rules. To reduce client-perceived latency, the module first delivers email to the recipient and then, for fresh stamps, asynchronously executes the SET.

6 Evaluation of the Enforcer

The analysis (§4.1, appendix) accurately reflects how actual failures affect observed stamp reuse. Even with 20% of the nodes down, the average number of reuses is under 1.5.	§6.2
Microbenchmarks (§6.3) predict the enforcer's performance exactly. The bottleneck is disk seeks.	§6.4
The enforcer can handle current email volume with a few thousand high-end PCs.	§6.5
The scheme to avoid livelock (§4.3) is effective.	§6.6

Table 1: Summary of evaluation results.

In this section, we evaluate the enforcer experimentally. We first investigate how its observed fault-tolerance-in terms of the average number of stamp reuses as a function of the number of faulty machines-matches the analysis in §4.1. We next investigate the capacity of a single enforcer node, measure how this capacity scales with multiple nodes, and then estimate the number of dedicated enforcer nodes needed to handle 100 billion emails per day (our target volume; see §2.2). Finally, we evaluate the livelock avoidance scheme from §4.3. Table 1 summarizes our results.

All of our experiments use the Emulab testbed [18]. In these experiments, between one and 64 enforcer nodes are connected to a single LAN, modeling a clustered network service with a high-speed access link.

6.1 Environment

Each enforcer node runs on a separate Emulab host. To simulate clients and to test the enforcer under load, we run up to 25 instances of an open-loop tester, U (again, one per Emulab host). All hosts run Linux FC4 (2.6 kernel) and are Emulab's "PC 3000s", which have 3 GHz Xeon processors, 2 GBytes of RAM, 100 Mbit/s Ethernet interfaces, and 10,000 RPM SCSI disks.

Each U follows a Poisson process to generate TESTs and selects the portal for each TEST uniformly at random. This process models various email servers sending TESTs to various enforcer nodes. (As argued in [45], Poisson processes appropriately model a collection of many random, unrelated session arrivals in the Internet.) The proportion of reused TESTs (stamps⁵ previously SET by U) to fresh TESTs (stamps never SET by U) is configurable. These two TEST types model an email server receiving a spam or non-spam message, respectively. In response to a "not found" reply-which happens either if the stamp is fresh or if the enforcer lost the reused stamp-U issues a SET to the portal it chose for the TEST.

Our reported experiments run for 12 or 30 minutes. Separately, we ran a 12-hour test to verify that the performance of the enforcer does not degrade over time.

6.2 Fault Tolerance

We investigate whether failures in the implemented system reflect the analysis. Recall that this analysis (in §4.1 and the appendix) upper bounds the average number of stamp uses in terms of p, where p is the probability a node is bad, i.e., that it is ever down while a given stamp is relevant (two days). Below, we model "bad" with crash faults, only (see §4.5 for the relationship between Byzantine and crash faults).

We run two experiments in which we vary the number of bad nodes. These experiments measure how often the enforcer-because some of its nodes have crashed-fails to "find" stamps it has already "heard" about.

In the first experiment, called crashed, the bad nodes are never up. In the second, called churning, the bad nodes repeat a 90-second cycle of 45 seconds of down time followed by 45 seconds of up time. Both experiments run for 30 minutes. The Us issue TESTs and SETs to the up nodes, as described in §6.1. Half the TESTs are for fresh stamps, and the other half are for a reuse group-843,750 reused stamps that are each queried 32 times during the experiment. This group of TESTs models an adversary trying to reuse a stamp. The Us count the number of "not found" replies for each stamp in the reuse group; each such reply counts as a stamp use. We set n = 40, and the number of bad nodes is between 6 and 10, so p varies between 0.15 and 0.25. For the replication factor (§4.1), we set r=3.

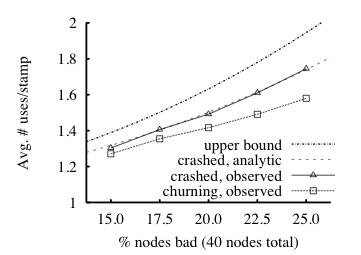Fig. 7: Effect of "bad" nodes on stamp reuse for two types of "bad". Observed uses obey the upper bound from the analysis (see §4.1 and the appendix). The crashed case can be analyzed exactly; the observations track this analysis closely.

The results are depicted in Figure 7. The two "observed" lines plot the average number of times a stamp in the "reuse group" was used successfully. These observations obey the model's least upper bound. This bound, from equation (1) in the appendix, is 1 +[3/2]p + 3p² + p³[40(1−p) − (1 +[3/2] + 3)] and is labeled "upper bound".⁶ The crashed experiment is amenable to an exact expectation calculation. The resulting expression⁷ is depicted by the line labeled "crashed, analytic"; it matches the observations well.

6.3 Single-node Microbenchmarks

We now examine the performance of a single-node enforcer. We begin with RAM and ask how it limits the number of PUTs. Each key-value pair consumes roughly 5.2 bytes of memory in expectation (§4.2), and each is stored for two days (§3.3). Thus, with one GByte of RAM, a node can store slightly fewer than 200 million key-value pairs, which, over two days, is roughly 1100 PUTs per second. A node can certainly accept a higher average rate over any given period but must limit the total number of PUTs it accepts each day to 100 million for every GByte of RAM. Our implementation does not currently rate-limit inbound PUTs.

Operation	Ops/sec	bottleneck
PUT	1,100	RAM
pessimistic GET	400	disk
non-pessimistic GET	38,000	CPU

Table 2: Single-node performance, assuming 1 GByte of RAM.

We next ask how the disk limits GETs. (The disk does not bottleneck PUTs because writes are sequential and because disk space is ample.) Consider a key k requested at a node d. We call a GET slow if d stores k on disk (if so, d has an entry for k in its index) and k is not in d's RAM cache (see §4.2). We expect d's ability to respond to slow GETs to be limited by disk seeks. To verify this belief, an instance of U sends TESTs and SETs at a high rate to a single-node enforcer, inducing local GETs and PUTs. The node runs with its cache of key-value pairs disabled. The node responds to an average of 400 slow GETs per second (measured over 5-second intervals, with standard deviation less than 10% of the mean). This performance agrees with our disk benchmark utility, which does random access reads in a tight loop.

We next consider fast GETs, which are GETs on keys k for which the node has k cached or is not storing k. In either case, the node can reply quickly. For this type of GET, we expect the bottleneck to be the CPU. To test this hypothesis, U again sends many TESTs and SETs. Indeed, CPU usage reaches 100% (again, measured over 5-second intervals with standard deviation as above), after which the node can handle no more than 38,000 RPCs. A profile of our implementation indicates that the specific CPU bottleneck is malloc().

Table 2 summarizes the above findings.

6.4 Capacity of the Enforcer

We now measure the capacity of multiple-node enforcers and seek to explain the results using the microbenchmarks just given. We define capacity as the maximum rate at which the system can respond correctly to the reused requests. Knowing the capacity as a function of the number of nodes will help us, in the next section, answer the dual question: how many nodes the enforcer must comprise to handle a given volume of email (assuming each email generates a TEST).

Of course, the measured capacity will depend on the workload: the ratio of fresh to reused TESTs determines whether RAM or disk is the bottleneck. The former TESTs consume RAM because the SETs that follow induce PUTs, while the latter TESTs may incur a disk seek.

Note that the resources consumed by a TEST are different in the multiple-node case. A TEST now generates r (or r−1, if the portal is an assigned node) GET RPCs, each of which consumes CPU cycles at the sender and receiver. A reused TEST still incurs only one disk seek in the entire enforcer (since the portal stops GETing once a node replies affirmatively).

32-node experiments We first determine the capacity of a 32-node enforcer. To emulate the per-node load of a several thousand-node deployment, we set r=5 (which we get because, from §4.1, r = 1 + log_1/p n; we take p=0.1 and n=8000, which is the upper bound in §6.5).

We run two groups of experiments in which 20 instances of U send half fresh and half reused TESTs at various rates to this enforcer. In the first group, called disk, the nodes' LRU caches are disabled, forcing a disk seek for every affirmative GET (§4.2). In the second group, called CPU, we enable the LRU caches and set them large enough that stamps will be stored in the cache for the duration of the experiment. The first group of experiments is fully pessimistic and models a disk-bound workload whereas the second is (unrealistically) optimistic and models a workload in which RPC processing is the bottleneck. We ignore the RAM bottleneck in these experiments but consider it at the end of the section.

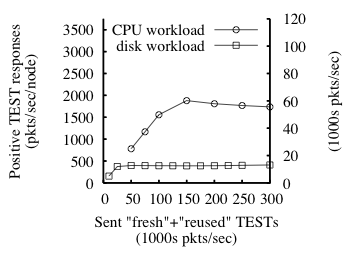
Each node reports how many reused TESTs it served over the last 5 seconds (if too many arrive, the node's kernel silently drops). Each experiment run happens at a different TEST rate. For each run, we produce a value by averaging together all of the nodes' 5-second reports. Figure 8 graphs the positive response rate as a function of the TEST rate. The left and right y-axes show, respectively, a per-node per-second mean and a per-second mean over all nodes; the x-axis is the aggregate sent TEST rate. (The standard deviations are less than 9% of the means.) The graph shows that maximum per-node capacity is 400 reused TESTs/sec when the disk is the bottleneck and 1875 reused TESTs/sec when RPC processing is the bottleneck; these correspond to 800 and 3750 total TESTs/sec (recall that half of the sent TESTs are reused).

The microbenchmarks explain these numbers. The per-node disk capacity is given by the disk benchmark. We now connect the per-node TEST-processing rate (3750 per second) to the RPC-processing microbenchmark (38,000 per second). Recall that a TEST generates multiple GET requests and multiple GET responses (how many depends on whether the TEST is fresh). Also, if the stamp was fresh, a TEST induces a SET request, a PUT request, and a PUT response. Taking all of these "requests" together (and counting responses as "requests" because each response also causes the node to do work), the average TEST generates 10.1 "requests" in this experiment (see [66] for details). Thus, 3750 TEST requests per node per second is 37,875 "requests" per node per second, which is within 0.5% of the microbenchmark from §6.3 (last row of Table 2).

One might notice that the CPU line in Figure 8 degrades after 1875 positive responses per second per node (the enforcer's RPC-processing capacity). The reason is as follows. Giving the enforcer more TESTs and SETs than it can handle causes it to drop some. Dropped SETs cause some future reused TESTs to be seen as fresh by the enforcer-but fresh TESTs induce more GETs (r or r−1) than reused TESTs (roughly (r+1)/2 on average since the portal stops querying when it gets a positive response). Thus, the degradation happens because extra RPCs from fresh-looking TESTs consume capacity. This degradation is not ideal, but it does not continue indefinitely.

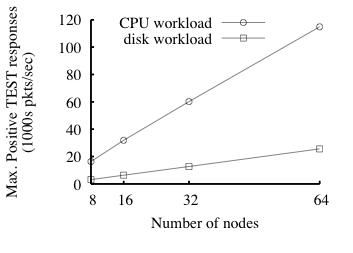
Scaling We now measure the enforcer's capacity as a function of the number of nodes, hypothesizing near-linear scaling. We run the same experiments as for 32 nodes but with enforcers of 8, 16, and 64 nodes. Figure 9 plots the maximum point from each experiment. (The standard deviations are smaller than 10% of the means.) The results confirm our hypothesis across this (limited) range of system sizes: an additional node at the margin lets the enforcer handle, depending on the workload, an additional 400 or 1875 TESTs/sec-the per-node averages for the 32-node experiment.


Fig. 8: For a 32-node enforcer, mean response rate to TEST requests as function of sent TEST rate for disk- and CPU-bound workloads. The two y-axes show the response rate in different units: (1) per-node and (2) over the enforcer in aggregate. Here, r=5, and each reported sample's standard deviation is less than 9% of its mean.	Fig. 9: Enforcer capacity under two workloads as a function of number of nodes in the enforcer. The y-axis is the same as the right-hand y-axis in Fig. 8. Standard deviations are smaller than 10% of the reported means.

We now view the enforcer's scaling properties in terms of its request mix. Assume pessimistically that all reused TEST requests cost a disk seek. Then, doubling the rate of spam (reused TEST requests) will double the required enforcer size. However, doubling the rate of non-spam (fresh TEST requests) will not change the required enforcer size at first. The rate of non-spam will only affect the required enforcer size when the ratio of the rates of reused TESTs to fresh TESTs matches the ratio of a single node's performance limits, namely 400 reused TESTs/sec to 1100 fresh TESTs/sec for every GByte of RAM. The reason is that fresh TESTs are followed by SETs, and these SETs are a bottleneck only if nodes see more than 1100 PUTs per second per GByte of RAM; see Table 2.

6.5 Estimating the Enforcer Size

100 billion	emails daily (target from §2.2)
65%	spam [43,7]
65 billion	disk seeks / day (pessimistic)
400	disk seeks/second/node (§6.3)
86400	seconds/day
1881	nodes (from three quantities above)

Table 3: Estimate of enforcer size (based on average rates).

We now give a rough estimate of the number of dedicated enforcer nodes required to handle current email volumes. The calculation is summarized in Table 3. Some current estimates suggest 84 billion email messages per day [30] and a spam rate of roughly 65% [43]. (Brightmail reported a similar figure for the spam percentage in July 2004 [7].) We assume 100 billion messages daily and follow the lower bound on capacity in Figure 9, i.e., every reused TEST-each of which models a spam message-causes the enforcer to do a disk seek. In this case, the enforcer must do 65 billion disk seeks per day and, since the required size scales with the number of disks (§6.4), a straightforward calculation gives the required number of machines. For the disks in our experiments, the number is about 2000 machines. The required network bandwidth is small, about 3 Mbits/s per node.

So far we have considered only average request rates. We must ask how many machines the enforcer needs to handle peak email loads while bounding reply latency. To answer this question, we would need to determine the peak-to-average ratio of email reception rates at email servers (their workload induces the enforcer workload). As one data point, we analyzed the logs of our research group's email server, dividing a five-week period in early 2006 into 10-minute windows. The maximum window saw 4 times the volume of the average window. Separately, we verified with a 14-hour test that a 32-node enforcer can handle a workload of like burstiness with worst-case latency of 10 minutes. Thus, if global email is this bursty, the enforcer would need 8000 machines (the peak-to-average ratio times the 2000 machines derived above) to give the same worst-case latency.

However, global email traffic is likely far smoother than one server's workload. And spam traffic may be smoother still: the spam in [32]'s 2004 data exhibits-over ten minute windows, as above-a peak-to-average ratio of 1.9:1. Also, Gomes et al. [22] claim that spam is less variable than legitimate email. Thus, many fewer than 8000 machines may be required. On the other hand, the enforcer may need some over-provisioning for spurious TESTs (§4.4). For now, we conclude that the enforcer needs "a few thousand" machines and leave to future work a study of email burstiness and attacker ability.

6.6 Avoiding "Distributed Livelock"

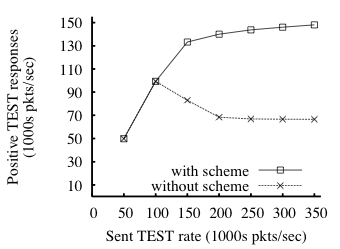Fig. 10: Effect of livelock avoidance scheme from §4.3. As the sent TEST rate increases, the ability of an enforcer without the scheme to respond accurately to reused TESTs degrades.

We now briefly evaluate the scheme to avoid livelock (from §4.3). The goal of the scheme is to maximize correct TEST responses under high load. To verify that the scheme meets this goal, we run the following experiment: 20 U instances send TEST requests (half fresh, half reused) at high rates, first, to a 32-node enforcer with the scheme and then, for comparison, to an otherwise identical enforcer without the scheme. Here, r=5 and the nodes' caches are enabled. Also, each stamp is used no more than twice; TESTs thus generate multiple GETs, some of which are dropped by the enforcer without the scheme. Figure 10 graphs the positive responses as a function of the sent TEST rate. At high sent TEST rates, an enforcer with the scheme gives twice as many positive responses-that is, blocks more than twice as much spam-as an enforcer without the scheme.

6.7 Limitations

Although we have tested the enforcer under heavy load to verify that it does not degrade, we have not tested a flash crowd in which a single stamp s is GETed by all (several thousand) of the enforcer nodes. Note, however, that handling several thousand simultaneous GETs is not difficult because after a single disk seek for s, an assigned node has the needed key-value pair in its cache.

We have also not addressed heterogeneity. For static heterogeneity, i.e., nodes that have unequal resources (e.g., CPU, RAM), the bunker can adjust the load-balanced assignment of keys to values. Dynamic heterogeneity, i.e., when certain nodes are busy, will be handled by the enforcer's robustness to unresponsive nodes and by the application's insensitivity to latency.

7 Related Work

We first place DQE in context with a survey of work on spam control (though space precludes a full list) and then compare the enforcer to related distributed systems.

7.1 Spam Control

Spam filters (e.g., [59,25]) analyze incoming email to classify it as spam or legitimate. While these tools certainly offer inboxes much relief, they do not achieve our top-level goal of reliable email (see §1). Moreover, filters and spammers are in an arms race that makes classification ever harder.

The recently-proposed Re: [21] shares our reliable email goal. Re: uses friend-of-friend relationships to let correspondents whitelist each other automatically. In contrast to DQE, Re: allows some false positives (for non-whitelisted senders), but on the other hand does not require globally trusted entities (like the quota allocators and bunker, in our case). Templeton [62] proposes an infrastructure formed by cooperating ISPs to handle worldwide email; the infrastructure throttles email from untrusted sources that send too much. Like DQE, this proposal tries to control volumes but unlike DQE presumes the enforcement infrastructure is trusted. Other approaches include single-purpose addresses [31] and techniques by which email service providers can stop outbound spam [24].

In postage proposals (e.g., [20,52]), senders pay receivers for each email; well-behaved receivers will not collect if the email is legitimate. This class of proposals is critiqued by Levine [38] and Abadi et al. [1]. Levine argues that creating a micropayment infrastructure to handle the world's email is infeasible and that potential cheating is fatal. Abadi et al. argue that micropayments raise difficult issues because "protection against double spending [means] making currency vendor-specific .... There are numerous other issues ... when considering the use of a straight micro-commerce system. For example, sending email from your email account at your employer to your personal account at home would in effect steal money from your employer" [1].

With pairwise postage, receivers charge CPU cycles [17,8,4] or memory cycles [2,16] (the latter being fairer because memory bandwidths are more uniform than CPU bandwidths) by asking senders to exhibit the solution of an appropriate puzzle. Similarly, receivers can demand human attention (e.g., [60]) from a sender before reading an email.

Abadi et al. pioneered bankable postage [1]. Senders get tickets from a "Ticket Server" (TS) (perhaps by paying in memory cycles) and attach them to emails. Receivers check tickets for freshness, cancel them with the TS, and optionally refund them. Abadi et al. note that, compared to pairwise schemes, this approach offers: asynchrony (senders get tickets "off-line" without disrupting their workflow), stockpiling (senders can get tickets from various sources, e.g., their ISPs), and refunds (which conserve tickets when the receiver is friendly, giving a higher effective price to spammers, whose receivers would not refund).

DQE is a bankable postage scheme, but TS differs from DQE in three ways: first, it does not separate allocation and enforcement (see §2); second, it relies on a trusted central server; and third, it does not preserve sender-receiver email privacy. Another bankable postage scheme, SHRED [36], also has a central, trusted cancellation authority. Unlike TS and SHRED, DQE does not allow refunds (letting it do so is future work for us), though receivers can abstain from canceling stamps of known correspondents; see §8.1.

Goodmail [23]-now used by two major email providers [13]-resembles TS. (See also Bonded Sender [6], which is not a postage proposal but has the same goal as Goodmail.) Goodmail accredits bulk mailers, trying to ensure that they send only solicited email, and tags their email as "certified". The providers then bypass filters to deliver such email to their customers directly. However, Goodmail does not eliminate false positives because only "reputable bulk mailers" get this favored treatment. Moreover, like TS, Goodmail combines allocation and enforcement and does not preserve privacy.

7.2 Related Distributed Systems

Because the enforcer stores key-value pairs, DHTs seemed a natural substrate, and our first design used one. However, we abandoned them because (1) most DHTs do not handle mutually untrusting nodes and (2) in most DHTs, nodes route requests for each other, which can decrease throughput if request handling is a bottleneck. Castro et al. [9] address (1) but use considerable mechanism to handle untrusting nodes that route requests for each other. Conversely, one-hop DHTs [28,29] eschew routing, but nodes must trust each other to propagate membership information. In contrast, the enforcer relies on limited scale to avoid routing and on a trusted entity, the bunker (§4), to determine its membership.

Such static configuration is common; it is used by distributed systems that take the replicated state machine approach [55] to fault tolerance (e.g., the Byzantine Fault Tolerant (BFT) literature [10], the recently proposed BAR model [3], and Rosebud [53]) as well as by Byzantine quorum solutions (e.g., [41,40]) and by cluster-based systems with strong semantics (e.g., [26]).

What makes the enforcer unusual compared to the work just mentioned is that, to tolerate faults (Byzantine or otherwise), the enforcer does not need mechanism beyond the bunker: enforcer nodes do not need to know which other nodes are currently up (in contrast to replicated state machine solutions), and neither enforcer nodes nor enforcer clients try to protect data or ensure its consistency (in contrast to the Byzantine quorum literature and cluster-based systems with strong semantics). The reason the enforcer gets away with this simplicity is weak semantics. It stores only immutable data, and the entire application is robust to lost data.

8 Deployment and Economics

Though the following discussion is in the context of DQE, much of it applies to bankable postage [1] (or quota-based) proposals in general.

8.1 Deployment, Usage, Mailing Lists

Deployment

We now speculate about paths to adoption. First, large email providers have an interest in reducing spam. A group of them could agree on a stamp format, allocate quotas to their users, and run the enforcer cooperatively. If each provider ran its own, separate enforcer, our design still applies: each enforcer must cope with a large universe of stamps. Another possibility is organization-by-organization adoption (the incremental benefit being that spoofed intra-organization spam no longer benefits from a "whitelist") or even individual-by-individual (the incremental benefit being that stamping one's email and sending to another DQE-enabled user ensures one's email will not be caught in a spam filter). In these cases, the deployment challenge is agreeing on a quota allocator and establishing an enforcer. The local changes (to email servers; email clients need not change) are less daunting.

Usage

The amount of stamped spam will be negligible (see below for a rough argument). Thus, following the "no false positives" goal, stamped email should always be passed to the human user. For unstamped email: before DQE is widely deployed, this email should go through content filters (again risking false positives), and under widespread DQE deployment, this email can be considered spam. Conversely, DQE can incorporate whitelists, where people agree not to cancel the stamps of their frequent correspondents. Senders still stamp their mails to prevent spoofing, but such stamps do not "count" against the sender's quota. Such a social protocol is similar to TS's refunds [1].

Mailing lists

For moderated lists, senders can spend a single stamp, and the list owner can then either sign the message or spend stamps for each receiver. Unmoderated, open mailing lists are problematic: spammers can multiply their effect while spending only one stamp. Partially-moderated lists might become more common under DQE. Here, messages from new contributors would be moderated (requiring only a glance to determine if the email is spam), and messages from known valid senders-based on past contributions and identified by the public key in the stamp-would be automatically sent to the list, again using either the list owner's public key or stamps for each recipient. In such lists, the moderation needed would be little (proportional to the number of messages from new contributors), so more lists could convert to this form.

8.2 Economics of Stamps

A quota allocation policy is effective whenever stamps cost a scarce resource. However, for simplicity, we view quotas as imposing a per-email monetary cost and do not discuss how to translate currencies like CPU [1], identity [5] or human attention [64] into money. Likewise, we only briefly consider how quotas should be allocated.

Basic analysis

We give a rough argument about the effectiveness of a per-email cost. Assume that spammers are profit-maximizing and that, today, the industry (or individual spammers) make a maximal profit of P by sending m spam messages. Now assume that DQE is deployed and induces a stamp cost of c. Then, the maximum number of messages with fresh stamps that profit-maximizing spammers can send under DQE must be less than [P/c]: more would consume the entire maximal profit. To reduce spam (i.e., m) by a factor f, one need only set c = f[P/m]. That is, to reduce spam by factor f, the price per message must be f times the profit-per-message.

The preceding analysis assumes that each stamp is reused only once, but adversaries can reuse each stamp a little more than once; see §4.1. Nevertheless, the analysis is very pessimistic: consider a variety of scams, each with a different profit-per-message when sent in the optimal amount. If, as we expect, most scams yield low profit, and few yield high profit, then setting a price c will prevent all scams with rate-of-return less than c. For example, if each scam sends the same amount, and if the number of scams returning more than a given amount q exponentially decays with q, then additive price increases in stamps result in multiplicative decreases in spam.

Pricing and allocation

From the preceding analysis, the quota allocator should set a "price" according to a target reduction goal (f) and an estimate of spammer profits (P). Another option is for the quota allocator to monitor spam levels and find a price adaptively (though the feedback may occur on time scales that are too long). One problem is that, as argued by Laurie and Clayton in the context of computational puzzles [37], no price exists that affects spammers and not legitimate heavy users. In response, we note first that heavy users are the ones most affected by spam and might be willing to pay to reduce the problem. Second, the analysis in [37] does not take into account refunds (or uncanceled stamps, in our context), which, as Abadi et al. [1] point out, will strongly differentiate between a spammer (whose stamps will be canceled) and a legitimate heavy user.

A difficult policy question is: how can quota allocation give the poor fair sending rights without allowing spammers to send? We are not experts in this area and just mention one possibility. Perhaps a combination of explicit allocation in poor areas of the world, bundled quotas elsewhere (e.g., with an email account comes free stamps), and pricing for additional usage could impose the required price while making only heavy users pay.

9 Conclusion

The way DQE is supposed to work is that the economic mechanism of quotas will make stamps expensive for spammers while a technical mechanism-the enforcer-will keep stamps from "losing value" through too much reuse. Whether the first part of this supposition is wishful thinking is not a question we can answer, and our speculations about various policies and the future trajectory of email should be recognized as such. We are more confident, however, about the second part. Based on our work, we believe an enforcer that comprises a moderate number of dedicated, mutually untrusting hosts can handle stamp queries at the volume of the world's email. Such an infrastructure, together with the other technical mechanisms in DQE, meets the design goals in §2.

The enforcer's simplicity-particularly the minimal trust assumptions-encourages our belief in its practicality. Nevertheless, the enforcer was not an "easy problem." Its external structure, though now spare, is the end of a series of designs-and a few implementations-that we tried. By accepting that the bunker is a reasonable assumption and that lost data is not calamitous, we have arrived at what we believe is a novel design point: a set of nodes that implement a simple storage abstraction but avoid neighbor maintenance, replica maintenance, and mutual trust. Moreover, the "price of distrust" in this system-in terms of what extra mechanisms are required because of mutual mistrust-is zero. We wonder whether this basic design would be useful in other contexts.

Appendix: Detailed Analysis

In this appendix, we justify the upper bound from §4.1 on the expected number of uses of a stamp. We make a worst-case assumption that an adversary tries to reuse each stamp an infinite number of times. Observe that each use induces a PUT to an assigned node, and once the stamp is PUT to a good assigned node-good is defined in §4.1-the adversary can no longer reuse that stamp successfully. Since PUTs are random, some will be to a node that has already received a PUT for the stamp (in which case the node is bad), while others are to "new" nodes. Each time a PUT happens on a new node, there is a 1−p chance that the node is good.

Let I_i be an indicator random variable for the event that the stamp needs to be PUT to at least i−1 distinct nodes before hitting a good one, and let T_i be the number of PUTs, after i−1 distinct nodes have been tried, needed to get to the i^th distinct node. As a special case, let T_r+1=n −∑_j=1^r T_j to reflect the fact that if all r assigned nodes are bad, an adversary can reuse the stamp once at each portal. E[I_i]=Pr[I_i = 1]=pⁱ⁻¹ and E[T_i]=r/(r−i+1) since each attempt for the stamp has a (r−i+1)/r chance of selecting a new node. Then, assuming adversaries try to reuse each stamp ad infinitum, the expected number of PUTs (i.e., uses of the stamp) is

E[I₁T₁+I₂T₂+…+I_rT_r+I_r+1T_r+1]

E[I₁]E[T₁]+…+E[I_r]E[T_r]+E[I_r+1]E[T_r+1]

1+p

r−1

+…+p^r−1

+p^r

[

n −

r
∑
j=1

r−j+1

]

r−1
∑
i=0

pⁱ

r−i

+ p^r

[

n −

r
∑
j=1

r−j+1

]

(1)

An upper bound for this expression is ∑_i=0^r−1 pⁱ[r/(r−i)]+p^rn, which we can further bound by noting that [r/(r−i)] ≤ 2ⁱ and assuming p ≤ 1/2, giving an upper bound of

1−2p

+p^rn.

(2)

Acknowledgments

We thank: Russ Cox, Dina Katabi, Sachin Katti, Sara Su, Arvind Thiagarajan, Mythili Vutukuru, and the anonymous reviewers, for their comments on drafts; David Andersen, Russ Cox, Sean Rhea, and Rodrigo Rodrigues, for useful conversations; Russ Cox, Frank Dabek, Maxwell Krohn, and Emil Sit, for implementation suggestions; Shabsi Walfish, for many cryptography pointers; and Michel Goraczko and Emulab [18], for their invaluable help with experiments. This work was supported by the National Science Foundation under grants CNS-0225660 and CNS-0520241, by an NDSEG Graduate Fellowship, and by British Telecom.

Source code for the implementation described in §5 is available at: https://nms.csail.mit.edu/dqe

References

[1]: M. Abadi, A. Birrell, M. Burrows, F. Dabek, and T. Wobber. Bankable postage for network services. In Proc. Asian Computing Science Conference, Dec. 2003.
[2]: M. Abadi, M. Burrows, M. Manasse, and T. Wobber. Moderately hard, memory-bound functions. In NDSS, 2003.
[3]: A. S. Aiyer, L. Alvisi, A. Clement, M. Dahlin, J.-P. Martin, and C. Porth. BAR fault tolerance for cooperative services. In SOSP, Oct. 2005.
[4]: A. Back. Hashcash. https://www.cypherspace.org/adam/hashcash/.
[5]: H. Balakrishnan and D. Karger. Spam-i-am: A proposal to combat spam using distributed quota management. In HotNets, Nov. 2004.
[6]: Bonded Sender Program. https://www.bondedsender.com/info_center.jsp.
[7]: Brightmail, Inc.: Spam percentages and spam categories. https://web.archive.org/web/20040811090755/https://www.brightmail.com/spamstats.html.
[8]: Camram. https://www.camram.org/.
[9]: M. Castro, P. Druschel, A. Ganesh, A. Rowstron, and D. S. Wallach. Secure routing for structured peer-to-peer overlay networks. In OSDI, Dec. 2002.
[10]: M. Castro and B. Liskov. Practical Byzantine fault tolerance and proactive recovery. ACM TOCS, 20(4):398-461, Nov. 2002.
[11]: ClickZ News. Costs of blocking legit e-mail to soar, Jan. 2004. https://www.clickz.com/news/article.php/3304671.
[12]: ClickZ News. Spam blocking experts: False positives inevitable, Feb. 2004. https://www.clickz.com/news/article.php/3315541.
[13]: ClickZ News. AOL to implement e-mail certification program, Jan. 2006. https://www.clickz.com/news/article.php/3581301.
[14]: F. Dabek et al. Designing a DHT for low latency and high throughput. In NSDI, Mar. 2004.
[15]: P. Druschel and G. Banga. Lazy receiver processing (LRP): A network subsystem architecture for server systems. In OSDI, Oct. 1996.
[16]: C. Dwork, A. Goldberg, and M. Naor. On memory-bound functions for fighting spam. In CRYPTO, 2003.
[17]: C. Dwork and M. Naor. Pricing via processing or combatting junk mail. In CRYPTO, 1992.
[18]: Emulab. https://www.emulab.net.
[19]: Enterprise IT Planet. False positives: Spam's casualty of war costing billions, Aug. 2003. https://www.enterpriseitplanet.com/security/news/article.php/2246371.
[20]: S. E. Fahlman. Selling interrupt rights: A way to control unwanted e-mail and telephone calls. IBM Systems Journal, 41(4):759-766, 2002.
[21]: S. Garriss, M. Kaminsky, M. J. Freedman, B. Karp, D. Mazières, and H. Yu. Re: Reliable email. In NSDI, May 2006.
[22]: L. H. Gomes, C. Cazita, J. M. Almeida, V. Almeida, and W. Meira Jr. Charaterizing a spam traffic. In IMC, Oct. 2004.
[23]: Goodmail Systems. https://www.goodmailsystems.com.
[24]: J. Goodman and R. Rounthwaite. Stopping outgoing spam. In ACM Conf. on Electronic Commerce (EC), May 2004.
[25]: P. Graham. Better bayesian filtering. https://www.paulgraham.com/better.html.
[26]: S. Gribble, E. A. Brewer, J. M. Hellerstein, and D. Culler. Scalable, distributed data structures for internet service construction. In OSDI, Oct. 2000.
[27]: R. F. Guilmette. ANNOUNCE: MONKEYS.COM: Now retired from spam fighting. newsgroup posting: news.admin.net-abuse.email, Sept. 2003.
[28]: A. Gupta, B. Liskov, and R. Rodrigues. Efficient routing for peer-to-peer overlays. In NSDI, Mar. 2004.
[29]: I. Gupta, K. Birman, P. Linka, A. Demers, and R. van Renesse. Building an efficient and stable P2P DHT through increased memory and background overhead. In IPTPS, Feb. 2003.
[30]: IDC. Worldwide email usage forecast, 2005-2009: Email's future depends on keeping its value high and its cost low. https://www.idc.com/, Dec. 2005.
[31]: J. Ioannidis. Fighting spam by encapsulating policy in email addresses. In NDSS, 2003.
[32]: J. Jung and E. Sit. An empirical study of spam traffic and the use of DNS black lists. In IMC, Oct. 2004.
[33]: D. Karger et al. Consistent hashing and random trees: Distributed caching protocols for relieving hot spots on the World Wide Web. In ACM STOC, May 1997.
[34]: D. E. Knuth. The Art of Computer Programming, chapter 6.4. Addison-Wesley, second edition, 1998.
[35]: H. Krawzyk, M. Bellare, and R. Canetti. HMAC: Keyed-hashing for message authentication, Feb. 1997. RFC 2104.
[36]: B. Krishnamurthy and E. Blackmond. SHRED: Spam harassment reduction via economic disincentives. https://www.research.att.com/~bala/papers/shred-ext.ps, 2004.
[37]: B. Laurie and R. Clayton. "Proof-of-Work" proves not to work; version 0.2, Sept. 2004. https://www.cl.cam.ac.uk/users/rnc1/proofwork2.pdf.
[38]: J. R. Levine. An overview of e-postage. Taughannock Networks, https://www.taugh.com/epostage.pdf, 2003.
[39]: J. Li, M. N. Krohn, D. Mazières, and D. Shasha. Secure untrusted data repository (SUNDR). In OSDI, Dec. 2004.
[40]: D. Malkhi and M. K. Reiter. Byzantine quorum systems. In ACM STOC, 1997.
[41]: D. Malkhi and M. K. Reiter. Secure and scalable replication in phalanx. In IEEE Symp. on Reliable Distrib. Systems, Oct. 1998.
[42]: D. Mazières. A toolkit for user-level file systems. In USENIX Technical Conference, June 2001.
[43]: MessageLabs Ltd. https://www.messagelabs.com/Threat_Watch/Threat_Statistics/Spam_Intercepts, 2006.
[44]: J. Mirkovic and P. Reiher. A taxonomy of DDoS attacks and DDoS defense mechanisms. CCR, 34(2), Apr. 2004.
[45]: V. Paxson and S. Floyd. Wide area traffic: the failure of Poisson modeling. IEEE ACM TON, 3(3):226-244, 1995.
[46]: PC World. Spam-proof your in-box, June 2004. https://www.pcworld.com/reviews/article/0,aid,115885,00.asp.
[47]: The Penny Black Project. https://research.microsoft.com/research/sv/PennyBlack/.
[48]: X. Qie, R. Pang, and L. Peterson. Defensive programming: Using an annotation toolkit to build DoS-resistant software. In OSDI, Dec. 2002.
[49]: S. Quinlan and S. Dorward. Venti: A new approach to archival storage. In USENIX FAST, Jan. 2002.
[50]: Radicati Group Inc.: Market Numbers Quarterly Update Q2 2003.
[51]: E. Ratliff. The zombie hunters. The New Yorker, Oct. 10 2005.
[52]: F.-R. Rideau. Stamps vs spam: Postage as a method to eliminate unsolicited commercial email. https://fare.tunes.org/articles/stamps_vs_spam.html.
[53]: R. Rodrigues and B. Liskov. Rosebud: A scalable Byzantine-fault-tolerant storage architecture. Technical Report TR/932, MIT LCS, Dec. 2003.
[54]: M. Rosenblum and J. Ousterhout. The design and implementation of a log-structured file system. ACM TOCS, 10(1):26-52, 1992.
[55]: F. B. Schneider. Implementing fault-tolerant services using the state machine approach: A tutorial. ACM Computing Surveys, 22(4):299-319, Dec. 1990.
[56]: SecurityFocus. FBI busts alleged DDoS mafia, Aug. 2004. https://www.securityfocus.com/news/9411.
[57]: K. Shen, H. Tang, T. Yang, and L. Chu. Integrated resource management for cluster-based internet services. In OSDI, Dec. 2002.
[58]: M. Sherr, M. Greenwald, C. A. Gunter, S. Khanna, and S. S. Venkatesh. Mitigating DoS attack through selective bin verification. In 1st Wkshp. on Secure Netwk. Protcls., Nov. 2005.
[59]: SpamAssassin. https://spamassassin.apache.org/.
[60]: Spambouncer. https://www.spambouncer.org.
[61]: I. Stoica et al. Chord: A scalable peer-to-peer lookup protocol for Internet applications. IEEE/ACM Transactions on Networking, 11(1):17-32, Feb. 2003.
[62]: B. Templeton. Best way to end spam. https://www.templetons.com/brad/spam/endspam.html.
[63]: The Spamhaus Project. Spammers release virus to attack spamhaus.org. https://www.spamhaus.org/news.lasso?article=13, Nov. 2003.
[64]: L. von Ahn, M. Blum, and J. Langford. Telling humans and computers apart automatically. CACM, 47(2), Feb. 2004.
[65]: M. Walfish, H. Balakrishnan, D. Karger, and S. Shenker. DoS: Fighting fire with fire. In HotNets, Nov. 2005.
[66]: M. Walfish, J. D. Zamfirescu, H. Balakrishnan, D. Karger, and S. Shenker. Supplement to "Distributed Quota Enforcement for Spam Control". Technical report, MIT CSAIL, Apr. 2006. Available from https://nms.csail.mit.edu/dqe.
[67]: X. Wang, Y. L. Yin, and H. Yu. Finding collisions in the full SHA-1. In CRYPTO, Aug. 2005.
[68]: M. Welsh and D. Culler. Adaptive overload control for busy Internet servers. In USENIX USITS, Mar. 2003.
[69]: M. Welsh, D. Culler, and E. Brewer. SEDA: An architecture for well-conditioned, scalable Internet services. In SOSP, Oct. 2001.

Footnotes:

¹Although spam control is our motivating application, and certain details are specific to it, the general approach of issuing and canceling stamps can apply to any computational service (as noted before in [1]).

²Most of the ideas in §3.1 and §3.2 first appeared in [5].

³One might wonder why receivers will SET after they have already received "service" from the enforcer in the form of a TEST. Our answer is that executing these requests is inexpensive, automatic, and damaging to spammers.

⁴Our implementation uses SHA-1, which has recently been found to be weaker than previously thought [67]. We don't believe this weakness significantly affects our system because DQE stamps are valid for only two days, and, at least for the near future, any attack on SHA-1 is likely to require more computing resources than can be marshaled in this time. Moreover, DQE can easily move to another hash function.

⁵In this section (§6), we often use "stamp" to refer to the key-value pair associated with the stamp.

⁶We take n=40(1−p) instead of n=40 because, as mentioned above, the Us issue TESTs and SETs only to the "up" nodes.

⁷The expression, with m = 40(1−p), is (1−p)³(1) + 3p²(1−p)α+ 3p(1−p)²β+ p³m(1 − ([(m − 1)/m])³²). α is ∑_i=1^m i([2/3])ⁱ⁻¹ [1/m] (1 + [(m−i)/3]), and β is ∑_i=1^m−1 i ([1/3])ⁱ⁻¹ [(m−i)/(m(m−1))](2 + [2/3](m −(i+1))). See [66] for a derivation.

File translated from T_EX by T_TH, version 3.74.
On 10 Apr 2006, 18:48.

This paper was originally published in the Proceedings of the 3rd Symposium on Networked Systems Design and Implementation (NSDI '06)
May 8–10, 2006, San Jose, CA

Last changed: 3 May 2006 jel