|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
NSDI '05 Paper
[NSDI '05 Technical Program]
Cashmere: Resilient Anonymous RoutingLi Zhuang, Feng Zhou
AbstractAnonymous routing protects user communication from identification by third-party observers. Existing anonymous routing layers utilize Chaum-Mixes for anonymity by relaying traffic through relay nodes called mixes. The source defines a static forwarding path through which traffic is relayed to the destination. The resulting path is fragile and shortlived: failure of one mix in the path breaks the forwarding path and results in data loss and jitter before a new path is constructed. In this paper, we propose Cashmere, a resilient anonymous routing layer built on a structured peer-to-peer overlay. Instead of single-node mixes, Cashmere selects regions in the overlay namespace as mixes. Any node in a region can act as the MIX, drastically reducing the probability of a mix failure. We analyze Cashmere's anonymity and measure its performance through simulation and measurements, and show that it maintains high anonymity while providing orders of magnitude improvement in resilience to network dynamics and node failures.
1 IntroductionIn many applications it is desirable to hide the identity of the communicating parties from each other and third-party observers. The ability to anonymously route packets is used in many applications, such as anonymous web browsing [1], anonymous voting and in peer-to-peer applications wanting to ensure fair resource sharing [19].
The first-generation of applications that used anonymous routing, including
the Anonymizer [1], were centralized, with central points of
failure. More recent anonymous routing
proposals [22,30,11] extend
Chaum-Mixes [3] by forwarding traffic through a sequence of
relays. Each relay is a single network endpoint. They attempt to
ensure that the identity of the message source is never revealed to
the destination, and the source and destination identities are
hidden from relays and third-party observers. They achieve
this by wrapping the payload and the sequence of relays through which a
message is to be forwarded in layers of public key encryption, with one
layer for each relay to be used. This requires that a set of
relays be statically chosen at the beginning of a communication
session. In general, if
Successful end-to-end message delivery requires that every relay We propose a failure resilient anonymous routing system called Cashmere. Cashmere achieves resilience by using a set of distributed endpoints as a single virtual relay rather than a single endpoint. We refer to these endpoints as relay groups, and the forwarding path used in Cashmere is a sequence of relay groups. All members of a relay group share a public/private key pair. Layered encryption is still used on the forwarding path, using the public key of the relay group. Every member of the relay group has the ability to independently decrypt the next layer in the forwarding path. A forwarding path is valid as long as each relay group used in the forwarding path has at least one single live reachable member. While Chaum-Mixes route to the destination as the last hop, the destination in Cashmere is a member of any one of the relay groups on the forwarding path. The source randomly orders the relay groups to hide the destination relay group. When a message arrives at a member of a relay group, the receiver both anycasts the message to the next relay group and broadcasts the decrypted contents to all other members of the relay group. This ensures that if the destination is a member of the current group, it will receive the message.
The rest of this paper is structured as follows. We give an overview of related work and their limitations in Section 2. Next, we present the design of Cashmere in Section 3. We then discuss details of our current Cashmere implementation in Section 4. In Section 5, we analyze the level of anonymity in Cashmere and evaluate its security and performance using both simulation and measurements from an actual implementation. Finally, we outline future work and conclude in Section 6.
|
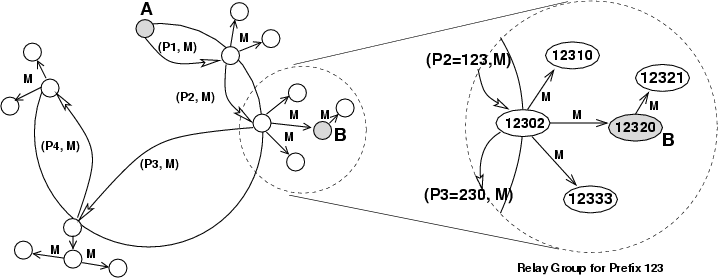
Relay group membership management in Cashmere exploits properties of the
identifier space maintained by prefix-routing based structured overlays. In
particular, for each ![]() -bit nodeID there are
-bit nodeID there are ![]() unique prefixes. For
example, the 6-bit nodeID 101011 has prefixes: 1, 10, 101, 1010, 10101 and 101011. In general, if there
are
unique prefixes. For
example, the 6-bit nodeID 101011 has prefixes: 1, 10, 101, 1010, 10101 and 101011. In general, if there
are ![]() nodes it is expected that
nodes it is expected that ![]() will share the same
will share the same ![]() -bit prefix.
-bit prefix.
In Cashmere, each relay group has a groupID which is an ![]() -bit
identifier, where
-bit
identifier, where
![]() . A node is a member of that relay
group if the groupID is a prefix of its nodeID. Since nodeIDs are
randomly assigned, nodes in a relay group are a random subset of the
overlay nodes and exhibit independent failure patterns. Each prefix
requires a public/private key pair and all nodes that share that
prefix need both the public and private key. We assume these are
generated and distributed using an off-line CA. In general, a user
wishing to contribute a node to the system must obtain from the CA a
signed
. A node is a member of that relay
group if the groupID is a prefix of its nodeID. Since nodeIDs are
randomly assigned, nodes in a relay group are a random subset of the
overlay nodes and exhibit independent failure patterns. Each prefix
requires a public/private key pair and all nodes that share that
prefix need both the public and private key. We assume these are
generated and distributed using an off-line CA. In general, a user
wishing to contribute a node to the system must obtain from the CA a
signed ![]() -bit nodeID and the set of
-bit nodeID and the set of ![]() public/private keys
associated with its nodeID and must have access to all the public keys
of the other prefixes. Each nodeID must be unique, so the
public/private key for the
public/private keys
associated with its nodeID and must have access to all the public keys
of the other prefixes. Each nodeID must be unique, so the
public/private key for the ![]() -bit prefix will be unique to this
nodeID.
-bit prefix will be unique to this
nodeID.
The structured overlay routes messages between relay groups. The groupID is used as the key as a message is routed using KBR. As the message is routed, the first node that receives the message and shares the groupID prefix processes the message on behalf of the relay group. This node is referred to as the relay group root. Therefore, routing a message to a groupID is effectively performing an anycast to the relay group members.
Generally, if node ![]() wants to route a message to node
wants to route a message to node ![]() anonymously, it selects a random sequence of
anonymously, it selects a random sequence of ![]() -bit groupIDs that
defines the set of relay groups and includes the
-bit groupIDs that
defines the set of relay groups and includes the ![]() -bit prefix of
-bit prefix of
![]() . These are used to construct a forwarding path, i.e. a
sequence of relay groups the message routes through. Since
. These are used to construct a forwarding path, i.e. a
sequence of relay groups the message routes through. Since ![]() selects
the groupIDs randomly, the path cannot be predicted by others. The
value of
selects
the groupIDs randomly, the path cannot be predicted by others. The
value of ![]() controls the expected size of the relay group, and
consequently the resilience against failures and malicious nodes.
controls the expected size of the relay group, and
consequently the resilience against failures and malicious nodes. ![]() encrypts the forwarding path in multiple layers using the public keys
associated with each relay group. The overlay routes the message to
the first relay group using its groupID. When any node matching the
current prefix receives the message, it becomes the relay group root
for that message, and uses the relay group's private key to decrypt
the next layer of the path. This reveals the next groupID and the
message is routed through the overlay to that prefix.
encrypts the forwarding path in multiple layers using the public keys
associated with each relay group. The overlay routes the message to
the first relay group using its groupID. When any node matching the
current prefix receives the message, it becomes the relay group root
for that message, and uses the relay group's private key to decrypt
the next layer of the path. This reveals the next groupID and the
message is routed through the overlay to that prefix.
Unlike other Chaum-Mixes based systems, Cashmere decouples the payload from the encrypted forwarding path, and encrypts the payload separately. This has the advantage that a source can reuse a forwarding path, avoiding multiple public key encryptions. The source caches the forwarding path, and only needs to perform a single public key encryption on each message using the destination's unique public key.
The source needs to encrypt each message payload such that it can only
be decrypted by the true destination and such that each relay sees a
different value for the payload (as do eavesdroppers). Suppose there
are ![]() relay groups in the forwarding path:
relay groups in the forwarding path:
![]() and the
destination node
and the
destination node ![]() is in relay group
is in relay group ![]() where
where
![]() . In
order to encrypt the payload the source generates a symmetric key
(
. In
order to encrypt the payload the source generates a symmetric key
(![]() ) for each relay group
) for each relay group ![]() , where
, where
![]() . The source
generates the payload:
. The source
generates the payload:
 |
where
![]() is the
real payload encrypted by the destination's public key and
is the
real payload encrypted by the destination's public key and
![]() indicates the content is encrypted using the key on
the subscript. The source generates a forwarding path by:
indicates the content is encrypted using the key on
the subscript. The source generates a forwarding path by:
 |
The source then anycasts the tuple
![]() to the first relay group
to the first relay group ![]() . In general, the
. In general, the
![]() -th relay group root receives messages
-th relay group root receives messages
![]() from the previous relay group. The
from the previous relay group. The ![]() -th relay
group root uses the groups public key to decrypt the outer layer of
-th relay
group root uses the groups public key to decrypt the outer layer of
![]() , revealing
, revealing
![]() , the identity of
the next relay group,
, the identity of
the next relay group, ![]() and the symmetric key
and the symmetric key ![]() . The
. The
![]() -th relay group root decrypts
-th relay group root decrypts
![]() using
using ![]() ,
generating
,
generating
![]() . Provided
. Provided
![]() is
not
is
not ![]() then the relay group root anycasts the tuple
then the relay group root anycasts the tuple
![]() to the next relay
group
to the next relay
group ![]() . During a single session, the source caches
. During a single session, the source caches
![]() and generates
and generates
![]() for each message.
for each message.
This process ensures that
![]() and
and
![]() if
if ![]() . In
particular, the source only encrypts the payload with the symmetric
keys for the relay groups
. In
particular, the source only encrypts the payload with the symmetric
keys for the relay groups
![]() . The path has embedded
within it the symmetric keys
. The path has embedded
within it the symmetric keys
![]() . At each of the relay
groups
. At each of the relay
groups
![]() the payload will be decrypted using
appropriate symmetric key, resulting in the forwarded payload being a
random number. This ensures that
the payload will be decrypted using
appropriate symmetric key, resulting in the forwarded payload being a
random number. This ensures that
![]() if
if ![]() .
.
 |
However, there is no guarantee that when the message reaches ![]() that the relay group root will be node
that the relay group root will be node ![]() , as any member of a relay
group can receive a message for its relay group. To ensure
, as any member of a relay
group can receive a message for its relay group. To ensure ![]() receives the message, we multicast the payload to the entire relay
group. If node
receives the message, we multicast the payload to the entire relay
group. If node ![]() receives the message (thus becoming the relay group
root for the message), then
receives the message (thus becoming the relay group
root for the message), then ![]() decrypts the relay group's layer from
the path in the message and decrypts the payload with the revealed
decrypts the relay group's layer from
the path in the message and decrypts the payload with the revealed
![]() .
. ![]() caches the map
caches the map
![]() to reduce the
computational load when further messages from the same session are
received.
to reduce the
computational load when further messages from the same session are
received. ![]() forwards the message to the next relay group and
broadcasts
forwards the message to the next relay group and
broadcasts
![]() to all members of the relay group (we
discuss the exact mechanism in Section 4). No
matter what position
to all members of the relay group (we
discuss the exact mechanism in Section 4). No
matter what position ![]() 's relay group is in the path,
's relay group is in the path, ![]() will
receive the message either directly or via a broadcast when the
message routes to a member of its relay group. Only
will
receive the message either directly or via a broadcast when the
message routes to a member of its relay group. Only ![]() will be able
decrypt the payload successfully. An example of this Cashmere routing
is shown in Figure 2.
will be able
decrypt the payload successfully. An example of this Cashmere routing
is shown in Figure 2.
The use of a broadcast has two implications addressed below; (i) that each node in a relay group has to perform an asymmetric decryption for each packet in a session; and (ii) malicious nodes can either drop messages or not broadcast them to the relay group. While such actions do not compromise anonymity they do negatively impact performance. We rely on end-to-end acknowledgments to detect failures and malicious nodes: if the source receives no acknowledgments, it can use timeouts to guide retransmission.
We eliminate the need to perform asymmetric encrypt/decrypt operations
on the data payload by encrypting it using a symmetric key
![]() chosen when a source creates a path. In addition
to the next relay group prefix,
chosen when a source creates a path. In addition
to the next relay group prefix, ![]() , and a group session key,
, and a group session key,
![]() , we embed another value
, we embed another value ![]() into the layered encrypted
path. If destination
into the layered encrypted
path. If destination ![]() is in relay group
is in relay group ![]() , then
, then
Now relay group roots broadcast
![]() to all members in the relay group.
to all members in the relay group. ![]() decrypts
decrypts ![]() and identifies
and identifies
![]() , thereby knowing that it is the destination. Using
, thereby knowing that it is the destination. Using
![]()
![]() can decrypt
can decrypt ![]() . All other members of this
relay group cache
. All other members of this
relay group cache ![]() . For future packets in the same session, they
remember they are not the destination node and without further
decryption operations.
. For future packets in the same session, they
remember they are not the destination node and without further
decryption operations. ![]() caches
caches
![]() and
associates it with
and
associates it with ![]() and therefore only needs to perform symmetric
decryption for subsequent session payloads.
and therefore only needs to perform symmetric
decryption for subsequent session payloads.
This also has the advantage that relay group roots can cache
![]() if they have
already forwarded messages for the same session. Relay group roots can
identify messages using
if they have
already forwarded messages for the same session. Relay group roots can
identify messages using
![]() as the session ID, hence no
asymmetric decryption is necessary.
as the session ID, hence no
asymmetric decryption is necessary.
A destination can reply to a source without sacrificing source anonymity or requiring state to be stored in the relay groups in the forwarding path. The destination can reply to the source either a pre-formatted reply message (e.g. an acknowledgment) or a message containing an arbitrary payload. The reply message shares all of the performance and security benefits with the anonymous messages from source to destination.
Node ![]() wishes to send an anonymous message to
wishes to send an anonymous message to ![]() and receive a
reply.
and receive a
reply. ![]() creates a forwarding path to
creates a forwarding path to ![]() as described, but also
generates a return forwarding path from
as described, but also
generates a return forwarding path from ![]() to
to ![]() .
. ![]() does this by
randomly selecting
does this by
randomly selecting ![]() relay groups (
relay groups (
![]() ). The set of
relay groups used in the return forwarding path may or may not
intersect with the set of relay groups used in the forwarding path
from
). The set of
relay groups used in the return forwarding path may or may not
intersect with the set of relay groups used in the forwarding path
from ![]() to
to ![]() .
. ![]() ensures that a relay group containing itself,
ensures that a relay group containing itself,
![]() , is included in the return path.
, is included in the return path. ![]() sends
sends
![]() as part of the payload to
as part of the payload to ![]() , where:
, where:
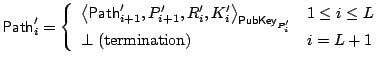 |
 |
where ![]() and
and ![]() are selected uniformly at random,
are selected uniformly at random,
![]() . If
. If ![]() wants to send a payload
wants to send a payload ![]() to
to ![]() , it sends
, it sends
![]() as
as
![]() to
to ![]() . While
. While
![]() is created by
is created by ![]() , it knows nothing about the path and the source. The
root of each relay group
, it knows nothing about the path and the source. The
root of each relay group ![]() decrypts
decrypts
![]() the same
as in the forwarding path, while it encrypts
the same
as in the forwarding path, while it encrypts
![]() with
with ![]() to get
to get
![]() Node
Node ![]() who is located in
relay group
who is located in
relay group ![]() will receive message
will receive message
![]() , where
, where
![]() is
the layered encryption of
is
the layered encryption of
![]() by
by
![]() . After
. After ![]() decrypts
decrypts ![]() using
using
![]() ,
, ![]() can use
can use
![]() to identify
which session the reply belongs to, and thus the keys
to identify
which session the reply belongs to, and thus the keys ![]() (
(![]() ) to decrypt
) to decrypt
![]() . All caching schemes used
in the forwarding path also apply to the return path.
. All caching schemes used
in the forwarding path also apply to the return path.
The final issue is how a source selects groupIDs for relay groups. Observation 1 shows the relation between the length of groupIDs and relay group sizes.
OBSERVATION 1: (Distribution of Relay Group Sizes) Let ![]() be the number of nodes in the overlay and nodeIDs are
assigned to all nodes uniformly at random. The size of relay groups
defined by a
be the number of nodes in the overlay and nodeIDs are
assigned to all nodes uniformly at random. The size of relay groups
defined by a ![]() -digit groupID is Poisson distributed with parameter
-digit groupID is Poisson distributed with parameter
![]() . The expected size of the relay group is
. The expected size of the relay group is
![]() . [Proof omitted]
. [Proof omitted]
A valid groupID requires that there exists at least one node that has
the groupID as a prefix. As ![]() is much smaller than the size of the
nodeID identifier space, there will be many invalid groupIDs. From
Observation 1, the probability that a groupID is valid is
is much smaller than the size of the
nodeID identifier space, there will be many invalid groupIDs. From
Observation 1, the probability that a groupID is valid is
![]() . When a node forms a path by selecting groupIDs
uniformly at random, the chance that the path contains only valid
groupIDs is
. When a node forms a path by selecting groupIDs
uniformly at random, the chance that the path contains only valid
groupIDs is
![]() , where
, where ![]() is the number of
relay groups used in the path. The expected number of tries to
generate a valid path, one that is composed on only valid groupIDs, is
is the number of
relay groups used in the path. The expected number of tries to
generate a valid path, one that is composed on only valid groupIDs, is
![]() . Table 1 shows the average
number of tries to generate a valid path is slightly larger than
. Table 1 shows the average
number of tries to generate a valid path is slightly larger than ![]() under typical
under typical ![]() and
and ![]() values.
values.
In Cashmere, nodes independently (without external communication)
select per-session values of ![]() (which determines
(which determines ![]() ) and
) and ![]() to
control tradeoffs between churn resilience, anonymity and overhead. We
discuss this in Section 5.1. In general, choosing a
value of between 3 and 5 for
to
control tradeoffs between churn resilience, anonymity and overhead. We
discuss this in Section 5.1. In general, choosing a
value of between 3 and 5 for ![]() , and a value of
, and a value of ![]() between
between ![]() and
and ![]() provides a good combination of efficiency and resiliency.
Because nodeIDs are uniformly distributed, nodes can locally estimate
provides a good combination of efficiency and resiliency.
Because nodeIDs are uniformly distributed, nodes can locally estimate
![]() using their routing tables. From Observation 1, a node can always
get the average relay group size (
using their routing tables. From Observation 1, a node can always
get the average relay group size (![]() ) it wants by selecting a
proper prefix length
) it wants by selecting a
proper prefix length ![]() . The design of Cashmere removes the high
cost of maintaining complete or near-complete overlay membership
information.
. The design of Cashmere removes the high
cost of maintaining complete or near-complete overlay membership
information.
|
We implemented Cashmere on top of FreePastry [12], a Java implementation of Pastry [26]. The implementation uses RSA (with 512-bit key length) and Blowfish (with 128-bit key length) as the asymmetric key and symmetric key ciphers, and uses the Cryptix [5] crypto library.
Applications use a simple Cashmere API. The source creates an AnonymousChannel object specifying a destination nodeID, and uses it to forward payloads. An application instance running on the destination node receives an up-call with the payload.
The Cashmere implementation ensures that relay
group roots cache
![]() information and all nodes
cache
information and all nodes
cache ![]() as described in the previous section.
as described in the previous section.
Our implementation performs relay group broadcast of
![]() using the leaf sets that
are maintained by each node [26]. The leaf set is a set of pointers
to the immediate
using the leaf sets that
are maintained by each node [26]. The leaf set is a set of pointers
to the immediate ![]() neighbors in the identifier space, where typical
neighbors in the identifier space, where typical
![]() . If the leaf set does not contain all members of the relay group,
nodes on the edge of the leaf set forward the message to their leaf set
members. This recursive process continues until all members of
the relay group have received the message.
. If the leaf set does not contain all members of the relay group,
nodes on the edge of the leaf set forward the message to their leaf set
members. This recursive process continues until all members of
the relay group have received the message.
One practical issue in the encoding of the path is that it is desirable for it to have the same length all along the forwarding path. This way no information about the route can be obtained by simply observing the size changes of the path onion. Previous work discussed these length-preserving Chaum-Mixes. A simple scheme is implemented in Mixmaster [18], and [17] presents a more sophisticated, provably secure scheme. Our prototype currently uses the basic layered encryption, and thus the path size decreases after each relay group. Changing the encoding scheme to preserve message length is straightforward and orthogonal to the design and performance of the overall system.
We analyze two types of anonymity provided by Cashmere: source anonymity and unlinkability of source and destination. We quantify Cashmere's anonymity parameterized by:
The parameter ![]() has two implications: (i) the probability that
compromised nodes are on the relay path; and (ii) the fraction
of relay group private keys known by the attacker. For each
compromised nodeID the attacker will know the relay group private keys
for all prefixes associated with the nodeID. The probability that the
attacker knows a
has two implications: (i) the probability that
compromised nodes are on the relay path; and (ii) the fraction
of relay group private keys known by the attacker. For each
compromised nodeID the attacker will know the relay group private keys
for all prefixes associated with the nodeID. The probability that the
attacker knows a ![]() -bit prefix private key is
-bit prefix private key is
![]() .
The attacker can obtain prefix private keys either by compromising
other nodes or through obtaining nodeIDs from the CA. We assume prefix
private keys are leaking slowly, and the offline CA can slowly issue
new prefix keys and revoke prior prefix keys over time. If the
attacker knows the private key for a relay group we refer to the relay
group as being compromised.
.
The attacker can obtain prefix private keys either by compromising
other nodes or through obtaining nodeIDs from the CA. We assume prefix
private keys are leaking slowly, and the offline CA can slowly issue
new prefix keys and revoke prior prefix keys over time. If the
attacker knows the private key for a relay group we refer to the relay
group as being compromised.
Our anonymity measurement follows the anonymity definition by
Pfitzmann et al. [20]: ``Anonymity is the state of being
not identifiable within a set of subjects, the anonymity set.''
In a network with a finite set ![]() (
(
![]() ) of nodes, ideal anonymity is achieved when all nodes look equally likely to be
the source or destination to an attacker, e.g. the anonymity set is
) of nodes, ideal anonymity is achieved when all nodes look equally likely to be
the source or destination to an attacker, e.g. the anonymity set is
![]() . In reality, based on information leaked from the system,
some nodes look more likely to be the source or destination than
others. That is, the attacker knows that the source (or destination)
is in
. In reality, based on information leaked from the system,
some nodes look more likely to be the source or destination than
others. That is, the attacker knows that the source (or destination)
is in ![]() with probability
with probability
![]() 2, where
2, where
![]() . For example, the
worst anonymity is the attacker identifies the source or
destination as
. For example, the
worst anonymity is the attacker identifies the source or
destination as ![]() ;
; ![]() is assigned with probability
is assigned with probability ![]() and
and
![]() with probability 0. We use the metric
proposed in [8,28] to measure the anonymity of our
design as a proportion of the ideal entropy achievable in a given
network. We briefly describe the entropy-based metric as follows:
with probability 0. We use the metric
proposed in [8,28] to measure the anonymity of our
design as a proportion of the ideal entropy achievable in a given
network. We briefly describe the entropy-based metric as follows:
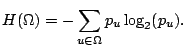
If we have ideal anonymity, all nodes look equal to attackers:
![]() ,
,
![]() . The entropy of ideal
anonymity is
. The entropy of ideal
anonymity is
![]() , which is the maximum
entropy achieved in a network of
, which is the maximum
entropy achieved in a network of ![]() nodes.
nodes.
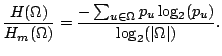
Definition 5.2 shows that the anonymity of a system is
measured by the real entropy of a system over the maximum (i.e. ideal
anonymity) entropy the system could achieve:
![]() .
.
The entropy definition above is more precise than the straightforward
probability definition of the probability that the attacker knows
the sender or receiver. For example, let us consider source
anonymity in network of ![]() nodes. In an anonymity system
nodes. In an anonymity system ![]() with
attacker
with
attacker ![]() :
:

The entropy definition is more precise, capturing that
![]() provides better anonymity. In
provides better anonymity. In ![]() the attacker knows more
information about the sources than in
the attacker knows more
information about the sources than in ![]() .
.
The anonymity of Cashmere is determined by ![]() and
and ![]() given the
fraction of compromised nodes. Anonymity increases with larger values
of
given the
fraction of compromised nodes. Anonymity increases with larger values
of ![]() . Intuitively, the destination is hidden among all relay group
members and
. Intuitively, the destination is hidden among all relay group
members and ![]() and
and ![]() determine the number of nodes in all relay
groups. However, as
determine the number of nodes in all relay
groups. However, as ![]() increases, which means a shorter prefix is
selected for groupID and the attacker has more chance to know
consecutive relay groups, the anonymity decreases. Larger
increases, which means a shorter prefix is
selected for groupID and the attacker has more chance to know
consecutive relay groups, the anonymity decreases. Larger ![]() also
means more resilience and a higher relay group broadcast overhead.
From analysis and experimentation, good typical values for
also
means more resilience and a higher relay group broadcast overhead.
From analysis and experimentation, good typical values for ![]() are
between
are
between ![]() to
to ![]() . In this section, we perform simulations with a
network of
. In this section, we perform simulations with a
network of ![]() nodes. GroupIDs have a prefix length of
nodes. GroupIDs have a prefix length of ![]() bits, such that the expected size of relay groups
bits, such that the expected size of relay groups ![]() nodes. We
compute unlinkability and source anonymity using the entropy
definition. We first assume that attackers only see their own
traffic, and simulate unlinkability and source anonymity given
different parameters of
nodes. We
compute unlinkability and source anonymity using the entropy
definition. We first assume that attackers only see their own
traffic, and simulate unlinkability and source anonymity given
different parameters of ![]() . We then analyze the security of
Cashmere against traffic analysis attacks.
. We then analyze the security of
Cashmere against traffic analysis attacks.
In our simulations, the attacker gathers information observed from
compromised nodes and maintains, for each pair of nodes ![]() , a
probability
, a
probability ![]() that the pair are a source and destination.
that the pair are a source and destination.
Using the entropy definition, we can measure unlinkability using the relative entropy to ideal unlinkability:
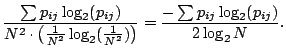
We assume the attacker determines the exact number of relay groups ![]() used for a message3. We
also assume the attacker knows a chain of
used for a message3. We
also assume the attacker knows a chain of ![]() consecutive relay groups
on the path of a message, each containing
consecutive relay groups
on the path of a message, each containing ![]() nodes. Assuming
there is enough cover traffic, the attacker cannot attribute discrete
chains in the path to the same session, because the path onion and the
observed payload are completely different at each relay group.
Therefore, the attacker's knowledge about a message only comes from
one consecutive chain on the relay path.
nodes. Assuming
there is enough cover traffic, the attacker cannot attribute discrete
chains in the path to the same session, because the path onion and the
observed payload are completely different at each relay group.
Therefore, the attacker's knowledge about a message only comes from
one consecutive chain on the relay path.
The source is indistinguishable from the relay group root of the
immediately preceding relay group. When the first relay group root on
the chain is non-malicious and known by the attacker, the attacker
infers that the source is the first root with probability
![]() and the source is among all other non-malicious
nodes with probability
and the source is among all other non-malicious
nodes with probability
![]() . That is, for each
non-malicious node
. That is, for each
non-malicious node ![]() , the attacker assigns probability of
, the attacker assigns probability of ![]() being
the source as:
being
the source as:
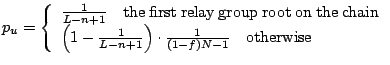
Let ![]() be the set of nodes that are in the chain of relay groups
known by the attacker,
be the set of nodes that are in the chain of relay groups
known by the attacker,
![]() . The set of
. The set of ![]() is
composed of both a set
is
composed of both a set ![]() of malicious nodes and a set
of malicious nodes and a set ![]() of
non-malicious nodes:
of
non-malicious nodes:
![]() ,
,
![]() and
and
![]() . The expected number of nodes in all relay groups is
. The expected number of nodes in all relay groups is
![]() . If the destination is among
. If the destination is among ![]() , the attacker knows the
destination and unlinkability becomes the source anonymity problem that we
discuss in Section 5.1.2. If the destination is among
, the attacker knows the
destination and unlinkability becomes the source anonymity problem that we
discuss in Section 5.1.2. If the destination is among
![]() , the attacker infers that each node in
, the attacker infers that each node in ![]() is the destination
with probability
is the destination
with probability
![]() and the destination is among
other nodes outside
and the destination is among
other nodes outside ![]() with probability
with probability
![]() . That is, for each node
. That is, for each node ![]() not in
not in
![]() , the attacker assigns the probability of
, the attacker assigns the probability of ![]() being the
destination as:
being the
destination as:

The number of relay groups compromised (i.e. ![]() ) is closely related
to the fraction
) is closely related
to the fraction ![]() of compromised nodes. If the compromised node was
not the relay group root then the attacker would only learn the value
of
of compromised nodes. If the compromised node was
not the relay group root then the attacker would only learn the value
of ![]() and the payload, which is broadcast to the relay group. When
the compromised node is the relay group root for a message the
attacker also discovers the identity of the next relay group. If the
compromised node is on the intermediate overlay hops between two relay
group the attacker knows the previous or/and the next relay group
root.
and the payload, which is broadcast to the relay group. When
the compromised node is the relay group root for a message the
attacker also discovers the identity of the next relay group. If the
compromised node is on the intermediate overlay hops between two relay
group the attacker knows the previous or/and the next relay group
root.
In Figure 4, we compare through simulation Cashmere's
unlinkability metric to that of Chaum-Mixes approaches under different
parameters of ![]() , ignoring eavesdropping and traffic analysis
(see Section 5.1.3). In the simulation, we setup a
relay path of length
, ignoring eavesdropping and traffic analysis
(see Section 5.1.3). In the simulation, we setup a
relay path of length ![]() , assign each node on the path and in the
relay groups as compromised consistent with parameter
, assign each node on the path and in the
relay groups as compromised consistent with parameter ![]() , count the
probability
of different cases that the attacker knows
, count the
probability
of different cases that the attacker knows ![]() consecutive groups, and
compute the entropy in all cases. Then the entropy of the system is
the average over all cases [8,28].
consecutive groups, and
compute the entropy in all cases. Then the entropy of the system is
the average over all cases [8,28].
The results show that Cashmere has similar anonymity to Chaum-Mixes.
Cashmere even behaves better than Chaum-Mixes for small ![]() and
and ![]() near
near ![]() , when the whole Chaum-Mixes path is controlled by attackers
with high probability while Cashmere still benefits from the anonymity
among relay group members. We also measured how the level of
unlinkability varies with network size and, as expected, unlinkability
is largely independent of network size. Increasing network size from
20K nodes to 2 million nodes results in less than 3% variation in
unlinkability. Reducing the network size to 64 provides similar
unlinkability under the same
, when the whole Chaum-Mixes path is controlled by attackers
with high probability while Cashmere still benefits from the anonymity
among relay group members. We also measured how the level of
unlinkability varies with network size and, as expected, unlinkability
is largely independent of network size. Increasing network size from
20K nodes to 2 million nodes results in less than 3% variation in
unlinkability. Reducing the network size to 64 provides similar
unlinkability under the same ![]() as large networks as long as
as large networks as long as ![]() and
and ![]() are set the same. Thus, bootstrapping Cashmere requires a
small initial network of trusted nodes and then other nodes can join
the network while maintaining the fraction of malicious nodes in the
network as
are set the same. Thus, bootstrapping Cashmere requires a
small initial network of trusted nodes and then other nodes can join
the network while maintaining the fraction of malicious nodes in the
network as ![]() .
.
In source anonymity, the destination colludes with other malicious
nodes to find the source's identity. If Cashmere is being used
for one-way communication (anonymous message) the attacker infers the
first relay group root on the chain (which includes the destination's
relay group) as the source with probability
![]() if the
first root is non-malicious, where
if the
first root is non-malicious, where ![]() is the length of the chain.
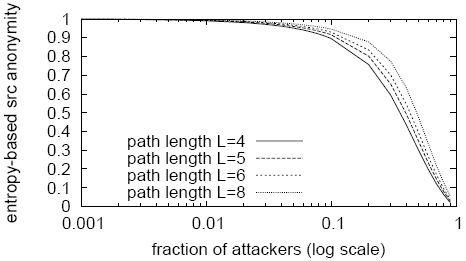
Figure 5 compares the source anonymity of Cashmere with
Chaum-Mixes, assuming no traffic analysis attacks, for one-way
communication. We see that like Chaum-Mixes, Cashmere has high source
anonymity when
is the length of the chain.
Figure 5 compares the source anonymity of Cashmere with
Chaum-Mixes, assuming no traffic analysis attacks, for one-way
communication. We see that like Chaum-Mixes, Cashmere has high source
anonymity when ![]() and increasing
and increasing ![]() improves anonymity.
improves anonymity.
If Cashmere is being used for two-way communication (anonymous
channel), the attacker has two ways to discover the source; (i)
discover the first relay group root on the chain of consecutive relay
groups which includes the destination's relay group (as for one-way),
or (ii) the attacker compromises consecutive relay groups used
on the return path from the destination to the source. Even if the
attacker compromises all ![]() of the return path relay groups, the
attacker only knows the source is a member of one of these relay
groups (the probability is the same as in
Section 5.1.1).
of the return path relay groups, the
attacker only knows the source is a member of one of these relay
groups (the probability is the same as in
Section 5.1.1).
Figure 6 shows the results for anonymous channels. The results show anonymous channels provide lower anonymity compared to anonymous messages due to the vulnerability of the return path. Finally, we also analyzed the impact of network size on source anonymity and, as before, increasing or decreasing the network size had negligible impact.

Our previous simulations disregarded the impact of traffic analysis.
In practice, however, attackers may monitor part or all of the network
traffic and use patterns to trace session paths. With each message,
the same decoupled path component is sent from a relay root. For
example, an attacker observes that a node ![]() receives
receives
![]() and sends out
and sends out
![]() to
to ![]() . Later it
observes
. Later it
observes ![]() receiving
receiving
![]() with a different payload, and
sending
with a different payload, and
sending
![]() with other another payload to
with other another payload to ![]() . The
attacker can then recognize all messages with path component
. The
attacker can then recognize all messages with path component
![]() as parts of a session involving
as parts of a session involving ![]() and
and
![]() . We simulate the robustness of Cashmere in unlinkability and
source anonymity against an attacker observing increasing amounts of
network traffic. There are two attacker models: (i) the attacker
analyzes a fixed fraction of all network traffic, e.g.
. We simulate the robustness of Cashmere in unlinkability and
source anonymity against an attacker observing increasing amounts of
network traffic. There are two attacker models: (i) the attacker
analyzes a fixed fraction of all network traffic, e.g. ![]() ,
, ![]() ,
,
![]() , etc.; or (ii) the attacker analyzes a fraction,
, etc.; or (ii) the attacker analyzes a fraction, ![]() ,
of traffic proportional to the fraction of malicious nodes (
,
of traffic proportional to the fraction of malicious nodes (![]() ) in
the network. For example,
) in
the network. For example, ![]() of malicious nodes can analyze
of malicious nodes can analyze
![]() of all traffic. The second is a more realistic model.
of all traffic. The second is a more realistic model.
We simulate unlinkability and source anonymity for anonymous channels
(since it is weaker than anonymous messages), and plot the results in
Figures 7 and 8, using parameters
![]() . We see that Cashmere is vulnerable to traffic analysis if the
attacker observes a significant portion (
. We see that Cashmere is vulnerable to traffic analysis if the
attacker observes a significant portion (![]() ) of all network
traffic. But Cashmere can still provide high levels of anonymity in
the more realistic proportional traffic analysis model.
) of all network
traffic. But Cashmere can still provide high levels of anonymity in
the more realistic proportional traffic analysis model.
Cashmere can completely disable traffic analysis attacks with a small
modification. Each node in the underlying structured overlay can
exchange symmetric keys with peers in its routing table. This sets up
secure channels between all node pairs and encrypts all messages using
a symmetric cipher. Thus source anonymity and unlinkability are
protected against the strongest attacker who can monitor all network
traffic. The key-exchange cost is done once per lifetime of a node, in
contrast to previous approaches that require per-session key
exchanges [11]. Additionally, the small (![]() ) number
of neighbors for each node limits number of key exchanges, whereas
approaches like Onion Routing require
) number
of neighbors for each node limits number of key exchanges, whereas
approaches like Onion Routing require ![]() keys. Finally, the
secure channel is established lazily when the first message is routed
through that link.
keys. Finally, the
secure channel is established lazily when the first message is routed
through that link.
Previous anonymous systems use single nodes as relays. Nodes joining and failing in the system can lead to forwarding paths failing. Here we examine the resilience of Cashmere to node churn and intermittent link failures.
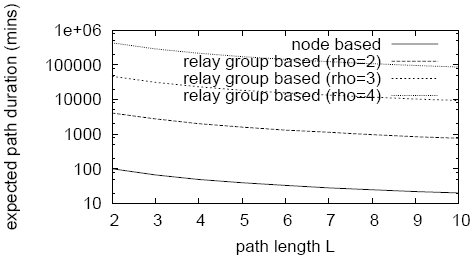
We refer to the time between a forwarding relay path is formed and its failure as the relay path duration. When a path fails, the sender needs to detect the failure via end-to-end timeouts and establish a new path. If relay path durations are too short, path construction time will dominate. Nodes will constantly be rebuilding failed paths and unable to deliver a message to a destination. Frequent path reconstruction also makes the layer more vulnerable to the degradation attack [32] discussed in Section 2.
In contrast, in Cashmere a relay is usable as long as at least one single node in the network has the relay group's groupID as a prefix. Changes in the membership of the relay group due to node joining and failing are transparent. We first compare the path duration and resilience of Cashmere to previous works.
Measurements on real systems have shown that peer-to-peer networks exhibit high node churn [27,13]. Since most anonymous routing layers are implemented on overlay networks, they must be resilient to high node churn in order to be useful.
Previous studies [25,13,27] use session
time as a metric of churn-rate.
We approximate this using an exponential distribution with parameter
![]() . This churn model is consistent with those used in previous studies of
the effect of churn in peer-to-peer systems [15,25].
Our network model is as follows:
. This churn model is consistent with those used in previous studies of
the effect of churn in peer-to-peer systems [15,25].
Our network model is as follows:
Figure 9 shows the expected path durations for forwarding paths using relay groups compared to using single nodes as relays. As expected, the use of relay groups increases the expected path duration exponentially, making Cashmere much more resilient to node churn.
We now simulate Cashmere's tolerance to short-term intermittent
failures. We model the mean time between failure (MTBF) as
![]() and mean time to repair (MTTR) as
and mean time to repair (MTTR) as
![]() . We assume the failure is a Poisson process with
failure event rate
. We assume the failure is a Poisson process with
failure event rate ![]() and time to repair is exponential
distributed with parameter
and time to repair is exponential
distributed with parameter ![]() . We assume MTBF
. We assume MTBF
![]() min, and MTTR
min, and MTTR
![]() min.
min.
Figure 10 shows that Cashmere completely masks all
intermittent network failures: the expected path duration is more than
![]() minutes (about
minutes (about ![]() days) when we set
days) when we set ![]() . This is an
improvement of several orders of magnitude over previous node-based
approaches.
. This is an
improvement of several orders of magnitude over previous node-based
approaches.

We examine how Cashmere's good path duration properties translate into stability for a real application. We simulate the fetching of objects in a file-sharing application, and examine the number of path repairs required during the object fetches. We model node churn and intermittent failures using parameters from the previous two sections. The distribution of object download times is long-tailed and generated using measurements from the Kazaa network. The Kazaa data [13] has distributions of download times for small objects (10MB) and large objects (100MB).
We simulate ![]() object download sessions on top of both
node-based relays and Cashmere's group-based relays. Both systems use
relay paths of length
object download sessions on top of both
node-based relays and Cashmere's group-based relays. Both systems use
relay paths of length ![]() , and Cashmere uses average relay group
size
, and Cashmere uses average relay group
size ![]() . Using object download times from the Kazaa
data, Figure 11 shows the distribution of expected
frequencies that each download needs to construct the relay path. It
shows that 81% of these small object download sessions
using Cashmere would not require any path rebuilds (i.e. number of
path builds is 1) and no sessions require more than about 500
rebuilds. This compares to 28% using node-based relays, and 10% of
all sessions requiring between 100 and 25000 path rebuilds.
The maximum number of path builds is very large (i.e. 500 and
25000) because Kazaa object download times are long-tail distributed
where some objects take extremely long time to download.
. Using object download times from the Kazaa
data, Figure 11 shows the distribution of expected
frequencies that each download needs to construct the relay path. It
shows that 81% of these small object download sessions
using Cashmere would not require any path rebuilds (i.e. number of
path builds is 1) and no sessions require more than about 500
rebuilds. This compares to 28% using node-based relays, and 10% of
all sessions requiring between 100 and 25000 path rebuilds.
The maximum number of path builds is very large (i.e. 500 and
25000) because Kazaa object download times are long-tail distributed
where some objects take extremely long time to download.
The average number of path builds under different parameters
![]() for small object downloads are shown in
Figure 12. Clearly, increasing relay group size
increases path duration significantly, and Cashmere provides more than
an order of magnitude improvement over node-based
approaches. Measurements for large file downloads are nearly identical
and omitted for brevity.
for small object downloads are shown in
Figure 12. Clearly, increasing relay group size
increases path duration significantly, and Cashmere provides more than
an order of magnitude improvement over node-based
approaches. Measurements for large file downloads are nearly identical
and omitted for brevity.
In this section we analyze the relative costs in operating Cashmere compared to previous node-based relay approaches. We observe that the operating costs of node-based relay path systems include:
We first examine communication costs in network maintenance and relay
discovery. In node-based relay approaches, nodes are expected to
actively maintain information about the other nodes in the network,
with a total cost of ![]() . In contrast, Cashmere decouples
maintenance and relay discovery, and relay discovery requires no
communication. Nodes estimate the number of nodes in the network by
examining their local routing tables, and choose an appropriate prefix
length to establish relay groups of average size
. In contrast, Cashmere decouples
maintenance and relay discovery, and relay discovery requires no
communication. Nodes estimate the number of nodes in the network by
examining their local routing tables, and choose an appropriate prefix
length to establish relay groups of average size ![]() . Nodes then
choose random prefixes of the desired length as relay
groupIDs. Cashmere relies on the underlying structured overlay,
and hence has a total cost of
. Nodes then
choose random prefixes of the desired length as relay
groupIDs. Cashmere relies on the underlying structured overlay,
and hence has a total cost of
![]() .
.
However, Cashmere incurs a higher bandwidth cost to gain
resilience. Total number of messages sent is ![]() while
node-based approaches requires
while
node-based approaches requires ![]() . The extra messages are
required to perform the per-relay group broadcast of the payload, and
do not adversely impact end-to-end latency or throughput
at the overlay layer. This broadcast traffic does
contribute to a node's cover traffic that it has to generate.
. The extra messages are
required to perform the per-relay group broadcast of the payload, and
do not adversely impact end-to-end latency or throughput
at the overlay layer. This broadcast traffic does
contribute to a node's cover traffic that it has to generate.
We now examine computational cost. High per-message computation is
often seen as a key obstacle to the wide-spread deployment of
Chaum-Mixes based systems. Given a path of length ![]() , a Chaum-Mixes
source node performs
, a Chaum-Mixes
source node performs ![]() asymmetric encryption operations on every
message. In addition, each node on the path performs one asymmetric
decryption per message that it forwards. The high cost of asymmetric
cryptographic operations limits the message send rate at the source
and the message forwarding rate at intermediate nodes.
asymmetric encryption operations on every
message. In addition, each node on the path performs one asymmetric
decryption per message that it forwards. The high cost of asymmetric
cryptographic operations limits the message send rate at the source
and the message forwarding rate at intermediate nodes.
Optimizations have been proposed to reduce computation for session-based communication on Chaum-Mixes by using symmetric key encryption for payload messages and amortizing asymmetric crypto operations across an entire session. Both Tarzan [11] and our solution fall into this category.
Assume the cost of asymmetric encryption and decryption are
![]() and
and ![]() respectively. For each relay group path, Cashmere
incurs computational cost that includes encryption cost of
respectively. For each relay group path, Cashmere
incurs computational cost that includes encryption cost of
![]() at the source, decryption cost of
at the source, decryption cost of ![]() at relay group root,
decryption cost of
at relay group root,
decryption cost of ![]() at each relay group member, and additional
operations to refresh caches after relay group root failures.
However, these cost are amortized over a much longer path duration
than node-based systems and dwarfed by the cost of rebuilding paths in
node-based systems.
at each relay group member, and additional
operations to refresh caches after relay group root failures.
However, these cost are amortized over a much longer path duration
than node-based systems and dwarfed by the cost of rebuilding paths in
node-based systems.
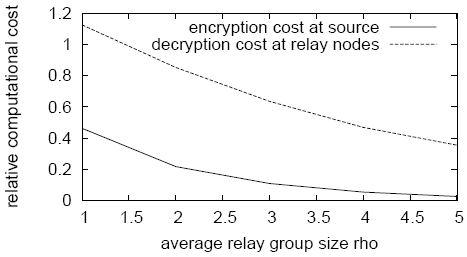 |
Based on previous results of expected durations, Figure 13
plots the cost of our ``relay group''-based approach relative to that
of node-based session solutions on a realistic network. As ![]() increases, the path duration increases and the per-session cost
drops. For
increases, the path duration increases and the per-session cost
drops. For ![]() , the encryption cost at the source in Cashmere is
roughly
, the encryption cost at the source in Cashmere is
roughly ![]() of the cost at source nodes in node-based
solutions. The aggregate decryption cost at relay group members in
Cashmere is
of the cost at source nodes in node-based
solutions. The aggregate decryption cost at relay group members in
Cashmere is ![]() of the cost at intermediate nodes in node-based
solutions. The reduction in encryption computation is from amortizing
the one time path setup costs across the long path durations of
Cashmere. The reduction in decryption costs is from per-node caching
of the path component and whether a node is the destination, and reducing
the number of asymmetric crypto operations to just one per session for
nodes who are not the destination.
of the cost at intermediate nodes in node-based
solutions. The reduction in encryption computation is from amortizing
the one time path setup costs across the long path durations of
Cashmere. The reduction in decryption costs is from per-node caching
of the path component and whether a node is the destination, and reducing
the number of asymmetric crypto operations to just one per session for
nodes who are not the destination.
We ran experiments to determine the latency, throughput and computational overheads of Cashmere.
We deployed and evenly distributed ![]() Cashmere nodes on
Cashmere nodes on ![]() machines
from PlanetLab that are geographically distributed all over the United
States. We define groupIDs to be
machines
from PlanetLab that are geographically distributed all over the United
States. We define groupIDs to be ![]() -bit prefixes, so relay groups
have average size of
-bit prefixes, so relay groups
have average size of ![]() nodes. We measure latency in:
nodes. We measure latency in:
We show the average latency in Cashmere, Fake Cashmere, Pastry
vs. direct IP latency in Figure 14. The ``stretch'' is
computed as each sample of Cashmere/Fake Cashmere/Pastry latency
divided by average IP latency for the same destination. To plot the
graph, we put all stretch samples into bins of ![]() ms intervals of
average IP latency. Figure 14 shows that the stretches
decrease while the IP latency between source and destination
increases. For a pair of end nodes that are very close to each other
(i.e.
ms intervals of
average IP latency. Figure 14 shows that the stretches
decrease while the IP latency between source and destination
increases. For a pair of end nodes that are very close to each other
(i.e. ![]() ms), Cashmere stretches are about two times of Pastry. The extra
delays introduced by the Cashmere layer is
significant compared to small IP latency values. Most samples of IP
latency are from
ms), Cashmere stretches are about two times of Pastry. The extra
delays introduced by the Cashmere layer is
significant compared to small IP latency values. Most samples of IP
latency are from ![]() ms to
ms to ![]() ms. In this range, Cashmere stretches
are between
ms. In this range, Cashmere stretches
are between ![]() to
to ![]() , which is quite close to Pastry
(
, which is quite close to Pastry
(![]() to
to ![]() ). This means Cashmere layer introduces a relatively small
delay on the overlay. Comparing stretches between Cashmere
and fake Cashmere shows that delay caused by cryptographic computation
in Cashmere is negligible. This is attributed to no per message
asymmetric encryption/decryption in Cashmere. We also measured that
the average number of IP messages per Cashmere message is
). This means Cashmere layer introduces a relatively small
delay on the overlay. Comparing stretches between Cashmere
and fake Cashmere shows that delay caused by cryptographic computation
in Cashmere is negligible. This is attributed to no per message
asymmetric encryption/decryption in Cashmere. We also measured that
the average number of IP messages per Cashmere message is ![]() and
the average number of IP messages per Pastry message is
and
the average number of IP messages per Pastry message is ![]() . The
larger number of IP message comes from the relay and broadcast
messages in Cashmere.
. The
larger number of IP message comes from the relay and broadcast
messages in Cashmere.
To measure computation cost, we utilize FreePastry's network emulation capabilities. We created 64 virtual FreePastry nodes inside the same Java virtual machine on a 2.4Ghz Pentium IV PC. The virtual nodes are connected together using local loopback (called ``direct'' network in FreePastry) network transport. There is no CPU contention between the nodes because the emulation is event-driven and at most one virtual node is running at a time. Cashmere is set up similarly as above. We obtain highly accurate time measurements by calling the RDTSC instruction supported by the Pentium architecture via Java Native Interface (JNI).
In the first experiment, we approximate throughput of relay group
roots by measuring per-message latency across 1000 random
source-destination pairs. For each source and destination pair, we
send a single message to set up the path and allow relay group roots
to set up their caches, then measure the latency taken to process a
second payload message. We then approximate the throughput as
![]() . Table 2 shows the results for
forwarding throughput of relay group roots for different message
sizes.
. Table 2 shows the results for
forwarding throughput of relay group roots for different message
sizes.
In the second experiment we measure the computational overheads for the source, the relay group root nodes, the non-root relay group nodes and the destination, for both the first and subsequent messages. 1000 empty messages are sent from random source to destination with and without the routes already set up. Table 3 summarizes the results, showing the average CPU time incurred per node role with the standard deviation in brackets. The first message invokes RSA on each hop and therefore is relatively expensive. The subsequent messages to the same destination, using the same forwarding path, utilize cached routing information on each node. Therefore they only invoke Blowfish which is less expensive.
|
We also evaluated the space overhead during the experiment. At the source nodes the overhead for each message is 456 bytes for the path element and any necessary padding bytes to round the payload to RSA block sizes (64 bytes).
We present Cashmere, a resilient anonymous routing infrastructure that leverages the flexible anycast routing inherent in structured overlay networks to significantly improve path durations compared to node-based relay approaches. Cashmere also decouples the encrypted path component of each session from the payload, and uses symmetric session keys to encrypt message payloads. Anonymous source nodes in Cashmere can choose their own per-session parameters to tradeoff between anonymity, resilience and computation overhead.
We compare Cashmere to previous node-based Chaum-Mixes approaches through analysis and simulation. We find that Cashmere provides similar anonymity properties while providing one to two orders of magnitude improvement in path durations under both node churn and intermittent failures. This translates into significantly lower path reconstructions across an anonymous application session. Performance optimizations in Cashmere avoid asymmetric crypto operations, resulting in lower per-session computation costs compared to other session-based Chaum-Mixes approaches. Finally, we provide measurements of a real Cashmere deployment and show that it provides reasonable throughput while incurring a small latency overhead over structure overlay routing.
Ongoing work on Cashmere includes issues related to key management and key revocation in particular. We are also interested in better understanding the impact of network dynamics on key discovery. A straight-forward yet very useful extension to Cashmere is to support anonymous object location in DOLR [6,34] overlays like Pastry and Tapestry. Finally, we are working on a stable wide-area deployment on PlanetLab and a software package for public release.
We would like to thank the anonymous reviewers for their comments and Vern Paxson our shepherd. We also thank Stefan Saroiu and Krishna Gummadi for providing us with data on filesharing session statistics.
1Cashmere only requires each node generates a small amount of traffic. When the real traffic is not sufficient, nodes send out dummy messages as cover traffic.
2Nodes in
![]() are equal, each with probability
are equal, each with probability
![]() to be the source (or
destination).
to be the source (or
destination).
3This is a worst case assumption. In reality the attacker can only estimate this by monitoring certain network latencies and system overheads. For example, the more relay groups are used, the more computation a source will perform.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons cashmere.tex
The translation was initiated by on 2005-03-27
2005-03-27|
This paper was originally published in the
Proceedings of the 2nd Symposium on Networked Systems Design and Implementation,
May 2–4, 2005, Boston, MA, USA Last changed: 2 May 2005 aw |
|