Achieving target loss rate $q$

We will describe a hybrid solution which uses a combination of FEC and ARQ to construct a CLVL. Recall that a CLVL abstraction aims to bound the bundle loss rate to a small value $q$. Since burstiness of cross-traffic is usually unpredictable, we define $q$ as a statistical bound on the average loss rate observed over some larger period of time (on the order of seconds).

FEC vs ARQ trade-off: The main distinction between FEC and ARQ is in the trade-off between bandwidth overhead and packet recovery time. While FEC can help in quickly recovering from packet losses, the bandwidth overhead can be high especially over virtual links experiencing bursty losses [22]. On the other hand, an ARQ based solution will have a high packet recovery time if the $RTT$ between two overlay nodes is large. To strike a balance between these two approaches, we present a hybrid approach that uses the best features of both these mechanisms.

We will first briefly describe how one will construct a CLVL using purely ARQ or FEC and combine these approaches to obtain a hybrid CLVL construction.

ARQ-based CLVL: A purely ARQ-based solution for building CLVLs is easy to construct. In a reliable transmission ($q=0$), a packet is repeatedly retransmitted until the sender receives an acknowledgment from the receiver. Similarly, to achieve a non-zero target loss rate, $q$, it is enough to retransmit any lost packet $L=~\log_{\bar p} q -1$ times, where $\bar p$ represents the average loss rate over the interval over which we want to bound $q$. However, if $L>1$, a pure-ARQ based CLVL is unattractive since it uses multiple RTTs to achieve the bound $q$.

FEC-based CLVL: In an FEC-based approach, we divide time into windows of period, $T_r$, where a window is a unit of encoding/decoding. We consider an erasure code such as Reed-Solomon, characterized by $(n, k)$, where $k$ is the number of packets arriving at the entry node during the window, and $(n-k)$ represents the number of redundant packets added. Let $r$ denote the redundancy factor, where $r=(n-k)/n$. The FEC problem reduces then to determining a minimum redundancy factor, $r$, such that the target loss rate $q$ is achieved. Since the hybrid approach (i.e., FEC+ARQ based CLVLs) presented below outperforms the FEC based CLVLs in most of the cases, we skip the description of our algorithm for computing the ideal value of $r$.

FEC+ARQ based CLVL: Due to delay constraints for loss recovery, we restrict the number of retransmissions to at most one. We divide packets into windows and add an FEC redundancy factor of $r_1$ for each window in the first round. In the second round, if a window is non-recoverable, the entry node retransmits the lost packets with a redundancy factor $r_2$.

We need to estimate the parameters, $r_1$ and $r_2$. Let $f(p)$ denote the PDF of the loss rate $p$, where each value of $p$ is measured over an encoding/decoding window. FEC offers loss protection within a window if the fraction of packets lost in a window, $p$, is less than the amount of redundancy added for that window. Given a redundancy factor, $r$, the expected packet loss rate after recovering from FEC is given by:

$$G(r) = \int_{r}^{1} p f(p) dp$$

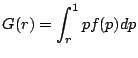
Hence the expected packet loss rate after the two rounds in the hybrid approach is equal to $L(r_1,r_2)= G(r_1) \times G(r_2)$. Given a target loss-rate, $q$, we require:

$$L(r_1,r_2) \leq q$$

For a given window, $r_1$ is the FEC overhead in the first round, $G(r_1)$ is the expected number of retransmitted packets and $G(r_1) \times r_2$, the expected overhead in the second round. The expected bandwidth overhead is given by

$$O(r_1,r_2)= r_1 + G(r_1) (1+ r_2)$$

This yields the following optimization problem: Given a target loss rate $q$, determine the redundancy factors $r_1$ and $r_2$ that minimizes the expected overhead, $O(r_1,r_2)$ subject to the target loss constraint: $L(r_1,r_2) \leq q$.

For many loss distributions that occur in practice, the optimal solution for this problem is when $r_1=0$. This solution implies that it is better not to use FEC in the first round, and use FEC only to protect retransmitted packets. When $r_1=0$ and $r_2=0$, an FEC+ARQ CLVL reduces to a pure ARQ based CLVL. This happens when $q <p_{avg}^2$ where $p_{avg}=G(0)$ is the average loss-rate along the virtual link. An FEC+ARQ CLVL can be made adaptive to sudden variations in the loss characteristics by always applying a minimal amount of FEC ($r_2 >0$), to the retransmitted packets in a window.

We made a simplistic assumption in the above calculation. We used the same distribution $f(p)$ to model the fraction of losses during both the first and second round. Since the number of packets in a retransmitted window may be much smaller than the original window, the same distribution $f(p)$ may not apply. To overcome this problem, we estimate a table of loss distributions (rather than one $f(p)$) across different time-scales and apply the appropriate distribution based on the number of retransmitted packets.