|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
LISA 2001 Paper
[LISA '01 Tech Program Index]
Scheduling Partially Ordered Events In A Randomized Framework - Empirical Results And Implications For Automatic Configuration ManagementAbstractAutomatic configuration management involves maintaining a set of shared and distributed resources in such a way that they serve a community of users fairly, promptly and reliably. In this context, this paper discusses experiments that measure the effect of adding randomized scheduling of partially ordered events to configuration management tools. Three characteristics of randomized scheduling are investigated: efficiency, robustness and security. A configuration management process is efficient if it minimizes the use of resources. It is robust if it is not vulnerable to malicious acts or inadvertent human errors. It is secure if its management model is hidden from observers. Several experiments suggest that randomized scheduling of partially ordered events has advantages over commonly used deterministic strategies, on average producing more efficient schedules. Further, randomized scheduling greatly degrades the accuracy of observer predictions of future behavior. In addition, randomized scheduling obscures the management model such that an observer will have to make a large number of observations in order to obtain the complete management model. The results of the study support the use of randomization in automatic configuration management tools. IntroductionSeveral protocols have been designed with distributed system administration in mind. For instance the Simple Network Management Protocol (SNMP) [14, 24], as well as higher level, abstract languages for policy based management [2, 4, 9, 11]. These languages allow the administrator to define what actions to be taken in certain situations. There are also a several tools providing automatic and distributed configuration management such as cfengine [4] or IBM's Tivoli [3, 10, 18, 20]. Typical actions include the creation, copying, modification and deletion of files, setting ownership and permissions and process control. These tools in some sense understand the concepts of events and responses. An event can for example be a particular time of day or the absence or presence of some entity such as a file or a process. Usually, an event triggers a set of responses from the configuration management tool. Such responses are themselves events and are usually related by a partial ordering that can be represented by a directed acyclic graph. These responses must be performed in a sequence satisfying the partial ordering, via a process called scheduling. Current tools such as cfengine version 1 employ very simple scheduling algorithms where events are scheduled in a deterministic fixed order. However, it has recently been suggested that the use of randomization can greatly improve the efficiency and security of a configuration management system [7]. This work supports some of the claims in [7] through a set of three experiments. The first set of experiments measure the effect of randomized scheduling strategy upon the efficiency of the configuration management process. It is an established fact in the parallel computing literature that scheduling of tasks greatly affects the resource utilization in a distributed system. However, to the best of our knowledge, this has not previously been studied from a completely randomized viewpoint. Most work on scheduling focusses upon specialized scheduling algorithms designed to find optimal schedules, exhibiting maximum efficiency. These algorithms solve single objective optimization problems. However, our problem of configuration management can be viewed as a multi-objective optimization problem, where the objective is to achieve good efficiency, but also sufficient security, fairness and availability of service. The second set of experiments measure the extent to which randomization can contribute to the security of the configuration process. As discussed in [7], the configuration management process can be viewed as a competition between forces: destructive forces that attempt to disorder the system, and constructive forces that try to re-order the system. In such systems, the destructive forces may want to predict the next move triggered by the constructive force in order to sabotage the system. It is trivial for an observer to predict the order of configuration steps if the observer knows the configuration management model a priori. By replacing a deterministic model with one based on randomness it becomes more difficult for an observer to make accurate predictions. A second set of experiments were set up to quantify, in terms of probabilities, how difficult it is for an observer to predict the configuration management actions under a randomized regime. Obscurity is studied as part of a dynamic and reactive security policy for maintaining resource availability in the presence of resource abuse. The third set of experiments was designed to quantify the extent to which an observer may monitor configuration management actions and use these observations to reconstruct the management model. The impact of randomization on hiding the model from the observer is studied. In real life, an observer usually does not know the management model beforehand. But the observer may learn the management model by continuously observing the system over time and identifying trends. A deterministic fixed-order model is trivial to capture - but what about a random model? The algorithm used in this experiment falls into the same category as algorithms described in a totally independent study by Couch and Daniels [8] where the precedence hierarchy of troubleshooting procedures are uncovered over time through a series of observations. The three experiments are presented sequentially in self-contained sections with background material, a description of the experimental method, results and discussion. Finally, a discussion on how the results can be used to improve the design of automatic configuration management tools is provided. However, before examining the details of the experiments, scheduling is discussed in the context of distributed configuration management. Management, Resource Allocation, and SchedulingScheduling takes many forms, such as job-shop scheduling, production scheduling, silicon chip design, multiprocessor scheduling and so on. It can take place within any extent of time, space or other dimension. Scheduling algorithms are usually dynamic or static. Dynamic scheduling involves continuously allocating a set of resources to a time-variant problem. Modern operating system kernels provide good examples of dynamic scheduling in the way processes are scheduled and the processor resource is time-sliced. The set of resources - total processing power, primary and secondary storage units, network bandwidth, etc. - remain fixed. The scheduling problem is time-variant as processes are continuously started, stopped, resumed and killed by the users of the system, either explicitly or implicitly. The scheduling objective is to maximize the use of available resources in any given situation. Static scheduling involves assigning a set of fixed resources to a fixed and constant problem. For example, scheduling timetables in schools and universities involves static scheduling, as different classes of students have to be assigned classrooms and lecture theaters, and students and teachers must not have overlapping timeslots. The classes, the courses and the lecture rooms are known a priori. In general, static scheduling problems are NP hard. Static scheduling involves assigning the vertices (tasks) of an acyclic, directed graph onto a set of resources, such that the total time to process all the tasks are minimized. The actual time it takes to process all the tasks is usually referred to as the makespan. An additional objective is often to achieve a short makespan while minimizing the use of resources. Such multi-objective optimization problems involve complex trade- offs and compromises, and good scheduling strategies are based on a detailed and deep understanding of the specific problem domains. Most approaches belong to the family of priority-list scheduling algorithms, differentiated by the way in which task priorities are assigned to the set of resources. Traditionally, heuristics have been employed in the search for high-quality solutions [13]. Over the last decade heuristics have been combined with modern search techniques such as simulated annealing and genetic algorithms [1]. Scheduling Objectives and Configuration ManagementThe scheduling problem occurs naturally in distributed configuration management. Within a single configuration rule there is often a set of classes or triggers that are interrelated by precedence relations. These relations constrain the order in which configuration actions can be applied; these graphs can be described formally. A set of precedence relations can be represented by a directed graph, G=(V,E), containing a finite, nonempty set of vertices, V, and a finite set of directed edges, E, connecting the vertices. The collection of vertices, V={v1, v2, ..., vn }, represents the set of n configuration actions to be applied and the directed edges, E={eij}, define the precedence relations that exists between these configuration actions (eij denotes a directed edge from configuration action vi to vj). This graph can be cyclic or acyclic. Cyclic graphs consist of inter-cycle and intra-cycle edges, where the inter-cycle edges are dependencies within a cycle and intra-cycle edges represent dependencies across cycles. Management models in system administration are typically cyclic and the cycles have to be broken prior to scheduling. However, this discussion is limited to acyclic graphs. Literature addressing cyclic graphs include [6, 15, 17, 21, 23]. The reader is also referred to [19] for information on graph algorithms and [22] for general graph theory. Configuration management is a mixture of dynamic and static scheduling. It is dynamic in the sense that it is an ongoing real-time process where configuration actions are triggered as a result of the environment. It is static in the sense that all configuration actions are known a priori. Configuration actions can be added, changed and removed arbitrarily and dynamically. However, this does not violate the static model because such changes would typically be made during a time-interval in which the configuration tool were idle or offline. The hierarchal configuration management model remains static, in the reference frame of each configuration, but may change dynamically between successive frames of configuration. See [7] for an in-depth discussion of dynamic and static scheduling in configuration management. Few studies have been conducted into randomized scheduling as the scheduling objectives usually are to find the most efficient schedules with the shortest makespan. However, in this work efficiency is just one of several goals, and the main emphasis is on improving security and obscuring the information that can be gained by observers by watching the configuration process as it occurs. Security and RandomizationAll scheduling problems are resolved by traversing the graph using topological sorting. In simple terms, a topological sort of a directed graph is a list of the vertices of the graph in an order that preserves the precedences in the graph. If the vertices represent tasks, a topological sort of the tasks is an order in which they can be accomplished while satisfying the precedences between them. Most topological sorting algorithms are based on the concept of a freelist. One starts by filling the freelist with the entry nodes, i.e., nodes with no parents. At any time one can freely select, or schedule, any element in the freelist. Once all the parents of a node have been scheduled, the node can be added to the freelist. Scheduling strategies differ in the way elements are selected from the freelist. Most scheduling algorithms attempt to select freelist elements so that the schedule can be completed in the shortest possible time. A popular heuristic for achieving a short schedule is the Critical Path/Most Immediate Successor First (CP/MISF) [13]. Tasks are scheduled with respect to their levels in the graph. Whenever there is a tie between tasks (when tasks are on the same level) the tasks with the largest number of successors are given the highest priority. The critical path is defined as the longest path from an entry node to an exit node. In configuration management, the selection of nodes from the freelist is often viewed as a trivial problem, and the freelist may, for instance, be processed from left to right, then updated, in an iterative manner. If instead one employs a strategy such as the CP/MISF, one can make modifications to a system more efficiently in a shorter time than by trivial strategy. A system can be prone to attacks when it is managed deterministically. By introducing randomness into the system, it becomes significantly harder to execute repetitive attacks on the system. One can therefore use a random configuration action implementation when selecting elements from the freelist. A randomized scheduling algorithm adhering to the above description is outlined later in this article. In the next section the effect of randomized scheduling on efficiency is investigated quantitatively through a series of experiments. Part I: EfficiencyConfiguration management includes activities such as process monitoring and control and the management of files and file- structures, involving operations such as copying, moving, deleting and modification of files. Operations on files are typically amongst the most time-consuming and resource-demanding since they require mechanical movement. There are two fundamental classes of management operations - local and remote. Local interactions involve operations on files residing on the disk-drives attached to the local machine. Remote operations include file accesses on remote machines accessible via a computer network. Common to all computer hardware manufactured during the last decades are disk drives and networking peripherals equipped with the well known Direct Memory Access (DMA) controllers. A DMA controller allows content to be transferred asynchronously between the system memory and a peripheral device - such as a disk drive or a network card - without wasting processor cycles. Thus, in true parallel fashion most computers can, for example, copy huge files and do number crunching simultaneously. In this article asynchronous operations refer to those that can be initiated and performed in parallel without intervention from the processor. Synchronous operations refer to operations that cannot be performed in the background, or parallel, resulting in a processor in a busy state until the completion of the operation. The notion of time-sharing and multitasking is not included in this discussion as it represents pseudo-parallelism that does not lead to any efficiency gains. Further, most remote operations can be executed asynchronously on a remote machine. First the local machine issues some form of remote procedure call (RPC). The remote procedure call is sent, received, and its parameters un-marshalled at the remote machine, and the remote procedure initiated by the remote processor. While the remote procedure call is in progress at the remote machine the local processor can either wait for the remote procedure call to complete, or perform some other task simultaneously. In this case, the local machine must at some later point in time check that the remote procedure call completed successfully or obtain this information via an interrupt, callback or a signal. Thus computer systems embody two forms of true parallelism, parallelism within a machine due to parallel peripheral devices and parallelism achieved by the ``delegation'' of tasks to independent processing nodes on the same network. In a system that provides these forms of parallelism, the sequence in which events are scheduled affects efficiency. This fact is supported by the vast body of literature on parallel processing and task scheduling. For example, suppose we one is given a hardware configuration consisting of a central computer with two disk drives A and B, and a remote computer with a disk drive C. Suppose the configuration management tasks to be performed include copying a configuration file from disk A to disk B on the local computer and the same file to disk C on the remote computer. Then, the file is to be modified by replacing an identifier string occurring in the file with the hostname of the machine to which the file has been copied. This problem can be broken down into four logical operations:
The schedules resulting from these sequences are given in Figure 1. Clearly, the makespans vary from 2.5 to 4.5 - the worst makespan being nearly twice as long as the shortest or the optimal makespan. Clearly, the sequences 1342 and 3142 are both optimal and symmetric to each other. In the sequence 1342, Task 1 is initiated asynchronously, followed by the remote initiation of the asynchronous task 3. Upon completion of task 3, task 4 is initiated asynchronously followed by synchronous initiation of task 2. This sequence leads to a good exploitation of the available hardware with the least idle time. On the other hand the sequence 1234 (and 3412) yields a poor result since the second task cannot be started before the first task 1 has completed, although task 1 is asynchronous. The second task 2 is synchronous and the third task cannot be started before the processor is available after processing task 2. Further, the final task 4 depends on the completion of task 3. Why Is Randomness Better?Assuming that the scheduling order can affect the makespan of the schedule, how can a random order be better than a fixed order? In the traditional scheduling context there are few differences between a fixed order and a random order, because a fixed order is simply one of the random orders. With a fixed order, however, there is a probability of picking a good, medium or poor schedule. With some luck it is a good schedule, but it could equally well be a poor schedule. In any case, since it is a fixed order, and the process is repeated, the scheduling algorithm is locked into this configuration. Thus, the effect of a poor selection is multiplied over time.
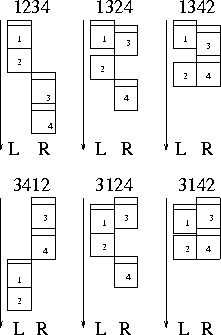 Conversely, with the random strategy, a different order is selected each time - sampling the entire spectrum of makespans. Thus over all executions the schedules will yield average makespans. MethodThe Graph Test Suite The suite of random directed acyclic graphs (DAGs) used in the
experiments was generated by defining a n 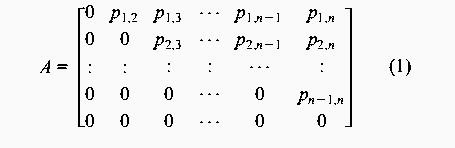 Two sets totalling 19 graphs were generated, where graph size and density were varied. The size n of the graphs was varied from 10 to 100 vertices in steps of 10, and the graph density was varied in nine steps by adjusting the probability p from 0.1 to 0.9 in steps of 0.1. A graph with an element probability of 1 has all the upper triangular elements set to 1, and represents a fully connected graph. When all the transitive edges are removed the resulting graph is a linear chain or a completely ordered sequence of events. On the other hand, if the probability is 0 then there are no dependencies between the events and all the events are independent. Thus, there is no ordering. Probabilities in the range of 0.1 to 0.9 yield graphs with varying degrees of partial ordering from the completely ordered linear chain of events to the unordered independent set of events. For an interesting discussion on graph structures see [12]. One may argue that authentic dependence graphs are more realistic than artificial graphs. Authentic graphs fall into one of the classes of commonly occurring graph topologies (trees, meshes etc.). Random graphs allow graph characteristics to be varied enabling crucial relationships to be identified. Such relationships might not be revealed by using a biased set of graphs. 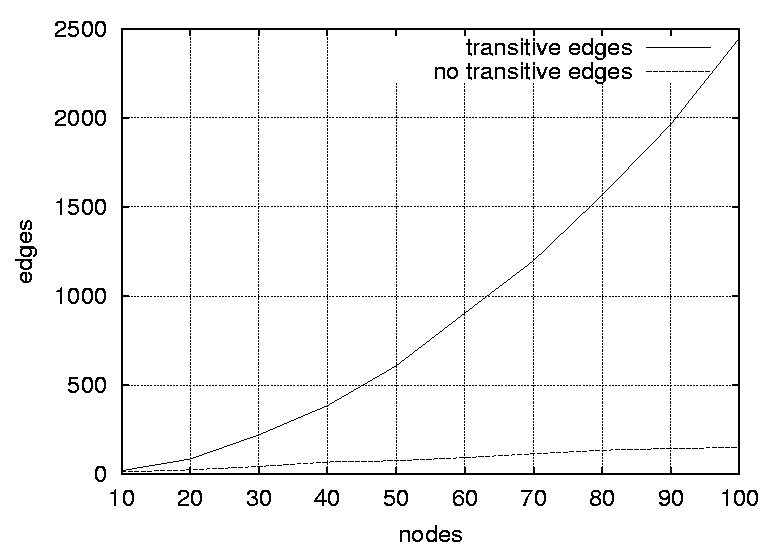 Figures 2 and 3 show the number of non-transitive and transitive edges in the suite of random graphs, where the number of edges are plotted against graph size and graph density respectively. Note that the number of transitive edges increases quadratically with graph size while the number of non-transitive edges increases linearly. Also note the interesting fact that although an increase in the adjacency matrix probability leads to an increase in the number of transitive edges, it also leads to a decrease in the number of non transitive edges. 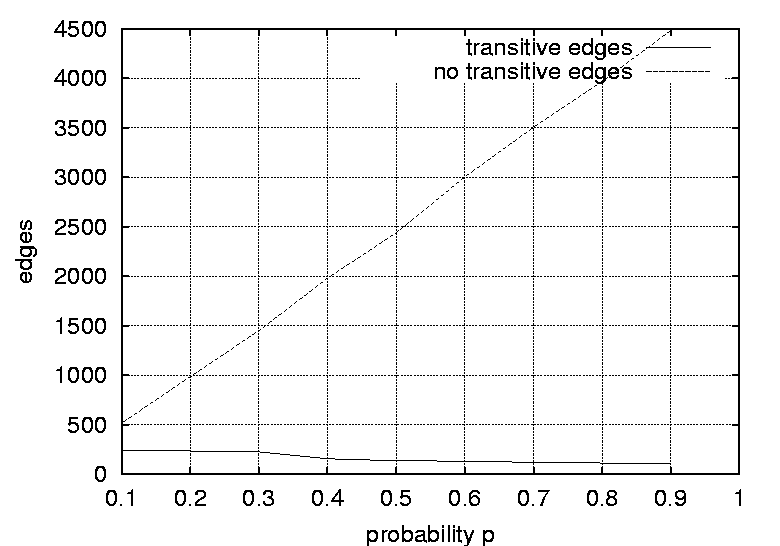 Graph Pre-processingRandom graphs were pre-processed by removing all the transitive dependencies. A transitive dependency can be defined as follows; If vertex y depends on x and vertex z depends on y, then z also depends on x. Therefore, a transitive relation such as z depends on x can be removed from the graph since it is transitively implied by the two relationships z depends on y and y depends on x. The purpose of removing the ``unnecessary'' transitive dependencies is to simplify and purify the graphs. Graphs with no transitive edges are more efficient to process and two graphs are easier to compare if they contain no transitive edges. A graph with transitive edges and a graph with no transitive edges may express the same partial ordering of the vertices, however they have different topological structures. The precedence relations are conserved when the transitive edges are removed. Transitive edges were removed using the following strategy:
For each node in graph
For each parent of the node
If parent is in any of the
ancestors of the other parents
of the node
Then remove the edge from
the node to the parent as
it is transitive.
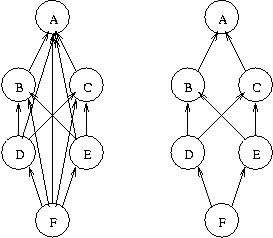
Figure 4 shows an example of a graph with (left) and without
transitive dependencies (right). Clearly, D and E are transitively
dependent on A, since D depends on B which again depends on A
and E depends on C which also depends on A. Further node F is
transitively dependent on both A, B and C, since it depends on
D and E.
 Scheduling StrategyIn the first experiment the graphs were scheduled using a randomized scheduling algorithm that can be outlined as follows:
freelist := all_entry_nodes;
unscheduled := all_nodes;
while (not unscheduled.empty())
begin
node := freelist[random];
process(node);
scheduled.add(node);
freelist.remove(node);
for all nodes in unscheduled whose
parents are all scheduled
begin
freelist.add(nodes);
unscheduled.remove(nodes);
end
end
Notice that elements were selected randomly from the freelist. Events were scheduled onto the first available timeslot on the resource or later depending on the completion times of parent tasks, as all parent tasks of a task must have completed before the task can commence. Resource allocations where fixed. Four resources were used and tasks were allocated to a resource with an index matching the modulo 4 of the task index. Each task was given unity execution and communication/setup delays. The resources represented individual DMA controllers managing individual devices such as local disk drives and network cards allowing connectivity to remote disk drives. However, any number of resources greater than one could be employed to demonstrate the differences in efficiency. ResultsThe results of the scheduling experiment are shown in Tables 2 and 3. Table 2 lists the number of nodes in the graph, the smallest makespan, the largest makespan, the mean makespan, its variance, and the variation in makespan as a percentage of the longest makespan. Table 3 lists the same data where the first column describes the graph density.
DiscussionTable 2 shows that the makespan generally increases with an increase in the number of nodes. This is logical, as if one is increasing the workload without adding resources it will take longer to service the jobs. Also, the variance in makespans do not change significantly with the graph size. Thus, there is room for improvement, regardless of the graph size. Table 3 is even more interesting. When the graph size is fixed and the graph density is increased there is a seemingly linear reduction in makespan. This is because a more connected graph in general provides more parallelism than a less connected graph, and this parallelism is thus exploited during scheduling. Further, the variance of the graph increases with the density. Thus, a dense graph is both more efficiently scheduled but also provides more variance in its makespan. The presence of variance in makespan proves that the order in which the tasks are scheduled have an significant effect on the makespan, and, thus the efficiency of carrying out the configuration management task. From this one can conclude that a dense graph provides more room for improvement than a sparse graph. As it also results in shorter makespans, a management topology should be designed with a maximum number of non-transitive dependencies with the view to improve the performance of the configuration management task. Finally, this experiment confirm that the processing order of the elements has an impact on performance and that the random strategy can produce better results than a fixed-order strategy. Part II: Malicious InterventionIn this part of the experiment three assumptions are made. First, an observer has complete knowledge of the configuration management structure (precedence relations). Second, an observer is able to monitor transactions. Third, the observer is capable of, and has the desire to, intervene. The scenario can be viewed as a game between two parties; see Burgess [5] for a discussion on game theory applied to configuration management. The system administrator, or operator, is responsible for maintaining the operation of his or her computer system, ensuring a high quality of service to its users or subscribers. The observer possesses the ill-intended desire of sabotaging the operation of the computer system. The operator issues an action and the observer tries to pre-empt the action by a guess or a prediction. If the operator follows a predictable pattern, the observer will know the next move of the operator. However, if the operator employs a non-deterministic pattern then it is difficult for the observer to predict the next move, and the prediction becomes a gamble. 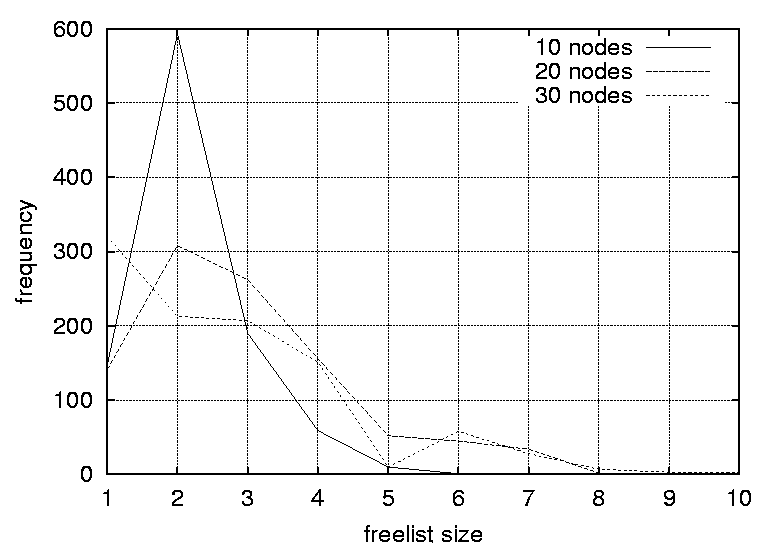 This can be illustrated with a practical example. Imagine that a
computer system consist of two temporary storage areas: /tmp and
/audio/tmp, each cleared at regular times. Suppose that the operator
has configured a configuration action where the /tmp directory is
cleared every night at 2 am, and /audio/tmp is cleared every day at 6
am. Further, there is an inconsiderate user that wants to store huge
amounts of data exceeding the allowed quota. A well-known trick is to
use a shared temporary areas. Such areas usually have large
capacities. The result is that one user hogs the temporary space of
other users, preventing them from carrying out their work. Further, if
this ill-intended user knows the cleanup configuration action, it is
quite easy to sustain this antisocial state by moving the files around
to prevent the files from being deleted. The files are moved from /tmp
to /audio/tmp sometime in the interval between 6 am and 2 am the
following night, and in the interval between 2 am to 6 am the files
are moved back from /audio/tmp to /tmp. Thus accurate predictions of
the management activities can be exploited by the observer. The result
is that the user gets away with unfair exploitation of resources.
However, if a random strategy is applied to scheduling these two
maintenance events, then it becomes impossible for the observer to
predict the next move accurately. The observer is not able to know
whether, or when, the /tmp or /audio/tmp directory are cleared. The
probability of the malicious user losing his or her data in this
situation is 0.5, and at the next iteration the probability is 0.5 and
so forth. And the total probability of keeping the data is therefore
0.5i where i are the number of iterations. In general,
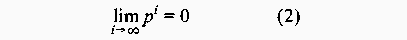 Thus, the random strategy has a measurable reinforcing effect on the sturdiness of the system. The objective of this experiment was to evaluate what is gained by introducing randomness into the scheduling of the configuration management actions and how much randomness that will typically be available. If an operator is given a choice of k actions and one is chosen randomly, then the observer is able to guess or predict the next move with probability p = 1 / k. Clearly, it is desirable to operate with a small probability p as possible. Thus the scheduling framework should ideally be designed to maximize k. MethodFor each of the randomly generated graphs in the test suite, 1000 valid random sequences were generated through random scheduling. For each iteration of the scheduling algorithm, the size of the freelist was recorded, where the freelist contains the list of possible alternatives. The data obtained for each graph were used to generate a set of histograms, illustrating freelist size distributions for the different graph configurations. ResultsFigures 5, 6, 7, and 8 depict the distribution of freelist sizes obtained over 1000 iterations. The different plots represents graphs with a varying number of vertices. Figures 9, 10 and 11 demonstrate the distribution of freelist sizes obtained over 1000 iterations. The different plots represents graphs with a varying graph density. Tables 4 and 5 summarize the results for the size experiment and
the density experiments respectively. The first column describes the
experiment parameter (size and density). The second column shows the
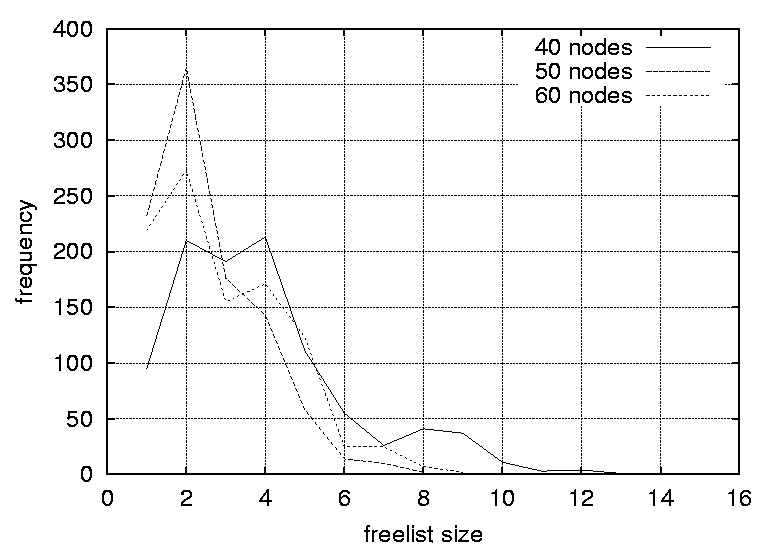 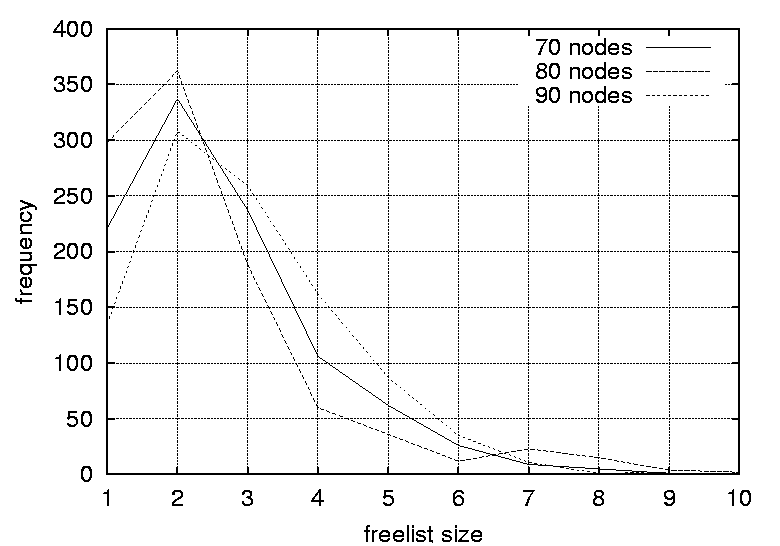 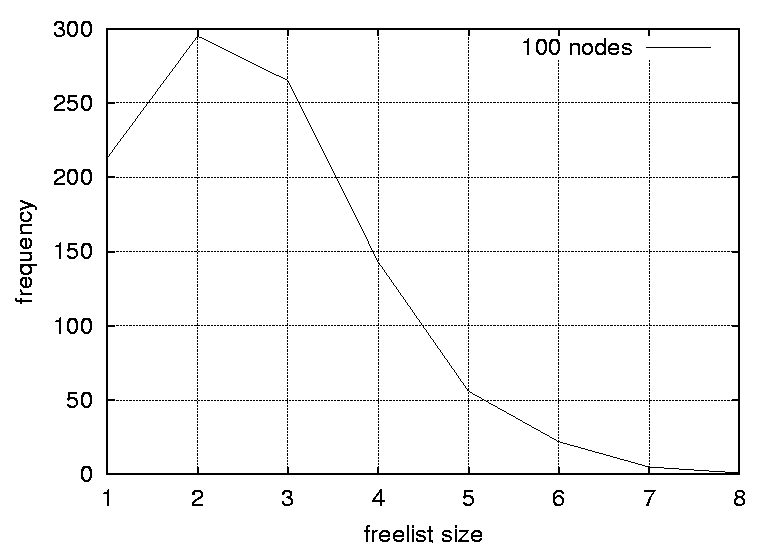 percentage of freelists with size 1 (the percentage of completely deterministic scheduling situations). Column three shows the percentage of freelists with a size greater than one (the percentage of non-deterministic scheduling situations). Column four shows the positions of the peak in the distributions. Column five 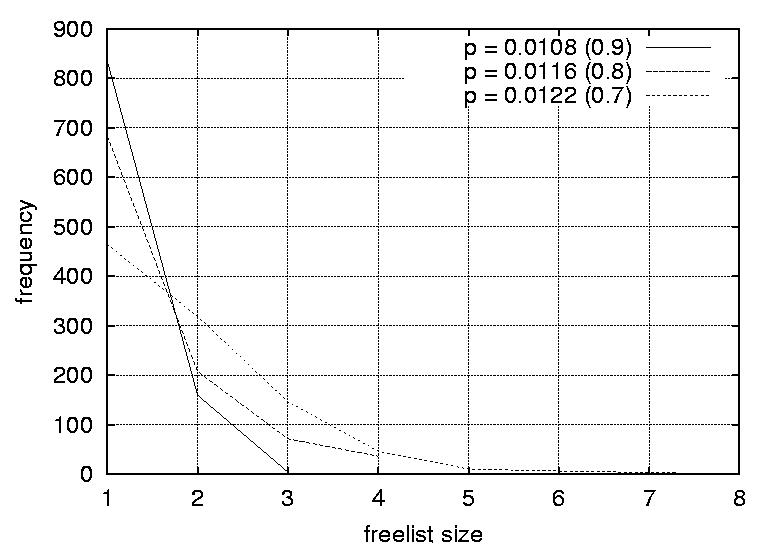 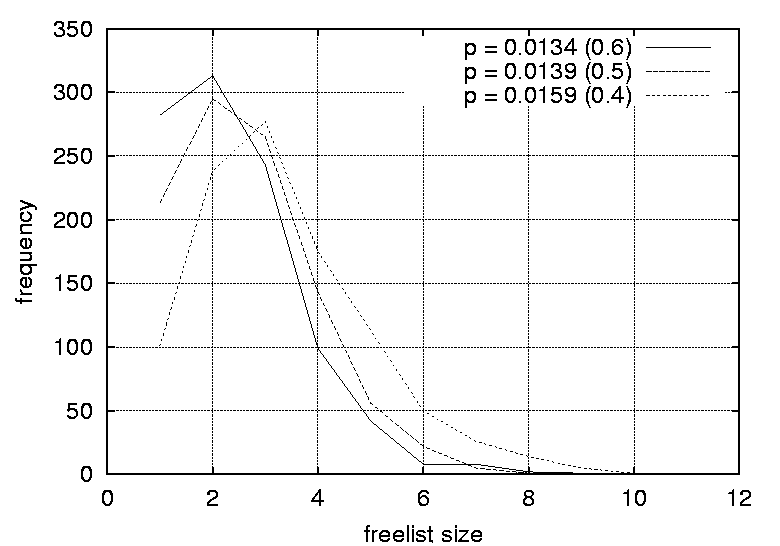 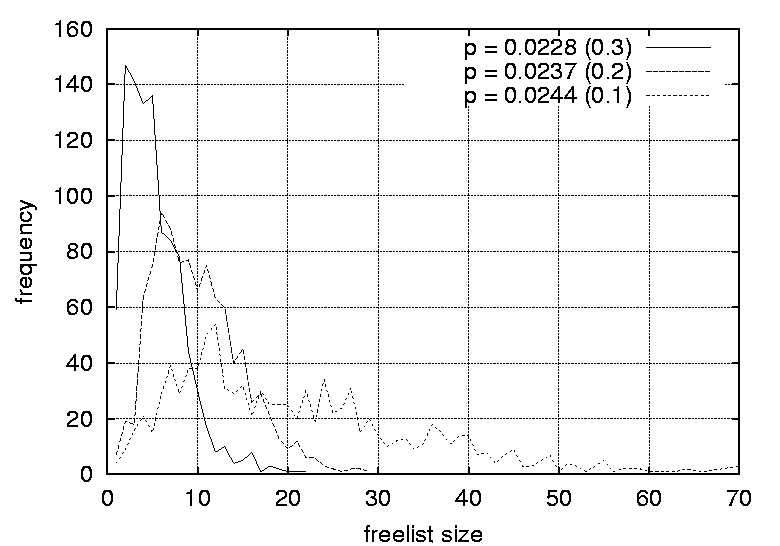 shows the magnitudes of the distribution peaks and the final column shows the widths of the distributions. DiscussionThe results indicate that the distributions of freelist sizes for smaller graphs are narrow with most freelist vectors of size 2 (59.3%) and some freelists with size 1 and 3 elements (about 20% each). As the number of nodes in the graphs is increased the distribution is smeared outwards spanning a larger sized freelist. The distribution peaks are still at 2, but the peaks are smaller at approximately 30%. For example, the graph with 100 nodes contains around 27% occurrences of freelists of size 3, 15% of lists with size 4, and 5% of freelists with size 5. However, as the number of vertices is increased, there is no significant difference in the distributions, thus size is not a crucial factor.
One implication of this data is that even the most trivial of graphs can benefit from a randomized strategy, as only a fraction of the freelists (approximately 20%) has a size of one and is completely deterministic. A freelist with a size of two adds a sufficient level of uncertainty (p = 0.5) in making a prediction, for an observer. As the graphs are increased in size the proportion of predictable scenarios (having a freelist size of one) does not change significantly. However, the proportion of freelists with a size greater than two increases, reducing the probability of successful predictions significantly. For example, a size of 3 yields a probability of 0.33 for a successful prediction, a size of 4 yields a probability of 0.25 and so forth. For the graphs where the graph density was varied, the distributions are strongly affected by the density parameters. Again, the peaks decrease and the distributions become more smeared as the densities are increased. For graphs with a density of 0.0108 the largest freelist has a size of 3, while by increasing the graph density to 0.0244 one obtain freelists with as many as 70 elements. The smearing effect is especially strong as the graph densities approach 1.0 (which generates fully connected graphs). Peaks start at 1 for graphs with a density of 0.0108, 0.0116 and 0.0122. The peak moves to 2 for graphs with a density of 0.0134 and 0.0139, and to 3 for a graph with a density of 0.0159. For the graphs with densities of 0.0228, 0.0237 and 0.0244 distributions peak at 2, 6 and 12 respectively. Further, the proportion of situations where the freelist has a size of one decreases from 83.5% to 4% as the graph density is increased. Clearly, the density of a graph has a strong effect on the freelist size distributions and thus the random scheduling of these graphs. The more dense a graph, the more random its scheduling can become and thus the more difficult it is for an observer to perform accurate predictions. For large graph densities the probabilities of correct predictions become diminishingly small. Since the nature of the graph affects the random scheduling, the structure of the precedence relations should be taken into consideration when designing the configuration management topology. The results of this section lead to the following design guidelines.
At first sight these results might seem surprising, especially as the vertices of a graph with zero density (with totally independent nodes) can be scheduled arbitrarily, and a graph with a density of 1 has a fixed scheduling order. However, a graph with a density of 0.0108 is easier to predict than one with a density of 0.0244. The mistake is to assume that a graph with a density of 0.0108 consists of more independent nodes than one with a density of 0.0244. Either the nodes are independent or they are not. If we investigate a ten-node graph with density 0.1, the probability of 0.1 ensures that nearly every row of its adjacency matrix would contain a 1, or an edge. The corresponding graph would therefore be some loosely connected structure with perhaps one or two independent satellite nodes. In fact, one does not need many 1's in the adjacency matrix to connect the nodes. The result is a narrow and long chain-like structure. A similar argument can be applied when comparing the graphs with densities of 0.9 and 1. Part III: Malicious SurveillanceIn the previous experiment the focus was on the prediction of events and how well one can prevent prediction by scrambling events randomly. The goal of this experiment is to identify how an observer can monitor a system and identify the management structure and configuration patterns. In particular, what is the impact of employing a randomized scheduling strategy on the ability of an observer to identify and reconstruct an accurate model of the configuration management task topology? In this experiment, it is assumed that the observer is able to monitor the actions of the system administrator, either explicitly or implicitly through observing the results of actions. We also assume that the observer is able to uniquely identify each action. The example given in the previous experiment can be extended to illustrate this. Assume a user is interested in storing huge files on the system but is aware that there are cleanup configuration actions in place. The user also knows that there are two independent storage areas on the computer system, namely /tmp and /audio/tmp. By writing a simple script that lists the content of these two directories to a file every hour, the user will after one day collect fairly good evidence that /tmp is deleted around 2 am and /audio/tmp around 6 am. Repeating this exercise for several consecutive days confirms the findings. The user has identified the sequence of these two events. This is a trivial example. However, when observing larger number of tasks it is still trivial to identify the patterns as long as the system administrator employs a deterministic strategy that often results in the same repeated sequence of effects. When the same sequence is repeated, the events belonging to the sequence can be modelled using a graph with a linear chain structure, or a total order. However, if the system administrator employs a random strategy on a graph with a complex topology, the observer can reveal the structure as shown in the following example: A user observes five events over a period of 10 days. Even if the user does not know that there are five events, the user can identify this by observing the recurrence of events. Through the occurrence of the events the user realizes that each event occurs once every day and can therefore deduce that the five events occur in one-day cycles. Each day a sequence of events is observed, for example: 01 : 2 1 3 4 5 02 : 1 2 3 4 5 03 : 1 2 3 4 5 04 : 1 2 3 4 5 05 : 2 3 1 4 5 06 : 2 1 3 4 5 07 : 2 1 3 4 5 08 : 2 3 4 1 5 09 : 2 3 4 1 5 10 : 2 1 3 4 5By analyzing these sequences [Note 1] it is possible to deduce the partial ordering of the five tasks. Obviously, tasks 1 and 2 are entry nodes as they are the only tasks occurring in the first position, and task 5 is the only exit task since it is always in the last position. Further, task 3 depends on task 2 since it always occur somewhere after task 2, and task 4 depends on task 3 since it always occur somewhere after task 3. Task five depends on all the other tasks. After, all the transitive dependencies have been removed, one obtains the graph G represented by the adjacency matrix: 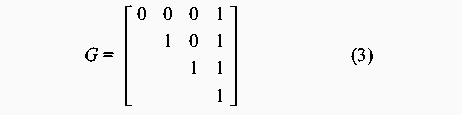 A formal procedure for deducing partial orderings from sequences is provided later in this article. In this small example, the complete structure was uncovered in only a few iterations. However, real world graphs would contain a larger number of vertices. It is possible to make some general statements regarding the time it takes to discover the structure of a graph. If the graph is a linear chain, or a total order, then one observation suffices. However, if the graph consists of N independent vertices, i.e., no ordering, then N! (distinct) observations are necessary in order to establish the fact that all the nodes are independent. As mentioned earlier, the graph usually represents a partial ordering. The number of observations needed to capture the entire structure for large graphs is huge. The few first observations provide a rough indication of the graph topology, and the estimate is refined as further observations are made. However, a large number of observations are needed to uncover all the details. This discussion is based on the assumption that the reference graph remains constant. However, in real life the management structures are modified on a daily basis to reflect the dynamic needs of the users. Consequently, the graph can be viewed as a time-varying entity. One implication of this is that it is even more difficult for an observer to identify the management structure. However, time varying management structures are beyond the scope of this article. This experiment sets out to answer how many iterations are necessary in order to identify a configuration management model? MethodThe experiment was carried out by setting up a sequence generator and a sequence observer. The generator produced 300 valid random partial orders from each of the graphs in the test suite. The observer observed each of the generated sequences without any knowledge of the graph topology. For each iteration the information embedded in the sequence was accumulated in a process known as training. For evaluation and graphing purposes a graph was generated from the accumulated information, all the transitive dependencies were removed and the resulting graph was compared to the reference graph providing the sequences. Each of these steps will be described in the following paragraphs. A data structure was built up while observing the sequences. The data structure consisted of a list of two sets - a pair of sets for each element, or vertex, in the graph. One of the sets consisted of elements succeeding the current element in the sequence - the successors, and the other set of elements preceding the current element in the sequence - the predecessors. These sets grew as the observer was introduced to new sequences. This procedure is captured in the following algorithm:
for i:=1 to sizeof(S) do
begin
suc[i] := union(suc[i], head(S,i-1));
pro[i] := union(pro[i], tail(S,i+1));
end
S is an array containing the sequence of events. Sizeof
is a function that returns the size of the sequence, suc and
pre are arrays of sets containing the set of successors and
predecessors, union is a function returning the union of two
sets and head and tail return sets consisting of the
head and the tail of the array respectively.
Equipped with this data structure it is possible to reconstruct the reference graph, either fully or partially, depending on the number of observations made. The graph building algorithm used is based on the following observations:
The algorithm for extracting the graph is outlined as follows:
for i:=1 to n do
begin
P[i] := suc[i] - isct(suc[i],pre[i]);
end
P is an array of sets containing the parents of the nodes of
the graph, suc and pre are arrays of sets containing the
set of successors and predecessors, and isct is a function
returning the intersection of two sets. The minus (-) operator removes
the elements in the right hand set from the elements of the left hand
set.
Transitive dependencies were removed. Graphs free of transitive dependencies were a prerequisite for performing graph comparisons. The reference graph and the predicted graphs were compared as follows: The parents of each vertex in the reference graph was compared to the parents of the corresponding vertex in the predicted graph. The number of common parents where counted and divided by the total number of parents for that vertex (in the reference graph). These ratios were then summed. This procedure be described formally using the following expression: 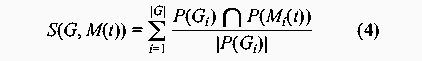 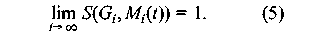 ResultsFigures 12, 13, 14 and 15 depict the similarity between the reference graph and the reconstructed graph plotted against time, where time is measured in iterations. The different graphs represent structures with a varying number of vertices. 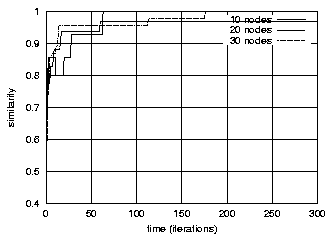 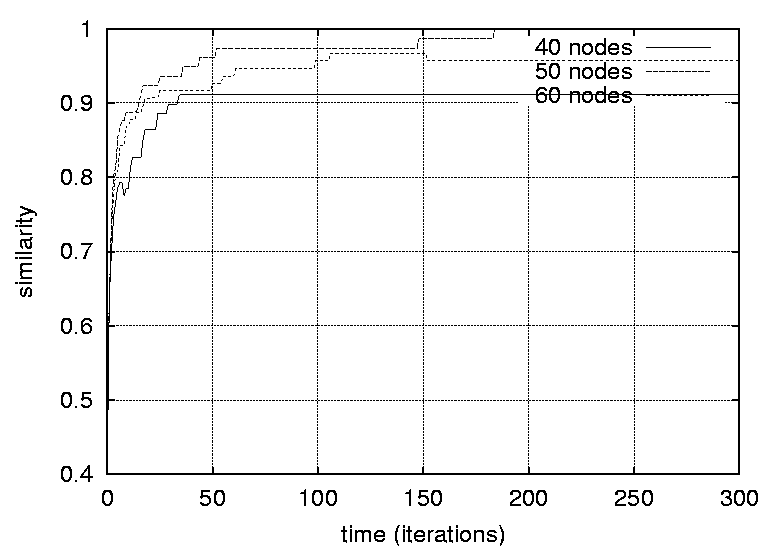 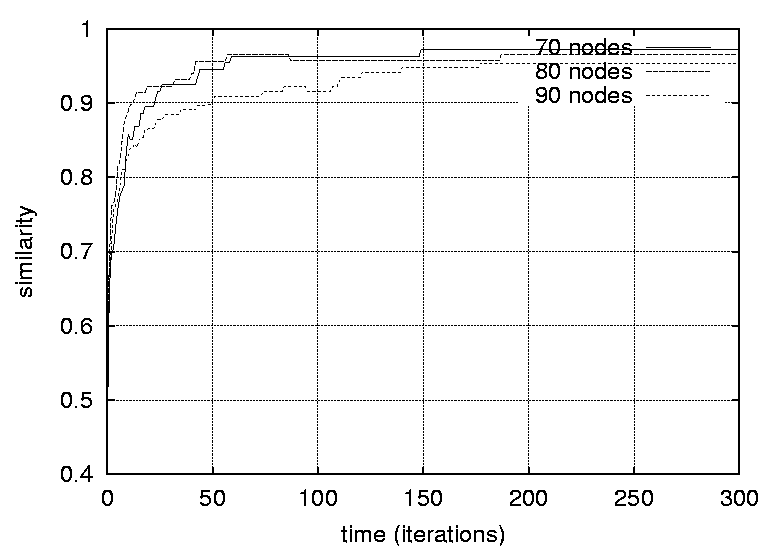 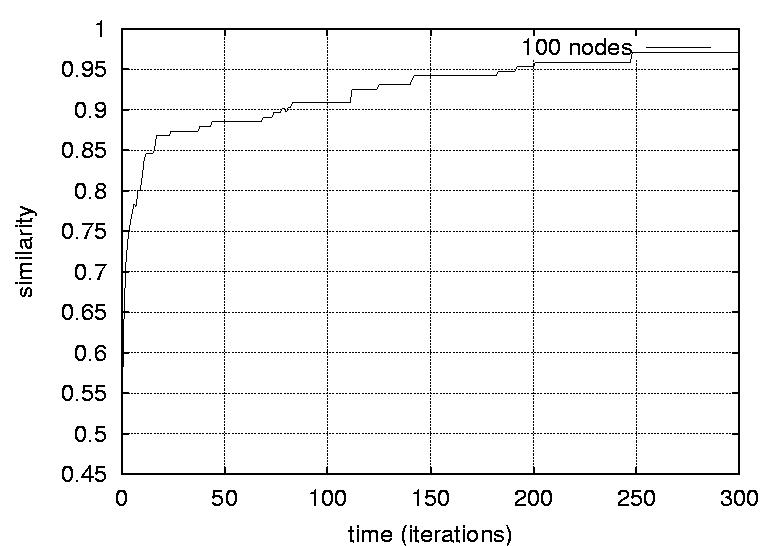 Figures 16, 17 and 18 depict the similarity between the reference
graph and the reconstructed graph plotted against time, where time is
measured in iterations. The different graphs represent structures with
a varying graph density. 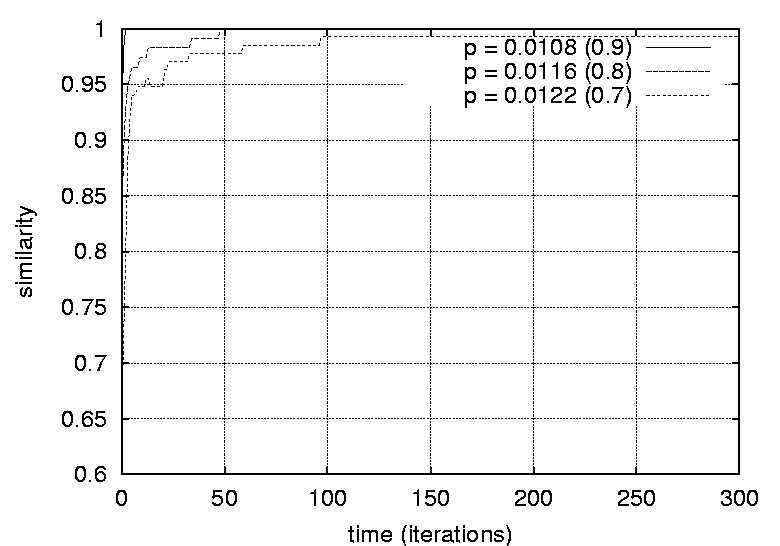 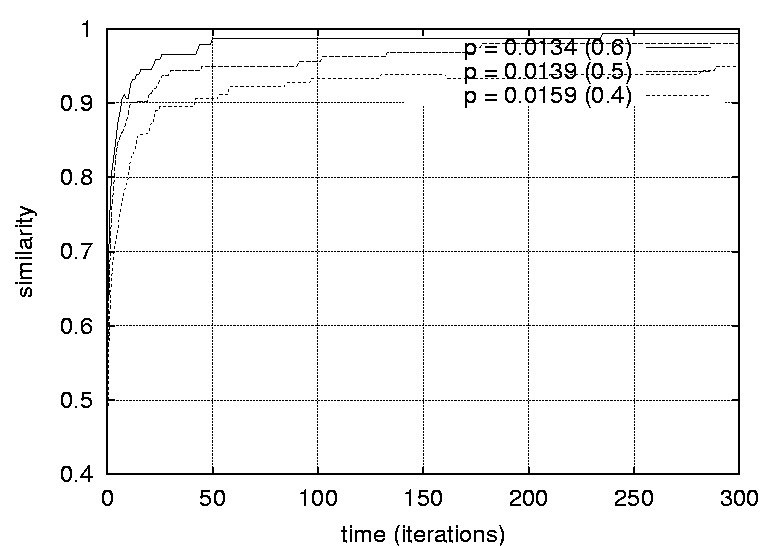 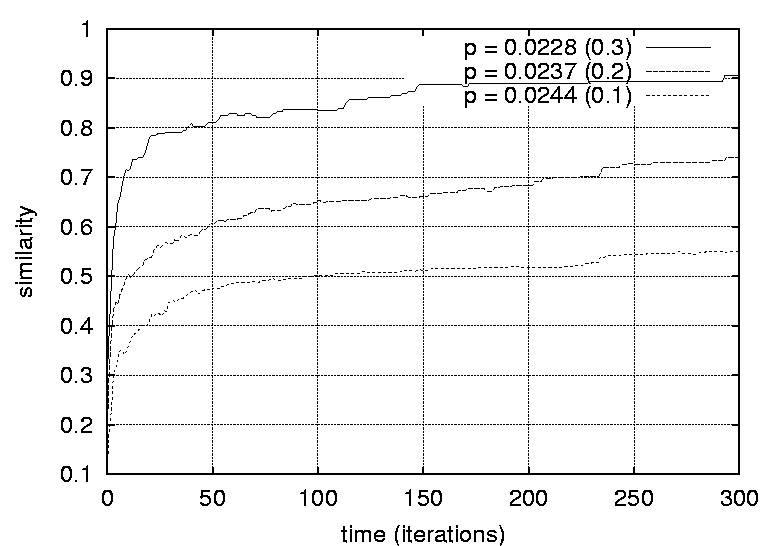 Figures 19 and 20 show graphs of the number of iterations required
to reach a similarity levels of 70%, 80%, 90% and 95% for graphs of
different sizes and densities respectively. 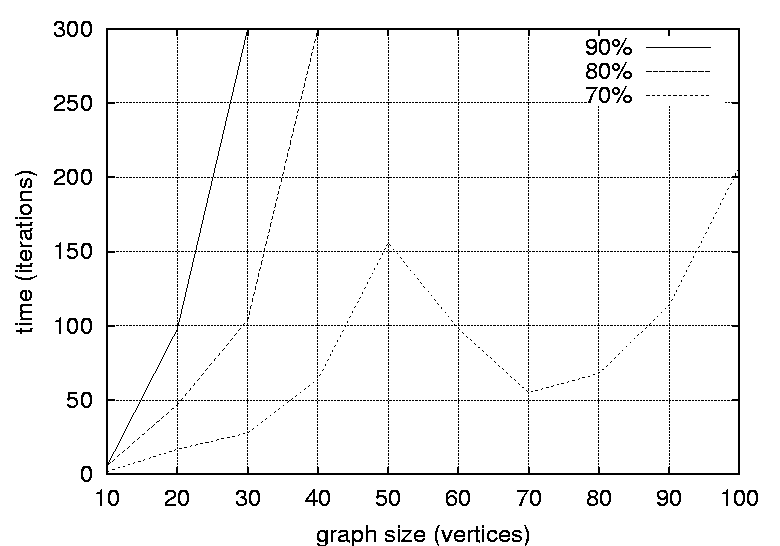 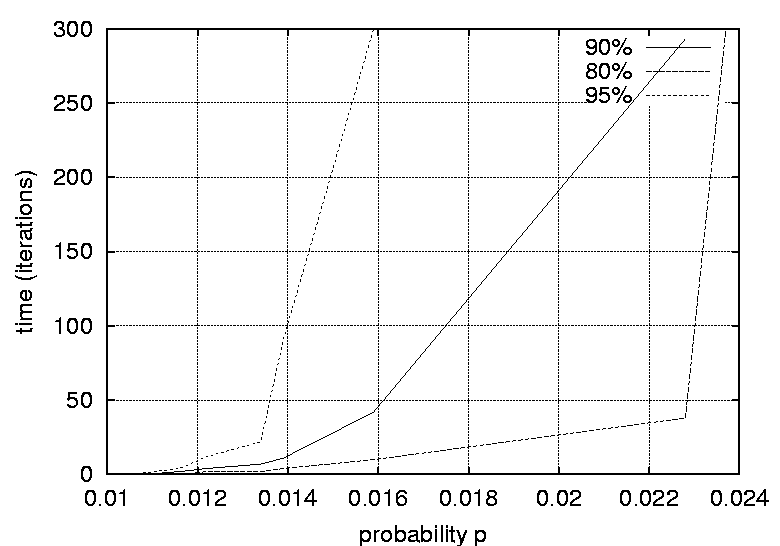 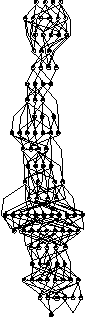 Figures 21, 22, 23 and 24 depict graphs at various stages of recognition, namely graphs with similarity levels of 0.67, 0.77, 0.82 and 1.0 respectively. Only, graphs with relatively high similarity factors could be included in this article, as graphs with lower similarity factors had a large depth unsuitable for printed material. These graphs indicate that the depth of the graphs decrease as they become more similar to the reference graph. Similarly the width of the graphs increases as the predicted graphs more similar to the reference graphs. The VCG (Visualizing Compiler Graph) tool was used to generate the graphs [16]. Note that the ``minimize depth'' option was selected to fit the graphs into these proceedings, as a more natural level by level layout would yield long and narrow graphs. 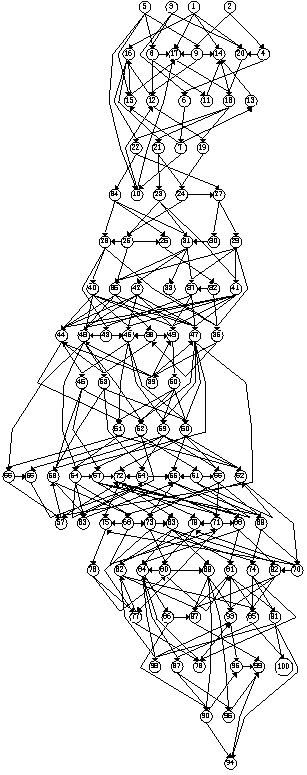 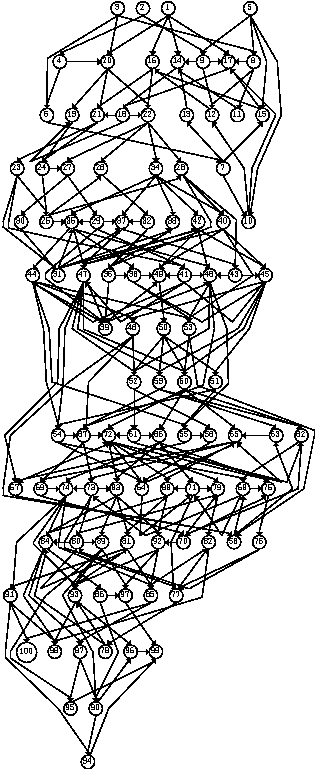 DiscussionA common attribute of all the graphs where the similarity level is plotted against time (Figures 12, 13, 14 and 15) is that they appear asymptotic - converging towards 1 or some positive value less than 1. Further, results show that graph size has a moderate effect on obscuring the graph topologies. A larger graph is harder to identify than a smaller graph; more observations are necessary in order to fully identify a large than a small reference graph. This phenomenon is more evident in Figure 19 which plots the number of observations required to obtain a given similarity level against size. The graphs with 50 nodes, or more, appear to converge onto similarity levels of less than 1, after 300 iterations. This data supports the claim that a randomized strategy obscures the topology of the management structure making it more difficult for an observer to identify it. 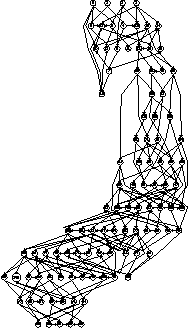 Graph density appears to have a dramatic and noticeable effect on obscuring graph topologies. For low densities such as 0.0108, 0.0116 and 0.0122 (Figure 16) the observer is able to identify the complete structure or a very similar structure simply after a few iterations. For graphs with medium density, such as 0.0134, 0.0139 and 0.0159 (Figure 17), the similarity graphs converge at significantly lower levels. Finally, the graphs with densities 0.0228, 0.0237 and 0.0244 (Figure 18) are just about starting to converge at the 300th iteration and are still at noticeably low levels of similarity - 0.9, 0.7 and 0.5 respectively. Figure 20 shows the number of iterations to reach the similarity levels of 80%, 90% and 95% are plotted against the graph density, and strongly indicates that the density of a graph has an exponential effect on obscuring the management topology, i.e., with a linear increase in graph density, one achieves an exponential increase in the time required for an observer to reconstruct the structure from the observations. The visualization of graphs at various stages of recognition (Figures 21, 22, 23 and 24) show that less similar graphs tend to have a larger depth and smaller width than more similar graphs, and that the reference graph itself is the widest and most shallow. This is because initially all nodes are assumed independent, then a few edges are detected, connecting the nodes together in a sparse and deep structure. As more edges are discovered the vertices of the graph are tied more strongly together such that each level becomes wider and the depth becomes more shallow. Clearly, the experiments indicate that management structures with many nodes are preferable to those with fewer nodes. Further, management topologies with a strong connectivity are drastically less predictable than sparse structures. These observations should be taken into consideration when designing management structures to obscure the management structure to an onlooker. An Optimal TopologyWhen given the freedom to design a structure, what topologies yield the strongest connectivity? If one assumes that a graph with N vertices is acyclic and contains no transitive dependencies, then it is obvious that the graph must have a layered structure with L levels, where the d sub i nodes of level iis a member of L are dependent on all the nodes in the previous level i-1 (all other dependencies would be transitive or cyclic). If we assume, for simplicity, that each level contains an equivalent number of elements, i.e., d i = dj where i, j is a member of L, such that d L = N, then the total number of edges E in the graph is given by 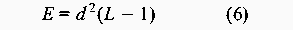 Such a graph has a rectangular shaped structure when drawn in a layered manner. Further, E is maximized by maximizing d, i.e, L = 2 and d = N/2. The resulting graph is a wide structure with two fully connected levels, E = N2 / 4 edges, and a connectivity of p = N/2(N-1). (Note that the transitive edges are not counted). ConclusionsThis paper addresses randomized scheduling of events in a distributed configuration management context. Three, aspects of the impact of randomized scheduling were investigated - namely, efficiency of resource utilization during configuration management, predictability and exploitability by malicious observers, and the extent to which observers are capable of monitoring and identifying the configuration management topology. The experiments show that randomized scheduling has advantages over fixed order strategies - on average resulting in more efficient schedules. Further, most graphs yield sufficiently large freelists that makes the job of predicting management action difficult. Finally, randomized scheduling makes it more difficult for an observer to identify the complete management topology, and if the management topology is viewed as a time-variant entity this difficulty increase even further. When it is difficult to identify the model, then it is also difficult to make accurate predictions. The conclusion to draw from this is that randomized scheduling, in the context of distributed configuration management, can be advantageous compared to a trivial strategy, providing a good compromise between efficiency and security. As random scheduling is an extremely simple strategy to understand and implement it is recommended that it is incorporated into automatic distributed configuration management tools, such as cfengine. The experiments confirm claims by Burgess [5] that it is advisable to introduce changes into the management model, and continuously change its structure, to increase robustness. Also, as pointed out in [7], randomness can also be introduced in other aspects of the management process such as the timing of the events to improve the robustness. AcknowledgementsThe author would like to acknowledge everyone in the system administrations research group at Oslo University College for enlightening discussions. Further, the author acknowledges Mark Burgess and Alva Couch for insightful and inspirational comments and the anonymous reviewers for their comments greatly enhancing the quality of this manuscript. Finally, the author is grateful to the management at the Oslo University College for recognizing the importance of this work, providing the necessary financial support and a stimulating working environment. Author InformationFrode Eika Sandnes received the B.Sc. degree in computing science from the University of Newcastle Upon Tyne, England, in 1993, and the Ph.D. degree in computer science from the University of Reading, England, in 1997. He has worked for several years in the space industry developing data handling systems and communications equipment for low earth orbit satellites. He is currently an associate professor in the Department of Computer Science, Faculty of Engineering at Oslo University College, Norway. His research interests include applications of coding theory, signal processing, parallel and distributed processing and especially distributed configuration management. Dr. Sandnes is a member of the IEEE Computer Society. Reach him electronically at Frode-Eika.Sandnes@iu.hio.no. Bibliography[1] Imtiaz Ahmad and Muhammed K. Dhodhi, ``Multiprocessor Scheduling in a Genetic Paradigm,'' Parallel Computing, vol 22, pp. 395-406, 1996.[2] P. Anderson, ``Towards a high level machine configuration system,'' Proceedings of the Eighth Systems, Administration Conference (LISA VIII) USENIX Association, Berkeley, CA, 1994. [3] Lee Bruno, ``Sophisticated Network Management,'' Open Computing, 11(12), p. 100, December, 1994. [4] M. Burgess, ``A Site Configuration Engine,'' Computing Systems, MIT Press, Cambridge, MA, Vol. 8, p.309, 1995. [5] M. Burgess, ``Theoretical System Administration,'' Proceedings of the Fourteenth Systems Administration Conference (LISA XIV), USENIX Association, Berkeley, CA, p. 1, 2000. [6] M. Burgess and D. Skipitaris, ``Adaptive Locks For Frequently Scheduled Tasks With Unpredictable Runtimes,'' Proceedings of the Eleventh Systems Administration Conference (LISA XI), USENIX Association: Berkeley, CA, p. 113, 1997. [7] Mark Burgess and Frode Eika Sandnes, ``Predictable Configuration Management in a Randomized Scheduling Framework,'' in Proceedings of the 12th International Workshop on Distributed System Operation and Management, DSOM'2001, INRIA Press, October, 2001. [8] Alva L. Couch and Noah Daniels, ``The Maelstrom: Network Service Debugging via Ineffective Procedures,'' in Proceedings of the 15th Systems Administration Conference LISA 2001, USENIX, December, 2001. [9] N. Damianou, N. Dulay, E. C. Lupu, and M. Sloman, ``Ponder: A Language for Specifying Security and Management Policies for Distributed Systems,'' Imperial College Research Report DoC 2000/1, 2000. [10] Rik Farrow, ``Object-Oriented Network Management,'' UNIX/world, Vol. 9, Num. 11, p. 93, November, 1992. [11] B. Hagemark and K. Zadeck, ``Site: A Language and System for Configuring Many Computers As One Computer Site,'' Proceedings of the Workshop on Large Installation Systems Administration III, USENIX Association, Berkeley, CA, 1989, p. 1, 1989. [12] B. Jereb and L. Pipan, ``Measuring Parallelism in Algorithms,'' Microprocessing and Microprogramming, The Euromicro Journal, Vol 34, pp. 49-52, 1992. [13] Hironori Kasahara and Seinosuke Narita, ``Practical Multiprocessor Scheduling Algorithms for Efficient Parallel Processing,'' IEEE Transactions on Computers, Vol C-33, Num. 11, pp. 1023-1029, 1984. [14] S. Omari, R. Boutaba, and O. Cherakaoui, ``Policies in SNMPv3-Based Management,'' Proceedings of the VI IFIP/IEEE IM Conference on Network Management, p. 797, 1999. [15] Raymond Reitter, ``Scheduling Parallel Computations,'' Journal of the Association for Computing Machinery (ACM), Vol. 15, Num. 4, pp. 590-599, 1968. [16] G. Sander, ``Graph Layout Through the VCG Tool,'' in Proceedings DIMACS International Workshop GD'94, Lecture Notes in Computer Science 894, pp. 194-205, Springer Verlag, October, 1995. [17] Frode Eika Sandnes and G. M. Megson, ``Improved Static Multiprocessor Scheduling Using Cyclic Task Graphs: A Genetic Approach,'' PARALLEL COMPUTING: Fundamentals, Applications and New Directions, North-Holland, Vol 12, pp. 703-710, 1998. [18] Stéphane Schitter, ``Integration of Intrusion Detection Products in the Tivoli Enterprise Console,'' Master's Thesis, Eurécom Institute, June, 1999. [19] Robert Sedgewick, Algorithms, Second Edition, Addison-Wesley, 1989. [20] Stefan Uelpenich, ``Extending the Reach of Tivoli Distributed Monitoring - Creating a Custom Monitoring Collection,'' The Managed View, Vol. 3, Num. 2, pp. 21-40, Spring, 1999. [21] Herbert Weinblatt, ``A New Algorithm for Finding the Simple Cycles of a Finite Directed Graph,'' Journal of the Association for Computing Machinery (ACM), Vol. 19, Num. 1, pp. 45-56, 1972. [22] Douglas B. West, Introduction to Graph Theory Second edition, Prentice Hall, 2001. [23] Tao Yang and Cong Fu, ``Heuristic Algorithms for Scheduling Iterative Task Computations on Distributed Memory Machines,'' IEEE Transactions on Parallel and Distributed Systems, Vol. 8m, Num. 6, 1997. [24] M. Zapf, K. Herrmann, K. Geihs, and J. Wolfang, ``Decentralized SNMP Management with Mobile Agents,'' Proceedings of the VI IFIP/ IEEE IM Conference on Network Management, p. 623, 1999. Footnotes: Note 1: The sequences should be read from left to right. |
|
This paper was originally published in the
Proceedings of the LISA 2001 15th System Administration Conference, December 2-7, 2001, San Diego, California, USA.
Last changed: 2 Jan. 2002 ml |
|