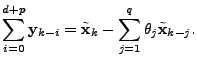|
IMC '05 Paper
[IMC '05 Technical Program]


Network Anomography
Yin Zhang , Zihui Ge , Zihui Ge , Albert
Greenberg , Albert
Greenberg , and Matthew Roughan , and Matthew Roughan
 Department of Computer Sciences, University of Texas at Austin, Austin, TX 78712, USA Department of Computer Sciences, University of Texas at Austin, Austin, TX 78712, USA
 AT&T Labs - Research, Florham Park, NJ 07932, USA AT&T Labs - Research, Florham Park, NJ 07932, USA
 School of Mathematical Science, University of Adelaide, SA 5005, Australia School of Mathematical Science, University of Adelaide, SA 5005, Australia
Abstract:
Anomaly detection is a first and important step needed to respond to
unexpected problems and to assure high performance and security in IP
networks. We introduce a framework and a powerful class of algorithms
for network anomography, the problem of inferring network-level
anomalies from widely available data aggregates. The framework
contains novel algorithms, as well as a recently published approach
based on Principal Component Analysis (PCA). Moreover, owing to its
clear separation of inference and anomaly detection, the framework
opens the door to the creation of whole families of new algorithms.
We introduce several such algorithms here, based on ARIMA modeling,
the Fourier transform, Wavelets, and Principal Component Analysis. We
introduce a new dynamic anomography algorithm, which effectively
tracks routing and traffic change, so as to alert with high fidelity
on intrinsic changes in network-level traffic, yet not on internal
routing changes. An additional benefit of dynamic anomography is that
it is robust to missing data, an important operational reality. To the
best of our knowledge, this is the first anomography algorithm that
can handle routing changes and missing data. To evaluate these
algorithms, we used several months of traffic data collected from the
Abilene network and from a large Tier-1 ISP network. To compare
performance, we use the methodology put forward earlier for the
Abilene data set. The findings are encouraging. Among the new
algorithms introduced here, we see: high accuracy in detection (few
false negatives and few false positives), and high robustness (little
performance degradation in the presence of measurement noise, missing
data and routing changes).
1 Introduction
The first step in fixing a problem is knowing it exists. This is no
less true in networking than anywhere else - we need to know about a
problem before we can repair it.
Networking vendors typically build alarms into network equipment to
facilitate fast, accurate detection and diagnosis of
problems. However, in practice, there are many problems for which
explicit alarms are either absent (for new or uncommon problems), or
intrinsically hard to produce. In these cases we must infer the
problem from other data sources. For instance, many types of network
problems cause abnormal patterns to appear in the network
traffic. Such traffic anomalies may be caused by problems
ranging from security threats such as Distributed Denial of Service
(DDoS) attacks and network worms, to unusual traffic events such as
flash crowds, to vendor implementation bugs, to network
misconfigurations. We refer to the problem of inferring anomalies
from indirect measurement as network anomography (combining
``anomalous'' with ``tomography,'' a general approach to such inference
problems).
Network tomography [31] bears some resemblance, in that both
involve the solution of a linear inverse problem. Examples include
inference of individual link performance characteristics from path
performance characteristics, and inference of traffic matrices from
individual link load measurements. For example, the traffic matrix
estimation problem arises because the obvious source of data for
direct measurement (flow-level data) can be hard to obtain
network-wide [5,14,22,23,28,31,34,35].
On the other hand, Simple Network Management Protocol (SNMP) data on
individual link loads is available almost ubiquitously. Fortunately,
the link loads and traffic matrices are simply related by a linear
equation
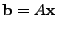 |
(1) |
The vector
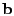 contains the link measurements, and contains the link measurements, and 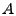 is
the routing matrix (defined formally below). We wish to infer is
the routing matrix (defined formally below). We wish to infer
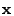 , which contains the unknown traffic matrix elements
written as a vector. Tomographic inference techniques seek to invert
this relationship to find , which contains the unknown traffic matrix elements
written as a vector. Tomographic inference techniques seek to invert
this relationship to find
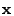 . .
The anomography problem is different and somewhat more complex.
First, note that anomaly detection is performed on a series of
measurements over a period of time, rather than from a single
snapshot. In addition to changes in the traffic, the solution must
build in the ability to deal with changes in routing. Second, note
that the anomalies that we wish to infer may have dramatically
different properties from a traffic matrix, and so different methods
than those used for network tomography may be called for. Indeed, we
find that simple extensions to network tomography methods perform fair poorly
here. Techniques that transform the measurements prior to attempting
to solve the inverse problem are preferable.
As a simple example, imagine trying to detect an anomalous traffic
pattern caused by a flash crowd or DDoS attack on a web site. This
type of event will cause increases in traffic flows headed towards a
particular set of destinations. It may be hard to rapidly identify
which of the tens of thousands of ingress links on a large network
might be primarily responsible, as large surges at a network egress
link may arise from small surges on several ingress links.
We must infer the change in the pattern of traffic to the particular site
from the complete set of link data, considered together, rather than
as individual time series. This illustrates an important feature of
anomography - it extends anomaly detection to network-level
problems (automatically building in correlation across the network)
where link-level anomaly detection might be inadequate or unreliable.
Many approaches to anomography are possible. In pioneering work,
Lakhina et al. introduced a novel approach based on Principal Component
Analysis (PCA) [19]. Our paper
makes three major contributions to understanding and solving
anomography problems:
- We present a simple and powerful framework that encompasses a wide
class of methods for network anomography. We will see that the method
of [19] is a member of this class.
The framework clearly decouples the inference and anomaly detection
steps, and so immediately opens the door to the development of new
algorithms where one makes different choices for each step.
Accordingly, we introduce several such new algorithms here, based on
ARIMA modeling, the Fourier transform, Wavelets, and Principal
Component Analysis. Moreover, the framework is not restricted to the
analysis of link traffic data, and in particular also applies to the
dual problem of inferring performance anomalies from end-to-end
performance measurements.
- We introduce a new algorithm for dynamic anomography, which
identifies network level traffic anomalies and works in the presence
of routing changes. That is, dynamic anomography tracks routing and
traffic change - signaling traffic anomalies, but not internal
network routing changes (which may dramatically change internal
traffic patterns but may leave the traffic matrix, describing how
traffic enters and exits the network, stable). In IP networks,
routing changes occur as part of the normal ``self-healing'' behavior
of the network, and so isolating these from traffic anomalies is
advantageous. An additional benefit of dynamic anomography is that it
is robust to missing link load measurements, an important operational
reality (see Section 4 for why missing data may result
in changes in the routing matrix). To the best of our knowledge, this
is the first anomography algorithm that can handle routing changes and
missing data.
- Using data sets collected from a large Tier-1 ISP and from Internet2's
Abilene network, we report on the results of an extensive and thorough
evaluation of a set of anomography methods. To understand the
fidelity of the methods and to compare different methods, we apply the
methodology introduced in [19].
Under this methodology, we find that in general the new temporal
anomography methods introduced here exhibit consistently high
fidelity.
In particular, we find that the most successful method (of those
examined) is a variation of dynamic anomography, combining Box-Jenkins
modeling (ARIMA) with
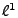 norm minimization. Further evaluation
suggests that this algorithm can cope well with measurement noise, and
degrade gracefully in the presence of missing or corrupted data. norm minimization. Further evaluation
suggests that this algorithm can cope well with measurement noise, and
degrade gracefully in the presence of missing or corrupted data.
The paper is organized as follows. Section 2
summarizes background and related work. In
Section 3 we describe our framework, and the
anomography algorithms examined in this paper, in the context of fixed
routing. In Section 4 we extend the Box-Jenkins
anomography to the case where routing may change over time. In
Section 5 we describe our evaluation methodology,
and Section 6 presents the results.
Section 7 provides final remarks.
2 Background
Network tomography describes several problems: inferring
link performance of a network from end-to-end measurements, or
inferring Origin-Destination (OD) traffic demands from link load
measurements. These problems can be written as linear inverse problems
where one seeks to find unknowns
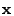 from measurements from measurements
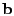 given a linear relationship (1),
where given a linear relationship (1),
where 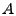 is the routing matrix. For a network with is the routing matrix. For a network with 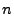 links, and links, and 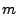 OD flows, we define the routing matrix to be the
OD flows, we define the routing matrix to be the
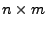 matrix matrix
![$ A=[a_{ij}]$](img16.gif) where where 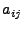 indicates the fraction of traffic from
flow indicates the fraction of traffic from
flow 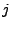 to appear on link to appear on link 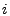 . .
SNMP provides link measurements of traffic volumes (bytes and
packets), typically at 5 minute intervals (this data is described in
more detail in, for example [34]).
We shall
assume data of this type is the input to our algorithms, and we wish
to infer anomalous traffic matrix elements, but note that anomography
is not limited to this problem, and could equally be applied to
inferring anomalous link performance from end-to-end measurements.
An additional source of data used here comes from the routing
protocols used to build the forwarding tables within each router. We
use routing data (e.g., gathered from a route monitor as in
[27]) along with a route simulator (as in
[10]) to predict the results of these
distributed computations, and determine the network routing.
The problem of inferring the OD traffic-matrix has been much studied
recently (e.g., [5,14,22,23,28,31,34,35]).
The problem's key characteristic is that it is massively
underconstrained: there will be approximately 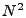 OD flows to
estimate and only OD flows to
estimate and only 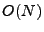 link measurements. Hence tomography methods
seek to introduce additional information, often in the form of some
kind of traffic model (for instance a Poisson model in
[31,28], a Gaussian model in [5], or a gravity
model in [34,35]). Anomography
problems are also highly underconstrained, but the models used to
describe traffic are inappropriate for anomalies -- by definition
these events are generated by completely different processes from
normal network traffic. Moreover, in anomography we combine
detection with inference, whereas in standard network tomography
we seek only to infer a set of traffic matrix elements. Hence
there are important differences between this paper and network
tomography. link measurements. Hence tomography methods
seek to introduce additional information, often in the form of some
kind of traffic model (for instance a Poisson model in
[31,28], a Gaussian model in [5], or a gravity
model in [34,35]). Anomography
problems are also highly underconstrained, but the models used to
describe traffic are inappropriate for anomalies -- by definition
these events are generated by completely different processes from
normal network traffic. Moreover, in anomography we combine
detection with inference, whereas in standard network tomography
we seek only to infer a set of traffic matrix elements. Hence
there are important differences between this paper and network
tomography.
It is also important to note that routing matrices change over
time. In much previous work, routing matrices are taken to be constant
(an exception being [23], where the traffic is
assumed to be somewhat constant, while the routing varies), but it is
important (see [29]) to
allow for the fact that routing is not constant, and neither is the
traffic. In order to allow for variable routing, we index not just the
traffic measurements over time, but also the routing matrix. Given
these, we may write the relationship between the link traffic, and OD
traffic matrix as
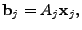 |
(2) |
where 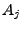 is an is an
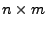 routing matrix, routing matrix,
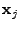 is a length- is a length-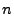 vector of unknown OD flow traffic volumes, and
vector of unknown OD flow traffic volumes, and
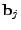 is a length- is a length-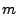 vector of link loads1, at
time interval
vector of link loads1, at
time interval 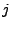 . .
Lakhina et al. carried out the pioneering work in the area of inference
of anomalies at network level,
[19,18,20],
and adapted Principal Components Analysis (PCA) to this setting.
Donoho [8,9] introduced a powerful mathematical
treatment for tomography-like problems, wherein one seeks solutions
that maximize sparsity (intuitively, solutions with fewest
explanations). These papers inspired our development of the new
methods introduced here, and our development of a framework in which a
very wide class of methods all fit.
Anomaly detection is a burgeoning field.
A great deal of research in network anomaly detection relies
on some type of inference step, taking a set of
alarms [13,15,16,25,30] as input.
While anomography includes methods of this type, our results indicate
that it is better to delay alarm generation until after the inference step.
In that way, a single constructive alarm may be generated, rather than a storm
of redundant alarms. Moreover, in delaying the alarm generation
until after the inference step, we can in some cases greatly improve
the sensitivity of detection, as was demonstrated in
[19].
We approach the network anomaly detection
problem from the point of detecting unknown anomalous behavior, rather
than looking for particular signatures in the data, the focus
of much work in the security community.
A large component of the work on machine learning, signal processing
and time-series analysis
is devoted to detecting outliers or anomalies in time-series.
This literature has been applied to networks in a
number of cases; for examples see
[1,4,15,17,30,32].
These methods range in sophistication from [4], which
suggests the use of the standard Holt-Winters forecasting technique for
network anomaly detection, to [1], which uses a
sophisticated wavelet based method with great potential.
These methods focus on single time series rather than the multi-dimensional
time series that arise in anomography.
Most earlier work ignores noise or provides weak tests of
robustness to noise (which can destroy utility).
A strength of the work presented here is that we provide tests
of effectiveness of the methods in the presence of noise,
always a factor in practice.
3 Network Anomography
In this section, we shall assume that the routing matrices 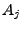 are
time-invariant and are denoted by are
time-invariant and are denoted by 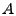 . (We will extend our work to
time-varying . (We will extend our work to
time-varying 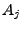 in Section 4.) Under this
assumption, we can combine all in Section 4.) Under this
assumption, we can combine all 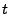 linear systems (2)
into a single equation using matrix notation: linear systems (2)
into a single equation using matrix notation:
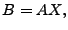 |
(3) |
where
![$ B= [\mathbf{b}_1 \mathbf{b}_2 \cdots \mathbf{b}_t]$](img28.gif) is the matrix formed by
having is the matrix formed by
having
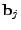 as its column vectors, and similarly as its column vectors, and similarly
![$ X = [\mathbf{x}_1 \mathbf{x}_2 \cdots
\mathbf{x}_t]$](img29.gif) . .
We identify two basic solution strategies to network anomography: (i)
early inverse, and (ii) late inverse. Early-inverse
approaches may appear more intuitive.
The early-inverse approach tackles the problem in
two steps. The first is the network tomography step, where
OD flow data at each interval 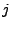 are inferred from the link load
measurements by solving the ill-posed linear inverse problem
(2).
Given the estimated OD flow data are inferred from the link load
measurements by solving the ill-posed linear inverse problem
(2).
Given the estimated OD flow data
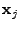 at
different time points at
different time points 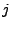 , in the second step, anomaly
detection can then be applied to the , in the second step, anomaly
detection can then be applied to the
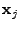 . For this step,
there are many widely used spatial and temporal analysis techniques,
which we will describe later in this section. . For this step,
there are many widely used spatial and temporal analysis techniques,
which we will describe later in this section.
Early-inverse methods, although conceptually simple, have an obvious
drawback -- errors in the first step, which are unavoidable due to
the ill-posed nature of the inference problem, can contaminate the
second step, sabotaging overall performance. Another disadvantage is
that early-inverse methods apply a potentially computationally
expensive anomaly detection step to high-dimensional data: on a
network of 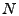 nodes, one must perform this step on all nodes, one must perform this step on all 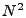 OD
pairs. As we will see, late-inverse performs anomaly detection
on only OD
pairs. As we will see, late-inverse performs anomaly detection
on only 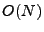 dimensional data. We focus on late-inverse methods in this paper for
these reasons, though we shall provide some comparisons between early-
and late-inverse methods.
dimensional data. We focus on late-inverse methods in this paper for
these reasons, though we shall provide some comparisons between early-
and late-inverse methods.
The idea of the late-inverse method is to defer ``lossy'' inference to
the last step. Specifically, late inverse approaches extract the
anomalous traffic from the link load observation, then form and solve
a new set of inference problems:
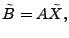 |
(4) |
where
![$ \tilde{B} = [\tilde{\mathbf{b}}_1 \tilde{\mathbf{b}}_2 \cdots \tilde{\mathbf{b}}_t]$](img32.gif) is the matrix of anomalous traffic in the observables, and
is the matrix of anomalous traffic in the observables, and
![$ \tilde{X} =
[\tilde{\mathbf{x}}_1 \tilde{\mathbf{x}}_2 \cdots \tilde{\mathbf{x}}_t]$](img33.gif) is the matrix of
OD flow anomalies to be diagnosed, over is the matrix of
OD flow anomalies to be diagnosed, over 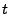 time intervals. time intervals.
While the new inference problems (4) share the same
linear-inverse structure as in network tomography (3),
the characteristics of the unknowns are very different, and so is the
solution strategy, which we will explore in Section 3.4.
We now introduce a simple framework for late-inverse anomography
methods. In this framework, 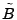 is formed by multiplying is formed by multiplying 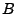 with a transformation matrix
with a transformation matrix 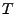 . Depending on whether we use a left
or right multiplying transformation matrix, we can further divide the
framework into the following two classes: . Depending on whether we use a left
or right multiplying transformation matrix, we can further divide the
framework into the following two classes:
- spatial anomography, where a left multiplying
transformation matrix
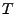 is used to form is used to form 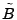 , i.e., , i.e.,
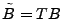 ; ;
- temporal anomography, where a right multiplying
transformation matrix
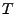 is used to form is used to form 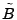 , i.e., , i.e.,
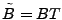 . .
Our framework encompasses a number of analysis
techniques for extracting anomalous traffic 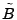 from link load
observations from link load
observations 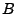 , as we next illustrate. , as we next illustrate.
3.2 Spatial Anomography
Data elements in high dimensional data sets, such as the link load
observations, usually have dependencies. The intrinsic dependency
structure among the data elements can thus be exploited for filtering
anomalous behavior by discovering data points that violate the normal
dependency structure. In our context, the process of detecting such
data points can be performed by left-multiplication by a
transformation matrix 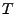 such that such that
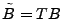 . An example of
such an approach is a recent study by Lakhina et al. [19], where Principal Component
Analysis (PCA) is used in finding dominant patterns. We describe this
method, and in particular its instantiation as a left-multiplication
operation in the following section. . An example of
such an approach is a recent study by Lakhina et al. [19], where Principal Component
Analysis (PCA) is used in finding dominant patterns. We describe this
method, and in particular its instantiation as a left-multiplication
operation in the following section.
3.2.1 Spatial PCA
In [19], Lakhina et al. proposed a
subspace analysis of link traffic for anomaly detection, which can be
summarized as follows.
-
1.
- Identify a coordinate transformation of
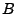 such that the link
traffic data under the new coordinate systems have the greatest degree
of variance along the first axis, the second greatest degree of
variance along the second axis, and so forth. These axes are
called the principal axes or principal components. such that the link
traffic data under the new coordinate systems have the greatest degree
of variance along the first axis, the second greatest degree of
variance along the second axis, and so forth. These axes are
called the principal axes or principal components.
Recall that
![$ B= [\mathbf{b}_1 \mathbf{b}_2 \cdots \mathbf{b}_t]$](img28.gif) is the collection of link traffic
data at is the collection of link traffic
data at 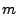 links over links over 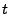 time intervals, where each row time intervals, where each row 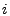 ( (
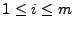 ) denotes the time series of the ) denotes the time series of the 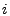 -th link and each column -th link and each column
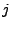 ( (
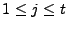 ) represents an instance of all the link loads at
time interval ) represents an instance of all the link loads at
time interval 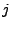 . The principal components, . The principal components,
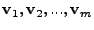 can
be computed iteratively as follows: can
be computed iteratively as follows:
The coordinate transformation matrix can thus be obtained by arranging
the principal components as rows of a matrix
![$ P = [\mathbf{v}_1 \mathbf{v}_2 ... \mathbf{v}_m]^T$](img43.gif) . .
-
2.
- Divide the link traffic space into the normal subspace and
the anomalous subspace.
Lakhina et al. [19] developed a
threshold-based separation method by examining the projection of the
time series of link traffic data on each principal axis in order. As
soon as a projection is found that contains a 3
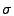 deviation from
the mean, that principal axis and all subsequent axes are assigned to
the anomalous subspace. All previous principal axis are assigned to
the normal subspace. deviation from
the mean, that principal axis and all subsequent axes are assigned to
the anomalous subspace. All previous principal axis are assigned to
the normal subspace.
We use
![$ P_a=[\mathbf{v}_r \mathbf{v}_{r+1} ... \mathbf{v}_m]^T$](img45.gif) to denote the matrix of
the principal axes in the anomalous subspace, where to denote the matrix of
the principal axes in the anomalous subspace, where
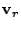 is the
first axis that fails to pass the threshold test. is the
first axis that fails to pass the threshold test.
-
3.
- The anomalous traffic can now by extracted from link load observation
by first projecting the data into the anomalous subspace and then
transforming it back, by taking
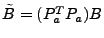 , and so we
obtain the transformation matrix , and so we
obtain the transformation matrix
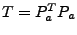 . .
We call the above method spatial PCA because it exploits the
correlation between traffic on different links (across space).
Later in Section 3.3.4, we will describe temporal PCA,
which exploits temporal correlation by applying PCA to identify dominant
patterns across time.
3.3 Temporal Anomography
The anomalous link traffic can also be separated by performing
temporal analysis on the time series for each link. Consider a set of
link traffic data over time 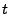 : :
![$ B= [\mathbf{b}_1 \mathbf{b}_2 ... \mathbf{b}_t]$](img49.gif) . The
process of extracting anomalies by exploiting the temporal structure
within the data points can be modeled as a linear transformation of
the time series: . The
process of extracting anomalies by exploiting the temporal structure
within the data points can be modeled as a linear transformation of
the time series:
![$ \tilde{B} =[\tilde{\mathbf{b}}_1 \tilde{\mathbf{b}}_2
... \tilde{\mathbf{b}}_t] = B T$](img50.gif) , where the transformation matrix , where the transformation matrix 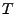 can be
either explicit or implicit. In this paper, we consider four types of
temporal analysis: ARIMA, Fourier, Wavelet, and PCA (for identifying
dominant patterns across time). Although it may not be obvious at
first glance, all these methods indeed fit in our framework of linear
matrix transformation, as we will see next. can be
either explicit or implicit. In this paper, we consider four types of
temporal analysis: ARIMA, Fourier, Wavelet, and PCA (for identifying
dominant patterns across time). Although it may not be obvious at
first glance, all these methods indeed fit in our framework of linear
matrix transformation, as we will see next.
3.3.1 ARIMA Modeling
Univariate time series. The Box-Jenkins methodology, or
AutoRegressive Integrated Moving Average (ARIMA) modeling
technique [2,3], is a class of linear time-series
forecasting techniques that capture the linear dependency of the
future values on the past. It is able to model a wide spectrum of
time-series behavior, and has been extensively used for anomaly
detection in univariate time-series.
An ARIMA model includes three order parameters: the autoregressive
parameter (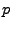 ), the number of differencing passes ( ), the number of differencing passes (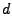 ), and the
moving average parameter ( ), and the
moving average parameter (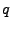 ). In the notation introduced by Box and
Jenkins, models are summarized as
ARIMA ). In the notation introduced by Box and
Jenkins, models are summarized as
ARIMA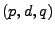 . A model
described as
ARIMA . A model
described as
ARIMA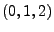 means that it contains means that it contains 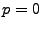 (zero)
autoregressive parameters and (zero)
autoregressive parameters and 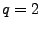 moving-average parameters which
were computed for the time series after it was differenced once
( moving-average parameters which
were computed for the time series after it was differenced once
(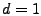 ). ).
A general ARIMA model of order 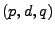 can be expressed as: can be expressed as:
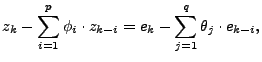 |
(5) |
where 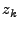 is obtained by differencing the original time series is obtained by differencing the original time series 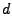 times (when
times (when 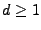 ) or by subtracting the mean from the original
time series (when ) or by subtracting the mean from the original
time series (when 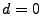 ), ), 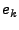 is the forecast error at time is the forecast error at time 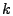 , ,
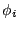 ( (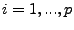 ) and ) and 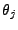 ( (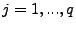 ) are the
autoregression and moving-average coefficients, respectively. ) are the
autoregression and moving-average coefficients, respectively.
Many commonly used smoothing models are special instances of ARIMA
models. For example, the Exponentially Weighted Moving Average
(EWMA), is equivalent to
ARIMA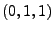 ; linear exponential
smoothing, also known as Holt-Winters, is equivalent to
ARIMA ; linear exponential
smoothing, also known as Holt-Winters, is equivalent to
ARIMA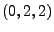 .
See [26] for detailed equations for various
smoothing models and their equivalence with ARIMA models. .
See [26] for detailed equations for various
smoothing models and their equivalence with ARIMA models.
There are well known techniques for estimating the parameters
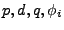 and and 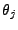 for a given time
series [2,3], and given the parameters, the model
is simply applied to get for a given time
series [2,3], and given the parameters, the model
is simply applied to get 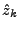 a prediction of a prediction of 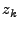 (using for
instance the Durbin-Levinson algorithm [3]). The prediction
errors are then (using for
instance the Durbin-Levinson algorithm [3]). The prediction
errors are then
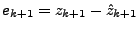 , which then form
our anomalous traffic (the traffic which does not fit the model). In
practice the parameters used in the ARIMA model are sometimes chosen
to meet particular goals intended by the implementor (see
[4] for some discussion of these choices),
rather than being estimated from the data set, because the parameters
of a data set may change over time. However, we prefer to use adaptive
techniques to overcome this problem. , which then form
our anomalous traffic (the traffic which does not fit the model). In
practice the parameters used in the ARIMA model are sometimes chosen
to meet particular goals intended by the implementor (see
[4] for some discussion of these choices),
rather than being estimated from the data set, because the parameters
of a data set may change over time. However, we prefer to use adaptive
techniques to overcome this problem.
If we consider the time series to be vectors of length 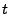 , then the
above results can be written in matrix form. Taking the
measurements , then the
above results can be written in matrix form. Taking the
measurements
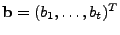 , we can obtain the errors , we can obtain the errors
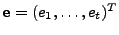 , via right-multiplication by a
transformation matrix , via right-multiplication by a
transformation matrix
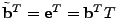 . Specifically,
let . Specifically,
let 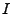 denote the
denote the
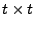 identity matrix, identity matrix,
 denote the
``back shift'' matrix, and denote the
``back shift'' matrix, and
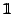 denote the denote the
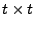 unit matrix, i.e.,
unit matrix, i.e.,
The differencing result,
![$ \mathbf{z}= [z_1 z_2 ... z_t]^T$](img81.gif) , is then , is then
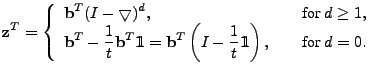 |
(6) |
Equation (5) can be written in matrix notation as
or equivalently,
Extending ARIMA based models to
multivariate time series is straightforward.
As noted earlier, we
construct the matrix 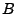 with the measurements at each time period with the measurements at each time period
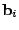 as its columns. Via the above transformations,
we obtain as its columns. Via the above transformations,
we obtain
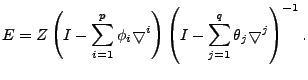 |
(7) |
ARIMA based anomography. Replacing 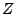 by the matrix form of
(6), we see that by the matrix form of
(6), we see that 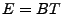 is indeed a transformation
given by right-multiplying is indeed a transformation
given by right-multiplying 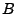 with a matrix with a matrix 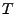 . In fact, any linear filtration of the elements of a time series can be modeled by
a right multiplying matrix transformation. . In fact, any linear filtration of the elements of a time series can be modeled by
a right multiplying matrix transformation.
To get back to anomaly detection, we simply
identify the forecast errors as anomalous link traffic,
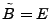 . That is, traffic behavior that cannot be well captured
by the model is considered anomalous. . That is, traffic behavior that cannot be well captured
by the model is considered anomalous.
3.3.2 Fourier Analysis
Fourier analysis [21] is the process of
decomposing a complex periodic waveform into a set of sinusoids with
different amplitudes, frequencies and phases. The sum of these
sinusoids can exactly match the original waveform. This lossless
transform presents a new perspective of the signal under study (in the
frequency domain), which has proved useful in very many applications.
For a discrete-time signal
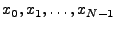 , the Discrete
Fourier Transform (DFT) is defined by , the Discrete
Fourier Transform (DFT) is defined by
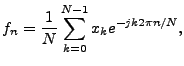 for 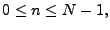
where 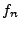 is a complex number that captures the amplitude and phase
of the signal at the is a complex number that captures the amplitude and phase
of the signal at the 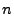 -th harmonic frequency (with base frequency -th harmonic frequency (with base frequency
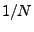 ). Note that for a real signal ). Note that for a real signal 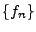 is symmetric, i.e., is symmetric, i.e.,
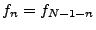 . Lower . Lower 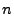 corresponds to a lower frequency
component, with corresponds to a lower frequency
component, with 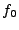 being the DC component, or the average of the
input series, and being the DC component, or the average of the
input series, and 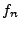 with with 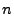 close to close to 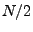 corresponding to high
frequencies. corresponding to high
frequencies.
The Inverse Discrete Fourier Transform (IDFT) is used to reconstruct
the signal in the time domain by
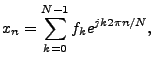 for 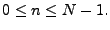
An efficient way to implement the DFT and IDFT is through an algorithm
called the Fast Fourier Transform (FFT). The computational complexity
of the FFT is
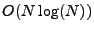 . .
FFT based anomography. The idea of using the FFT to extract
anomalous link traffic, 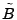 is to filter out the low frequency
components in the link traffic time series. In general, low frequency
components capture the daily and weekly traffic patterns, while high
frequency components represent the sudden changes in traffic
behavior. Working in the frequency domain provides us with the
opportunity to distinguish these two kinds of behaviors. is to filter out the low frequency
components in the link traffic time series. In general, low frequency
components capture the daily and weekly traffic patterns, while high
frequency components represent the sudden changes in traffic
behavior. Working in the frequency domain provides us with the
opportunity to distinguish these two kinds of behaviors.
We summarize FFT based anomography as follows.
-
4.
- Transform link traffic
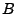 into the frequency domain: into the frequency domain:
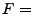 FFT FFT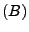 :
apply the FFT on each row of :
apply the FFT on each row of 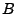 . (Recall that a row corresponds to
the time series of traffic data on one link.)
The result is the corresponding frequency domain series, in each row of . (Recall that a row corresponds to
the time series of traffic data on one link.)
The result is the corresponding frequency domain series, in each row of 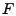 . .
-
5.
- Remove low frequency components: i.e. set
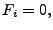 for for ![$ i \in
[1,c]\cup [N-c, N]$](img106.gif) , where , where 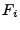 is the is the 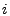 -th column of -th column of 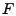 and and 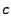 is a cut-off frequency. (For example, for the results presented in
Section 6, we use 10-minute aggregated link traffic
data of one week duration, and
is a cut-off frequency. (For example, for the results presented in
Section 6, we use 10-minute aggregated link traffic
data of one week duration, and
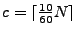 , corresponding to a frequency
of one cycle per hour.) , corresponding to a frequency
of one cycle per hour.)
-
6.
- Transform back into the time domain: i.e. we take
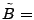 IFFT IFFT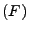 . The result is the high frequency components in
the traffic data, which we will use as anomalous link traffic, . The result is the high frequency components in
the traffic data, which we will use as anomalous link traffic, 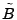 . .
The DFT and IDFT may be represented as right-matrix
products. In setting columns of 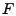 to zero, and performing the IDFT
we are taking a linear combination of the columns of to zero, and performing the IDFT
we are taking a linear combination of the columns of 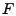 , which in
turn are a linear combination of those of , which in
turn are a linear combination of those of 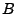 . Hence, the overall
process above can be modeled as a right-multiplying matrix
transformation . Hence, the overall
process above can be modeled as a right-multiplying matrix
transformation
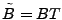 . Note also that in thresholding at
frequency . Note also that in thresholding at
frequency  we preserve the symmetry of we preserve the symmetry of  , and so although , and so although 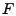 may
contain complex elements, the resulting transform will be real. may
contain complex elements, the resulting transform will be real.
3.3.3 Wavelet Analysis
Wavelets [7,12,21] are mathematical
functions that cut up data into different frequency components, and
then study each component with a resolution matched to its scale.
They provide a powerful means for isolating characteristics of signals
via a combined time-frequency representation and are often considered
superior to traditional Fourier methods especially in situations where
the signal contains transients, such as discontinuities and sharp
spikes.
In [1], Barford et al. have developed a wavelet-based
algorithm for detecting anomalies in the link traffic data. It shares
the same principle as the FFT based approaches -- exposing anomalies
by filtering low frequency components. More specifically, it uses
wavelets to decompose the original signal into low-, mid-, and
high-frequency components and then detects anomalies by close
examination of the mid- and high-frequency components.
Below we compute 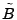 as the high-frequency components of link
traffic as the high-frequency components of link
traffic 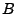 . We can also compute . We can also compute 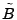 as the mid-frequency
components of as the mid-frequency
components of 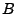 in essentially the same way. in essentially the same way.
-
7.
- Use wavelets to decompose
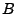 into different frequency levels: into different frequency levels:
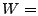 WAVEDEC WAVEDEC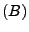 , by applying a multi-level , by applying a multi-level 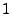 -D wavelet
decomposition on each row of -D wavelet
decomposition on each row of 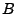 . The result is a wavelet
decomposition vector, which we save as one row in matrix . The result is a wavelet
decomposition vector, which we save as one row in matrix 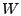 . The
wavelet we use is the Daubechies wavelet [6] of order 6. . The
wavelet we use is the Daubechies wavelet [6] of order 6.
-
8.
- Then remove low- and mid-frequency components in
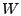 by setting
all coefficients at frequency levels higher than by setting
all coefficients at frequency levels higher than 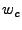 to 0. Here to 0. Here
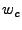 is a cut-off frequency level. For the results presented in
Section 6, we use is a cut-off frequency level. For the results presented in
Section 6, we use 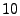 -minute aggregated link
traffic data of one week duration, and -minute aggregated link
traffic data of one week duration, and 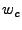 is set at is set at 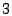 . That
is, we only keep coefficients at frequency levels . That
is, we only keep coefficients at frequency levels 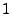 , , 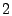 , and , and 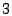 ,
which is consistent with [1]. ,
which is consistent with [1].
-
9.
- Reconstruct the signal:
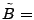 WAVEREC WAVEREC . The
result is the high-frequency components in the traffic data. . The
result is the high-frequency components in the traffic data.
It is easy to verify that the process of WAVEDEC and WAVEREC only
involves linear combinations of columns of  . As a result, the . As a result, the
 derived through the wavelet based anomography can also be
modeled as right multiplying matrix transformation. derived through the wavelet based anomography can also be
modeled as right multiplying matrix transformation.
3.3.4 Temporal PCA
In Section 3.2.1, we presented a method of applying PCA
to find dominant patterns among different link-load time series. A
similar method can be used in identifying dominant patterns across
time.
Consider the link load matrix
![$ B= [\mathbf{b}_1 \mathbf{b}_2 ... \mathbf{b}_t]$](img49.gif) . We can
think of each row as a . We can
think of each row as a 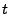 -dimensional vector. What we are looking for
is a new coordinate system, -dimensional vector. What we are looking for
is a new coordinate system,
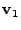 , ,
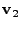 , ... , , ... ,
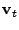 , such that
the projection of the , such that
the projection of the 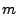 links (on links (on
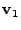 , ,
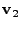 , ..., , ...,
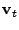 )
has energy concentrated on the first several axes. This is exactly
what PCA provides. The only difference is that we now apply PCA on )
has energy concentrated on the first several axes. This is exactly
what PCA provides. The only difference is that we now apply PCA on
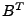 as opposed to as opposed to 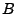 (as used in spatial PCA). Then we follow the
same procedure to define an anomalous subspace and to extract
anomalies that have projections in the anomalous subspace. In this
way, we obtain a left multiplying transformation matrix (as used in spatial PCA). Then we follow the
same procedure to define an anomalous subspace and to extract
anomalies that have projections in the anomalous subspace. In this
way, we obtain a left multiplying transformation matrix 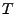 , i.e., , i.e.,
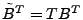 . Taking transpose on both side of the equation,
we have . Taking transpose on both side of the equation,
we have
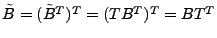 where where 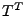 is a right multiplying transformation matrix that extracts anomalies
from
is a right multiplying transformation matrix that extracts anomalies
from 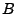 . .
3.4 Inference Algorithms
Once we obtain the matrix of link anomalies 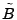 , the next step
is to reconstruct OD flow anomalies , the next step
is to reconstruct OD flow anomalies 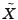 by solving a series of
ill-posed linear inverse problems by solving a series of
ill-posed linear inverse problems
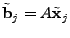 . For
example, Lakhina et al [19]
proposed to find the single largest anomaly in each time interval . For
example, Lakhina et al [19]
proposed to find the single largest anomaly in each time interval 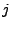 by applying a greedy algorithm. We present below three common
inference algorithms for solving these problems. All three algorithms
deal with the underconstrained linear system by searching for a
solution that minimizes some notions of vector norm, three examples of
which are
by applying a greedy algorithm. We present below three common
inference algorithms for solving these problems. All three algorithms
deal with the underconstrained linear system by searching for a
solution that minimizes some notions of vector norm, three examples of
which are
3.4.1 Pseudoinverse Solution
A standard solution to
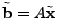 is the pseudoinverse
solution is the pseudoinverse
solution
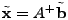 , where , where 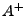 is the
pseudoinverse (or Moore-Penrose inverse) of matrix is the
pseudoinverse (or Moore-Penrose inverse) of matrix 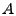 .
It is known that .
It is known that
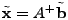 is the solution to the
problem is the solution to the
problem
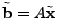 that minimizes the that minimizes the 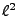 norm
of the anomaly vector, i.e. it solves: norm
of the anomaly vector, i.e. it solves:
minimize 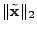 subject to subject to 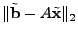 is minimal is minimal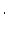 |
(8) |
In practice, we expect only a few anomalies at any one time, so
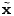 typically has only a small number of large values.
Hence it is natural to proceed by maximizing the sparsity of typically has only a small number of large values.
Hence it is natural to proceed by maximizing the sparsity of
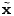 , i.e., solving the following , i.e., solving the following 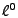 norm minimization
problem: norm minimization
problem:
minimize 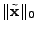 subject to subject to 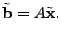 |
(9) |
The 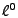 norm is not convex and is notoriously difficult to
minimize, so in practice one needs to either approximate the norm is not convex and is notoriously difficult to
minimize, so in practice one needs to either approximate the 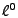 norm with a convex function or use heuristics, for example the greedy
algorithm of Lakhina et al [19].
norm with a convex function or use heuristics, for example the greedy
algorithm of Lakhina et al [19].
3.4.2.1 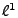 norm minimization norm minimization
One common approach to approximate 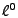 norm minimization is to
convexify (9) by replacing the norm minimization is to
convexify (9) by replacing the 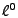 norm with an norm with an
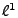 norm, so that we seek a solution to norm, so that we seek a solution to
minimize 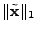 subject to subject to 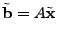 |
(10) |
As shown in [8,9], 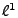 norm
minimization results in the sparsest solution for many large
under-determined linear systems. norm
minimization results in the sparsest solution for many large
under-determined linear systems.
In the presence of measurement noise, the constraints
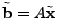 may not always be satisfiable. In this case, we can add a
penalty term may not always be satisfiable. In this case, we can add a
penalty term
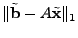 to the objective and
reformulate (10) as: to the objective and
reformulate (10) as:
minimize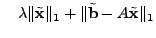 |
(11) |
where
![$ \lambda \in [0,1]$](img149.gif) controls the degree to which the constraints controls the degree to which the constraints
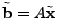 are satisfied.
As shown in Section 6,
the algorithm is not very sensitive to the choice of are satisfied.
As shown in Section 6,
the algorithm is not very sensitive to the choice of 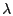 . In
the rest of this paper, unless noted otherwise, we use . In
the rest of this paper, unless noted otherwise, we use
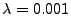 , which gives satisfactory results. , which gives satisfactory results.
We can cast (11) into the following equivalent Linear
Programming (LP) problem, for which solutions are available even when
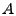 is very large, owing to modern interior-point linear programming
methods. is very large, owing to modern interior-point linear programming
methods.
 |
(12) |
3.4.2.2 Greedy algorithm
Another common heuristic solution for 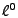 norm minimization is to
apply the greedy algorithm. For example, the greedy heuristic has
been successfully applied to wavelet decomposition, where it goes by
the name of Orthogonal Matching Pursuit (OMP) [24].
In the same spirit here, we develop a greedy solution to
maximize the sparsity of norm minimization is to
apply the greedy algorithm. For example, the greedy heuristic has
been successfully applied to wavelet decomposition, where it goes by
the name of Orthogonal Matching Pursuit (OMP) [24].
In the same spirit here, we develop a greedy solution to
maximize the sparsity of
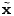 .
The algorithm starts with an empty set .
The algorithm starts with an empty set
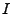 of non-zero positions for of non-zero positions for
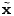 and then iteratively adds new
non-zero positions to and then iteratively adds new
non-zero positions to 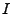 . During each iteration, for each position . During each iteration, for each position
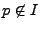 , the algorithm tests how much it can reduce the residual , the algorithm tests how much it can reduce the residual
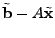 by including by including 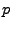 as a non-zero position. More
specifically, let as a non-zero position. More
specifically, let
 . The algorithm estimates the
values for the non-zero elements of . The algorithm estimates the
values for the non-zero elements of
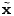 (denoted as (denoted as
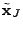 ) by solving the following least squares problem ) by solving the following least squares problem
minimize 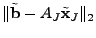 |
(13) |
where
![$ A_J = A[.,J]$](img157.gif) is a submatrix of is a submatrix of 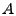 formed by the column
vectors of formed by the column
vectors of 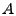 corresponding to positions in corresponding to positions in 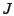 . The residual is
then computed as . The residual is
then computed as
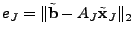 . The algorithm
then greedily chooses the position . The algorithm
then greedily chooses the position 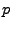 that gives the smallest that gives the smallest
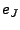 and adds it to and adds it to 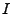 . The algorithm stops whenever either the
residual energy falls below some tolerance to inaccuracy . The algorithm stops whenever either the
residual energy falls below some tolerance to inaccuracy 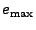 or
the number of non-zero positions exceeds some threshold or
the number of non-zero positions exceeds some threshold
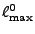 . .
4 Dynamic Network Anomography
Up to this point, we have assumed that the routing matrices are
constant. However, we wish to allow for dynamic routing changes, and
so we must allow 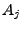 to vary over time. In IP networks, routing
changes occur as part of the normal ``self-healing'' behavior of the
network, and so it is advantageous to isolate these from traffic
anomalies and only signal traffic anomalies. In addition, if some
measurements are missing (say at time to vary over time. In IP networks, routing
changes occur as part of the normal ``self-healing'' behavior of the
network, and so it is advantageous to isolate these from traffic
anomalies and only signal traffic anomalies. In addition, if some
measurements are missing (say at time 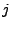 ), we may still form a
consistent problem by setting the appropriate rows of ), we may still form a
consistent problem by setting the appropriate rows of 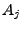 to
zero. Thus, for realistic SNMP measurements where missing data are
often an issue, we still wish to vary to
zero. Thus, for realistic SNMP measurements where missing data are
often an issue, we still wish to vary 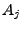 even for static routing.
Routing measurements may be obtained using a route monitor, to provide
accurate, up-to-date measurements of routing (at least at the time
scale of SNMP measurements, e.g. minutes). even for static routing.
Routing measurements may be obtained using a route monitor, to provide
accurate, up-to-date measurements of routing (at least at the time
scale of SNMP measurements, e.g. minutes).
Where the tomography step can be done separately at each time interval
(for instance see [34,35]), it is
simple to adapt early-inverse methods to dynamic network
anomography by inverting (2) at each time step. Given
the straight forward approach for early-inverse methods, We seek here
to generalize late-inverse methods to dynamic network anomography.
4.1 Dynamic Temporal Anomography
When the routing matrix is non-constant, there is no reason to believe
that the measurements 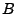 should follow a simple model such as an ARIMA
model. Even where the traffic itself follows such a model, a simple
routing change may change a link load measurement by 100%, for
instance by routing traffic completely away from a particular link. If
we were to apply the ARIMA model to the measurements should follow a simple model such as an ARIMA
model. Even where the traffic itself follows such a model, a simple
routing change may change a link load measurement by 100%, for
instance by routing traffic completely away from a particular link. If
we were to apply the ARIMA model to the measurements 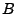 , we would see
such a change in routing as a level-shift anomaly. However, its cause
is not an unknown change in , we would see
such a change in routing as a level-shift anomaly. However, its cause
is not an unknown change in 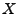 (to be discovered), but rather a known
change in the routing matrices (to be discovered), but rather a known
change in the routing matrices 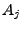 . Likewise, it no longer makes
sense to try to exploit spatial correlations which arose from a
particular routing, to the case of another routing. . Likewise, it no longer makes
sense to try to exploit spatial correlations which arose from a
particular routing, to the case of another routing.
However, it is no less reasonable to approximate the traffic matrix
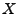 by an ARIMA model (than by an ARIMA model (than 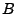 when the routing is constant), even
when routing may change. Under such a modeling assumption, we can
write when the routing is constant), even
when routing may change. Under such a modeling assumption, we can
write
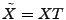 . We know also that the measurements are given
by (2). A reasonable approach to the solution is
therefore to seek a solution . We know also that the measurements are given
by (2). A reasonable approach to the solution is
therefore to seek a solution 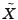 which is consistent with
these equations, but also minimizes one of the norms (described above)
at each time step. We choose to minimize the which is consistent with
these equations, but also minimizes one of the norms (described above)
at each time step. We choose to minimize the 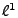 norm norm
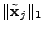 here because (i) it allows us to naturally
incorporate link load constraints at multiple time intervals, and (ii)
it is more accurate than both the pseudoinverse and the greedy
algorithms for static anomography (as we will show in
Section 6). here because (i) it allows us to naturally
incorporate link load constraints at multiple time intervals, and (ii)
it is more accurate than both the pseudoinverse and the greedy
algorithms for static anomography (as we will show in
Section 6).
Unfortunately, for transform based methods (the Fourier, wavelet and
PCA methods) the number of constraints becomes very large (as 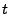 grows). On the other hand, the set of constraints for the ARIMA model
can be written in a form such that it does not grow with
grows). On the other hand, the set of constraints for the ARIMA model
can be written in a form such that it does not grow with 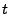 . Hence,
in the following we concentrate on generalizing the ARIMA approach. We
present the algorithm for ARIMA . Hence,
in the following we concentrate on generalizing the ARIMA approach. We
present the algorithm for ARIMA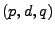 models with models with 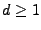 (Section 4.2). We have also extended the algorithm to
handle ARIMA models with
(Section 4.2). We have also extended the algorithm to
handle ARIMA models with 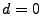 , though we omit this treatment here for
brevity (as it is a straightforward extension). Due to space limits,
we will leave out the discussion on model selection and parameter
estimation, two important issues for applying ARIMA-based
anomography. Interested readers can find this in our technical report
[33]. , though we omit this treatment here for
brevity (as it is a straightforward extension). Due to space limits,
we will leave out the discussion on model selection and parameter
estimation, two important issues for applying ARIMA-based
anomography. Interested readers can find this in our technical report
[33].
4.2 Algorithm for ARIMA Models (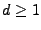 ) )
We are going to seek solutions that are consistent with the
measurements
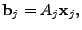 for for
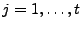 , and an ARIMA
model that gives , and an ARIMA
model that gives
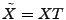 where where 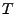 is the same
transformation matrix implicitly defined by (6) and
(7). Importantly, we do not wish to have to estimate is the same
transformation matrix implicitly defined by (6) and
(7). Importantly, we do not wish to have to estimate
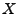 (or we may as well use an early-inverse method). The advantage of
the ARIMA model, is we do not need to know (or we may as well use an early-inverse method). The advantage of
the ARIMA model, is we do not need to know 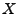 , but only linear
combinations of , but only linear
combinations of 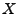 . .
Let 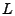 be the backshift operator, whose effect on a process be the backshift operator, whose effect on a process
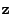 can be summarized as
can be summarized as
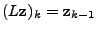 . Let the AR polynomial . Let the AR polynomial
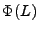 be be
Let
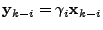 . We now identify . We now identify
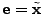 in the ARIMA model described in (5) (or
rather its multivariate extension). By definition the sum in the ARIMA model described in (5) (or
rather its multivariate extension). By definition the sum
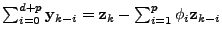 , and so, for , and so, for 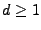 , the ARIMA model (5)
can be rewritten , the ARIMA model (5)
can be rewritten
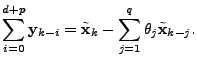 |
(14) |
Define
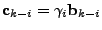 , then as , then as
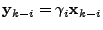 , the measurement equation (2) implies , the measurement equation (2) implies
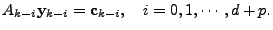 |
(15) |
We can compute
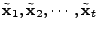 iteratively by solving a series of
iteratively by solving a series of 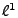 norm minimization
problems norm minimization
problems
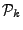 ( (
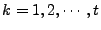 ): ):
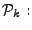 minimize minimize 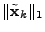 subject to (14) and (15). subject to (14) and (15). |
(16) |
As an example, consider the simplest ARIMA model,
ARIMA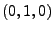 . In this case, . In this case, 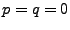 , so we have , so we have
so
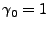 and and
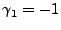 , and (14)
becomes , and (14)
becomes
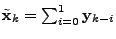 , thus problem , thus problem
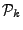 is simply is simply
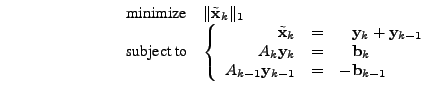 |
(17) |
As in Section 3.4.2, we can accommodate measurement
noise by incorporating penalty terms into the objective to penalize
against violation of constraints (14) and
(15). We can then solve the resulting 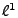 norm
minimization problem by reformulating it as an equivalent LP problem.
We omit such details in the interest of brevity. norm
minimization problem by reformulating it as an equivalent LP problem.
We omit such details in the interest of brevity.
We have also developed two techniques to significantly reduce the size
of the above minimization problems
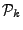 by exploiting the
fact that changes in routing matrices tend to be infrequent (i.e., not
in every time interval) and local (i.e., only in a small subset of
rows). Interested readers please refer to our technical report
[33] for details. by exploiting the
fact that changes in routing matrices tend to be infrequent (i.e., not
in every time interval) and local (i.e., only in a small subset of
rows). Interested readers please refer to our technical report
[33] for details.
5 Evaluation Methodology
We apply our techniques to real network measurement data gathered from
two large backbone networks - Internet2's Abilene network and a
Tier-1 ISP network. Both networks span the continental USA.
The Abilene backbone is
relatively small, with 12 core routers, 15 backbone links and 144 OD
flow elements in its traffic matrix.
The Tier-1 ISP network is much larger, consisting of hundreds of
routers, thousands of links and tens of thousands of different OD
flows. To reduce computation complexity without loss of utility, we
use the technique in [34] to lump edge
routers with topologically equivalent connectivity. This reduces the
total number of OD flows to about 6000.
The primary data inputs for our anomaly diagnosis are the time series
of link loads (bytes across interfaces) for every network, gathered
through SNMP. We use flow level data, where available, for
validation. As is often the case, the flow data is incomplete. The
flow data are collected at the edge of the network where data packets
are sampled and aggregated by the IP source and destination address,
and the TCP port number. Adjusted for sampling rate and combined with
BGP and ISIS/OSPF routing information, these sampled IP flow
statistics are then aggregated into a real traffic matrix
[11], where each element is an OD flow with the
origin and destination being the ingress and egress point of the flow
to/from the network. Consistent with
[19], we aggregate these
measurements into bins of 10 minutes to avoid any synchronization
issues that could have arisen in the data collection.
Ideally, to evaluate the methods, one would like complete flow level
data, SNMP link load measurements, and continuous tracking of routing
information, providing a consistent, comprehensive view of the network
in operation. Unfortunately, we do not have the complete set of flow
level data across the edge of the network (due to problems in vendor
implementations or in data collection), and our routing information is
only ``quasi-'' real time (we rely on snapshots available from table dumps
carried out every 8 hours). As a result, inconsistencies sometimes
arise between these measurements. To overcome these problems and
provide a consistent means for
evaluating the algorithms, we adopt the method in
[34] and reconstruct the link traffic data
by simulating the network routing on the OD flow traffic matrix
generated from the available set of flow level data. Note that we use
derived link load measurements for validation purposes only. In
practice, our methods are applicable to direct measurement of traffic
data as obtained from SNMP.
We conduct our evaluation in two steps. First, we compare the
different solution techniques for the inverse problem
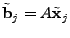 (as described in Section 3.4). The
inverse problem is common to all the late-inverse anomography methods
discussed in Section 3, so for simplicity we choose
to use the simplest temporal forecasting model, ARIMA (as described in Section 3.4). The
inverse problem is common to all the late-inverse anomography methods
discussed in Section 3, so for simplicity we choose
to use the simplest temporal forecasting model, ARIMA , for
evaluation. This model predicts the next observation to have the same
value as the current one. Thus, the inverse problem on the prediction
error can be constructed by simply taking the difference between
consecutive link load observations: , for
evaluation. This model predicts the next observation to have the same
value as the current one. Thus, the inverse problem on the prediction
error can be constructed by simply taking the difference between
consecutive link load observations:
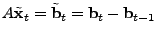 . The performance of the inversion technique is
measured by comparing the inferred solution, . The performance of the inversion technique is
measured by comparing the inferred solution,
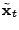 , to the
direct difference of the OD flow, , to the
direct difference of the OD flow,
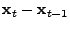 ; the closer
the values are, the better the result. In the context of anomaly
detection, it is often the case that the large elements (large volume
changes) are of chief interest to network management. Hence, we
defined a metric - detection rate - to compare the top ranked ; the closer
the values are, the better the result. In the context of anomaly
detection, it is often the case that the large elements (large volume
changes) are of chief interest to network management. Hence, we
defined a metric - detection rate - to compare the top ranked 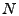 elements (sorted by size) in solution
elements (sorted by size) in solution
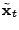 to the top to the top 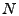 prediction errors
prediction errors
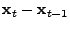 for for 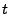 spanning a period of
one week.
As we will see
in Section 6, the top anomalies in our data are
easily resolved by magnitude (close ties are rare).
The detection rate is the ratio of the overlap between
the two sets. Note that the detection rate avoids some problems with
comparing false-alarm versus detection probabilities, as it combines
both into one measure. A high detection rate indicates good
performance. Detection rate is used to compare inference techniques in
Section 6.1, to assess sensitivity to spanning a period of
one week.
As we will see
in Section 6, the top anomalies in our data are
easily resolved by magnitude (close ties are rare).
The detection rate is the ratio of the overlap between
the two sets. Note that the detection rate avoids some problems with
comparing false-alarm versus detection probabilities, as it combines
both into one measure. A high detection rate indicates good
performance. Detection rate is used to compare inference techniques in
Section 6.1, to assess sensitivity to 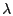 ,
robustness to noise in Section 6.2,
and the effectiveness of the methods for time-varying routing in
Section 6.3. ,
robustness to noise in Section 6.2,
and the effectiveness of the methods for time-varying routing in
Section 6.3.
In Section 6.4.2 we step away from the simple
anomaly detection algorithm applied to test the inference component,
and compare the complete set of anomography methods described in
Section 3. As before we use detection rate to
measure whether the anomaly detection method produces similar results
when applied to the OD pairs directly, or applied to the link load
data, along with an inversion method -- we use the Sparsity-L1 method
(the best performing of the methods tested using the methodology
above).
In other words, we benchmark the anomography method against the anomalies
seen in direct analysis of the OD flows.
Since different methods may find different sets of benchmark anomalies,
we need an objective measure for assessing the performance of the methods.
Ideally, we would like to compare the set
of anomalies identified by each of the methods to the set of ``true''
network anomalies. However, isolating and verifying all genuine
anomalies in an operational network is, although important, a very
difficult task. It involves correlating traffic changes with other
data sources (e.g., BGP/OSPF routing events, network alarms, and
operator logs), an activity that often involves case-by-case analysis.
Instead, we perform pair-wise comparisons, based on the top ranked
anomalies identified by each of the anomography methods, an
approach also taken in Lakhina et al. [19].
Specifically, for each of the anomography methods, we apply the
underlying anomaly detection method directly to the OD flow data.
We think of the top ranked 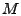 anomalies, denoted by the set anomalies, denoted by the set
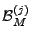 for anomaly detection method for anomaly detection method 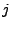 as a benchmark.
For each of the anomography methods as a benchmark.
For each of the anomography methods 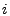 , we examine
the set of , we examine
the set of 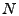 largest anomalies largest anomalies
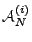 inferred from
link load data.
To help understand the fidelity of the anomography methods we
consider
the overlap between the benchmark and the anomography method, inferred from
link load data.
To help understand the fidelity of the anomography methods we
consider
the overlap between the benchmark and the anomography method,
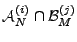 , across the benchmarks
and the anomography methods.
We allow a
small amount of slack (within one ten-minute time shift) in the
comparison between events, in order that phase differences between
methods not unduly impact the results. , across the benchmarks
and the anomography methods.
We allow a
small amount of slack (within one ten-minute time shift) in the
comparison between events, in order that phase differences between
methods not unduly impact the results.
We are interested in understanding both false positives and false
negatives:
- (i)
- False Positives.
Taking
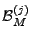 as the benchmark, the false positives produced
by anomography method
as the benchmark, the false positives produced
by anomography method 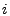 are are
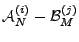 .
The
magnitudes of the anomalies in .
The
magnitudes of the anomalies in
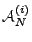 and
and
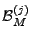 may vary. Yet, intuitively
if one of the
may vary. Yet, intuitively
if one of the 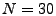 top anomalies in top anomalies in
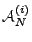 is not among the top
is not among the top 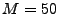 from the benchmark, then this anomaly in from the benchmark, then this anomaly in
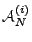 is likely a false positive.
This leads to the following heuristic for detecting false positives.
We choose (reasonable) parameters
is likely a false positive.
This leads to the following heuristic for detecting false positives.
We choose (reasonable) parameters 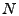 and and 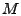 , with , with 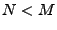 , and count
the false positives as the size of , and count
the false positives as the size of
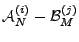 . .
- (ii)
- False Negatives.
Our reasoning is similar.
Taking
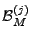 as the benchmark, the false negatives produced
by anomography method
as the benchmark, the false negatives produced
by anomography method 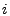 are are
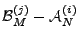 .
Intuitively
if one of the .
Intuitively
if one of the 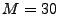 top anomalies in
the benchmark
is not among the top top anomalies in
the benchmark
is not among the top 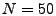 anomalies in
anomalies in
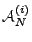 then
this anomaly in
then
this anomaly in
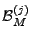 is missed by the anomography method is missed by the anomography method 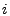 , and
is a false negative.
This leads to the following heuristic for detecting false negatives.
We choose (reasonable) parameters , and
is a false negative.
This leads to the following heuristic for detecting false negatives.
We choose (reasonable) parameters 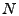 and and 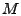 , with , with 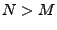 , and count
the false negatives as the size of , and count
the false negatives as the size of
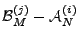 . .
For our reports in the next section,
we choose the smaller of 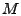 and and 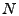 to be 30, since
this roughly represents the number of traffic anomalies that network
engineers might have the resources to analyze deeply on a weekly
basis. We would like to show comparative results where the larger
parameter varies, but cannot within a reasonable amount of space, and
so show results for one fixed value to be 30, since
this roughly represents the number of traffic anomalies that network
engineers might have the resources to analyze deeply on a weekly
basis. We would like to show comparative results where the larger
parameter varies, but cannot within a reasonable amount of space, and
so show results for one fixed value 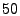 . It is important to note that
the results we obtained for other values of . It is important to note that
the results we obtained for other values of 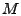 and and 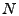 change none of
our qualitative conclusions. change none of
our qualitative conclusions.
6 Results
We obtained six months (03/01/04-09/04/04) of measurements for the
Abilene network and one month (10/06/04-11/02/04) for the Tier-1 ISP
network. We partitioned the data into sets spanning one week each, and
evaluated the methods on each data set. Due to space limits, we
present only one set of representative results - Tier-1 ISP
(10/6/04-10/12/04). In our technical report [33], we also report
results in other weeks for the Tier-1 ISP network as well as for the
Abilene network. These results are qualitatively similar to those
reported here.
6.1 Comparison of Inference Techniques
We first compare different solution techniques for the inference
problem
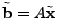 . More specifically, we consider three
late inverse algorithms: Pseudoinverse (Section
3.4.1), Sparsity-Greedy (Section
3.4.2), and Sparsity-L1 (Section
3.4.2), and one early inverse technique: Early
Inverse-Tomogravity. We choose to use the tomogravity method
[35] as the early inverse technique since it has
demonstrated high accuracy and robustness for estimating traffic
matrix for real operational networks [14,35]. . More specifically, we consider three
late inverse algorithms: Pseudoinverse (Section
3.4.1), Sparsity-Greedy (Section
3.4.2), and Sparsity-L1 (Section
3.4.2), and one early inverse technique: Early
Inverse-Tomogravity. We choose to use the tomogravity method
[35] as the early inverse technique since it has
demonstrated high accuracy and robustness for estimating traffic
matrix for real operational networks [14,35].
Figure 1:
Anomalies by Size
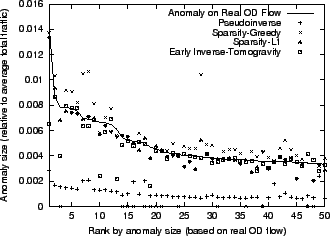 |
Figure 1 plots the sizes of the top 50 anomalies
(the forecast errors) of the OD flows (the solid lines) and the
corresponding values diagnosed by the different inference techniques
(the points) for 10/6/04 to 10/12/04, for the Tier-1 ISP network. The
y-axis provides the size of the anomalies normalized by the average
total traffic volume on the network. The x-axis is the rank by the
size of anomalies directly computed from the OD flows. We observe that
there are very few large changes - among more than 6 million elements
( 6000 OD flows at 1007 data points), there is one instance
where the size of anomaly is more than 1% of total traffic and there
are 18 cases where the disturbances constitute more than 0.5% of
total traffic. This agrees with our intuition on the sparsity of
network anomalies. 6000 OD flows at 1007 data points), there is one instance
where the size of anomaly is more than 1% of total traffic and there
are 18 cases where the disturbances constitute more than 0.5% of
total traffic. This agrees with our intuition on the sparsity of
network anomalies.
We see that Pseudoinverse significantly underestimates the size of the
anomalies. Intuitively, Pseudoinverse finds the least square solution
which distributes the ``energy'' of the anomaly evenly to all
candidate flows that may have contributed to the anomaly, under the
link load constraint. This is directly opposed to the sparsity
maximization philosophy. Among the sparsity maximization techniques,
Sparsity-L1 performs the best. Sparsity-L1 always finds solutions close
to the real anomalies. Sparsity-Greedy, in general, is more effective
than Pseudoinverse, although it sometimes
overestimates the size of anomalies. As a representative of the early
inverse technique, Tomogravity also performs well. With few
exceptions, tomogravity finds solutions that track the real OD flow
anomalies. Intuitively, when a proportionality condition holds,
i.e., when the size of the anomalies are proportional to the sizes of
the OD flows, then early inverse methods work well. However, where the
proportionality condition does not hold, the error can be significant.
Figure 2:
Detection Rate by Various Inference Techniques
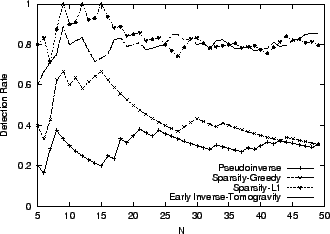 |
Figure 2 presents the detection rate for the
different inference techniques. We observe that for the Tier-1 ISP
network, Sparsity-L1 and Tomogravity, which have about 0.8 detection
rate, significantly outperform other methods.
Due to space limits, we will consider only Sparsity-L1 and
Tomogravity in the rest of the evaluation, as these method demonstrate
the greatest performance and flexibility in dealing with problems such
as missing data and routing changes.
6.2 Robustness
Figure 3:
Sensitivity to Parameter Choice: 
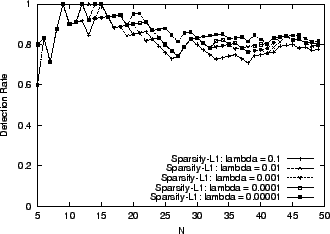 |
 in Sparsity-L1.
Sparsity-L1 involves a parameter in Sparsity-L1.
Sparsity-L1 involves a parameter 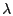 in its formulation
(Eq. 11). Figure 3 investigates the
sensitivity to the parameter choice. Specifically,
Figure 3 plots the detection rate of Sparsity-L1
for in its formulation
(Eq. 11). Figure 3 investigates the
sensitivity to the parameter choice. Specifically,
Figure 3 plots the detection rate of Sparsity-L1
for
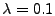 , ,  , ,  , ,  and and 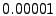 .
All .
All 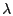 in this range achieve good performance.
This is reassuring, since it suggests that little training or parameter
tuning is needed to match the method to a different network or traffic
pattern. in this range achieve good performance.
This is reassuring, since it suggests that little training or parameter
tuning is needed to match the method to a different network or traffic
pattern.
Measurement Noise.
Thus far, we have assumed perfect link load information for anomaly
detection. However, in real networks, SNMP byte counts are collected
from all routers across the network. Inevitably, measurement issues
such as lack of time synchronization may introduce noise. Below we
evaluate the impact of measurement noise by multiplying white noise
terms
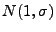 with each element of the link load, and then using
the result as input to our inference algorithms. with each element of the link load, and then using
the result as input to our inference algorithms.
Figure 4:
Sensitivity to Measurement Noise
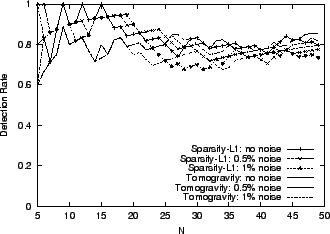 |
Figure 4 compares how well the methods perform with no
noise, to how well they do with noise levels
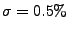 and and
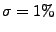 . Note that measurement errors near 1% throughout the
network are quite significant, since the size of the largest anomalies
are themselves near 1% of the total traffic (Figure
1). It is a challenging task to accurately diagnose
anomalies given the comparable level of noise. Nevertheless, we find
that both Sparsity-L1 and Tomogravity are quite robust to measurement
noise. For the Tier-1 ISP network, the detection rate remains above
0.8 for big anomalies (small . Note that measurement errors near 1% throughout the
network are quite significant, since the size of the largest anomalies
are themselves near 1% of the total traffic (Figure
1). It is a challenging task to accurately diagnose
anomalies given the comparable level of noise. Nevertheless, we find
that both Sparsity-L1 and Tomogravity are quite robust to measurement
noise. For the Tier-1 ISP network, the detection rate remains above
0.8 for big anomalies (small  ) and above 0.7 for the top 50
anomalies.
These results demonstrate the strength of our
algorithms in dealing with imperfect measurements. ) and above 0.7 for the top 50
anomalies.
These results demonstrate the strength of our
algorithms in dealing with imperfect measurements.
6.3 Time Varying Routing Matrices
Missing Data.
Missing measurement data, arising from problems such as packet loss
during data collection, is common in real networks. Indeed, this can
be tricky to deal with, since the loss of link load data has the
effect of producing time varying routing matrices in the anomography
formulation. Fortunately, as discussed in Section 4,
our extended Sparsity-L1 algorithm can handle this situation.
Figure 5:
Impact of Missing Data
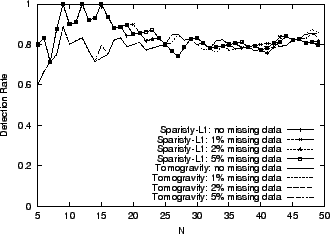 |
Figure 5 shows the performance of the
inference algorithms with up to 5% of the data missing - missing
values are selected uniformly at random. We see that both
Sparsity-L1 and Tomogravity suffer only minor (almost negligible)
performance impact, in terms of detection rate.
The low sensitivity to missing data is an important feature of these
methods, which is critical for real implementation.
Routing Changes.
In an operational network, the routing matrix is unlikely to remain
unchanged over a few days. Hardware failures, engineering operations,
maintenance and upgrades all may cause traffic to be rerouted on
alternative paths. Here we evaluate the impact of
routing changes on the performance of our algorithms. We introduce
routing changes by simulating faults on internal links.
Figure 6:
Impact of Route Change
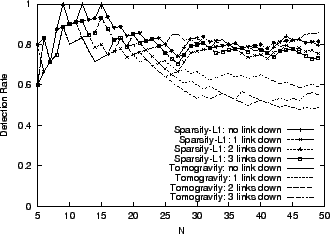 |
Figure 6 presents results where we have randomly
failed/repaired up to 3 links at each time instance. We observe that
Sparsity-L1 is very robust to such a disturbance in the routing
structure, while Tomogravity suffers significant performance impact.
It appears that Tomogravity suffers here because errors in the (early)
inference step, being computed from different routing matrices, add to
become comparable to the anomalies themselves.
This demonstrates another advantage of the late-inverse over the
early-inverse approach.
6.4 Comparison of Anomography Methods
Thus far, we have compared the performance of Sparsity-L1 and Early
Inverse-Tomogravity, under the simple temporal model (forecasting the
next data point using the current value). We found that Sparsity-L1 in
general outperforms the Early Inverse approach.
We also observed that Sparsity-L1 is robust to measurement noise,
is insensitive to parameter choice, and is able to handle missing data
and route changes. We now evaluate overall performance when applying
Sparsity-L1 with other temporal and spatial anomography methods. In
particular, we compare FFT (Section 3.3.2), Wavelet (Section 3.3.3), PCA (Section
3.2.1), TPCA (Section 3.3.4), and
four ARIMA based methods, Diff (the simple forecasting model of
the last section), Holt-Winters, EWMA, and general ARIMA, which determines the appropriate model using the method in
[33].
As noted in Section 5, for each model considered,
we compute
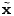 directly from the OD flow traffic data and use
it as the benchmark. Next, we compute directly from the OD flow traffic data and use
it as the benchmark. Next, we compute
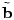 with the same
anomography model, and construct the with the same
anomography model, and construct the
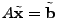 inference problem. We compare the solution derived through
Sparsity-L1 with the benchmark. Figure 7
presents the detection rate for these approaches. To avoid
overcrowding the graph, we divide the anomography methods into two
groups.
Figure 7 (a) plots
the results for
the ARIMA family of anomography approaches and
Figure 7 (b) plots
the results for the rest. We
observe that for all the ARIMA based approaches, Sparsity-L1 finds
very good solutions. With the traffic data aggregated at the 10-minute
level, simple Diff and EWMA can sufficiently extract the anomalous
traffic and warrant a solution that maximizes the sparsity of the
anomalies. Holt-Winters produces better performance than Diff and
EWMA. This is because the model is more sophisticated, and thus is
able to capture more complex temporal trends exhibited in the traffic
data. Further sophistication, as incorporated in ARIMA, however,
cannot significantly improve performance. In the family of ARIMA
models, Holt-Winters appears to provide the best
complexity-performance trade-off.
inference problem. We compare the solution derived through
Sparsity-L1 with the benchmark. Figure 7
presents the detection rate for these approaches. To avoid
overcrowding the graph, we divide the anomography methods into two
groups.
Figure 7 (a) plots
the results for
the ARIMA family of anomography approaches and
Figure 7 (b) plots
the results for the rest. We
observe that for all the ARIMA based approaches, Sparsity-L1 finds
very good solutions. With the traffic data aggregated at the 10-minute
level, simple Diff and EWMA can sufficiently extract the anomalous
traffic and warrant a solution that maximizes the sparsity of the
anomalies. Holt-Winters produces better performance than Diff and
EWMA. This is because the model is more sophisticated, and thus is
able to capture more complex temporal trends exhibited in the traffic
data. Further sophistication, as incorporated in ARIMA, however,
cannot significantly improve performance. In the family of ARIMA
models, Holt-Winters appears to provide the best
complexity-performance trade-off.
From Figure 7 (b), we observe that
Sparsity-L1 can also achieve high detection rate under FFT, Wavelet
and TPCA. However, it doesn't work well with PCA2. This can be explained as follows. When we
apply spatial PCA on the real traffic matrix 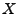 and the link load
matrix and the link load
matrix 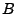 , we obtain two linear transformation , we obtain two linear transformation
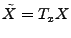 ,
and ,
and
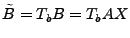 , respectively. However, the two
transformation matrices , respectively. However, the two
transformation matrices 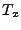 and and 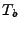 may differ significantly
because the spatial correlation among link loads and that among OD
flows are rather different. Even if we use may differ significantly
because the spatial correlation among link loads and that among OD
flows are rather different. Even if we use 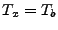 , we cannot
ensure that , we cannot
ensure that
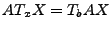 (i.e., (i.e.,
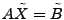 (Note
that this last comment applies to spatial anomography methods in
general). Thus, the spatial PCA anomography solution is not expected
to completely overlap with the (Note
that this last comment applies to spatial anomography methods in
general). Thus, the spatial PCA anomography solution is not expected
to completely overlap with the
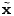 identified by directly
applying spatial PCA on the OD traffic flows. In contrast, the
temporal anomography methods are self-consistent in that given identified by directly
applying spatial PCA on the OD traffic flows. In contrast, the
temporal anomography methods are self-consistent in that given
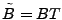 , if we apply the same transformation , if we apply the same transformation 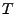 on on 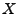 and
obtain and
obtain
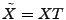 , we guarantee that , we guarantee that
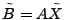 (
(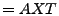 ). ).
Figure 7:
Sparsity-L1 with Various Anomography Methods
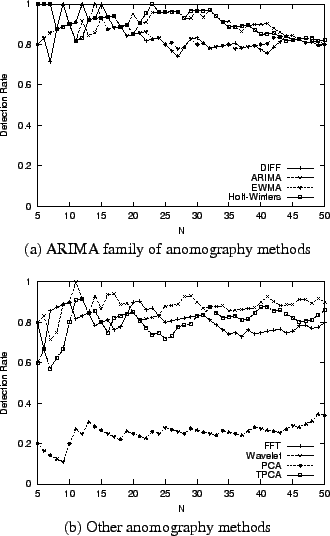 |
6.4.2 Cross Validation for Different Methods
We now turn to comparing the various anomography methods . To do
so, we use a set of benchmarks, as described in
Section 5, each derived from applying anomaly
detection algorithm directly to the OD flows. For each benchmark,
we report on the success of all of the anomography methods. The hope
is that methods emerge that achieve both low false positives and low false negatives
for nearly all of the benchmarks.
Table 1:
False positives seen in the top  inferred anomalies compared against the top inferred anomalies compared against the top  benchmark anomalies. benchmark anomalies.
|
|
False Positives with Top 50 Benchmark |
|
Top 30 Inferred |
Diff |
ARIMA |
EWMA |
H-W |
FFT |
Wavelet |
PCA |
TPCA |
|
Diff |
3 |
6 |
3 |
6 |
6 |
4 |
14 |
14 |
|
ARIMA |
4 |
1 |
4 |
1 |
8 |
3 |
10 |
13 |
|
EWMA |
3 |
6 |
3 |
6 |
7 |
5 |
15 |
13 |
|
Holt-Winters |
4 |
1 |
4 |
1 |
8 |
3 |
10 |
13 |
|
FFT |
6 |
6 |
6 |
7 |
2 |
6 |
18 |
19 |
|
Wavelet |
6 |
6 |
6 |
6 |
8 |
1 |
12 |
13 |
|
TPCA |
17 |
17 |
17 |
17 |
20 |
13 |
14 |
0 |
|
PCA |
18 |
18 |
18 |
18 |
20 |
14 |
14 |
1 |
|
PCA*(37) |
18 |
17 |
18 |
17 |
23 |
16 |
11 |
8 |
|
Table 2:
False negatives seen in the top  inferred anomalies compared against the top inferred anomalies compared against the top 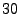 benchmark anomalies. benchmark anomalies.
|
|
False Negatives with Top 30 Benchmark |
|
Top 50 Inferred |
Diff |
ARIMA |
EWMA |
H-W |
FFT |
Wavelet |
PCA |
TPCA |
|
Diff |
0 |
1 |
0 |
1 |
5 |
5 |
12 |
17 |
|
ARIMA |
1 |
0 |
1 |
0 |
6 |
4 |
12 |
18 |
|
EWMA |
0 |
1 |
0 |
1 |
5 |
5 |
12 |
17 |
|
Holt-Winters |
1 |
0 |
1 |
0 |
6 |
4 |
12 |
18 |
|
FFT |
3 |
8 |
4 |
8 |
1 |
7 |
18 |
19 |
|
Wavelet |
0 |
2 |
1 |
2 |
5 |
0 |
11 |
13 |
|
TPCA |
14 |
14 |
14 |
14 |
19 |
15 |
15 |
3 |
|
PCA |
10 |
13 |
10 |
13 |
15 |
11 |
13 |
1 |
|
PCA*(37) |
17 |
18 |
18 |
18 |
21 |
19 |
16 |
8 |
|
In Table 1 (a) we present the false positives
for the Tier-1 ISP network with 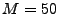 and and 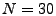 (see Section
5). We found results for
different values of (see Section
5). We found results for
different values of  and and 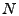 to be qualitatively quite similar.
To align our results with the methodology reported in
[19], we include the bottom row,
labeled PCA*, where we use a squared
prediction error (SPE) based scheme to determine the set of time
intervals at which big anomalies occur, and the greedy
approach (Section 3.4.2) to solve the inference problem.
Note that the number of anomalies reported by PCA*
may be less than to be qualitatively quite similar.
To align our results with the methodology reported in
[19], we include the bottom row,
labeled PCA*, where we use a squared
prediction error (SPE) based scheme to determine the set of time
intervals at which big anomalies occur, and the greedy
approach (Section 3.4.2) to solve the inference problem.
Note that the number of anomalies reported by PCA*
may be less than 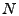 . We therefore report the actual number of anomalies
in the table next to the label PCA*. . We therefore report the actual number of anomalies
in the table next to the label PCA*.
From the table, we observe from the upper left
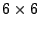 quadrant
that the ARIMA, FFT and Wavelet approaches tend to have relative low
false positives among detected anomalies. Thus,
the top 30 ranked anomalies derived through
these approaches indeed appear to be anomalous traffic events that are worth
investigating. quadrant
that the ARIMA, FFT and Wavelet approaches tend to have relative low
false positives among detected anomalies. Thus,
the top 30 ranked anomalies derived through
these approaches indeed appear to be anomalous traffic events that are worth
investigating.
The PCA based approaches, however, exhibit a higher false positives
when benchmarked against other approaches.
This appears to be partially due to PCA identifying anomalies of
a different type than those identified by the methods.
Consider, for example, a sudden increase of traffic for an OD
flow that persists for a couple of hours. PCA methods may
identify every instance within the two-hour period as anomalous.
ARIMA based approaches detect abrupt traffic changes.
Hence ARIMA based methods likely extract only the ``edges'' -
the first and
last instance - of the two-hour period.
Another factor contributing to PCA's false positives may be
its lack of self-consistency: anomalies present in
the OD pairs but not detected by the method in the link loads.
In addition,
unlike ARIMA, FFT, or wavelet based tomography, both spatial
PCA and temporal PCA cannot fully utilize temporal ordering
information in the measured time series data.
For example, any reordering of the time
series,
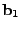 , ,
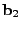 , ..., , ...,
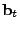 , does not affect the outcome of the
algorithm. , does not affect the outcome of the
algorithm.
Table 2 presents the number of false negatives
for 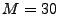 and and 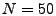 , where we are interested in
the number
of large anomalies that are not identified by each approach. We
observe that the ARIMA methods, FFT and Wavelet anomography approaches
have superb performance - the number of false negatives are very low.
This indicates
that very few important traffic anomalies can pass undetected by these
approaches. The PCA based approaches, however, identify about half of
the anomalies. , where we are interested in
the number
of large anomalies that are not identified by each approach. We
observe that the ARIMA methods, FFT and Wavelet anomography approaches
have superb performance - the number of false negatives are very low.
This indicates
that very few important traffic anomalies can pass undetected by these
approaches. The PCA based approaches, however, identify about half of
the anomalies.
7 Conclusions
In this paper, we introduced network anomography, the problem
of inferring network-level anomalies from widely available data
aggregates.
Our major advances are:
- We introduced a powerful framework for anomography that cleanly
separates the anomaly detection component from the inference
component.
The framework opens up a wide field for innovation and for the
development of families of new algorithms.
The novel method of Lakhina et al. based on PCA falls within the
framework.
- Within the framework, we put forward a number of novel
algorithms,
taking advantage of
the range of choices for anomaly detection and inference
components and choosing between temporal versus spatial approaches.
- We developed a new dynamic anomography algorithm, which
tracks both routing and traffic measurements, and so enables
alerting with high fidelity on traffic matrix anomalies, without
alerting on internal routing changes that leave the traffic matrix
relatively stable. As routing changes are often due to normal
internal self-healing behavior separating these changes from
intrinsic traffic anomalies is advantageous. An additional benefit
of dynamic anomography is that is robust to missing data, an
important operational reality.
- Using extensive data from Internet2's Abilene network and a Tier-1
ISP, we evaluated these anomography methods.
The findings are encouraging.
Specifically, the results indicate that the new set of temporal
anomography methods introduced here have better fidelity, particularly
when using
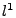 minimization for the inference step.
Dynamic anomography using ARIMA based methods and minimization for the inference step.
Dynamic anomography using ARIMA based methods and
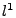 norm minimization shows uniformly high fidelity (low false
positive and false negatives) and high robustness (to routing changes
and missing or corrupted data). norm minimization shows uniformly high fidelity (low false
positive and false negatives) and high robustness (to routing changes
and missing or corrupted data).
While we believe our work represents a significant advance in the
state of the art, we recognize that the
the ultimate test of performance is significant operational experience:
utility is bringing to light in the field new anomalies that
were ``flying under the radar'' of other techniques, while producing very
few false alarms.
Our larger goal in future work is to explore the feasibility and
performance of automated traffic management systems, which incorporate
anomaly detection, root cause diagnosis and traffic and route control
for operational networks.
- 1
-
P. Barford, J. Kline, D. Plonka, and A. Ron.
A signal analysis of network traffic anomalies.
In ACM Internet Measurement Workshop, Nov. 2002.
- 2
-
G. E. P. Box, G. M. Jenkins, and G. C. Reinsel.
Time Series Analysis, Forecasting and Control.
Prentice-Hall, Englewood Cliffs, 1994.
- 3
-
P. J. Brockwell and R. A. Davis.
Introduction to Time Series and Forecasting.
Springer-Varlang, 2nd edition, 2002.
- 4
-
J. D. Brutag.
Aberrant behavior detection and control in time series for network
monitoring.
In 14th Systems Administration Conference (LISA 2000), Dec.
2000.
- 5
-
J. Cao, D. Davis, S. V. Wiel, and B. Yu.
Time-varying network tomography.
J. Amer. Statist. Assoc, 95(452):1063-1075, 2000.
- 6
-
I. Daubechies.
Orthonormal bases of compactly supported wavelets.
Communications on Pure and Applied Mathematics, 41:909-996,
1988.
- 7
-
I. Daubechies.
Ten Lectures on Wavelets, volume 41 of CBMS-NSF Regional
Conference Series in Applied Mathematics.
SIAM, 1992.
- 8
-
D. L. Donoho.
For most large underdetermined systems of equations, the minimal
l1-norm near-solution approximates the sparsest near-solution, Aug. 2004.
https://www-stat.stanford.edu/~donoho/Reports/.
- 9
-
D. L. Donoho.
For most large underdetermined systems of equations, the minimal
l1-norm solution is also the sparsest solution, Sept. 2004.
https://www-stat.stanford.edu/~donoho/Reports/.
- 10
-
A. Feldmann, A. Greenberg, C. Lund, N. Reingold, and J. Rexford.
Netscope: Traffic engineering for IP networks.
IEEE Network Magazine, pages 11-19, Mar./Apr. 2000.
- 11
-
A. Feldmann, A. Greenberg, C. Lund, N. Reingold, J. Rexford, and F. True.
Deriving traffic demands for operational IP networks: Methodology
and experience.
IEEE/ACM Transactions on Networking, 9(3):265-279, 2001.
- 12
-
A. Graps.
Amara's wavelet page, 2004.
https://www.amara.com/current/wavelet.html.
- 13
-
M. Grossglauser, N. Koudas, Y. Park, and A. Variot.
FALCON: Fault management via alarm warehousing and mining.
In NRDM 2001 Workshop, May 2001.
- 14
-
A. Gunnar, M. Johansson, and T. Telkamp.
Traffic matrix estimation on a large IP backbone: A comparison on
real data.
In ACM Internet Measurement Conference, Oct. 2004.
- 15
-
C. Hood and C. Ji.
Proactive network fault detection.
IEEE Trans. Reliability, 46(3):333-341, 1997.
- 16
-
Katzela and Schwartz.
Schemes for fault identification in communication networks.
IEEE/ACM Transactions on Networking, 3(6):753-764, 1995.
- 17
-
B. Krishnamurthy, S. Sen, Y. Zhang, and Y. Chen.
Sketch-based change detection: Methods, evaluation, and applications.
In ACM Internet Measurement Conference, Oct. 2003.
- 18
-
A. Lakhina, M. Crovella, and C. Diot.
Characterization of network-wide anomalies in traffic flows.
In ACM Internet Measurement Conference, Oct. 2004.
- 19
-
A. Lakhina, M. Crovella, and C. Diot.
Diagnosing network-wide traffic anomalies.
In ACM SIGCOMM, Aug. 2004.
- 20
-
A. Lakhina, K. Papagiannaki, C. D. Mark Crovella, E. D. Kolaczyk, and N. Taft.
Structural analysis of network traffic flows.
In ACM SIGMETRICS, 2004.
- 21
-
S. Mallat.
A Wavelet Tour of Signal Processing.
Academic Press, San Diego, 2nd edition, 2001.
- 22
-
A. Medina, N. Taft, K. Salamatian, S. Bhattacharyya, and C. Diot.
Traffic matrix estimation: Existing techniques and new directions.
In ACM SIGCOMM, Aug. 2002.
- 23
-
A. Nucci, R. Cruz, N. Taft, and C. Diot.
Design of IGP link weights for estimation of traffic matrices.
In IEEE Infocom, Mar. 2004.
- 24
-
Y. C. Pati, R. Rezaiifar, and P. S. Krishnaprasad.
Orthogonal matching pursuit: Recursive function approximation with
applications to wavelet decomposition.
In 27th Annual Asilomar Conference on Signals, Systems, and
Computers, 1993.
- 25
-
M. Roughan, T. Griffin, M. Mao, A. Greenberg, and B. Freeman.
IP forwarding anomalies and improving their detection using
multiple data sources.
In ACM SIGCOMM Workshop on Network Troubleshooting, pages
307-312, Sept. 2004.
- 26
-
SAS 9 online document.
Equations for the smoothing models, Jan. 2004.
https://support.sas.com/91doc/getDoc/hpfug.hlp/hpfdet_sect7.htm.
- 27
-
A. Shaikh, C. Isett, A. Greenberg, M. Roughan, and J. Gottlieb.
A case study of OSPF behavior in a large enterprise network.
In ACM Internet Measurement Workshop, 2002.
- 28
-
C. Tebaldi and M. West.
Bayesian inference on network traffic using link count data.
J. Amer. Statist. Assoc, 93(442):557-576, 1998.
- 29
-
R. Teixeira, N. Duffield, J. Rexford, and M. Roughan.
Traffic matrix reloaded: Impact of routing changes renata teixeira.
In Workshop on Passive and Active Measurements (PAM), 2005.
- 30
-
M. Thottan and C. Ji.
Proactive anomaly detection using distributed intelligent agents.
IEEE Network, Sept/Oct 1998.
- 31
-
Y. Vardi.
Network tomography: estimating source-destination traffic intensities
from link data.
J. Amer. Statist. Assoc., 91(433):365-377, 1996.
- 32
-
A. Ward, P. Glynn, and K. Richardson.
Internet service performance failure detection.
ACM SIGMETRICS Performance Evaluation Review archive,
26(3):38-43, Dec. 1998.
- 33
-
Y. Zhang, Z. Ge, A. Greenberg, and M. Roughan.
Network anomography.
UT-Austin Technical Report, 2005.
https://www.cs.utexas.edu/~yzhang/papers/.
- 34
-
Y. Zhang, M. Roughan, N. Duffield, and A. Greenberg.
Fast accurate computation of large-scale ip traffic matrices from
link loads.
In ACM SIGMETRICS, June 2003.
- 35
-
Y. Zhang, M. Roughan, C. Lund, and D. Donoho.
An information-theoretic approach to traffic matrix estimation.
In ACM SIGCOMM, Aug. 2003.
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -image_type gif paper.tex
The translation was initiated by Yin Zhang on 2005-08-10
Footnotes
- ... loads1
- Note that the
link load vector
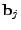 includes the aggregated traffic at
different ingress/egress points; the corresponding rows in includes the aggregated traffic at
different ingress/egress points; the corresponding rows in 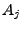 encode the OD flows that enter/exit the network at these points.
encode the OD flows that enter/exit the network at these points.
- ... PCA2
- We have
verified that Pseudoinverse and Sparsity-Greedy work even worse than
Sparsity-L1 for PCA.


Yin Zhang
2005-08-10
|
![]() to vary over time. In IP networks, routing
changes occur as part of the normal ``self-healing'' behavior of the
network, and so it is advantageous to isolate these from traffic
anomalies and only signal traffic anomalies. In addition, if some
measurements are missing (say at time
to vary over time. In IP networks, routing
changes occur as part of the normal ``self-healing'' behavior of the
network, and so it is advantageous to isolate these from traffic
anomalies and only signal traffic anomalies. In addition, if some
measurements are missing (say at time ![]() ), we may still form a
consistent problem by setting the appropriate rows of
), we may still form a
consistent problem by setting the appropriate rows of ![]() to
zero. Thus, for realistic SNMP measurements where missing data are
often an issue, we still wish to vary
to
zero. Thus, for realistic SNMP measurements where missing data are
often an issue, we still wish to vary ![]() even for static routing.
Routing measurements may be obtained using a route monitor, to provide
accurate, up-to-date measurements of routing (at least at the time
scale of SNMP measurements, e.g. minutes).
even for static routing.
Routing measurements may be obtained using a route monitor, to provide
accurate, up-to-date measurements of routing (at least at the time
scale of SNMP measurements, e.g. minutes).
![]() should follow a simple model such as an ARIMA
model. Even where the traffic itself follows such a model, a simple
routing change may change a link load measurement by 100%, for
instance by routing traffic completely away from a particular link. If
we were to apply the ARIMA model to the measurements
should follow a simple model such as an ARIMA
model. Even where the traffic itself follows such a model, a simple
routing change may change a link load measurement by 100%, for
instance by routing traffic completely away from a particular link. If
we were to apply the ARIMA model to the measurements ![]() , we would see
such a change in routing as a level-shift anomaly. However, its cause
is not an unknown change in
, we would see
such a change in routing as a level-shift anomaly. However, its cause
is not an unknown change in ![]() (to be discovered), but rather a known
change in the routing matrices
(to be discovered), but rather a known
change in the routing matrices ![]() . Likewise, it no longer makes
sense to try to exploit spatial correlations which arose from a
particular routing, to the case of another routing.
. Likewise, it no longer makes
sense to try to exploit spatial correlations which arose from a
particular routing, to the case of another routing.
![]() by an ARIMA model (than
by an ARIMA model (than ![]() when the routing is constant), even
when routing may change. Under such a modeling assumption, we can
write
when the routing is constant), even
when routing may change. Under such a modeling assumption, we can
write
![]() . We know also that the measurements are given
by (2). A reasonable approach to the solution is
therefore to seek a solution
. We know also that the measurements are given
by (2). A reasonable approach to the solution is
therefore to seek a solution ![]() which is consistent with
these equations, but also minimizes one of the norms (described above)
at each time step. We choose to minimize the
which is consistent with
these equations, but also minimizes one of the norms (described above)
at each time step. We choose to minimize the ![]() norm
norm
![]() here because (i) it allows us to naturally
incorporate link load constraints at multiple time intervals, and (ii)
it is more accurate than both the pseudoinverse and the greedy
algorithms for static anomography (as we will show in
Section 6).
here because (i) it allows us to naturally
incorporate link load constraints at multiple time intervals, and (ii)
it is more accurate than both the pseudoinverse and the greedy
algorithms for static anomography (as we will show in
Section 6).
![]() grows). On the other hand, the set of constraints for the ARIMA model
can be written in a form such that it does not grow with
grows). On the other hand, the set of constraints for the ARIMA model
can be written in a form such that it does not grow with ![]() . Hence,
in the following we concentrate on generalizing the ARIMA approach. We
present the algorithm for ARIMA
. Hence,
in the following we concentrate on generalizing the ARIMA approach. We
present the algorithm for ARIMA![]() models with
models with ![]() (Section 4.2). We have also extended the algorithm to
handle ARIMA models with
(Section 4.2). We have also extended the algorithm to
handle ARIMA models with ![]() , though we omit this treatment here for
brevity (as it is a straightforward extension). Due to space limits,
we will leave out the discussion on model selection and parameter
estimation, two important issues for applying ARIMA-based
anomography. Interested readers can find this in our technical report
[33].
, though we omit this treatment here for
brevity (as it is a straightforward extension). Due to space limits,
we will leave out the discussion on model selection and parameter
estimation, two important issues for applying ARIMA-based
anomography. Interested readers can find this in our technical report
[33].
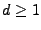 )
)
![]() for
for
![]() , and an ARIMA
model that gives
, and an ARIMA
model that gives
![]() where
where ![]() is the same
transformation matrix implicitly defined by (6) and
(7). Importantly, we do not wish to have to estimate
is the same
transformation matrix implicitly defined by (6) and
(7). Importantly, we do not wish to have to estimate
![]() (or we may as well use an early-inverse method). The advantage of
the ARIMA model, is we do not need to know
(or we may as well use an early-inverse method). The advantage of
the ARIMA model, is we do not need to know ![]() , but only linear
combinations of
, but only linear
combinations of ![]() .
.
![]() be the backshift operator, whose effect on a process
be the backshift operator, whose effect on a process
![]() can be summarized as
can be summarized as
![]() . Let the AR polynomial
. Let the AR polynomial
![]() be
be
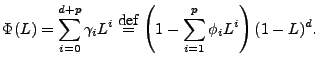
![]() . In this case,
. In this case, ![]() , so we have
, so we have
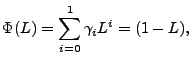
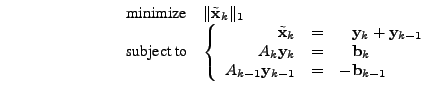
![]() norm
minimization problem by reformulating it as an equivalent LP problem.
We omit such details in the interest of brevity.
norm
minimization problem by reformulating it as an equivalent LP problem.
We omit such details in the interest of brevity.
![]() by exploiting the
fact that changes in routing matrices tend to be infrequent (i.e., not
in every time interval) and local (i.e., only in a small subset of
rows). Interested readers please refer to our technical report
[33] for details.
by exploiting the
fact that changes in routing matrices tend to be infrequent (i.e., not
in every time interval) and local (i.e., only in a small subset of
rows). Interested readers please refer to our technical report
[33] for details.
![]() anomalies, denoted by the set
anomalies, denoted by the set
![]() for anomaly detection method
for anomaly detection method ![]() as a benchmark.
For each of the anomography methods
as a benchmark.
For each of the anomography methods ![]() , we examine
the set of
, we examine
the set of ![]() largest anomalies
largest anomalies
![]() inferred from
link load data.
To help understand the fidelity of the anomography methods we
consider
the overlap between the benchmark and the anomography method,
inferred from
link load data.
To help understand the fidelity of the anomography methods we
consider
the overlap between the benchmark and the anomography method,
![]() , across the benchmarks
and the anomography methods.
We allow a
small amount of slack (within one ten-minute time shift) in the
comparison between events, in order that phase differences between
methods not unduly impact the results.
, across the benchmarks
and the anomography methods.
We allow a
small amount of slack (within one ten-minute time shift) in the
comparison between events, in order that phase differences between
methods not unduly impact the results.
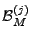 as the benchmark, the false positives produced
by anomography method
as the benchmark, the false positives produced
by anomography method  are
are
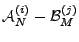 .
The
magnitudes of the anomalies in
.
The
magnitudes of the anomalies in
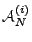 and
and
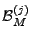 may vary. Yet, intuitively
if one of the
may vary. Yet, intuitively
if one of the  top anomalies in
top anomalies in
 is not among the top
is not among the top 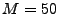 from the benchmark, then this anomaly in
from the benchmark, then this anomaly in
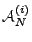 is likely a false positive.
This leads to the following heuristic for detecting false positives.
We choose (reasonable) parameters
is likely a false positive.
This leads to the following heuristic for detecting false positives.
We choose (reasonable) parameters  and
and 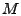 , with
, with 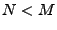 , and count
the false positives as the size of
, and count
the false positives as the size of
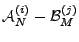 .
.
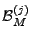 as the benchmark, the false negatives produced
by anomography method
as the benchmark, the false negatives produced
by anomography method  are
are
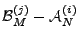 .
Intuitively
if one of the
.
Intuitively
if one of the  top anomalies in
the benchmark
is not among the top
top anomalies in
the benchmark
is not among the top  anomalies in
anomalies in
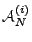 then
this anomaly in
then
this anomaly in
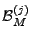 is missed by the anomography method
is missed by the anomography method 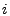 , and
is a false negative.
This leads to the following heuristic for detecting false negatives.
We choose (reasonable) parameters
, and
is a false negative.
This leads to the following heuristic for detecting false negatives.
We choose (reasonable) parameters 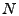 and
and 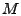 , with
, with 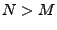 , and count
the false negatives as the size of
, and count
the false negatives as the size of
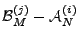 .
.
![]() and
and ![]() to be 30, since
this roughly represents the number of traffic anomalies that network
engineers might have the resources to analyze deeply on a weekly
basis. We would like to show comparative results where the larger
parameter varies, but cannot within a reasonable amount of space, and
so show results for one fixed value
to be 30, since
this roughly represents the number of traffic anomalies that network
engineers might have the resources to analyze deeply on a weekly
basis. We would like to show comparative results where the larger
parameter varies, but cannot within a reasonable amount of space, and
so show results for one fixed value ![]() . It is important to note that
the results we obtained for other values of
. It is important to note that
the results we obtained for other values of ![]() and
and ![]() change none of
our qualitative conclusions.
change none of
our qualitative conclusions.
![]() . More specifically, we consider three
late inverse algorithms: Pseudoinverse (Section
3.4.1), Sparsity-Greedy (Section
3.4.2), and Sparsity-L1 (Section
3.4.2), and one early inverse technique: Early
Inverse-Tomogravity. We choose to use the tomogravity method
[35] as the early inverse technique since it has
demonstrated high accuracy and robustness for estimating traffic
matrix for real operational networks [14,35].
. More specifically, we consider three
late inverse algorithms: Pseudoinverse (Section
3.4.1), Sparsity-Greedy (Section
3.4.2), and Sparsity-L1 (Section
3.4.2), and one early inverse technique: Early
Inverse-Tomogravity. We choose to use the tomogravity method
[35] as the early inverse technique since it has
demonstrated high accuracy and robustness for estimating traffic
matrix for real operational networks [14,35].
![]() 6000 OD flows at 1007 data points), there is one instance
where the size of anomaly is more than 1% of total traffic and there
are 18 cases where the disturbances constitute more than 0.5% of
total traffic. This agrees with our intuition on the sparsity of
network anomalies.
6000 OD flows at 1007 data points), there is one instance
where the size of anomaly is more than 1% of total traffic and there
are 18 cases where the disturbances constitute more than 0.5% of
total traffic. This agrees with our intuition on the sparsity of
network anomalies.
![]() in Sparsity-L1.
Sparsity-L1 involves a parameter
in Sparsity-L1.
Sparsity-L1 involves a parameter ![]() in its formulation
(Eq. 11). Figure 3 investigates the
sensitivity to the parameter choice. Specifically,
Figure 3 plots the detection rate of Sparsity-L1
for
in its formulation
(Eq. 11). Figure 3 investigates the
sensitivity to the parameter choice. Specifically,
Figure 3 plots the detection rate of Sparsity-L1
for
![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
All
.
All ![]() in this range achieve good performance.
This is reassuring, since it suggests that little training or parameter
tuning is needed to match the method to a different network or traffic
pattern.
in this range achieve good performance.
This is reassuring, since it suggests that little training or parameter
tuning is needed to match the method to a different network or traffic
pattern.
![]() and
and
![]() . Note that measurement errors near 1% throughout the
network are quite significant, since the size of the largest anomalies
are themselves near 1% of the total traffic (Figure
1). It is a challenging task to accurately diagnose
anomalies given the comparable level of noise. Nevertheless, we find
that both Sparsity-L1 and Tomogravity are quite robust to measurement
noise. For the Tier-1 ISP network, the detection rate remains above
0.8 for big anomalies (small
. Note that measurement errors near 1% throughout the
network are quite significant, since the size of the largest anomalies
are themselves near 1% of the total traffic (Figure
1). It is a challenging task to accurately diagnose
anomalies given the comparable level of noise. Nevertheless, we find
that both Sparsity-L1 and Tomogravity are quite robust to measurement
noise. For the Tier-1 ISP network, the detection rate remains above
0.8 for big anomalies (small ![]() ) and above 0.7 for the top 50
anomalies.
These results demonstrate the strength of our
algorithms in dealing with imperfect measurements.
) and above 0.7 for the top 50
anomalies.
These results demonstrate the strength of our
algorithms in dealing with imperfect measurements.
![]() directly from the OD flow traffic data and use
it as the benchmark. Next, we compute
directly from the OD flow traffic data and use
it as the benchmark. Next, we compute
![]() with the same
anomography model, and construct the
with the same
anomography model, and construct the
![]() inference problem. We compare the solution derived through
Sparsity-L1 with the benchmark. Figure 7
presents the detection rate for these approaches. To avoid
overcrowding the graph, we divide the anomography methods into two
groups.
Figure 7 (a) plots
the results for
the ARIMA family of anomography approaches and
Figure 7 (b) plots
the results for the rest. We
observe that for all the ARIMA based approaches, Sparsity-L1 finds
very good solutions. With the traffic data aggregated at the 10-minute
level, simple Diff and EWMA can sufficiently extract the anomalous
traffic and warrant a solution that maximizes the sparsity of the
anomalies. Holt-Winters produces better performance than Diff and
EWMA. This is because the model is more sophisticated, and thus is
able to capture more complex temporal trends exhibited in the traffic
data. Further sophistication, as incorporated in ARIMA, however,
cannot significantly improve performance. In the family of ARIMA
models, Holt-Winters appears to provide the best
complexity-performance trade-off.
inference problem. We compare the solution derived through
Sparsity-L1 with the benchmark. Figure 7
presents the detection rate for these approaches. To avoid
overcrowding the graph, we divide the anomography methods into two
groups.
Figure 7 (a) plots
the results for
the ARIMA family of anomography approaches and
Figure 7 (b) plots
the results for the rest. We
observe that for all the ARIMA based approaches, Sparsity-L1 finds
very good solutions. With the traffic data aggregated at the 10-minute
level, simple Diff and EWMA can sufficiently extract the anomalous
traffic and warrant a solution that maximizes the sparsity of the
anomalies. Holt-Winters produces better performance than Diff and
EWMA. This is because the model is more sophisticated, and thus is
able to capture more complex temporal trends exhibited in the traffic
data. Further sophistication, as incorporated in ARIMA, however,
cannot significantly improve performance. In the family of ARIMA
models, Holt-Winters appears to provide the best
complexity-performance trade-off.
![]() and the link load
matrix
and the link load
matrix ![]() , we obtain two linear transformation
, we obtain two linear transformation
![]() ,
and
,
and
![]() , respectively. However, the two
transformation matrices
, respectively. However, the two
transformation matrices ![]() and
and ![]() may differ significantly
because the spatial correlation among link loads and that among OD
flows are rather different. Even if we use
may differ significantly
because the spatial correlation among link loads and that among OD
flows are rather different. Even if we use ![]() , we cannot
ensure that
, we cannot
ensure that
![]() (i.e.,
(i.e.,
![]() (Note
that this last comment applies to spatial anomography methods in
general). Thus, the spatial PCA anomography solution is not expected
to completely overlap with the
(Note
that this last comment applies to spatial anomography methods in
general). Thus, the spatial PCA anomography solution is not expected
to completely overlap with the
![]() identified by directly
applying spatial PCA on the OD traffic flows. In contrast, the
temporal anomography methods are self-consistent in that given
identified by directly
applying spatial PCA on the OD traffic flows. In contrast, the
temporal anomography methods are self-consistent in that given
![]() , if we apply the same transformation
, if we apply the same transformation ![]() on
on ![]() and
obtain
and
obtain
![]() , we guarantee that
, we guarantee that
![]() (
(![]() ).
).
![]() quadrant
that the ARIMA, FFT and Wavelet approaches tend to have relative low
false positives among detected anomalies. Thus,
the top 30 ranked anomalies derived through
these approaches indeed appear to be anomalous traffic events that are worth
investigating.
quadrant
that the ARIMA, FFT and Wavelet approaches tend to have relative low
false positives among detected anomalies. Thus,
the top 30 ranked anomalies derived through
these approaches indeed appear to be anomalous traffic events that are worth
investigating.
![]() ,
,
![]() , ...,
, ...,
![]() , does not affect the outcome of the
algorithm.
, does not affect the outcome of the
algorithm.
![]() and
and ![]() , where we are interested in
the number
of large anomalies that are not identified by each approach. We
observe that the ARIMA methods, FFT and Wavelet anomography approaches
have superb performance - the number of false negatives are very low.
This indicates
that very few important traffic anomalies can pass undetected by these
approaches. The PCA based approaches, however, identify about half of
the anomalies.
, where we are interested in
the number
of large anomalies that are not identified by each approach. We
observe that the ARIMA methods, FFT and Wavelet anomography approaches
have superb performance - the number of false negatives are very low.
This indicates
that very few important traffic anomalies can pass undetected by these
approaches. The PCA based approaches, however, identify about half of
the anomalies.
 minimization for the inference step.
Dynamic anomography using ARIMA based methods and
minimization for the inference step.
Dynamic anomography using ARIMA based methods and
 norm minimization shows uniformly high fidelity (low false
positive and false negatives) and high robustness (to routing changes
and missing or corrupted data).
norm minimization shows uniformly high fidelity (low false
positive and false negatives) and high robustness (to routing changes
and missing or corrupted data).
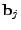 includes the aggregated traffic at
different ingress/egress points; the corresponding rows in
includes the aggregated traffic at
different ingress/egress points; the corresponding rows in 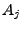 encode the OD flows that enter/exit the network at these points.
encode the OD flows that enter/exit the network at these points.


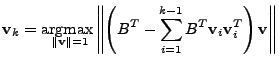
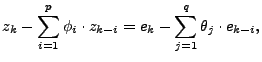
![\begin{displaymath}
I = \left[
\begin{array}{c}1 0 0 ... 0 0 0 1 ...
... 1 ... 1 1 1 1 1 ... 1 1\end{array}
\right].
\end{displaymath}](img80.gif)
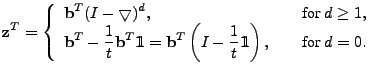
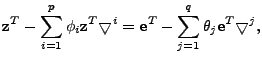
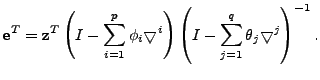
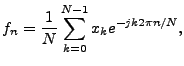 for
for 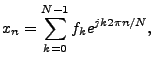 for
for