IMC '05 Paper    [IMC '05 Technical Program]

1 Introduction

The Internet has witnessed a rapid growth in the popularity of various Peer-to-Peer (P2P) applications during recent years. In particular, today’s P2P file-sharing applications (e.g., FastTrack, eDonkey, Gnutella) are extremely popular with millions of simultaneous clients and contribute a significant portion of the total Internet traffic [1, 13, 14]. These applications have changed in many ways to accommodate growing numbers of participating peers. In these applications, participating peers form an overlay which provides connectivity among the peers to search for desired files. Typically, these overlays are unstructured where peers select neighbors through a predominantly random process, contrasting with structured overlays, i.e., distributed hash tables such as Chord [29] and CAN [22]. Most modern file-sharing networks use a two-tier topology where a subset of peers, called ultrapeers, form an unstructured mesh while other participating peers, called leaf peers, are connected to the top-level overlay through one or multiple ultrapeers. More importantly, the overlay topology is continuously reshaped by both user-driven dynamics of peer participation as well as protocol-driven dynamics of neighbor selection. In a nutshell, as participating peers join and leave, they collectively, in a decentralized fashion, form an unstructured and dynamically changing overlay topology.

The design and simulation-based evaluation of new search and replication techniques has received much attention in recent years. These studies often make certain assumptions about topological characteristics of P2P networks (e.g., power-law degree distribution) and usually ignore the dynamic aspects of overlay topologies. However, little is known about the topological characteristics of popular P2P file sharing applications, particularly about overlay dynamics. An important factor to note is that properties of unstructured overlay topologies cannot be easily derived from the neighbor selection mechanisms due to implementation heterogeneity and dynamic peer participation. Without a solid understanding of topological characteristics in file-sharing applications, the actual performance of the proposed search and replication techniques in practice is unknown, and cannot be meaningfully simulated.

Accurately characterizing the overlay topology of a large scale P2P network is challenging [33]. A common approach is to examine properties of snapshots of the overlay captured by a topology crawler. However, capturing accurate snapshots is inherently difficult for two reasons: (i) the dynamic nature of overlay topologies, and (ii) a non-negligible fraction of discovered peers in each snapshot are not directly reachable by the crawler. Furthermore, the accuracy of captured snapshots is difficult to verify due to the lack of any accurate reference snapshot.

Previous studies that captured P2P overlay topologies with a crawler either deployed slow crawlers, which inevitably lead to significantly distorted snapshots of the overlay [23], or partially crawled the overlay [24, 18] which is likely to capture biased (and non-representative) snapshots. These studies have not examined the accuracy of their captured snapshots and only conducted limited analysis of the overlay topology. More importantly, these few studies (except [18]) are outdated (more than three years old) since P2P filesharing applications have significantly increased in size and incorporated several new topological features over the past few years. An interesting recent study [18] presented a high level characterization of the two-tier Kazaa overlay topology. However, the study does not contain detailed graph-related properties of the overlay. Finally, to our knowledge, the dynamics of unstructured P2P overlay topologies have not been studied in detail in any prior work.

We have recently developed a set of measurement techniques and incorporated them into a parallel P2P crawler, called Cruiser [30]. Cruiser can accurately capture a complete snapshot of the Gnutella network with more than one million peers in just a few minutes. Its speed is several orders of magnitude faster than any previously reported P2P crawler and thus its captured snapshots are significantly more accurate. Capturing snapshots rapidly also allows us to examine the dynamics of the overlay over a much shorter time scale, which was not feasible in previous studies. This paper presents detailed characterizations of both graph-related properties as well as the dynamics of unstructured overlay topologies based on recent large-scale and accurate measurements of the Gnutella network.

1.1 Contributions

Using Cruiser, we have captured more than 18,000 snapshots of the Gnutella network during the past year. We use these snapshots to characterize the Gnutella topology at two levels:

• Graph-related Properties of Individual Snapshots: We treat individual snapshots of the overlay as graphs and apply different forms of graph analysis to examine their properties¹.
• Dynamics of the Overlay: We present new methodologies to examine the dynamics of the overlay and its evolution over different timescales.

We investigate the underlying causes of the observed properties and dynamics of the overlay topology. To the extent possible, we conduct our analysis in a generic (i.e., Gnutella-independent) fashion to ensure applicability to other P2P systems. Our main findings can be summarized as follows:

• In contrast to earlier studies [7, 23, 20], we find that node degree does not exhibit a power-law distribution. We show how power-law degree distributions can result from measurement artifacts.
• While the Gnutella network has dramatically grown and changed in many ways, it still exhibits the clustering and the short path lengths of a small world network. Furthermore, its overlay topology is highly resilient to random peer departure and even systematic removal of high-degree peers.
• Long-lived ultrapeers form a stable and densely connected core overlay, providing stable and efficient connectivity among participating peers despite the high degree of dynamics in peer participation.
• The longer a peer remains in the overlay, the more it becomes clustered with other long-lived peers with similar uptime². In other words, connectivity within the core overlay exhibits an “onion-like” bias where most long-lived peers form a well-connected core, and a group of peers with shorter uptime form a layer with a relatively biased connectivity to each other and to peers with higher uptime (i.e., internal layers).

1.2 Why Examine Gnutella?

eDonkey, FastTrack, and Gnutella are the three most popular P2P file-sharing applications today, according to Slyck.com [1], a website which tracks the number of users for different P2P applications. We elected to first focus on the Gnutella network due to a number of considerations.

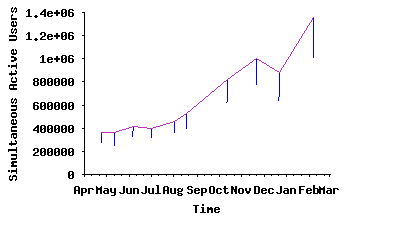
First, a variety of evidence indicates that the Gnutella network has a large and growing population of active users and generates considerable traffic volume. Figure 1 depicts the average size of the Gnutella network over an eleven month period ending February 2005, indicating that network size has more than tripled (from 350K to 1.3 million peers) during our measurement period. We also observed time-of-day effects in the size of captured snapshots, which is a good indication of active user participations in the Gnutella network. Also, examination of Internet2 measurement logs³ reveal that the estimated Gnutella traffic measured on that network is considerable and growing. For example, for the 6 week period 10∕11∕04 - 11∕21∕04, the Gnutella traffic on Internet2 was estimated to be 79.69 terabytes, up from 21.52 terabytes for a 6 week period (02∕02∕04 - 03∕14∕04) earlier that year.

Second, Gnutella, which was the first decentralized P2P system, has evolved significantly since its inception in 2000. While it is among the most studied P2P networks in the literature, prior studies are at least 2–3 years old, and mostly considered the earlier flat-network incarnation. A detailed measurement study of the modern two-tier Gnutella network is therefore timely and allows us to compare and contrast the behavior today from the earlier measurement studies, and to gain insights into the behavior and impact of the two-tier, unstructured overlay topologies which have been adopted by most modern P2P systems.

Third, our choice was also influenced by the fact that Gnutella is the most popular P2P file-sharing network with an open and well-documented protocol specification. This eliminates (or at least significantly reduces) any incompatibility error in our measurement that could potentially occur in other proprietary P2P applications that have been reverse-engineered, such as FastTrack/Kazaa and eDonkey.

The rest of this paper is organized as follows: Section 2 provides a description of the modern Gnutella P2P overlay network and describes the fundamental challenges in capturing accurate snapshots. We present a brief overview of our crawler in Section 3. Section 4 presents a detailed characterization of graph-related properties of individual snapshots as well as the implications of our findings. In Section 5, we examine overlay dynamics, their underlying causes, and their implications on design and evaluation of P2P applications. Section 6 presents an overview of related work and Section 7 concludes the paper.

2 Background

To accurately characterize P2P overlay topologies, we need to capture complete and accurate snapshots. By “snapshot”, we refer to a graph that presents all participating peers (as nodes) and the connections between them (as edges) at a single instance in time. The most reliable, and thus common, approach to capture a snapshot is to crawl the overlay. Given information about a handful of initial peers, the crawler progressively contacts participating peers and collects information about their neighbors. In practice, capturing accurate snapshots is challenging for two reasons:

(i) The Dynamic Nature of Overlays: Crawlers are not instantaneous and require time to capture a complete snapshot. Because of the dynamic nature of peer participation and neighbor selection, the longer a crawl takes, the more changes occur in participating peers and their connections, and the more distorted the captured snapshot becomes. More specifically, any connection that is established or closed during a crawl (i.e., changing connections) is likely to be reported only by one end of the connection. We note that there is no reliable way to accurately resolve the status of changing peers or changing connections. In a nutshell, any captured snapshot by a crawler will be distorted, where the degree of distortion is a function of the crawl duration relative to the rate of change in the overlay.

(ii) Unreachable Peers: A significant portion of discovered peers in each snapshot are not directly reachable since they have departed, reside behind a firewall, or are overloaded [30]. Therefore, information about the edges of the overlay that are connected between these unreachable peers will be missing from the captured snapshots.

We argue that sampling a snapshot of unstructured networks through partial crawls [24] or passive monitoring [25] is not a reliable technique for an initial characterization of the overlay topology for the following reasons: (i) in the absence of adequate knowledge about the properties and dynamics of the overlay topology, it is difficult to collect unbiased samples. For example, partial crawling of the network can easily result in a snapshot that is biased towards peers with higher degree; (ii) some graph-level characteristics of the overlay topology, such as the mean shortest path between peers (which we discuss in Subsection 4.2) cannot be accurately derived from partial snapshots. Because of these reasons, we attempt to capture snapshots as complete as possible and use them for our characterizations.

To describe our measurement methodology for addressing the above challenges, we provide a brief description of modern Gnutella as an example of a two-tier P2P file-sharing application.

2.1 Modern Gnutella

In the original Gnutella protocol, participating peers form a flat unstructured overlay and use TTL-scoped flooding of search queries to other peers. This approach has limited scalability. To improve the scalability of the Gnutella protocol, most modern Gnutella clients adopt a new overlay structure along with a new query distribution mechanism as follows:

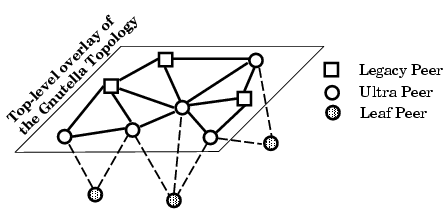
(i) Two-tier Overlay: A new generation of popular file-sharing applications have adopted a two-tier overlay architecture to improve their scalability: a subset of peers, called ultrapeers, form a top-level overlay while other participating peers, called leaf peers, are connected to the top-level overlay through one or multiple ultrapeers (Figure 2). FastTrack (or Kazaa), Gnutella, and eDonkey all use some variation of this model. Those peers that do not implement the ultrapeer feature, called legacy peers, can only reside in the top-level overlay and do not accept any leaves. When a leaf connects to an ultrapeer, it uploads a set of hashes of its filename keywords to that ultrapeer. This allows the ultrapeer to only forward messages to the leaves who might have matching files. This approach reduces the number of forwarded messages towards leaf peers which in turn increases the scalability of the network by a constant factor. Leaf peers never forward messages.

(ii) Dynamic Query: The Gnutella developer community has adopted a new scheme for query distribution called Dynamic Querying [9]. The goal in this scheme is to only gather enough results to satisfy the user (typically 50 to 200 results). Rather than forwarding a query to all neighbors, ultrapeers manage the queries for their leaves. Toward this end, an ultrapeer begins by forwarding a query to a subset of top-level connections using a low TTL. From that point on, the query is flooded outward until the TTL expires. The ultrapeer then waits for the results, and uses the ratio between the number of results and the estimated number of visited peers to determine how rare matches are. If matches are rare (i.e., there are few or no responses), the query is sent through more connections with a relatively high TTL. If matches are more common but not sufficient, the query is sent down a few more connections with a low TTL. This process is repeated until the desired number of results are collected or the ultrapeer gives up. Each ultrapeer estimates the number of visited ultrapeers through each neighbor based on the following formula: ∑ _i=0^TTL-1(d - 1)ⁱ. This formula assumes that all peers have the same node degree, d. When Dynamic Querying was introduced, the number of neighbors each ultrapeer attempts to maintain was increased to allow more fine-grained control with Dynamic Querying by giving ultrapeers more neighbors to choose from.

3 Capturing Accurate Snapshots

In this section, we present an overview of our data collection and post-processing steps. Cruiser: We have developed a set of measurement techniques into a parallel Gnutella crawler, called Cruiser [30]. While the basic crawling strategy by Cruiser is similar to other crawlers, it improves the accuracy of captured snapshots by significantly increasing the crawling speed (i.e., reducing crawl duration) primarily by using the following techniques: First, Cruiser employs a master-slave architecture in order to achieve a high degree of concurrency and to effectively utilize available resources on multiple PCs. Using a master-slave architecture also allows us to deploy Cruiser in a distributed fashion if Cruiser’s access link becomes a bottleneck. The master process coordinates multiple slave processes that crawl disjoint portions of the network in parallel. Each slave crawler opens hundreds of parallel connections, contributing a speed-up of nearly three orders of magnitude.

Second, Cruiser leverages the two-tier structure of the modern Gnutella network by only crawling the top-level peers (i.e., ultrapeers and legacy peers). Since each leaf must be connected to an ultrapeer, this approach enables us to capture all the nodes and links of the overlay by contacting a relatively small fraction of all peers. Overall, this strategy leads to around an 85% reduction in the duration of a crawl without any loss of information.

These techniques collectively result in a significant increase in crawling speed. Cruiser can capture the Gnutella network with one million peers in around 7 minutes using six off-the-shelf 1 GHz GNU/Linux boxes in our lab. Cruiser’s crawling speed is about 140K peers/minute (by directly contacting 22K peers/minute), This is orders of magnitude faster than previously reported crawlers (i.e., 2 hours for 30K peers (250/minute) in [23], and 2 minutes for 5K peer (2.5K/minute) in [24]). It is worth clarifying that while our crawling strategy is aggressive and our crawler requires considerable local resources, its behavior is not intrusive since each top-level peer is contacted only once per crawl.

Post-Processing: Once information is collected from all reachable peers, we perform some post-processing to remove any obvious inconsistencies that might have been introduced due to changes in the topology during the crawling period. Specifically, we include edges even if they are only reported by one peer, and treat a peer as an ultrapeer if it neighbors with another ultrapeer or has any leaves. Due to the inconsistencies, we might over-count edges by about 1% and ultrapeers by about 0.5%.

Unreachable Peers: We have carefully examined the effect of unreachable peers on the accuracy of captured snapshots [33]. Previous studies assumed that these unreachable peers departed the network or are legacy peers that reside behind a firewall (or NAT), and simply excluded this large group of unreachable peers from their snapshot. It is important to determine what portion of unreachable peers are departed or NATed because each group introduces a different error on the snapshot. However, there is no reliable test to distinguish between departed and firewalled peers because firewalls can time out or refuse connections depending on their configuration.

In summary, our investigation revealed that in each crawl, 30%–38% of discovered peers are unreachable. In this group, the breakdown is as follows: 2%–3% are departed peers, 15%–24% are firewalled, and the remaining unreachable peers (3%–21%) are either also firewalled or overwhelmed ultrapeers. However, since Cruiser only needs to contact either end of an edge, it is able to discover at least 85%–91% of edges. Since firewalled peers cannot directly connect together (i.e., cannot be located at both ends of a missing edge) and they constitute more than half of the unreachable peers, the actual portion of missing edges is considerably smaller.

Quantifying Snapshot Accuracy: We rigorously examined the effect of crawling speed and duration on two dimensions of snapshot accuracy: completeness and distortion. Our evaluations [30] revealed that (i) Cruiser captures nearly all ultrapeers and the pair-wise connections between them and the majority of connections to leaves; (ii) Both node distortion and edge distortion in captured snapshots increases linearly with the crawl duration; and (iii) snapshots captured by Cruiser have little distortion. For example, we found that two back-to-back snapshots differed only 4% in their peer populations.

Data Set: We have captured more than 18,000 snapshots of the Gnutella network during the past eleven months (Apr. 2004–Feb. 2005) with Cruiser. In particular, we collected back-to-back snapshots for several one-week intervals as well as randomly distributed snapshots during various times of the day to ensure that captured snapshots are representative. In Section 4, we use four of these snapshots to illustrate graph properties of the overlay topology. In Section 5, we use sets of hundreds of back-to-back snapshots to examine how the overlay topology evolves with time.

4 Overlay Graph Properties

The two-tier overlay topology in modern Gnutella (as well as other unstructured P2P networks) consists of ultrapeers that form a “spaghetti-like” top-level overlay and a large group of leaf peers that are connected to the top-level through multiple ultrapeers. We treat individual snapshots of the overlay as graphs and apply different forms of graph analysis to examine their properties. We pay special attention to the top-level overlay since it is the core component of the topology. Throughout our analysis, we compare our findings with similar results reported in previous studies. However, it is important to note that we are unable to determine whether the reported differences (or similarities) are due to changes in the Gnutella network or due to inaccuracy in the captured snapshots of previous studies.

Table 1 presents summary information of four sample snapshots after post-processing. The results in this section are primarily from the snapshots in Table 1. However, we have examined many other snapshots and observed similar trends and behaviors. Therefore, we believe the presented results are representative. Presenting different angles of the same subset of snapshots allows us to conduct cross comparisons and also relate various findings.

In this section, we explore the node degree distribution in Subsection 4.1, the reachability and pairwise distance properties of the overlay in Subsection 4.2, small world characteristics in Subsection 4.3, and the resilience of the overlay in Subsection 4.4.

Implementation Heterogeneity: The open nature of the Gnutella protocol has led to several known (and possibly many unknown) implementations. It is important to determine the distribution of different implementations (and configurations) among participating peers since their design choices directly affect the overall properties of the overlay topology. This will help us explain some of the observed properties of the overlay.

Table 2 presents the distribution of different implementations across discovered ultrapeers. This table shows that a clear majority of contacted ultrapeers use the LimeWire implementation. We also discovered that a majority of LimeWire ultrapeers (around 94%) use the most recent version of the software available at the time of the crawl. These results reveal that while heterogeneity exists, nearly all Gnutella users run LimeWire or BearShare.

(a) Top-level Degree Distribution (b) Reachable Degree Distribution (c) Unreachable Degree Distribution Figure 3: Different angles of the top-level degree distribution in Gnutella topology

We are particularly interested in the number of connections that are used by each implementation since this design choice directly affects the degree distribution of the overall topology. This information can be obtained from available LimeWire source code. However, not all implementations are open, and users can always change the source code of open implementations. Thus, we need to collect this information from running ultrapeers in action.

Our measurements reveal that LimeWire’s and BearShare’s ultrapeer implementations prefer to serve 30 and 45 leaves, respectively, whereas both try to maintain around 30 neighbors in the top-level overlay.

4.1 Node Degree Distributions

The introduction of the two-tier architecture in the overlay topology along with the distinction between ultrapeers and leaf peers in the modern Gnutella protocol demands a close examination of the different degree distributions among different group of peers.

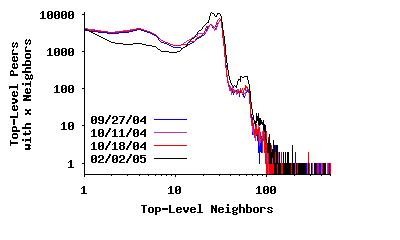
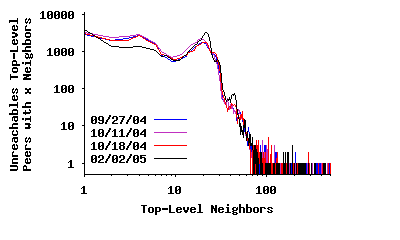
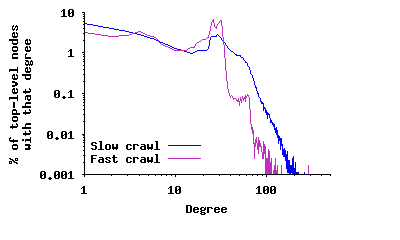
Node Degree in the Top-Level Overlay: Previous studies reported that the distribution of node degree in the Gnutella network exhibited a power-law distribution [23, 2, 7] and later changed to a two-segment power-law distribution [20, 23]. To verify this property for the modern Gnutella network, Figure 3(a) depicts the distribution of node degree among all peers (both unreachable and reachable) in the top-level overlay for the four sample snapshots presented in Table 1. This distribution has a spike around 30 and does not follow a power-law⁴. A key question is to what extent this difference in degree distribution is due to the change in the overlay structure versus error in captured snapshots by earlier studies. To examine this question, we captured a distorted snapshot by a slow crawler⁵ which is similar to the 50-connection crawler used in an earlier study [23]. Figure 4(a) depicts the degree distribution based on this distorted snapshot, which is significantly more similar to a two-piece power-law distribution⁶. If we further slow down the crawling speed, the resulting snapshots contains a higher degree of edge distortion, and the derived degree distribution looks more similar to a single-piece power-law distribution, the result reported by earlier studies [2, 7]. To a slow crawler, peers with long uptimes appear as high degree because many short-lived peers report them as neighbors. However, this is a mischaracterization since these short-lived peers are not all present at the same time. More importantly, this finding demonstrates that using distorted snapshots that are captured by slow crawlers can easily lead to incorrect characterizations of P2P overlays.

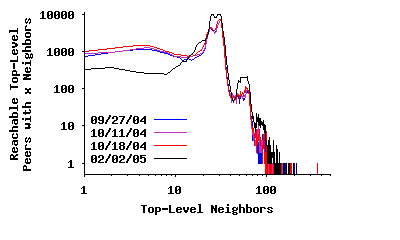
Because we were unable to contact every top-level peer, the distribution in Figure 3(a) is biased slightly low since it does not include all edges. To address this problem, we split the data into Figures 3(b) and 3(c), which depict the neighbor degree distribution for reachable and unreachable peers, respectively. The data in Figure 3(b) is unbiased since we contacted each peer successfully, i.e., we discovered every edge connected to these peers. The spike around a degree of 30 is more pronounced in this figure. Figure 3(c) presents the observed degree distribution for unreachable top-level peers (i.e., overloaded or NATed). This distribution is biased low since we cannot observe the connections between pairs of these peers. In this data, a much greater fraction of peers have an observed degree below 30. Many of these peers probably have a true degree closer to 30, with the true distribution likely similar to that in Figure 3(b).

(a) Observed top-level degree distributions of a slow and a fast crawl (b) Degree distribution from ultrapeers to leaves (c) Leaf Parents Figure 4: Different angles of degree distribution in Gnutella

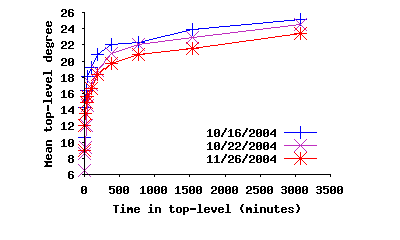
The degree distribution among contacted top-level peers has two distinct segments around a spike in degree of 30, resulting from LimeWire and BearShare’s behavior of attempting to maintain 30 neighbors. The peers with higher degree represent other implementations that try to maintain a higher node degree or the rare user who has modified their client software. The peers with lower degree are peers which have not yet established 30 connections. In other words, the observed degree for these peers is temporary. They are in a state of flux, working on opening more connections to increase their degree. To verify this hypothesis, we plot the mean degree of peers as a function of their uptime in Figure 5. The standard deviation for these measurements is quite large (around 7 - 13), indicating high variability. When peers first arrive, they quickly establish several connections. However, since node churn is high, they are constantly losing connections and establishing new ones. As time passes, long-lived peers gradually accumulate stable connections to other long-lived peers. We further explore this issue in Section 5 when we examine overlay dynamics.

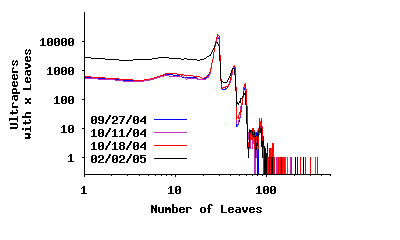
Node Degree For Leaves: To characterize properties of the two-tier topology, we have examined the degree distribution between the top-level overlay and leaves, and vice versa. Figure 4(b) presents the degree distribution of connections from ultrapeers to leaf peers. Distinct spikes at 30, 45 and 75 degree are visible. The first two spikes are due to the corresponding parameters used in LimeWire and BearShare implementations, respectively. The third spike is due to a less common implementation. This figure shows that a significant minority of ultrapeers are connected to less than 30 leaf peers, which indicates availability in the system to accommodate more leaf peers.

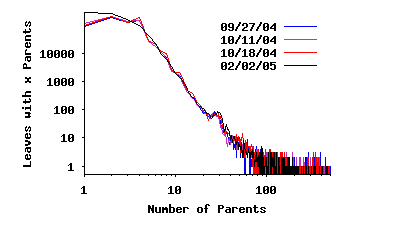
In Figure 4(c), we present the degree of connectivity for leaf peers. This result reveals that most leaf peers connect to three ultrapeers or fewer (the behavior of LimeWire), a small fraction of leaves connect to several ultrapeers, and a few leaves (< 0.02%) connect to an extremely large number of ultrapeers (100–3000).

(a) Correlation between ultrapeer’s degree and its mean distance from other ultrapeers from the 10/18/04 snapshot (b) Mean Top-Level Peers Searched by TTL from the 9/27/2004 snapshot (c) Cumulative Top-Level Peers Searched CDF Figure 6: reachability, diameter, and shortest path in Gnutella topology

(a) Ultrapeer-to-ultrapeer shortest paths (b) Distribution of path lengths across all pairs of peers (c) Distribution of Eccentricity in the Top-level Overlay Figure 7: Different angles on path lengths

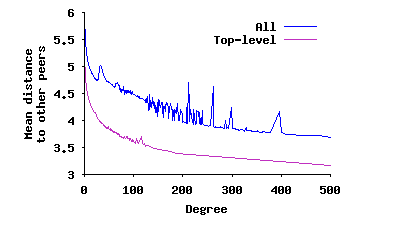
Implications of High Degree Peers: We observed a few outlier peers with an unusually high degree of connectivity in all degree distributions in this subsection. The main incentive for these peers is to reduce their mean distance to other peers. To quantify the benefit of this approach, Figure 6(a) presents the mean distance to other peers as a function of node degree, averaged across peers with the same degree. We show this for both the top-level overlay and across all peers. This figure shows that the mean path to participating peers exponentially decreases with degree. In other words, there are steeply diminishing returns from increasing degree as a way of decreasing distance to other peers.

Turning our attention to the effects of high-degree peers on the overlay, for scoped flood-based querying, the traffic these nodes must handle is proportional to their degree for leaves and proportional to the square of their degree for ultrapeers. Note that high-degree ultrapeers may not be able, or may not choose, to route all of the traffic between their neighbors. Thus, they may not actually provide as much connectivity as they appear to, affecting the performance of the overlay.

During our analysis, we discovered around 20 ultrapeers (all on the same /24 subnet) with an extremely high degree (between 2500 to 3500) in our snapshots. These high-degree peers are widely visible throughout the overlay, and thus receive a significant portion of exchanged queries among other peers. We directly connected to these high degree peers and found they do not actually forward any traffic⁷. We removed these inactive high degree peers from our snapshots when considering path lengths since their presence would artificially improve the apparent connectivity of the overlay.

4.2 Reachability

The degree distribution suggests the overlay topology might have a low diameter, given the moderately high degree of most peers. To explore the distances between peers in more detail, we examine two equally important properties of overlay topologies that express the reachability of queries throughout the overlay: (i) the reachability of flood-based queries, and (ii) the pairwise distance between arbitrary pairs of peers.

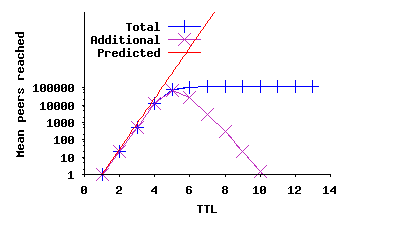
Reachability of Flood-Based Query: Figure 6(b) depicts the mean number of newly visited peers and its cumulative value as a function of TTL, averaged across top-level peers in a single snapshot. The shape of this figure is similar to the result that was reported by Lv et al. (Figure 3 in [20]) which was captured in October 2000, with a significantly smaller number of peers (less than 5000). Both results indicate that the number of newly visited peers exponentially grows with increasing TTL up to a certain threshold and has diminishing returns afterwards. This illustrates that the dramatic growth of network size has been effectively balanced by the introduction of ultrapeers and an increase in node degree. Thus, while the network has changed in many ways, the percentage (but not absolute number) of newly reached peers per TTL has remained relatively stable. Figure 6(b) also shows the number of newly visited peers predicted by the Dynamic Querying formula (assuming a node degree of 30), which we presented in Section 2.1. This result indicates that the formula closely predicts the number of newly visited peers for TTL values less than 5. Beyond 5, the query has almost completely saturated the network.

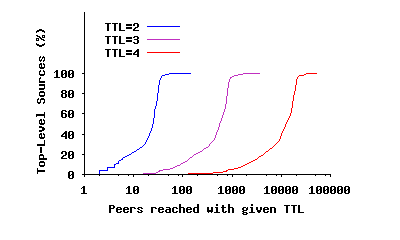
Figure 6(c) shows a different angle of reachability for the same snapshot by presenting the Cumulative Distribution Function (CDF) of the number of visited peers from top-level peers for different TTL values. This figure shows the distribution of reachability for flood-based queries among participating peers. We use a logarithmic x-scale to magnify the left part of the figure for lower TTL values. The figure illustrates two interesting points: First, the total number of visited peers using a TTL of n is almost always an order of magnitude higher compared to using a TTL of (n- 1). In other words, TTL is the primary determinant of the mean number of newly visited peers independent of a peer’s location. Second, the distribution of newly visited peers for each TTL is not uniform among all peers. As TTL increases, this distribution becomes more skewed (considering the logarithmic scale for x axis). This is a direct effect of node degree. More specifically, if a peer or one of its neighbors has a very high degree, its flood-based query reaches a proportionally larger number of peers.

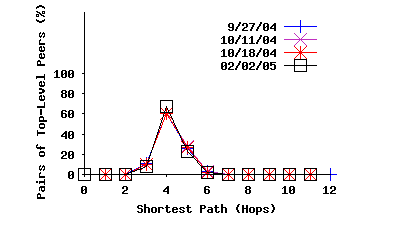
Pair-wise Distance: Figure 7(a) shows the distribution of shortest-path lengths in terms of overlay hops among all pairs of top-level peers from four snapshots. Ripeanu et al. [23] presented a similar distribution for the shortest-path length based on snapshots that were collected between November 2000 and June 2001 with 30,000 peers. Comparing these results reveals two differences: (i) the pairwise path between peers over the modern Gnutella topology is significantly more homogeneous in length, with shorter mean value compared with a few years ago. More specifically, the old snapshot shows 40% and 50% of all paths having a length of 4 and 5 hops whereas our results show a surprising 60% of all paths having a length of 4. (ii) the results from our snapshots are nearly identical; whereas in [23], there is considerable variance from one crawl to another. In summary, the path lengths have become shorter, more homogeneous, and more stable.

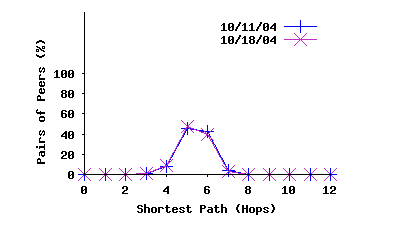
Effect of Two-Tier Topology: To examine the effect of the two-tier overlay topology on path length, we also plot the path length between all peers (including leaves) in 7(b). If each leaf had only one ultrapeer, the distribution of path length between leaves would look just like the top-level path lengths (Figure 7(a)), but right-shifted by two. However, since each leaf peer has multiple parents, the path length distribution between leaves (and thus for all peers) has a more subtle relationship with Figure 7(a). Comparing Figures 7(a) and 7(b) shows us the cost introduced by using a two-tier overlay. In the top-level, most paths are of length 4. Among leaves, we see that around 50% of paths are of length 5 and the other 50% are of length 6. Thus, getting to and from the top-level overlay introduces an increase of 1 to 2 overlay hops.

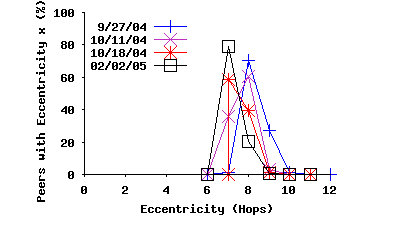
Eccentricity: The longest observed path in these four snapshots was 12 hops, however the vast majority (99.5%) of paths have a length of 5 hops or less. To further explore the longest paths in the topology, we examined the distribution of eccentricity in the top-level overlay. The eccentricity of a peer is the distance from that peer to the most distant other peer. More formally, given the function P(i,j) that returns the shortest path distance between nodes i and j, the eccentricity, E_i of node i is defined as follows: E_i = max(P(i,j), ∀j). Figure 7(c) shows the distribution of eccentricity in four topology snapshots. This figure shows that the distribution of eccentricity is rather homogeneous and low which is an indication that the overlay graph is a relatively balanced and well-connected mesh, rather than a chain of multiple groups of peers.

4.3 Small World

Recent studies have shown that many biological and man-made graphs (e.g., collaborations among actors, the electrical grid, and the WWW graph) exhibit “small world” properties. In these graphs, the mean pairwise distance between nodes is small and nodes are highly clustered compared to random graphs with the same number of vertices and edges. A study by Jovanovic et al. [12] in November–December 2000 concluded that the Gnutella network exhibits small world properties as well. Our goal is to verify to what extent recent top-level topologies of the Gnutella network still exhibit small world properties despite growth in overlay population, an increase in node degree, and changes in overlay structure. The clustering coefficient of a graph, C_actual, represents how frequently each node’s neighbors are also neighbors, and is defined as follows [35]:

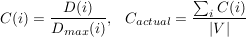
D(i), D_max(i) and ∣V ∣ denote the number of edges between neighbors of node i, the maximum possible edges between neighbors of node i, and the number of vertices in the graph, respectively. For example, if node A has 3 neighbors, they could have at most 3 edges between them, so D_max(A) = 3. If only two of them are connected together, that’s one edge and we have D(A) = 1 and C(A) = . C(i) is not defined for nodes with fewer than 2 neighbors. Thus, we simply exclude these nodes from the computation of C_actual. Table 3 presents ranges for the clustering coefficient (C_actual) and mean path length (L_actual) for the Gnutella snapshots from Table 1 as well as the mean values from four random graphs with the same number of vertices and edges (i.e., C_random and L_random). Because computing the true mean path lengths (L_random) is computationally expensive for large graphs, we used the mean of 500 sample paths selected uniformly at random. We also include the information presented by Jovanovic et al. [12] and three classic small world graphs [35].

A graph is loosely identified as a small world when its mean path length is close to random graphs with the same number of edge and vertices, but its clustering coefficient is orders of magnitude larger than the corresponding random graph (i.e., L_actual and L_random are close, but C_actual is orders of magnitude larger than C_random). All three classic small world graphs in the table exhibit variants of these conditions. Snapshots of modern Gnutella clearly satisfy these conditions which means that modern Gnutella still exhibits small world properties.

Comparing the clustering coefficient between modern Gnutella and old Gnutella shows that modern Gnutella has less clustering. A plausible explanation is the increased size, which provides the opportunity for more diverse connectivity to other peers. A high clustering coefficient implies a larger fraction of redundant messages in flood-based querying. The observed clustering could be a result of factors like peer bootstrapping, the peer discovery mechanism, and overlay dynamics. Further analysis is needed to better understand the underlying causes. Section 5 shows how peer churn is one factor that contributes to clustering.

4.4 Resilience

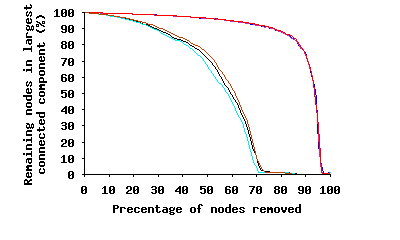
We also examine the resilience in different snapshots of the Gnutella overlay topology using two different types of node removal: (i) random removal, and (ii) pathologically removing the highest-degree nodes first. An early study [24] conducted the same analysis on Gnutella based on a partial topology snapshot, finding that the overlay is resilient to random departures, but under pathological node removal quickly becomes very fragmented (after removing just 4% of nodes).

Figure 8 depicts the fraction of remaining nodes in the topology which remain still connected in both the random and pathological node removal. This figure clearly shows the Gnutella overlay is not only extremely robust to random peer removals, but it also exhibits high resilience to pathological node removal. Even after removing 85% of peers randomly, 90% of the remaining nodes are still connected. For the pathological case, after removing the 50% of peers with the highest-degree, 75% of the remaining nodes remain connected. There are two possible factors contributing to this difference with earlier results [24]: (i) the higher median node degree of most nodes in modern Gnutella, and (ii) a non-negligible number of missing nodes and edges in the partial snapshot of the earlier study. Our result implies that complex overlay construction algorithms (e.g.,  [36]) are not always a necessary prerequisite for ensuring resilience in unstructured overlays.

5 Overlay Dynamics

In Section 4, we characterized the graph-related properties of individual snapshots of the overlay topology. However, in practice the overlay topology is inherently dynamic since connections (i.e., edges) are constantly changing. These dynamics can significantly affect the main functionality of the overlay which is to provide connectivity and efficiently route the messages (e.g., queries, responses) among participating peers. Characterizing overlay dynamics enables us to examine their impact on performance of P2P applications. For example, a query or response message can be routed differently or even dropped as a result of changes in the edges of the overlay. To our knowledge, aggregate dynamics of unstructured P2P overlay have not been studied. There are two basic causes for observed dynamics in the overlay topology as follows:

• Dynamics of Peer Participation: When a peer joins (or departs) the network, it establishes (or tears down) its connections to other participating peers in the overlay. Therefore, these changes in overlay edges are user-driven⁸.
• Dynamics of Neighbor Selection: Two existing peers in the overlay may establish a new (or tear down an existing) connection between them. Such a change in edges is not triggered by users and thus considered protocol-driven.

Note that the user-driven dynamics of peer participation are likely to exhibit similar heavy-tailed distributions in different P2P applications [31, 28]. Therefore, characterization of user-driven dynamics in the overlay provides a useful insight for design of other Gnutella-like unstructured P2P overlays.

(a) Percentage of top-level peers with uptime at least x (b) Percentage of top-level peers with uptime at least x (zoomed in) (c) Percentage of increased clustering among stable nodes, relative to a randomized topology for 5 different snapshots Figure 9: Number of stable peers and their external connectivity for different τ

(a) Percentage of peers in the stable core that are part of the core’s largest connect component (b) Diameter (top) and characteristic path length (bottom) of the largest connected component of the stable core (c) Clustering coefficient within the largest connected component of the stable core Figure 10: Different angles of connectivity with the stable core

In this section, we characterize the dynamics of the Gnutella network. More specifically, we want to investigate (i) whether a subset of participating peers form a relatively stable core for the overlay, (ii) what properties (such as size, diameter, degree of connectivity or clustering) this stable core exhibits, and (iii) what underlying factors contribute to the formation and properties of such a stable core.

Methodology: Our main goal is to determine whether observed dynamics (i.e., the rate of change in the edges of the overlay) are different at various regions of the overlay. We primarily focus on the top-level overlay in our analysis, because leaf nodes do not forward traffic and therefore do not provide meaningful connectivity between peers. One key issue is to define a core region for the “spaghetti-like” overlay. We use the following methodology to identify and characterize any potentially stable core for the overlay. Intuitively, if the overlay has a stable core, it must contain the long-lived peers of the overlay. Therefore, to identify the stable core of the overlay at any point of time, we select the subset of participating peers who have been part of the overlay for at least τ minutes, i.e., all peers whose uptime is longer than a threshold τ. We call this subset of peers the stable peers, or SP(τ), and only focus on this subset in our analysis. However, by changing τ, we can control the minimum uptime of selected peers and thus the relative stability and size of SP(τ).

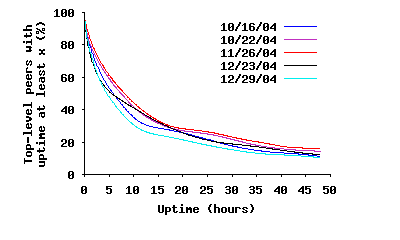
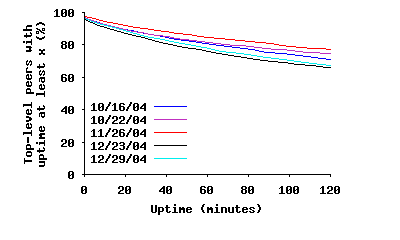
To conduct this analysis, we use several slices of our dataset where each slice is a period of 48 hours of continuous back-to-back topology snapshots, with hundreds of snapshots per slice. Let’s consider the last captured snapshot over each 48 hour period as a reference snapshot. Any peer in the reference snapshot must have joined the overlay either before or during our measurement period. By looking back through the snapshots, we can determine (with accuracy of a few minutes) the arrival time of all peers that joined during the measurement period. For those peers that were present for the entire measurement period, we can conclude that their uptime is at least 48 hours. Having this information, we can annotate all peers in the reference snapshot with their uptime information. Figure 9(a) depicts the CCDF of uptime among existing peers in the reference snapshot for several slices (Figure 9(b) presents the initial part of the same graph). In essence, this figure presents the distribution of uptime among participating peers in steady state, implying that the size of SP(τ) exponentially decreases with τ. This is more visible over longer time scales. Furthermore, this also implies that the total number of possible connections within SP(τ) dramatically decreases with τ.

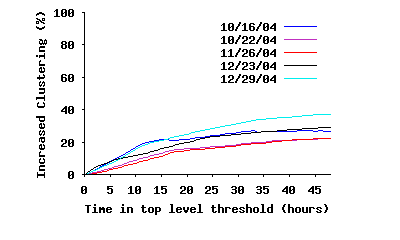
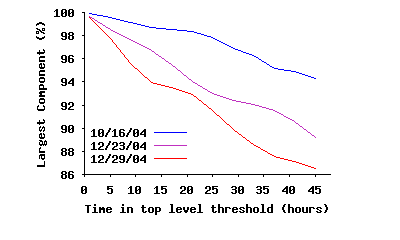
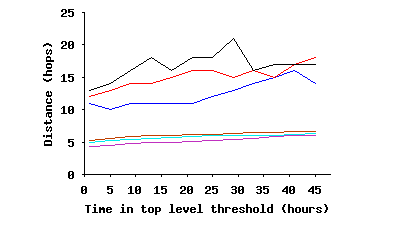
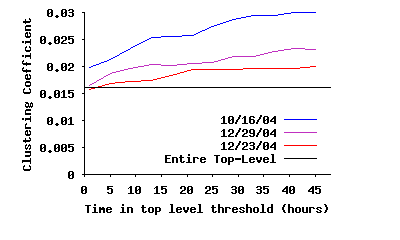
Internal Connectivity Within the Stable Core: To study different angles of connectivity among ultrapeers within SP(τ), we focus only on the connections of the overlay where both end points are inside SP(τ), i.e., we remove all edges to peers outside SP(τ). We call this the stable core overlay or SC(τ). The first question is: whether SC(τ) is fully connected? Figure 10(a) depicts the fraction of ultrapeers within SC(τ) that are in the largest connected component, as a function of τ. This figure clearly demonstrates that while the fraction of connected peers slightly decreases with τ over long times scales, a significant majority (86%–94%) of peers within SC(τ) remain fully connected. The minor drop in the percentage of connected peers is due to exponential decrease in number of peers within SC(τ), which in turn reduces the number of edges among peers, and thus affects the opportunity for pairwise connectivity. The second question is: how clustered and dense is the connected portion of the core overlay? Figure 10(b) shows the diameter and characteristic (mean) path length among fully connected peers in the stable core overlay. Interestingly, both the mean path length and the diameter of the stable core overlay remain relatively stable as τ increases, despite the dramatic drop in number of edges. Furthermore, the mean path length for the stable core overlay, even when it has a very small population (only 10% of top-level peers for τ=45h), is around 5 hops, very close to the mean path length for the entire top-level overlay (4.17–4.23 from the first row of Table 3). Finally, Figure 10(c) depicts the evolution of the clustering coefficient for the stable core overlay as τ increases, along with the clustering coefficient for the entire top-level overlay in the reference snapshot. This figure shows two important points: (i) peers within the stable core overlay are more clustered together than the entire top-level overlay on average, and, more importantly, (ii) connectivity among peers within the stable core overlay becomes increasingly more clustered with τ. This latter point implies that the longer a peer remains in the overlay, the more likely it establishes connections to peers with equal or higher uptimes, i.e., the more biased its connectivity becomes toward peers with higher uptime. Since connections for all participating peers exhibit the same behavior, connectivity of the overlay exhibits a biased “onion-like” layering where peers with similar uptime (a layer) have a tendency to be connected to peers with the same or higher uptime (internal layers of the onion). Since the size of SP(τ) decreases with τ, this means that internal layers are both smaller and more clustered.

External Connectivity to/from the Stable Core: To quantify the connectivity between SC(τ) and the rest of the overlay we examined whether peers within SC(τ) have a higher tendency to connect to each other rather than peers outside the core. To quantify any potential tendency, we calculate the ratio of internal edges to the total number of edges and compare that with the same ratio for a randomly generated graph with the same number of nodes, same degree distribution among nodes, and same number of edges. For a fair comparison, we present the notion of a half edge for a graph as follows: we cut the edge E_ij between two nodes i and j, and define HalfEdge(i,j) as the half of E_ij that is connected to node i. Then, the ratio of internal to total half-edges can be calculated as follows:

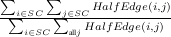
Figure 9(c) depicts (R_g - R_r)∕R_r as a function of τ where R_g and R_r denote the value of R for several snapshots and their corresponding randomly generated graphs, respectively. This figure demonstrates that the longer a peer remains in the network, its connectivity becomes more biased towards peers with the same or higher uptime. This is another evidence that peers exhibit an onion-like biased connectivity and the degree of such bias increases with uptime.

Implications of Stable and Layered Core Overlay: The connectivity of the core overlay implies that all peers within the core do not depend on peers outside the core for reachability. In other words, the core overlay provides a stable and efficient backbone for the entire top-level overlay that ensures connectivity among all participating peers despite the high rate of dynamics among peers outside the core.

(a) Removed edges (b) Added edges Figure 11: Contribution of user- and protocol-driven dynamics in variations of edges in the overlay

5.1 Examining Underlying Causes

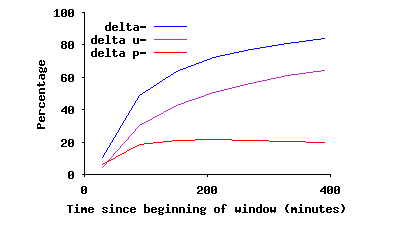
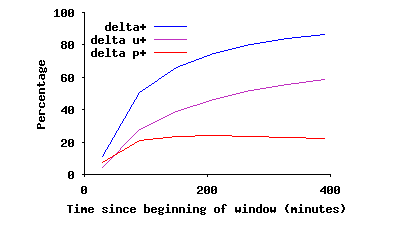
A key question is: how does this onion-like layered connectivity form in the overlay in an unintentional and uncoordinated fashion? To address this issue, we quantify the contribution of user-driven and protocol-driven dynamics in changes of the edges of the overlay. We can distinguish protocol-driven versus user-driven changes in edges between two snapshots of the overlay as follows: if at least one of the endpoints for a changing edge has arrived (or departed) between two snapshots, that change is user-driven. Otherwise, a changing edge is considered protocol-driven. To answer the above question, we examine a 48-hour slice of back-to-back snapshots from 10/14/2004 to 10/16/2004, using the first snapshot as a reference. Given a slice, we can detect new or missing edges in any snapshot compared to the reference snapshot, for peers in both snapshots. Let δ_p- and δ_u- (δ_p+ and δ_u+) denote the normalized ratio of missing (and new) edges in a snapshot due to protocol-driven (p) and user-driven (u) causes, normalized by the number of edges in the reference snapshot. Figure 11(a) and 11(b) depict δ_-=δ_p-+δ_u- and δ₊=δ_p++δ_u+ for back-to-back snapshots for the slice under investigation. Each figure also depicts the breakdown of changes in edges into two groups: protocol-driven and user-driven changes. Note that δ_p and δ_u are by definition cumulative. The left graph (δ_-) shows that around 20% and 30% of edges in the overlay are removed due to protocol-driven and user-driven factors during the first 100 minutes, respectively. After this period, almost all removed edges are due to departing peers. Similarly, from the right graph, many edges are added during the first 100 minutes due to both protocol-driven factors and the arrival of new peers. After this period, almost all new edges involve a newly arriving peer. These results shows two important points: First, each peer may establish and tear down many connections to other peers during the initial 100 minutes of its uptime. But peers with higher uptime (i.e., peers inside SC(τ) for τ ≥ 100 min), maintain their connections to their remaining long-lived neighbors, and only add (or drop) connections to arriving (or departing) peers. This behavior appears to explain the formation of the biased onion-like layering in connectivity within the overlay. Second, user-driven dynamics are the dominant factor in long-term changes of the overlay. Since dynamics of peer participations exhibit similar dynamics in different P2P systems [31], other Gnutella-like overlays are likely to show similar behavior. We plan to conduct further investigations to better understand the underlying dynamics that contribute to this behavior.

6 Related Work

As listed throughout this paper, there are a handful of prior studies on characterizing peer-to-peer overlay topologies in file-sharing applications [23, 2, 20, 12]. These studies are more than three years old, did not verify the accuracy of their captured snapshots, and conducted only limited analysis. A recent study [18] used both passive measurement and active probing of 900 super nodes to study behavior of the Kaaza overlay. They have mostly focused on the number of observed connections (within the top-level overlay and from the top-level overlay to leaf nodes) and their evolution with time. However they have not examined detailed graph-related properties of the overlay, or collective dynamics of the entire overlay topology, both of which are investigated in this paper.

There has been a wealth of measurement research on other properties of peer-to-peer systems. These studies cover several topics: (i) file characteristics [6, 17, 3, 19], (ii) transfer characteristics [10, 17], (iii) peer characteristics [25, 24], (vi) query characteristics [26, 3, 16, 4], and (v) comparisons of different implementations [15, 11]. Since they explore different aspects of peer-to-peer networks, these studies complement our work. There have also been several modeling and simulation-based studies on improvement of search in Gnutella-like P2P networks [5, 38, 37, 27]. Our characterization can be directly used by these studies as a reference for comparison of suggested topology models, and our captured overlay snapshots can be used for trace-driven simulation of their proposed search mechanisms.

Finally, the research studies on characterization of the Internet topology (e.g., [8]) and network topology generators (e.g., [34]) are closely related to our work. However, these studies focus on the Internet topology rather than an overlay topology. We plan to conduct further characterization of the Gnutella topology by applying some of the suggested graph analysis in these studies to the Gnutella overlay topology.

7 Conclusions

In this paper, using Gnutella, we presented the first detailed characterization of an unstructured two-tier overlay topology that is typical of modern popular P2P systems, based on accurate and complete snapshots. We described fundamental challenges in capturing accurate snapshots, and demonstrated that inaccurate snapshots can lead to erroneous conclusions—such as a power-law degree distribution. We characterized the graph-related properties of individual snapshots, the dynamics of the overlay topology across different time scales, and investigated the underlying causes and implications. Our main findings are summarized in Section 1.1.

This study developed essential insights into the behavior of overlay topologies which are necessary to improve the design and evaluation of peer-to-peer file-sharing applications. The existence of a stable well-connected core of long-lived peers suggests that there may be benefits in terms of increasing search resilience in the face ofd the overlay dynamics, by biasing/directing the search towards longer lived peers and therefore towards this core. It may also be useful to cache indexes or content at long-lived peers in order to reduce load on the stable core, especially if the biased forwarding of queries is adopted. For example, the idea of one-hop replication [21], intended for power-law topologies, can be changed to a probabilistic one-hop replication biased towards peers with longer uptime.

We are continuing this work along a number of directions. We are actively monitoring the Gnutella network and plan to further examine the dynamics of peer participation over short time scales, explore any longer term trends in the topology, and observe variations in several key properties (e.g., small-world coefficient, degree distribution, and mean pairwise distance) with time. We are applying our techniques to develop characterizations of the eDonkey/Overnet and BitTorrent P2P networks in ongoing work.

References

Notes

¹An earlier version of our work on graph-related properties of Gnutella appeared as an extended abstract in SIGMETRICS 2005 [32].

²Throughout this paper, by “uptime” we mean the time that has elapsed since the peer has arrived.

³https://netflow.internet2.edu/weekly/

⁴The degree distribution for all the presented results is limited to 500, which includes all but a handful of peers with larger degree that are discussed later.

⁵To reduce the crawling speed, we simply limited the degree of concurrency (i.e., number of parallel connections) to 60 in Cruiser.

⁶To properly compare these snapshots with different sizes, the y-axis in Figure 4(a) was normalized by number of peers in the snapshot

⁷To our surprise, it appears that these peers monitor exchanged messages among other participating peers. They could be trying to locate copyright infringement among Gnutella users or collecting ratings information to measure which songs consumers might like to buy.

⁸Note that Gnutella does not run as a daemon. Therefore, peer arrival/departure is a reliable indication of user action. We are mindful that dynamic IP addresses could force some peers to leave and rejoin the network with a new address. However, this does not affect our analysis since we examine the effect of each departure/arrival event on the overlay dynamics.

Need help? Last changed: 22 Sept. 2005 aw

IMC Technical Program IMC Home USENIX Home